| Latest Maths NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Example 1 to 13 (Before Exercise 14.1) | Exercise 14.1 | |
Chapter 14 Probability
Welcome to the solutions guide for Chapter 14, "Probability," from the latest Class 10 NCERT mathematics textbook for the academic session 2024-25. This chapter deals with the fascinating mathematical study of chance and uncertainty, providing tools to quantify the likelihood of various events occurring. Understanding probability is essential not only in mathematics but also in fields like science, economics, insurance, and even everyday decision-making. These solutions offer clear explanations and systematic approaches to solving problems based on the fundamental principles of probability theory, particularly focusing on the classical definition.
The core concept explored in this chapter is the Classical (or Theoretical) Definition of Probability. Assuming that all outcomes of a random experiment are equally likely, the probability of an event $E$, denoted as $P(E)$, is defined as the ratio: $\mathbf{P(E) = \frac{\text{Number of outcomes favourable to E}}{\text{Total number of possible outcomes}}}$ The solutions begin by reinforcing the basic terminology: understanding a random experiment (an action with uncertain results), identifying the sample space (the set of all possible outcomes, e.g., for a coin toss $S = \{H, T\}$; for rolling a die $S = \{1, 2, 3, 4, 5, 6\}$), defining an event (a subset of the sample space), and correctly counting the favourable outcomes for that specific event. Systematic listing of the sample space and careful identification of favourable outcomes are emphasized as crucial first steps.
The solutions demonstrate the calculation of probabilities for a wide variety of standard random experiments, including:
- Tossing one, two, or three fair coins.
- Rolling one or two fair dice (including finding probabilities related to the sum of the numbers).
- Drawing a card from a well-shuffled standard deck of 52 playing cards (involving suits, colours, face cards, number cards).
- Selecting an object (like a ball of a certain colour) from a bag containing multiple objects.
A vital concept covered is that of Complementary Events. The event 'not E' represents the complement of event E. The solutions explain and apply the fundamental relationship: $\mathbf{P(E) + P(\text{not } E) = 1}$. This relationship is often very useful, as sometimes calculating the probability of an event not occurring, $P(\text{not } E)$, is easier than calculating $P(E)$ directly, allowing us to find $P(E)$ as $1 - P(\text{not } E)$. The solutions address problems involving both single events and simple compound events, ensuring students can correctly identify and count the total and favourable outcomes in each scenario. Careful attention to the wording of problems (e.g., "at least," "at most," "or," "and") is highlighted.
Regarding the rationalized syllabus for 2024-25, Chapter 14, "Probability" (formerly Chapter 15), retains its core focus on the classical definition of probability and its application to simple experiments. The rationalization primarily involved removing the introductory discussion contrasting experimental and theoretical probability and potentially streamlining some very complex compound event scenarios. The fundamental concepts and calculations related to coins, dice, cards, etc., remain central. By diligently working through these comprehensive solutions, students can solidify their understanding of basic probability definitions and properties, develop systematic approaches for listing outcomes and calculating probabilities, and build confidence in solving diverse probability-based problems.
Example 1 to 13 (Before Exercise 14.1)
Example 1. Find the probability of getting a head when a coin is tossed once. Also find the probability of getting a tail.
Answer:
When a coin is tossed once, the possible outcomes are either a Head (H) or a Tail (T).
The total number of possible outcomes is 2.
Let E be the event of getting a Head.
The number of favorable outcomes for event E (getting a Head) is 1 (which is H).
The formula for probability of an event is:
$P(E) = \frac{\text{Number of favorable outcomes}}{\text{Total number of possible outcomes}}$
The probability of getting a Head is:
$P(\text{Head}) = \frac{1}{2}$
Let F be the event of getting a Tail.
The number of favorable outcomes for event F (getting a Tail) is 1 (which is T).
The probability of getting a Tail is:
$P(\text{Tail}) = \frac{1}{2}$
Example 2. A bag contains a red ball, a blue ball and a yellow ball, all the balls being of the same size. Kritika takes out a ball from the bag without looking into it. What is the probability that she takes out the
(i) yellow ball?
(ii) red ball?
(iii) blue ball?
Answer:
In this problem, there are 3 balls in the bag: one red, one blue, and one yellow. All balls are of the same size, meaning each outcome is equally likely.
The total number of possible outcomes when Kritika takes out a ball is the total number of balls in the bag.
Total number of possible outcomes = 3.
(i) Probability of taking out the yellow ball:
Let Y be the event of getting a yellow ball.
The number of favorable outcomes for event Y is the number of yellow balls in the bag.
Number of favorable outcomes for Y = 1.
Using the probability formula $P(E) = \frac{\text{Number of favorable outcomes}}{\text{Total number of possible outcomes}}$, we get:
$P(\text{Yellow ball}) = \frac{\text{Number of yellow balls}}{\text{Total number of balls}}$
$P(\text{Yellow ball}) = \frac{1}{3}$
(ii) Probability of taking out the red ball:
Let R be the event of getting a red ball.
The number of favorable outcomes for event R is the number of red balls in the bag.
Number of favorable outcomes for R = 1.
$P(\text{Red ball}) = \frac{\text{Number of red balls}}{\text{Total number of balls}}$
$P(\text{Red ball}) = \frac{1}{3}$
(iii) Probability of taking out the blue ball:
Let B be the event of getting a blue ball.
The number of favorable outcomes for event B is the number of blue balls in the bag.
Number of favorable outcomes for B = 1.
$P(\text{Blue ball}) = \frac{\text{Number of blue balls}}{\text{Total number of balls}}$
$P(\text{Blue ball}) = \frac{1}{3}$
Example 3. Suppose we throw a die once.
(i) What is the probability of getting a number greater than 4 ?
(ii) What is the probability of getting a number less than or equal to 4 ?
Answer:
When a die is thrown once, the possible outcomes are the numbers 1, 2, 3, 4, 5, and 6.
The total number of possible outcomes is 6.
(i) Probability of getting a number greater than 4:
Let A be the event of getting a number greater than 4. The outcomes greater than 4 are 5 and 6.
The favorable outcomes for event A are $\{5, 6\}$.
The number of favorable outcomes for A is 2.
Using the formula $P(E) = \frac{\text{Number of favorable outcomes}}{\text{Total number of possible outcomes}}$, we have:
$P(\text{number} > 4) = \frac{\text{Number of outcomes} > 4}{\text{Total number of outcomes}}$
$P(\text{number} > 4) = \frac{2}{6} = \frac{1}{3}$
(ii) Probability of getting a number less than or equal to 4:
Let B be the event of getting a number less than or equal to 4. The numbers less than or equal to 4 are 1, 2, 3, and 4.
The favorable outcomes for event B are $\{1, 2, 3, 4\}$.
The number of favorable outcomes for B is 4.
Using the probability formula:
$P(\text{number} \le 4) = \frac{\text{Number of outcomes} \le 4}{\text{Total number of outcomes}}$
$P(\text{number} \le 4) = \frac{4}{6} = \frac{2}{3}$
Alternate Solution for (ii):
The event "getting a number less than or equal to 4" is the complement of the event "getting a number greater than 4".
Let A be the event of getting a number greater than 4, and A' be the event of getting a number less than or equal to 4.
We know that $P(A') = 1 - P(A)$.
From part (i), $P(A) = P(\text{number} > 4) = \frac{1}{3}$.
So, $P(A') = P(\text{number} \le 4) = 1 - P(\text{number} > 4)$
$P(\text{number} \le 4) = 1 - \frac{1}{3} = \frac{3}{3} - \frac{1}{3} = \frac{2}{3}$.
Example 4. One card is drawn from a well-shuffled deck of 52 cards. Calculate the probability that the card will
(i) be an ace,
(ii) not be an ace.
Answer:
Given: A well-shuffled deck of 52 cards.
To Find: The probability of drawing:
(i) an ace.
(ii) not an ace.
Solution:
The total number of possible outcomes when drawing one card from a deck of 52 cards is 52.
Total number of possible outcomes = 52.
(i) Probability of getting an ace:
Let A be the event that the card drawn is an ace.
There are 4 aces in a standard deck of 52 cards (Ace of Spades, Ace of Hearts, Ace of Diamonds, Ace of Clubs).
The number of favorable outcomes for event A is 4.
The probability of drawing an ace is given by:
$P(A) = \frac{\text{Number of favorable outcomes for A}}{\text{Total number of possible outcomes}}$
$P(\text{Ace}) = \frac{4}{52}$
$P(\text{Ace}) = \frac{1}{13}$
(ii) Probability of not getting an ace:
Let A' be the event that the card drawn is not an ace.
The number of cards that are not aces is the total number of cards minus the number of aces.
Number of cards that are not aces = $52 - 4 = 48$.
The number of favorable outcomes for event A' is 48.
The probability of drawing a card that is not an ace is given by:
$P(A') = \frac{\text{Number of favorable outcomes for A'}}{\text{Total number of possible outcomes}}$
$P(\text{Not an Ace}) = \frac{48}{52}$
$P(\text{Not an Ace}) = \frac{12}{13}$
Alternate Solution for (ii):
The event "not getting an ace" is the complement of the event "getting an ace".
If A is the event of getting an ace, then A' is the event of not getting an ace.
We know that the sum of the probabilities of an event and its complement is 1, i.e., $P(A) + P(A') = 1$.
From part (i), we found that $P(A) = P(\text{Ace}) = \frac{1}{13}$.
So, $P(\text{Not an Ace}) = 1 - P(\text{Ace})$
$P(\text{Not an Ace}) = 1 - \frac{1}{13}$
$P(\text{Not an Ace}) = \frac{13}{13} - \frac{1}{13}$
$P(\text{Not an Ace}) = \frac{12}{13}$
Example 5. Two players, Sangeeta and Reshma, play a tennis match. It is known that the probability of Sangeeta winning the match is 0.62. What is the probability of Reshma winning the match?
Answer:
Given:
The probability of Sangeeta winning the match is 0.62.
$P(\text{Sangeeta wins}) = 0.62$
To Find:
The probability of Reshma winning the match.
$P(\text{Reshma wins})$
Solution:
In a tennis match between two players, there are only two possible outcomes: either Sangeeta wins or Reshma wins. These two events are complementary.
The sum of the probabilities of an event and its complementary event is always 1.
So, $P(\text{Sangeeta wins}) + P(\text{Reshma wins}) = 1$.
We are given $P(\text{Sangeeta wins}) = 0.62$.
Substitute the given value into the equation:
$0.62 + P(\text{Reshma wins}) = 1$
To find the probability of Reshma winning, subtract 0.62 from 1:
$P(\text{Reshma wins}) = 1 - 0.62$
$P(\text{Reshma wins}) = 0.38$
Therefore, the probability of Reshma winning the match is 0.38.
Example 6. Savita and Hamida are friends. What is the probability that both will have
(i) different birthdays?
(ii) the same birthday? (ignoring a leap year).
Answer:
Given: Two friends, Savita and Hamida. Ignoring a leap year.
To Find:
(i) Probability that they have different birthdays.
(ii) Probability that they have the same birthday.
Solution:
Since we are ignoring a leap year, there are 365 days in a year.
Savita's birthday can be any of the 365 days.
Hamida's birthday can also be any of the 365 days.
The total number of possible outcomes for the pair of birthdays is the number of choices for Savita's birthday multiplied by the number of choices for Hamida's birthday.
Total number of possible outcomes $= 365 \times 365$.
(i) Probability of having different birthdays:
For Savita and Hamida to have different birthdays, Hamida's birthday must be on a day different from Savita's birthday.
Savita can have her birthday on any of the 365 days.
Hamida can have her birthday on any day except the day Savita was born. So, there are $365 - 1 = 364$ favorable days for Hamida's birthday.
The number of favorable outcomes for them having different birthdays is the number of choices for Savita's birthday multiplied by the number of favorable choices for Hamida's birthday.
Number of favorable outcomes for different birthdays $= 365 \times 364$.
The probability of having different birthdays is:
$P(\text{Different birthdays}) = \frac{\text{Number of favorable outcomes for different birthdays}}{\text{Total number of possible outcomes}}$
$P(\text{Different birthdays}) = \frac{365 \times 364}{365 \times 365}$
$P(\text{Different birthdays}) = \frac{364}{365}$
(ii) Probability of having the same birthday:
For Savita and Hamida to have the same birthday, Hamida's birthday must be on the exact same day as Savita's birthday.
Savita can have her birthday on any of the 365 days.
Once Savita's birthday is fixed, there is only 1 favorable day for Hamida's birthday (the same day as Savita's).
The number of favorable outcomes for them having the same birthday is the number of choices for Savita's birthday multiplied by the number of favorable choices for Hamida's birthday.
Number of favorable outcomes for same birthday $= 365 \times 1 = 365$.
The probability of having the same birthday is:
$P(\text{Same birthday}) = \frac{\text{Number of favorable outcomes for same birthday}}{\text{Total number of possible outcomes}}$
$P(\text{Same birthday}) = \frac{365}{365 \times 365}$
$P(\text{Same birthday}) = \frac{1}{365}$
Alternate Solution for (i) using the Complement:
The events "having different birthdays" and "having the same birthday" are complementary events.
Let E be the event that they have the same birthday. Then E' is the event that they have different birthdays.
We know that $P(E) + P(E') = 1$.
From part (ii), we found $P(\text{Same birthday}) = \frac{1}{365}$.
So, $P(\text{Different birthdays}) = 1 - P(\text{Same birthday})$.
$P(\text{Different birthdays}) = 1 - \frac{1}{365}$
$P(\text{Different birthdays}) = \frac{365}{365} - \frac{1}{365}$
$P(\text{Different birthdays}) = \frac{365 - 1}{365}$
$P(\text{Different birthdays}) = \frac{364}{365}$
Example 7. There are 40 students in Class X of a school of whom 25 are girls and 15 are boys. The class teacher has to select one student as a class representative. She writes the name of each student on a separate card, the cards being identical. Then she puts cards in a bag and stirs them thoroughly. She then draws one card from the bag. What is the probability that the name written on the card is the name of
(i) a girl?
(ii) a boy?
Answer:
Given:
Total number of students in Class X = 40.
Number of girls = 25.
Number of boys = 15.
To Find:
(i) Probability that the selected student is a girl.
(ii) Probability that the selected student is a boy.
Solution:
The class teacher selects one student randomly from the 40 students. Each student's name is on an identical card, and the cards are thoroughly stirred, ensuring each student has an equal chance of being selected.
The total number of possible outcomes is the total number of students.
Total number of possible outcomes = 40.
(i) Probability of selecting a girl:
Let G be the event that the selected student is a girl.
The number of favorable outcomes for event G is the number of girls in the class.
Number of favorable outcomes for G = 25.
The probability of selecting a girl is given by:
$P(G) = \frac{\text{Number of favorable outcomes for G}}{\text{Total number of possible outcomes}}$
$P(\text{Girl}) = \frac{25}{40}$
Simplifying the fraction by cancelling the common factor 5:
$P(\text{Girl}) = \frac{\cancel{25}^{5}}{\cancel{40}_{8}} = \frac{5}{8}$
(ii) Probability of selecting a boy:
Let B be the event that the selected student is a boy.
The number of favorable outcomes for event B is the number of boys in the class.
Number of favorable outcomes for B = 15.
The probability of selecting a boy is given by:
$P(B) = \frac{\text{Number of favorable outcomes for B}}{\text{Total number of possible outcomes}}$
$P(\text{Boy}) = \frac{15}{40}$
Simplifying the fraction by cancelling the common factor 5:
$P(\text{Boy}) = \frac{\cancel{15}^{3}}{\cancel{40}_{8}} = \frac{3}{8}$
Alternate Solution for (ii) using the Complement:
The event "selecting a boy" is the complement of the event "selecting a girl".
Let G be the event of selecting a girl, and B be the event of selecting a boy.
Since the selected student must be either a girl or a boy, the sum of their probabilities is 1: $P(G) + P(B) = 1$.
From part (i), we found $P(G) = \frac{5}{8}$.
So, $P(B) = 1 - P(G)$
$P(\text{Boy}) = 1 - \frac{5}{8}$
$P(\text{Boy}) = \frac{8}{8} - \frac{5}{8}$
$P(\text{Boy}) = \frac{8 - 5}{8}$
$P(\text{Boy}) = \frac{3}{8}$
Example 8. A box contains 3 blue, 2 white, and 4 red marbles. If a marble is drawn at random from the box, what is the probability that it will be
(i) white?
(ii) blue?
(iii) red?
Answer:
Given:
Number of blue marbles = 3
Number of white marbles = 2
Number of red marbles = 4
To Find:
The probability of drawing:
(i) a white marble.
(ii) a blue marble.
(iii) a red marble.
Solution:
The total number of marbles in the box is the sum of the number of marbles of each color.
Total number of marbles = Number of blue marbles + Number of white marbles + Number of red marbles
Total number of marbles = $3 + 2 + 4 = 9$.
The total number of possible outcomes when drawing one marble is 9.
Total number of possible outcomes = 9.
(i) Probability of drawing a white marble:
Let W be the event that the marble drawn is white.
The number of favorable outcomes for event W is the number of white marbles.
Number of favorable outcomes for W = 2.
The probability of drawing a white marble is:
$P(W) = \frac{\text{Number of favorable outcomes for W}}{\text{Total number of possible outcomes}}$
$P(\text{White}) = \frac{2}{9}$
(ii) Probability of drawing a blue marble:
Let B be the event that the marble drawn is blue.
The number of favorable outcomes for event B is the number of blue marbles.
Number of favorable outcomes for B = 3.
The probability of drawing a blue marble is:
$P(B) = \frac{\text{Number of favorable outcomes for B}}{\text{Total number of possible outcomes}}$
$P(\text{Blue}) = \frac{3}{9}$
Simplifying the fraction:
$P(\text{Blue}) = \frac{1}{3}$
(iii) Probability of drawing a red marble:
Let R be the event that the marble drawn is red.
The number of favorable outcomes for event R is the number of red marbles.
Number of favorable outcomes for R = 4.
The probability of drawing a red marble is:
$P(R) = \frac{\text{Number of favorable outcomes for R}}{\text{Total number of possible outcomes}}$
$P(\text{Red}) = \frac{4}{9}$
Example 9. Harpreet tosses two different coins simultaneously (say, one is of ₹1 and other of ₹ 2). What is the probability that she gets at least one head?
Answer:
Given:
Harpreet tosses two different coins simultaneously (one $\textsf{₹}$1 coin and one $\textsf{₹}$2 coin).
To Find:
The probability of getting at least one head.
Solution:
When two different coins are tossed simultaneously, the possible outcomes are:
- Head on the $\textsf{₹}$1 coin and Head on the $\textsf{₹}$2 coin (HH)
- Head on the $\textsf{₹}$1 coin and Tail on the $\textsf{₹}$2 coin (HT)
- Tail on the $\textsf{₹}$1 coin and Head on the $\textsf{₹}$2 coin (TH)
- Tail on the $\textsf{₹}$1 coin and Tail on the $\textsf{₹}$2 coin (TT)
The set of all possible outcomes (the sample space) is S = $\{HH, HT, TH, TT\}$.
The total number of possible outcomes is 4.
Let E be the event of getting at least one head. This means the outcome has one or two heads.
The outcomes favorable to event E are $\{HH, HT, TH\}$.
The number of favorable outcomes for E is 3.
The probability of an event E is given by the formula:
$P(E) = \frac{\text{Number of favorable outcomes}}{\text{Total number of possible outcomes}}$
So, the probability of getting at least one head is:
$P(\text{at least one head}) = \frac{3}{4}$
Alternate Solution using the Complement:
The event "getting at least one head" is the complement of the event "getting no heads".
Getting no heads means getting tails on both coins (TT).
Let E' be the event of getting no heads (i.e., getting two tails).
The favorable outcome for event E' is $\{TT\}$.
The number of favorable outcomes for E' is 1.
The probability of getting no heads is:
$P(\text{no heads}) = P(TT) = \frac{\text{Number of favorable outcomes for E'}}{\text{Total number of possible outcomes}} = \frac{1}{4}$
The probability of getting at least one head is $P(E) = 1 - P(E')$.
$P(\text{at least one head}) = 1 - P(\text{no heads})$
$P(\text{at least one head}) = 1 - \frac{1}{4}$
$P(\text{at least one head}) = \frac{4}{4} - \frac{1}{4} = \frac{3}{4}$
Example 10. In a musical chair game, the person playing the music has been advised to stop playing the music at any time within 2 minutes after she starts playing. What is the probability that the music will stop within the first half-minute after starting?
Answer:
Given:
The music stops at any random time within a total duration of 2 minutes after starting.
Total time interval = 2 minutes.
To Find:
The probability that the music will stop within the first half-minute.
Solution:
This is a problem of continuous probability, where the outcome is any point in a given time interval. The probability of the music stopping within a specific sub-interval is the ratio of the length of the sub-interval to the length of the total interval.
Total duration for the music to stop = 2 minutes.
Favorable duration (music stopping within the first half-minute) = half-minute = 0.5 minutes.
The probability is given by:
$P(\text{event}) = \frac{\text{Length of the favorable interval}}{\text{Length of the total interval}}$
Probability that the music stops within the first half-minute:
$P(\text{music stops within first half-minute}) = \frac{0.5 \text{ minutes}}{2 \text{ minutes}}$
$P = \frac{0.5}{2} = \frac{1/2}{2} = \frac{1}{4}$
Alternatively, using seconds:
Total duration = 2 minutes $= 2 \times 60 = 120$ seconds.
Favorable duration = half-minute $= 0.5 \times 60 = 30$ seconds.
$P(\text{music stops within first half-minute}) = \frac{30 \text{ seconds}}{120 \text{ seconds}}$
$P = \frac{30}{120} = \frac{1}{4}$
The probability that the music will stop within the first half-minute after starting is $\frac{1}{4}$.
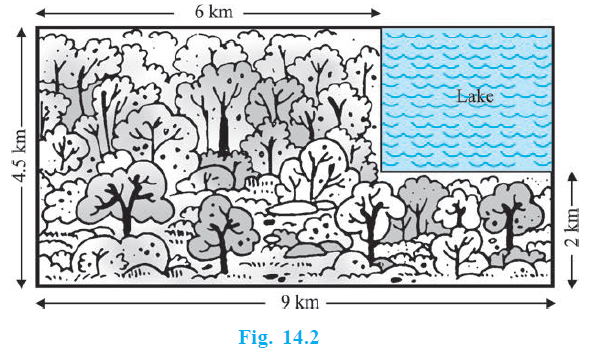
Example 11. A missing helicopter is reported to have crashed somewhere in the rectangular region shown in Fig. 14.2. What is the probability that it crashed inside the lake shown in the figure?
Answer:
Given:
The helicopter crashed somewhere in the rectangular region shown in the figure.
From the figure, the dimensions of the rectangular region are: Length = $9 \text{ km}$ and Width = $4.5 \text{ km}$.
The lake within the rectangular region is also rectangular with dimensions: Length = $3 \text{ km}$ and Width = $2.5 \text{ km}$.
To Find:
The probability that the helicopter crashed inside the lake.
Solution:
The problem is a case of geometric probability. The probability of the helicopter crashing inside the lake is the ratio of the area of the lake to the area of the entire rectangular region.
Area of the rectangular region = Length $\times$ Width
$= 9 \text{ km} \times 4.5 \text{ km}$
$= (9 \times 4.5) \text{ km}^2$
$= 40.5 \text{ km}^2$
Area of the lake = Length $\times$ Width
$= 3 \text{ km} \times 2.5 \text{ km}$
$= (3 \times 2.5) \text{ km}^2$
$= 7.5 \text{ km}^2$
The event that the helicopter crashed inside the lake is a favorable event. The sample space is the entire rectangular region where the helicopter could have crashed.
Probability of the helicopter crashing inside the lake = $\frac{\text{Area of the lake}}{\text{Area of the rectangular region}}$
$P(\text{crash in lake}) = \frac{7.5 \text{ km}^2}{40.5 \text{ km}^2}$
$P(\text{crash in lake}) = \frac{7.5}{40.5}$
To simplify the fraction, we can multiply the numerator and denominator by 10 to remove the decimal point:
$P(\text{crash in lake}) = \frac{75}{405}$
Now, simplify the fraction $\frac{75}{405}$ by dividing the numerator and denominator by their greatest common divisor. Both are divisible by 5.
$75 = 5 \times 15$
$405 = 5 \times 81$
$P(\text{crash in lake}) = \frac{\cancel{75}^{15}}{\cancel{405}^{81}}$
Now, simplify the fraction $\frac{15}{81}$. Both are divisible by 3.
$15 = 3 \times 5$
$81 = 3 \times 27$
$P(\text{crash in lake}) = \frac{\cancel{15}^{5}}{\cancel{81}^{27}}$
The simplified probability is $\frac{5}{27}$.
Answer:
The probability that the helicopter crashed inside the lake is $\frac{5}{27}$.
Example 12. A carton consists of 100 shirts of which 88 are good, 8 have minor defects and 4 have major defects. Jimmy, a trader, will only accept the shirts which are good, but Sujatha, another trader, will only reject the shirts which have major defects. One shirt is drawn at random from the carton. What is the probability that
(i) it is acceptable to Jimmy?
(ii) it is acceptable to Sujatha?
Answer:
Given:
Total number of shirts in the carton = 100.
Number of good shirts = 88.
Number of shirts with minor defects = 8.
Number of shirts with major defects = 4.
To Find:
(i) The probability that the drawn shirt is acceptable to Jimmy.
(ii) The probability that the drawn shirt is acceptable to Sujatha.
Solution:
One shirt is drawn at random from the carton of 100 shirts. This means each shirt has an equal probability of being drawn.
The total number of possible outcomes is the total number of shirts.
Total number of possible outcomes = 100.
(i) Probability that the shirt is acceptable to Jimmy:
Jimmy accepts only the shirts which are good.
The number of shirts acceptable to Jimmy is the number of good shirts.
Number of favorable outcomes for Jimmy = 88.
The probability that the shirt is acceptable to Jimmy is:
$P(\text{acceptable to Jimmy}) = \frac{\text{Number of shirts acceptable to Jimmy}}{\text{Total number of shirts}}$
$P(\text{acceptable to Jimmy}) = \frac{88}{100}$
Simplifying the fraction by cancelling the common factor 4:
$P(\text{acceptable to Jimmy}) = \frac{\cancel{88}^{22}}{\cancel{100}_{25}} = \frac{22}{25}$
(ii) Probability that the shirt is acceptable to Sujatha:
Sujatha will only reject the shirts which have major defects. This means she will accept shirts that are good or have minor defects.
The number of shirts acceptable to Sujatha is the sum of the number of good shirts and the number of shirts with minor defects.
Number of good shirts = 88.
Number of shirts with minor defects = 8.
Number of shirts acceptable to Sujatha $= 88 + 8 = 96$.
The probability that the shirt is acceptable to Sujatha is:
$P(\text{acceptable to Sujatha}) = \frac{\text{Number of shirts acceptable to Sujatha}}{\text{Total number of shirts}}$
$P(\text{acceptable to Sujatha}) = \frac{96}{100}$
Simplifying the fraction by cancelling the common factor 4:
$P(\text{acceptable to Sujatha}) = \frac{\cancel{96}^{24}}{\cancel{100}_{25}} = \frac{24}{25}$
Alternate way to find shirts acceptable to Sujatha:
Total shirts = 100.
Shirts rejected by Sujatha = shirts with major defects = 4.
Shirts acceptable to Sujatha = Total shirts - Shirts rejected by Sujatha
Shirts acceptable to Sujatha $= 100 - 4 = 96$.
This gives the same number of favorable outcomes as calculated previously, leading to the same probability $\frac{96}{100} = \frac{24}{25}$.
Example 13. Two dice, one blue and one grey, are thrown at the same time. Write down all the possible outcomes. What is the probability that the sum of the two numbers appearing on the top of the dice is
(i) 8?
(ii) 13?
(iii) less than or equal to 12?
Answer:
Given:
Two dice (one blue and one grey) are thrown at the same time.
To Find:
All possible outcomes.
The probability that the sum of the numbers is:
(i) 8
(ii) 13
(iii) less than or equal to 12
Solution:
When two dice are thrown, the possible outcomes are pairs of numbers, where the first number represents the outcome on the blue die and the second number represents the outcome on the grey die. Each die can show a number from 1 to 6.
The set of all possible outcomes (sample space) is:
S = $\{(1,1), (1,2), (1,3), (1,4), (1,5), (1,6), $
$(2,1), (2,2), (2,3), (2,4), (2,5), (2,6), $
$(3,1), (3,2), (3,3), (3,4), (3,5), (3,6), $
$(4,1), (4,2), (4,3), (4,4), (4,5), (4,6), $
$(5,1), (5,2), (5,3), (5,4), (5,5), (5,6), $
$(6,1), (6,2), (6,3), (6,4), (6,5), (6,6)\}$
The total number of possible outcomes is $6 \times 6 = 36$.
Total number of possible outcomes = 36.
(i) Probability that the sum is 8:
Let E$_1$ be the event that the sum of the numbers on the two dice is 8.
The favorable outcomes for E$_1$ are the pairs whose sum is 8. These are:
$(2,6), (3,5), (4,4), (5,3), (6,2)$
The number of favorable outcomes for E$_1$ is 5.
The probability of event E$_1$ is:
$P(E_1) = \frac{\text{Number of favorable outcomes for } E_1}{\text{Total number of possible outcomes}}$
$P(\text{sum = 8}) = \frac{5}{36}$
(ii) Probability that the sum is 13:
Let E$_2$ be the event that the sum of the numbers on the two dice is 13.
The maximum possible sum when throwing two dice is $6 + 6 = 12$. It is impossible to get a sum of 13.
The number of favorable outcomes for E$_2$ is 0.
The probability of event E$_2$ is:
$P(E_2) = \frac{\text{Number of favorable outcomes for } E_2}{\text{Total number of possible outcomes}}$
$P(\text{sum = 13}) = \frac{0}{36}$
$P(\text{sum = 13}) = 0$
This is an impossible event.
(iii) Probability that the sum is less than or equal to 12:
Let E$_3$ be the event that the sum of the numbers on the two dice is less than or equal to 12.
As noted earlier, the maximum possible sum when throwing two dice is $6 + 6 = 12$. Therefore, the sum of the numbers on any outcome in the sample space will always be less than or equal to 12.
All the possible outcomes (36 outcomes) result in a sum less than or equal to 12.
The number of favorable outcomes for E$_3$ is 36.
The probability of event E$_3$ is:
$P(E_3) = \frac{\text{Number of favorable outcomes for } E_3}{\text{Total number of possible outcomes}}$
$P(\text{sum} \le 12) = \frac{36}{36}$
$P(\text{sum} \le 12) = 1$
This is a sure event.
Exercise 14.1
Question 1. Complete the following statements:
(i) Probability of an event E + Probability of the event ‘not E’ = _____________.
(ii) The probability of an event that cannot happen is ________________. Such an event is called .
(iii) The probability of an event that is certain to happen is _________________. Such an event is called .
(iv) The sum of the probabilities of all the elementary events of an experiment is ________________.
(v) The probability of an event is greater than or equal to _______________and less than or equal to .
Answer:
(i) Probability of an event E + Probability of the event ‘not E’ = 1.
(ii) The probability of an event that cannot happen is 0. Such an event is called an impossible event.
(iii) The probability of an event that is certain to happen is 1. Such an event is called a sure event (or certain event).
(iv) The sum of the probabilities of all the elementary events of an experiment is 1.
(v) The probability of an event is greater than or equal to 0 and less than or equal to 1.
Question 2. Which of the following experiments have equally likely outcomes? Explain.
(i) A driver attempts to start a car. The car starts or does not start.
(ii) A player attempts to shoot a basketball. She/he shoots or misses the shot.
(iii) A trial is made to answer a true-false question. The answer is right or wrong.
(iv) A baby is born. It is a boy or a girl.
Answer:
Outcomes are considered equally likely if each outcome of the experiment has the same chance or probability of happening.
(i) A driver attempts to start a car. The car starts or does not start.
The outcomes are 'car starts' and 'car does not start'. These outcomes are not equally likely. The chance of the car starting depends on many things like if the car is in good condition, if there is fuel, if the battery is charged, etc. It's not guaranteed that starting the car and not starting the car have the same chance.
(ii) A player attempts to shoot a basketball. She/he shoots or misses the shot.
The outcomes are 'shoots (makes the shot)' and 'misses the shot'. These outcomes are not equally likely. The chance of making the shot depends on the player's skill. A skilled player has a higher chance of making the shot than a new player. So the probabilities are different.
(iii) A trial is made to answer a true-false question. The answer is right or wrong.
The outcomes are 'answer is right' and 'answer is wrong'. If you are simply guessing the answer to a true-false question, there are only two possible outcomes (True or False), and choosing either one has an equal chance of being correct. So, the chance of being right is the same as the chance of being wrong if you guess. Therefore, these outcomes are equally likely.
(iv) A baby is born. It is a boy or a girl.
The outcomes are 'it is a boy' and 'it is a girl'. When a baby is born, there are two possible outcomes: either it is a boy or it is a girl. Each of these outcomes has the same chance of happening. Therefore, these outcomes are equally likely.
Question 3. Why is tossing a coin considered to be a fair way of deciding which team should get the ball at the beginning of a football game?
Answer:
Tossing a coin is considered a fair way of deciding which team should get the ball at the beginning of a football game because the outcome of a coin toss is considered to be a random event with equally likely outcomes.
When a standard, unbiased coin is tossed, there are only two possible outcomes: getting a Head or getting a Tail.
Assuming the coin is fair, the probability of getting a Head is $\frac{1}{2}$, and the probability of getting a Tail is also $\frac{1}{2}$. This means that both outcomes have an equal chance of occurring.
Since the result of the toss (Head or Tail) determines which team gets the ball, and both outcomes are equally likely, neither team has any pre-determined advantage before the toss. There is no way for either team to influence the outcome of the toss.
Therefore, the decision made by the coin toss is based purely on chance, making it a fair method for both competing teams.
Question 4. Which of the following cannot be the probability of an event?
(A) $\frac{2}{3}$
(B) –1.5
(C) 15%
(D) 0.7
Answer:
The probability of any event E, denoted by $P(E)$, must be a number between 0 and 1, inclusive.
Mathematically, this is expressed as $0 \le P(E) \le 1$.
Let's examine each option:
(A) $\frac{2}{3}$: This value is approximately 0.67. Since $0 \le 0.67 \le 1$, $\frac{2}{3}$ can be the probability of an event.
(B) –1.5: This value is less than 0. The probability of an event cannot be negative. Therefore, –1.5 cannot be the probability of an event.
(C) 15%: This can be written as a decimal $0.15$. Since $0 \le 0.15 \le 1$, 15% can be the probability of an event.
(D) 0.7: This value is between 0 and 1. Since $0 \le 0.7 \le 1$, 0.7 can be the probability of an event.
The only option that is not between 0 and 1 (inclusive) is –1.5.
Therefore, the correct answer is (B) –1.5.
Question 5. If P(E) = 0.05, what is the probability of ‘not E’?
Answer:
Given:
The probability of event E is $P(E) = 0.05$.
To Find:
The probability of the event 'not E', denoted as $P(\text{not } E)$ or $P(\overline{E})$ or $P(E')$.
Solution:
The event 'not E' is the complementary event of E. The sum of the probability of an event and the probability of its complementary event is always 1.
$P(E) + P(\text{not } E) = 1$
Substitute the given value of $P(E)$ into the equation:
$0.05 + P(\text{not } E) = 1$
To find $P(\text{not } E)$, subtract 0.05 from 1:
$P(\text{not } E) = 1 - 0.05$
$P(\text{not } E) = 0.95$
Therefore, the probability of ‘not E’ is 0.95.
Question 6. A bag contains lemon flavoured candies only. Malini takes out one candy without looking into the bag. What is the probability that she takes out
(i) an orange flavoured candy?
(ii) a lemon flavoured candy?
Answer:
Given:
A bag contains only lemon flavoured candies.
Malini takes out one candy at random.
To Find:
(i) Probability of taking out an orange flavoured candy.
(ii) Probability of taking out a lemon flavoured candy.
Solution:
Let the total number of candies in the bag be $N$. All $N$ candies are lemon flavoured.
The total number of possible outcomes when drawing one candy is $N$.
Total number of possible outcomes = $N$.
(i) Probability of taking out an orange flavoured candy:
Let O be the event of taking out an orange flavoured candy.
The number of orange flavoured candies in the bag is 0, because the bag contains only lemon flavoured candies.
Number of favorable outcomes for O = 0.
The probability of event O is:
$P(O) = \frac{\text{Number of favorable outcomes for O}}{\text{Total number of possible outcomes}}$
$P(\text{Orange}) = \frac{0}{N}$
$P(\text{Orange}) = 0$
This is an impossible event.
(ii) Probability of taking out a lemon flavoured candy:
Let L be the event of taking out a lemon flavoured candy.
The number of lemon flavoured candies in the bag is $N$, because all candies in the bag are lemon flavoured.
Number of favorable outcomes for L = $N$.
The probability of event L is:
$P(L) = \frac{\text{Number of favorable outcomes for L}}{\text{Total number of possible outcomes}}$
$P(\text{Lemon}) = \frac{N}{N}$
$P(\text{Lemon}) = 1$
This is a sure event.
Question 7. It is given that in a group of 3 students, the probability of 2 students not having the same birthday is 0.992. What is the probability that the 2 students have the same birthday?
Answer:
Given:
In a group of 3 students, the probability of 2 students not having the same birthday is 0.992.
Let E be the event that the 2 students have the same birthday.
The event 'not E' is that the 2 students do not have the same birthday.
$P(\text{not E}) = 0.992$
To Find:
The probability that the 2 students have the same birthday, i.e., $P(E)$.
Solution:
The event that the 2 students have the same birthday and the event that the 2 students do not have the same birthday are complementary events.
For any event E and its complement 'not E', the sum of their probabilities is 1.
$P(E) + P(\text{not E}) = 1$
Substitute the given value $P(\text{not E}) = 0.992$ into the equation:
$P(E) + 0.992 = 1$
To find $P(E)$, subtract 0.992 from 1:
$P(E) = 1 - 0.992$
$P(E) = 0.008$
Therefore, the probability that the 2 students have the same birthday is 0.008.
Question 8. A bag contains 3 red balls and 5 black balls. A ball is drawn at random from the bag. What is the probability that the ball drawn is
(i) red ?
(ii) not red?
Answer:
Given:
Number of red balls = 3
Number of black balls = 5
To Find:
(i) Probability of drawing a red ball.
(ii) Probability of drawing a ball that is not red.
Solution:
The total number of balls in the bag is the sum of red and black balls.
Total number of balls = Number of red balls + Number of black balls
Total number of balls = $3 + 5 = 8$.
The total number of possible outcomes when drawing one ball is 8.
Total number of possible outcomes = 8.
(i) Probability of drawing a red ball:
Let R be the event that the ball drawn is red.
The number of favorable outcomes for event R is the number of red balls.
Number of favorable outcomes for R = 3.
The probability of drawing a red ball is:
$P(R) = \frac{\text{Number of favorable outcomes for R}}{\text{Total number of possible outcomes}}$
$P(\text{Red}) = \frac{3}{8}$
(ii) Probability of drawing a ball that is not red:
A ball that is not red must be a black ball.
Let 'not R' be the event that the ball drawn is not red.
The number of favorable outcomes for event 'not R' is the number of black balls.
Number of favorable outcomes for 'not R' = 5.
The probability of drawing a ball that is not red is:
$P(\text{not R}) = \frac{\text{Number of favorable outcomes for not R}}{\text{Total number of possible outcomes}}$
$P(\text{not Red}) = \frac{5}{8}$
Alternate Solution for (ii) using the Complement:
The event "drawing a ball that is not red" is the complement of the event "drawing a red ball".
$P(\text{not Red}) = 1 - P(\text{Red})$
From part (i), we found $P(\text{Red}) = \frac{3}{8}$.
So, $P(\text{not Red}) = 1 - \frac{3}{8}$
$P(\text{not Red}) = \frac{8}{8} - \frac{3}{8} = \frac{5}{8}$
Question 9. A box contains 5 red marbles, 8 white marbles and 4 green marbles. One marble is taken out of the box at random. What is the probability that the marble taken out will be
(i) red ?
(ii) white ?
(iii) not green?
Answer:
Given:
Number of red marbles = 5
Number of white marbles = 8
Number of green marbles = 4
To Find:
The probability of drawing:
(i) a red marble.
(ii) a white marble.
(iii) a marble that is not green.
Solution:
The total number of marbles in the box is the sum of the number of marbles of each color.
Total number of marbles = Number of red marbles + Number of white marbles + Number of green marbles
Total number of marbles = $5 + 8 + 4 = 17$.
The total number of possible outcomes when drawing one marble at random is 17.
Total number of possible outcomes = 17.
(i) Probability of drawing a red marble:
Let R be the event that the marble drawn is red.
The number of favorable outcomes for event R is the number of red marbles.
Number of favorable outcomes for R = 5.
The probability of drawing a red marble is:
$P(R) = \frac{\text{Number of favorable outcomes for R}}{\text{Total number of possible outcomes}}$
$P(\text{Red}) = \frac{5}{17}$
(ii) Probability of drawing a white marble:
Let W be the event that the marble drawn is white.
The number of favorable outcomes for event W is the number of white marbles.
Number of favorable outcomes for W = 8.
The probability of drawing a white marble is:
$P(W) = \frac{\text{Number of favorable outcomes for W}}{\text{Total number of possible outcomes}}$
$P(\text{White}) = \frac{8}{17}$
(iii) Probability of drawing a marble that is not green:
A marble that is not green is either a red marble or a white marble.
Let 'not G' be the event that the marble drawn is not green.
The number of favorable outcomes for event 'not G' is the sum of the number of red marbles and the number of white marbles.
Number of favorable outcomes for 'not G' = Number of red marbles + Number of white marbles = $5 + 8 = 13$.
The probability of drawing a marble that is not green is:
$P(\text{not G}) = \frac{\text{Number of favorable outcomes for not G}}{\text{Total number of possible outcomes}}$
$P(\text{not Green}) = \frac{13}{17}$
Alternate Solution for (iii) using the Complement:
The event "drawing a marble that is not green" is the complement of the event "drawing a green marble".
Let G be the event that the marble drawn is green.
The number of favorable outcomes for event G is the number of green marbles = 4.
The probability of drawing a green marble is $P(G) = \frac{4}{17}$.
The probability of not drawing a green marble is $P(\text{not G}) = 1 - P(G)$.
$P(\text{not Green}) = 1 - \frac{4}{17}$
$P(\text{not Green}) = \frac{17}{17} - \frac{4}{17} = \frac{17 - 4}{17} = \frac{13}{17}$
Both methods yield the same result.
Question 10. A piggy bank contains hundred 50p coins, fifty ₹1 coins, twenty ₹ 2 coins and ten ₹5 coins. If it is equally likely that one of the coins will fall out when the bank is turned upside down, what is the probability that the coin
(i) will be a 50 p coin ?
(ii) will not be a ₹ 5 coin?
Answer:
Given:
Number of 50p coins = 100.
Number of $\textsf{₹}$1 coins = 50.
Number of $\textsf{₹}$2 coins = 20.
Number of $\textsf{₹}$5 coins = 10.
To Find:
(i) The probability that the coin is a 50p coin.
(ii) The probability that the coin is not a $\textsf{₹}$5 coin.
Solution:
The total number of coins in the piggy bank is the sum of the numbers of coins of each denomination.
Total number of coins = $100 + 50 + 20 + 10 = 180$.
Since it is equally likely that any one coin will fall out, the total number of possible outcomes is 180.
Total number of possible outcomes = 180.
(i) Probability that the coin will be a 50p coin:
Let A be the event that the coin is a 50p coin.
The number of favorable outcomes for event A is the number of 50p coins.
Number of favorable outcomes for A = 100.
The probability of event A is given by:
$P(A) = \frac{\text{Number of favorable outcomes for A}}{\text{Total number of possible outcomes}}$
$P(\text{50p coin}) = \frac{100}{180}$
Simplifying the fraction:
$P(\text{50p coin}) = \frac{10}{18} = \frac{5}{9}$
(ii) Probability that the coin will not be a $\textsf{₹}$5 coin:
Let B be the event that the coin is not a $\textsf{₹}$5 coin.
The coins that are not $\textsf{₹}$5 coins are the 50p coins, $\textsf{₹}$1 coins, and $\textsf{₹}$2 coins.
Number of coins that are not $\textsf{₹}$5 coins = Number of 50p coins + Number of $\textsf{₹}$1 coins + Number of $\textsf{₹}$2 coins
Number of favorable outcomes for B = $100 + 50 + 20 = 170$.
The probability of event B is given by:
$P(B) = \frac{\text{Number of favorable outcomes for B}}{\text{Total number of possible outcomes}}$
$P(\text{not a } \textsf{₹}5 \text{ coin}) = \frac{170}{180}$
Simplifying the fraction:
$P(\text{not a } \textsf{₹}5 \text{ coin}) = \frac{17}{18}$
Alternate Solution for (ii) using the Complement:
Let C be the event that the coin is a $\textsf{₹}$5 coin.
The number of $\textsf{₹}$5 coins is 10.
The probability of getting a $\textsf{₹}$5 coin is $P(C) = \frac{10}{180} = \frac{1}{18}$.
The event "not being a $\textsf{₹}$5 coin" is the complement of the event "being a $\textsf{₹}$5 coin".
$P(\text{not a } \textsf{₹}5 \text{ coin}) = 1 - P(\text{₹}5 \text{ coin})$
$P(\text{not a } \textsf{₹}5 \text{ coin}) = 1 - \frac{1}{18}$
$P(\text{not a } \textsf{₹}5 \text{ coin}) = \frac{18}{18} - \frac{1}{18} = \frac{17}{18}$
Both methods yield the same result.
Question 11. Gopi buys a fish from a shop for his aquarium. The shopkeeper takes out one fish at random from a tank containing 5 male fish and 8 female fish (see Fig. 14.4). What is the probability that the fish taken out is a male fish?

Answer:
Given:
Number of male fish in the tank = 5.
Number of female fish in the tank = 8.
To Find:
The probability that the fish taken out is a male fish.
Solution:
The total number of fish in the tank is the sum of the male and female fish.
Total number of fish = Number of male fish + Number of female fish
Total number of fish $= 5 + 8 = 13$.
Since the shopkeeper takes out one fish at random, the total number of possible outcomes is the total number of fish.
Total number of possible outcomes = 13.
Let M be the event that the fish taken out is a male fish.
The number of favorable outcomes for event M is the number of male fish in the tank.
Number of favorable outcomes for M = 5.
The probability of an event is given by the formula:
$P(E) = \frac{\text{Number of favorable outcomes}}{\text{Total number of possible outcomes}}$
The probability of taking out a male fish is:
$P(\text{Male fish}) = \frac{\text{Number of male fish}}{\text{Total number of fish}}$
$P(\text{Male fish}) = \frac{5}{13}$
Therefore, the probability that the fish taken out is a male fish is $\frac{5}{13}$.
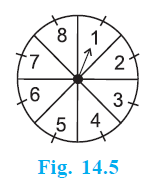
Question 12. A game of chance consists of spinning an arrow which comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8 (see Fig. 14.5 ), and these are equally likely outcomes. What is the probability that it will point at
(i) 8 ?
(ii) an odd number?
(iii) a number greater than 2?
(iv) a number less than 9?
Answer:
Given:
A game of chance involves spinning an arrow pointing at numbers from 1 to 8. The outcomes are equally likely.
To Find:
The probability that the arrow will point at:
(i) 8
(ii) an odd number
(iii) a number greater than 2
(iv) a number less than 9
Solution:
The possible outcomes when the arrow is spun are the numbers 1, 2, 3, 4, 5, 6, 7, 8.
The total number of possible outcomes is 8.
Total number of possible outcomes = 8.
(i) Probability of pointing at 8:
Let E$_1$ be the event that the arrow points at 8.
The favorable outcome for E$_1$ is $\{8\}$.
The number of favorable outcomes for E$_1$ is 1.
The probability of pointing at 8 is:
$P(\text{pointing at 8}) = \frac{\text{Number of favorable outcomes for } E_1}{\text{Total number of possible outcomes}}$
$P(\text{pointing at 8}) = \frac{1}{8}$
(ii) Probability of pointing at an odd number:
Let E$_2$ be the event that the arrow points at an odd number.
The odd numbers in the possible outcomes are 1, 3, 5, 7.
The favorable outcomes for E$_2$ are $\{1, 3, 5, 7\}$.
The number of favorable outcomes for E$_2$ is 4.
The probability of pointing at an odd number is:
$P(\text{pointing at an odd number}) = \frac{\text{Number of favorable outcomes for } E_2}{\text{Total number of possible outcomes}}$
$P(\text{pointing at an odd number}) = \frac{4}{8}$
Simplifying the fraction:
$P(\text{pointing at an odd number}) = \frac{1}{2}$
(iii) Probability of pointing at a number greater than 2:
Let E$_3$ be the event that the arrow points at a number greater than 2.
The numbers greater than 2 in the possible outcomes are 3, 4, 5, 6, 7, 8.
The favorable outcomes for E$_3$ are $\{3, 4, 5, 6, 7, 8\}$.
The number of favorable outcomes for E$_3$ is 6.
The probability of pointing at a number greater than 2 is:
$P(\text{pointing at a number} > 2) = \frac{\text{Number of favorable outcomes for } E_3}{\text{Total number of possible outcomes}}$
$P(\text{pointing at a number} > 2) = \frac{6}{8}$
Simplifying the fraction:
$P(\text{pointing at a number} > 2) = \frac{3}{4}$
(iv) Probability of pointing at a number less than 9:
Let E$_4$ be the event that the arrow points at a number less than 9.
The numbers less than 9 in the possible outcomes are 1, 2, 3, 4, 5, 6, 7, 8.
The favorable outcomes for E$_4$ are $\{1, 2, 3, 4, 5, 6, 7, 8\}$.
The number of favorable outcomes for E$_4$ is 8.
The probability of pointing at a number less than 9 is:
$P(\text{pointing at a number} < 9) = \frac{\text{Number of favorable outcomes for } E_4}{\text{Total number of possible outcomes}}$
$P(\text{pointing at a number} < 9) = \frac{8}{8}$
$P(\text{pointing at a number} < 9) = 1$
This is a sure event.
Question 13. A die is thrown once. Find the probability of getting
(i) a prime number;
(ii) a number lying between 2 and 6;
(iii) an odd number.
Answer:
Given:
A die is thrown once.
To Find:
The probability of getting:
(i) a prime number.
(ii) a number lying between 2 and 6.
(iii) an odd number.
Solution:
When a standard die is thrown once, the possible outcomes are the numbers 1, 2, 3, 4, 5, 6.
The total number of possible outcomes is 6.
Total number of possible outcomes = 6.
(i) Probability of getting a prime number:
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself.
The prime numbers in the possible outcomes (1, 2, 3, 4, 5, 6) are 2, 3, and 5.
The favorable outcomes for getting a prime number are $\{2, 3, 5\}$.
The number of favorable outcomes for getting a prime number is 3.
The probability of getting a prime number is:
$P(\text{prime number}) = \frac{\text{Number of favorable outcomes}}{\text{Total number of possible outcomes}}$
$P(\text{prime number}) = \frac{3}{6}$
Simplifying the fraction:
$P(\text{prime number}) = \frac{\cancel{3}^{1}}{\cancel{6}_{2}} = \frac{1}{2}$
(ii) Probability of getting a number lying between 2 and 6:
The numbers lying strictly between 2 and 6 in the possible outcomes are 3, 4, and 5.
The favorable outcomes for getting a number between 2 and 6 are $\{3, 4, 5\}$.
The number of favorable outcomes is 3.
The probability of getting a number lying between 2 and 6 is:
$P(\text{number between 2 and 6}) = \frac{\text{Number of favorable outcomes}}{\text{Total number of possible outcomes}}$
$P(\text{number between 2 and 6}) = \frac{3}{6}$
Simplifying the fraction:
$P(\text{number between 2 and 6}) = \frac{\cancel{3}^{1}}{\cancel{6}_{2}} = \frac{1}{2}$
(iii) Probability of getting an odd number:
The odd numbers in the possible outcomes are 1, 3, and 5.
The favorable outcomes for getting an odd number are $\{1, 3, 5\}$.
The number of favorable outcomes is 3.
The probability of getting an odd number is:
$P(\text{odd number}) = \frac{\text{Number of favorable outcomes}}{\text{Total number of possible outcomes}}$
$P(\text{odd number}) = \frac{3}{6}$
Simplifying the fraction:
$P(\text{odd number}) = \frac{\cancel{3}^{1}}{\cancel{6}_{2}} = \frac{1}{2}$
Question 14. One card is drawn from a well-shuffled deck of 52 cards. Find the probability of getting
(i) a king of red colour
(ii) a face card
(iii) a red face card
(iv) the jack of hearts
(v) a spade
(vi) the queen of diamonds
Answer:
Given:
One card is drawn from a well-shuffled deck of 52 cards.
To Find:
The probability of drawing:
(i) a king of red colour.
(ii) a face card.
(iii) a red face card.
(iv) the jack of hearts.
(v) a spade.
(vi) the queen of diamonds.
Solution:
The total number of possible outcomes when drawing one card from a deck of 52 cards is 52.
Total number of possible outcomes = 52.
(i) Probability of getting a king of red colour:
There are two red suits: Hearts and Diamonds.
Each suit has one King.
So, there are 2 Kings of red colour (King of Hearts and King of Diamonds).
Number of favorable outcomes = 2.
$P(\text{King of red colour}) = \frac{\text{Number of Kings of red colour}}{\text{Total number of cards}}$
$P(\text{King of red colour}) = \frac{2}{52}$
Simplifying the fraction:
$P(\text{King of red colour}) = \frac{\cancel{2}^{1}}{\cancel{52}_{26}} = \frac{1}{26}$
(ii) Probability of getting a face card:
In a standard deck, face cards are Jack, Queen, and King.
There are 4 suits, and each suit has 3 face cards (Jack, Queen, King).
Total number of face cards = $3 \times 4 = 12$.
Number of favorable outcomes = 12.
$P(\text{Face card}) = \frac{\text{Number of face cards}}{\text{Total number of cards}}$
$P(\text{Face card}) = \frac{12}{52}$
Simplifying the fraction by cancelling the common factor 4:
$P(\text{Face card}) = \frac{\cancel{12}^{3}}{\cancel{52}_{13}} = \frac{3}{13}$
(iii) Probability of getting a red face card:
The red suits are Hearts and Diamonds.
Each red suit has 3 face cards (Jack, Queen, King).
Total number of red face cards = Number of face cards in Hearts + Number of face cards in Diamonds = $3 + 3 = 6$.
Number of favorable outcomes = 6.
$P(\text{Red face card}) = \frac{\text{Number of red face cards}}{\text{Total number of cards}}$
$P(\text{Red face card}) = \frac{6}{52}$
Simplifying the fraction by cancelling the common factor 2:
$P(\text{Red face card}) = \frac{\cancel{6}^{3}}{\cancel{52}_{26}} = \frac{3}{26}$
(iv) Probability of getting the jack of hearts:
There is only one Jack of Hearts in a deck of 52 cards.
Number of favorable outcomes = 1.
$P(\text{Jack of hearts}) = \frac{\text{Number of Jack of hearts}}{\text{Total number of cards}}$
$P(\text{Jack of hearts}) = \frac{1}{52}$
(v) Probability of getting a spade:
There are 13 cards of spade in a deck of 52 cards (Ace, 2, 3, ..., 10, Jack, Queen, King).
Number of favorable outcomes = 13.
$P(\text{a spade}) = \frac{\text{Number of spades}}{\text{Total number of cards}}$
$P(\text{a spade}) = \frac{13}{52}$
Simplifying the fraction by cancelling the common factor 13:
$P(\text{a spade}) = \frac{\cancel{13}^{1}}{\cancel{52}_{4}} = \frac{1}{4}$
(vi) Probability of getting the queen of diamonds:
There is only one Queen of Diamonds in a deck of 52 cards.
Number of favorable outcomes = 1.
$P(\text{the queen of diamonds}) = \frac{\text{Number of Queen of diamonds}}{\text{Total number of cards}}$
$P(\text{the queen of diamonds}) = \frac{1}{52}$
Question 15. Five cards—the ten, jack, queen, king and ace of diamonds, are well-shuffled with their face downwards. One card is then picked up at random.
(i) What is the probability that the card is the queen?
(ii) If the queen is drawn and put aside, what is the probability that the second card picked up is (a) an ace? (b) a queen?
Answer:
Given:
A set of five cards: the ten, jack, queen, king, and ace of diamonds.
Initially, one card is picked up at random from these five cards.
To Find:
(i) The probability that the first card picked is the queen.
(ii) If the queen is drawn and put aside, the probability that the second card picked up is (a) an ace, (b) a queen.
Solution:
Initially, there are 5 cards in the set: Ten of Diamonds, Jack of Diamonds, Queen of Diamonds, King of Diamonds, and Ace of Diamonds.
The total number of possible outcomes when picking one card at random is 5.
Total number of possible outcomes (first draw) = 5.
(i) Probability that the card is the queen:
Let E$_1$ be the event that the first card drawn is the queen.
There is only one queen in the initial set of 5 cards.
The number of favorable outcomes for E$_1$ is 1.
The probability of drawing the queen in the first draw is:
$P(E_1) = \frac{\text{Number of favorable outcomes}}{\text{Total number of possible outcomes}}$
$P(\text{Queen}) = \frac{1}{5}$
(ii) If the queen is drawn and put aside:
After drawing the queen and putting it aside, the remaining cards are: Ten of Diamonds, Jack of Diamonds, King of Diamonds, and Ace of Diamonds.
The total number of cards remaining is 4.
Total number of possible outcomes (second draw) = 4.
(a) Probability that the second card picked up is an ace:
Let E$_{2a}$ be the event that the second card drawn is an ace, given that the queen was drawn first and put aside.
From the remaining 4 cards, there is one ace (Ace of Diamonds).
The number of favorable outcomes for E$_{2a}$ is 1.
The probability of drawing an ace as the second card is:
$P(\text{Ace in second draw}) = \frac{\text{Number of favorable outcomes}}{\text{Total number of remaining outcomes}}$
$P(\text{Ace in second draw}) = \frac{1}{4}$
(b) Probability that the second card picked up is a queen:
Let E$_{2b}$ be the event that the second card drawn is a queen, given that the queen was drawn first and put aside.
Since the queen was drawn in the first step and put aside, there are no queens left in the remaining 4 cards.
The number of favorable outcomes for E$_{2b}$ is 0.
The probability of drawing a queen as the second card is:
$P(\text{Queen in second draw}) = \frac{\text{Number of favorable outcomes}}{\text{Total number of remaining outcomes}}$
$P(\text{Queen in second draw}) = \frac{0}{4}$
$P(\text{Queen in second draw}) = 0$
Question 16. 12 defective pens are accidentally mixed with 132 good ones. It is not possible to just look at a pen and tell whether or not it is defective. One pen is taken out at random from this lot. Determine the probability that the pen taken out is a good one.
Answer:
Given:
Number of defective pens = 12.
Number of good pens = 132.
To Find:
The probability that the pen taken out at random is a good one.
Solution:
The total number of pens in the lot is the sum of the good pens and the defective pens.
Total number of pens = Number of good pens + Number of defective pens
Total number of pens $= 132 + 12 = 144$.
When one pen is taken out at random, the total number of possible outcomes is 144.
Total number of possible outcomes = 144.
Let G be the event that the pen taken out is a good one.
The number of favorable outcomes for event G is the number of good pens in the lot.
Number of favorable outcomes for G = 132.
The probability of an event E is given by the formula:
$P(E) = \frac{\text{Number of favorable outcomes}}{\text{Total number of possible outcomes}}$
The probability of taking out a good pen is:
$P(\text{good pen}) = \frac{\text{Number of good pens}}{\text{Total number of pens}}$
$P(\text{good pen}) = \frac{132}{144}$
Simplifying the fraction $\frac{132}{144}$:
Both 132 and 144 are divisible by 12.
$132 = 12 \times 11$
$144 = 12 \times 12$
$P(\text{good pen}) = \frac{\cancel{132}^{11}}{\cancel{144}_{12}} = \frac{11}{12}$
Therefore, the probability that the pen taken out is a good one is $\frac{11}{12}$.
Question 17. (i) A lot of 20 bulbs contain 4 defective ones. One bulb is drawn at random from the lot. What is the probability that this bulb is defective?
(ii) Suppose the bulb drawn in (i) is not defective and is not replaced. Now one bulb is drawn at random from the rest. What is the probability that this bulb is not defective ?
Answer:
Given:
Total number of bulbs in the lot = 20.
Number of defective bulbs = 4.
Number of good (not defective) bulbs = Total bulbs - Number of defective bulbs $= 20 - 4 = 16$.
(i) Probability that the bulb drawn is defective:
To Find:
The probability that the bulb drawn at random is defective.
Solution:
One bulb is drawn at random from the lot of 20 bulbs.
The total number of possible outcomes is 20.
Total number of possible outcomes (first draw) = 20.
Let D be the event that the bulb drawn is defective.
The number of favorable outcomes for event D is the number of defective bulbs.
Number of favorable outcomes for D = 4.
The probability of drawing a defective bulb is:
$P(D) = \frac{\text{Number of favorable outcomes for D}}{\text{Total number of possible outcomes}}$
$P(\text{Defective}) = \frac{4}{20}$
Simplifying the fraction by cancelling the common factor 4:
$P(\text{Defective}) = \frac{\cancel{4}^{1}}{\cancel{20}_{5}} = \frac{1}{5}$
(ii) Probability that the second bulb drawn is not defective (given the first was not defective and not replaced):
Given:
The bulb drawn in (i) was not defective and is not replaced.
To Find:
The probability that the second bulb drawn at random from the remaining bulbs is not defective.
Solution:
After drawing one not defective bulb and not replacing it, the number of bulbs in the lot changes.
Original total bulbs = 20.
One not defective bulb is removed.
Number of remaining bulbs = $20 - 1 = 19$.
Original number of good bulbs = 16.
One good bulb is removed.
Number of remaining good bulbs = $16 - 1 = 15$.
The number of defective bulbs remains the same = 4.
Now, one bulb is drawn at random from the remaining 19 bulbs.
The total number of possible outcomes for the second draw is 19.
Total number of possible outcomes (second draw) = 19.
Let G' be the event that the second bulb drawn is not defective.
The number of favorable outcomes for event G' is the number of remaining not defective (good) bulbs.
Number of favorable outcomes for G' = 15.
The probability of drawing a not defective bulb in the second draw is:
$P(\text{not defective in second draw}) = \frac{\text{Number of remaining not defective bulbs}}{\text{Total number of remaining bulbs}}$
$P(\text{not defective in second draw}) = \frac{15}{19}$
Therefore, the probability that the second bulb drawn is not defective is $\frac{15}{19}$.
Question 18. A box contains 90 discs which are numbered from 1 to 90. If one disc is drawn at random from the box, find the probability that it bears
(i) a two-digit number
(ii) a perfect square number
(iii) a number divisible by 5.
Answer:
Given:
A box contains 90 discs numbered from 1 to 90.
One disc is drawn at random.
To Find:
The probability that the disc drawn bears:
(i) a two-digit number.
(ii) a perfect square number.
(iii) a number divisible by 5.
Solution:
The numbers on the discs are 1, 2, 3, ..., 90.
The total number of possible outcomes when drawing one disc is 90.
Total number of possible outcomes = 90.
(i) Probability of getting a two-digit number:
The numbers from 1 to 9 are one-digit numbers.
Number of one-digit numbers = 9.
The two-digit numbers are from 10 to 90.
Number of two-digit numbers = Total numbers - Number of one-digit numbers
Number of two-digit numbers $= 90 - 9 = 81$.
The number of favorable outcomes is 81.
The probability of getting a two-digit number is:
$P(\text{two-digit number}) = \frac{\text{Number of two-digit numbers}}{\text{Total number of discs}}$
$P(\text{two-digit number}) = \frac{81}{90}$
Simplifying the fraction by cancelling the common factor 9:
$P(\text{two-digit number}) = \frac{\cancel{81}^{9}}{\cancel{90}_{10}} = \frac{9}{10}$
(ii) Probability of getting a perfect square number:
The perfect squares between 1 and 90 (inclusive) are the squares of integers whose squares are less than or equal to 90.
These are: $1^2=1$, $2^2=4$, $3^2=9$, $4^2=16$, $5^2=25$, $6^2=36$, $7^2=49$, $8^2=64$, $9^2=81$.
The next integer square is $10^2=100$, which is greater than 90.
The perfect square numbers are $\{1, 4, 9, 16, 25, 36, 49, 64, 81\}$.
The number of favorable outcomes is 9.
The probability of getting a perfect square number is:
$P(\text{perfect square number}) = \frac{\text{Number of perfect square numbers}}{\text{Total number of discs}}$
$P(\text{perfect square number}) = \frac{9}{90}$
Simplifying the fraction by cancelling the common factor 9:
$P(\text{perfect square number}) = \frac{\cancel{9}^{1}}{\cancel{90}_{10}} = \frac{1}{10}$
(iii) Probability of getting a number divisible by 5:
The numbers divisible by 5 between 1 and 90 are 5, 10, 15, ..., 90.
These numbers are of the form $5 \times k$, where $k$ is an integer.
For $5 \times k \le 90$, we have $k \le \frac{90}{5}$, so $k \le 18$.
Since the smallest number is 5 ($5 \times 1$), $k$ ranges from 1 to 18.
The numbers divisible by 5 are $\{5 \times 1, 5 \times 2, ..., 5 \times 18\}$.
The number of favorable outcomes is 18.
The probability of getting a number divisible by 5 is:
$P(\text{number divisible by 5}) = \frac{\text{Number of numbers divisible by 5}}{\text{Total number of discs}}$
$P(\text{number divisible by 5}) = \frac{18}{90}$
Simplifying the fraction by cancelling the common factor 18:
$P(\text{number divisible by 5}) = \frac{\cancel{18}^{1}}{\cancel{90}_{5}} = \frac{1}{5}$
Question 19. A child has a die whose six faces show the letters as given below:

The die is thrown once. What is the probability of getting
(i) A?
(ii) D?
Answer:
Given:
A die with six faces showing the letters A, B, C, D, E, A.
The die is thrown once.
To Find:
(i) The probability of getting the letter A.
(ii) The probability of getting the letter D.
Solution:
The possible outcomes when the die is thrown once are the letters on its six faces: A, B, C, D, E, A.
The total number of possible outcomes is 6.
Total number of possible outcomes = 6.
(i) Probability of getting A:
Let E$_1$ be the event of getting the letter A.
From the faces (A, B, C, D, E, A), the letter A appears on 2 faces.
The number of favorable outcomes for E$_1$ is 2.
The probability of getting A is:
$P(\text{A}) = \frac{\text{Number of favorable outcomes for A}}{\text{Total number of possible outcomes}}$
$P(\text{A}) = \frac{2}{6}$
Simplifying the fraction:
$P(\text{A}) = \frac{1}{3}$
(ii) Probability of getting D:
Let E$_2$ be the event of getting the letter D.
From the faces (A, B, C, D, E, A), the letter D appears on 1 face.
The number of favorable outcomes for E$_2$ is 1.
The probability of getting D is:
$P(\text{D}) = \frac{\text{Number of favorable outcomes for D}}{\text{Total number of possible outcomes}}$
$P(\text{D}) = \frac{1}{6}$
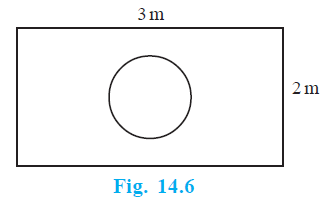
Question 20. Suppose you drop a die at random on the rectangular region shown in Fig. 14.6. What is the probability that it will land inside the circle with diameter 1m?
Answer:
Given:
A rectangular region with dimensions length = 3 m and width = 2 m.
A circle within the rectangle with diameter = 1 m.
A die is dropped at random on the rectangular region.
To Find:
The probability that the die will land inside the circle.
Solution:
In geometric probability problems, the probability is calculated as the ratio of the favorable area to the total area.
The total area where the die can land is the area of the rectangular region.
Area of rectangular region = Length $\times$ Width
Area of rectangular region $= 3 \text{ m} \times 2 \text{ m} = 6 \text{ m}^2$.
The favorable area where the die lands inside the circle is the area of the circle.
The diameter of the circle is 1 m.
The radius of the circle is $r = \frac{\text{Diameter}}{2} = \frac{1}{2} \text{ m} = 0.5 \text{ m}$.
Area of circle $= \pi r^2$
Area of circle $= \pi (0.5)^2 \text{ m}^2 = \pi (0.25) \text{ m}^2 = 0.25 \pi \text{ m}^2$.
The probability that the die lands inside the circle is:
$P(\text{landing inside the circle}) = \frac{\text{Area of circle}}{\text{Area of rectangular region}}$
$P(\text{landing inside the circle}) = \frac{0.25 \pi \text{ m}^2}{6 \text{ m}^2}$
$P(\text{landing inside the circle}) = \frac{0.25 \pi}{6}$
$P(\text{landing inside the circle}) = \frac{\frac{1}{4} \pi}{6} = \frac{\pi}{4 \times 6} = \frac{\pi}{24}$
Therefore, the probability that the die will land inside the circle is $\frac{\pi}{24}$.
Question 21. A lot consists of 144 ball pens of which 20 are defective and the others are good. Nuri will buy a pen if it is good, but will not buy if it is defective. The shopkeeper draws one pen at random and gives it to her. What is the probability that
(i) She will buy it ?
(ii) She will not buy it ?
Answer:
Given:
Total number of ball pens = 144.
Number of defective pens = 20.
Number of good pens = Total pens - Number of defective pens $= 144 - 20 = 124$.
Nuri buys a pen if it is good and does not buy it if it is defective.
To Find:
(i) The probability that Nuri will buy the pen.
(ii) The probability that Nuri will not buy the pen.
Solution:
The shopkeeper draws one pen at random from the lot of 144 pens.
The total number of possible outcomes is 144.
Total number of possible outcomes = 144.
(i) Probability that she will buy it:
Nuri will buy the pen if it is good.
Let B be the event that Nuri buys the pen.
The number of favorable outcomes for event B is the number of good pens.
Number of favorable outcomes for B = 124.
The probability that she will buy the pen is:
$P(\text{She will buy it}) = \frac{\text{Number of good pens}}{\text{Total number of pens}}$
$P(\text{She will buy it}) = \frac{124}{144}$
Simplifying the fraction by cancelling the common factor 4:
$P(\text{She will buy it}) = \frac{\cancel{124}^{31}}{\cancel{144}_{36}} = \frac{31}{36}$
(ii) Probability that she will not buy it:
Nuri will not buy the pen if it is defective.
Let NB be the event that Nuri will not buy the pen.
The number of favorable outcomes for event NB is the number of defective pens.
Number of favorable outcomes for NB = 20.
The probability that she will not buy the pen is:
$P(\text{She will not buy it}) = \frac{\text{Number of defective pens}}{\text{Total number of pens}}$
$P(\text{She will not buy it}) = \frac{20}{144}$
Simplifying the fraction by cancelling the common factor 4:
$P(\text{She will not buy it}) = \frac{\cancel{20}^{5}}{\cancel{144}_{36}} = \frac{5}{36}$
Alternate Solution for (ii) using the Complement:
The event "she will not buy it" is the complement of the event "she will buy it".
$P(\text{She will not buy it}) = 1 - P(\text{She will buy it})$
From part (i), we found $P(\text{She will buy it}) = \frac{31}{36}$.
So, $P(\text{She will not buy it}) = 1 - \frac{31}{36}$
$P(\text{She will not buy it}) = \frac{36}{36} - \frac{31}{36} = \frac{36 - 31}{36} = \frac{5}{36}$
Both methods yield the same result.
Question 22. Refer to Example 13.
(i) Complete the following table:
| Event : ‘Sum on 2 dice’ | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Probability | $\frac{1}{36}$ | $\frac{5}{36}$ | $\frac{1}{36}$ |
(ii) A student argues that ‘there are 11 possible outcomes 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12. Therefore, each of them has a probability $\frac{1}{11}$ Do you agree with this argument? Justify your answer.
Answer:
Given:
Two dice (one blue and one grey) are thrown at the same time. The possible outcomes from a single die are 1, 2, 3, 4, 5, 6.
Solution for (i):
When two distinct dice are thrown, the total number of possible outcomes is $6 \times 6 = 36$. These 36 outcomes are equally likely pairs (blue die result, grey die result), as listed in Example 13.
To complete the table, we need to find the number of pairs that sum up to each value from 2 to 12 and then calculate the probability by dividing by the total number of outcomes (36).
- Sum = 2: (1,1) - 1 outcome
- Sum = 3: (1,2), (2,1) - 2 outcomes
- Sum = 4: (1,3), (2,2), (3,1) - 3 outcomes
- Sum = 5: (1,4), (2,3), (3,2), (4,1) - 4 outcomes
- Sum = 6: (1,5), (2,4), (3,3), (4,2), (5,1) - 5 outcomes
- Sum = 7: (1,6), (2,5), (3,4), (4,3), (5,2), (6,1) - 6 outcomes
- Sum = 8: (2,6), (3,5), (4,4), (5,3), (6,2) - 5 outcomes
- Sum = 9: (3,6), (4,5), (5,4), (6,3) - 4 outcomes
- Sum = 10: (4,6), (5,5), (6,4) - 3 outcomes
- Sum = 11: (5,6), (6,5) - 2 outcomes
- Sum = 12: (6,6) - 1 outcome
The probabilities are calculated as $\frac{\text{Number of favorable outcomes}}{\text{Total number of outcomes}} = \frac{\text{Number of pairs for the sum}}{36}$.
Completed Table:
| Event : ‘Sum on 2 dice’ | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Probability | $\frac{1}{36}$ | $\frac{2}{36}$ | $\frac{3}{36}$ | $\frac{4}{36}$ | $\frac{5}{36}$ | $\frac{6}{36}$ | $\frac{5}{36}$ | $\frac{4}{36}$ | $\frac{3}{36}$ | $\frac{2}{36}$ | $\frac{1}{36}$ |
Solution for (ii):
No, I do not agree with the student's argument.
Justification:
The student's argument is based on the assumption that each of the 11 possible sum values (2, 3, ..., 12) is an equally likely outcome. However, this assumption is incorrect.
The elementary equally likely outcomes when throwing two distinct dice are the 36 ordered pairs of numbers that can appear on the faces of the two dice (from (1,1) to (6,6)). Each of these 36 pairs has a probability of $\frac{1}{36}$ of occurring.
A specific sum value is obtained from different numbers of these equally likely elementary outcomes. For example:
- The sum 2 can only be obtained in 1 way: (1,1).
- The sum 7 can be obtained in 6 ways: (1,6), (2,5), (3,4), (4,3), (5,2), (6,1).
Since the number of ways to obtain each sum is different (e.g., 1 way for sum 2, 6 ways for sum 7), the probabilities of these sums are not equal. The probability of a sum is calculated by dividing the number of ways to get that sum by the total number of equally likely elementary outcomes (36).
As shown in the table in part (i), the probabilities for the different sums are: $\frac{1}{36}, \frac{2}{36}, \frac{3}{36}, \frac{4}{36}, \frac{5}{36}, \frac{6}{36}, \frac{5}{36}, \frac{4}{36}, \frac{3}{36}, \frac{2}{36}, \frac{1}{36}$, which are clearly not all equal to $\frac{1}{11}$.
Question 23. A game consists of tossing a one rupee coin 3 times and noting its outcome each time. Hanif wins if all the tosses give the same result i.e., three heads or three tails, and loses otherwise. Calculate the probability that Hanif will lose the game.
Answer:
Given:
A game consists of tossing a one rupee coin 3 times.
Hanif wins if the outcome is three heads (HHH) or three tails (TTT).
Hanif loses for all other outcomes.
To Find:
The probability that Hanif will lose the game.
Solution:
When a coin is tossed 3 times, the possible outcomes for each toss are Head (H) or Tail (T).
The set of all possible outcomes for tossing the coin 3 times (the sample space) is:
S = $\{HHH, HHT, HTH, THH, HTT, THT, TTH, TTT\}$.
The total number of possible outcomes is 8.
Total number of possible outcomes = 8.
Let W be the event that Hanif wins the game.
Hanif wins if he gets three heads or three tails. The favorable outcomes for event W are $\{HHH, TTT\}$.
The number of favorable outcomes for W is 2.
The probability that Hanif wins is:
$P(W) = \frac{\text{Number of favorable outcomes for W}}{\text{Total number of possible outcomes}}$
$P(\text{Win}) = \frac{2}{8} = \frac{1}{4}$
Let L be the event that Hanif loses the game.
Hanif loses if the outcome is not three heads and not three tails. The outcomes where Hanif loses are $\{HHT, HTH, THH, HTT, THT, TTH\}$.
The number of favorable outcomes for L is 6.
The probability that Hanif loses is:
$P(L) = \frac{\text{Number of favorable outcomes for L}}{\text{Total number of possible outcomes}}$
$P(\text{Lose}) = \frac{6}{8} = \frac{3}{4}$
Alternate Solution using the Complement:
The event that Hanif loses is the complement of the event that Hanif wins.
$P(\text{Lose}) = 1 - P(\text{Win})$
From our calculation above, $P(\text{Win}) = \frac{1}{4}$.
So, $P(\text{Lose}) = 1 - \frac{1}{4}$
$P(\text{Lose}) = \frac{4}{4} - \frac{1}{4} = \frac{3}{4}$
Both methods yield the same result.
Therefore, the probability that Hanif will lose the game is $\frac{3}{4}$.
Question 24. A die is thrown twice. What is the probability that
(i) 5 will not come up either time?
(ii) 5 will come up at least once?
[Hint: Throwing a die twice and throwing two dice simultaneously are treated as the same experiment]
Answer:
Given:
A die is thrown twice (or two dice are thrown simultaneously).
To Find:
(i) The probability that 5 will not come up either time.
(ii) The probability that 5 will come up at least once.
Solution:
When a die is thrown twice, the possible outcomes are ordered pairs $(x, y)$, where $x$ is the result of the first throw and $y$ is the result of the second throw, with $x, y \in \{1, 2, 3, 4, 5, 6\}$.
The total number of possible outcomes is the number of outcomes for the first throw multiplied by the number of outcomes for the second throw.
Total number of possible outcomes = $6 \times 6 = 36$.
(i) Probability that 5 will not come up either time:
Let E$_1$ be the event that 5 will not come up on either throw.
This means the outcome of the first throw is not 5 (i.e., 1, 2, 3, 4, or 6), AND the outcome of the second throw is not 5 (i.e., 1, 2, 3, 4, or 6).
Number of outcomes for the first throw (not 5) = 5.
Number of outcomes for the second throw (not 5) = 5.
The number of favorable outcomes for E$_1$ is the number of pairs $(x, y)$ where $x \in \{1, 2, 3, 4, 6\}$ and $y \in \{1, 2, 3, 4, 6\}$.
Number of favorable outcomes for E$_1$ = $5 \times 5 = 25$.
The probability of event E$_1$ is:
$P(\text{5 will not come up either time}) = \frac{\text{Number of favorable outcomes for } E_1}{\text{Total number of possible outcomes}}$
$P(\text{5 will not come up either time}) = \frac{25}{36}$
(ii) Probability that 5 will come up at least once:
Let E$_2$ be the event that 5 will come up at least once.
This means 5 comes up on the first throw, or on the second throw, or on both throws.
The outcomes where 5 comes up at least once are:
(5,1), (5,2), (5,3), (5,4), (5,5), (5,6) (5 on the first throw)
(1,5), (2,5), (3,5), (4,5), (6,5) (5 on the second throw, excluding (5,5) which is already listed)
The favorable outcomes for E$_2$ are $\{ (5,1), (5,2), (5,3), (5,4), (5,5), (5,6), (1,5), (2,5), (3,5), (4,5), (6,5) \}$.
The number of favorable outcomes for E$_2$ is 6 + 5 = 11.
The probability of event E$_2$ is:
$P(\text{5 will come up at least once}) = \frac{\text{Number of favorable outcomes for } E_2}{\text{Total number of possible outcomes}}$
$P(\text{5 will come up at least once}) = \frac{11}{36}$
Alternate Solution for (ii) using the Complement:
The event "5 will come up at least once" is the complement of the event "5 will not come up either time".
Let A be the event "5 will not come up either time" (calculated in part i).
Let A' be the event "5 will come up at least once".
The sum of the probabilities of complementary events is 1: $P(A) + P(A') = 1$.
From part (i), $P(A) = P(\text{5 will not come up either time}) = \frac{25}{36}$.
So, $P(A') = P(\text{5 will come up at least once}) = 1 - P(\text{5 will not come up either time})$
$P(\text{5 will come up at least once}) = 1 - \frac{25}{36}$
$P(\text{5 will come up at least once}) = \frac{36}{36} - \frac{25}{36}$
$P(\text{5 will come up at least once}) = \frac{36 - 25}{36} = \frac{11}{36}$
Both methods yield the same result.
Question 25. Which of the following arguments are correct and which are not correct? Give reasons for your answer.
(i) If two coins are tossed simultaneously there are three possible outcomes—two heads, two tails or one of each. Therefore, for each of these outcomes, the probability is $\frac{1}{3}$ .
(ii) If a die is thrown, there are two possible outcomes—an odd number or an even number. Therefore, the probability of getting an odd number is $\frac{1}{2}$ .
Answer:
(i) Argument: If two coins are tossed simultaneously there are three possible outcomes—two heads, two tails or one of each. Therefore, for each of these outcomes, the probability is $\frac{1}{3}$ .
This argument is not correct.
Reason:
When two coins are tossed simultaneously, the list of all possible **equally likely** outcomes (the sample space) is:
S = $\{HH, HT, TH, TT\}$.
The total number of equally likely outcomes is 4.
- The event 'two heads' corresponds to the outcome $\{HH\}$, which has 1 favorable outcome. The probability is $P(\text{two heads}) = \frac{1}{4}$.
- The event 'two tails' corresponds to the outcome $\{TT\}$, which has 1 favorable outcome. The probability is $P(\text{two tails}) = \frac{1}{4}$.
- The event 'one of each' corresponds to the outcomes $\{HT, TH\}$, which have 2 favorable outcomes. The probability is $P(\text{one of each}) = \frac{2}{4} = \frac{1}{2}$.
Since the probabilities of these outcomes are $\frac{1}{4}, \frac{1}{4}, \frac{1}{2}$, they are not equally likely. The student's argument incorrectly assumed that the listed outcomes (two heads, two tails, one of each) constitute an equally likely sample space.
(ii) Argument: If a die is thrown, there are two possible outcomes—an odd number or an even number. Therefore, the probability of getting an odd number is $\frac{1}{2}$ .
This argument is correct.
Reason:
When a standard die is thrown, the list of all possible **equally likely** outcomes (the sample space) is:
S = $\{1, 2, 3, 4, 5, 6\}$.
The total number of equally likely outcomes is 6.
- The event 'an odd number' corresponds to the outcomes $\{1, 3, 5\}$. The number of favorable outcomes is 3. The probability is $P(\text{odd number}) = \frac{3}{6} = \frac{1}{2}$.
- The event 'an even number' corresponds to the outcomes $\{2, 4, 6\}$. The number of favorable outcomes is 3. The probability is $P(\text{even number}) = \frac{3}{6} = \frac{1}{2}$.
In this case, the two outcomes listed by the student ('an odd number' and 'an even number') correspond to events that have an equal number of elementary outcomes (3 each) from the equally likely sample space $\{1, 2, 3, 4, 5, 6\}$. Thus, these two events are themselves equally likely, each with a probability of $\frac{1}{2}$.

