| Latest Maths NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Example 1 (Before Exercise 2.1) | Exercise 2.1 | Example 2 to 5 (Before Exercise 2.2) |
| Exercise 2.2 | ||
Chapter 2 Polynomials
Welcome to the solutions guide for Chapter 2, "Polynomials," from the latest Class 10 NCERT mathematics textbook prescribed for the academic session 2024-25. This chapter delves deeper into the study of polynomials, building upon the foundations laid in Class 9. It focuses particularly on quadratic polynomials, exploring the crucial relationship between their zeros and coefficients, and interpreting their graphical representations. Understanding these concepts is fundamental for advanced algebra, calculus, and various applications. These solutions provide detailed walkthroughs and clear explanations for all exercises within the current syllabus, ensuring a solid grasp of the core ideas.
A key aspect explored in this chapter is the geometrical meaning of the zeros of a polynomial. The solutions help interpret the graphs of polynomials, specifically linear and quadratic ones. Students will learn to identify the number of zeros of a polynomial by observing the points where its graph intersects the x-axis. For instance, the graph of a quadratic polynomial (a parabola) can intersect the x-axis at two distinct points, touch it at one point, or not intersect it at all, corresponding to two distinct real zeros, one real zero (or two equal zeros), or no real zeros, respectively. The solutions clarify this visual connection between the algebraic concept of zeros and the geometric graph.
The core algebraic focus of this chapter lies in the relationship between the zeros and the coefficients of a quadratic polynomial. For a standard quadratic polynomial $ax^2 + bx + c$ (where $a \neq 0$), let its zeros be denoted by $\alpha$ and $\beta$. The solutions meticulously demonstrate how to:
- Find the zeros ($\alpha, \beta$) of a given quadratic polynomial, often using the method of factorization (splitting the middle term) learned in Class 9.
- Verify the fundamental relationships between these zeros and the coefficients:
- Sum of zeros: $\alpha + \beta = -\frac{b}{a}$ (negative of the coefficient of $x$ divided by the coefficient of $x^2$)
- Product of zeros: $\alpha \beta = \frac{c}{a}$ (the constant term divided by the coefficient of $x^2$)
- Conversely, construct a quadratic polynomial when the sum ($\alpha + \beta$) and product ($\alpha \beta$) of its zeros are provided. A common form used is $k[x^2 - (\text{sum of zeros})x + (\text{product of zeros})]$, where $k$ is any non-zero constant.
Regarding the rationalized syllabus for 2024-25, Chapter 2, "Polynomials," in the Class 10 NCERT textbook has undergone significant revision. The sections dealing with the Division Algorithm for Polynomials (including polynomial long division) and exercises based on it have been completely removed. Consequently, problems involving finding remaining zeros of cubic or biquadratic polynomials using polynomial division are no longer part of the syllabus. Furthermore, the relationship between zeros and coefficients for cubic polynomials has also been removed. The current chapter focuses exclusively on quadratic polynomials – their geometrical interpretation, finding zeros, and the relationship between zeros and coefficients. By diligently working through these focused solutions, students can master the techniques for finding zeros of quadratic polynomials, thoroughly understand the vital connection between their zeros and coefficients, interpret their graphs effectively, and build a strong foundation for related topics in mathematics.
Example 1 (Before Exercise 2.1)
Example 1. Look at the graphs in figure below. Each is the graph of y = p(x), where p(x) is a polynomial. For each of the graphs, find the number of zeroes of p(x).
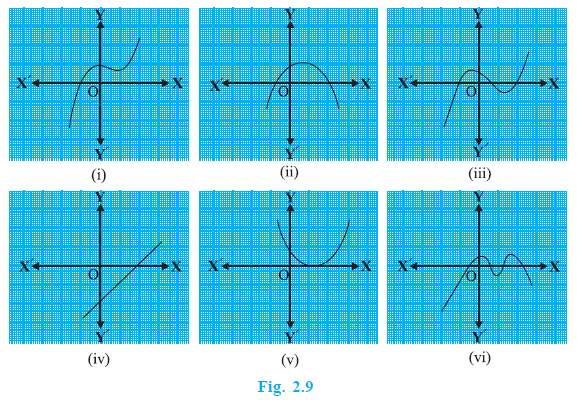
Answer:
The number of zeroes of a polynomial $p(x)$ is equal to the number of times the graph of $y = p(x)$ intersects the x-axis.
(i) In the first graph, the graph intersects the x-axis at one point.
Therefore, the number of zeroes of $p(x)$ is 1.
(ii) In the second graph, the graph intersects the x-axis at two points.
Therefore, the number of zeroes of $p(x)$ is 2.
(iii) In the third graph, the graph intersects the x-axis at three points.
Therefore, the number of zeroes of $p(x)$ is 3.
(iv) In the fourth graph, the graph intersects the x-axis at one point.
Therefore, the number of zeroes of $p(x)$ is 1.
(v) In the fifth graph, the graph intersects the x-axis at one point.
Therefore, the number of zeroes of $p(x)$ is 1.
(vi) In the sixth graph, the graph intersects the x-axis at four points.
Therefore, the number of zeroes of $p(x)$ is 4.
Exercise 2.1
Question 1. The graphs of y = p(x) are given in figure below, for some polynomials p(x). Find the number of zeroes of p(x), in each case.

Answer:
The number of zeroes of a polynomial $p(x)$ is equal to the number of times the graph of $y = p(x)$ intersects the x-axis.
(i) In the first graph, the graph does not intersect the x-axis at any point.
Therefore, the number of zeroes of $p(x)$ is 0.
(ii) In the second graph, the graph intersects the x-axis at one distinct points.
Therefore, the number of zeroes of $p(x)$ is 1.
(iii) In the third graph, the graph intersects the x-axis at three distinct points.
Therefore, the number of zeroes of $p(x)$ is 3.
(iv) In the fourth graph, the graph intersects the x-axis at two point.
Therefore, the number of zeroes of $p(x)$ is 2.
(v) In the fifth graph, the graph intersects the x-axis at four point.
Therefore, the number of zeroes of $p(x)$ is 4.
(vi) In the sixth graph, the graph intersects the x-axis at three distinct points.
Therefore, the number of zeroes of $p(x)$ is 3.
Example 2 to 5 (Before Exercise 2.2)
Example 2. Find the zeroes of the quadratic polynomial x2 + 7x + 10, and verify the relationship between the zeroes and the coefficients.
Answer:
Given:
The quadratic polynomial is $p(x) = x^2 + 7x + 10$.
To Find:
The zeroes of the polynomial and verify the relationship between the zeroes and the coefficients.
Solution:
To find the zeroes of the polynomial, we need to find the values of $x$ for which $p(x) = 0$.
$x^2 + 7x + 10 = 0$
We can factor the quadratic expression by splitting the middle term. We look for two numbers that multiply to 10 and add up to 7. These numbers are 2 and 5.
$x^2 + 2x + 5x + 10 = 0$
Group the terms and factor:
$(x^2 + 2x) + (5x + 10) = 0$
$x(x + 2) + 5(x + 2) = 0$
Factor out the common binomial $(x + 2)$:
$(x + 2)(x + 5) = 0$
To find the zeroes, set each factor equal to zero:
$x + 2 = 0 \quad$ or $\quad x + 5 = 0$
$x = -2 \quad$ or $\quad x = -5$
The zeroes of the polynomial $x^2 + 7x + 10$ are $-2$ and $-5$.
Verification of the relationship between zeroes and coefficients:
Let the zeroes be $\alpha = -2$ and $\beta = -5$.
The given quadratic polynomial is $x^2 + 7x + 10$. Comparing this with the standard form $ax^2 + bx + c$, we have:
$a = 1$
$b = 7$
$c = 10$
Relationship between zeroes and coefficients:
1. Sum of zeroes: $\alpha + \beta = \frac{-b}{a}$
Left Hand Side (LHS): $\alpha + \beta = (-2) + (-5) = -7$
Right Hand Side (RHS): $\frac{-b}{a} = \frac{-(7)}{1} = -7$
$-7 = -7$
... (i)
The sum of zeroes is verified.
2. Product of zeroes: $\alpha \times \beta = \frac{c}{a}$
Left Hand Side (LHS): $\alpha \times \beta = (-2) \times (-5) = 10$
Right Hand Side (RHS): $\frac{c}{a} = \frac{10}{1} = 10$
$10 = 10$
... (ii)
The product of zeroes is verified.
Since both relationships are satisfied, the verification is complete.
Example 3. Find the zeroes of the polynomial x2 – 3 and verify the relationship between the zeroes and the coefficients.
Answer:
Given:
The quadratic polynomial is $p(x) = x^2 - 3$.
To Find:
The zeroes of the polynomial and verify the relationship between the zeroes and the coefficients.
Solution:
To find the zeroes of the polynomial, we need to find the values of $x$ for which $p(x) = 0$.
$x^2 - 3 = 0$
Add 3 to both sides:
$x^2 = 3$
Take the square root of both sides:
$x = \pm\sqrt{3}$
The zeroes of the polynomial $x^2 - 3$ are $\sqrt{3}$ and $-\sqrt{3}$.
Verification of the relationship between zeroes and coefficients:
Let the zeroes be $\alpha = \sqrt{3}$ and $\beta = -\sqrt{3}$.
The given quadratic polynomial is $x^2 - 3$. We can write it in the standard form $ax^2 + bx + c$ as $x^2 + 0x - 3$. Comparing, we have:
$a = 1$
$b = 0$
$c = -3$
Relationship between zeroes and coefficients:
1. Sum of zeroes: $\alpha + \beta = \frac{-b}{a}$
Left Hand Side (LHS): $\alpha + \beta = \sqrt{3} + (-\sqrt{3}) = 0$
Right Hand Side (RHS): $\frac{-b}{a} = \frac{-(0)}{1} = 0$
$0 = 0$
... (i)
The sum of zeroes is verified.
2. Product of zeroes: $\alpha \times \beta = \frac{c}{a}$
Left Hand Side (LHS): $\alpha \times \beta = (\sqrt{3}) \times (-\sqrt{3}) = -(\sqrt{3})^2 = -3$
Right Hand Side (RHS): $\frac{c}{a} = \frac{(-3)}{1} = -3$
$-3 = -3$
... (ii)
The product of zeroes is verified.
Since both relationships are satisfied, the verification is complete.
Example 4. Find a quadratic polynomial, the sum and product of whose zeroes are – 3 and 2, respectively.
Answer:
Given:
Sum of the zeroes = $-3$
Product of the zeroes = $2$
To Find:
A quadratic polynomial whose sum and product of zeroes are given.
Solution:
A quadratic polynomial with sum of zeroes $\alpha + \beta$ and product of zeroes $\alpha \times \beta$ can be written in the form:
$p(x) = k(x^2 - (\text{Sum of zeroes})x + (\text{Product of zeroes}))$
where $k$ is any non-zero real number.
Substitute the given values for the sum and product of zeroes:
$p(x) = k(x^2 - (-3)x + (2))$
Simplify the expression:
$p(x) = k(x^2 + 3x + 2)$
For simplicity, we can take $k = 1$.
So, a quadratic polynomial is $x^2 + 3x + 2$.
Answer:
A quadratic polynomial is $x^2 + 3x + 2$.
Example 5. Verify that 3, –1, $-\frac{1}{3}$ are the zeroes of the cubic polynomial p(x) = 3x3 – 5x2 – 11x – 3, and then verify the relationship between the zeroes and the coefficients.
Answer:
Given:
The cubic polynomial $p(x) = 3x^3 - 5x^2 - 11x - 3$.
The given potential zeroes are $3$, $-1$, and $-\frac{1}{3}$.
To Verify:
1. That $3$, $-1$, and $-\frac{1}{3}$ are the zeroes of $p(x)$.
2. The relationship between the zeroes and the coefficients of $p(x)$.
Solution:
Verification of Zeroes:
A number $k$ is a zero of a polynomial $p(x)$ if $p(k) = 0$. We substitute the given values into the polynomial $p(x)$.
For $x = 3$:
$p(3) = 3(3)^3 - 5(3)^2 - 11(3) - 3$
$p(3) = 3(27) - 5(9) - 33 - 3$
$p(3) = 81 - 45 - 33 - 3$
$p(3) = 81 - (45 + 33 + 3)$
$p(3) = 81 - 81$
$p(3) = 0$
... (1)
Since $p(3)=0$, $3$ is a zero of the polynomial $p(x)$.
For $x = -1$:
$p(-1) = 3(-1)^3 - 5(-1)^2 - 11(-1) - 3$
$p(-1) = 3(-1) - 5(1) - (-11) - 3$
$p(-1) = -3 - 5 + 11 - 3$
$p(-1) = (-3 - 5 - 3) + 11$
$p(-1) = -11 + 11$
$p(-1) = 0$
... (2)
Since $p(-1)=0$, $-1$ is a zero of the polynomial $p(x)$.
For $x = -\frac{1}{3}$:
$p(-\frac{1}{3}) = 3(-\frac{1}{3})^3 - 5(-\frac{1}{3})^2 - 11(-\frac{1}{3}) - 3$
$p(-\frac{1}{3}) = 3(-\frac{1}{27}) - 5(\frac{1}{9}) + \frac{11}{3} - 3$
$p(-\frac{1}{3}) = -\frac{3}{27} - \frac{5}{9} + \frac{11}{3} - 3$
$p(-\frac{1}{3}) = -\frac{1}{9} - \frac{5}{9} + \frac{11}{3} - 3$
$p(-\frac{1}{3}) = \frac{-1}{9} - \frac{5}{9} + \frac{11 \times 3}{3 \times 3} - \frac{3 \times 9}{1 \times 9}$
$p(-\frac{1}{3}) = \frac{-1 - 5}{9} + \frac{33}{9} - \frac{27}{9}$
$p(-\frac{1}{3}) = \frac{-6 + 33 - 27}{9}$
$p(-\frac{1}{3}) = \frac{27 - 27}{9} = \frac{0}{9}$
$p(-\frac{1}{3}) = 0$
... (3)
Since $p(-\frac{1}{3})=0$, $-\frac{1}{3}$ is a zero of the polynomial $p(x)$.
Thus, we have verified that $3$, $-1$, and $-\frac{1}{3}$ are the zeroes of the cubic polynomial $p(x) = 3x^3 - 5x^2 - 11x - 3$.
Verification of the relationship between zeroes and coefficients:
Let the zeroes be $\alpha = 3$, $\beta = -1$, and $\gamma = -\frac{1}{3}$.
The given cubic polynomial is $p(x) = 3x^3 - 5x^2 - 11x - 3$.
Comparing this polynomial with the standard form of a cubic polynomial, $ax^3 + bx^2 + cx + d$, we identify the coefficients:
$a = 3$
... (4)
$b = -5$
... (5)
$c = -11$
... (6)
$d = -3$
... (7)
The relationships between the zeroes ($\alpha, \beta, \gamma$) and the coefficients ($a, b, c, d$) of a cubic polynomial are given by:
1. Sum of zeroes: $\alpha + \beta + \gamma = -\frac{b}{a}$
2. Sum of the products of zeroes taken two at a time: $\alpha\beta + \beta\gamma + \gamma\alpha = \frac{c}{a}$
3. Product of zeroes: $\alpha\beta\gamma = -\frac{d}{a}$
Let's verify these relationships using the given zeroes and the coefficients we found.
Relationship 1: Sum of zeroes
LHS: $\alpha + \beta + \gamma = 3 + (-1) + (-\frac{1}{3})$
$\alpha + \beta + \gamma = 3 - 1 - \frac{1}{3}$
$\alpha + \beta + \gamma = 2 - \frac{1}{3}$
$\alpha + \beta + \gamma = \frac{6 - 1}{3} = \frac{5}{3}$
... (8)
RHS: $-\frac{b}{a}$
Using values from (5) and (4):
$-\frac{b}{a} = -\frac{-5}{3} = \frac{5}{3}$
... (9)
From (8) and (9), we see that LHS = RHS. The first relationship is verified.
Relationship 2: Sum of the products of zeroes taken two at a time
LHS: $\alpha\beta + \beta\gamma + \gamma\alpha = (3)(-1) + (-1)(-\frac{1}{3}) + (-\frac{1}{3})(3)$
$\alpha\beta + \beta\gamma + \gamma\alpha = -3 + \frac{1}{3} - \frac{3}{3}$
$\alpha\beta + \beta\gamma + \gamma\alpha = -3 + \frac{1}{3} - 1$
$\alpha\beta + \beta\gamma + \gamma\alpha = -4 + \frac{1}{3}$
$\alpha\beta + \beta\gamma + \gamma\alpha = \frac{-12 + 1}{3} = -\frac{11}{3}$
... (10)
RHS: $\frac{c}{a}$
Using values from (6) and (4):
$\frac{c}{a} = \frac{-11}{3}$
... (11)
From (10) and (11), we see that LHS = RHS. The second relationship is verified.
Relationship 3: Product of zeroes
LHS: $\alpha\beta\gamma = (3)(-1)(-\frac{1}{3})$
$\alpha\beta\gamma = (-3)(-\frac{1}{3})$
$\alpha\beta\gamma = \frac{3}{3} = 1$
... (12)
RHS: $-\frac{d}{a}$
Using values from (7) and (4):
$-\frac{d}{a} = -\frac{-3}{3} = -(-1) = 1$
... (13)
From (12) and (13), we see that LHS = RHS. The third relationship is verified.
All the relationships between the zeroes and the coefficients of the polynomial have been verified.
Exercise 2.2
Question 1. Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients.
(i) x2 – 2x – 8
(ii) 4s2 – 4s + 1
(iii) 6x2 – 3 – 7x
(iv) 4u2 + 8u
(v) t2 – 15
(vi) 3x2 – x – 4
Answer:
Solution (i): x² – 2x – 8
Given:
The quadratic polynomial $p(x) = x^2 - 2x - 8$.
To Find:
1. The zeroes of the polynomial.
2. Verify the relationship between the zeroes and the coefficients.
Solution:
To find the zeroes, we set the polynomial equal to zero:
$x^2 - 2x - 8 = 0$
We factorize the quadratic expression:
$x^2 - 4x + 2x - 8 = 0$
$x(x - 4) + 2(x - 4) = 0$
$(x - 4)(x + 2) = 0$
Setting each factor to zero gives the zeroes:
$x - 4 = 0 \implies x = 4$
$x + 2 = 0 \implies x = -2$
So, the zeroes of the polynomial $x^2 - 2x - 8$ are $4$ and $-2$.
Let $\alpha = 4$ and $\beta = -2$.
Now, we identify the coefficients of the polynomial $x^2 - 2x - 8$. Comparing it with the standard form $ax^2 + bx + c$, we have:
$a = 1$
... (1)
$b = -2$
... (2)
$c = -8$
... (3)
Verification of Relationship:
1. Sum of zeroes ($\alpha + \beta$):
LHS: $\alpha + \beta = 4 + (-2) = 4 - 2 = 2$
RHS: $-\frac{b}{a} = -\frac{-2}{1} = \frac{2}{1} = 2$
LHS = RHS. The sum of zeroes is verified.
2. Product of zeroes ($\alpha \beta$):
LHS: $\alpha \beta = (4)(-2) = -8$
RHS: $\frac{c}{a} = \frac{-8}{1} = -8$
LHS = RHS. The product of zeroes is verified.
Solution (ii): 4s² – 4s + 1
Given:
The quadratic polynomial $p(s) = 4s^2 - 4s + 1$.
To Find:
1. The zeroes of the polynomial.
2. Verify the relationship between the zeroes and the coefficients.
Solution:
To find the zeroes, we set the polynomial equal to zero:
$4s^2 - 4s + 1 = 0$
We factorize the quadratic expression. This is a perfect square trinomial:
$(2s)^2 - 2(2s)(1) + (1)^2 = 0$
$(2s - 1)^2 = 0$
Taking the square root of both sides:
$2s - 1 = 0$
$2s = 1$
$s = \frac{1}{2}$
This is a repeated zero. So, the zeroes of the polynomial $4s^2 - 4s + 1$ are $\frac{1}{2}$ and $\frac{1}{2}$.
Let $\alpha = \frac{1}{2}$ and $\beta = \frac{1}{2}$.
Now, we identify the coefficients of the polynomial $4s^2 - 4s + 1$. Comparing it with the standard form $as^2 + bs + c$, we have:
$a = 4$
... (4)
$b = -4$
... (5)
$c = 1$
... (6)
Verification of Relationship:
1. Sum of zeroes ($\alpha + \beta$):
LHS: $\alpha + \beta = \frac{1}{2} + \frac{1}{2} = \frac{1+1}{2} = \frac{2}{2} = 1$
RHS: $-\frac{b}{a} = -\frac{-4}{4} = \frac{4}{4} = 1$
LHS = RHS. The sum of zeroes is verified.
2. Product of zeroes ($\alpha \beta$):
LHS: $\alpha \beta = (\frac{1}{2})(\frac{1}{2}) = \frac{1}{4}$
RHS: $\frac{c}{a} = \frac{1}{4}$
LHS = RHS. The product of zeroes is verified.
Solution (iii): 6x² – 3 – 7x
Given:
The quadratic polynomial $p(x) = 6x^2 - 3 - 7x$.
To Find:
1. The zeroes of the polynomial.
2. Verify the relationship between the zeroes and the coefficients.
Solution:
First, we write the polynomial in the standard form $ax^2 + bx + c$:
$p(x) = 6x^2 - 7x - 3$
To find the zeroes, we set the polynomial equal to zero:
$6x^2 - 7x - 3 = 0$
We factorize the quadratic expression by splitting the middle term ($(-9) \times 2 = -18$ and $-9 + 2 = -7$):
$6x^2 - 9x + 2x - 3 = 0$
$3x(2x - 3) + 1(2x - 3) = 0$
$(2x - 3)(3x + 1) = 0$
Setting each factor to zero gives the zeroes:
$2x - 3 = 0 \implies 2x = 3 \implies x = \frac{3}{2}$
$3x + 1 = 0 \implies 3x = -1 \implies x = -\frac{1}{3}$
So, the zeroes of the polynomial $6x^2 - 7x - 3$ are $\frac{3}{2}$ and $-\frac{1}{3}$.
Let $\alpha = \frac{3}{2}$ and $\beta = -\frac{1}{3}$.
Now, we identify the coefficients of the polynomial $6x^2 - 7x - 3$. Comparing it with the standard form $ax^2 + bx + c$, we have:
$a = 6$
... (7)
$b = -7$
... (8)
$c = -3$
... (9)
Verification of Relationship:
1. Sum of zeroes ($\alpha + \beta$):
LHS: $\alpha + \beta = \frac{3}{2} + (-\frac{1}{3}) = \frac{3}{2} - \frac{1}{3} = \frac{3 \times 3 - 1 \times 2}{6} = \frac{9 - 2}{6} = \frac{7}{6}$
RHS: $-\frac{b}{a} = -\frac{-7}{6} = \frac{7}{6}$
LHS = RHS. The sum of zeroes is verified.
2. Product of zeroes ($\alpha \beta$):
LHS: $\alpha \beta = (\frac{3}{2})(-\frac{1}{3}) = -\frac{3}{6} = -\frac{1}{2}$
RHS: $\frac{c}{a} = \frac{-3}{6} = -\frac{1}{2}$
LHS = RHS. The product of zeroes is verified.
Solution (iv): 4u² + 8u
Given:
The quadratic polynomial $p(u) = 4u^2 + 8u$.
To Find:
1. The zeroes of the polynomial.
2. Verify the relationship between the zeroes and the coefficients.
Solution:
To find the zeroes, we set the polynomial equal to zero:
$4u^2 + 8u = 0$
We can factor out the common term $4u$:
$4u(u + 2) = 0$
Setting each factor to zero gives the zeroes:
$4u = 0 \implies u = 0$
$u + 2 = 0 \implies u = -2$
So, the zeroes of the polynomial $4u^2 + 8u$ are $0$ and $-2$.
Let $\alpha = 0$ and $\beta = -2$.
Now, we identify the coefficients of the polynomial $4u^2 + 8u$. Comparing it with the standard form $au^2 + bu + c$, we have:
$a = 4$
... (10)
$b = 8$
... (11)
$c = 0$
... (12)
Verification of Relationship:
1. Sum of zeroes ($\alpha + \beta$):
LHS: $\alpha + \beta = 0 + (-2) = -2$
RHS: $-\frac{b}{a} = -\frac{8}{4} = -2$
LHS = RHS. The sum of zeroes is verified.
2. Product of zeroes ($\alpha \beta$):
LHS: $\alpha \beta = (0)(-2) = 0$
RHS: $\frac{c}{a} = \frac{0}{4} = 0$
LHS = RHS. The product of zeroes is verified.
Solution (v): t² – 15
Given:
The quadratic polynomial $p(t) = t^2 - 15$.
To Find:
1. The zeroes of the polynomial.
2. Verify the relationship between the zeroes and the coefficients.
Solution:
To find the zeroes, we set the polynomial equal to zero:
$t^2 - 15 = 0$
$t^2 = 15$
Taking the square root of both sides:
$t = \pm \sqrt{15}$
So, the zeroes of the polynomial $t^2 - 15$ are $\sqrt{15}$ and $-\sqrt{15}$.
Let $\alpha = \sqrt{15}$ and $\beta = -\sqrt{15}$.
Now, we identify the coefficients of the polynomial $t^2 - 15$. We can write it as $t^2 + 0t - 15$. Comparing it with the standard form $at^2 + bt + c$, we have:
$a = 1$
... (13)
$b = 0$
... (14)
$c = -15$
... (15)
Verification of Relationship:
1. Sum of zeroes ($\alpha + \beta$):
LHS: $\alpha + \beta = \sqrt{15} + (-\sqrt{15}) = \sqrt{15} - \sqrt{15} = 0$
RHS: $-\frac{b}{a} = -\frac{0}{1} = 0$
LHS = RHS. The sum of zeroes is verified.
2. Product of zeroes ($\alpha \beta$):
LHS: $\alpha \beta = (\sqrt{15})(-\sqrt{15}) = -(\sqrt{15})^2 = -15$
RHS: $\frac{c}{a} = \frac{-15}{1} = -15$
LHS = RHS. The product of zeroes is verified.
Solution (vi): 3x² – x – 4
Given:
The quadratic polynomial $p(x) = 3x^2 - x - 4$.
To Find:
1. The zeroes of the polynomial.
2. Verify the relationship between the zeroes and the coefficients.
Solution:
To find the zeroes, we set the polynomial equal to zero:
$3x^2 - x - 4 = 0$
We factorize the quadratic expression by splitting the middle term ($(-4) \times 3 = -12$ and $3 - 4 = -1$):
$3x^2 + 3x - 4x - 4 = 0$
$3x(x + 1) - 4(x + 1) = 0$
$(x + 1)(3x - 4) = 0$
Setting each factor to zero gives the zeroes:
$x + 1 = 0 \implies x = -1$
$3x - 4 = 0 \implies 3x = 4 \implies x = \frac{4}{3}$
So, the zeroes of the polynomial $3x^2 - x - 4$ are $-1$ and $\frac{4}{3}$.
Let $\alpha = -1$ and $\beta = \frac{4}{3}$.
Now, we identify the coefficients of the polynomial $3x^2 - x - 4$. Comparing it with the standard form $ax^2 + bx + c$, we have:
$a = 3$
... (16)
$b = -1$
... (17)
$c = -4$
... (18)
Verification of Relationship:
1. Sum of zeroes ($\alpha + \beta$):
LHS: $\alpha + \beta = -1 + \frac{4}{3} = \frac{-3 + 4}{3} = \frac{1}{3}$
RHS: $-\frac{b}{a} = -\frac{-1}{3} = \frac{1}{3}$
LHS = RHS. The sum of zeroes is verified.
2. Product of zeroes ($\alpha \beta$):
LHS: $\alpha \beta = (-1)(\frac{4}{3}) = -\frac{4}{3}$
RHS: $\frac{c}{a} = \frac{-4}{3}$
LHS = RHS. The product of zeroes is verified.
Question 2. Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively.
(i) $\frac{1}{4}$ , −1
(ii) $\sqrt{2}$ , $\frac{1}{3}$
(iii) 0 , $\sqrt{5}$
(iv) 1 , 1
(v) $-\frac{1}{4}$ , $\frac{1}{4}$
(vi) 4, 1
Answer:
The general form of a quadratic polynomial whose zeroes are $\alpha$ and $\beta$ is $p(x) = k(x^2 - (\alpha + \beta)x + \alpha\beta)$, where $k$ is any non-zero real number.
Given the sum of zeroes $(\alpha + \beta)$ and the product of zeroes $(\alpha\beta)$, the polynomial can be written as $p(x) = k(x^2 - (\text{Sum of Zeroes})x + (\text{Product of Zeroes}))$.
We can find one such polynomial by taking $k=1$ or a suitable value to clear denominators.
Solution (i): Sum = $\frac{1}{4}$, Product = $-1$
Given:
Sum of zeroes $= \frac{1}{4}$
Product of zeroes $= -1$
To Find:
A quadratic polynomial with the given sum and product of zeroes.
Solution:
Using the formula with $k=1$:
$p(x) = x^2 - (\frac{1}{4})x + (-1)$
$p(x) = x^2 - \frac{1}{4}x - 1$
To get a polynomial with integer coefficients, we can choose $k=4$:
$p(x) = 4(x^2 - \frac{1}{4}x - 1)$
$p(x) = 4x^2 - x - 4$
One quadratic polynomial is $\mathbf{4x^2 - x - 4}$.
Solution (ii): Sum = $\sqrt{2}$, Product = $\frac{1}{3}$
Given:
Sum of zeroes $= \sqrt{2}$
Product of zeroes $= \frac{1}{3}$
To Find:
A quadratic polynomial with the given sum and product of zeroes.
Solution:
Using the formula with $k=1$:
$p(x) = x^2 - (\sqrt{2})x + (\frac{1}{3})$
$p(x) = x^2 - \sqrt{2}x + \frac{1}{3}$
To get a polynomial with integer coefficients in the denominators, we can choose $k=3$:
$p(x) = 3(x^2 - \sqrt{2}x + \frac{1}{3})$
$p(x) = 3x^2 - 3\sqrt{2}x + 1$
One quadratic polynomial is $\mathbf{3x^2 - 3\sqrt{2}x + 1}$.
Solution (iii): Sum = $0$, Product = $\sqrt{5}$
Given:
Sum of zeroes $= 0$
Product of zeroes $= \sqrt{5}$
To Find:
A quadratic polynomial with the given sum and product of zeroes.
Solution:
Using the formula with $k=1$:
$p(x) = x^2 - (0)x + (\sqrt{5})$
$p(x) = x^2 - 0x + \sqrt{5}$
$p(x) = x^2 + \sqrt{5}$
One quadratic polynomial is $\mathbf{x^2 + \sqrt{5}}$.
Solution (iv): Sum = $1$, Product = $1$
Given:
Sum of zeroes $= 1$
Product of zeroes $= 1$
To Find:
A quadratic polynomial with the given sum and product of zeroes.
Solution:
Using the formula with $k=1$:
$p(x) = x^2 - (1)x + (1)$
$p(x) = x^2 - x + 1$
One quadratic polynomial is $\mathbf{x^2 - x + 1}$.
Solution (v): Sum = $-\frac{1}{4}$, Product = $\frac{1}{4}$
Given:
Sum of zeroes $= -\frac{1}{4}$
Product of zeroes $= \frac{1}{4}$
To Find:
A quadratic polynomial with the given sum and product of zeroes.
Solution:
Using the formula with $k=1$:
$p(x) = x^2 - (-\frac{1}{4})x + (\frac{1}{4})$
$p(x) = x^2 + \frac{1}{4}x + \frac{1}{4}$
To get a polynomial with integer coefficients, we can choose $k=4$:
$p(x) = 4(x^2 + \frac{1}{4}x + \frac{1}{4})$
$p(x) = 4x^2 + x + 1$
One quadratic polynomial is $\mathbf{4x^2 + x + 1}$.
Solution (vi): Sum = $4$, Product = $1$
Given:
Sum of zeroes $= 4$
Product of zeroes $= 1$
To Find:
A quadratic polynomial with the given sum and product of zeroes.
Solution:
Using the formula with $k=1$:
$p(x) = x^2 - (4)x + (1)$
$p(x) = x^2 - 4x + 1$
One quadratic polynomial is $\mathbf{x^2 - 4x + 1}$.

