| Latest Maths NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Exercise 6.1 | Example 1 to 3 (Before Exercise 6.2) | Exercise 6.2 |
| Example 4 to 8 (Before Exercise 6.3) | Exercise 6.3 | |
Chapter 6 Triangles
Welcome to the comprehensive solutions guide for Chapter 6, "Triangles," from the latest Class 10 NCERT mathematics textbook for the academic session 2024-25. This pivotal chapter marks a significant progression from the concept of congruence (studied in Class 9) to the broader and highly applicable concept of similarity of geometric figures, particularly triangles. While congruent figures are identical in shape and size, similar figures maintain the same shape but may differ in size, implying proportional relationships between their corresponding parts. Mastering similarity criteria and related theorems is fundamental for advanced geometry, trigonometry, and real-world applications like scaling maps or architectural drawings. These solutions offer detailed explanations, rigorous proofs, and systematic applications for all exercises within the current syllabus.
A primary focus of this chapter, meticulously addressed in the solutions, is understanding and applying the criteria for similarity of triangles. Two triangles are similar if their corresponding angles are equal and their corresponding sides are in the same ratio (proportional). The solutions demonstrate the application of the key similarity criteria:
- AA (Angle-Angle) Similarity Criterion: If two angles of one triangle are respectively equal to two angles of another triangle, then the two triangles are similar. (Often extended to AAA).
- SAS (Side-Angle-Side) Similarity Criterion: If one angle of a triangle is equal to one angle of another triangle and the sides including these angles are proportional.
- SSS (Side-Side-Side) Similarity Criterion: If in two triangles, the sides of one triangle are proportional to the sides of the other triangle.
Central to the study of similarity are two fundamental theorems related to proportionality within triangles. The solutions provide rigorous proofs and numerous applications for:
- Basic Proportionality Theorem (BPT or Thales Theorem): This theorem states that if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then the other two sides are divided in the same ratio. (e.g., If DE || BC in $\triangle ABC$, then $\frac{AD}{DB} = \frac{AE}{EC}$).
- Converse of the Basic Proportionality Theorem: This states that if a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.
Furthermore, this chapter revisits the essential Pythagoras Theorem, often providing a proof based on the concepts of similar triangles. The theorem states that in a right-angled triangle, the square of the hypotenuse ($c$) is equal to the sum of the squares of the other two sides ($a, b$): $\mathbf{a^2 + b^2 = c^2}$. The solutions also cover the Converse of the Pythagoras Theorem, which states that if the square of one side of a triangle is equal to the sum of the squares of the other two sides, then the angle opposite the first side is a right angle. Applications of both the theorem and its converse are extensively demonstrated in solving various geometric problems, especially those involving finding lengths in right triangles embedded within other shapes.
Throughout the solutions for proof-based problems, a structured, logical approach is consistently maintained, typically outlining 'Given', 'To Prove', 'Construction' (if needed), and the 'Proof' with clear justifications for each deductive step, reinforcing formal geometric reasoning.
Regarding the rationalized syllabus for 2024-25, Chapter 6, "Triangles," in the Class 10 NCERT textbook has seen a significant adjustment. The theorem regarding the ratio of the areas of two similar triangles (stating the ratio of areas is equal to the square of the ratio of corresponding sides) and all exercises based on it have been removed. The curriculum now focuses primarily on similarity criteria, BPT and its converse, and the Pythagoras theorem and its converse. By diligently using these focused solutions, students can master the concepts of similarity, learn to construct rigorous proofs, and effectively apply BPT and Pythagoras theorem to solve a wide range of geometric problems.
Exercise 6.1
Question 1. Fill in the blanks using the correct word given in brackets :
(i) All circles are ______________ (congruent, similar)
(ii) All squares are ____________. (similar, congruent)
(iii) All _______________triangles are similar. (isosceles, equilateral)
(iv) Two polygons of the same number of sides are similar, if (a) their corresponding angles are _____________________and (b) their corresponding sides are .(equal,)
Answer:
Solution:
(i) All circles are similar.
Circles can vary in size (radius) but always maintain the same fundamental shape. Corresponding angles (e.g., angles subtended by corresponding arcs at the center) are equal, and the ratio of corresponding lengths (like radii) is constant. Congruent circles must have the same radius.
(ii) All squares are similar.
Squares can vary in side length but always have four right angles ($90^\circ$) and four equal sides. Thus, corresponding angles are always equal, and corresponding sides are always in the same ratio. Congruent squares must have the same side length.
(iii) All equilateral triangles are similar.
All equilateral triangles have three equal angles, each measuring $60^\circ$. This means their corresponding angles are always equal. Also, the ratio of corresponding sides is constant. Isosceles triangles, however, can have varying apex angles and base angles, so they are not necessarily similar to each other.
(iv) Two polygons of the same number of sides are similar, if (a) their corresponding angles are equal and (b) their corresponding sides are equal.
Based on the options provided in the brackets "(equal,)" for filling the blanks in part (iv), the word "equal" is the only option available and is used for both (a) and (b).
Note: The standard geometric definition for similar polygons requires corresponding angles to be equal and corresponding sides to be proportional (in the same ratio), not necessarily equal. However, adhering strictly to the provided options, "equal" is used here for both blanks.
Question 2. Give two different examples of pair of
(i) similar figures.
(ii) non-similar figures.
Answer:
Solution:
(i) Examples of similar figures:
1. Two circles with different radii.
2. Two squares with different side lengths.
(ii) Examples of non-similar figures:
1. A triangle and a square.
2. A circle and a rectangle.
Question 3. State whether the following quadrilaterals are similar or not:

Answer:
Given:
Two quadrilaterals: a rhombus PQRS and a square ABCD.
Side lengths: PQ = QR = RS = SP = 1.5 cm.
Side lengths: AB = BC = CD = DA = 3 cm.
To Determine:
Whether the given quadrilaterals are similar or not.
Solution:
Two polygons with the same number of sides are similar if and only if both of the following conditions are satisfied:
1. Their corresponding angles are equal.
2. The ratio of their corresponding sides is the same.
Let's examine the given quadrilaterals:
Quadrilateral ABCD is a square. In a square, all interior angles are equal to $90^\circ$. So, $\angle A = \angle B = \angle C = \angle D = 90^\circ$.
Quadrilateral PQRS is a rhombus. In a rhombus that is not a square, the angles are not all $90^\circ$. From the figure, it is clear that the angles of the rhombus are not $90^\circ$. For instance, $\angle P$ and $\angle R$ appear to be acute angles, while $\angle Q$ and $\angle S$ appear to be obtuse angles.
For the two quadrilaterals to be similar, their corresponding angles must be equal. This means, if we consider the correspondence P $\leftrightarrow$ A, Q $\leftrightarrow$ B, R $\leftrightarrow$ C, S $\leftrightarrow$ D, then we must have $\angle P = \angle A$, $\angle Q = \angle B$, $\angle R = \angle C$, and $\angle S = \angle D$.
However, $\angle A = 90^\circ$, and $\angle P$ is not $90^\circ$. Similarly, $\angle B = 90^\circ$, and $\angle Q$ is not $90^\circ$, and so on for other angles.
Thus, the corresponding angles of the rhombus and the square are not equal.
Although the ratio of corresponding sides is constant (since all sides of the rhombus are equal, and all sides of the square are equal, $\frac{1.5}{3} = \frac{1}{2}$ for any pair of corresponding sides), the condition that corresponding angles are equal is not satisfied.
Since the first condition for similarity (equality of corresponding angles) is not met, the two quadrilaterals are not similar.
Answer:
The given quadrilaterals are not similar because their corresponding angles are not equal.
Example 1 to 3 (Before Exercise 6.2)
Example 1. If a line intersects sides AB and AC of a ∆ ABC at D and E respectively and is parallel to BC, prove that $\frac{AD}{AB}$ = $\frac{AE}{AC}$ (see Fig. 6.13).

Answer:
Given:
In $ \triangle ABC $:
A line intersects side AB at D and side AC at E.
The line segment DE is parallel to BC ($DE || BC$).
To Prove:
$ \frac{AD}{AB} = \frac{AE}{AC} $
Proof:
Consider $ \triangle ADE $ and $ \triangle ABC $.
We are given that the line segment DE is parallel to BC ($DE || BC$).
When a transversal line intersects two parallel lines, the corresponding angles are equal.
Considering AB as a transversal intersecting parallel lines DE and BC:
$ \angle ADE = \angle ABC $
(Corresponding angles)
Considering AC as a transversal intersecting parallel lines DE and BC:
$ \angle AED = \angle ACB $
(Corresponding angles)
The angle at vertex A is common to both triangles $ \triangle ADE $ and $ \triangle ABC $.
$ \angle DAE = \angle BAC $
(Common angle)
Now, we have shown that the three angles of $ \triangle ADE $ are respectively equal to the three corresponding angles of $ \triangle ABC $.
By the Angle-Angle-Angle (AAA) similarity criterion, if the corresponding angles of two triangles are equal, then the triangles are similar.
Therefore, $ \triangle ADE \sim \triangle ABC $.
When two triangles are similar, the ratio of their corresponding sides is equal.
The corresponding sides are AD and AB, AE and AC, and DE and BC.
Thus, we can write the proportionality of corresponding sides:
$ \frac{AD}{AB} = \frac{AE}{AC} = \frac{DE}{BC} $
From this set of equalities, we can take the required part:
$ \frac{AD}{AB} = \frac{AE}{AC} $
Hence Proved.
Example 2. ABCD is a trapezium with AB || DC. E and F are points on non-parallel sides AD and BC respectively such that EF is parallel to AB (see Fig. 6.14). Show that $\frac{AE}{ED}$ = $\frac{BF}{FC}$ .

Answer:
Given:
ABCD is a trapezium with $AB || DC$.
E is a point on side AD and F is a point on side BC.
$EF || AB$.
To Prove:
$\frac{AE}{ED} = \frac{BF}{FC}$
Construction Required:
Draw a diagonal AC, intersecting EF at point G.
Proof:
We are given that $AB || DC$ and $EF || AB$.
Since $EF || AB$ and $AB || DC$, by the property of parallel lines, we have $EF || DC$.
Thus, $EF || AB || DC$.
Now, consider the triangle $ \triangle ADC $. The line segment EG is a part of EF, and we know $EF || DC$. Therefore, $EG || DC$.
In $ \triangle ADC $, we have EG || DC, E is on AD, and G is on AC.
According to the Basic Proportionality Theorem (BPT), if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then the other two sides are divided in the same ratio.
Applying BPT to $ \triangle ADC $ with $EG || DC$:
$\frac{AE}{ED} = \frac{AG}{GC}$
(By BPT in $\triangle ADC$) ... (1)
Next, consider the triangle $ \triangle ABC $. The line segment GF is a part of EF, and we know $EF || AB$. Therefore, $GF || AB$.
In $ \triangle ABC $, we have GF || AB, G is on AC, and F is on BC.
Applying BPT to $ \triangle ABC $ with $GF || AB$:
$\frac{CG}{GA} = \frac{CF}{FB}$
(By BPT in $\triangle ABC$) ... (2)
From equation (2), we can take the reciprocal of both sides:
$\frac{GA}{CG} = \frac{FB}{CF}$
This can be rewritten as:
$\frac{AG}{GC} = \frac{BF}{FC}$
... (3)
Now, comparing equation (1) and equation (3), we see that both $\frac{AE}{ED}$ and $\frac{BF}{FC}$ are equal to $\frac{AG}{GC}$.
Therefore, by the transitive property of equality, we can conclude that:
$\frac{AE}{ED} = \frac{BF}{FC}$
Hence Proved.
Example 3. In Fig. 6.16, $\frac{PS}{SQ}$ = $\frac{PT}{TR}$ and ∠PST = ∠PRQ. Prove that PQR is an isosceles triangle.

Answer:
Given:
In $ \triangle PQR $, S is a point on PQ and T is a point on PR.
$ \frac{PS}{SQ} = \frac{PT}{TR} $
$ \angle PST = \angle PRQ $
To Prove:
$ \triangle PQR $ is an isosceles triangle.
Proof:
We are given that $ \frac{PS}{SQ} = \frac{PT}{TR} $.
In $ \triangle PQR $, the line segment ST divides the sides PQ and PR in the same ratio.
By the converse of the Basic Proportionality Theorem (BPT), if a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.
Therefore, ST is parallel to QR.
$ ST || QR $
(By converse of BPT)
Since $ ST || QR $, and PQ is a transversal, the corresponding angles are equal.
$ \angle PST = \angle PQR $
(Corresponding angles) ... (1)
We are also given that:
$ \angle PST = \angle PRQ $
(Given) ... (2)
From equations (1) and (2), since both are equal to $ \angle PST $, they must be equal to each other.
$ \angle PQR = \angle PRQ $
(From (1) and (2))
In $ \triangle PQR $, angles $ \angle PQR $ and $ \angle PRQ $ are the angles opposite to sides PR and PQ respectively.
If two angles of a triangle are equal, then the sides opposite to them are also equal.
$ PQ = PR $
(Sides opposite to equal angles are equal)
Since $ \triangle PQR $ has two sides of equal length (PQ = PR), it is an isosceles triangle.
Hence Proved.
Exercise 6.2
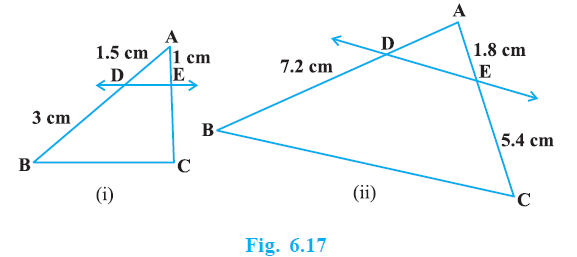
Question 1. In Fig. 6.17, (i) and (ii), DE || BC. Find EC in (i) and AD in (ii).
Answer:
Solution for Part (i):
Given:
In $\triangle ABC$, DE || BC.
AD = $1.5$ cm
DB = $3$ cm
AE = $1$ cm
To Find:
EC
Calculation:
Since DE || BC, by the Basic Proportionality Theorem (BPT), we have:
$\frac{AD}{DB} = \frac{AE}{EC}$
Substitute the given values:
$\frac{1.5}{3} = \frac{1}{EC}$
Cross-multiply:
$1.5 \times EC = 3 \times 1$
$1.5 \times EC = 3$
Divide by 1.5:
$EC = \frac{3}{1.5}$
To remove the decimal, multiply numerator and denominator by 10:
$EC = \frac{30}{15}$
$EC = 2$
The value of EC is $2$ cm.
Solution for Part (ii):
Given:
In $\triangle ABC$, DE || BC.
DB = $7.2$ cm
AE = $1.8$ cm
EC = $5.4$ cm
To Find:
AD
Calculation:
Since DE || BC, by the Basic Proportionality Theorem (BPT), we have:
$\frac{AD}{DB} = \frac{AE}{EC}$
Substitute the given values:
$\frac{AD}{7.2} = \frac{1.8}{5.4}$
Simplify the right side:
$\frac{AD}{7.2} = \frac{1.8}{1.8 \times 3}$
$\frac{AD}{7.2} = \frac{1}{3}$
Now, solve for AD by multiplying both sides by 7.2:
$AD = \frac{1}{3} \times 7.2$
$AD = \frac{7.2}{3}$
$AD = 2.4$
The value of AD is $2.4$ cm.
Question 2. E and F are points on the sides PQ and PR respectively of a ∆ PQR. For each of the following cases, state whether EF || QR :
(i) PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm
(ii) PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm
(iii) PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm
Answer:
According to the Converse of Basic Proportionality Theorem (BPT), if a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side. In $\triangle PQR$, EF will be parallel to QR if $\frac{PE}{EQ} = \frac{PF}{FR}$.
Case (i):
Given:
PE = $3.9$ cm, EQ = $3$ cm, PF = $3.6$ cm, FR = $2.4$ cm.
To Determine:
Whether EF || QR.
Solution:
Calculate the ratio $\frac{PE}{EQ}$:
$\frac{PE}{EQ} = \frac{3.9}{3}$
$\frac{PE}{EQ} = \frac{39}{30}$
$\frac{PE}{EQ} = \frac{\cancel{39}^{13}}{\cancel{30}^{10}} = \frac{13}{10} = 1.3$
Calculate the ratio $\frac{PF}{FR}$:
$\frac{PF}{FR} = \frac{3.6}{2.4}$
$\frac{PF}{FR} = \frac{36}{24}$
$\frac{PF}{FR} = \frac{\cancel{36}^{3}}{\cancel{24}^{2}} = \frac{3}{2} = 1.5$
Compare the ratios:
$\frac{PE}{EQ} = 1.3$ and $\frac{PF}{FR} = 1.5$
Since $\frac{PE}{EQ} \neq \frac{PF}{FR}$, the line segment EF does not divide the sides PQ and PR in the same ratio.
Therefore, by the converse of BPT, EF is not parallel to QR.
Case (ii):
Given:
PE = $4$ cm, QE = $4.5$ cm, PF = $8$ cm, RF = $9$ cm.
To Determine:
Whether EF || QR.
Solution:
Calculate the ratio $\frac{PE}{QE}$:
$\frac{PE}{QE} = \frac{4}{4.5}$
$\frac{PE}{QE} = \frac{40}{45}$
$\frac{PE}{QE} = \frac{\cancel{40}^{8}}{\cancel{45}^{9}} = \frac{8}{9}$
Calculate the ratio $\frac{PF}{RF}$:
$\frac{PF}{RF} = \frac{8}{9}$
Compare the ratios:
$\frac{PE}{QE} = \frac{8}{9}$ and $\frac{PF}{RF} = \frac{8}{9}$
Since $\frac{PE}{QE} = \frac{PF}{RF}$, the line segment EF divides the sides PQ and PR in the same ratio.
Therefore, by the converse of BPT, EF is parallel to QR.
Case (iii):
Given:
PQ = $1.28$ cm, PR = $2.56$ cm, PE = $0.18$ cm, PF = $0.36$ cm.
To Determine:
Whether EF || QR.
Solution:
We can use the proportionality of segments or the proportionality of segment to the full side. Using the latter form of converse of BPT, EF || QR if $\frac{PE}{PQ} = \frac{PF}{PR}$.
Calculate the ratio $\frac{PE}{PQ}$:
$\frac{PE}{PQ} = \frac{0.18}{1.28}$
$\frac{PE}{PQ} = \frac{18}{128}$
$\frac{PE}{PQ} = \frac{\cancel{18}^9}{\cancel{128}^{64}} = \frac{9}{64}$
Calculate the ratio $\frac{PF}{PR}$:
$\frac{PF}{PR} = \frac{0.36}{2.56}$
$\frac{PF}{PR} = \frac{36}{256}$
$\frac{PF}{PR} = \frac{\cancel{36}^9}{\cancel{256}^{64}} = \frac{9}{64}$ (Dividing both by 4)
Compare the ratios:
$\frac{PE}{PQ} = \frac{9}{64}$ and $\frac{PF}{PR} = \frac{9}{64}$
Since $\frac{PE}{PQ} = \frac{PF}{PR}$, the line segment EF divides the sides PQ and PR proportionally.
Therefore, by the converse of BPT, EF is parallel to QR.
Question 3. In Fig. 6.18, if LM || CB and LN || CD, prove that $\frac{AM}{AB}$ = $\frac{AN}{AD}$ .

Answer:
Given:
In the given figure:
LM || CB, where M is a point on AB and L is a point on AC.
LN || CD, where N is a point on AD and L is a point on AC.
To Prove:
$\frac{AM}{AB} = \frac{AN}{AD}$
Proof:
Consider $ \triangle ABC $. We are given that LM is parallel to CB ($LM || CB$).
The line segment LM intersects sides AB and AC at points M and L respectively.
According to the Basic Proportionality Theorem (BPT), if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then the other two sides are divided in the same ratio.
Applying BPT to $ \triangle ABC $ with $LM || CB$, we get:
$ \frac{AM}{MB} = \frac{AL}{LC} $
An extension of the BPT states that if a line parallel to one side of a triangle intersects the other two sides, then the ratio of the segments of one side is equal to the ratio of the corresponding segments of the other side, and also equal to the ratio of a segment to the whole side.
Using the extended BPT on $ \triangle ABC $ with $LM || CB$, considering the ratio of segment to the whole side:
$ \frac{AM}{AB} = \frac{AL}{AC} $
... (1)
Next, consider $ \triangle ADC $. We are given that LN is parallel to CD ($LN || CD$).
The line segment LN intersects sides AD and AC at points N and L respectively.
Applying the extended BPT to $ \triangle ADC $ with $LN || CD$, considering the ratio of segment to the whole side:
$ \frac{AN}{AD} = \frac{AL}{AC} $
... (2)
Now, compare the equations (1) and (2).
From equation (1), we have $ \frac{AM}{AB} = \frac{AL}{AC} $.
From equation (2), we have $ \frac{AN}{AD} = \frac{AL}{AC} $.
Since both $\frac{AM}{AB}$ and $\frac{AN}{AD}$ are equal to the same ratio $\frac{AL}{AC}$, they must be equal to each other by the transitive property of equality.
Therefore, we can conclude that:
$ \frac{AM}{AB} = \frac{AN}{AD} $
Hence Proved.
Question 4. In Fig. 6.19, DE || AC and DF || AE. Prove that $\frac{BF}{FE}$ = $\frac{BE}{EC}$ .

Answer:
Given:
In $ \triangle ABC $:
DE || AC, where D is a point on AB and E is a point on BC.
DF || AE, where D is a point on AB and F is a point on BE.
To Prove:
$\frac{BF}{FE} = \frac{BE}{EC}$
Proof:
Consider $ \triangle ABE $. We are given that DF is parallel to AE ($DF || AE$).
The line segment DF intersects sides AB at D and BE at F.
According to the Basic Proportionality Theorem (BPT), if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then the other two sides are divided in the same ratio.
Applying BPT to $ \triangle ABE $ with $DF || AE$, we get:
$ \frac{BD}{DA} = \frac{BF}{FE} $
... (1)
Next, consider $ \triangle ABC $. We are given that DE is parallel to AC ($DE || AC$).
The line segment DE intersects sides AB at D and BC at E.
Applying BPT to $ \triangle ABC $ with $DE || AC$, we get:
$ \frac{BD}{DA} = \frac{BE}{EC} $
... (2)
Now, compare the equations (1) and (2).
From equation (1), we have $ \frac{BD}{DA} = \frac{BF}{FE} $.
From equation (2), we have $ \frac{BD}{DA} = \frac{BE}{EC} $.
Since both $\frac{BF}{FE}$ and $\frac{BE}{EC}$ are equal to the same ratio $\frac{BD}{DA}$, they must be equal to each other by the transitive property of equality.
Therefore, we can conclude that:
$ \frac{BF}{FE} = \frac{BE}{EC} $
Hence Proved.
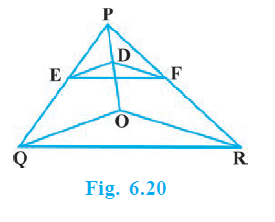
Question 5. In Fig. 6.20, DE || OQ and DF || OR. Show that EF || QR.
Answer:
Given:
In the given figure:
DE || OQ, where E is a point on PQ and D is a point on PO.
DF || OR, where F is a point on PR and D is a point on PO.
To Show:
EF || QR
Proof:
Consider $ \triangle POQ $. We are given that DE is parallel to OQ ($DE || OQ$).
The line segment DE intersects side PO at D and side PQ at E.
According to the Basic Proportionality Theorem (BPT), if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then the other two sides are divided in the same ratio.
Applying BPT to $ \triangle POQ $ with $DE || OQ$, we get:
$ \frac{PD}{DO} = \frac{PE}{EQ} $
... (1)
Next, consider $ \triangle POR $. We are given that DF is parallel to OR ($DF || OR$).
The line segment DF intersects side PO at D and side PR at F.
Applying BPT to $ \triangle POR $ with $DF || OR$, we get:
$ \frac{PD}{DO} = \frac{PF}{FR} $
... (2)
Now, compare the equations (1) and (2).
From equation (1), we have $ \frac{PD}{DO} = \frac{PE}{EQ} $.
From equation (2), we have $ \frac{PD}{DO} = \frac{PF}{FR} $.
Since both $\frac{PE}{EQ}$ and $\frac{PF}{FR}$ are equal to the same ratio $\frac{PD}{DO}$, they must be equal to each other by the transitive property of equality.
Therefore, we have:
$ \frac{PE}{EQ} = \frac{PF}{FR} $
Now, consider $ \triangle PQR $. The points E and F are on sides PQ and PR respectively, and we have just shown that the line segment EF divides these sides in the same ratio, i.e., $ \frac{PE}{EQ} = \frac{PF}{FR} $.
According to the converse of the Basic Proportionality Theorem (BPT), if a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.
Applying the converse of BPT to $ \triangle PQR $ based on the ratio $ \frac{PE}{EQ} = \frac{PF}{FR} $, we conclude that the line segment EF is parallel to the side QR.
Thus, EF || QR.
Hence Showed.
Question 6. In Fig. 6.21, A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.

Answer:
Given:
Points A, B, and C are on OP, OQ, and OR respectively.
AB || PQ
AC || PR
To Show:
BC || QR
Proof:
Consider $ \triangle OPQ $. We are given that AB is parallel to PQ ($AB || PQ$).
The line segment AB intersects side OP at A and side OQ at B.
According to the Basic Proportionality Theorem (BPT), if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then the other two sides are divided in the same ratio.
Applying BPT to $ \triangle OPQ $ with $AB || PQ$, considering the ratios of the segments from vertex O:
$ \frac{OA}{AP} = \frac{OB}{BQ} $
... (1)
Next, consider $ \triangle OPR $. We are given that AC is parallel to PR ($AC || PR$).
The line segment AC intersects side OP at A and side OR at C.
Applying BPT to $ \triangle OPR $ with $AC || PR$, considering the ratios of the segments from vertex O:
$ \frac{OA}{AP} = \frac{OC}{CR} $
... (2)
Now, compare the equations (1) and (2).
From equation (1), we have $ \frac{OA}{AP} = \frac{OB}{BQ} $.
From equation (2), we have $ \frac{OA}{AP} = \frac{OC}{CR} $.
Since both $\frac{OB}{BQ}$ and $\frac{OC}{CR}$ are equal to the same ratio $\frac{OA}{AP}$, they must be equal to each other by the transitive property of equality.
Therefore, we have:
$ \frac{OB}{BQ} = \frac{OC}{CR} $
Now, consider $ \triangle OQR $. The points B and C are on sides OQ and OR respectively, and we have just shown that the line segment BC divides these sides in the same ratio, i.e., $ \frac{OB}{BQ} = \frac{OC}{CR} $.
According to the converse of the Basic Proportionality Theorem (BPT), if a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.
Applying the converse of BPT to $ \triangle OQR $ based on the ratio $ \frac{OB}{BQ} = \frac{OC}{CR} $, we conclude that the line segment BC is parallel to the side QR.
Thus, BC || QR.
Hence Showed.
Question 7. Using Theorem 6.1, prove that a line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side. (Recall that you have proved it in Class IX).
Answer:
Theorem 6.1 (Basic Proportionality Theorem or Thales Theorem): If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then the other two sides are divided in the same ratio.
Statement to be Proved: A line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side.
Given:
In $ \triangle ABC $:
D is the midpoint of side AB.
A line passes through D and is parallel to BC, intersecting AC at E.
D is the midpoint of AB
(Given)
$DE || BC$
(Given)
To Prove:
E is the midpoint of AC, i.e., $AE = EC$.
Proof:
Since D is the midpoint of the side AB, the segment AD has the same length as the segment DB.
$AD = DB$
(Definition of midpoint)
We can write this equality as a ratio:
$ \frac{AD}{DB} = 1 $
Now, consider $ \triangle ABC $. We are given that the line segment DE is parallel to the side BC ($DE || BC$). The line DE intersects the other two sides, AB and AC, at distinct points D and E, respectively.
According to the Basic Proportionality Theorem (Theorem 6.1), if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then the other two sides are divided in the same ratio.
Applying the Basic Proportionality Theorem to $ \triangle ABC $ with the line $DE || BC$, we get the ratio of the segments on sides AB and AC:
$ \frac{AD}{DB} = \frac{AE}{EC} $
(By Basic Proportionality Theorem) ... (1)
We already established that $ \frac{AD}{DB} = 1 $ because D is the midpoint of AB.
Substitute the value of $ \frac{AD}{DB} $ into equation (1):
$ 1 = \frac{AE}{EC} $
Multiply both sides of this equation by EC:
$ 1 \times EC = AE $
$ EC = AE $
This result means that the distance from A to E is equal to the distance from E to C. Therefore, the point E divides the side AC into two equal parts.
Hence, E is the midpoint of AC, which means the line DE bisects the side AC.
Hence Proved.
Question 8. Using Theorem 6.2, prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side. (Recall that you have done it in Class IX).
Answer:
Theorem 6.2 (Converse of Basic Proportionality Theorem or Converse of Thales Theorem): If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.
Statement to be Proved: The line joining the mid-points of any two sides of a triangle is parallel to the third side.
Given:
In $ \triangle ABC $:
D is the midpoint of side AB.
E is the midpoint of side AC.
To Prove:
DE || BC
Proof:
Since D is the midpoint of the side AB, the length of the segment AD is equal to the length of the segment DB.
$AD = DB$
(By definition of midpoint)
Dividing both sides by DB (since DB is a segment of a triangle side, its length is non-zero), we get the ratio:
$ \frac{AD}{DB} = 1 $
... (1)
Similarly, since E is the midpoint of the side AC, the length of the segment AE is equal to the length of the segment EC.
$AE = EC$
(By definition of midpoint)
Dividing both sides by EC (since EC is a segment of a triangle side, its length is non-zero), we get the ratio:
$ \frac{AE}{EC} = 1 $
... (2)
Now, compare equation (1) and equation (2). Both the ratios $\frac{AD}{DB}$ and $\frac{AE}{EC}$ are equal to 1.
Therefore, by the transitive property of equality, we can conclude that:
$ \frac{AD}{DB} = \frac{AE}{EC} $
This equation shows that the line segment DE divides the sides AB and AC of the triangle in the same ratio.
According to the Converse of the Basic Proportionality Theorem (Theorem 6.2), if a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.
Since the line segment DE divides sides AB and AC in the same ratio ($ \frac{AD}{DB} = \frac{AE}{EC} $), applying Theorem 6.2 to $ \triangle ABC $, we conclude that DE is parallel to the third side BC.
Thus, $DE || BC$.
Hence Proved.
Question 9. ABCD is a trapezium in which AB || DC and its diagonals intersect each other at the point O. Show that $\frac{AO}{BO}$ = $\frac{CO}{DO}$.
Answer:
Given:
ABCD is a trapezium in which AB || DC.
The diagonals AC and BD intersect each other at the point O.
To Show:
$\frac{AO}{BO} = \frac{CO}{DO}$
Construction Required:
Draw a line through the point O, parallel to AB, intersecting AD at point E.
Since $AB || DC$ (given) and we construct $EO || AB$, by the property of parallel lines, we also have $EO || DC$.
Thus, $EO || AB || DC$.
Proof:
Consider the triangle $ \triangle DAB $. We have constructed the line segment EO parallel to side AB ($EO || AB$).
The line segment EO intersects the side DA at E and the side DB at O.
According to the Basic Proportionality Theorem (BPT), if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then the other two sides are divided in the same ratio.
Applying BPT to $ \triangle DAB $ with $EO || AB$, we get the ratio of the segments on sides DA and DB:
$ \frac{DE}{EA} = \frac{DO}{OB} $
(By BPT in $\triangle DAB$) ... (1)
Now, consider the triangle $ \triangle ADC $. We have established that the line segment EO is parallel to side DC ($EO || DC$).
The line segment EO intersects the side AD at E and the side AC at O.
Applying BPT to $ \triangle ADC $ with $EO || DC$, we get the ratio of the segments on sides AD and AC:
$ \frac{AE}{ED} = \frac{AO}{OC} $
(By BPT in $\triangle ADC$) ... (2)
Consider equation (1): $ \frac{DE}{EA} = \frac{DO}{OB} $.
Consider equation (2): $ \frac{AE}{ED} = \frac{AO}{OC} $. Notice that the ratio $\frac{AE}{ED}$ in equation (2) is the reciprocal of the ratio $\frac{DE}{EA}$ in equation (1).
Let's take the reciprocal of both sides of equation (1):
$ \frac{EA}{DE} = \frac{OB}{DO} $
... (3)
Now, we have two expressions for the ratio $\frac{AE}{ED}$ (or $\frac{EA}{DE}$):
From (2): $ \frac{AE}{ED} = \frac{AO}{OC} $
From (3): $ \frac{EA}{DE} = \frac{OB}{DO} $
Since $ \frac{AE}{ED} $ is the same as $ \frac{EA}{DE} $, by the transitive property of equality, the quantities they are equal to must also be equal:
$ \frac{AO}{OC} = \frac{OB}{DO} $
We want to show that $\frac{AO}{BO} = \frac{CO}{DO}$. We can rearrange the terms in the equation $\frac{AO}{OC} = \frac{OB}{DO}$ by cross-multiplication or by swapping the denominators (BO and OC):
$ AO \times DO = OC \times OB $
Divide both sides by $BO \times DO$ (assuming $BO \neq 0$ and $DO \neq 0$, which is true for intersecting diagonals):
$ \frac{AO \times DO}{BO \times DO} = \frac{OC \times OB}{BO \times DO} $
Cancel out the common terms:
$ \frac{AO}{BO} = \frac{OC}{DO} $
This is the required result.
Hence Showed.
Question 10. The diagonals of a quadrilateral ABCD intersect each other at the point O such that $\frac{AO}{BO}$ = $\frac{CO}{DO}$.
Answer:
Given:
ABCD is a quadrilateral.
The diagonals AC and BD intersect each other at the point O.
The intersection satisfies the ratio: $\frac{AO}{BO} = \frac{CO}{DO}$.
To Show:
ABCD is a trapezium (i.e., we need to show that AB || DC).
Construction Required:
Draw a line through the point O, parallel to side AB, intersecting the side AD at point E.
Draw $ EO || AB $
(Construction)
Proof:
Consider the triangle $ \triangle DAB $.
In this triangle, we have constructed the line segment EO such that it is parallel to the side AB ($EO || AB$). The line EO intersects the side DA at E and the side DB at O.
According to the Basic Proportionality Theorem (BPT), if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then the other two sides are divided in the same ratio.
Applying BPT to $ \triangle DAB $ with the line $EO || AB$, we get the following proportion for the segments on sides DA and DB:
$ \frac{DE}{EA} = \frac{DO}{OB} $
(By BPT in $\triangle DAB$) ... (1)
We are given the condition that the diagonals intersect such that $\frac{AO}{BO} = \frac{CO}{DO}$.
$ \frac{AO}{BO} = \frac{CO}{DO} $
(Given)
We can rearrange this given proportion by swapping the terms BO and CO (cross-multiplying and then rearranging, or simply swapping the means):
$ \frac{AO}{CO} = \frac{BO}{DO} $
... (2)
Now, let's look back at equation (1): $ \frac{DE}{EA} = \frac{DO}{OB} $. We can take the reciprocal of both sides of this equation:
$ \frac{EA}{DE} = \frac{OB}{DO} $
... (3)
From equation (2), we have $\frac{AO}{CO} = \frac{BO}{DO}$.
From equation (3), we have $\frac{EA}{DE} = \frac{OB}{DO}$.
Notice that the right-hand sides of equation (2) and equation (3) involve the same ratio $\frac{BO}{DO}$ (or $\frac{OB}{DO}$).
Therefore, by the transitive property of equality, the left-hand sides of equation (2) and equation (3) must be equal:
$ \frac{EA}{DE} = \frac{AO}{CO} $
This means $ \frac{AE}{ED} = \frac{AO}{OC} $.
Now, consider the triangle $ \triangle ADC $. The line segment EO intersects the side AD at E and the side AC at O. We have shown that the ratio of the segments on side AD ($\frac{AE}{ED}$) is equal to the ratio of the segments on side AC ($\frac{AO}{OC}$).
According to the Converse of the Basic Proportionality Theorem (Theorem 6.2), if a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.
Applying the Converse of BPT to $ \triangle ADC $, based on the ratio $ \frac{AE}{ED} = \frac{AO}{OC} $, we conclude that the line segment EO is parallel to the third side DC.
$ EO || DC $
(By Converse of BPT)
We began our proof by constructing the line segment EO to be parallel to AB.
$ EO || AB $
(By Construction)
Now we have shown that $EO || DC$.
Since both line segments AB and DC are parallel to the same line segment EO, they must be parallel to each other.
$ AB || DC $
By definition, a quadrilateral with at least one pair of opposite sides parallel is called a trapezium.
Since AB is parallel to DC, the quadrilateral ABCD is a trapezium.
Hence Showed.
Example 4 to 8 (Before Exercise 6.3)
Example 4. In Fig. 6.29, if PQ || RS, prove that ∆ POQ ~ ∆ SOR.

Answer:
Given:
In the given figure, PQ || RS.
The line segments PS and RQ intersect at point O.
To Prove:
$\triangle POQ \sim \triangle SOR$.
Proof:
Consider the triangles $ \triangle POQ $ and $ \triangle SOR $.
We are given that the line segment PQ is parallel to RS ($PQ || RS$).
Consider the angles formed at the intersection point O:
$ \angle POQ = \angle SOR $
(Vertically opposite angles)
Now, consider the transversal PS intersecting the parallel lines PQ and RS.
The alternate interior angles formed are equal:
$ \angle OPQ = \angle OSR $
(Alternate interior angles)
Next, consider the transversal QR intersecting the parallel lines PQ and RS.
The alternate interior angles formed are also equal:
$ \angle OQP = \angle ORS $
(Alternate interior angles)
Now, in $ \triangle POQ $ and $ \triangle SOR $, we have shown that the three corresponding angles are equal:
- $\angle POQ = \angle SOR$
- $\angle OPQ = \angle OSR$
- $\angle OQP = \angle ORS$
By the Angle-Angle-Angle (AAA) similarity criterion, if the corresponding angles of two triangles are equal, then the triangles are similar.
Matching the corresponding vertices based on equal angles (P $\leftrightarrow$ S, O $\leftrightarrow$ O, Q $\leftrightarrow$ R), we conclude that:
$ \triangle POQ \sim \triangle SOR $
Hence Proved.
Example 5. Observe Fig. 6.30 and then find ∠P.

Answer:
Given:
Two triangles $ \triangle ABC $ and $ \triangle PQR $ with the following side lengths and angles as shown in the figure:
In $ \triangle ABC $:
AB = $3.8$ cm
BC = $6$ cm
CA = $3\sqrt{3}$ cm
$ \angle A = 80^\circ $
$ \angle B = 60^\circ $
In $ \triangle PQR $:
PQ = $7.6$ cm
QR = $12$ cm
RP = $6\sqrt{3}$ cm
To Find:
The measure of $ \angle P $.
Solution:
First, let's find the measure of the third angle in $ \triangle ABC $ using the angle sum property of a triangle.
In $ \triangle ABC $, $ \angle A + \angle B + \angle C = 180^\circ $ (Angle sum property of a triangle).
Substitute the given angle values:
$ 80^\circ + 60^\circ + \angle C = 180^\circ $
$ 140^\circ + \angle C = 180^\circ $
$ \angle C = 180^\circ - 140^\circ $
$ \angle C = 40^\circ $
Now we have all angles of $ \triangle ABC $: $ \angle A = 80^\circ $, $ \angle B = 60^\circ $, $ \angle C = 40^\circ $.
Next, we compare the ratios of the side lengths of $ \triangle ABC $ and $ \triangle PQR $ to check for similarity. Let's try to find the ratios of corresponding sides by comparing the smallest side of $ \triangle ABC $ with the smallest side of $ \triangle PQR $, and so on, or simply check all possible pairings to find proportional ones.
Side lengths of $ \triangle ABC $: 3.8, 6, $3\sqrt{3}$ (approx $3 \times 1.732 = 5.196$)
Side lengths of $ \triangle PQR $: 7.6, 12, $6\sqrt{3}$ (approx $6 \times 1.732 = 10.392$)
Let's calculate the ratios:
$ \frac{AB}{RQ} = \frac{3.8}{12}$
$ \frac{BC}{PQ} = \frac{6}{7.6}$
$ \frac{CA}{RP} = \frac{3\sqrt{3}}{6\sqrt{3}} = \frac{3}{6} = \frac{1}{2} $
Let's try a different pairing based on the side lengths values:
$ \frac{AB}{PQ} = \frac{3.8}{7.6} = \frac{38}{76} = \frac{1}{2} $
$ \frac{BC}{QR} = \frac{6}{12} = \frac{1}{2} $
$ \frac{CA}{RP} = \frac{3\sqrt{3}}{6\sqrt{3}} = \frac{3}{6} = \frac{1}{2} $
Since the ratios of the corresponding sides are equal ($ \frac{AB}{PQ} = \frac{BC}{QR} = \frac{CA}{RP} = \frac{1}{2} $), the triangles $ \triangle ABC $ and $ \triangle PQR $ are similar by the Side-Side-Side (SSS) similarity criterion.
When two triangles are similar, their corresponding angles are equal. The correspondence of vertices is determined by the sides in proportion:
- The angle opposite side AB ($\angle C$) corresponds to the angle opposite side PQ ($\angle R$). So, $ \angle C = \angle R $.
- The angle opposite side BC ($\angle A$) corresponds to the angle opposite side QR ($\angle P$). So, $ \angle A = \angle P $.
- The angle opposite side CA ($\angle B$) corresponds to the angle opposite side RP ($\angle Q$). So, $ \angle B = \angle Q $.
We found $ \angle C = 40^\circ $. This means $ \angle R = 40^\circ $. From the figure of $\triangle PQR$, this matches the angle $R$.
We are given $ \angle A = 80^\circ $. Since $ \angle A = \angle P $, we have $ \angle P = 80^\circ $.
We are given $ \angle B = 60^\circ $. Since $ \angle B = \angle Q $, we have $ \angle Q = 60^\circ $. From the figure of $\triangle PQR$, this matches the angle $Q$.
We can verify the angles in $ \triangle PQR $: $ \angle P + \angle Q + \angle R = 80^\circ + 60^\circ + 40^\circ = 180^\circ $.
The value of $ \angle P $ is $80^\circ$.
Answer:
$ \angle P = 80^\circ $.
Example 6. In Fig. 6.31,
OA . OB = OC . OD.
Show that ∠A = ∠C and ∠B = ∠D.

Answer:
Given:
Two line segments AB and CD intersect at point O.
$OA \cdot OB = OC \cdot OD$
To Show:
$ \angle A = \angle C $
$ \angle B = \angle D $
Proof:
We are given the equation $OA \cdot OB = OC \cdot OD$.
We can rearrange this equation to form a ratio of lengths. Divide both sides by $OB \cdot OC$ (assuming $OB \neq 0$ and $OC \neq 0$, which is true since O is the intersection point and A, B, C, D are distinct points):
$ \frac{OA \cdot OB}{OB \cdot OC} = \frac{OC \cdot OD}{OB \cdot OC} $
Cancel out the common terms:
$ \frac{OA}{\cancel{OB} \cdot OC} = \frac{\cancel{OC} \cdot OD}{OB \cdot \cancel{OC}} $
$ \frac{OA}{OC} = \frac{OD}{OB} $
This gives us a proportionality relation between the segments of the intersecting lines AC and BD:
$ \frac{OA}{OC} = \frac{OD}{OB} $
... (1)
Now, consider $ \triangle AOD $ and $ \triangle COB $.
Let's consider the angles formed at the intersection point O.
$ \angle AOD = \angle COB $
(Vertically opposite angles)
Now, consider $ \triangle AOD $ and $ \triangle COB $ again. We have:
Since $\frac{OA}{OC} = \frac{OD}{OB}$ and $\angle AOD = \angle COB$, by SAS similarity, $\triangle AOD \sim \triangle COB$.
When two triangles are similar, their corresponding angles are equal. The corresponding angles in similar triangles $ \triangle AOD \sim \triangle COB $ are:
- $ \angle A $ corresponds to $ \angle C $ (opposite sides OD and OB)
- $ \angle D $ corresponds to $ \angle B $ (opposite sides OA and OC)
- $ \angle AOD $ corresponds to $ \angle COB $ (which are already known to be equal)
Therefore, we have:
$ \angle A = \angle C $
(Corresponding angles of similar triangles)
$ \angle D = \angle B $
(Corresponding angles of similar triangles)
This is equivalent to $ \angle B = \angle D $.
Hence Showed that $ \angle A = \angle C $ and $ \angle B = \angle D $.
Example 7. A girl of height 90 cm is walking away from the base of a lamp-post at a speed of 1.2 m/s. If the lamp is 3.6 m above the ground, find the length of her shadow after 4 seconds.
Answer:
Given:
Height of the girl (CD) = 90 cm.
Height of the lamp-post (AB) = 3.6 m.
Speed of the girl = 1.2 m/s.
Time taken = 4 seconds.
To Find:
The length of the girl's shadow after 4 seconds.
Solution:
First, let's convert the height of the girl from centimeters to meters:
Height of the girl (CD) = 90 cm $= \frac{90}{100}$ m $= 0.9$ m.
The girl is walking away from the base of the lamp-post at a speed of 1.2 m/s. In 4 seconds, the distance she walks away from the base of the lamp-post (distance BD) is:
Distance = Speed $\times$ Time
$ \text{BD} = 1.2 \text{ m/s} \times 4 \text{ s} $
$ \text{BD} = 4.8 \text{ m} $
Let the length of the girl's shadow be $x$ meters. The shadow starts from the point where the girl is standing (D) and extends to the point E. So, DE = $x$ meters.
The lamp-post is AB, and the girl is CD. Both are standing perpendicular to the ground. The light source is at A, and the shadow of the girl ends at E.
Consider the two triangles $ \triangle ABE $ (formed by the lamp-post, the ground, and the ray of light to the tip of the shadow) and $ \triangle CDE $ (formed by the girl, the ground, and the ray of light to the tip of her shadow).
In $ \triangle ABE $ and $ \triangle CDE $:
- $ \angle ABE = \angle CDE = 90^\circ $ (Since both the lamp-post and the girl are vertical to the ground)
- $ \angle AEB = \angle CED $ (These are common angles, as E is the tip of the shadow for both the lamp-post and the girl)
Since two corresponding angles of $ \triangle ABE $ and $ \triangle CDE $ are equal, the triangles are similar by the Angle-Angle (AA) similarity criterion.
$ \triangle ABE \sim \triangle CDE $
For similar triangles, the ratio of corresponding sides is equal.
The side AB (height of lamp-post) corresponds to side CD (height of girl).
The side BE (distance from base of lamp-post to shadow tip) corresponds to side DE (length of shadow).
$ \frac{AB}{CD} = \frac{BE}{DE} $
(Ratio of corresponding sides of similar triangles) ... (1)
We know AB = 3.6 m, CD = 0.9 m, DE = $x$ m, and BE = BD + DE = $4.8 + x$ m.
Substitute these values into equation (1):
$ \frac{3.6}{0.9} = \frac{4.8 + x}{x} $
Calculate the ratio on the left side:
$ \frac{3.6}{0.9} = \frac{36}{9} = 4 $
So, the equation becomes:
$ 4 = \frac{4.8 + x}{x} $
Now, solve for $x$. Multiply both sides by $x$:
$ 4 \times x = 4.8 + x $
$ 4x = 4.8 + x $
Subtract $x$ from both sides:
$ 4x - x = 4.8 $
$ 3x = 4.8 $
Divide both sides by 3:
$ x = \frac{4.8}{3} $
$ x = 1.6 $
The length of her shadow after 4 seconds is 1.6 meters.
Answer:
The length of her shadow after 4 seconds is 1.6 m.
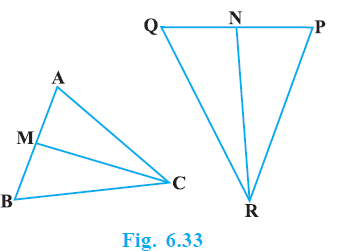
Example 8. In Fig. 6.33, CM and RN are respectively the medians of ∆ ABC and ∆ PQR. If ∆ ABC ~ ∆ PQR, prove that :
(i) ∆ AMC ~ ∆ PNR
(ii) $\frac{CN}{RN}$ = $\frac{AB}{PQ}$
(iii) ∆ CMB ~ ∆ RNQ
Answer:
Given:
$\triangle$ ABC $\sim$ $\triangle$ PQR
CM is the median of $\triangle$ ABC.
RN is the median of $\triangle$ PQR.
To Prove:
(i) $\triangle$ AMC $\sim$ $\triangle$ PNR
(ii) $\frac{\text{CM}}{\text{RN}}$ = $\frac{\text{AB}}{\text{PQ}}$
(iii) $\triangle$ CMB $\sim$ $\triangle$ RNQ
Proof:
Since $\triangle$ ABC $\sim$ $\triangle$ PQR, their corresponding angles are equal and the ratio of their corresponding sides is equal.
$\angle$ A = $\angle$ P
(Corresponding angles of similar triangles)
$\angle$ B = $\angle$ Q
(Corresponding angles of similar triangles)
$\frac{\text{AB}}{\text{PQ}} = \frac{\text{BC}}{\text{QR}} = \frac{\text{AC}}{\text{PR}}$
(Ratio of corresponding sides of similar triangles)
CM is the median to AB, so M is the midpoint of AB. Therefore, $AM = MB = \frac{1}{2}\text{AB}$.
RN is the median to PQ, so N is the midpoint of PQ. Therefore, $PN = NQ = \frac{1}{2}\text{PQ}$.
From $\frac{\text{AB}}{\text{PQ}} = \frac{\text{AC}}{\text{PR}}$, we can write $\frac{2\text{AM}}{2\text{PN}} = \frac{\text{AC}}{\text{PR}}$ which simplifies to:
$\frac{\text{AM}}{\text{PN}} = \frac{\text{AC}}{\text{PR}}$
... (i)
Similarly, from $\frac{\text{AB}}{\text{PQ}} = \frac{\text{BC}}{\text{QR}}$, we can write $\frac{2\text{MB}}{2\text{NQ}} = \frac{\text{BC}}{\text{QR}}$ which simplifies to:
$\frac{\text{MB}}{\text{NQ}} = \frac{\text{BC}}{\text{QR}}$
... (ii)
(i) To prove $\triangle$ AMC $\sim$ $\triangle$ PNR:
Consider $\triangle$ AMC and $\triangle$ PNR.
$\frac{\text{AM}}{\text{PN}} = \frac{\text{AC}}{\text{PR}}$
(From (i))
$\angle$ A = $\angle$ P
(Given $\triangle$ ABC $\sim$ $\triangle$ PQR)
Therefore, by SAS similarity criterion,
$\triangle$ AMC $\sim$ $\triangle$ PNR.
(ii) To prove $\frac{\text{CM}}{\text{RN}}$ = $\frac{\text{AB}}{\text{PQ}}$:
Since $\triangle$ AMC $\sim$ $\triangle$ PNR (Proved in (i)), the ratio of their corresponding sides is equal.
$\frac{\text{AM}}{\text{PN}} = \frac{\text{AC}}{\text{PR}} = \frac{\text{CM}}{\text{RN}}$
(Corresponding sides of similar triangles)
We also know that $\frac{\text{AM}}{\text{PN}} = \frac{\frac{1}{2}\text{AB}}{\frac{1}{2}\text{PQ}} = \frac{\text{AB}}{\text{PQ}}$.
Combining these, we get:
$\frac{\text{CM}}{\text{RN}} = \frac{\text{AM}}{\text{PN}} = \frac{\text{AB}}{\text{PQ}}$
Thus, $\frac{\text{CM}}{\text{RN}}$ = $\frac{\text{AB}}{\text{PQ}}$.
(iii) To prove $\triangle$ CMB $\sim$ $\triangle$ RNQ:
Consider $\triangle$ CMB and $\triangle$ RNQ.
$\frac{\text{MB}}{\text{NQ}} = \frac{\text{BC}}{\text{QR}}$
(From (ii))
$\angle$ B = $\angle$ Q
(Given $\triangle$ ABC $\sim$ $\triangle$ PQR)
Therefore, by SAS similarity criterion,
$\triangle$ CMB $\sim$ $\triangle$ RNQ.
Hence, all three parts are proved.
Exercise 6.3
Question 1. State which pairs of triangles in Fig. 6.34 are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form :

Answer:
We will examine each pair of triangles given in the figure to determine if they are similar based on the standard similarity criteria: AAA, SSS, and SAS.
Pair (i): $\triangle$ ABC and $\triangle$ PQR
Given angles:
$\angle$ A = $60^\circ$
$\angle$ B = $80^\circ$
$\angle$ C = $40^\circ$
and
$\angle$ P = $60^\circ$
$\angle$ Q = $80^\circ$
$\angle$ R = $40^\circ$
Comparing the angles of the two triangles:
$\angle$ A = $\angle$ P = $60^\circ$
$\angle$ B = $\angle$ Q = $80^\circ$
$\angle$ C = $\angle$ R = $40^\circ$
Since all corresponding angles are equal, the triangles are similar by the AAA similarity criterion.
Symbolic form: $\triangle$ ABC $\sim \triangle$ PQR.
Pair (ii): $\triangle$ ABC and $\triangle$ PQR
Given sides:
$\triangle$ ABC: AB = 2, BC = 2.5, AC = 3
$\triangle$ PQR: PQ = 6, QR = 4, PR = 5
Let's check the ratio of corresponding sides. Arrange the sides in increasing order for both triangles:
$\triangle$ ABC: 2, 2.5, 3
$\triangle$ PQR: 4, 5, 6
Let's check the ratios of the sides:
$\frac{AB}{QR} = \frac{2}{4} = \frac{1}{2}$
$\frac{BC}{PR} = \frac{2.5}{5} = \frac{2.5 \times 2}{5 \times 2} = \frac{5}{10} = \frac{1}{2}$
$\frac{AC}{PQ} = \frac{3}{6} = \frac{1}{2}$
Since the ratios of all corresponding sides are equal, the triangles are similar by the SSS similarity criterion.
The correspondence of vertices is based on the ratios: AB $\leftrightarrow$ QR (C opposite AB, P opposite QR $\implies$ C $\leftrightarrow$ P), BC $\leftrightarrow$ PR (A opposite BC, Q opposite PR $\implies$ A $\leftrightarrow$ Q), AC $\leftrightarrow$ PQ (B opposite AC, R opposite PQ $\implies$ B $\leftrightarrow$ R).
Symbolic form: $\triangle$ ABC $\sim \triangle$ QRP.
Pair (iii): $\triangle$ LMP and $\triangle$ DEF
Given sides:
$\triangle$ LMP: LM = 2.7, MP = 2, LP = 3
$\triangle$ DEF: DE = 4, EF = 5, DF = 6
Let's check the ratio of corresponding sides. Arrange the sides in increasing order for both triangles:
$\triangle$ LMP: 2, 2.7, 3
$\triangle$ DEF: 4, 5, 6
Let's check the ratios of the sides (smallest to smallest, middle to middle, largest to largest):
$\frac{MP}{DE} = \frac{2}{4} = \frac{1}{2}$
$\frac{LM}{EF} = \frac{2.7}{5} = \frac{27}{50}$
$\frac{LP}{DF} = \frac{3}{6} = \frac{1}{2}$
Since $\frac{27}{50} \neq \frac{1}{2}$, the ratios of corresponding sides are not equal.
Therefore, the triangles are not similar.
Pair (iv): $\triangle$ MNL and $\triangle$ PQR
Given sides and angle:
$\triangle$ MNL: $\angle$ M = $70^\circ$, LM = 5, MN = 2.5
$\triangle$ PQR: $\angle$ Q = $70^\circ$, PQ = 5, QR = 10
We have $\angle$ M = $\angle$ Q = $70^\circ$. This is one angle equal.
Let's check the ratio of the sides including these angles.
In $\triangle$ MNL, the sides including $\angle$ M are MN and ML (or LM).
In $\triangle$ PQR, the sides including $\angle$ Q are PQ and QR.
Let's check the ratios:
$\frac{MN}{PQ} = \frac{2.5}{5} = \frac{25}{50} = \frac{1}{2}$
$\frac{ML}{QR} = \frac{5}{10} = \frac{1}{2}$
Since $\frac{MN}{PQ} = \frac{ML}{QR}$ and the included angles are equal ($\angle$ M = $\angle$ Q), the triangles are similar by the SAS similarity criterion.
The correspondence is M $\leftrightarrow$ Q, N $\leftrightarrow$ P, L $\leftrightarrow$ R.
Symbolic form: $\triangle$ MNL $\sim \triangle$ QPR.
Pair (v): $\triangle$ ABC and $\triangle$ FDE
Given sides and angle:
$\triangle$ ABC: AB = 2.5, BC = 3, $\angle$ A = $80^\circ$
$\triangle$ FDE: FE = 6, FD = 5, $\angle$ F = $80^\circ$
We have $\angle$ A = $\angle$ F = $80^\circ$. This is one angle equal.
For SAS similarity, this equal angle must be included between the proportional sides in both triangles.
In $\triangle$ ABC, $\angle$ A is included between sides AB and AC. We are given AB=2.5 and BC=3, but not AC.
In $\triangle$ FDE, $\angle$ F is included between sides FD and FE. We are given FD=5 and FE=6.
The given angle $\angle$ A in $\triangle$ ABC is not the angle between the given sides AB and BC (it is opposite to side BC).
The given angle $\angle$ F in $\triangle$ FDE IS the angle between the given sides FD and FE.
To apply SAS, we would need $\frac{AB}{FD} = \frac{AC}{FE}$ or $\frac{AB}{FE} = \frac{AC}{FD}$, with $\angle$ A = $\angle$ F. Or, we might check if the ratio of sides around $\angle$ A (AB, AC) is proportional to sides around $\angle$ F (FD, FE).
Let's check the ratios of the given sides around the angle F in $\triangle$ FDE (FD, FE) with the given sides in $\triangle$ ABC (AB, BC):
$\frac{AB}{FD} = \frac{2.5}{5} = \frac{1}{2}$
$\frac{BC}{FE} = \frac{3}{6} = \frac{1}{2}$
While the ratio of two pairs of sides is equal ($\frac{AB}{FD} = \frac{BC}{FE}$), the equal angle ($\angle$ A = $\angle$ F) is not the angle included between these sides in both triangles. $\angle$ F is included between FD and FE, but $\angle$ A is opposite to BC.
Therefore, the triangles are not similar by the SAS similarity criterion with the given information.
Pair (vi): $\triangle$ DEF and $\triangle$ PQR
Given angles:
$\triangle$ DEF: $\angle$ D = $70^\circ$, $\angle$ E = $80^\circ$
$\triangle$ PQR: $\angle$ Q = $80^\circ$, $\angle$ R = $30^\circ$
First, let's find the third angle in each triangle using the angle sum property of a triangle.
In $\triangle$ DEF:
$\angle$ D + $\angle$ E + $\angle$ F = $180^\circ$
$70^\circ$ + $80^\circ$ + $\angle$ F = $180^\circ$
$150^\circ$ + $\angle$ F = $180^\circ$
$\angle$ F = $180^\circ - 150^\circ = 30^\circ$
In $\triangle$ PQR:
$\angle$ P + $\angle$ Q + $\angle$ R = $180^\circ$
$\angle$ P + $80^\circ$ + $30^\circ$ = $180^\circ$
$\angle$ P + $110^\circ$ = $180^\circ$
$\angle$ P = $180^\circ - 110^\circ = 70^\circ$
Now, let's compare the angles of the two triangles:
$\angle$ D = $70^\circ = \angle$ P
$\angle$ E = $80^\circ = \angle$ Q
$\angle$ F = $30^\circ = \angle$ R
Since all corresponding angles are equal, the triangles are similar by the AAA similarity criterion.
Symbolic form: $\triangle$ DEF $\sim \triangle$ PQR.
Question 2. In Fig. 6.35, ∆ ODC ~ ∆ OBA, ∠BOC = 125° and ∠CDO = 70°. Find ∠DOC, ∠DCO and ∠OAB.

Answer:
Given:
$\triangle$ ODC $\sim$ $\triangle$ OBA
$\angle$ BOC = $125^\circ$
$\angle$ CDO = $70^\circ$
To Find:
$\angle$ DOC, $\angle$ DCO, and $\angle$ OAB.
Solution:
The line segment BD is a straight line. The angles $\angle$ DOC and $\angle$ BOC form a linear pair.
Therefore, the sum of angles in a linear pair is $180^\circ$.
$ \angle\text{DOC} + \angle\text{BOC} = 180^\circ $
$\angle\text{DOC} + 125^\circ = 180^\circ$
(Linear Pair)
$ \angle\text{DOC} = 180^\circ - 125^\circ $
$ \angle\text{DOC} = 55^\circ $
Thus, the first angle found is $\angle$ DOC = $55^\circ$.
Now, consider $\triangle$ ODC. The sum of angles in a triangle is $180^\circ$.
$ \angle\text{DOC} + \angle\text{CDO} + \angle\text{DCO} = 180^\circ $
$55^\circ + 70^\circ + \angle\text{DCO} = 180^\circ$
(Angle sum property of $\triangle$ ODC)
$ 125^\circ + \angle\text{DCO} = 180^\circ $
$ \angle\text{DCO} = 180^\circ - 125^\circ $
$ \angle\text{DCO} = 55^\circ $
Thus, the second angle found is $\angle$ DCO = $55^\circ$.
We are given that $\triangle$ ODC $\sim$ $\triangle$ OBA.
For similar triangles, the corresponding angles are equal.
The corresponding vertices are O $\leftrightarrow$ O, D $\leftrightarrow$ B, and C $\leftrightarrow$ A.
Therefore, $\angle$ DCO corresponds to $\angle$ BAO (or $\angle$ OAB), $\angle$ CDO corresponds to $\angle$ ABO (or $\angle$ OBA), and $\angle$ DOC corresponds to $\angle$ BOA.
$\angle\text{DCO} = \angle\text{OAB}$
(Corresponding angles of similar triangles)
Since we found $\angle$ DCO = $55^\circ$, we have:
$ \angle\text{OAB} = 55^\circ $
Thus, the third angle found is $\angle$ OAB = $55^\circ$.
We can also find $\angle$ OBA:
$\angle\text{CDO} = \angle\text{OBA}$
(Corresponding angles of similar triangles)
Since $\angle$ CDO = $70^\circ$, we have:
$ \angle\text{OBA} = 70^\circ $
Also, $\angle$ DOC and $\angle$ BOA are vertically opposite angles, so $\angle$ BOA = $\angle$ DOC = $55^\circ$.
In $\triangle$ OBA, $\angle$ OAB + $\angle$ OBA + $\angle$ BOA = $55^\circ + 70^\circ + 55^\circ = 180^\circ$, which confirms the angle sum property for $\triangle$ OBA.
The required angles are $\angle$ DOC = $55^\circ$, $\angle$ DCO = $55^\circ$, and $\angle$ OAB = $55^\circ$.
Question 3. Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using a similarity criterion for two triangles, show that $\frac{OA}{OC}$ = $\frac{OB}{OD}$.
Answer:
Given:
ABCD is a trapezium in which AB is parallel to DC ($AB \parallel DC$).
The diagonals AC and BD intersect each other at the point O.
To Prove:
$ \frac{\text{OA}}{\text{OC}} = \frac{\text{OB}}{\text{OD}} $
Construction Required:
Draw the trapezium ABCD with AB parallel to DC. Draw the diagonals AC and BD intersecting at point O.
Proof:
Consider the two triangles $\triangle$ AOB and $\triangle$ COD.
Since AB is parallel to DC and AC is a transversal intersecting AB and DC,
$\angle\text{OAB} = \angle\text{OCD}$
(Alternate interior angles)
Since AB is parallel to DC and BD is a transversal intersecting AB and DC,
$\angle\text{OBA} = \angle\text{ODC}$
(Alternate interior angles)
The angles $\angle$ AOB and $\angle$ COD are vertically opposite angles formed by the intersection of diagonals AC and BD.
$\angle\text{AOB} = \angle\text{COD}$
(Vertically opposite angles)
In $\triangle$ AOB and $\triangle$ COD, we have:
$\angle\text{OAB} = \angle\text{OCD}$
$\angle\text{OBA} = \angle\text{ODC}$
$\angle\text{AOB} = \angle\text{COD}$
Since all three corresponding angles are equal, by AAA similarity criterion,
$ \triangle\text{AOB} \sim \triangle\text{COD} $
When two triangles are similar, the ratio of their corresponding sides is equal.
Therefore, the ratio of the sides opposite to the equal angles must be proportional:
The side opposite $\angle$ OAB ($=\angle$ OCD) in $\triangle$ AOB is OB. The side opposite $\angle$ OCD in $\triangle$ COD is OD.
The side opposite $\angle$ OBA ($=\angle$ ODC) in $\triangle$ AOB is OA. The side opposite $\angle$ ODC in $\triangle$ COD is OC.
The side opposite $\angle$ AOB ($=\angle$ COD) in $\triangle$ AOB is AB. The side opposite $\angle$ COD in $\triangle$ COD is CD.
So, we can write the proportion of corresponding sides as:
$ \frac{\text{OA}}{\text{OC}} = \frac{\text{OB}}{\text{OD}} = \frac{\text{AB}}{\text{CD}} $
Considering the first two ratios, we get:
$ \frac{\text{OA}}{\text{OC}} = \frac{\text{OB}}{\text{OD}} $
Hence, proved.
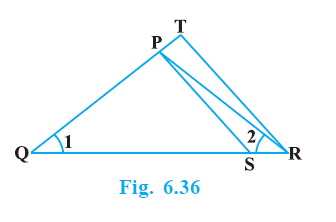
Question 4. In fig. 6.36, $\frac{QR}{QS}$ = $\frac{QT}{PR}$ and ∠1 = ∠2. Show that ∆ PQS ~ ∆ TQR.
Answer:
Given:
In the given figure, $\frac{\text{QR}}{\text{QS}}$ = $\frac{\text{QT}}{\text{PR}}$ and $\angle 1$ = $\angle 2$.
To Prove:
$\triangle$ PQS $\sim$ $\triangle$ TQR.
Proof:
In $\triangle$ PQR, we are given that $\angle 1 = \angle 2$.
In any triangle, sides opposite to equal angles are equal.
Therefore, in $\triangle$ PQR, the side opposite to $\angle 1$ (which is $\angle$ PQR) is PR, and the side opposite to $\angle 2$ (which is $\angle$ PRQ) is PQ.
PQ = PR
(Sides opposite equal angles in $\triangle$ PQR)
We are given the ratio:
$\frac{\text{QR}}{\text{QS}} = \frac{\text{QT}}{\text{PR}}$
(Given)
Substitute PR = PQ into the given ratio:
$\frac{\text{QR}}{\text{QS}} = \frac{\text{QT}}{\text{PQ}}$
... (i)
Now, consider the triangles $\triangle$ PQS and $\triangle$ TQR that we need to prove similar.
From the figure, the angle $\angle 1$ is common to both triangles. $\angle 1$ is $\angle$ PQR, which is the same as $\angle$ PQS in $\triangle$ PQS and $\angle$ TQR in $\triangle$ TQR.
$\angle \text{PQS} = \angle \text{TQR}$
(Both are equal to $\angle 1$)
Let's rearrange the equation (i) to match the sides of $\triangle$ PQS and $\triangle$ TQR that include the common angle $\angle 1$. The sides including $\angle$ PQS in $\triangle$ PQS are PQ and QS. The sides including $\angle$ TQR in $\triangle$ TQR are QT and QR.
From equation (i), $\frac{\text{QR}}{\text{QS}} = \frac{\text{QT}}{\text{PQ}}$. By cross-multiplication, $\text{QR} \cdot \text{PQ} = \text{QS} \cdot \text{QT}$. Dividing by $\text{QS} \cdot \text{QT}$, we get:
$\frac{\text{PQ}}{\text{QT}} = \frac{\text{QS}}{\text{QR}}$
... (ii)
In $\triangle$ PQS and $\triangle$ TQR, we have:
$\angle \text{PQS} = \angle \text{TQR}$
$\frac{\text{PQ}}{\text{QT}} = \frac{\text{QS}}{\text{QR}}$
(From (ii))
We have shown that one angle of $\triangle$ PQS is equal to one angle of $\triangle$ TQR, and the sides including these angles are proportional.
Therefore, by SAS similarity criterion,
$ \triangle\text{PQS} \sim \triangle\text{TQR} $
Hence, proved.
Question 5. S and T are points on sides PR and QR of ∆ PQR such that ∠P = ∠RTS. Show that ∆ RPQ ~ ∆ RTS.
Answer:
Given:
S is a point on side PR of $\triangle$ PQR.
T is a point on side QR of $\triangle$ PQR.
$\angle$ P = $\angle$ RTS.
To Prove:
$\triangle$ RPQ $\sim$ $\triangle$ RTS.
Construction Required:
Draw a triangle PQR. Mark point S on PR and point T on QR such that $\angle$ P = $\angle$ RTS.
Proof:
Consider the two triangles $\triangle$ RPQ and $\triangle$ RTS.
We are given that $\angle$ P = $\angle$ RTS.
$\angle\text{QPR} = \angle\text{RTS}$
(Given)
The angle $\angle$ R is common to both triangles $\triangle$ RPQ and $\triangle$ RTS.
$\angle\text{PRQ} = \angle\text{TRS}$
(Common angle)
In $\triangle$ RPQ and $\triangle$ RTS, we have shown that two corresponding angles are equal.
$\angle\text{QPR} = \angle\text{RTS}$
$\angle\text{PRQ} = \angle\text{TRS}$
Therefore, by AA similarity criterion,
$ \triangle\text{RPQ} \sim \triangle\text{RTS} $
Hence, proved.
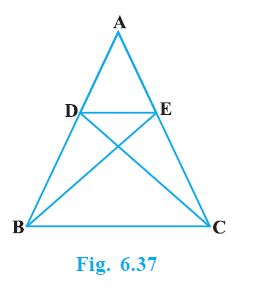
Question 6. In Fig. 6.37, if ∆ ABE ≅ ∆ ACD, show that ∆ ADE ~ ∆ ABC.
Answer:
Given:
In the given figure, $\triangle$ ABE $\cong$ $\triangle$ ACD.
To Prove:
$\triangle$ ADE $\sim$ $\triangle$ ABC.
Proof:
Since $\triangle$ ABE $\cong$ $\triangle$ ACD, the corresponding parts of the congruent triangles are equal (CPCT).
Therefore,
AB = AC
(CPCT)
AE = AD
(CPCT)
Now, consider the triangles $\triangle$ ADE and $\triangle$ ABC.
Both triangles share the common angle $\angle$ A.
$\angle\text{DAE} = \angle\text{BAC}$
(Common angle)
From the results of congruence, we have AE = AD and AB = AC.
Let's consider the ratio of the sides including the common angle $\angle$ A in $\triangle$ ADE and $\triangle$ ABC.
For $\triangle$ ADE, the sides are AD and AE.
For $\triangle$ ABC, the sides are AB and AC.
We can write the ratios as $\frac{\text{AD}}{\text{AB}}$ and $\frac{\text{AE}}{\text{AC}}$.
Since AD = AE and AB = AC, the ratio $\frac{\text{AD}}{\text{AB}}$ can be written as $\frac{\text{AE}}{\text{AC}}$ by substituting AE for AD in the numerator and AC for AB in the denominator. Thus,
$\frac{\text{AD}}{\text{AB}} = \frac{\text{AE}}{\text{AC}}$
Therefore, in $\triangle$ ADE and $\triangle$ ABC, we have:
$\angle\text{DAE} = \angle\text{BAC}$
$\frac{\text{AD}}{\text{AB}} = \frac{\text{AE}}{\text{AC}}$
According to the SAS similarity criterion, if one angle of a triangle is equal to one angle of the other triangle and the sides including these angles are proportional, then the two triangles are similar.
By SAS similarity criterion,
$ \triangle\text{ADE} \sim \triangle\text{ABC} $
Hence, proved.
Question 7. In Fig. 6.38, altitudes AD and CE of ∆ ABC intersect each other at the point P. Show that:
(i) ∆AEP ~ ∆CDP
(ii) ∆ABD ~ ∆CBE
(iii) ∆AEP ~ ∆ADB
(iv) ∆ PDC ~ ∆BEC

Answer:
Given:
AD and CE are altitudes of $\triangle$ ABC.
AD $\perp$ BC and CE $\perp$ AB.
AD and CE intersect at point P.
To Prove:
(i) $\triangle$ AEP $\sim$ $\triangle$ CDP
(ii) $\triangle$ ABD $\sim$ $\triangle$ CBE
(iii) $\triangle$ AEP $\sim$ $\triangle$ ADB
(iv) $\triangle$ PDC $\sim$ $\triangle$ BEC
Proof:
(i) To prove $\triangle$ AEP ~ $\triangle$ CDP:
Consider $\triangle$ AEP and $\triangle$ CDP.
$\angle\text{AEP} = 90^\circ$
(Since CE $\perp$ AB)
$\angle\text{CDP} = 90^\circ$
(Since AD $\perp$ BC)
$\angle\text{APE} = \angle\text{CPD}$
(Vertically opposite angles)
By AA similarity criterion,
$ \triangle\text{AEP} \sim \triangle\text{CDP} $
Hence proved.
(ii) To prove $\triangle$ ABD ~ $\triangle$ CBE:
Consider $\triangle$ ABD and $\triangle$ CBE.
$\angle\text{ADB} = 90^\circ$
(Since AD $\perp$ BC)
$\angle\text{CEB} = 90^\circ$
(Since CE $\perp$ AB)
$\angle\text{ABD} = \angle\text{CBE}$
(Common angle $\angle$ B)
By AA similarity criterion,
$ \triangle\text{ABD} \sim \triangle\text{CBE} $
Hence proved.
(iii) To prove $\triangle$ AEP ~ $\triangle$ ADB:
Consider $\triangle$ AEP and $\triangle$ ADB.
$\angle\text{AEP} = 90^\circ$
(Since CE $\perp$ AB)
$\angle\text{ADB} = 90^\circ$
(Since AD $\perp$ BC)
$\angle\text{PAE} = \angle\text{DAB}$
(Common angle $\angle$ A)
By AA similarity criterion,
$ \triangle\text{AEP} \sim \triangle\text{ADB} $
Hence proved.
(iv) To prove $\triangle$ PDC ~ $\triangle$ BEC:
Consider $\triangle$ PDC and $\triangle$ BEC.
$\angle\text{PDC} = 90^\circ$
(Since AD $\perp$ BC)
$\angle\text{BEC} = 90^\circ$
(Since CE $\perp$ AB)
$\angle\text{PCD} = \angle\text{BCE}$
(Common angle $\angle$ C)
By AA similarity criterion,
$ \triangle\text{PDC} \sim \triangle\text{BEC} $
Hence proved.
Question 8. E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that ∆ ABE ~ ∆ CFB.
Answer:
Given:
ABCD is a parallelogram.
E is a point on the side AD produced.
BE intersects CD at F.
To Prove:
$\triangle$ ABE $\sim$ $\triangle$ CFB.
Construction Required:
Draw a parallelogram ABCD. Produce side AD to point E. Draw the line segment BE intersecting side CD at point F.
Proof:
Consider the two triangles $\triangle$ ABE and $\triangle$ CFB.
In a parallelogram ABCD, opposite angles are equal.
$\angle\text{DAB} = \angle\text{BCD}$
(Opposite angles of parallelogram)
Since E is on the line AD produced, $\angle$ DAB is the same as $\angle$ BAE.
Thus, $\angle$ BAE = $\angle$ BCD. Since F is a point on CD, $\angle$ BCD is the same as $\angle$ FCB.
$\angle\text{BAE} = \angle\text{FCB}$
In a parallelogram ABCD, opposite sides are parallel.
So, AB $\parallel$ DC.
Since F is a point on the line segment DC, it means AB $\parallel$ CF.
Now, consider AB $\parallel$ CF and BE as a transversal line intersecting these parallel lines.
The angles $\angle$ ABE and $\angle$ CFB are alternate interior angles.
$\angle\text{ABE} = \angle\text{CFB}$
(Alternate interior angles)
Now, let's examine $\triangle$ ABE and $\triangle$ CFB again.
We have found two pairs of corresponding angles that are equal:
$\angle\text{BAE} = \angle\text{FCB}$
$\angle\text{ABE} = \angle\text{CFB}$
By the AA similarity criterion, if two angles of one triangle are equal to two corresponding angles of another triangle, then the triangles are similar.
Therefore,
$ \triangle\text{ABE} \sim \triangle\text{CFB} $
Hence, proved.
Question 9. In Fig. 6.39, ABC and AMP are two right triangles, right angled at B and M respectively. Prove that:
(i) ∆ABC ~ ∆AMP
(ii) $\frac{CA}{PA}$ = $\frac{BC}{MP}$

Answer:
Given:
$\triangle$ ABC is a right triangle, right-angled at B ($\angle$ ABC = $90^\circ$).
$\triangle$ AMP is a right triangle, right-angled at M ($\angle$ AMP = $90^\circ$).
To Prove:
(i) $\triangle$ ABC $\sim$ $\triangle$ AMP
(ii) $\frac{\text{CA}}{\text{PA}} = \frac{\text{BC}}{\text{MP}}$
Proof:
(i) To prove $\triangle$ ABC ~ $\triangle$ AMP:
Consider the two triangles $\triangle$ ABC and $\triangle$ AMP.
We are given that both triangles are right-angled.
$\angle\text{ABC} = 90^\circ$
(Given)
$\angle\text{AMP} = 90^\circ$
(Given)
From the figure, it is clear that $\angle$ BAC is the same angle as $\angle$ PAM. This angle is common to both triangles $\triangle$ ABC and $\triangle$ AMP.
$\angle\text{BAC} = \angle\text{PAM}$
(Common angle $\angle$ A)
In $\triangle$ ABC and $\triangle$ AMP, we have shown that two corresponding angles are equal.
$\angle$ ABC = $\angle$ AMP (Both are $90^\circ$)
$\angle$ BAC = $\angle$ PAM (Common angle)
Therefore, by AA similarity criterion,
$ \triangle\text{ABC} \sim \triangle\text{AMP} $
Hence proved part (i).
(ii) To prove $\frac{\text{CA}}{\text{PA}} = \frac{\text{BC}}{\text{MP}}$:
Since we have already proved that $\triangle$ ABC $\sim$ $\triangle$ AMP (from part (i)), the ratio of their corresponding sides must be equal.
The corresponding vertices are A $\leftrightarrow$ A, B $\leftrightarrow$ M, and C $\leftrightarrow$ P.
Thus, the corresponding sides are AB and AM, BC and MP, AC and AP.
The ratio of corresponding sides is:
$\frac{\text{AB}}{\text{AM}} = \frac{\text{BC}}{\text{MP}} = \frac{\text{AC}}{\text{AP}}$
(Corresponding sides of similar triangles)
From this equality, we can take the second and third ratios:
$ \frac{\text{BC}}{\text{MP}} = \frac{\text{AC}}{\text{AP}} $
Rearranging the terms to match the required expression:
$ \frac{\text{AC}}{\text{AP}} = \frac{\text{BC}}{\text{MP}} $
This is the same as:
$ \frac{\text{CA}}{\text{PA}} = \frac{\text{BC}}{\text{MP}} $
Hence proved part (ii).
Question 10. CD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ∆ ABC and ∆ EFG respectively. If ∆ABC ~ ∆ FEG, show that:
(i) $\frac{CD}{GH}$ = $\frac{AC}{FG}$
(ii) ∆ DCB ~ ∆ HGE
(iii) ∆ DCA ~ ∆ HGF
Answer:
Given:
$\triangle$ ABC $\sim$ $\triangle$ FEG.
CD is the bisector of $\angle$ ACB, with point D on side AB of $\triangle$ ABC.
GH is the bisector of $\angle$ EGF, with point H on side FE of $\triangle$ EFG.
To Prove:
(i) $ \frac{\text{CD}}{\text{GH}} = \frac{\text{AC}}{\text{FG}} $
(ii) $ \triangle\text{DCB} \sim \triangle\text{HGE} $
(iii) $ \triangle\text{DCA} \sim \triangle\text{HGF} $
Construction Required:
Draw two triangles ABC and FEG such that $\triangle$ ABC is similar to $\triangle$ FEG. Draw the angle bisector CD of $\angle$ ACB, with D on AB. Draw the angle bisector GH of $\angle$ EGF, with H on FE.
Proof:
Since it is given that $ \triangle\text{ABC} \sim \triangle\text{FEG} $, their corresponding angles are equal and the ratio of their corresponding sides is equal.
$\angle\text{A} = \angle\text{F}$
(Corresponding angles of similar triangles)
$\angle\text{B} = \angle\text{E}$
(Corresponding angles of similar triangles)
$\angle\text{ACB} = \angle\text{FEG}$
(Corresponding angles of similar triangles)
Also, the ratio of corresponding sides is:
$\frac{\text{AB}}{\text{FE}} = \frac{\text{BC}}{\text{EG}} = \frac{\text{AC}}{\text{FG}}$
(Ratio of corresponding sides of similar triangles)
CD is the bisector of $\angle$ ACB, so it divides the angle into two equal halves:
$\angle\text{ACD} = \angle\text{BCD} = \frac{1}{2}\angle\text{ACB}$
GH is the bisector of $\angle$ EGF, so it divides the angle into two equal halves:
$\angle\text{EGH} = \angle\text{FGH} = \frac{1}{2}\angle\text{EGF}$
Since $\angle$ ACB = $\angle$ EGF, it follows that their halves are also equal:
$\frac{1}{2}\angle\text{ACB} = \frac{1}{2}\angle\text{EGF}$
Therefore,
$\angle\text{ACD} = \angle\text{BCD} = \angle\text{EGH} = \angle\text{FGH}$
... (i)
(i) To prove $ \frac{\text{CD}}{\text{GH}} = \frac{\text{AC}}{\text{FG}} $:
Consider $\triangle$ DCA and $\triangle$ HGF.
We have:
$\angle\text{A} = \angle\text{F}$
(Given $\triangle$ ABC $\sim$ $\triangle$ FEG)
$\angle\text{ACD} = \angle\text{FGH}$
(From (i))
Since two corresponding angles are equal, by AA similarity criterion,
$ \triangle\text{DCA} \sim \triangle\text{HGF} $
When two triangles are similar, the ratio of their corresponding sides is equal.
Therefore, the ratio of the sides opposite to the equal angles must be proportional:
The side opposite $\angle$ A (= $\angle$ F) in $\triangle$ DCA is CD. The side opposite $\angle$ F in $\triangle$ HGF is GH.
The side opposite $\angle$ ACD (= $\angle$ FGH) in $\triangle$ DCA is AD. The side opposite $\angle$ FGH in $\triangle$ HGF is FH.
The side opposite $\angle$ ADC (= $\angle$ HFG) in $\triangle$ DCA is AC. The side opposite $\angle$ HFG in $\triangle$ HGF is FG.
So, we can write the proportion of corresponding sides as:
$ \frac{\text{CD}}{\text{GH}} = \frac{\text{AD}}{\text{FH}} = \frac{\text{AC}}{\text{FG}} $
From the first and third ratios, we get:
$ \frac{\text{CD}}{\text{GH}} = \frac{\text{AC}}{\text{FG}} $
Hence, proved part (i).
(ii) To prove $ \triangle\text{DCB} \sim \triangle\text{HGE} $:
Consider $\triangle$ DCB and $\triangle$ HGE.
We have:
$\angle\text{B} = \angle\text{E}$
(Given $\triangle$ ABC $\sim$ $\triangle$ FEG)
$\angle\text{BCD} = \angle\text{EGH}$
(From (i))
Since two corresponding angles are equal, by AA similarity criterion,
$ \triangle\text{DCB} \sim \triangle\text{HGE} $
Hence, proved part (ii).
(iii) To prove $ \triangle\text{DCA} \sim \triangle\text{HGF} $:
This was already proved in part (i).
Consider $\triangle$ DCA and $\triangle$ HGF.
We have:
$\angle\text{A} = \angle\text{F}$
(Given $\triangle$ ABC $\sim$ $\triangle$ FEG)
$\angle\text{ACD} = \angle\text{FGH}$
(From (i))
By AA similarity criterion,
$ \triangle\text{DCA} \sim \triangle\text{HGF} $
Hence, proved part (iii).
Question 11. In Fig. 6.40, E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD⊥BC and EF⊥AC, prove that ∆ ABD ~ ∆ ECF.

Answer:
Given:
$\triangle$ ABC is an isosceles triangle with AB = AC.
E is a point on the side CB produced.
AD $\perp$ BC, where D is on BC.
EF $\perp$ AC, where F is on AC.
To Prove:
$\triangle$ ABD $\sim$ $\triangle$ ECF.
Proof:
In $\triangle$ ABC, since AB = AC, the angles opposite to these sides are equal.
$\angle\text{ABC} = \angle\text{ACB}$
(Angles opposite to equal sides of an isosceles triangle are equal)
Since D is a point on BC, $\angle$ ABC is the same as $\angle$ ABD.
Since E is a point on CB produced, $\angle$ ACB is the same as $\angle$ ECF (they are the same angle). Note that $\angle$ ACB and $\angle$ ECF are vertically opposite angles only if B lies between C and E, but here E is on CB *produced*, so C lies between B and E, and $\angle$ ACB and $\angle$ ECF are the same angle $\angle$ C.
So, from $\angle$ ABC = $\angle$ ACB, we have:
$\angle\text{ABD} = \angle\text{ECF}$
... (i)
Now, consider the two triangles $\triangle$ ABD and $\triangle$ ECF.
We are given that AD $\perp$ BC, so $\angle$ ADB is a right angle.
$\angle\text{ADB} = 90^\circ$
(Given AD $\perp$ BC)
We are given that EF $\perp$ AC, so $\angle$ EFC is a right angle.
$\angle\text{EFC} = 90^\circ$
(Given EF $\perp$ AC)
Thus, we have one pair of equal angles:
$\angle\text{ADB} = \angle\text{EFC}$
(Both are $90^\circ$)
From equation (i), we have the second pair of equal angles:
$\angle\text{ABD} = \angle\text{ECF}$
(Proved above)
In $\triangle$ ABD and $\triangle$ ECF, we have:
$\angle$ ADB = $\angle$ EFC (Both $90^\circ$)
$\angle$ ABD = $\angle$ ECF (Proved)
By AA similarity criterion, if two angles of one triangle are respectively equal to two angles of another triangle, then the two triangles are similar.
Therefore,
$ \triangle\text{ABD} \sim \triangle\text{ECF} $
Hence, proved.
Question 12. Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of ∆ PQR (see Fig. 6.41). Show that ∆ ABC ~ ∆ PQR.
Answer:
Given:
In $\triangle$ ABC, AD is the median to side BC.
In $\triangle$ PQR, PM is the median to side QR.
The sides are proportional as $\frac{\text{AB}}{\text{PQ}} = \frac{\text{BC}}{\text{QR}} = \frac{\text{AD}}{\text{PM}}$.
To Prove:
$\triangle$ ABC $\sim$ $\triangle$ PQR.
Proof:
We are given that AD is the median of $\triangle$ ABC. This means D is the midpoint of BC.
Therefore, $\text{BD} = \text{DC} = \frac{1}{2}\text{BC}$.
We are given that PM is the median of $\triangle$ PQR. This means M is the midpoint of QR.
Therefore, $\text{QM} = \text{MR} = \frac{1}{2}\text{QR}$.
We are given the proportionality of sides and medians:
$\frac{\text{AB}}{\text{PQ}} = \frac{\text{BC}}{\text{QR}} = \frac{\text{AD}}{\text{PM}}$
(Given)
Substitute $\text{BC} = 2\text{BD}$ and $\text{QR} = 2\text{QM}$ into the ratio $\frac{\text{BC}}{\text{QR}}$:
$ \frac{\text{BC}}{\text{QR}} = \frac{2\text{BD}}{2\text{QM}} = \frac{\text{BD}}{\text{QM}} $
So, the given proportionality can be rewritten as:
$\frac{\text{AB}}{\text{PQ}} = \frac{\text{BD}}{\text{QM}} = \frac{\text{AD}}{\text{PM}}$
... (i)
Now, consider $\triangle$ ABD and $\triangle$ PQM.
From equation (i), we have $\frac{\text{AB}}{\text{PQ}} = \frac{\text{BD}}{\text{QM}} = \frac{\text{AD}}{\text{PM}}$.
This shows that the three sides of $\triangle$ ABD are proportional to the three sides of $\triangle$ PQM.
By SSS similarity criterion,
$ \triangle\text{ABD} \sim \triangle\text{PQM} $
Since $\triangle$ ABD is similar to $\triangle$ PQM, their corresponding angles are equal.
$\angle\text{ABD} = \angle\text{PQM}$
(Corresponding angles of similar triangles)
Since D lies on BC and M lies on QR, the angles $\angle$ ABD and $\angle$ ABC are the same angle, and the angles $\angle$ PQM and $\angle$ PQR are the same angle.
$\angle\text{ABC} = \angle\text{PQR}$
... (ii)
Now, consider the triangles $\triangle$ ABC and $\triangle$ PQR.
We are given the proportionality:
$\frac{\text{AB}}{\text{PQ}} = \frac{\text{BC}}{\text{QR}}$
... (iii) (Given)
And we have shown that the included angle between these sides is equal:
$\angle\text{ABC} = \angle\text{PQR}$
(From (ii))
In $\triangle$ ABC and $\triangle$ PQR, we have two pairs of corresponding sides proportional and the included angles equal.
By SAS similarity criterion,
$ \triangle\text{ABC} \sim \triangle\text{PQR} $
Hence, proved.
Question 13. D is a point on the side BC of a triangle ABC such that ∠ADC = ∠BAC. Show that CA2 = CB.CD.
Answer:
Given:
In $\triangle$ ABC, D is a point on the side BC such that $\angle$ ADC = $\angle$ BAC.
To Prove:
$ \text{CA}^2 = \text{CB} \cdot \text{CD} $
Construction Required:
Draw a triangle ABC. Mark a point D on the side BC such that the angle $\angle$ ADC is equal to $\angle$ BAC.
Proof:
Consider the two triangles $\triangle$ ABC and $\triangle$ DAC.
In $\triangle$ ABC and $\triangle$ DAC:
$\angle\text{BAC} = \angle\text{ADC}$
(Given)
The angle $\angle$ C is common to both triangles $\triangle$ ABC (specifically $\angle$ ACB) and $\triangle$ DAC (specifically $\angle$ DCA).
$\angle\text{ACB} = \angle\text{DCA}$
(Common angle $\angle$ C)
Since two angles of $\triangle$ ABC are equal to two corresponding angles of $\triangle$ DAC, the triangles are similar by AA similarity criterion.
$ \triangle\text{ABC} \sim \triangle\text{DAC} $
When two triangles are similar, the ratio of their corresponding sides is equal. The corresponding vertices are matched based on the equal angles: $\angle$ BAC = $\angle$ ADC (A $\leftrightarrow$ D), $\angle$ ACB = $\angle$ DCA (C $\leftrightarrow$ C). The remaining vertex B in $\triangle$ ABC corresponds to A in $\triangle$ DAC (B $\leftrightarrow$ A).
So, we can write the proportionality of corresponding sides as:
$ \frac{\text{AB}}{\text{DA}} = \frac{\text{BC}}{\text{AC}} = \frac{\text{AC}}{\text{DC}} $
Taking the last two ratios, we have:
$\frac{\text{BC}}{\text{AC}} = \frac{\text{AC}}{\text{DC}}$
Now, cross-multiply the terms:
$ \text{BC} \cdot \text{DC} = \text{AC} \cdot \text{AC} $
$ \text{BC} \cdot \text{CD} = \text{AC}^2 $
Rearranging the terms to match the required form:
$ \text{CA}^2 = \text{CB} \cdot \text{CD} $
Hence, proved.
Question 14. Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that ∆ABC ~ ∆ PQR.
Answer:
Given:
Two triangles $\triangle$ ABC and $\triangle$ PQR.
AD is the median to side BC in $\triangle$ ABC, so D is the midpoint of BC.
PM is the median to side QR in $\triangle$ PQR, so M is the midpoint of QR.
The sides AB and AC and median AD of $\triangle$ ABC are proportional to sides PQ and PR and median PM of $\triangle$ PQR.
$\frac{\text{AB}}{\text{PQ}} = \frac{\text{AC}}{\text{PR}} = \frac{\text{AD}}{\text{PM}}$
To Prove:
$ \triangle\text{ABC} \sim \triangle\text{PQR} $
Construction Required:
Extend median AD to a point E such that AD = DE. Join CE.
Extend median PM to a point N such that PM = MN. Join RN.
Proof:
Consider $\triangle$ ABD and $\triangle$ ECD.
We have:
AD = DE
(By Construction)
BD = DC
(AD is the median to BC, so D is midpoint of BC)
$\angle\text{ADB} = \angle\text{EDC}$
(Vertically Opposite Angles)
Therefore, by SAS Congruence Criterion,
$\triangle\text{ABD} \cong \triangle\text{ECD}$
By Corresponding Parts of Congruent Triangles (CPCT), we have:
AB = CE
$\angle\text{BAD} = \angle\text{CED}$
Similarly, consider $\triangle$ PQM and $\triangle$ RNM.
We have:
PM = MN
(By Construction)
QM = MR
(PM is the median to QR, so M is midpoint of QR)
$\angle\text{PMQ} = \angle\text{RMN}$
(Vertically Opposite Angles)
Therefore, by SAS Congruence Criterion,
$\triangle\text{PQM} \cong \triangle\text{RNM}$
By Corresponding Parts of Congruent Triangles (CPCT), we have:
PQ = RN
$\angle\text{QPM} = \angle\text{RMN}$
We are given that $ \frac{\text{AB}}{\text{PQ}} = \frac{\text{AC}}{\text{PR}} = \frac{\text{AD}}{\text{PM}} $.
Substitute AB = CE and PQ = RN into the proportion $ \frac{\text{AB}}{\text{PQ}} = \frac{\text{AC}}{\text{PR}} $:
$\frac{\text{CE}}{\text{RN}} = \frac{\text{AC}}{\text{PR}}$
Now, consider the ratio $ \frac{\text{AD}}{\text{PM}} $. From construction, AE = AD + DE = AD + AD = 2AD, and PN = PM + MN = PM + PM = 2PM.
So, $ \frac{\text{AD}}{\text{PM}} = \frac{2\text{AD}}{2\text{PM}} = \frac{\text{AE}}{\text{PN}} $.
Thus, the given proportionality becomes:
$\frac{\text{CE}}{\text{RN}} = \frac{\text{AC}}{\text{PR}} = \frac{\text{AE}}{\text{PN}}$
Now consider $\triangle$ ACE and $\triangle$ PRN.
We have shown that their corresponding sides are proportional:
$\frac{\text{AC}}{\text{PR}} = \frac{\text{CE}}{\text{RN}} = \frac{\text{AE}}{\text{PN}}$
Therefore, by SSS Similarity Criterion,
$\triangle\text{ACE} \sim \triangle\text{PRN}$
Due to similarity, corresponding angles are equal. The angle opposite to CE in $\triangle$ ACE is $\angle$ CAE. The angle opposite to RN in $\triangle$ PRN is $\angle$ RPN.
So,
$\angle\text{CAE} = \angle\text{RPN}$
... (i)We know that $\angle$ CAE is the same as $\angle$ CAD (since D lies on AE). $\angle$ RPN is the same as $\angle$ RPM (since M lies on PN).
So, from (i), $ \angle\text{CAD} = \angle\text{RPM} $.
From $\triangle$ ABD $\cong$ $\triangle$ ECD, we have $\angle$ BAD = $\angle$ CED. Since E lies on the line AD produced, $\angle$ CED is the same as $\angle$ CEA (angle at E in $\triangle$ ACE).
So, $ \angle\text{BAD} = \angle\text{CEA} $. From $\triangle$ ACE $\sim$ $\triangle$ PRN, we have $\angle$ CEA = $\angle$ PNR.
From $\triangle$ PQM $\cong$ $\triangle$ RNM, we have $\angle$ QPM = $\angle$ RMN. Since N lies on the line PM produced, $\angle$ RMN is the same as $\angle$ RNP (angle at N in $\triangle$ PRN).
So, $ \angle\text{QPM} = \angle\text{RNP} $.
Since $\angle$ CEA = $\angle$ PNR, we have $\angle$ BAD = $\angle$ QPM.
$\angle\text{BAD} = \angle\text{QPM}$
... (ii)Now, let's add the angles from equation (i) and (ii):
$\angle\text{CAD} + \angle\text{BAD} = \angle\text{RPM} + \angle\text{QPM}$
The sum of $\angle$ CAD and $\angle$ BAD is the entire angle $\angle$ BAC.
The sum of $\angle$ RPM and $\angle$ QPM is the entire angle $\angle$ QPR.
Thus,
$\angle\text{BAC} = \angle\text{QPR}$
Now consider $\triangle$ ABC and $\triangle$ PQR.
We are given that sides AB and AC are proportional to PQ and PR:
$\frac{\text{AB}}{\text{PQ}} = \frac{\text{AC}}{\text{PR}}$
We have also shown that the angle included between these sides is equal:
$\angle\text{BAC} = \angle\text{QPR}$
Therefore, by SAS Similarity Criterion,
$\triangle\text{ABC} \sim \triangle\text{PQR}$
Hence, proved.
Question 15. A vertical pole of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
Answer:
Given:
Length of the vertical pole = $6\text{ m}$
Length of the shadow cast by the pole = $4\text{ m}$
Length of the shadow cast by the tower = $28\text{ m}$
To Find:
The height of the tower.
Construction Required:
Draw a diagram representing a vertical pole and its shadow, and a vertical tower and its shadow, at the same time. These should form two right-angled triangles with the sun's rays making the same angle with the ground.
Solution:
At the same time of the day, the sun is in the same position in the sky. This means the angle of elevation of the sun (the angle made by the sun's rays with the ground) is the same for both the pole and the tower.
Consider the triangle formed by the vertical pole, its shadow on the ground, and the line from the top of the pole to the end of the shadow. This is a right-angled triangle.
Similarly, consider the triangle formed by the vertical tower, its shadow on the ground, and the line from the top of the tower to the end of the shadow. This is also a right-angled triangle.
Let the height of the pole be denoted by $P$ and its shadow by $S_P$.
Let the height of the tower be denoted by $T$ and its shadow by $S_T$.
We have $P = 6\text{ m}$, $S_P = 4\text{ m}$, and $S_T = 28\text{ m}$. We need to find $T$.
Let $\triangle$ABC represent the triangle formed by the pole and its shadow, where AB is the height of the pole (perpendicular to the ground), BC is the length of the shadow (on the ground), and $\angle$C is the angle of elevation of the sun.
Let $\triangle$PQR represent the triangle formed by the tower and its shadow, where PQ is the height of the tower (perpendicular to the ground), QR is the length of the shadow (on the ground), and $\angle$R is the angle of elevation of the sun.
In $\triangle$ ABC and $\triangle$ PQR:
$\angle\text{B} = \angle\text{Q} = 90^\circ$
(Both the pole and the tower are vertical to the ground)
$\angle\text{C} = \angle\text{R}$
(Angle of elevation of the sun at the same time)
Since two corresponding angles are equal, by AA similarity criterion,
$\triangle\text{ABC} \sim \triangle\text{PQR}$
When two triangles are similar, the ratio of their corresponding sides is equal.
Therefore, the ratio of the height of the pole to the height of the tower is equal to the ratio of the length of the pole's shadow to the length of the tower's shadow.
$\frac{\text{AB}}{\text{PQ}} = \frac{\text{BC}}{\text{QR}}$
Substitute the given values:
$\frac{6}{T} = \frac{4}{28}$
Simplify the fraction on the right side:
$\frac{4}{28} = \frac{\cancel{4}^{1}}{\cancel{28}_{7}} = \frac{1}{7}$
So the equation becomes:
$\frac{6}{T} = \frac{1}{7}$
To find $T$, we can cross-multiply:
$6 \times 7 = T \times 1$
$42 = T$
So, the height of the tower is $42\text{ m}$.
Answer:
The height of the tower is $42\text{ m}$.
Question 16. If AD and PM are medians of triangles ABC and PQR, respectively where ∆ ABC ~ ∆ PQR, prove that $\frac{AB}{PQ}$ = $\frac{AD}{PM}$.
Answer:
Given:
$\triangle$ ABC $\sim$ $\triangle$ PQR.
AD is the median of $\triangle$ ABC, which means D is the midpoint of BC.
PM is the median of $\triangle$ PQR, which means M is the midpoint of QR.
To Prove:
$ \frac{\text{AB}}{\text{PQ}} = \frac{\text{AD}}{\text{PM}} $
Construction Required:
Draw two triangles ABC and PQR such that they are similar ($\triangle$ ABC $\sim$ $\triangle$ PQR). Draw the median AD from A to BC and the median PM from P to QR.
Proof:
Since it is given that $ \triangle\text{ABC} \sim \triangle\text{PQR} $, their corresponding angles are equal and the ratio of their corresponding sides is equal.
Therefore, we have:
$\angle\text{B} = \angle\text{Q}$
(Corresponding angles of similar triangles)
And the ratio of corresponding sides is:
$\frac{\text{AB}}{\text{PQ}} = \frac{\text{BC}}{\text{QR}} = \frac{\text{AC}}{\text{PR}}$
(Ratio of corresponding sides of similar triangles)
Since AD is the median to BC, D is the midpoint of BC. So, BC = 2BD (or BD = $\frac{1}{2}$ BC).
Since PM is the median to QR, M is the midpoint of QR. So, QR = 2QM (or QM = $\frac{1}{2}$ QR).
Now, consider the ratio of sides $ \frac{\text{BC}}{\text{QR}} $ from the similarity of $\triangle$ ABC and $\triangle$ PQR:
$\frac{\text{BC}}{\text{QR}} = \frac{2\text{BD}}{2\text{QM}} = \frac{\text{BD}}{\text{QM}}$
From the property of similar triangles, we also have $ \frac{\text{AB}}{\text{PQ}} = \frac{\text{BC}}{\text{QR}} $.
Combining these results, we get:
$\frac{\text{AB}}{\text{PQ}} = \frac{\text{BD}}{\text{QM}}$
... (i)
Now, consider the two triangles $\triangle$ ABD and $\triangle$ PQM.
In $\triangle$ ABD and $\triangle$ PQM:
We have the ratio of sides:
$\frac{\text{AB}}{\text{PQ}} = \frac{\text{BD}}{\text{QM}}$
(From (i))
We also have the included angle:
$\angle\text{B} = \angle\text{Q}$
(From $\triangle$ ABC $\sim$ $\triangle$ PQR)
Since two pairs of sides are proportional ($ \frac{\text{AB}}{\text{PQ}} = \frac{\text{BD}}{\text{QM}} $) and the included angles are equal ($ \angle\text{B} = \angle\text{Q} $), by SAS similarity criterion,
$\triangle\text{ABD} \sim \triangle\text{PQM}$
When two triangles are similar, the ratio of their corresponding sides is equal.
Therefore, the ratio of the side AB to PQ must be equal to the ratio of the corresponding median AD to PM:
$ \frac{\text{AB}}{\text{PQ}} = \frac{\text{AD}}{\text{PM}} $
Hence, proved.

