| Latest Maths NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Exercise 13.1 | Example 1 (Before Exercise 13.2) | Exercise 13.2 |
| Example 2 (Before Exercise 13.3) | Exercise 13.3 | Exercise 13.4 |
Chapter 13 Visualising Solid Shapes
Welcome to the fascinating world of three-dimensional geometry presented in Chapter 13, "Visualising Solid Shapes," from the latest Class 7 NCERT mathematics textbook for the academic session 2024-25. This chapter serves as a crucial bridge, helping students develop the ability to perceive, understand, and represent the three-dimensional objects that populate our physical world using two-dimensional mediums like paper. It's about training the mind's eye to see depth, structure, and different perspectives. These solutions provide comprehensive guidance for the exercises designed to build these essential spatial reasoning skills.
A primary challenge in studying solid shapes is depicting them accurately on a flat surface. This chapter explores several key techniques for this translation. One fundamental method involves understanding and drawing Nets. A net is a 2D pattern that can be folded along its edges to form a 3D solid. The solutions meticulously guide students in identifying, drawing, and verifying nets for various common solids, including:
- Cubes
- Cuboids
- Cylinders
- Cones
- Pyramids (various bases)
- Prisms (various bases)
Beyond nets, the chapter explores direct drawing techniques for representing solids on paper. The solutions provide clear explanations and examples for creating:
- Oblique Sketches: These sketches attempt to show the depth of the object. While easy to draw, they often don't preserve the exact proportions or angles accurately.
- Isometric Sketches: Drawn typically on special isometric dot paper, these sketches provide a more realistic representation of the solid, maintaining the relative lengths of edges along the three main axes and giving a better sense of perspective. The solutions demonstrate step-by-step methods, especially for constructing isometric sketches of cubes and cuboids.
Another critical aspect of visualizing solids is understanding how they appear from different viewpoints. The solutions address problems requiring students to identify or draw the Front View, Top View, and Side View of various solid objects or structures (often built from unit cubes). This skill is essential in fields like engineering, architecture, and design. Furthermore, the fundamental components of solids, particularly polyhedrons (solids with flat faces, straight edges, and sharp vertices), are revisited. The concepts of Faces (F), Vertices (V), and Edges (E) are reinforced, and the solutions likely guide students in verifying the remarkable relationship known as Euler's Formula for polyhedrons: $F + V - E = 2$. Finally, the chapter might touch upon visualizing the 2D shapes (cross-sections) obtained when a solid is sliced either horizontally or vertically, and the solutions would help describe or sketch these resulting shapes.
Regarding the rationalized syllabus for 2024-25, Chapter 13, "Visualising Solid Shapes," in the Class 7 NCERT textbook maintains its focus on developing fundamental spatial visualization skills through nets, oblique and isometric sketching, different views of solids, and understanding basic properties including Euler's formula. The rationalization mainly involved streamlining the complexity and number of exercises related to constructing nets for complex shapes, drawing intricate isometric views, or analyzing complex composite solids, ensuring a strong grasp of core visualization techniques. By engaging with these detailed solutions, students can significantly improve their spatial reasoning, learn diverse methods for representing 3D shapes, understand the crucial link between 2D nets and 3D solids, and grasp foundational properties of polyhedrons.
Exercise 13.1
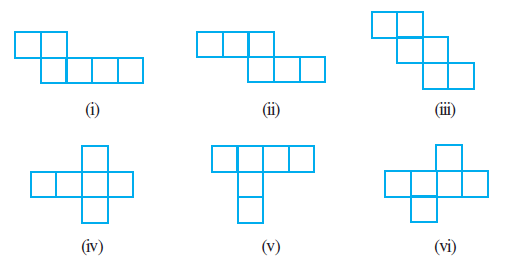
Question 1. Identify the nets which can be used to make cubes (cut out copies of the nets and try it):
Answer:
To identify which of the given nets can be used to make cubes, we need to determine if the arrangement of the 6 squares can be folded along the edges to form a closed cube without any overlaps or gaps.
(i)
The given net cannot be folded as a cube.
(ii)
The given net can be folded as a cube.
(iii)
The given net can be folded as a cube.
(iv)
The given net can be folded as a cube.
(v)
The given net cannot be folded as a cube.
(vi)
The given net can be folded as a cube.
By observing all the figures and their potential to be folded into a cube, the nets which can be used to make cubes are (ii), (iii), (iv), and (vi).
Question 2. Dice are cubes with dots on each face. Opposite faces of a die always have a total of seven dots on them.
Here are two nets to make dice (cubes); the numbers inserted in each square indicatethe number of dots in that box.
.png)
.png)
Insert suitable numbers in the blanks, remembering that the number on the opposite faces should total to 7.
Answer:
The problem states that in a standard die, the sum of the dots on opposite faces is always 7. We are given nets for dice with some numbers and blanks, and we need to fill the blanks such that this rule is followed.
(i)
By observing the above figure, which shows the completed net, the numbers are placed such that the sum of the numbers on the opposite faces is equal to 7.
So, the given net can be folded into a net of a die that follows the rule. The blanks in the original net are filled with the numbers 3, 5, and 2 as shown in the figure.
(ii)
By observing the above figure, which shows the completed net, the numbers are placed such that the sum of the numbers on the opposite faces is equal to 7.
So, the given net can be folded into a net of a die that follows the rule. The blanks in the original net are filled with the numbers 4, 5, and 6 as shown in the figure.
Question 3. Can this be a net for a die? Explain your answer.

Answer:
To determine if the given net can be a net for a die, we first check if it can be folded into a cube. If it can form a cube, we then check if the numbers on the opposite faces sum up to 7, as required for a standard die.
The given net can indeed be folded into a cube.
When the net is folded into a cube, the opposite faces will have the following pairs of numbers:
- The face with '1' is opposite the face with '4'.
- The face with '3' is opposite the face with '6'.
- The face with '2' is opposite the face with '5'.
Now, let's check the sum of the numbers on these opposite faces:
$1 + 4 = 5$
$3 + 6 = 9$
$2 + 5 = 7$
For a standard die, the sum of the numbers on opposite faces must always be 7. In this case, the pairs $(1, 4)$ and $(3, 6)$ do not sum up to 7 ($1+4=5$ and $3+6=9$).
Therefore, this net cannot be a net for a standard die because the numbers on the opposite faces do not sum to 7.
Question 4. Here is an incomplete net for making a cube. Complete it in at least two different ways. Remember that a cube has six faces. How many are there in the net here? (Give two separate diagrams. If you like, you may use a squared sheet for easy manipulation.)

Answer:
The given incomplete net has 3 faces. To make a cube, which has six faces, we need to add $6 - 3 = 3$ more faces (squares) to this net.
Here is one way to complete the net such that it can be folded into a cube:
This completed net is a valid net for a cube.
There are other ways to complete the given net to form a cube. Here is a second different way:
This completed net is also a valid net for a cube.
Question 5. Match the nets with appropriate solids:
(a) .png)
|
(i) .png)
|
(b) .png)
|
(ii) .png)
|
(c) .png)
|
(iii) .png)
|
(d) .png)
|
(iv) .png)
|
Answer:
We need to match each net with the appropriate solid figure it forms when folded.
(a)
Match: (a) (ii)
Because, the net (ii) can be folded as a square.
(b)
Match: (b) (iii)
Because, the net (iii) can be folded as a cylinder.
(c)
Match: (c) (iv)
Because, the net (iv) can be folded as a cone.
(d)
Match: (d) (i)
Because, the net (i) can be folded as a pyramid.
Example 1 (Before Exercise 13.2)
Example 1. Here is an oblique sketch of a cuboid [Fig 13.14(i)].

Draw an isometric sketch that matches this drawing.
Answer:
An isometric sketch is a representation of a 3D object on a 2D surface where lines parallel to the axes are drawn to true length along lines at $30^\circ$ or vertically on an isometric grid.
From the given oblique sketch, let's assume the dimensions of the cuboid are: Length = 4 units, Width (Depth) = 3 units, and Height = 2 units. We will draw the isometric sketch on isometric dot paper using these dimensions.
To draw the isometric sketch:
1. Choose a starting point for one corner.
2. Draw three edges from this point: one vertical (for height, 2 units), one at $30^\circ$ (for length, 4 units), and one at $30^\circ$ in the other direction (for width, 3 units).
3. Complete the base parallelogram by drawing lines parallel to the length and width.
4. From the corners of the base, draw vertical lines upwards for the height (2 units).
5. Connect the top ends of these vertical lines to form the top parallelogram, drawing lines parallel to the base edges.
6. The resulting figure is the isometric sketch of the cuboid.
Here is a possible isometric sketch based on the assumed dimensions:
Exercise 13.2
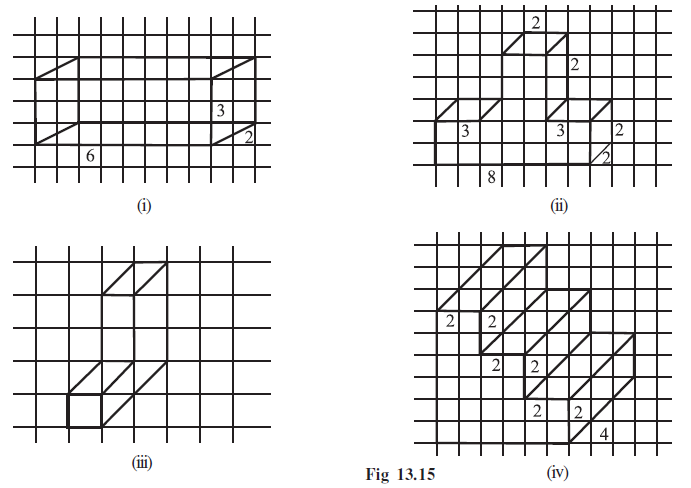
Question 1. Use isometric dot paper and make an isometric sketch for each one of the given shapes:
Answer:
An oblique sketch shows a solid where one face (usually the front) is drawn with actual measurements, and the receding lines are drawn parallel to each other, often at an angle like $45^\circ$. The lengths of the receding lines in an oblique sketch may not be the actual lengths of the edges.
An isometric sketch shows a solid where all three dimensions (length, width, and height) are drawn proportionally along three lines that meet at a point. Vertical lines are drawn vertically, and the other two sets of lines are drawn at $30^\circ$ to the horizontal. Isometric sketches are usually drawn on isometric dot paper, which helps in keeping the correct angles and proportions.
To make an isometric sketch from the given oblique sketches on a square grid, we first observe the dimensions (length, width, height) by counting the units shown in the oblique drawing. Then, we transfer these dimensions to isometric dot paper, drawing along the lines of the isometric grid.
Figure (a):
Figure (b):
Figure (c):
Figure (d):
Question 2. The dimensions of a cuboid are 5 cm, 3 cm and 2 cm. Draw three different isometric sketches of this cuboid.
Answer:
An isometric sketch allows us to draw a 3D shape on a flat surface (like paper) while keeping the actual lengths of the edges. We use isometric dot paper for this, which has dots arranged in a way that helps us draw vertical lines and lines at $30^\circ$ to the horizontal correctly.
A cuboid has three different dimensions given: 5 cm, 3 cm, and 2 cm. When we draw an isometric sketch, we can orient the cuboid in different ways by choosing which dimension goes in which direction (vertical, and the two directions at $30^\circ$). This will give us different views or sketches of the same cuboid.
We can make three different isometric sketches by arranging the 5 cm, 3 cm, and 2 cm dimensions along the three isometric directions in different ways. Let's consider the height (vertical direction) as the changing dimension.
Sketch 1: Height = 2 cm, Length = 5 cm, Width = 3 cm
To draw this sketch on isometric dot paper:
1. Pick a dot to start from.
2. From this dot, draw a line going straight up for 2 units (dots apart) to show the height.
3. From the starting dot, draw a line going upwards and to the right along the grid lines for 5 units to show the length.
4. From the starting dot, draw a line going upwards and to the left along the grid lines for 3 units to show the width.
5. Now, complete the base shape (a parallelogram) by drawing a line parallel to the 3-unit width line from the end of the 5-unit length line, and a line parallel to the 5-unit length line from the end of the 3-unit width line.
6. From the other three corners of the base, draw lines straight up for 2 units (height).
7. Connect the tops of these vertical lines to complete the top face.
Sketch 2: Height = 3 cm, Length = 5 cm, Width = 2 cm
To draw this sketch on isometric dot paper:
1. Pick a dot to start from.
2. From this dot, draw a line going straight up for 3 units to show the height.
3. From the starting dot, draw a line going upwards and to the right along the grid lines for 5 units to show the length.
4. From the starting dot, draw a line going upwards and to the left along the grid lines for 2 units to show the width.
5. Complete the base parallelogram (5 units by 2 units).
6. From the other three base corners, draw lines straight up for 3 units (height).
7. Connect the tops of these vertical lines to complete the top face.
Sketch 3: Height = 5 cm, Length = 3 cm, Width = 2 cm
To draw this sketch on isometric dot paper:
1. Pick a dot to start from.
2. From this dot, draw a line going straight up for 5 units to show the height.
3. From the starting dot, draw a line going upwards and to the right along the grid lines for 3 units to show the length.
4. From the starting dot, draw a line going upwards and to the left along the grid lines for 2 units to show the width.
5. Complete the base parallelogram (3 units by 2 units).
6. From the other three base corners, draw lines straight up for 5 units (height).
7. Connect the tops of these vertical lines to complete the top face.
Question 3. Three cubes each with 2 cm edge are placed side by side to form a cuboid. Sketch an oblique or isometric sketch of this cuboid.
Answer:
We are given three cubes, and each cube has an edge length of 2 cm. When these three cubes are placed side by side in a row, they form a single cuboid.
Let the edge length of each cube be $2\text{ cm}$.
When we place three cubes side by side, the dimension along the direction where they are placed next to each other will be the sum of their lengths. The other two dimensions will remain the same as the edge length of a single cube.
The dimensions of the resulting cuboid are:
Length $= 3 \times 2\text{ cm} = 6\text{ cm}$
Width $= 2\text{ cm}$
Height $= 2\text{ cm}$
So, the resulting cuboid has dimensions 6 cm $\times$ 2 cm $\times$ 2 cm.
We can draw either an oblique sketch and an isometric sketch of this cuboid.
Oblique Sketch:
In an oblique sketch, the front face is drawn with its true shape and measurements. Receding lines are drawn parallel to each other, often at an angle like $45^\circ$ to the horizontal. We can show the depth (width) using the true length or a reduced length. Let's draw the front face as the $6 \text{ cm} \times 2 \text{ cm}$ rectangle.
To draw the oblique sketch:
1. Draw a rectangle representing the front face, with length 6 units and height 2 units.
2. From each vertex of this rectangle, draw lines at an angle (e.g., $45^\circ$) representing the width (2 units). You can draw these lines with length 2 units (Cavalier sketch) or a shorter length (Cabinet sketch) to make it look more realistic. Let's use true length (2 units).
3. Connect the ends of these receding lines to form the back face, drawing lines parallel to the edges of the front face.
4. Show the divisions on the front face to indicate the three original cubes (draw vertical lines dividing the 6-unit length into three 2-unit sections). Similarly, show the divisions on the top face.
Isometric Sketch:
In an isometric sketch, we use isometric dot paper. Vertical edges are drawn vertically, and other edges are drawn along the $30^\circ$ lines of the grid. All measurements along these lines are kept proportional to the actual lengths.
To draw the isometric sketch of the cuboid with dimensions 6 units $\times$ 2 units $\times$ 2 units:
1. Choose a dot on your isometric dot paper as a starting corner.
2. From this dot, draw three lines along the isometric grid directions.
3. Let the height be 2 units, so draw a vertical line upwards for 2 units.
4. Let the length be 6 units, so draw a line along one $30^\circ$ direction (e.g., upwards and right) for 6 units.
5. Let the width be 2 units, so draw a line along the other $30^\circ$ direction (upwards and left) for 2 units.
6. From the ends of the length and width lines on the base, draw lines parallel to the initial width and length lines respectively to complete the base parallelogram (6 units $\times$ 2 units).
7. From the other three corners of the base, draw vertical lines upwards for 2 units (height).
8. Connect the top ends of these vertical lines with lines parallel to the base edges to form the top parallelogram.
You can also draw dotted lines on the visible faces to show the original cubes, creating divisions every 2 units along the 6-unit length.
Question 4. Make an oblique sketch for each one of the given isometric shapes:

Answer:
To make an oblique sketch from an isometric sketch, we typically choose one face to be the "front" face and draw it in its true shape on a squared grid. Then, we draw the receding edges parallel to each other at an angle (commonly $45^\circ$ or $30^\circ$) to the horizontal, often drawing their lengths to scale (Cavalier projection) or reduced (Cabinet projection). We will describe how to draw these sketches on a squared grid, assuming receding lines are at $45^\circ$ with true length for simplicity.
Sketch (a):
Sketch (b):
Question 5. Give (i) an oblique sketch and (ii) an isometric sketch for each of the following:
(a) A cuboid of dimensions 5 cm, 3 cm and 2 cm. (Is your sketch unique?)
(b) A cube with an edge 4 cm long.
An isometric sheet is attached at the end of the book. You could try to make on it some cubes or cuboids of dimensions specified by your friend.
Answer:
We are asked to provide sketches for a cuboid and a cube, showing both an oblique view and an isometric view. We also need to comment on the uniqueness of the sketches.
(a) A cuboid of dimensions 5 cm, 3 cm and 2 cm.
Let the dimensions of the cuboid be Length = 5 cm, Width = 3 cm, and Height = 2 cm.
(i) Oblique Sketch:
For an oblique sketch, we typically draw the front face in its true shape and size on a squared grid. The receding edges are drawn parallel to each other at an angle (usually $45^\circ$ or $30^\circ$) to the horizontal. The length of the receding edges can be drawn to true scale (Cavalier sketch) or reduced (Cabinet sketch). Let's draw a Cavalier oblique sketch on a squared grid.
- Choose a face to be the front. Let's choose the face with dimensions 5 cm (length) $\times$ 2 cm (height) as the front face.
- Draw a rectangle on the squared grid representing this front face, with a horizontal side of 5 units and a vertical side of 2 units.
- From each of the four vertices of this rectangle, draw a line parallel to the others, representing the depth (width) of the cuboid, which is 3 cm. Draw these lines at an angle, say $45^\circ$ upwards and to the right. Draw these lines with a length of 3 units (true length).
- Connect the ends of these four receding lines to form the back face of the cuboid. The edges of the back face will be parallel to the corresponding edges of the front face.
- Hidden edges can be shown as dotted lines if desired.
Sketch description: Draw a $5 \times 2$ rectangle. From each corner, draw a line 3 units long at $45^\circ$. Connect the ends of these lines.
(ii) Isometric Sketch:
For an isometric sketch, we use isometric dot paper. Vertical edges are drawn vertically, and edges along the other two principal directions are drawn along the $30^\circ$ lines of the grid. All lengths along these isometric axes are drawn to scale. Since the cuboid has three different dimensions, we can orient it in different ways on the isometric grid, leading to different sketches.
- Choose a starting dot on the isometric paper.
- From this dot, draw three edges representing the length (5 cm), width (3 cm), and height (2 cm) along the three isometric grid directions (vertical, $30^\circ$ left, $30^\circ$ right). There are multiple ways to assign the dimensions to these directions. For example, we can set Height = 2, Length = 5, Width = 3.
- Draw a vertical line upwards for 2 units. Draw a line along one $30^\circ$ direction for 5 units. Draw a line along the other $30^\circ$ direction for 3 units.
- Complete the base parallelogram (5 units $\times$ 3 units) by drawing lines parallel to the initial length and width lines.
- From the other three vertices of the base, draw vertical lines upwards for 2 units (height).
- Connect the top ends of these vertical lines to complete the top face.
- Hidden edges can be shown as dotted lines.
Sketch description (Example Orientation): From a dot, draw up 2 units, along one $30^\circ$ line 5 units, along the other $30^\circ$ line 3 units. Complete the box using parallel lines.
Is your sketch unique?
For the oblique sketch, the sketch is generally not unique. The specific appearance depends on:
- Which face is chosen as the front face (e.g., 5x2, 5x3, or 3x2).
- The angle at which the receding lines are drawn (commonly $45^\circ$ or $30^\circ$).
- Whether the receding lines are drawn to true length (Cavalier) or reduced length (Cabinet).
For the isometric sketch of a cuboid with different dimensions, the sketch is also not unique. As shown above, you can assign the three dimensions (5, 3, 2) to the three isometric axes (vertical, $30^\circ$ left, $30^\circ$ right) in different combinations, resulting in different views of the cuboid. There are $3! = 6$ possible assignments if all dimensions were different, but since the axes directions are fixed relative to each other on the paper, we get distinct visual sketches depending on which dimension is vertical (3 possibilities) and then which of the remaining two is assigned to which $30^\circ$ axis (2 possibilities for each vertical choice), leading to 3 fundamentally different visual orientations.
(b) A cube with an edge 4 cm long.
Let the edge length of the cube be $s = 4\text{ cm}$.
(i) Oblique Sketch:
Use a squared grid sheet.
- Draw the front face as a square with side length 4 units on the grid. This is the true shape.
- From each vertex of the square, draw parallel receding lines at an angle (e.g., $45^\circ$ upwards and to the right).
- Draw the length of these receding lines to represent the depth, which is 4 cm. Using true length (4 units) for a Cavalier sketch.
- Connect the ends of the receding lines to form the back square.
- Show hidden edges as dotted lines.
Sketch description: Draw a $4 \times 4$ square. From each corner, draw a line 4 units long at $45^\circ$. Connect the ends.
(ii) Isometric Sketch:
Use isometric dot paper.
- Choose a starting dot.
- From this dot, draw three edges along the isometric grid lines, each of length 4 units (representing the height, length, and width). One is vertical, the other two are at $30^\circ$ to the horizontal.
- Complete the cube by drawing parallel lines of length 4 units along the grid directions from the other vertices.
- Hidden edges can be shown as dotted lines.
Sketch description: From a dot, draw a line 4 units vertically, a line 4 units along one slanted grid line, and a line 4 units along the other slanted grid line. Complete the box using parallel lines of length 4 units.
Is your sketch unique?
For the oblique sketch, if we fix the angle and scaling of the receding lines (e.g., $45^\circ$ Cavalier), then the sketch is essentially unique, as the front face must be a $4 \times 4$ square, and the receding edges must follow the chosen rule. Without fixing the convention (angle/scaling), it's not strictly unique in appearance, but the core representation is standard.
For the isometric sketch of a cube, since all edge lengths are equal, rotating the cube into different orientations on the isometric paper results in sketches that are visually identical (unless hidden lines are included differently). Therefore, the isometric sketch of a cube is considered essentially unique.
Example 2 (Before Exercise 13.3)
Example 2. If two cubes of dimensions 2 cm by 2cm by 2cm are placed side by side, what would the dimensions of the resulting cuboid be?
Answer:
We are given two cubes. Each cube has dimensions 2 cm by 2 cm by 2 cm. This means that the length, width, and height of each cube are all 2 cm.
When two such cubes are placed side by side, they are joined along one of their square faces. Let's assume they are placed side by side along the direction which we consider the length.
The dimensions of the resulting cuboid will be:
- The length will be the sum of the lengths of the two cubes placed side by side:
Length $= 2\text{ cm} + 2\text{ cm} = 4\text{ cm}$
- The width will remain the width of a single cube:
Width $= 2\text{ cm}$
- The height will remain the height of a single cube:
Height $= 2\text{ cm}$
Therefore, the dimensions of the resulting cuboid are 4 cm $\times$ 2 cm $\times$ 2 cm.
Exercise 13.3
Question 1. What cross-sections do you get when you give a
(i) vertical cut
(ii) horizontal cut
to the following solids?
(a) A brick
(b) A round apple
(c) A die
(d) A circular pipe
(e) An ice cream cone
Answer:
A cross-section is the shape that you see when you slice through a 3D solid with a flat surface (like a knife). We need to figure out the shape of this slice when we make a vertical cut (a cut that goes straight up and down) and a horizontal cut (a cut that goes straight across, parallel to the ground or base) through different solid objects.
(a) A brick (We can think of a brick as a rectangular box, or a cuboid).
(i) Vertical cut: If you slice a brick vertically (straight up and down), the shape of the cut surface will be a rectangle.
(ii) Horizontal cut: If you slice a brick horizontally (straight across, like slicing a cake), the shape of the cut surface will also be a rectangle, which is the same shape as its base.
(b) A round apple (We can think of a round apple as being roughly like a sphere).
(i) Vertical cut: If you slice a round apple vertically, the shape of the cut surface will be a circle (or very close to a circle), unless you slice it right at the very edge.
(ii) Horizontal cut: If you slice a round apple horizontally, the shape of the cut surface will also be a circle (or very close to a circle), unless you slice it right at the very edge.
(c) A die (A die is a cube).
(i) Vertical cut: If you slice a die vertically, parallel to one of its faces, the shape of the cut surface will be a square, which is the shape of its face.
(ii) Horizontal cut: If you slice a die horizontally, parallel to its base, the shape of the cut surface will also be a square, which is the shape of its base.
(d) A circular pipe (A circular pipe is like a cylinder).
(i) Vertical cut: If you slice a circular pipe vertically (along its length), the shape of the cut surface will be a rectangle.
(ii) Horizontal cut: If you slice a circular pipe horizontally (across its width), the shape of the cut surface will be a circle, which is the shape of its opening.
(e) An ice cream cone (We can think of an ice cream cone as a cone).
(i) Vertical cut: If you slice an ice cream cone vertically through its pointed tip (vertex), the shape of the cut surface will be a triangle.
(ii) Horizontal cut: If you slice an ice cream cone horizontally, parallel to the round opening at the top (base), the shape of the cut surface will be a circle.
Exercise 13.4
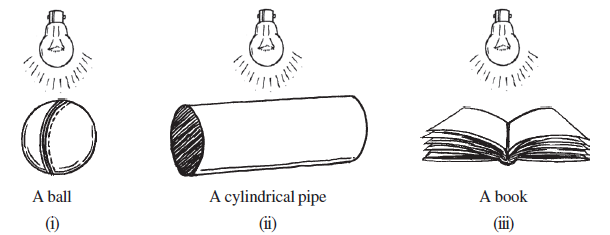
Question 1. A bulb is kept burning just right above the following solids. Name the shape of the shadows obtained in each case. Attempt to give a rough sketch of the shadow. (You may try to experiment first and then answer these questions).
Answer:
When a light source, like a bulb, is placed directly above a solid object, the shadow formed on a flat surface below is the projection of the solid's outline onto that surface. The shape of the shadow depends on the shape of the solid and its orientation relative to the light source and the surface.
(a) A ball (This is a sphere). The light is directly above the sphere.
Shape of the shadow: The projection of a sphere onto a flat surface when the light source is directly above is always a Circle.
Rough sketch description: Draw a simple circular outline.
(b) A cylindrical pipe (Assuming it is placed upright on a flat surface). The light is directly above the top horizontal curve.
Shape of the shadow: When an upright cylinder is lit from directly above, the shadow formed is the projection of its curve onto the surface. Since the flat curve is a rectangle, the shadow is nearly rectangular.
Rough sketch description: Draw a simple rectangular outline.
(c) A book (Assuming it is placed flat on a surface). A book is like a rectangular prism. The light is directly above the top rectangular face.
Shape of the shadow: When a flat rectangular prism is lit from directly above, the shadow formed is the projection of its top rectangular face onto the surface below. The shadow is a Rectangle.
Rough sketch description: Draw a simple rectangular outline.
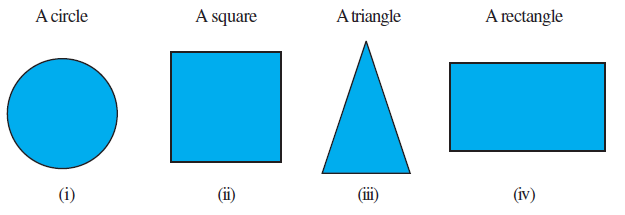
Question 2. Here are the shadows of some 3-D objects, when seen under the lamp of an overhead projector. Identify the solid(s) that match each shadow. (There may be multiple answers for these!)
Answer:
When a solid object is placed under the lamp of an overhead projector (assuming the lamp is directly above the object and the shadow is cast on a flat surface below), the shape of the shadow is determined by the projection of the solid's outline onto the surface.
Here are the solids that can produce the given shadows:
(a) Shadow is a Circle.
- A Sphere (e.g., a ball) placed on the surface.
- A Cylinder placed upright on its circular base.
- A Cone placed upright on its circular base.
(b) Shadow is a Square.
- A Cube placed with any face flat on the surface.
- A Square pyramid placed on its square base.
- A Square prism (a cuboid with a square base) placed on its square base.
(c) Shadow is a Triangle.
- A Triangular pyramid placed on its triangular base.
- A Triangular prism placed on one of its triangular bases.
- A Cone (if the light source is positioned off-center or the cone is tilted, although typically under a direct overhead lamp, the shadow of an upright cone on its base is a circle). However, if the question implies a view of the silhouette from a specific direction, a cone can project a triangular silhouette. Sticking to the overhead lamp scenario, the triangular pyramid/prism on base is the likely intended answer.
(d) Shadow is a Rectangle.
- A Cuboid (rectangular prism) placed on any of its rectangular faces.
- A Triangular prism placed on one of its rectangular faces.
- A Cylinder placed horizontally on its curved surface.
Question 3. Examine if the following are true statements:
(i) The cube can cast a shadow in the shape of a rectangle.
(ii) The cube can cast a shadow in the shape of a hexagon.
Answer:
The shape of the shadow depends on the shape of the object casting the shadow, the type and position of the light source, and how the object is oriented.
(i) The cube can cast a shadow in the shape of a rectangle.
This statement is True.
Explanation:
- If you place a cube on a flat surface such that one of its faces is parallel to the surface, and shine light directly from above (like the sun, which sends parallel light rays), the shadow will be a square. A square is a type of rectangle.
- If you tilt the cube in a certain way, or if the light source is at a specific angle, the outline of the cube projected onto the flat surface can form a shape with four right angles and opposite sides equal in length, which is a rectangle (that is not a square).
(ii) The cube can cast a shadow in the shape of a hexagon.
This statement is True.
Explanation:
- A cube can indeed cast a hexagonal shadow.
- This happens when the light source is placed in such a position that when you look from the light source towards the cube, you can see three faces meeting at a vertex, and the outline you see is made up of six edges.
- When the light rays from the source go past these six outer edges of the cube and hit a flat surface, the shadow formed has six sides, which is a hexagon.
- An example where this occurs is when a point light source is placed directly above one of the vertices (corners) of the cube, and the shadow is cast on a surface parallel to the face opposite to that vertex.

