| Latest Maths NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Example 1 to 3 (Before Exercise 7.1) | Exercise 7.1 | Example 4 to 6 (Before Exercise 7.2) |
| Exercise 7.2 | Example 7 & 8 (Before Exercise 7.3) | Exercise 7.3 |
Chapter 7 Triangles
Welcome to the solutions guide for Chapter 7, "Triangles," from the latest Class 9 NCERT mathematics textbook for the academic session 2024-25. This crucial chapter delves deep into the concept of congruence – the idea of geometric figures being identical in shape and size. Understanding and proving triangle congruence is fundamental to developing rigorous geometric proof techniques and establishing many other geometric properties. These solutions provide detailed explanations and step-by-step applications of the criteria used to determine if two triangles are congruent, fostering logical reasoning and precision in geometric arguments.
The solutions provided here meticulously explain and apply the various criteria established for determining if two triangles are congruent. Master the application of:
- SAS (Side-Angle-Side) Congruence Rule: If two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle.
- ASA (Angle-Side-Angle) Congruence Rule: If two angles and the included side of one triangle are equal to two angles and the included side of another triangle.
- SSS (Side-Side-Side) Congruence Rule: If three sides of one triangle are equal to the three sides of another triangle.
- RHS (Right angle-Hypotenuse-Side) Congruence Rule: Specifically for right-angled triangles, if the hypotenuse and one side of one triangle are equal to the hypotenuse and one side of another triangle.
A vital technique demonstrated extensively in these solutions is the application of CPCT (Corresponding Parts of Congruent Triangles are Congruent/Equal). Once congruence between two triangles is established using one of the rules above, CPCT allows us to logically deduce that all other corresponding sides and angles of those triangles are also equal. This is a powerful tool frequently used in subsequent steps of geometric proofs to establish further equalities or relationships. Furthermore, the solutions provide clear proofs for key theorems related to isosceles triangles: the theorem stating that 'angles opposite equal sides of an isosceles triangle are equal,' and its important converse, 'sides opposite equal angles of a triangle are equal.' The application of these theorems in solving various problems involving isosceles triangles is clearly illustrated.
Regarding the rationalized syllabus for 2024-25, Chapter 7, "Triangles," in the Class 9 NCERT textbook has sharpened its focus primarily on the congruence criteria (SAS, ASA, SSS, RHS) and their applications, along with the properties of isosceles triangles derived from congruence. Notably, the section and related exercises concerning Triangle Inequalities (such as the sum of two sides being greater than the third, and relationships between angle size and opposite side length) have been removed from the curriculum for this academic session. This ensures a concentrated effort on mastering the core concept of congruence and its direct consequences. By diligently studying these focused solutions, students can master the application of congruence rules, significantly develop their formal geometric proof-writing skills, understand the key properties of isosceles triangles, and build a strong foundation for further geometric exploration.
Example 1 to 3 (Before Exercise 7.1)
Example 1. In Fig. 7.8, OA = OB and OD = OC. Show that
(i) ∆ AOD ≅ ∆ BOC and
(ii) AD || BC.
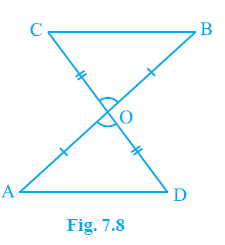
Answer:
Given:
In Fig. 7.8,
OA = OB
OD = OC
To Prove:
(i) $\Delta$ AOD $\cong$ $\Delta$ BOC
(ii) AD || BC
Proof:
(i) To prove $\Delta$ AOD $\cong$ $\Delta$ BOC
Consider the triangles $\Delta$ AOD and $\Delta$ BOC.
OA = OB
(Given)
OD = OC
(Given)
$\angle$AOD = $\angle$BOC
(Vertically Opposite Angles)
By SAS (Side-Angle-Side) congruence rule, if two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle, then the two triangles are congruent.
In $\Delta$ AOD and $\Delta$ BOC, we have two pairs of equal sides (OA = OB and OD = OC) and the included angles ($\angle$AOD and $\angle$BOC) are equal.
Therefore, by SAS congruence rule:
$\Delta$ AOD $\cong$ $\Delta$ BOC
(ii) To prove AD || BC
Since $\Delta$ AOD $\cong$ $\Delta$ BOC (as proved in part (i)), their corresponding parts are equal (CPCT).
Thus, we have the equality of corresponding angles:
$\angle$OAD = $\angle$OBC
These angles ($\angle$OAD and $\angle$OBC) are alternate interior angles formed by the transversal AB intersecting lines AD and BC.
Also, we have:
$\angle$ADO = $\angle$BCO
These angles ($\angle$ADO and $\angle$BCO) are alternate interior angles formed by the transversal BD intersecting lines AD and BC.
Since a pair of alternate interior angles is equal ($\angle$OAD = $\angle$OBC or $\angle$ADO = $\angle$BCO), the lines AD and BC must be parallel.
Therefore,
AD || BC
Hence Proved.
Example 2. AB is a line segment and line l is its perpendicular bisector. If a point P lies on l, show that P is equidistant from A and B.
Answer:
Given:
AB is a line segment.
Line l is the perpendicular bisector of AB.
Point P lies on line l.
To Prove:
P is equidistant from A and B, i.e., PA = PB.
Construction Required:
Let M be the point where the line l intersects the line segment AB.
Since l is the perpendicular bisector of AB, M is the midpoint of AB, and line l is perpendicular to AB at M.
Join PA and PB.
Proof:
We can consider two cases:
Case 1: P is the midpoint M of AB.
If the point P coincides with the midpoint M of the line segment AB, then the distance from P to A is MA, and the distance from P to B is MB.
Since M is the midpoint of AB, by the definition of a midpoint, we have AM = MB.
Therefore, PA = PB.
Case 2: P is any point on line l other than M.
Consider the two triangles formed: $\Delta$ PMA and $\Delta$ PMB.
We can show that these two triangles are congruent using the SAS (Side-Angle-Side) congruence rule.
1. Segment AM and segment MB are equal.
AM = MB
(M is the midpoint of AB, since l is the perpendicular bisector)
2. The angles $\angle$ PMA and $\angle$ PMB are right angles.
$\angle$ PMA = $\angle$ PMB = $90^\circ$
(Line l is perpendicular to AB at M)
3. The side PM is common to both triangles.
PM = PM
(Common side)
By the SAS congruence rule, $\Delta$ PMA is congruent to $\Delta$ PMB.
$\Delta$ PMA $\cong$ $\Delta$ PMB
Since the triangles are congruent, their corresponding parts are equal by CPCT (Corresponding Parts of Congruent Triangles are Congruent).
Therefore, the corresponding sides PA and PB are equal.
PA = PB
(CPCT)
In both cases (whether P is the midpoint or any other point on the perpendicular bisector), we have shown that PA = PB.
This proves that any point P on the perpendicular bisector l is equidistant from the points A and B.
Hence Proved.
Example 3. Line-segment AB is parallel to another line-segment CD. O is the mid-point of AD (see Fig. 7.15). Show that (i) ∆AOB ≅ ∆DOC (ii) O is also the mid-point of BC.
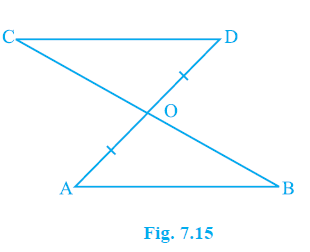
Answer:
Given:
AB || CD
O is the mid-point of AD.
To Prove:
(i) $\Delta$AOB $\cong$ $\Delta$DOC
(ii) O is also the mid-point of BC.
Proof:
(i) To prove $\Delta$AOB $\cong$ $\Delta$DOC
Consider the triangles $\Delta$ AOB and $\Delta$ DOC.
OA = OD
(O is the mid-point of AD)
$\angle$OAB = $\angle$ODC
(Alternate Interior Angles, since AB || CD and AD is a transversal)
$\angle$AOB = $\angle$DOC
(Vertically Opposite Angles)
Therefore, by ASA (Angle-Side-Angle) congruence rule:
$\Delta$ AOB $\cong$ $\Delta$ DOC
(ii) To prove O is also the mid-point of BC
Since $\Delta$ AOB $\cong$ $\Delta$ DOC (from part (i)), their corresponding parts are equal (CPCT).
Thus, the corresponding sides OB and OC are equal.
OB = OC
(CPCT)
Since O lies on the line segment BC and OB = OC, O is the mid-point of BC.
Hence Proved.
Exercise 7.1
Question 1. In quadrilateral ACBD, AC = AD and AB bisects ∠ A (see Fig. 7.16). Show that ∆ ABC ≅ ∆ ABD. What can you say about BC and BD?
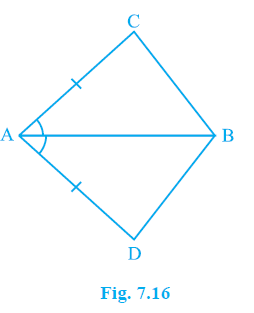
Answer:
Given:
In quadrilateral ACBD,
AC = AD
AB bisects $\angle$A.
To Prove:
(i) $\Delta$ ABC $\cong$ $\Delta$ ABD
(ii) What can be said about BC and BD.
Proof:
(i) To prove $\Delta$ ABC $\cong$ $\Delta$ ABD
Consider the triangles $\Delta$ ABC and $\Delta$ ABD.
AC = AD
(Given)
Since AB bisects $\angle$A, the angle $\angle$A is divided into two equal angles by AB.
$\angle$CAB = $\angle$DAB
(Given, AB bisects $\angle$A)
AB = AB
(Common side)
By SAS (Side-Angle-Side) congruence rule, if two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle, then the two triangles are congruent.
In $\Delta$ ABC and $\Delta$ ABD, we have two pairs of equal sides (AC = AD and AB = AB) and the included angles ($\angle$CAB and $\angle$DAB) are equal.
Therefore, by SAS congruence rule:
$\Delta$ ABC $\cong$ $\Delta$ ABD
(ii) What can be said about BC and BD
Since $\Delta$ ABC $\cong$ $\Delta$ ABD (as proved in part (i)), their corresponding parts are equal (CPCT).
BC and BD are corresponding sides in the two congruent triangles (BC corresponds to BD).
Therefore, their lengths are equal.
BC = BD
(CPCT)
Final Answer:
(i) $\Delta$ ABC $\cong$ $\Delta$ ABD by SAS congruence rule.
(ii) BC and BD are equal in length (BC = BD) because they are corresponding parts of congruent triangles.
Question 2. ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA (see Fig. 7.17). Prove that
(i) ∆ABD ≅ ∆BAC
(ii) BD = AC
(iii) ∠ABD = ∠BAC.
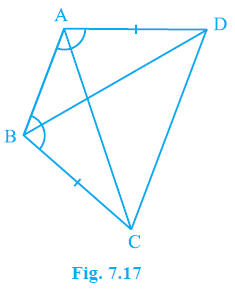
Answer:
Given:
In quadrilateral ABCD,
AD = BC
$\angle$DAB = $\angle$CBA
To Prove:
(i) $\Delta$ABD $\cong$ $\Delta$BAC
(ii) BD = AC
(iii) $\angle$ABD = $\angle$BAC
Proof:
(i) To prove $\Delta$ABD $\cong$ $\Delta$BAC
Consider the triangles $\Delta$ ABD and $\Delta$ BAC.
AD = BC
(Given)
$\angle$DAB = $\angle$CBA
(Given)
AB = BA
(Common side)
By SAS (Side-Angle-Side) congruence rule, if two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle, then the two triangles are congruent.
In $\Delta$ ABD and $\Delta$ BAC, we have two pairs of equal sides (AD = BC and AB = BA) and the included angles ($\angle$DAB and $\angle$CBA) are equal.
Therefore, by SAS congruence rule:
$\Delta$ ABD $\cong$ $\Delta$ BAC
(ii) To prove BD = AC
Since $\Delta$ ABD $\cong$ $\Delta$ BAC (as proved in part (i)), their corresponding parts are equal (CPCT).
BD and AC are corresponding sides in the two congruent triangles (BD corresponds to AC).
Therefore, their lengths are equal.
BD = AC
(CPCT)
(iii) To prove $\angle$ABD = $\angle$BAC
Since $\Delta$ ABD $\cong$ $\Delta$ BAC (as proved in part (i)), their corresponding parts are equal (CPCT).
$\angle$ABD and $\angle$BAC are corresponding angles in the two congruent triangles ($\angle$ABD corresponds to $\angle$BAC).
Therefore, their measures are equal.
$\angle$ABD = $\angle$BAC
(CPCT)
Hence Proved.
Question 3. AD and BC are equal perpendiculars to a line segment AB (see Fig. 7.18). Show that CD bisects AB.
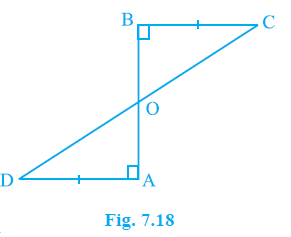
Answer:
Given:
AD $\perp$ AB and BC $\perp$ AB.
AD = BC.
To Prove:
CD bisects AB (i.e., the intersection point of CD and AB is the midpoint of AB).
Proof:
Let CD intersect AB at point O.
Consider the triangles $\Delta$ AOD and $\Delta$ BOC.
$\angle$DAO = $90^\circ$
(Given, AD $\perp$ AB)
$\angle$CBO = $90^\circ$
(Given, BC $\perp$ AB)
So,
$\angle$DAO = $\angle$CBO
$\angle$AOD = $\angle$BOC
(Vertically Opposite Angles)
AD = BC
(Given)
By AAS (Angle-Angle-Side) congruence rule, if two angles and a non-included side of one triangle are equal to the corresponding two angles and the non-included side of the other triangle, then the triangles are congruent.
In $\Delta$ AOD and $\Delta$ BOC, we have two pairs of equal angles ($\angle$DAO = $\angle$CBO and $\angle$AOD = $\angle$BOC) and a pair of non-included sides equal (AD = BC).
Therefore, by AAS congruence rule:
$\Delta$ AOD $\cong$ $\Delta$ BOC
Since $\Delta$ AOD $\cong$ $\Delta$ BOC, their corresponding parts are equal (CPCT).
Therefore, the corresponding sides AO and BO are equal.
AO = BO
(CPCT)
Since O is a point on the line segment AB and AO = BO, O is the midpoint of AB.
Thus, CD bisects AB at O.
Hence Proved.
Question 4. l and m are two parallel lines intersected by another pair of parallel lines p and q (see Fig. 7.19). Show that ∆ABC ≅ ∆CDA.
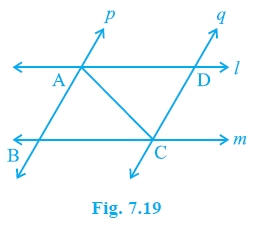
Answer:
Given:
l || m
p || q
To Prove:
$\Delta$ABC $\cong$ $\Delta$CDA
Proof:
Consider the triangles $\Delta$ ABC and $\Delta$ CDA.
Since lines l || m and AC is a transversal line intersecting them, the alternate interior angles are equal.
$\angle$BAC = $\angle$DCA
(Alternate Interior Angles)
Since lines p || q and AC is a transversal line intersecting them, the alternate interior angles are equal.
$\angle$BCA = $\angle$DAC
(Alternate Interior Angles)
Also, AC is a common side to both triangles $\Delta$ ABC and $\Delta$ CDA.
AC = CA
(Common Side)
By ASA (Angle-Side-Angle) congruence rule, if two angles and the included side of one triangle are equal to the corresponding two angles and the included side of another triangle, then the two triangles are congruent.
In $\Delta$ ABC and $\Delta$ CDA, we have two pairs of equal angles ($\angle$BAC = $\angle$DCA and $\angle$BCA = $\angle$DAC) and the included side (AC = CA) is common.
Therefore, by ASA congruence rule:
$\Delta$ABC $\cong$ $\Delta$CDA
Hence Proved.
Question 5. Line l is the bisector of an angle ∠A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A (see Fig. 7.20). Show that:
(i) ∆APB ≅ ∆AQB
(ii) BP = BQ or B is equidistant from the arms of ∠ A.
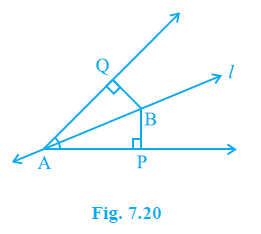
Answer:
Given:
Line l is the bisector of $\angle$A.
B is any point on line l.
BP $\perp$ arm AP (where P is a point on the arm of $\angle$A).
BQ $\perp$ arm AQ (where Q is a point on the arm of $\angle$A).
To Prove:
(i) $\Delta$APB $\cong$ $\Delta$AQB
(ii) BP = BQ (B is equidistant from the arms of $\angle$A)
Proof:
(i) To prove $\Delta$APB $\cong$ $\Delta$AQB
Consider the triangles $\Delta$ APB and $\Delta$ AQB.
Since line l is the bisector of $\angle$A and B lies on l, the ray AB is the angle bisector of $\angle$A. Thus, it divides $\angle$A into two equal angles.
$\angle$PAB = $\angle$QAB
(Given, AB is the angle bisector of $\angle$A)
We are given that BP and BQ are perpendiculars to the arms of $\angle$A.
$\angle$APB = $90^\circ$
(Given, BP $\perp$ arm)
$\angle$AQB = $90^\circ$
(Given, BQ $\perp$ arm)
So,
$\angle$APB = $\angle$AQB
AB is a common side to both triangles.
AB = AB
(Common side)
By AAS (Angle-Angle-Side) congruence rule, if two angles and a non-included side of one triangle are equal to the corresponding two angles and the non-included side of the other triangle, then the triangles are congruent.
In $\Delta$ APB and $\Delta$ AQB, we have $\angle$PAB = $\angle$QAB, $\angle$APB = $\angle$AQB, and AB = AB.
Therefore, by AAS congruence rule:
$\Delta$ APB $\cong$ $\Delta$ AQB
(ii) To prove BP = BQ
Since $\Delta$ APB $\cong$ $\Delta$ AQB (as proved in part (i)), their corresponding parts are equal (CPCT).
BP and BQ are corresponding sides in the two congruent triangles (BP corresponds to BQ).
Therefore, their lengths are equal.
BP = BQ
(CPCT)
This means that point B is equidistant from the arms of $\angle$A.
Hence Proved.
Question 6. In Fig. 7.21, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.
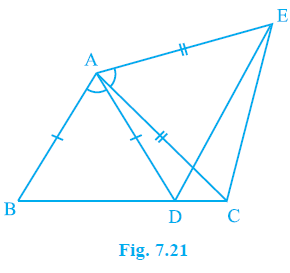
Answer:
Given:
In Fig. 7.21,
AC = AE
AB = AD
$\angle$BAD = $\angle$EAC
To Prove:
BC = DE
Proof:
We are given that $\angle$BAD = $\angle$EAC.
Add $\angle$DAC to both sides of the equation:
$\angle$BAD + $\angle$DAC = $\angle$EAC + $\angle$DAC
From the figure, $\angle$BAD + $\angle$DAC = $\angle$BAC and $\angle$EAC + $\angle$DAC = $\angle$DAE.
So, we have:
$\angle$BAC = $\angle$DAE
... (i)
Now consider the triangles $\Delta$ ABC and $\Delta$ ADE.
AB = AD
(Given)
$\angle$BAC = $\angle$DAE
(From equation (i))
AC = AE
(Given)
By SAS (Side-Angle-Side) congruence rule, if two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle, then the two triangles are congruent.
In $\Delta$ ABC and $\Delta$ ADE, we have two pairs of equal sides (AB = AD and AC = AE) and the included angles ($\angle$BAC and $\angle$DAE) are equal.
Therefore, by SAS congruence rule:
$\Delta$ ABC $\cong$ $\Delta$ ADE
Since $\Delta$ ABC $\cong$ $\Delta$ ADE, their corresponding parts are equal (CPCT).
BC and DE are corresponding sides in the two congruent triangles (BC corresponds to DE).
Therefore, their lengths are equal.
BC = DE
(CPCT)
Hence Proved.
Question 7. AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (see Fig. 7.22). Show that
(i) ∆DAP ≅ ∆EBP
(ii) AD = BE
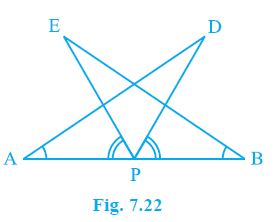
Answer:
Given:
AB is a line segment.
P is the mid-point of AB.
D and E are points on the same side of AB.
$\angle$BAD = $\angle$ABE
$\angle$EPA = $\angle$DPB
To Prove:
(i) $\Delta$DAP $\cong$ $\Delta$EBP
(ii) AD = BE
Proof:
(i) To prove $\Delta$DAP $\cong$ $\Delta$EBP
We are given that $\angle$EPA = $\angle$DPB.
Add $\angle$EPD to both sides of the equation:
$\angle$EPA + $\angle$EPD = $\angle$DPB + $\angle$EPD
From the figure, $\angle$EPA + $\angle$EPD = $\angle$DPA and $\angle$DPB + $\angle$EPD = $\angle$EPB.
So, we have:
$\angle$DPA = $\angle$EPB
... (i)
Now consider the triangles $\Delta$ DAP and $\Delta$ EBP.
$\angle$BAD = $\angle$ABE
(Given). In terms of the triangles, this is $\angle$DAP = $\angle$EBP.
AP = BP
(Given, P is the mid-point of AB)
$\angle$DPA = $\angle$EPB
(From equation (i))
By ASA (Angle-Side-Angle) congruence rule, if two angles and the included side of one triangle are equal to the corresponding two angles and the included side of another triangle, then the two triangles are congruent.
In $\Delta$ DAP and $\Delta$ EBP, we have two pairs of equal angles ($\angle$DAP = $\angle$EBP and $\angle$DPA = $\angle$EPB) and the included side (AP = BP) is equal.
Therefore, by ASA congruence rule:
$\Delta$ DAP $\cong$ $\Delta$ EBP
(ii) To prove AD = BE
Since $\Delta$ DAP $\cong$ $\Delta$ EBP (as proved in part (i)), their corresponding parts are equal (CPCT).
AD and BE are corresponding sides in the two congruent triangles (AD corresponds to BE).
Therefore, their lengths are equal.
AD = BE
(CPCT)
Hence Proved.
Question 8. In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see Fig. 7.23). Show that:
(i) ∆AMC ≅ ∆BMD
(ii) ∠DBC is a right angle.
(iii) ∆DBC ≅ ∆ACB
(iv) CM = $\frac{1}{2}$ AB
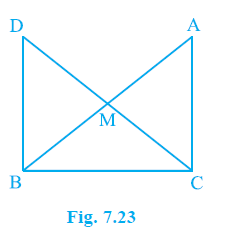
Answer:
Given:
In right triangle ABC, right angled at C, i.e., $\angle$ACB = $90^\circ$.
M is the mid-point of hypotenuse AB, so AM = MB.
C is joined to M and produced to a point D such that DM = CM.
Point D is joined to point B.
To Prove:
(i) $\Delta$AMC $\cong$ $\Delta$BMD
(ii) $\angle$DBC is a right angle ($= 90^\circ$).
(iii) $\Delta$DBC $\cong$ $\Delta$ACB
(iv) CM = $\frac{1}{2}$ AB
Proof:
(i) To prove $\Delta$AMC $\cong$ $\Delta$BMD
Consider the triangles $\Delta$ AMC and $\Delta$ BMD.
AM = BM
(Given, M is the mid-point of AB)
$\angle$AMC = $\angle$BMD
(Vertically Opposite Angles)
CM = DM
(Given)
By SAS (Side-Angle-Side) congruence rule, if two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle, then the two triangles are congruent.
Therefore, by SAS congruence rule:
$\Delta$ AMC $\cong$ $\Delta$ BMD
(ii) To prove $\angle$DBC is a right angle
Since $\Delta$ AMC $\cong$ $\Delta$ BMD (from part (i)), their corresponding parts are equal (CPCT).
$\angle$ACM = $\angle$BDM
(CPCT)
These angles ($\angle$ACM and $\angle$BDM) are alternate interior angles formed by the transversal CD intersecting lines AC and DB.
Since the alternate interior angles are equal, lines AC and DB must be parallel.
AC || DB
... (i)
Now consider the parallel lines AC and DB with BC as a transversal.
The consecutive interior angles $\angle$ACB and $\angle$DBC are supplementary.
$\angle$ACB + $\angle$DBC = $180^\circ$
(Consecutive Interior Angles)
We are given that $\angle$ACB = $90^\circ$. Substitute this value:
90$^\circ$ + $\angle$DBC = $180^\circ$
$\angle$DBC = $180^\circ - 90^\circ$
$\angle$DBC = $90^\circ$
Thus, $\angle$DBC is a right angle.
(iii) To prove $\Delta$DBC $\cong$ $\Delta$ACB
Consider the triangles $\Delta$ DBC and $\Delta$ ACB.
From part (i), we know that $\Delta$ AMC $\cong$ $\Delta$ BMD. By CPCT, corresponding sides are equal.
DB = AC
(CPCT from $\Delta$AMC $\cong$ $\Delta$BMD)
From part (ii), we know that $\angle$DBC = $90^\circ$. We are given that $\angle$ACB = $90^\circ$.
$\angle$DBC = $\angle$ACB = $90^\circ$
(Proved in (ii) and Given)
BC is a common side to both triangles.
BC = CB
(Common side)
By SAS (Side-Angle-Side) congruence rule, if two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle, then the two triangles are congruent.
In $\Delta$ DBC and $\Delta$ ACB, we have two pairs of equal sides (DB = AC and BC = CB) and the included angles ($\angle$DBC and $\angle$ACB) are equal.
Therefore, by SAS congruence rule:
$\Delta$ DBC $\cong$ $\Delta$ ACB
(iv) To prove CM = $\frac{1}{2}$ AB
Since $\Delta$ DBC $\cong$ $\Delta$ ACB (from part (iii)), their corresponding parts are equal (CPCT).
CD and AB are corresponding sides in the two congruent triangles (CD corresponds to AB).
CD = AB
(CPCT from $\Delta$DBC $\cong$ $\Delta$ACB)
From the construction and given information, D, M, C are collinear and DM = CM.
CD = CM + DM
CD = CM + CM
(Since DM = CM)
CD = 2CM
Substitute CD = 2CM into the equation CD = AB:
2CM = AB
Divide both sides by 2:
CM = $\frac{1}{2}$ AB
Hence Proved.
Example 4 to 6 (Before Exercise 7.2)
Example 4. In ∆ ABC, the bisector AD of ∠A is perpendicular to side BC (see Fig. 7.27). Show that AB = AC and ∆ ABC is isosceles.
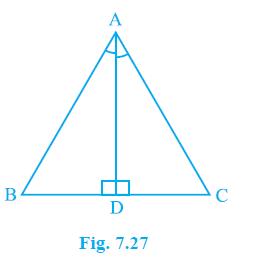
Answer:
Given:
In $\Delta$ ABC, AD is the bisector of $\angle$A.
AD $\perp$ BC.
To Prove:
AB = AC and $\Delta$ ABC is isosceles.
Proof:
Consider the triangles $\Delta$ ABD and $\Delta$ ACD.
Since AD is the bisector of $\angle$A, it divides $\angle$A into two equal angles.
$\angle$BAD = $\angle$CAD
(Given, AD bisects $\angle$A)
Since AD $\perp$ BC, the angle between AD and BC is $90^\circ$ at point D.
$\angle$ADB = $90^\circ$
(Given, AD $\perp$ BC)
$\angle$ADC = $90^\circ$
(Given, AD $\perp$ BC)
So,
$\angle$ADB = $\angle$ADC
AD is a common side to both triangles.
AD = AD
(Common side)
By ASA (Angle-Side-Angle) congruence rule, if two angles and the included side of one triangle are equal to the corresponding two angles and the included side of another triangle, then the two triangles are congruent.
In $\Delta$ ABD and $\Delta$ ACD, we have two pairs of equal angles ($\angle$BAD = $\angle$CAD and $\angle$ADB = $\angle$ADC) and the included side (AD = AD) is common.
Therefore, by ASA congruence rule:
$\Delta$ ABD $\cong$ $\Delta$ ACD
Since $\Delta$ ABD $\cong$ $\Delta$ ACD, their corresponding parts are equal (CPCT).
Therefore, the corresponding sides AB and AC are equal.
AB = AC
(CPCT)
By definition, a triangle with two equal sides is called an isosceles triangle.
Since AB = AC, $\Delta$ ABC is an isosceles triangle.
Hence Proved.
Example 5. E and F are respectively the mid-points of equal sides AB and AC of ∆ ABC (see Fig. 7.28). Show that BF = CE.
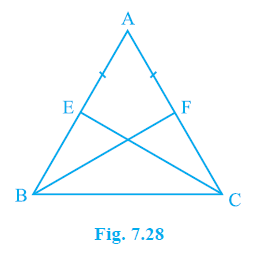
Answer:
Given:
In $\Delta$ ABC,
AB = AC
E is the mid-point of AB.
F is the mid-point of AC.
To Prove:
BF = CE
Proof:
Consider the triangles $\Delta$ ABF and $\Delta$ ACE.
AB = AC
(Given)
$\angle$A = $\angle$A
(Common angle)
Since E is the mid-point of AB, we have AE = $\frac{1}{2}$ AB.
Since F is the mid-point of AC, we have AF = $\frac{1}{2}$ AC.
Given AB = AC, multiplying both sides by $\frac{1}{2}$, we get:
$\frac{1}{2}$ AB = $\frac{1}{2}$ AC
By substitution, we have:
AE = AF
So, in $\Delta$ ABF and $\Delta$ ACE, we have:
AB = AC
(Given)
$\angle$A = $\angle$A
(Common angle)
AF = AE
(Proved above)
By SAS (Side-Angle-Side) congruence rule, if two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle, then the two triangles are congruent.
Therefore, by SAS congruence rule:
$\Delta$ ABF $\cong$ $\Delta$ ACE
Since $\Delta$ ABF $\cong$ $\Delta$ ACE, their corresponding parts are equal (CPCT).
BF and CE are corresponding sides in the two congruent triangles (BF corresponds to CE).
Therefore, their lengths are equal.
BF = CE
(CPCT)
Hence Proved.
Example 6. In an isosceles triangle ABC with AB = AC, D and E are points on BC such that BE = CD (see Fig. 7.29). Show that AD = AE.
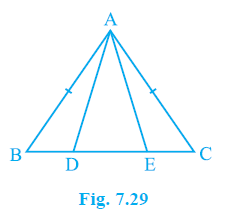
Answer:
Given:
In $\Delta$ ABC, AB = AC.
D and E are points on BC such that BE = CD.
To Prove:
AD = AE
Proof:
Consider the triangles $\Delta$ ABE and $\Delta$ ACD.
AB = AC
(Given)
Since AB = AC in $\Delta$ ABC, the angles opposite to these equal sides are also equal.
$\angle$ABC = $\angle$ACB
(Angles opposite to equal sides)
In $\Delta$ ABE, $\angle$ABE is the same as $\angle$ABC.
In $\Delta$ ACD, $\angle$ACD is the same as $\angle$ACB.
Therefore,
$\angle$ABE = $\angle$ACD
BE = CD
(Given)
By SAS (Side-Angle-Side) congruence rule, if two sides and the included angle of one triangle are equal to the corresponding two sides and the included angle of another triangle, then the two triangles are congruent.
In $\Delta$ ABE and $\Delta$ ACD, we have two pairs of equal sides (AB = AC and BE = CD) and the included angles ($\angle$ABE and $\angle$ACD) are equal.
Therefore, by SAS congruence rule:
$\Delta$ ABE $\cong$ $\Delta$ ACD
Since $\Delta$ ABE $\cong$ $\Delta$ ACD, their corresponding parts are equal (CPCT).
AD and AE are corresponding sides in the two congruent triangles (AE corresponds to AD).
Therefore, their lengths are equal.
AD = AE
(CPCT)
Hence Proved.
Exercise 7.2
Question 1. In an isosceles triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at O. Join A to O. Show that:
(i) OB = OC
(ii) AO bisects ∠A
Answer:
Given:
In $\Delta$ ABC, AB = AC.
BO is the bisector of $\angle$B.
CO is the bisector of $\angle$C.
To Prove:
(i) OB = OC
(ii) AO bisects $\angle$A
Figure:
Draw an isosceles triangle ABC with AB = AC. Draw the angle bisectors of $\angle$B and $\angle$C, which intersect at O. Join A to O.
Proof:
(i) To prove OB = OC
In $\Delta$ ABC, we are given that AB = AC.
In an isosceles triangle, the angles opposite to the equal sides are equal.
$\angle$ABC = $\angle$ACB
(Angles opposite to equal sides)
Since BO is the bisector of $\angle$B, it divides $\angle$B into two equal angles:
$\angle$OBC = $\frac{1}{2}\angle$ABC
Since CO is the bisector of $\angle$C, it divides $\angle$C into two equal angles:
$\angle$OCB = $\frac{1}{2}\angle$ACB
Since $\angle$ABC = $\angle$ACB, multiplying both sides by $\frac{1}{2}$, we get:
$\frac{1}{2}\angle$ABC = $\frac{1}{2}\angle$ACB
By substitution (using the definitions of angle bisectors), we have:
$\angle$OBC = $\angle$OCB
... (i)
Now consider $\Delta$ OBC.
In a triangle, the sides opposite to equal angles are equal.
Since $\angle$OBC = $\angle$OCB (from equation (i)), the side opposite $\angle$OBC (which is OC) must be equal to the side opposite $\angle$OCB (which is OB).
OC = OB
(Sides opposite to equal angles)
Therefore, OB = OC.
(ii) To prove AO bisects $\angle$A
Consider the triangles $\Delta$ ABO and $\Delta$ ACO.
1. Side AB and side AC are equal.
AB = AC
(Given)
2. Side OB and side OC are equal.
OB = OC
(Proved in part (i))
3. Side AO is common to both triangles.
AO = AO
(Common side)
By SSS (Side-Side-Side) congruence rule, if three sides of one triangle are equal to the corresponding three sides of another triangle, then the two triangles are congruent.
In $\Delta$ ABO and $\Delta$ ACO, we have three pairs of equal sides (AB = AC, OB = OC, and AO = AO).
Therefore, by SSS congruence rule:
$\Delta$ ABO $\cong$ $\Delta$ ACO
By CPCT (Corresponding Parts of Congruent Triangles), the corresponding angles of congruent triangles are equal.
The angle $\angle$BAO in $\Delta$ ABO corresponds to $\angle$CAO in $\Delta$ ACO.
$\angle$BAO = $\angle$CAO
(CPCT)
Since the ray AO divides $\angle$A into two equal angles ($\angle$BAO and $\angle$CAO), AO bisects $\angle$A.
Hence Proved.
Question 2. In ∆ABC, AD is the perpendicular bisector of BC (see Fig. 7.30). Show that ∆ABC is an isosceles triangle in which AB = AC.
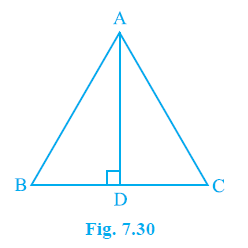
Answer:
Given:
In $\Delta$ ABC, AD is the perpendicular bisector of BC.
To Prove:
$\Delta$ ABC is an isosceles triangle with AB = AC.
Proof:
Since AD is the perpendicular bisector of BC, it means that AD is perpendicular to BC and D is the midpoint of BC.
From the definition of perpendicular bisector:
$\angle$ADB = $90^\circ$
(AD $\perp$ BC)
$\angle$ADC = $90^\circ$
(AD $\perp$ BC)
So, $\angle$ADB = $\angle$ADC.
BD = CD
(D is the midpoint of BC)
Now consider the triangles $\Delta$ ABD and $\Delta$ ACD.
BD = CD
(From perpendicular bisector definition)
$\angle$ADB = $\angle$ADC
(Both equal to $90^\circ$)
AD = AD
(Common side)
By SAS (Side-Angle-Side) congruence rule, if two sides and the included angle of one triangle are equal to the corresponding two sides and the included angle of another triangle, then the two triangles are congruent.
In $\Delta$ ABD and $\Delta$ ACD, we have two pairs of equal sides (BD = CD and AD = AD) and the included angles ($\angle$ADB and $\angle$ADC) are equal.
Therefore, by SAS congruence rule:
$\Delta$ ABD $\cong$ $\Delta$ ACD
Since $\Delta$ ABD $\cong$ $\Delta$ ACD, their corresponding parts are equal (CPCT).
Therefore, the corresponding sides AB and AC are equal.
AB = AC
(CPCT)
By definition, a triangle with two equal sides is called an isosceles triangle.
Since AB = AC, $\Delta$ ABC is an isosceles triangle.
Hence Proved.
Question 3. ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see Fig. 7.31). Show that these altitudes are equal.
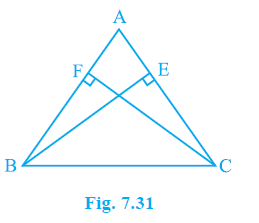
Answer:
Given:
In $\Delta$ ABC, AB = AC.
BE is an altitude to AC, so BE $\perp$ AC.
CF is an altitude to AB, so CF $\perp$ AB.
To Prove:
BE = CF (The altitudes are equal).
Proof:
Consider the triangles $\Delta$ ABE and $\Delta$ ACF.
$\angle$AEB = $90^\circ$
(Given, BE is an altitude to AC)
$\angle$AFC = $90^\circ$
(Given, CF is an altitude to AB)
So,
$\angle$AEB = $\angle$AFC
The angle $\angle$A is common to both triangles.
$\angle$BAE = $\angle$CAF
(Common angle $\angle$A)
We are given that AB = AC.
AB = AC
(Given)
By AAS (Angle-Angle-Side) congruence rule, if two angles and a non-included side of one triangle are equal to the corresponding two angles and the non-included side of the other triangle, then the triangles are congruent.
In $\Delta$ ABE and $\Delta$ ACF, we have two pairs of equal angles ($\angle$BAE = $\angle$CAF and $\angle$AEB = $\angle$AFC) and a pair of non-included sides equal (AB = AC).
Therefore, by AAS congruence rule:
$\Delta$ ABE $\cong$ $\Delta$ ACF
Since $\Delta$ ABE $\cong$ $\Delta$ ACF, their corresponding parts are equal (CPCT).
BE and CF are corresponding sides in the two congruent triangles (BE corresponds to CF).
Therefore, their lengths are equal.
BE = CF
(CPCT)
Hence Proved.
Alternate Proof:
Consider the triangles $\Delta$ BCE and $\Delta$ CBF.
$\angle$BEC = $90^\circ$
(Given, BE $\perp$ AC)
$\angle$CFB = $90^\circ$
(Given, CF $\perp$ AB)
So,
$\angle$BEC = $\angle$CFB
We are given that AB = AC.
In $\Delta$ ABC, the angles opposite to equal sides are also equal.
$\angle$ABC = $\angle$ACB
(Angles opposite equal sides AB and AC)
In $\Delta$ BCE, $\angle$EBC is the same as $\angle$ABC.
In $\Delta$ CBF, $\angle$FCB is the same as $\angle$ACB.
Therefore,
$\angle$EBC = $\angle$FCB
BC is a common side to both triangles.
BC = CB
(Common side)
By AAS (Angle-Angle-Side) congruence rule, if two angles and a non-included side of one triangle are equal to the corresponding two angles and the non-included side of the other triangle, then the triangles are congruent.
In $\Delta$ BCE and $\Delta$ CBF, we have two pairs of equal angles ($\angle$EBC = $\angle$FCB and $\angle$BEC = $\angle$CFB) and a pair of non-included sides equal (BC = CB).
Therefore, by AAS congruence rule:
$\Delta$ BCE $\cong$ $\Delta$ CBF
Since $\Delta$ BCE $\cong$ $\Delta$ CBF, their corresponding parts are equal (CPCT).
BE and CF are corresponding sides in the two congruent triangles (BE corresponds to CF).
Therefore, their lengths are equal.
BE = CF
(CPCT)
Hence Proved.
Question 4. ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see Fig. 7.32). Show that
(i) ∆ ABE ≅ ∆ ACF
(ii) AB = AC, i.e., ABC is an isosceles triangle.
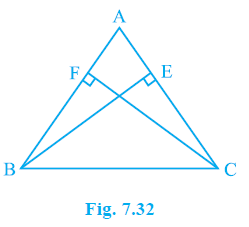
Answer:
Given:
In $\Delta$ ABC,
BE is an altitude to AC, so BE $\perp$ AC.
CF is an altitude to AB, so CF $\perp$ AB.
BE = CF.
To Prove:
(i) $\Delta$ ABE $\cong$ $\Delta$ ACF
(ii) AB = AC ($\Delta$ ABC is an isosceles triangle).
Proof:
(i) To prove $\Delta$ ABE $\cong$ $\Delta$ ACF
Consider the triangles $\Delta$ ABE and $\Delta$ ACF.
Since BE is an altitude to AC, $\angle$AEB = $90^\circ$.
Since CF is an altitude to AB, $\angle$AFC = $90^\circ$.
$\angle$AEB = $\angle$AFC = $90^\circ$
(Given altitudes)
The angle $\angle$A is common to both triangles.
$\angle$BAE = $\angle$CAF
(Common angle $\angle$A)
We are given that the altitudes BE and CF are equal.
BE = CF
(Given)
By AAS (Angle-Angle-Side) congruence rule, if two angles and a non-included side of one triangle are equal to the corresponding two angles and the non-included side of the other triangle, then the triangles are congruent.
In $\Delta$ ABE and $\Delta$ ACF, we have two pairs of equal angles ($\angle$BAE = $\angle$CAF and $\angle$AEB = $\angle$AFC) and a pair of non-included sides equal (BE = CF).
Therefore, by AAS congruence rule:
$\Delta$ ABE $\cong$ $\Delta$ ACF
(ii) To prove AB = AC
Since $\Delta$ ABE $\cong$ $\Delta$ ACF (as proved in part (i)), their corresponding parts are equal (CPCT).
AB and AC are corresponding sides in the two congruent triangles (AB corresponds to AC).
Therefore, their lengths are equal.
AB = AC
(CPCT)
By definition, a triangle with two equal sides is called an isosceles triangle.
Since AB = AC, $\Delta$ ABC is an isosceles triangle.
Hence Proved.
Alternate Proof for (i) using RHS:
Consider the right-angled triangles $\Delta$ BCE and $\Delta$ CBF.
$\angle$BEC = $90^\circ$
(Given, BE $\perp$ AC)
$\angle$CFB = $90^\circ$
(Given, CF $\perp$ AB)
So, both are right triangles.
BC is the hypotenuse for both right triangles $\Delta$ BCE and $\Delta$ CBF.
BC = CB
(Common hypotenuse)
We are given that the altitudes BE and CF are equal.
BE = CF
(Given)
By RHS (Right angle-Hypotenuse-Side) congruence rule, if in two right triangles the hypotenuse and one side of one triangle are equal to the hypotenuse and one side of the other triangle, then the two triangles are congruent.
In right triangles $\Delta$ BCE and $\Delta$ CBF, the hypotenuse BC is common, and a side (BE = CF) is equal.
Therefore, by RHS congruence rule:
$\Delta$ BCE $\cong$ $\Delta$ CBF
By CPCT, the corresponding angles are equal.
$\angle$EBC = $\angle$FCB
(CPCT)
In $\Delta$ ABC, $\angle$ABC is the same as $\angle$EBC, and $\angle$ACB is the same as $\angle$FCB.
So, $\angle$ABC = $\angle$ACB.
In $\Delta$ ABC, since $\angle$ABC = $\angle$ACB, the sides opposite to these angles are equal.
AC = AB
(Sides opposite equal angles)
Thus, AB = AC, and $\Delta$ ABC is an isosceles triangle.
This completes the proof for both parts (i) and (ii) using an alternative approach starting with RHS congruence of $\Delta$ BCE and $\Delta$ CBF.
Question 5. ABC and DBC are two isosceles triangles on the same base BC (see Fig. 7.33). Show that ∠ABD = ∠ACD.
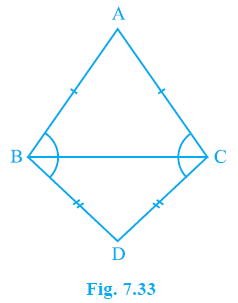
Answer:
Given:
$\Delta$ ABC is an isosceles triangle on base BC, with AB = AC.
$\Delta$ DBC is an isosceles triangle on the same base BC, with DB = DC.
To Prove:
$\angle$ABD = $\angle$ACD
Proof:
Consider $\Delta$ ABC.
We are given that AB = AC.
In a triangle, the angles opposite to equal sides are equal.
Therefore, the angle opposite to side AC ($\angle$ABC) is equal to the angle opposite to side AB ($\angle$ACB).
$\angle$ABC = $\angle$ACB
(Angles opposite to equal sides in $\Delta$ ABC) ... (i)
Now consider $\Delta$ DBC.
We are given that DB = DC.
In a triangle, the angles opposite to equal sides are equal.
Therefore, the angle opposite to side DC ($\angle$DBC) is equal to the angle opposite to side DB ($\angle$DCB).
$\angle$DBC = $\angle$DCB
(Angles opposite to equal sides in $\Delta$ DBC) ... (ii)
Now, we add equation (i) and equation (ii):
$\angle$ABC + $\angle$DBC = $\angle$ACB + $\angle$DCB
From the figure, we can see that $\angle$ABD is the sum of adjacent angles $\angle$ABC and $\angle$DBC.
$\angle$ABD = $\angle$ABC + $\angle$DBC
Similarly, $\angle$ACD is the sum of adjacent angles $\angle$ACB and $\angle$DCB.
$\angle$ACD = $\angle$ACB + $\angle$DCB
Substituting these sums into the result of adding equations (i) and (ii):
$\angle$ABD = $\angle$ACD
Thus, we have shown that $\angle$ABD is equal to $\angle$ACD.
Hence Proved.
Question 6. ∆ABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see Fig. 7.34). Show that ∠ BCD is a right angle.
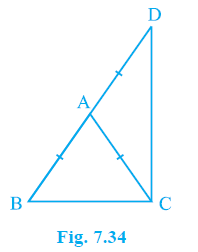
Answer:
Given:
In $\Delta$ ABC, AB = AC.
Side BA is produced to D such that AD = AB.
To Prove:
$\angle$BCD is a right angle, i.e., $\angle$BCD = $90^\circ$.
Proof:
In $\Delta$ ABC, we are given that AB = AC.
In an isosceles triangle, the angles opposite to the equal sides are equal.
$\angle$ABC = $\angle$ACB
(Angles opposite equal sides AB and AC)
Let $\angle$ABC = $\angle$ACB = x.
We are given that AD = AB. Since AB = AC, we also have AD = AC.
Now consider $\Delta$ ADC. We have AD = AC.
In $\Delta$ ADC, the angles opposite to the equal sides are equal.
$\angle$ADC = $\angle$ACD
(Angles opposite equal sides AC and AD)
Let $\angle$ADC = $\angle$ACD = y.
Now consider the triangle $\Delta$ BCD.
The angle $\angle$BCD is the sum of angles $\angle$BCA and $\angle$ACD.
$\angle$BCD = $\angle$BCA + $\angle$ACD
Substituting the values we assigned:
$\angle$BCD = x + y
... (i)
Now, apply the Angle Sum Property to $\Delta$ BCD.
Sum of angles in $\Delta$ BCD = $180^\circ$
(Angle Sum Property of a Triangle)
$\angle$DBC + $\angle$BCD + $\angle$BDC = $180^\circ$
Note that $\angle$DBC is the same as $\angle$ABC, which is x.
Note that $\angle$BDC is the same as $\angle$ADC, which is y.
Substitute these values and the expression for $\angle$BCD from (i):
x + (x + y) + y = $180^\circ$
Combine like terms:
2x + 2y = $180^\circ$
Divide the entire equation by 2:
x + y = $90^\circ$
From equation (i), we know that $\angle$BCD = x + y.
Substitute x + y = $90^\circ$ into the equation for $\angle$BCD:
$\angle$BCD = $90^\circ$
Therefore, $\angle$BCD is a right angle.
Hence Proved.
Question 7. ABC is a right angled triangle in which ∠A = 90° and AB = AC. Find ∠B and ∠C.
Answer:
Given:
In right angled triangle ABC,
$\angle$A = $90^\circ$
AB = AC
To Find:
The measures of $\angle$B and $\angle$C.
Figure:
Draw a right-angled triangle ABC where the angle at A is $90^\circ$, and sides AB and AC are equal in length.
Solution:
In $\Delta$ ABC, we are given that AB = AC.
In a triangle, the angles opposite to equal sides are equal.
$\angle$B = $\angle$C
(Angles opposite equal sides AB and AC) ... (i)
By the Angle Sum Property of a triangle, the sum of all interior angles in $\Delta$ ABC is $180^\circ$.
$\angle$A + $\angle$B + $\angle$C = $180^\circ$
(Angle Sum Property of a triangle) ... (ii)
Substitute the given value $\angle$A = $90^\circ$ and the relationship $\angle$C = $\angle$B (from equation (i)) into equation (ii):
90$^\circ$ + $\angle$B + $\angle$B = $180^\circ$
Combine the terms involving $\angle$B:
90$^\circ$ + $2\angle$B = $180^\circ$
Subtract $90^\circ$ from both sides of the equation:
2$\angle$B = $180^\circ - 90^\circ$
2$\angle$B = $90^\circ$
Divide both sides by 2 to find $\angle$B:
$\angle$B = $\frac{90^\circ}{2}$
$\angle$B = $45^\circ$
Since $\angle$C = $\angle$B (from equation (i)), we also have:
$\angle$C = $45^\circ$
Answer:
The measures of the angles are:
$\angle$B = $45^\circ$
$\angle$C = $45^\circ$
Question 8. Show that the angles of an equilateral triangle are 60° each.
Answer:
Given:
An equilateral triangle, let's call it $\Delta$ ABC.
By the definition of an equilateral triangle, all its sides are equal in length.
AB = BC = AC
(Sides of an equilateral triangle)
To Prove:
The measure of each angle in $\Delta$ ABC is $60^\circ$, i.e., $\angle$A = $\angle$B = $\angle$C = $60^\circ$.
Figure:
Draw a triangle with all three sides marked as equal.
Proof:
In $\Delta$ ABC, we are given that AB = AC.
In a triangle, the angles opposite to equal sides are equal.
The angle opposite to side AC is $\angle$B.
The angle opposite to side AB is $\angle$C.
$\angle$B = $\angle$C
(Angles opposite equal sides AB and AC) ... (i)
Also, in $\Delta$ ABC, we are given that BC = AC.
In a triangle, the angles opposite to equal sides are equal.
The angle opposite to side AC is $\angle$B.
The angle opposite to side BC is $\angle$A.
$\angle$B = $\angle$A
(Angles opposite equal sides AC and BC) ... (ii)
From equation (i) ($\angle$B = $\angle$C) and equation (ii) ($\angle$B = $\angle$A), we can conclude that all three angles are equal to each other.
$\angle$A = $\angle$B = $\angle$C
Let the measure of each angle be $m$ degrees.
$\angle$A = m, $\angle$B = m, and $\angle$C = m
By the Angle Sum Property of a triangle, the sum of the interior angles of $\Delta$ ABC is $180^\circ$.
$\angle$A + $\angle$B + $\angle$C = $180^\circ$
(Angle Sum Property of a triangle) ... (iii)
Substitute the value of each angle (m) into equation (iii):
m + m + m = $180^\circ$
Combine the terms:
3m = $180^\circ$
Divide both sides by 3 to find the value of m:
m = $\frac{180^\circ}{3}$
m = $60^\circ$
Since $\angle$A = $\angle$B = $\angle$C = m, we have:
$\angle$A = $60^\circ$
$\angle$B = $60^\circ$
$\angle$C = $60^\circ$
Thus, the angles of an equilateral triangle are $60^\circ$ each.
Hence Proved.
Example 7 & 8 (Before Exercise 7.3)
Example 7. AB is a line-segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (see Fig. 7.37). Show that the line PQ is the perpendicular bisector of AB.
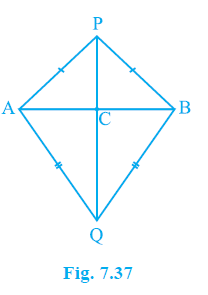
Answer:
Given:
AB is a line segment.
P and Q are points on opposite sides of AB.
P is equidistant from A and B, i.e., PA = PB.
Q is equidistant from A and B, i.e., QA = QB.
Line PQ and line segment AB intersect at point C.
To Prove:
The line PQ is the perpendicular bisector of AB.
Proof:
Consider the triangles $\Delta$ PAQ and $\Delta$ PBQ.
1. Side PA and side PB are equal.
PA = PB
(Given)
2. Side QA and side QB are equal.
QA = QB
(Given)
3. Side PQ is common to both triangles.
PQ = PQ
(Common side)
By the SSS (Side-Side-Side) congruence rule, $\Delta$ PAQ is congruent to $\Delta$ PBQ.
$\Delta$ PAQ $\cong$ $\Delta$ PBQ
Since $\Delta$ PAQ $\cong$ $\Delta$ PBQ, their corresponding parts are equal by CPCT (Corresponding Parts of Congruent Triangles are Congruent).
The angle $\angle$ APQ in $\Delta$ PAQ corresponds to $\angle$ BPQ in $\Delta$ PBQ.
$\angle$ APQ = $\angle$ BPQ
(CPCT) ... (i)
This means that line PQ bisects the angle $\angle$ APB. Point C lies on the line segment PQ.
Now consider the triangles $\Delta$ PAC and $\Delta$ PBC.
1. Side PA and side PB are equal.
PA = PB
(Given)
2. The angle $\angle$ APC and $\angle$ BPC are equal.
$\angle$ APC = $\angle$ BPC
(From $\angle$ APQ = $\angle$ BPQ, as C lies on PQ) ... (ii)
3. Side PC is common to both triangles.
PC = PC
(Common side)
By the SAS (Side-Angle-Side) congruence rule, $\Delta$ PAC is congruent to $\Delta$ PBC.
$\Delta$ PAC $\cong$ $\Delta$ PBC
Since $\Delta$ PAC $\cong$ $\Delta$ PBC, their corresponding parts are equal by CPCT.
The side AC in $\Delta$ PAC corresponds to the side BC in $\Delta$ PBC.
AC = BC
(CPCT) ... (iii)
This shows that point C is the midpoint of the line segment AB. Since PQ passes through C, the line PQ bisects the line segment AB.
Also by CPCT, the angle $\angle$ PCA in $\Delta$ PAC corresponds to the angle $\angle$ PCB in $\Delta$ PBC.
$\angle$ PCA = $\angle$ PCB
(CPCT) ... (iv)
Since $\angle$ PCA and $\angle$ PCB form a linear pair on the straight line segment AB, their sum is $180^\circ$.
$\angle$ PCA + $\angle$ PCB = $180^\circ$
(Linear Pair Axiom)
Substitute $\angle$ PCB = $\angle$ PCA (from equation (iv)) into the equation:
$\angle$ PCA + $\angle$ PCA = $180^\circ$
2$\angle$ PCA = $180^\circ$
Divide both sides by 2:
$\angle$ PCA = $\frac{180^\circ}{2}$
$\angle$ PCA = $90^\circ$
Since $\angle$ PCA = $90^\circ$, the line PQ is perpendicular to AB at point C.
From equation (iii), we showed that AC = BC, meaning C is the midpoint of AB.
Since line PQ passes through the midpoint C of AB and is perpendicular to AB at C, the line PQ is the perpendicular bisector of AB.
Hence Proved.
Example 8. P is a point equidistant from two lines l and m intersecting at point A (see Fig. 7.38). Show that the line AP bisects the angle between them.
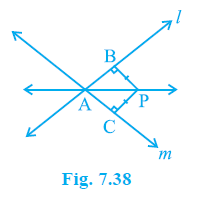
Answer:
Given:
Two lines l and m intersecting at point A.
P is a point such that it is equidistant from lines l and m.
To Prove:
The line AP bisects the angle between lines l and m, i.e., $\angle$PAB = $\angle$PAC, where AB is part of line l and AC is part of line m.
Proof:
Consider the right-angled triangles $\Delta$ PBA and $\Delta$ PCA.
$\angle$PBA = $90^\circ$
(By construction, PB $\perp$ line l)
$\angle$PCA = $90^\circ$
(By construction, PC $\perp$ line m)
So, both $\Delta$ PBA and $\Delta$ PCA are right triangles.
PB = PC
(Given, P is equidistant from lines l and m)
AP is the hypotenuse in both right triangles $\Delta$ PBA and $\Delta$ PCA.
AP = AP
(Common hypotenuse)
By RHS (Right angle-Hypotenuse-Side) congruence rule, if in two right triangles the hypotenuse and one side of one triangle are equal to the hypotenuse and one side of the other triangle, then the two triangles are congruent.
In right triangles $\Delta$ PBA and $\Delta$ PCA, we have the hypotenuse AP common and a side equal (PB = PC).
Therefore, by RHS congruence rule:
$\Delta$ PBA $\cong$ $\Delta$ PCA
Since $\Delta$ PBA $\cong$ $\Delta$ PCA, their corresponding parts are equal (CPCT).
The angle $\angle$PAB in $\Delta$ PBA corresponds to $\angle$PAC in $\Delta$ PCA.
Therefore,
$\angle$PAB = $\angle$PAC
(CPCT)
Since the ray AP divides the angle $\angle$BAC (the angle between lines l and m) into two equal angles ($\angle$PAB and $\angle$PAC), the line AP bisects the angle between them.
Hence Proved.
Exercise 7.3
Question 1. ∆ ABC and ∆ DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Fig. 7.39). If AD is extended to intersect BC at P, show that
(i) ∆ABD ≅ ∆ACD
(ii) ∆ABP ≅ ∆ACP
(iii) AP bisects ∠A as well as ∠D.
(iv) AP is the perpendicular bisector of BC.
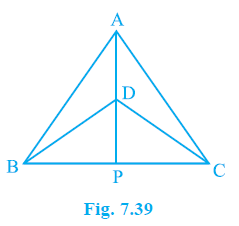
Answer:
Given:
$\Delta$ ABC is an isosceles triangle with base BC, so AB = AC.
$\Delta$ DBC is an isosceles triangle on the same base BC, so DB = DC.
AD is extended to intersect BC at P.
To Prove:
(i) $\Delta$ABD $\cong$ $\Delta$ACD
(ii) $\Delta$ABP $\cong$ $\Delta$ACP
(iii) AP bisects $\angle$A as well as $\angle$D.
(iv) AP is the perpendicular bisector of BC.
Proof:
(i) To prove $\Delta$ABD $\cong$ $\Delta$ACD
Consider the triangles $\Delta$ ABD and $\Delta$ ACD.
AB = AC
(Given)
DB = DC
(Given)
AD = AD
(Common side)
By SSS (Side-Side-Side) congruence rule, if three sides of one triangle are equal to the corresponding three sides of another triangle, then the two triangles are congruent.
Therefore, by SSS congruence rule:
$\Delta$ ABD $\cong$ $\Delta$ ACD
(ii) To prove $\Delta$ABP $\cong$ $\Delta$ACP
Consider the triangles $\Delta$ ABP and $\Delta$ ACP.
AB = AC
(Given)
Since $\Delta$ ABD $\cong$ $\Delta$ ACD (from part (i)), their corresponding parts are equal (CPCT).
Therefore, $\angle$BAD = $\angle$CAD.
Since P lies on the extension of AD, the ray AP is the same as the ray AD.
$\angle$BAP = $\angle$CAP
(Since $\angle$BAD = $\angle$CAD and P is on the extension of AD)
AP = AP
(Common side)
By SAS (Side-Angle-Side) congruence rule, if two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle, then the two triangles are congruent.
Therefore, by SAS congruence rule:
$\Delta$ ABP $\cong$ $\Delta$ ACP
(iii) To prove AP bisects $\angle$A as well as $\angle$D.
From the proof of part (ii), we used the fact that $\angle$BAP = $\angle$CAP (which is the same as $\angle$BAD = $\angle$CAD). This shows that the line segment AP (or ray AD extended to P) divides $\angle$A into two equal angles.
$\angle$BAP = $\angle$CAP
(Proved in part (ii))
Thus, AP bisects $\angle$A.
Now, consider the triangles $\Delta$ BDP and $\Delta$ CDP.
DB = DC
(Given)
Since $\Delta$ ABP $\cong$ $\Delta$ ACP (from part (ii)), their corresponding parts are equal (CPCT).
BP = CP
(CPCT from $\Delta$ABP $\cong$ $\Delta$ACP)
DP = DP
(Common side)
By SSS congruence rule, $\Delta$ BDP $\cong$ $\Delta$ CDP.
By CPCT, their corresponding angles are equal.
$\angle$BDP = $\angle$CDP
(CPCT)
Since P lies on the extension of AD, the line AP contains the line segment DP. The equality $\angle$BDP = $\angle$CDP shows that the line AP (or ray DP) divides $\angle$BDC (which is $\angle$D) into two equal angles.
Thus, AP bisects $\angle$D.
(iv) To prove AP is the perpendicular bisector of BC.
From part (ii), we have proved $\Delta$ ABP $\cong$ $\Delta$ ACP.
By CPCT, corresponding sides are equal:
BP = CP
(CPCT)
Since P lies on BC and BP = CP, P is the midpoint of BC. This means AP bisects BC.
Also by CPCT from $\Delta$ ABP $\cong$ $\Delta$ ACP, corresponding angles are equal:
$\angle$APB = $\angle$APC
(CPCT)
Since $\angle$APB and $\angle$APC form a linear pair on the line BC, their sum is $180^\circ$.
$\angle$APB + $\angle$APC = $180^\circ$
(Linear Pair Axiom)
Substitute $\angle$APB = $\angle$APC:
$\angle$APB + $\angle$APB = $180^\circ$
2$\angle$APB = $180^\circ$
$\angle$APB = $\frac{180^\circ}{2}$
$\angle$APB = $90^\circ$
Since $\angle$APB = $90^\circ$, AP is perpendicular to BC.
Since AP bisects BC at P and is perpendicular to BC at P, AP is the perpendicular bisector of BC.
Hence Proved.
Question 2. AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that
(i) AD bisects BC
(ii) AD bisects ∠A.
Answer:
Given:
In $\Delta$ ABC, AB = AC.
AD is an altitude from A to BC, which means AD $\perp$ BC.
To Prove:
(i) AD bisects BC (i.e., BD = CD)
(ii) AD bisects $\angle$A (i.e., $\angle$BAD = $\angle$CAD)
Figure:
Draw an isosceles triangle ABC with AB = AC. Draw a perpendicular line segment AD from vertex A to the base BC.
Proof:
(i) To prove AD bisects BC
Consider the triangles $\Delta$ ABD and $\Delta$ ACD.
Since AD is an altitude to BC, it means AD is perpendicular to BC at D.
$\angle$ ADB = $90^\circ$
(Given, AD $\perp$ BC)
Similarly,
$\angle$ ADC = $90^\circ$
(Given, AD $\perp$ BC)
So, both $\Delta$ ABD and $\Delta$ ACD are right triangles at D.
1. The hypotenuses AB and AC are equal.
AB = AC
(Given)
2. The side AD is common to both triangles.
AD = AD
(Common side)
By the RHS (Right angle-Hypotenuse-Side) congruence rule, if the hypotenuse and one side of a right triangle are equal to the hypotenuse and one side of another right triangle, then the triangles are congruent.
Therefore, by RHS congruence rule:
$\Delta$ ABD $\cong$ $\Delta$ ACD
Since $\Delta$ ABD $\cong$ $\Delta$ ACD, their corresponding parts are equal by CPCT (Corresponding Parts of Congruent Triangles are Congruent).
The corresponding sides BD and CD are equal.
BD = CD
(CPCT)
Since BD = CD, point D is the midpoint of BC. Thus, AD bisects BC.
(ii) To prove AD bisects $\angle$A
Since $\Delta$ ABD $\cong$ $\Delta$ ACD (as proved in part (i)), their corresponding parts are equal by CPCT.
The angle $\angle$ BAD in $\Delta$ ABD corresponds to the angle $\angle$ CAD in $\Delta$ ACD.
$\angle$ BAD = $\angle$ CAD
(CPCT)
Since $\angle$ BAD = $\angle$ CAD, the line segment AD bisects $\angle$A.
Hence Proved.
Question 3. Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of ∆ PQR (see Fig. 7.40). Show that:
(i) ∆ ABM ≅ ∆ PQN
(ii) ∆ ABC ≅ ∆ PQR
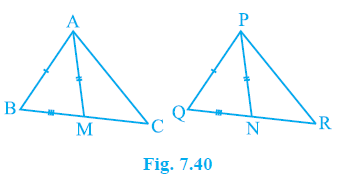
Answer:
Given:
In $\Delta$ ABC and $\Delta$ PQR,
AB = PQ
BC = QR
AM is the median to BC, so M is the midpoint of BC.
PN is the median to QR, so N is the midpoint of QR.
AM = PN
To Prove:
(i) $\Delta$ ABM $\cong$ $\Delta$ PQN
(ii) $\Delta$ ABC $\cong$ $\Delta$ PQR
Proof:
(i) To prove $\Delta$ ABM $\cong$ $\Delta$ PQN
We are given that BC = QR.
Since M is the midpoint of BC, BM = $\frac{1}{2}$ BC.
Since N is the midpoint of QR, QN = $\frac{1}{2}$ QR.
As BC = QR, multiplying both sides by $\frac{1}{2}$ gives $\frac{1}{2}$ BC = $\frac{1}{2}$ QR.
Therefore, BM = QN.
Now consider the triangles $\Delta$ ABM and $\Delta$ PQN.
AB = PQ
(Given)
BM = QN
(Proved above)
AM = PN
(Given)
By SSS (Side-Side-Side) congruence rule, if three sides of one triangle are equal to the corresponding three sides of another triangle, then the two triangles are congruent.
Therefore, by SSS congruence rule:
$\Delta$ ABM $\cong$ $\Delta$ PQN
(ii) To prove $\Delta$ ABC $\cong$ $\Delta$ PQR
Consider the triangles $\Delta$ ABC and $\Delta$ PQR.
AB = PQ
(Given)
Since $\Delta$ ABM $\cong$ $\Delta$ PQN (from part (i)), their corresponding parts are equal (CPCT).
Therefore, the corresponding angles $\angle$ABM and $\angle$PQN are equal.
The angle $\angle$ABM is the same as $\angle$ABC.
The angle $\angle$PQN is the same as $\angle$PQR.
$\angle$ABC = $\angle$PQR
(CPCT from $\Delta$ABM $\cong$ $\Delta$PQN)
BC = QR
(Given)
By SAS (Side-Angle-Side) congruence rule, if two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle, then the two triangles are congruent.
In $\Delta$ ABC and $\Delta$ PQR, we have two pairs of equal sides (AB = PQ and BC = QR) and the included angles ($\angle$ABC and $\angle$PQR) are equal.
Therefore, by SAS congruence rule:
$\Delta$ ABC $\cong$ $\Delta$ PQR
Hence Proved.
Question 4. BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
Answer:
Given:
In $\Delta$ ABC,
BE is an altitude to AC, so BE $\perp$ AC.
CF is an altitude to AB, so CF $\perp$ AB.
BE = CF.
To Prove:
$\Delta$ ABC is an isosceles triangle (i.e., AB = AC).
Figure:
Draw a triangle ABC and draw altitudes BE from B to AC and CF from C to AB. Mark the right angles at E and F and indicate that BE = CF.
Proof:
Consider the two right-angled triangles $\Delta$ BCE and $\Delta$ CBF.
1. They are right-angled triangles.
$\angle$ BEC = $90^\circ$
(Given, BE is an altitude to AC)
$\angle$ CFB = $90^\circ$
(Given, CF is an altitude to AB)
2. The hypotenuse BC is common to both triangles.
BC = CB
(Common hypotenuse)
3. The altitudes BE and CF are equal in length.
BE = CF
(Given)
By the RHS (Right angle-Hypotenuse-Side) congruence rule, if the hypotenuse and one side of one right triangle are equal to the hypotenuse and one side of another right triangle, then the triangles are congruent.
In right triangles $\Delta$ BCE and $\Delta$ CBF, we have the hypotenuse BC = CB, and side BE = side CF.
Therefore, by RHS congruence rule:
$\Delta$ BCE $\cong$ $\Delta$ CBF
By CPCT (Corresponding Parts of Congruent Triangles), the corresponding angles of congruent triangles are equal.
The angle $\angle$ EBC in $\Delta$ BCE corresponds to $\angle$ FCB in $\Delta$ CBF.
$\angle$ EBC = $\angle$ FCB
(CPCT)
In $\Delta$ ABC, $\angle$ ABC is the same as $\angle$ EBC, and $\angle$ ACB is the same as $\angle$ FCB.
So, we have $\angle$ ABC = $\angle$ ACB.
In $\Delta$ ABC, since $\angle$ ABC (angle at B) is equal to $\angle$ ACB (angle at C), the sides opposite to these angles are equal.
The side opposite $\angle$ ABC is AC.
The side opposite $\angle$ ACB is AB.
AC = AB
(Sides opposite equal angles)
Thus, AB = AC.
By definition, a triangle with two equal sides is called an isosceles triangle.
Since AB = AC, $\Delta$ ABC is an isosceles triangle.
Hence Proved.
Question 5. ABC is an isosceles triangle with AB = AC. Draw AP ⊥ BC to show that ∠B = ∠C.
Answer:
Given:
In $\Delta$ ABC, AB = AC.
To Prove:
$\angle$B = $\angle$C.
Construction Required:
Draw a line segment AP from vertex A perpendicular to the side BC, where P is a point on BC.
AP $\perp$ BC
Proof:
Since AP is perpendicular to BC by construction, the angles formed at point P are right angles.
$\angle$ APB = $90^\circ$
(By construction, AP $\perp$ BC)
$\angle$ APC = $90^\circ$
(By construction, AP $\perp$ BC)
So, $\Delta$ APB and $\Delta$ APC are right-angled triangles at P.
Consider the right-angled triangles $\Delta$ APB and $\Delta$ APC.
1. The angles at P are right angles.
$\angle$ APB = $\angle$ APC = $90^\circ$
(From construction)
2. The hypotenuses AB and AC are equal.
AB = AC
(Given, these are the hypotenuses of the right triangles)
3. The side AP is common to both triangles.
AP = AP
(Common side)
Using the RHS (Right angle-Hypotenuse-Side) congruence rule, if in two right triangles the hypotenuse and one side of one triangle are equal to the hypotenuse and one side of the other triangle, then the two triangles are congruent.
In right triangles $\Delta$ APB and $\Delta$ APC, we have the right angle at P, the hypotenuse AB = AC, and the common side AP = AP.
Therefore, by RHS congruence rule:
$\Delta$ APB $\cong$ $\Delta$ APC
By CPCT (Corresponding Parts of Congruent Triangles), the corresponding angles of congruent triangles are equal.
The angle $\angle$B in $\Delta$ APB corresponds to the angle $\angle$C in $\Delta$ APC.
Therefore,
$\angle$B = $\angle$C
(CPCT)
Thus, we have shown that the angles opposite the equal sides AB and AC in $\Delta$ ABC are equal.
Hence Proved.

