| Non-Rationalised NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Example 1 (Before Exercise 12.1) | Exercise 12.1 | Example 2 & 3 (Before Exercise 12.2) |
| Exercise 12.2 | Example 4 to 6 (Before Exercise 12.3) | Exercise 12.3 |
Chapter 12 Areas Related To Circles
This solutions guide explores Chapter 12: Areas Related to Circles, a chapter dedicated to extending our understanding of circles beyond their basic definitions. While we are familiar with calculating the total distance around a circle (its circumference) and the total space it occupies (its area), this chapter delves into the geometry of specific parts of a circle. We will learn how to precisely measure the lengths of curved boundaries (arcs) and calculate the areas of distinct regions within a circle, namely sectors and segments. These concepts are not merely abstract geometric exercises; they have direct applications in various practical fields, including design (e.g., creating patterns, logos, or decorative elements), architecture (e.g., designing curved windows or sections of domes), engineering (e.g., calculating cross-sectional areas of pipes or properties of gears), and even land measurement. Furthermore, a significant focus of this chapter lies in tackling problems involving combinations of plane figures, where circles or their parts are integrated with other shapes like squares, rectangles, and triangles. This requires a strategic approach, breaking down complex composite shapes into simpler, manageable components whose areas we can calculate using the formulas developed here and in previous studies. Mastering these techniques allows for the accurate quantification of areas and perimeters in intricate two-dimensional layouts.
We begin by revisiting the foundational formulas for a circle with radius $r$:
- Circumference: The total length of the boundary of the circle is given by $C = 2\pi r$.
- Area: The total region enclosed by the circle is given by $A = \pi r^2$.
Building upon these, we define and analyze specific regions within the circle:
A Sector of a circle is the region enclosed by two radii and the corresponding arc lying between them, resembling a slice of pizza. If the angle between the two radii at the center is $\theta$ (measured in degrees), the solutions demonstrate how to calculate:
- The Length of the arc of the sector: $L = \left(\frac{\theta}{360}\right) \times 2\pi r$. This represents the portion of the circle's circumference corresponding to the angle $\theta$.
- The Area of the sector: $A_{\text{sector}} = \left(\frac{\theta}{360}\right) \times \pi r^2$. This represents the fraction $\frac{\theta}{360}$ of the total circle's area.
A Segment of a circle is the region enclosed between a chord and its corresponding arc. It's like the piece sliced off a circle by a straight cut. The solutions explain that calculating the Area of a segment typically involves a two-step process:
- Find the area of the corresponding sector (formed by the radii to the endpoints of the chord).
- Find the area of the triangle formed by the chord and the two radii.
- Subtract the area of the triangle from the area of the sector: $A_{\text{segment}} = A_{\text{sector}} - A_{\text{triangle}}$.
Calculating the area of the triangle within the segment often requires careful consideration of the central angle $\theta$. For standard angles like $60^\circ$ (equilateral triangle) or $90^\circ$ (isosceles right triangle), basic geometric formulas suffice. For other angles, trigonometry might be needed, using the formula $Area = \frac{1}{2} r^2 \sin\theta$.
The most challenging and application-oriented part of this chapter involves calculating the areas of combinations of plane figures. These problems often present visually complex designs incorporating circles, semicircles, quadrants (quarter circles), sectors, segments, alongside squares, rectangles, triangles, etc. The solutions guide students through the critical strategy of decomposing these intricate shapes into simpler, recognizable geometric components. The required area (often a shaded region) is then found by carefully adding or subtracting the areas of these fundamental shapes. Common examples include finding the area of shaded regions bounded by intersecting circles, calculating the area accessible for grazing by an animal tethered with a rope (forming a sector), determining the area of intricate flower bed designs, or finding the area of running tracks with semicircular ends. Success in these problems hinges on correct identification of the shapes, accurate application of the relevant area formulas (including those for sectors and segments), careful algebraic manipulation, and meticulous calculation, paying close attention to the specified value of $\pi$ ($\frac{22}{7}$ or $3.14$) and ensuring the final answer includes appropriate units (e.g., $cm^2$, $m^2$).
Example 1 (Before Exercise 12.1)
Example 1. The cost of fencing a circular field at the rate of ₹ 24 per metre is ₹ 5280. The field is to be ploughed at the rate of ₹ 0.50 per m2 . Find the cost of ploughing the field (Take π = $\frac{22}{7}$ ).
Answer:
Given
The total cost of fencing a circular field is
The rate of fencing is
The rate of ploughing the field is
To Find
The cost of ploughing the field.
Solution
First, we need to find the circumference of the circular field, which is the length of the fence.
Circumference = $\frac{\text{Total cost of fencing}}{\text{Rate of fencing}}$
Circumference = $\frac{5280}{24}$ m
Circumference = $220$ m
Let the radius of the circular field be $r$ metres. We can find the radius using the formula for the circumference of a circle.
Circumference = $2\pi r$
$220 = 2 \times \frac{22}{7} \times r$
... (i)
$220 = \frac{44}{7} \times r$
$r = 220 \times \frac{7}{44}$
$r = \frac{\cancel{220}^{5}}{\cancel{44}_{1}} \times 7$
$r = 5 \times 7$
$r = 35$ m
Now, we find the area of the field to calculate the cost of ploughing. The formula for the area of a circle is:
Area = $\pi r^2$
Area = $\frac{22}{7} \times (35)^2$
Area = $\frac{22}{7} \times 35 \times 35$
Area = $22 \times \frac{\cancel{35}^{5}}{\cancel{7}_{1}} \times 35$
Area = $22 \times 5 \times 35$
Area = $110 \times 35$
Area = $3850$ m2
Finally, we calculate the cost of ploughing the field.
Cost of ploughing = Area of the field $\times$ Rate of ploughing
Cost of ploughing = $3850 \times \textsf{₹} 0.50$
Cost of ploughing =
Cost of ploughing =
Hence, the cost of ploughing the field is
Exercise 12.1
Unless stated otherwise, use π = $\frac{22}{7}$
Question 1. The radii of two circles are 19 cm and 9 cm respectively. Find the radius of the circle which has circumference equal to the sum of the circumferences of the two circles.
Answer:
Given
Radius of the first circle, $r_1 = 19$ cm.
Radius of the second circle, $r_2 = 9$ cm.
To Find
The radius of the new circle whose circumference is the sum of the circumferences of the two given circles.
Solution
Let the radius of the new circle be R.
Circumference of the first circle, $C_1 = 2\pi r_1 = 2\pi(19) = 38\pi$ cm.
Circumference of the second circle, $C_2 = 2\pi r_2 = 2\pi(9) = 18\pi$ cm.
Circumference of the new circle, $C = 2\pi R$.
According to the question, the circumference of the new circle is equal to the sum of the circumferences of the other two circles.
$C = C_1 + C_2$
$2\pi R = 38\pi + 18\pi$
$2\pi R = 56\pi$
Divide both sides by $2\pi$:
$R = \frac{56\pi}{2\pi}$
$R = 28$ cm.
Alternate Solution
Let the radii be $r_1$ and $r_2$, and the radius of the new circle be R.
According to the condition:
Circumference of new circle = Circumference of 1st circle + Circumference of 2nd circle
$2\pi R = 2\pi r_1 + 2\pi r_2$
Divide the entire equation by $2\pi$:
$R = r_1 + r_2$
Substitute the given values:
$R = 19 + 9 = 28$ cm.
The radius of the new circle is 28 cm.
Question 2. The radii of two circles are 8 cm and 6 cm respectively. Find the radius of the circle having area equal to the sum of the areas of the two circles.
Answer:
Given
Radius of the first circle, $r_1 = 8$ cm.
Radius of the second circle, $r_2 = 6$ cm.
To Find
The radius of the new circle whose area is the sum of the areas of the two given circles.
Solution
Let the radius of the new circle be R.
Area of the first circle, $A_1 = \pi r_1^2 = \pi(8)^2 = 64\pi$ cm2.
Area of the second circle, $A_2 = \pi r_2^2 = \pi(6)^2 = 36\pi$ cm2.
Area of the new circle, $A = \pi R^2$.
According to the question, the area of the new circle is equal to the sum of the areas of the other two circles.
$A = A_1 + A_2$
$\pi R^2 = 64\pi + 36\pi$
$\pi R^2 = 100\pi$
Divide both sides by $\pi$:
$R^2 = 100$
$R = \sqrt{100}$
$R = 10$ cm (Since radius cannot be negative).
Alternate Solution
Let the radii be $r_1$ and $r_2$, and the radius of the new circle be R.
According to the condition:
Area of new circle = Area of 1st circle + Area of 2nd circle
$\pi R^2 = \pi r_1^2 + \pi r_2^2$
Divide the entire equation by $\pi$:
$R^2 = r_1^2 + r_2^2$
Substitute the given values:
$R^2 = 8^2 + 6^2$
$R^2 = 64 + 36 = 100$
$R = \sqrt{100} = 10$ cm.
The radius of the new circle is 10 cm.
Question 3. Fig. 12.3 depicts an archery target marked with its five scoring regions from the centre outwards as Gold, Red, Blue, Black and White. The diameter of the region representing Gold score is 21 cm and each of the other bands is 10.5 cm wide. Find the area of each of the five scoring regions.

Answer:
Given
Diameter of the Gold scoring region = 21 cm.
Width of each of the other bands (Red, Blue, Black, White) = 10.5 cm.
To Find
The area of each of the five scoring regions.
Solution
First, we determine the radius of each of the five concentric circular regions.
Diameter of the Gold region = 21 cm.
Radius of the Gold region (first circle), $r_1 = \frac{21}{2} = 10.5$ cm.
The width of each band is 10.5 cm.
Radius of the circle including the Red region (second circle), $r_2 = 10.5 + 10.5 = 21$ cm.
Radius of the circle including the Blue region (third circle), $r_3 = 21 + 10.5 = 31.5$ cm.
Radius of the circle including the Black region (fourth circle), $r_4 = 31.5 + 10.5 = 42$ cm.
Radius of the circle including the White region (fifth circle), $r_5 = 42 + 10.5 = 52.5$ cm.
Area of the Gold Region:
This is the area of the innermost circle with radius $r_1 = 10.5$ cm.
Area of Gold region = $\pi r_1^2$
= $\frac{22}{7} \times (10.5)^2 = \frac{22}{7} \times 10.5 \times 10.5$
= $22 \times 1.5 \times 10.5$
= $346.5$ cm2
Area of the Gold region is 346.5 cm2.
Area of the Red Region:
This is the area of the ring between the second circle (radius $r_2$) and the first circle (radius $r_1$).
Area of Red region = Area of circle with radius $r_2$ - Area of Gold region
Area of circle with radius $r_2$ = $\pi r_2^2 = \frac{22}{7} \times (21)^2 \ $$ = \frac{22}{7} \times 21 \times 21 \ $$ = 22 \times 3 \times 21 = 1386$ cm2.
Area of Red region = $1386 - 346.5 = 1039.5$ cm2.
Area of the Red region is 1039.5 cm2.
Area of the Blue Region:
Area of Blue region = Area of circle with radius $r_3$ - Area of circle with radius $r_2$
Area of circle with radius $r_3$ = $\pi r_3^2 = \frac{22}{7} \times (31.5)^2 \ $$ = \frac{22}{7} \times 31.5 \times 31.5 \ $$ = 22 \times 4.5 \times 31.5 = 3118.5$ cm2.
Area of Blue region = $3118.5 - 1386 = 1732.5$ cm2.
Area of the Blue region is 1732.5 cm2.
Area of the Black Region:
Area of Black region = Area of circle with radius $r_4$ - Area of circle with radius $r_3$
Area of circle with radius $r_4$ = $\pi r_4^2 = \frac{22}{7} \times (42)^2 \ $$ = \frac{22}{7} \times 42 \times 42 \ $$ = 22 \times 6 \times 42 = 5544$ cm2.
Area of Black region = $5544 - 3118.5 = 2425.5$ cm2.
Area of the Black region is 2425.5 cm2.
Area of the White Region:
Area of White region = Area of circle with radius $r_5$ - Area of circle with radius $r_4$
Area of circle with radius $r_5$ = $\pi r_5^2 = \frac{22}{7} \times (52.5)^2 \ $$ = \frac{22}{7} \times 52.5 \times 52.5 \ $$ = 22 \times 7.5 \times 52.5 = 8662.5$ cm2.
Area of White region = $8662.5 - 5544 = 3118.5$ cm2.
Area of the White region is 3118.5 cm2.
Question 4. The wheels of a car are of diameter 80 cm each. How many complete revolutions does each wheel make in 10 minutes when the car is travelling at a speed of 66 km per hour?
Answer:
Given
Diameter of each wheel = 80 cm.
Speed of the car = 66 km/hr.
Time duration = 10 minutes.
To Find
The number of complete revolutions each wheel makes in 10 minutes.
Solution
First, we need to make sure all units are consistent. Let's convert everything to centimeters and minutes.
1. Find the circumference of the wheel:
Diameter = 80 cm
Radius, $r = \frac{\text{Diameter}}{2} = \frac{80}{2} = 40$ cm.
The distance covered by the wheel in one revolution is equal to its circumference.
Circumference = $2\pi r = 2 \times \frac{22}{7} \times 40 = \frac{1760}{7}$ cm.
2. Find the total distance travelled by the car:
Speed = 66 km/hr.
Convert speed to cm/minute:
1 km = 1000 m = 1000 $\times$ 100 cm = 100000 cm.
1 hour = 60 minutes.
Speed = $\frac{66 \times 100000 \text{ cm}}{60 \text{ minutes}} = 11 \times 10000$ cm/minute = 110000 cm/minute.
Now, calculate the total distance covered in 10 minutes:
Distance = Speed $\times$ Time
Distance = $110000 \text{ cm/minute} \times 10 \text{ minutes} = 1100000$ cm.
3. Find the number of revolutions:
The number of revolutions is the total distance covered divided by the distance covered in one revolution (circumference).
Number of revolutions = $\frac{\text{Total Distance}}{\text{Circumference}}$
Number of revolutions = $\frac{1100000}{\frac{1760}{7}}$
= $1100000 \times \frac{7}{1760}$
= $\frac{110000 \times 7}{176}$
We can simplify this by dividing by 11:
= $\frac{10000 \times 7}{16}$
Now, divide by 4:
= $\frac{2500 \times 7}{4}$
Divide by 4 again:
= $625 \times 7$
= $4375$
Each wheel makes 4375 complete revolutions.
The number of complete revolutions each wheel makes is 4375.
Question 5. Tick the correct answer in the following and justify your choice : If the perimeter and the area of a circle are numerically equal, then the radius of the circle is
(A) 2 units
(B) π units
(C) 4 units
(D) 7 units
Answer:
Given
The perimeter (circumference) and the area of a circle are numerically equal.
To Find
The radius of the circle.
Justification
Let the radius of the circle be $r$ units.
The formula for the perimeter (circumference) of a circle is $C = 2\pi r$.
The formula for the area of a circle is $A = \pi r^2$.
According to the given condition, the numerical values are equal:
Area = Perimeter
$\pi r^2 = 2\pi r$
We can divide both sides by $\pi$ (since $\pi \neq 0$):
$r^2 = 2r$
Since the radius $r$ must be a positive value for a circle to exist, we can divide both sides by $r$ (assuming $r \neq 0$):
$\frac{r^2}{r} = \frac{2r}{r}$
$r = 2$
The radius of the circle is 2 units.
Therefore, the correct option is (A) 2 units.
Example 2 & 3 (Before Exercise 12.2)
Example 2. Find the area of the sector of a circle with radius 4 cm and of angle 30°. Also, find the area of the corresponding major sector (Use π = 3.14).
Answer:
Given
Radius of the circle, $r = 4$ cm.
Angle of the minor sector, $\theta = 30^\circ$.
Value of $\pi = 3.14$.
To Find
1. The area of the minor sector.
2. The area of the corresponding major sector.
Solution
1. Area of the Minor Sector:
The formula for the area of a sector with angle $\theta$ in degrees is:
Area of sector = $\frac{\theta}{360} \times \pi r^2$
Substitute the given values into the formula:
Area of minor sector = $\frac{30}{360} \times 3.14 \times (4)^2$
= $\frac{1}{12} \times 3.14 \times 16$
= $\frac{3.14 \times 16}{12}$
= $\frac{3.14 \times 4}{3}$
= $\frac{12.56}{3}$
$\approx 4.1866...$ cm2
Rounding to two decimal places, the area of the minor sector is approximately 4.19 cm2.
2. Area of the Corresponding Major Sector:
The area of the major sector can be found in two ways:
Method 1: Using the angle of the major sector
The angle of the major sector is $360^\circ - \theta$.
Angle of major sector = $360^\circ - 30^\circ = 330^\circ$.
Area of major sector = $\frac{330}{360} \times 3.14 \times (4)^2$
= $\frac{11}{12} \times 3.14 \times 16$
= $\frac{11 \times 3.14 \times 4}{3}$
= $\frac{138.16}{3}$
$\approx 46.0533...$ cm2
Rounding to two decimal places, the area is approximately 46.05 cm2.
Method 2: Subtracting the area of the minor sector from the total area of the circle
First, calculate the total area of the circle:
Area of circle = $\pi r^2 = 3.14 \times (4)^2 = 3.14 \times 16 = 50.24$ cm2.
Area of major sector = Area of circle - Area of minor sector
= $50.24 - \frac{12.56}{3}$
= $\frac{150.72 - 12.56}{3}$
= $\frac{138.16}{3}$
$\approx 46.0533...$ cm2
Rounding to two decimal places, the area is approximately 46.05 cm2.
The area of the sector is $\frac{12.56}{3} \approx 4.19$ cm2.
The area of the corresponding major sector is $\frac{138.16}{3} \approx 46.05$ cm2.
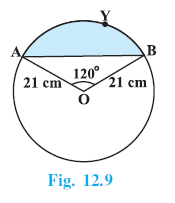
Example 3. Find the area of the segment AYB shown in Fig. 12.9, if radius of the circle is 21 cm and ∠AOB = 120°. (Use π = $\frac{22}{7}$ )
Answer:
Given
Radius of the circle, $r = 21$ cm.
Angle subtended by the chord AB at the centre, $\angle AOB = \theta = 120^\circ$.
Value of $\pi = \frac{22}{7}$.
To Find
The area of the minor segment AYB.
Solution
The area of a segment is found by subtracting the area of the corresponding triangle from the area of the corresponding sector.
Area of segment AYB = Area of sector OAYB - Area of $\triangle OAB$.
Step 1: Calculate the Area of the Sector OAYB
The formula for the area of a sector is:
Area of sector = $\frac{\theta}{360} \times \pi r^2$
Substitute the given values:
Area of sector OAYB = $\frac{120}{360} \times \frac{22}{7} \times (21)^2$
= $\frac{1}{3} \times \frac{22}{7} \times 21 \times 21$
= $\frac{1}{3} \times 22 \times 3 \times 21$
= $22 \times 21 = 462$ cm2.
Step 2: Calculate the Area of the Triangle OAB
The area of a triangle can be found using the formula $\frac{1}{2} r^2 \sin \theta$ when two sides (radii) and the included angle are known.
Area of $\triangle OAB = \frac{1}{2} r^2 \sin \theta$
= $\frac{1}{2} \times (21)^2 \times \sin 120^\circ$
We know that $\sin 120^\circ = \sin(180^\circ - 60^\circ) = \sin 60^\circ = \frac{\sqrt{3}}{2}$.
= $\frac{1}{2} \times 441 \times \frac{\sqrt{3}}{2}$
= $\frac{441\sqrt{3}}{4}$ cm2.
Step 3: Calculate the Area of the Segment AYB
Area of segment AYB = Area of sector OAYB - Area of $\triangle OAB$
= $(462 - \frac{441\sqrt{3}}{4})$ cm2.
Alternate Method for Area of $\triangle OAB$
To find the area of $\triangle OAB$, we can also use the formula $\frac{1}{2} \times \text{base} \times \text{height}$.
Draw a perpendicular OM from O to the chord AB. This perpendicular bisects the chord AB and the angle $\angle AOB$.
So, $\angle AOM = \angle BOM = \frac{120^\circ}{2} = 60^\circ$.
In the right-angled triangle OMA:
$\sin 60^\circ = \frac{AM}{OA} \implies \frac{\sqrt{3}}{2} = \frac{AM}{21} \implies AM = \frac{21\sqrt{3}}{2}$ cm.
$\cos 60^\circ = \frac{OM}{OA} \implies \frac{1}{2} = \frac{OM}{21} \implies OM = \frac{21}{2}$ cm.
The base of $\triangle OAB$ is AB = $2 \times AM = 2 \times \frac{21\sqrt{3}}{2} = 21\sqrt{3}$ cm.
The height of $\triangle OAB$ is OM = $\frac{21}{2}$ cm.
Area of $\triangle OAB = \frac{1}{2} \times AB \times OM$
= $\frac{1}{2} \times 21\sqrt{3} \times \frac{21}{2} = \frac{441\sqrt{3}}{4}$ cm2.
This result is the same as obtained before.
The final area of the segment AYB is:
Area of segment AYB = $(462 - \frac{441\sqrt{3}}{4})$ cm2.
Exercise 12.2
Unless stated otherwise, use π = $\frac{22}{7}$
Question 1. Find the area of a sector of a circle with radius 6 cm if angle of the sector is 60°.
Answer:
Given
Radius of the circle, $r = 6$ cm.
Angle of the sector, $\theta = 60^\circ$.
To Find
The area of the sector.
Solution
The formula for the area of a sector of a circle with radius $r$ and angle $\theta$ (in degrees) is given by:
Area of sector = $\frac{\theta}{360^\circ} \times \pi r^2$
Substitute the given values $r = 6$ cm, $\theta = 60^\circ$, and using $\pi = \frac{22}{7}$:
Area of sector = $\frac{60}{360} \times \frac{22}{7} \times (6)^2$
Area of sector = $\frac{1}{6} \times \frac{22}{7} \times 36$
Area of sector = $\frac{1}{\cancel{6}_1} \times \frac{22}{7} \times \cancel{36}^6$
Area of sector = $\frac{22 \times 6}{7}$
Area of sector = $\frac{132}{7}$ cm$^2$
As a decimal, this is approximately $18.86$ cm$^2$.
The area of the sector is $\frac{132}{7}$ cm2.
Question 2. Find the area of a quadrant of a circle whose circumference is 22 cm.
Answer:
Given
Circumference of the circle = 22 cm.
To Find
The area of a quadrant of the circle.
Solution
First, we need to find the radius of the circle from its circumference.
Let the radius of the circle be $r$.
Circumference = $2\pi r$
$22 = 2 \times \frac{22}{7} \times r$
$1 = \frac{2}{7} \times r$
$r = \frac{7}{2}$ cm.
A quadrant of a circle is a sector with an angle of $90^\circ$ (since $\frac{360^\circ}{4} = 90^\circ$).
The formula for the area of a sector (quadrant in this case) is:
Area of quadrant = $\frac{\theta}{360^\circ} \times \pi r^2$
Substitute $\theta = 90^\circ$ and $r = \frac{7}{2}$ cm:
Area of quadrant = $\frac{90}{360} \times \frac{22}{7} \times \left(\frac{7}{2}\right)^2$
= $\frac{1}{4} \times \frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}$
= $\frac{1}{4} \times \frac{\cancel{22}^{11}}{\cancel{7}_1} \times \frac{\cancel{7}^1 \times 7}{\cancel{2}_1 \times 2}$
= $\frac{11 \times 7}{4 \times 2} = \frac{77}{8}$ cm$^2$
As a decimal, this is $9.625$ cm$^2$.
The area of a quadrant of the circle is $\frac{77}{8}$ cm2.
Question 3. The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in 5 minutes.
Answer:
Given
Length of the minute hand (radius), $r = 14$ cm.
Time duration = 5 minutes.
To Find
The area swept by the minute hand in 5 minutes.
Solution
The minute hand completes one full circle (360°) in 60 minutes.
Angle swept by the minute hand in 60 minutes = $360^\circ$.
Angle swept by the minute hand in 1 minute = $\frac{360^\circ}{60} = 6^\circ$.
Therefore, the angle swept by the minute hand in 5 minutes is:
$\theta = 5 \times 6^\circ = 30^\circ$.
The area swept by the minute hand is the area of a sector with radius $r = 14$ cm and angle $\theta = 30^\circ$.
Area of sector = $\frac{\theta}{360^\circ} \times \pi r^2$
Substitute the values:
Area = $\frac{30}{360} \times \frac{22}{7} \times (14)^2$
= $\frac{1}{12} \times \frac{22}{7} \times 14 \times 14$
= $\frac{1}{12} \times 22 \times 2 \times 14$
= $\frac{1}{6} \times 22 \times 14$
= $\frac{1}{3} \times 11 \times 14 = \frac{154}{3}$ cm$^2$
As a decimal, this is approximately $51.33$ cm$^2$.
The area swept by the minute hand in 5 minutes is $\frac{154}{3}$ cm2.
Question 4. A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the corresponding :
(i) minor segment
(ii) major sector. (Use π = 3.14)
Answer:
Given
Radius of the circle, $r = 10$ cm.
Angle of the minor sector, $\theta = 90^\circ$.
Use $\pi = 3.14$.
(i) Area of the minor segment
Solution
Area of minor segment = Area of minor sector - Area of triangle formed by the radii and chord.
Area of minor sector:
Area = $\frac{\theta}{360^\circ} \times \pi r^2 = \frac{90}{360} \times 3.14 \times (10)^2$
= $\frac{1}{4} \times 3.14 \times 100 = \frac{314}{4} = 78.5$ cm$^2$.
Area of the triangle:
The triangle formed is a right-angled triangle with the two radii as its perpendicular sides.
Area = $\frac{1}{2} \times \text{base} \times \text{height} = \frac{1}{2} \times r \times r = \frac{1}{2} \times 10 \times 10 = 50$ cm$^2$.
Area of minor segment:
Area = $78.5 - 50 = 28.5$ cm$^2$.
(ii) Area of the major sector
Solution
The angle of the major sector = $360^\circ - 90^\circ = 270^\circ$.
Area of major sector = $\frac{270}{360} \times \pi r^2$
= $\frac{3}{4} \times 3.14 \times (10)^2 = \frac{3}{4} \times 314 = 3 \times 78.5 = 235.5$ cm$^2$.
Alternate method:
Area of major sector = Area of circle - Area of minor sector
Area of circle = $\pi r^2 = 3.14 \times (10)^2 = 314$ cm$^2$.
Area of major sector = $314 - 78.5 = 235.5$ cm$^2$.
The final answers are:
(i) Area of the minor segment is 28.5 cm2.
(ii) Area of the major sector is 235.5 cm2.
Question 5. In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find:
(i) the length of the arc
(ii) area of the sector formed by the arc
(iii) area of the segment formed by the corresponding chord
Answer:
Given
Radius of the circle, $r = 21$ cm.
Angle of the sector, $\theta = 60^\circ$.
(i) The length of the arc
Solution
Length of an arc = $\frac{\theta}{360^\circ} \times 2\pi r$
= $\frac{60}{360} \times 2 \times \frac{22}{7} \times 21$
= $\frac{1}{6} \times 2 \times 22 \times 3 = 22$ cm.
(ii) Area of the sector formed by the arc
Solution
Area of a sector = $\frac{\theta}{360^\circ} \times \pi r^2$
= $\frac{60}{360} \times \frac{22}{7} \times (21)^2$
= $\frac{1}{6} \times \frac{22}{7} \times 21 \times 21 = \frac{1}{6} \times 22 \times 3 \times 21 = 11 \times 21 = 231$ cm$^2$.
(iii) Area of the segment formed by the corresponding chord
Solution
Area of segment = Area of sector - Area of triangle.
The triangle formed by the two radii and the chord has two sides equal to the radius (21 cm) and the angle between them is 60°. This makes it an equilateral triangle with side length 21 cm.
Area of equilateral triangle = $\frac{\sqrt{3}}{4} \times (\text{side})^2$
= $\frac{\sqrt{3}}{4} \times (21)^2 = \frac{441\sqrt{3}}{4}$ cm$^2$.
Area of segment = $231 - \frac{441\sqrt{3}}{4}$ cm$^2$.
The final answers are:
(i) Length of the arc is 22 cm.
(ii) Area of the sector is 231 cm2.
(iii) Area of the segment is $\left(231 - \frac{441\sqrt{3}}{4}\right)$ cm2.
Question 6. A chord of a circle of radius 15 cm subtends an angle of 60° at the centre. Find the areas of the corresponding minor and major segments of the circle. (Use π = 3.14 and $\sqrt{3}$ = 1.73)
Answer:
Given
Radius of the circle, $r = 15$ cm.
Angle of the minor sector, $\theta = 60^\circ$.
Use $\pi = 3.14$ and $\sqrt{3} = 1.73$.
To Find
Areas of the minor and major segments.
Solution for Minor Segment
Area of minor segment = Area of minor sector - Area of triangle.
Area of minor sector:
Area = $\frac{60}{360} \times 3.14 \times (15)^2 = \frac{1}{6} \times 3.14 \times 225 = 117.75$ cm$^2$.
Area of the triangle:
The triangle is equilateral with side 15 cm (since the angle is 60° and two sides are radii).
Area = $\frac{\sqrt{3}}{4} \times (\text{side})^2 = \frac{1.73}{4} \times (15)^2 = \frac{1.73 \times 225}{4} = \frac{389.25}{4} = 97.3125$ cm$^2$.
Area of minor segment:
Area = $117.75 - 97.3125 = 20.4375$ cm$^2$.
Solution for Major Segment
Area of major segment = Area of circle - Area of minor segment.
Area of circle:
Area = $\pi r^2 = 3.14 \times (15)^2 = 3.14 \times 225 = 706.5$ cm$^2$.
Area of major segment:
Area = $706.5 - 20.4375 = 686.0625$ cm$^2$.
The final answers are:
Area of minor segment is 20.4375 cm2.
Area of major segment is 686.0625 cm2.
Question 7. A chord of a circle of radius 12 cm subtends an angle of 120° at the centre. Find the area of the corresponding segment of the circle. (Use π = 3.14 and $\sqrt{3}$ = 1.73)
Answer:
Given
Radius of the circle, $r = 12$ cm.
Angle subtended at the centre, $\theta = 120^\circ$.
Use $\pi = 3.14$ and $\sqrt{3} = 1.73$.
To Find
The area of the corresponding segment.
Solution
Area of segment = Area of sector - Area of triangle.
Area of sector:
Area = $\frac{\theta}{360^\circ} \times \pi r^2 = \frac{120}{360} \times 3.14 \times (12)^2$
= $\frac{1}{3} \times 3.14 \times 144 = 3.14 \times 48 = 150.72$ cm$^2$.
Area of the triangle:
The area of the triangle with two sides equal to radius $r$ and included angle $\theta$ is $\frac{1}{2}r^2 \sin\theta$.
Area = $\frac{1}{2} \times (12)^2 \times \sin(120^\circ)$
Since $\sin(120^\circ) = \sin(180^\circ-60^\circ) = \sin(60^\circ) = \frac{\sqrt{3}}{2}$:
Area = $\frac{1}{2} \times 144 \times \frac{\sqrt{3}}{2} = 36\sqrt{3}$ cm$^2$.
Using $\sqrt{3} = 1.73$:
Area = $36 \times 1.73 = 62.28$ cm$^2$.
Area of segment:
Area = $150.72 - 62.28 = 88.44$ cm$^2$.
The area of the corresponding segment is 88.44 cm2.
Question 8. A horse is tied to a peg at one corner of a square shaped grass field of side 15 m by means of a 5 m long rope (see Fig. 12.11). Find
(i) the area of that part of the field in which the horse can graze.
(ii) the increase in the grazing area if the rope were 10 m long instead of 5 m. (Use π = 3.14)

Answer:
Given
The field is a square with a side length of 15 m.
The horse is tied to a peg at one corner.
Initial length of the rope = 5 m.
New length of the rope = 10 m.
Use $\pi = 3.14$.
Analysis
The area the horse can graze is limited by the length of the rope and the boundaries of the square field. Since the horse is tied at a corner, the grazable area within the field will be a quadrant of a circle (a sector with a 90° angle), with the radius equal to the length of the rope.
(i) The area of that part of the field in which the horse can graze.
Solution
The length of the rope is the radius of the sector, so $r_1 = 5$ m.
The angle of the sector at the corner of a square is $\theta = 90^\circ$.
The area of the grazable region is the area of a quadrant of a circle with radius 5 m.
Area of grazable region = $\frac{\theta}{360^\circ} \times \pi r_1^2$
= $\frac{90}{360} \times 3.14 \times (5)^2$
= $\frac{1}{4} \times 3.14 \times 25$
= $\frac{78.5}{4}$
= $19.625$ m2.
The area the horse can graze is 19.625 m2.
(ii) The increase in the grazing area if the rope were 10 m long instead of 5 m.
Solution
First, we find the new grazable area with the longer rope.
The new length of the rope is the new radius, so $r_2 = 10$ m.
The angle of the sector remains the same, $\theta = 90^\circ$.
New grazable area = $\frac{90}{360} \times 3.14 \times (10)^2$
= $\frac{1}{4} \times 3.14 \times 100$
= $\frac{314}{4}$
= $78.5$ m2.
The increase in the grazing area is the difference between the new area and the original area.
Increase in area = (New grazable area) - (Original grazable area)
= $78.5 - 19.625$
= $58.875$ m2.
The increase in the grazing area is 58.875 m2.
Question 9. A brooch is made with silver wire in the form of a circle with diameter 35 mm. The wire is also used in making 5 diameters which divide the circle into 10 equal sectors as shown in Fig. 12.12. Find :
(i) the total length of the silver wire required.
(ii) the area of each sector of the brooch.

Answer:
Given
The brooch is a circle with a diameter of 35 mm.
5 diameters are used, which divide the circle into 10 equal sectors.
(i) The total length of the silver wire required.
Solution
The total length of the silver wire required is the sum of the wire used for the circular part (circumference) and the wire used for the 5 diameters.
Length for the circular part (Circumference):
Diameter, $d = 35$ mm.
Circumference = $\pi d$
Using $\pi = \frac{22}{7}$:
Circumference = $\frac{22}{7} \times 35 = 22 \times 5 = 110$ mm.
Length for the 5 diameters:
The length of one diameter is 35 mm.
Length of 5 diameters = $5 \times 35 = 175$ mm.
Total length of silver wire:
Total length = (Circumference) + (Length of 5 diameters)
Total length = $110 + 175 = 285$ mm.
The total length of the silver wire required is 285 mm.
(ii) The area of each sector of the brooch.
Solution
The circle is divided into 10 equal sectors.
First, let's find the total area of the circle.
Radius, $r = \frac{\text{Diameter}}{2} = \frac{35}{2}$ mm.
Area of circle = $\pi r^2$
= $\frac{22}{7} \times \left(\frac{35}{2}\right)^2 = \frac{22}{7} \times \frac{35}{2} \times \frac{35}{2}$
= $\frac{\cancel{22}^{11}}{\cancel{7}_1} \times \frac{\cancel{35}^5}{2} \times \frac{35}{2}$
= $\frac{11 \times 5 \times 35}{2} = \frac{1925}{2}$ mm2.
Since the circle is divided into 10 equal sectors, the area of each sector is $\frac{1}{10}$ of the total area.
Area of each sector = $\frac{1}{10} \times \text{Area of circle}$
= $\frac{1}{10} \times \frac{1925}{2} = \frac{1925}{20}$
Simplify the fraction by dividing the numerator and denominator by 5:
= $\frac{385}{4}$ mm2.
As a decimal, this is $96.25$ mm2.
Alternate Method:
The angle of each of the 10 equal sectors is $\theta = \frac{360^\circ}{10} = 36^\circ$.
Area of sector = $\frac{\theta}{360} \times \pi r^2 = \frac{36}{360} \times \frac{22}{7} \times \left(\frac{35}{2}\right)^2$
= $\frac{1}{10} \times \frac{22}{7} \times \frac{35 \times 35}{4} = \frac{1 \times 22 \times 5 \times 35}{10 \times 4} = \frac{110 \times 35}{40} = \frac{11 \times 35}{4} = \frac{385}{4} = 96.25$ mm2.
The area of each sector of the brooch is $\frac{385}{4}$ mm2 or 96.25 mm2.
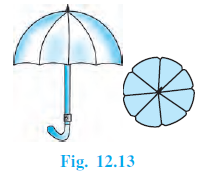
Question 10. An umbrella has 8 ribs which are equally spaced (see Fig. 12.13). Assuming umbrella to be a flat circle of radius 45 cm, find the area between the two consecutive ribs of the umbrella.
Answer:
Given
An umbrella has 8 equally spaced ribs.
When opened, the umbrella is assumed to be a flat circle.
Radius of the flat circle, $r = 45$ cm.
To Find
The area between two consecutive ribs of the umbrella.
Solution
The 8 equally spaced ribs divide the flat circle of the umbrella into 8 equal sectors.
The area between two consecutive ribs is the area of one of these sectors.
The total angle at the centre of the circle is $360^\circ$.
Since there are 8 equal sectors, the angle of each sector is:
$\theta = \frac{360^\circ}{8} = 45^\circ$.
Now, we can find the area of one sector using the formula:
Area of sector = $\frac{\theta}{360^\circ} \times \pi r^2$
Substitute the values $r = 45$ cm, $\theta = 45^\circ$, and using $\pi = \frac{22}{7}$:
Area = $\frac{45}{360} \times \frac{22}{7} \times (45)^2$
= $\frac{1}{8} \times \frac{22}{7} \times 45 \times 45$
Simplify the expression:
= $\frac{1}{\cancel{8}_4} \times \frac{\cancel{22}^{11}}{7} \times 45 \times 45$
= $\frac{11 \times 45 \times 45}{4 \times 7}$
= $\frac{11 \times 2025}{28}$
= $\frac{22275}{28}$ cm2.
As a decimal, this is approximately $795.5357$ cm2.
Therefore, the area between the two consecutive ribs of the umbrella is $\frac{22275}{28}$ cm2.
Question 11. A car has two wipers which do not overlap. Each wiper has a blade of length 25 cm sweeping through an angle of 115°. Find the total area cleaned at each sweep of the blades.
Answer:
Given
A car has two windscreen wipers.
The wipers do not overlap.
Length of each wiper blade (radius of the sector), $r = 25$ cm.
The angle of the sweep for each blade, $\theta = 115^\circ$.
To Find
The total area cleaned at each sweep of the blades.
Solution
The area cleaned by a single wiper blade is the area of a sector of a circle.
The radius of this sector is the length of the blade, $r = 25$ cm.
The angle of the sector is the angle of the sweep, $\theta = 115^\circ$.
The formula for the area of a sector is:
Area of one sector = $\frac{\theta}{360^\circ} \times \pi r^2$
Substitute the given values, using $\pi = \frac{22}{7}$:
Area cleaned by one wiper = $\frac{115}{360} \times \frac{22}{7} \times (25)^2$
First, simplify the fraction $\frac{115}{360}$ by dividing both by 5:
$\frac{115 \div 5}{360 \div 5} = \frac{23}{72}$
Now, substitute this back into the formula:
Area cleaned by one wiper = $\frac{23}{72} \times \frac{22}{7} \times 25 \times 25$
Simplify further:
= $\frac{23}{\cancel{72}_{36}} \times \frac{\cancel{22}^{11}}{7} \times 625$
= $\frac{23 \times 11 \times 625}{36 \times 7}$
= $\frac{253 \times 625}{252}$
= $\frac{158125}{252}$ cm2.
Since the car has two identical wipers and they do not overlap, the total area cleaned is twice the area cleaned by one wiper.
Total area cleaned = $2 \times$ (Area cleaned by one wiper)
= $2 \times \frac{158125}{252}$
= $\frac{158125}{126}$ cm2.
As a decimal, this is approximately $1254.96$ cm2.
Therefore, the total area cleaned at each sweep of the blades is $\frac{158125}{126}$ cm2.
Question 12. To warn ships for underwater rocks, a lighthouse spreads a red coloured light over a sector of angle 80° to a distance of 16.5 km. Find the area of the sea over which the ships are warned. (Use π = 3.14)
Answer:
Given
The light from the lighthouse spreads over a sector of a circle.
Angle of the sector, $\theta = 80^\circ$.
The distance the light spreads (radius of the sector), $r = 16.5$ km.
Value of $\pi$ to be used is 3.14.
To Find
The area of the sea over which the ships are warned.
Solution
The area over which the ships are warned is the area of the sector of the circle formed by the light.
The formula for the area of a sector is:
Area of sector = $\frac{\theta}{360^\circ} \times \pi r^2$
Substitute the given values into the formula:
Area = $\frac{80}{360} \times 3.14 \times (16.5)^2$
First, simplify the fraction $\frac{80}{360}$:
$\frac{80}{360} = \frac{8}{36} = \frac{2}{9}$
Now, substitute this back into the formula:
Area = $\frac{2}{9} \times 3.14 \times 16.5 \times 16.5$
Calculate the values:
$16.5 \times 16.5 = 272.25$
Area = $\frac{2}{9} \times 3.14 \times 272.25$
Area = $\frac{2 \times 854.865}{9}$
Area = $\frac{1709.73}{9}$
Area = $189.97$ km2.
Therefore, the area of the sea over which the ships are warned is 189.97 km2.
Question 13. A round table cover has six equal designs as shown in Fig. 12.14. If the radius of the cover is 28 cm, find the cost of making the designs at the rate of 0.35 per cm2 . (Use $\sqrt{3}$ = 1.7)

Answer:
Given
A round table cover with 6 equal designs.
Radius of the cover, $r = 28$ cm.
Cost of making the designs =
Use $\sqrt{3} = 1.7$.
To Find
The total cost of making the six designs.
Solution
The six equal designs are the six equal segments of the circle.
The chords connecting the endpoints of the designs form a regular hexagon inscribed in the circle.
A regular hexagon divides the circle into 6 equal sectors.
The angle of each sector at the centre is $\theta = \frac{360^\circ}{6} = 60^\circ$.
To find the area of one design (one segment), we will find the area of one sector and subtract the area of the corresponding triangle.
Area of one design = Area of one sector - Area of one triangle.
1. Area of one sector:
Area of sector = $\frac{\theta}{360^\circ} \times \pi r^2$
Substitute the values $r = 28$ cm, $\theta = 60^\circ$, and $\pi = \frac{22}{7}$:
Area of one sector = $\frac{60}{360} \times \frac{22}{7} \times (28)^2$
= $\frac{1}{6} \times \frac{22}{7} \times 28 \times 28$
= $\frac{1}{6} \times 22 \times 4 \times 28 = \frac{2464}{6} = \frac{1232}{3} \approx 410.67$ cm2.
2. Area of one triangle:
The triangle formed by the two radii and the chord has two sides equal to the radius (28 cm) and the angle between them is 60°. This makes the triangle an equilateral triangle with a side length of 28 cm.
Area of equilateral triangle = $\frac{\sqrt{3}}{4} \times (\text{side})^2$
Substitute the values side = 28 cm and $\sqrt{3} = 1.7$:
Area of one triangle = $\frac{1.7}{4} \times (28)^2 = \frac{1.7}{4} \times 784$
= $1.7 \times 196 = 333.2$ cm2.
3. Area of one design (segment):
Area of one design = $\frac{1232}{3} - 333.2$
$\approx 410.67 - 333.2 = 77.47$ cm2.
4. Total area of six designs:
Total area = $6 \times$ (Area of one design)
= $6 \times 77.47 = 464.82$ cm2.
Let's do the calculation with fractions to be more precise:
Total area = $6 \times \left(\frac{1232}{3} - 333.2\right) = 6 \times \frac{1232}{3} - 6 \times 333.2$
= $2 \times 1232 - 1999.2 = 2464 - 1999.2 = 464.8$ cm2.
5. Total cost of making the designs:
Total cost = (Total area of designs) $\times$ (Cost per cm2)
= $464.8 \times 0.35$
=
Therefore, the total cost of making the designs is
Question 14. Tick the correct answer in the following :
Area of a sector of angle p (in degrees) of a circle with radius R is
(A) $\frac{p}{180}$ × 2πR
(B) $\frac{p}{180}$ × πR2
(C) $\frac{p}{360}$ × 2πR
(D) $\frac{p}{720}$ × 2πR2
Answer:
To Find
The correct formula for the area of a sector with angle $p$ (in degrees) and radius R.
Solution and Justification
The standard formula for the area of a sector of a circle with radius $r$ and angle $\theta$ (in degrees) is:
Area of sector = $\frac{\theta}{360} \times \pi r^2$
In this question, the angle is given as $p$ and the radius is given as R.
Substituting these variables into the formula, we get:
Area of sector = $\frac{p}{360} \times \pi R^2$
Now, let's examine the given options to see which one is equivalent to this formula.
(A) $\frac{p}{180} \times 2\pi R$
This is the formula for the length of an arc, not the area of a sector. The standard arc length formula is $\frac{\theta}{360} \times 2\pi r$. This option is incorrect.
(B) $\frac{p}{180} \times \pi R^2$
This is similar to the area formula, but the denominator is 180 instead of 360. This option is incorrect.
(C) $\frac{p}{360} \times 2\pi R$
This is the formula for the length of an arc with angle $p$ and radius R. This option is incorrect.
(D) $\frac{p}{720} \times 2\pi R^2$
Let's simplify this expression:
$\frac{p}{720} \times 2\pi R^2 = \frac{p \times 2 \times \pi R^2}{720} = \frac{p \times \pi R^2}{360}$
This expression is exactly the same as the standard formula for the area of a sector that we derived: $\frac{p}{360} \times \pi R^2$.
The option has been written in a slightly different form, but it is mathematically equivalent.
Therefore, the correct answer is (D) $\frac{p}{720} \times 2\pi R^2$.
Example 4 to 6 (Before Exercise 12.3)
Example 4. In Fig. 12.15, two circular flower beds have been shown on two sides of a square lawn ABCD of side 56 m. If the centre of each circular flower bed is the point of intersection O of the diagonals of the square lawn, find the sum of the areas of the lawn and the flower beds.

Answer:
Given
A square lawn ABCD with side length, $s = 56$ m.
Two circular flower beds are on opposite sides of the lawn.
The centre of the circular flower beds is the intersection point O of the diagonals of the square.
To Find
The sum of the areas of the lawn and the flower beds.
Solution
Let's analyze the geometry of the figure. The total area is the sum of the area of the square lawn (ABCD) and the areas of the two flower beds (which are segments of a circle).
An alternative way to see the total area is to consider the four regions formed by the diagonals. The total area is the sum of the areas of the two sectors OAB and ODC and the areas of the two triangles OAD and OBC.
We will calculate the total area using this second approach as it is more direct.
1. Find the radius of the circular sectors:
The radius of the sectors is the distance from the centre O to any of the vertices A, B, C, or D. This is half the length of the diagonal of the square.
In the right-angled triangle ABC:
$AC^2 = AB^2 + BC^2$ (Pythagorean theorem)
$AC^2 = (56)^2 + (56)^2 = 2 \times (56)^2$
$AC = \sqrt{2 \times (56)^2} = 56\sqrt{2}$ m.
The radius, $r = OA = OB = OC = OD = \frac{1}{2} AC = \frac{1}{2} \times 56\sqrt{2} = 28\sqrt{2}$ m.
2. Find the area of the two sectors (OAB and ODC):
The diagonals of a square bisect each other at right angles. Therefore, the angle of each sector at the centre is $90^\circ$.
$\angle AOB = \angle COD = 90^\circ$.
Area of one sector = $\frac{\theta}{360} \times \pi r^2$
Area of sector OAB = $\frac{90}{360} \times \frac{22}{7} \times (28\sqrt{2})^2$
= $\frac{1}{4} \times \frac{22}{7} \times (28 \times 28 \times 2)$
= $\frac{1}{4} \times \frac{22}{7} \times 784 \times 2$
= $\frac{1}{4} \times 22 \times 112 \times 2 = 22 \times 56 = 1232$ m2.
Since the two sectors are identical, the sum of their areas is:
Area of two sectors = $2 \times 1232 = 2464$ m2.
3. Find the area of the two triangles (OAD and OBC):
The triangles OAD and OBC are right-angled isosceles triangles, with the right angle at O.
The lengths of the perpendicular sides are the radii, OA = OD = OB = OC = $28\sqrt{2}$ m.
Area of one triangle = $\frac{1}{2} \times \text{base} \times \text{height}$
Area of $\triangle OAD = \frac{1}{2} \times OA \times OD = \frac{1}{2} \times (28\sqrt{2}) \times (28\sqrt{2})$
= $\frac{1}{2} \times 28 \times 28 \times 2 = 28 \times 28 = 784$ m2.
Since the two triangles are identical, the sum of their areas is:
Area of two triangles = $2 \times 784 = 1568$ m2.
4. Find the total area:
Total Area = (Area of two sectors) + (Area of two triangles)
Total Area = $2464 + 1568 = 4032$ m2.
Hence, the sum of the areas of the lawn and the flower beds is 4032 m2.
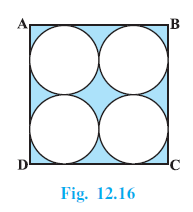
Example 5. Find the area of the shaded region in Fig. 12.16, where ABCD is a square of side 14 cm.
Answer:
Given
ABCD is a square with a side length of 14 cm.
Four identical circles are inscribed within the square such that each circle touches two sides of the square and two other circles.
To Find
The area of the shaded region.
Solution
The area of the shaded region can be found by subtracting the total area of the four circles from the area of the square.
Area of shaded region = Area of square ABCD - Area of 4 circles.
1. Find the Area of the Square:
Side of the square = 14 cm.
Area of square = $(\text{side})^2 = (14)^2 = 196$ cm2.
2. Find the Radius and Area of one Circle:
From the figure, we can see that the diameters of two adjacent circles add up to the length of the side of the square.
Let the diameter of one circle be $d$ and the radius be $r$.
$d + d = 14$ cm
$2d = 14$ cm
$d = 7$ cm
The radius of each circle is $r = \frac{d}{2} = \frac{7}{2}$ cm.
Now, find the area of one circle:
Area of one circle = $\pi r^2$
Using $\pi = \frac{22}{7}$:
Area of one circle = $\frac{22}{7} \times \left(\frac{7}{2}\right)^2 = \frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}$
= $\frac{22 \times 7}{4} = \frac{11 \times 7}{2} = \frac{77}{2} = 38.5$ cm2.
3. Find the Total Area of the Four Circles:
Total area of 4 circles = $4 \times$ (Area of one circle)
= $4 \times 38.5 = 154$ cm2.
4. Find the Area of the Shaded Region:
Area of shaded region = Area of square - Total area of 4 circles
= $196 - 154$
= $42$ cm2.
Hence, the area of the shaded region is 42 cm2.
Example 6. Find the area of the shaded design in Fig. 12.17, where ABCD is a square of side 10 cm and semicircles are drawn with each side of the square as diameter. (Use π = 3.14)
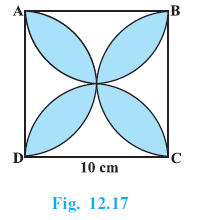
Answer:
Given
A square ABCD with side length = 10 cm.
Four semicircles are drawn with each side of the square as a diameter.
Use $\pi = 3.14$.
To Find
The area of the shaded design.
Solution
Let's denote the four semicircles drawn on sides AB, BC, CD, and DA as S1, S2, S3, and S4 respectively.
The shaded area can be found by adding the areas of the four semicircles and then subtracting the area of the square. Let's understand why this works.
Let the area of the four shaded leaf-like regions be $A_{shaded}$.
Let the area of the four unshaded regions be $A_{unshaded}$.
When we sum the areas of the four semicircles, the unshaded regions are counted once, while the shaded regions (which are formed by the overlapping of semicircles) are counted twice.
So, Area of 4 semicircles = $A_{unshaded} + 2 \times A_{shaded}$.
Also, we know that the area of the square is the sum of the shaded and unshaded regions:
Area of square = $A_{unshaded} + A_{shaded}$.
If we subtract the area of the square from the sum of the areas of the four semicircles, we get:
(Area of 4 semicircles) - (Area of square) = $(A_{unshaded} + 2 \times A_{shaded}) \ $$ - (A_{unshaded} + A_{shaded})$
= $A_{shaded}$.
Thus, Area of shaded region = (Area of 4 semicircles) - (Area of square ABCD).
Step 1: Calculate the Area of the Square
Side of the square = 10 cm.
Area of square ABCD = $(\text{side})^2 = (10)^2 = 100$ cm2.
Step 2: Calculate the Area of the Four Semicircles
The diameter of each semicircle is equal to the side of the square.
Diameter, $d = 10$ cm.
Radius of each semicircle, $r = \frac{d}{2} = \frac{10}{2} = 5$ cm.
Area of one semicircle = $\frac{1}{2} \pi r^2$
Area of four semicircles = $4 \times (\frac{1}{2} \pi r^2) = 2 \pi r^2$.
Substitute the values $r = 5$ cm and $\pi = 3.14$:
Area of 4 semicircles = $2 \times 3.14 \times (5)^2$
= $2 \times 3.14 \times 25$
= $50 \times 3.14$
= $157$ cm2.
Step 3: Calculate the Area of the Shaded Design
Area of shaded design = (Area of 4 semicircles) - (Area of square)
= $157 - 100$
= $57$ cm2.
Hence, the area of the shaded design is 57 cm2.
Exercise 12.3
Unless stated otherwise, use π = $\frac{22}{7}$
Question 1. Find the area of the shaded region in Fig. 12.19, if PQ = 24 cm, PR = 7 cm and O is the centre of the circle.

Answer:
Given:
In the given figure, O is the centre of the circle.
PQ = 24 cm
PR = 7 cm
RQ is the diameter of the circle.
To Find:
The area of the shaded region.
Solution:
Since RQ is the diameter passing through the centre O, the angle subtended by the diameter at any point on the circumference is $90^\circ$.
Therefore, the angle in the semicircle is a right angle.
$\angle RPQ = 90^\circ$
Now, consider the right-angled triangle $\triangle PQR$. By Pythagoras theorem:
$RQ^2 = PR^2 + PQ^2$
$RQ^2 = (7)^2 + (24)^2$
$RQ^2 = 49 + 576$
$RQ^2 = 625$
$RQ = \sqrt{625}$
$RQ = 25$ cm
Since RQ is the diameter of the circle, the radius of the circle (r) is:
$r = \frac{\text{Diameter}}{2} = \frac{RQ}{2} = \frac{25}{2}$ cm
Now, we find the area of the semicircle with diameter RQ.
Area of semicircle = $\frac{1}{2} \pi r^2$
Area of semicircle = $\frac{1}{2} \times \frac{22}{7} \times (\frac{25}{2})^2$
Area of semicircle = $\frac{1}{2} \times \frac{22}{7} \times \frac{25}{2} \times \frac{25}{2}$
Area of semicircle = $\frac{11}{7} \times \frac{625}{4}$
Area of semicircle = $\frac{6875}{28}$ cm$^2$
Next, we find the area of the right-angled triangle $\triangle PQR$.
Area of $\triangle PQR = \frac{1}{2} \times \text{Base} \times \text{Height}$
Area of $\triangle PQR = \frac{1}{2} \times PR \times PQ$
Area of $\triangle PQR = \frac{1}{2} \times 7 \times 24$
Area of $\triangle PQR = 7 \times 12$
Area of $\triangle PQR = 84$ cm$^2$
The area of the shaded region is the area of the semicircle minus the area of the triangle $\triangle PQR$.
Area of shaded region = Area of semicircle - Area of $\triangle PQR$
Area of shaded region = $(\frac{6875}{28} - 84)$ cm$^2$
Area of shaded region = $(\frac{6875 - 84 \times 28}{28})$ cm$^2$
Area of shaded region = $(\frac{6875 - 2352}{28})$ cm$^2$
Area of shaded region = $\frac{4523}{28}$ cm$^2$
Converting to decimal (optional):
Area of shaded region $\approx 161.53$ cm$^2$
Hence, the area of the shaded region is $\frac{4523}{28}$ cm$^2$.
Question 2. Find the area of the shaded region in Fig. 12.20, if radii of the two concentric circles with centre O are 7 cm and 14 cm respectively and ∠AOC = 40°.
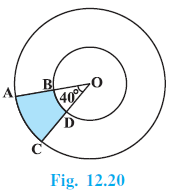
Answer:
Given:
Two concentric circles with centre O.
Radius of the outer circle (OA = OC), R = 14 cm.
Radius of the inner circle (OB = OD), r = 7 cm.
Angle subtended at the centre, $\angle AOC = \theta = 40^\circ$.
To Find:
The area of the shaded region ABDC.
Solution:
The shaded region ABDC can be found by subtracting the area of the smaller sector OBD from the area of the larger sector OAC.
The formula for the area of a sector with angle $\theta$ and radius $R$ is $\frac{\theta}{360^\circ} \times \pi R^2$.
Area of the larger sector OAC:
Area(OAC) = $\frac{\theta}{360^\circ} \times \pi R^2$
Area(OAC) = $\frac{40^\circ}{360^\circ} \times \pi (14)^2$
Area(OAC) = $\frac{1}{9} \times \frac{22}{7} \times 14 \times 14$
Area(OAC) = $\frac{1}{9} \times 22 \times 2 \times 14$
Area(OAC) = $\frac{616}{9}$ cm$^2$
Area of the smaller sector OBD:
Area(OBD) = $\frac{\theta}{360^\circ} \times \pi r^2$
Area(OBD) = $\frac{40^\circ}{360^\circ} \times \pi (7)^2$
Area(OBD) = $\frac{1}{9} \times \frac{22}{7} \times 7 \times 7$
Area(OBD) = $\frac{1}{9} \times 22 \times 7$
Area(OBD) = $\frac{154}{9}$ cm$^2$
Area of the shaded region ABDC = Area(OAC) - Area(OBD)
Area of shaded region = $\frac{616}{9} - \frac{154}{9}$
Area of shaded region = $\frac{616 - 154}{9}$
Area of shaded region = $\frac{462}{9}$
Area of shaded region = $\frac{\cancel{462}^{154}}{\cancel{9}_{3}}$
Area of shaded region = $\frac{154}{3}$ cm$^2$
Converting to decimal (optional):
Area of shaded region $\approx 51.33$ cm$^2$
Hence, the area of the shaded region is $\frac{154}{3}$ cm$^2$.
Question 3. Find the area of the shaded region in Fig. 12.21, if ABCD is a square of side 14 cm and APD and BPC are semicircles.
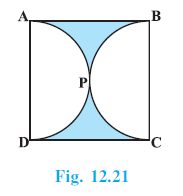
Answer:
Given:
ABCD is a square with side length $s = 14$ cm.
APD and BPC are semicircles drawn with sides AD and BC of the square as diameters, respectively.
To Find:
The area of the shaded region.
Solution:
First, calculate the area of the square ABCD.
Area of square = side $\times$ side = $s^2$
Area of square ABCD = $(14)^2 = 196$ cm$^2$.
Now, consider the semicircles APD and BPC.
The diameter of semicircle APD is the side AD of the square.
Diameter (d) = AD = 14 cm.
Radius of semicircle APD ($r$) = $\frac{\text{Diameter}}{2} = \frac{14}{2} = 7$ cm.
Similarly, the diameter of semicircle BPC is the side BC of the square.
Diameter (d) = BC = 14 cm.
Radius of semicircle BPC ($r$) = $\frac{\text{Diameter}}{2} = \frac{14}{2} = 7$ cm.
Both semicircles have the same radius, $r = 7$ cm.
Calculate the area of one semicircle.
Area of a semicircle = $\frac{1}{2} \pi r^2$
Area of semicircle APD = $\frac{1}{2} \times \frac{22}{7} \times (7)^2$
Area of semicircle APD = $\frac{1}{2} \times \frac{22}{7} \times 7 \times 7$
Area of semicircle APD = $\frac{1}{\cancel{2}_1} \times \frac{\cancel{22}^{11}}{\cancel{7}_1} \times \cancel{7} \times 7$
Area of semicircle APD = $11 \times 7 = 77$ cm$^2$.
Since both semicircles have the same radius, the area of semicircle BPC is also 77 cm$^2$.
The shaded region is the area of the square minus the areas of the two semicircles.
Area of shaded region = Area of square ABCD - (Area of semicircle APD + Area of semicircle BPC)
Area of shaded region = $196 - (77 + 77)$
Area of shaded region = $196 - 154$
Area of shaded region = $42$ cm$^2$.
Hence, the area of the shaded region is 42 cm$^2$.
Question 4. Find the area of the shaded region in Fig. 12.22, where a circular arc of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm as centre.
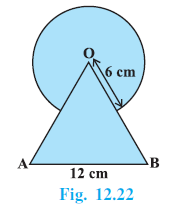
Answer:
Given:
OAB is an equilateral triangle with side length $s = 12$ cm.
A circular arc is drawn with centre O and radius $r = 6$ cm.
To Find:
The area of the shaded region.
Solution:
The shaded region consists of the area of the equilateral triangle OAB and the area of the major circular sector with centre O and radius 6 cm.
First, calculate the area of the equilateral triangle OAB.
Area of an equilateral triangle = $\frac{\sqrt{3}}{4} \times (\text{side})^2$
Area of $\triangle OAB = \frac{\sqrt{3}}{4} \times (12)^2$
Area of $\triangle OAB = \frac{\sqrt{3}}{4} \times 144$
Area of $\triangle OAB = 36\sqrt{3}$ cm$^2$.
Since OAB is an equilateral triangle, each angle is $60^\circ$.
Therefore, the angle at the centre O, $\angle AOB = 60^\circ$.
This angle corresponds to the minor sector formed by the arc within the triangle.
The angle of the major sector (part of the shaded region outside the triangle) is $360^\circ - \angle AOB$.
Angle of major sector $\theta = 360^\circ - 60^\circ = 300^\circ$.
Now, calculate the area of the major circular sector with radius $r=6$ cm and angle $\theta = 300^\circ$.
Area of major sector = $\frac{\theta}{360^\circ} \times \pi r^2$
Area of major sector = $\frac{300^\circ}{360^\circ} \times \pi (6)^2$
Area of major sector = $\frac{5}{6} \times \pi \times 36$
Area of major sector = $5 \times \pi \times 6$
Area of major sector = $30\pi$ cm$^2$.
Using $\pi = \frac{22}{7}$:
Area of major sector = $30 \times \frac{22}{7} = \frac{660}{7}$ cm$^2$.
The total area of the shaded region is the sum of the area of the equilateral triangle and the area of the major circular sector.
Total shaded area = Area of $\triangle OAB$ + Area of major sector
Total shaded area = $(36\sqrt{3} + \frac{660}{7})$ cm$^2$.
Alternate Solution:
The shaded region can also be seen as the sum of the area of the equilateral triangle and the area of the full circle, minus the area of the minor sector common to both.
Area of $\triangle OAB = 36\sqrt{3}$ cm$^2$. (Calculated above)
Area of the full circle with radius $r=6$ cm:
Area of circle = $\pi r^2 = \pi (6)^2 = 36\pi$ cm$^2$.
Using $\pi = \frac{22}{7}$:
Area of circle = $36 \times \frac{22}{7} = \frac{792}{7}$ cm$^2$.
Area of the minor sector with radius $r=6$ cm and angle $60^\circ$:
Area of minor sector = $\frac{60^\circ}{360^\circ} \times \pi r^2$
Area of minor sector = $\frac{1}{6} \times \pi (6)^2 = \frac{1}{6} \times 36\pi = 6\pi$ cm$^2$.
Using $\pi = \frac{22}{7}$:
Area of minor sector = $6 \times \frac{22}{7} = \frac{132}{7}$ cm$^2$.
Total shaded area = Area of $\triangle OAB$ + Area of circle - Area of minor sector
Total shaded area = $36\sqrt{3} + \frac{792}{7} - \frac{132}{7}$
Total shaded area = $36\sqrt{3} + \frac{792 - 132}{7}$
Total shaded area = $36\sqrt{3} + \frac{660}{7}$ cm$^2$.
Hence, the area of the shaded region is $(36\sqrt{3} + \frac{660}{7})$ cm$^2$.
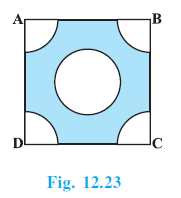
Question 5. From each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in Fig. 12.23. Find the area of the remaining portion of the square.
Answer:
Given:
A square ABCD with side length $s = 4$ cm.
Four quadrants of circles with radius $r_q = 1$ cm cut from each corner.
A circle with diameter $d_c = 2$ cm cut from the center.
To Find:
The area of the remaining portion of the square.
Solution:
First, calculate the area of the square ABCD.
Area of square = side $\times$ side = $s^2$
Area of square ABCD = $(4)^2 = 16$ cm$^2$.
Next, calculate the area of the four quadrants cut from the corners.
Radius of each quadrant, $r_q = 1$ cm.
Area of one quadrant = $\frac{1}{4} \pi r_q^2 = \frac{1}{4} \pi (1)^2 = \frac{1}{4} \pi$ cm$^2$.
The total area of the four quadrants is $4 \times \text{Area of one quadrant}$.
Total area of four quadrants = $4 \times \frac{1}{4} \pi = \pi$ cm$^2$.
(Alternatively, note that four quadrants of radius 1 cm form a complete circle of radius 1 cm, with area $\pi (1)^2 = \pi$ cm$^2$).
Using $\pi = \frac{22}{7}$:
Total area of four quadrants = $\frac{22}{7}$ cm$^2$.
Now, calculate the area of the circle cut from the center.
Diameter of the central circle, $d_c = 2$ cm.
Radius of the central circle, $r_c = \frac{d_c}{2} = \frac{2}{2} = 1$ cm.
Area of the central circle = $\pi r_c^2 = \pi (1)^2 = \pi$ cm$^2$.
Using $\pi = \frac{22}{7}$:
Area of central circle = $\frac{22}{7}$ cm$^2$.
The area of the remaining portion of the square is the area of the square minus the total area of the four quadrants and the area of the central circle.
Area of remaining portion = Area of square - (Total area of four quadrants + Area of central circle)
Area of remaining portion = $16 - (\pi + \pi)$
Area of remaining portion = $16 - 2\pi$
Substituting $\pi = \frac{22}{7}$:
Area of remaining portion = $16 - 2 \times \frac{22}{7}$
Area of remaining portion = $16 - \frac{44}{7}$
Area of remaining portion = $\frac{16 \times 7}{7} - \frac{44}{7}$
Area of remaining portion = $\frac{112 - 44}{7}$
Area of remaining portion = $\frac{68}{7}$ cm$^2$.
Hence, the area of the remaining portion of the square is $\frac{68}{7}$ cm$^2$.
Question 6. In a circular table cover of radius 32 cm, a design is formed leaving an equilateral triangle ABC in the middle as shown in Fig. 12.24. Find the area of the design.

Answer:
Given
A circular table cover with radius, $r = 32$ cm.
An equilateral triangle ABC is inscribed in the circle.
The design is the area of the circle excluding the area of the equilateral triangle.
To Find
The area of the design.
Solution
The area of the design can be found by subtracting the area of the equilateral triangle ABC from the total area of the circular cover.
Area of design = Area of circle - Area of equilateral $\triangle ABC$.
1. Calculate the Area of the Circle:
Radius of the circle, $r = 32$ cm.
Area of the circle = $\pi r^2$
Using $\pi = \frac{22}{7}$:
Area of the circle = $\frac{22}{7} \times (32)^2 = \frac{22}{7} \times 1024 = \frac{22528}{7}$ cm2.
2. Calculate the Area of the Equilateral Triangle ABC:
Let O be the centre of the circle. Since the triangle is equilateral, its vertices divide the circle into three equal sectors. The angle subtended by each side of the triangle at the centre O is:
$\theta = \frac{360^\circ}{3} = 120^\circ$.
So, $\angle AOB = \angle BOC = \angle COA = 120^\circ$.
The area of the equilateral triangle ABC is the sum of the areas of the three identical isosceles triangles: $\triangle AOB$, $\triangle BOC$, and $\triangle COA$.
Area of $\triangle ABC = 3 \times$ (Area of $\triangle AOB$).
The area of a triangle with two sides of length $r$ and an included angle $\theta$ is given by $\frac{1}{2} r^2 \sin \theta$.
Area of $\triangle AOB = \frac{1}{2} \times OA \times OB \times \sin(\angle AOB)$
= $\frac{1}{2} \times (32) \times (32) \times \sin(120^\circ)$
We know that $\sin(120^\circ) = \sin(180^\circ - 60^\circ) = \sin(60^\circ) = \frac{\sqrt{3}}{2}$.
Area of $\triangle AOB = \frac{1}{2} \times 1024 \times \frac{\sqrt{3}}{2} = 256\sqrt{3}$ cm2.
Now, the total area of the equilateral triangle ABC is:
Area of $\triangle ABC = 3 \times 256\sqrt{3} = 768\sqrt{3}$ cm2.
3. Calculate the Area of the Design:
Area of the design = Area of the circle - Area of $\triangle ABC$
Area of the design = $\left(\frac{22528}{7} - 768\sqrt{3}\right)$ cm2.
Hence, the area of the design is $\left(\frac{22528}{7} - 768\sqrt{3}\right)$ cm2.
Question 7. In Fig. 12.25, ABCD is a square of side 14 cm. With centres A, B, C and D, four circles are drawn such that each circle touch externally two of the remaining three circles. Find the area of the shaded region.

Answer:
Given:
ABCD is a square with side length $s = 14$ cm.
Four circles are drawn with centres A, B, C, and D.
Each circle touches two of the other circles externally.
To Find:
The area of the shaded region.
Solution:
First, calculate the area of the square ABCD.
Area of square = side $\times$ side = $s^2$
Area of square ABCD = $(14)^2 = 196$ cm$^2$.
Since the circles are drawn with centres A, B, C, D and each circle touches two other circles externally, the points of contact will be the midpoints of the sides AB, BC, CD, and DA.
Therefore, the radius of each circle (or sector within the square) is half the side length of the square.
Radius $r = \frac{\text{Side of square}}{2} = \frac{14}{2} = 7$ cm.
The portion of each circle inside the square forms a sector with the centre at the vertex of the square.
Since ABCD is a square, the angle at each vertex (A, B, C, D) is $90^\circ$.
So, each sector inside the square is a quadrant of a circle with radius $r=7$ cm and angle $\theta = 90^\circ$.
Area of one sector (quadrant) = $\frac{\theta}{360^\circ} \times \pi r^2$
Area of one sector = $\frac{90^\circ}{360^\circ} \times \pi (7)^2$
Area of one sector = $\frac{1}{4} \times \frac{22}{7} \times 7 \times 7$
Area of one sector = $\frac{1}{4} \times 22 \times 7$
Area of one sector = $\frac{154}{4} = \frac{77}{2}$ cm$^2$.
There are four such sectors, one at each corner of the square.
Total area of the four sectors = $4 \times \text{Area of one sector}$
Total area of four sectors = $4 \times \frac{77}{2} = 2 \times 77 = 154$ cm$^2$.
Alternatively: The four sectors together form a complete circle of radius $r=7$ cm. Area = $\pi r^2 = \frac{22}{7} \times (7)^2 = \frac{22}{7} \times 49 = 22 \times 7 = 154$ cm$^2$.
The area of the shaded region is the area of the square minus the total area of the four sectors.
Area of shaded region = Area of square ABCD - Total area of four sectors
Area of shaded region = $196 - 154$
Area of shaded region = $42$ cm$^2$.
Hence, the area of the shaded region is 42 cm$^2$.
Question 8. Fig. 12.26 depicts a racing track whose left and right ends are semicircular.
The distance between the two inner parallel line segments is 60 m and they are each 106 m long. If the track is 10 m wide, find :
(i) the distance around the track along its inner edge
(ii) the area of the track.

Answer:
Given
The shape of the racing track consists of a rectangle with two semicircles attached at its ends.
Length of the inner parallel line segments = 106 m.
Distance between the inner parallel line segments = 60 m.
Width of the track = 10 m.
(i) The distance around the track along its inner edge
Solution
The inner edge of the track consists of two straight line segments and two semicircular ends.
Length of each inner straight segment = 106 m.
The distance between the inner parallel segments is the diameter of the inner semicircles.
Diameter of inner semicircles = 60 m.
Radius of inner semicircles, $r_{inner} = \frac{60}{2} = 30$ m.
The length of the two inner semicircular parts is equal to the circumference of a circle with radius 30 m.
Length of inner curved parts = $2 \times (\pi r_{inner}) = 2\pi(30) = 60\pi$ m.
Total distance around the inner edge = (Length of two straight segments) + (Length of two semicircular parts)
= $(2 \times 106) + 60\pi$
Using $\pi = \frac{22}{7}$:
= $212 + 60 \times \frac{22}{7}$
= $212 + \frac{1320}{7}$
= $\frac{1484 + 1320}{7} = \frac{2804}{7}$ m.
The distance around the track along its inner edge is $\frac{2804}{7}$ m.
(ii) The area of the track.
Solution
The area of the track can be calculated by adding the area of the two rectangular sections and the area of the two semicircular ring sections.
Area of the rectangular sections:
There are two rectangular parts, each with a length of 106 m and a width of 10 m.
Area of one rectangular section = $106 \times 10 = 1060$ m2.
Area of two rectangular sections = $2 \times 1060 = 2120$ m2.
Area of the semicircular ring sections:
The two semicircular ends together form a circular ring (an annulus).
Radius of the inner circle, $r_{inner} = 30$ m.
Radius of the outer circle, $r_{outer} = r_{inner} + \text{width} = 30 + 10 = 40$ m.
Area of the circular ring = Area of outer circle - Area of inner circle
= $\pi r_{outer}^2 - \pi r_{inner}^2 = \pi (r_{outer}^2 - r_{inner}^2)$
= $\frac{22}{7} \times (40^2 - 30^2)$
= $\frac{22}{7} \times (1600 - 900)$
= $\frac{22}{7} \times 700 = 22 \times 100 = 2200$ m2.
Total area of the track:
Total area = (Area of two rectangular sections) + (Area of the circular ring)
= $2120 + 2200 = 4320$ m2.
The area of the track is 4320 m2.
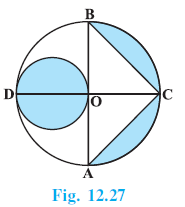
Question 9. In Fig. 12.27, AB and CD are two diameters of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region.
Answer:
Given:
A larger circle with centre O.
AB and CD are two perpendicular diameters of the larger circle.
OA (Radius of the larger circle) = R = 7 cm.
OD is the diameter of the smaller circle.
To Find:
The area of the shaded region.
Solution:
Since OA is the radius of the larger circle, R = 7 cm.
Because AB and CD are diameters, OA = OB = OC = OD = 7 cm.
The diameter of the smaller circle is OD = 7 cm.
Therefore, the radius of the smaller circle, $r = \frac{\text{Diameter}}{2} = \frac{OD}{2} = \frac{7}{2}$ cm.
Area of the smaller circle:
Area = $\pi r^2$
Area = $\frac{22}{7} \times (\frac{7}{2})^2$
Area = $\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}$
Area = $\frac{\cancel{22}^{11}}{\cancel{7}_1} \times \frac{\cancel{7}^1}{\cancel{2}_1} \times \frac{7}{2}$
Area = $11 \times \frac{7}{2} = \frac{77}{2}$ cm$^2$.
Area of the shaded segments in the larger circle:
Consider the semicircle ACB of the larger circle.
Radius of the larger circle, R = 7 cm.
Area of semicircle ACB = $\frac{1}{2} \pi R^2$
Area of semicircle ACB = $\frac{1}{2} \times \frac{22}{7} \times (7)^2$
Area of semicircle ACB = $\frac{1}{2} \times \frac{22}{7} \times 49$
Area of semicircle ACB = $\frac{1}{\cancel{2}_1} \times \frac{\cancel{22}^{11}}{\cancel{7}_1} \times \cancel{49}^7$
Area of semicircle ACB = $11 \times 7 = 77$ cm$^2$.
Now, consider the triangle ABC inscribed in the semicircle.
Since AB and CD are perpendicular diameters, OC is perpendicular to AB.
Base of $\triangle ABC$ = AB = Diameter of larger circle = $2 \times R = 2 \times 7 = 14$ cm.
Height of $\triangle ABC$ = OC = Radius of larger circle = 7 cm.
Area of $\triangle ABC = \frac{1}{2} \times \text{Base} \times \text{Height}$
Area of $\triangle ABC = \frac{1}{2} \times AB \times OC$
Area of $\triangle ABC = \frac{1}{2} \times 14 \times 7 = 7 \times 7 = 49$ cm$^2$.
The area of the two shaded segments (in the larger circle) is the area of the semicircle ACB minus the area of $\triangle ABC$.
Area of shaded segments = Area of semicircle ACB - Area of $\triangle ABC$
Area of shaded segments = $77 - 49 = 28$ cm$^2$.
Total shaded area:
The total area of the shaded region is the sum of the area of the smaller circle and the area of the two shaded segments in the larger circle.
Total shaded area = Area of smaller circle + Area of shaded segments
Total shaded area = $\frac{77}{2} + 28$
Total shaded area = $\frac{77}{2} + \frac{28 \times 2}{2} = \frac{77 + 56}{2}$
Total shaded area = $\frac{133}{2}$ cm$^2$.
Total shaded area = $66.5$ cm$^2$.
Hence, the area of the shaded region is $\frac{133}{2}$ cm$^2$ or 66.5 cm$^2$.
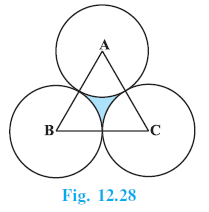
Question 10. The area of an equilateral triangle ABC is 17320.5 cm2 . With each vertex of the triangle as centre, a circle is drawn with radius equal to half the length of the side of the triangle (see Fig. 12.28). Find the area of the shaded region. (Use π = 3.14 and $\sqrt{3}$ = 1.73205)
Answer:
Given:
Area of equilateral triangle ABC = 17320.5 cm$^2$.
Circles are drawn with centres A, B, C.
Radius of each circle (r) = Half the length of the side of the triangle.
$\pi = 3.14$
$\sqrt{3} = 1.73205$
To Find:
The area of the shaded region.
Solution:
Let the side length of the equilateral triangle ABC be $s$.
The formula for the area of an equilateral triangle is:
Area = $\frac{\sqrt{3}}{4} s^2$
We are given that the area is 17320.5 cm$^2$.
$17320.5 = \frac{\sqrt{3}}{4} s^2$
Substitute the given value of $\sqrt{3} = 1.73205$:
$17320.5 = \frac{1.73205}{4} s^2$
$s^2 = \frac{17320.5 \times 4}{1.73205}$
$s^2 = \frac{173205 \times 10^{-1} \times 4}{173205 \times 10^{-5}}$
$s^2 = 10^{-1} \times 10^5 \times 4$
$s^2 = 4 \times 10^4 = 40000$
$s = \sqrt{40000} = 200$ cm.
The radius of each circle drawn from the vertices is half the side length.
Radius $r = \frac{s}{2} = \frac{200}{2} = 100$ cm.
Since ABC is an equilateral triangle, each interior angle is $60^\circ$.
Each circle cuts a sector of angle $\theta = 60^\circ$ from the triangle.
Area of one sector = $\frac{\theta}{360^\circ} \times \pi r^2$
Area of one sector = $\frac{60^\circ}{360^\circ} \times 3.14 \times (100)^2$
Area of one sector = $\frac{1}{6} \times 3.14 \times 10000$
Area of one sector = $\frac{31400}{6}$ cm$^2$.
There are three such sectors, one at each vertex.
Total area of the three sectors = $3 \times \text{Area of one sector}$
Total area of three sectors = $3 \times \frac{31400}{6}$
Total area of three sectors = $\frac{31400}{2} = 15700$ cm$^2$.
The area of the shaded region is the area of the equilateral triangle minus the total area of the three sectors.
Area of shaded region = Area of $\triangle ABC$ - Total area of three sectors
Area of shaded region = $17320.5 - 15700$
Area of shaded region = $1620.5$ cm$^2$.
Hence, the area of the shaded region is 1620.5 cm$^2$.
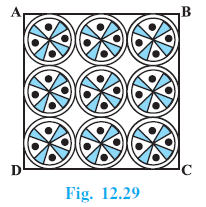
Question 11. On a square handkerchief, nine circular designs each of radius 7 cm are made (see Fig. 12.29). Find the area of the remaining portion of the handkerchief.
Answer:
Given:
A square handkerchief.
Nine circular designs are made on the handkerchief.
Radius of each circular design, $r = 7$ cm.
To Find:
The area of the remaining portion of the handkerchief.
Solution:
The nine circular designs are arranged in a 3x3 grid on the square handkerchief.
The diameter of each circular design is $d = 2r = 2 \times 7 = 14$ cm.
Since there are three circles arranged adjacently along each side of the square, the side length of the square handkerchief is equal to three times the diameter of one circle.
Side of the square, $s = 3 \times d = 3 \times 14 = 42$ cm.
Calculate the area of the square handkerchief.
Area of square = side $\times$ side = $s^2$
Area of square = $(42)^2 = 42 \times 42 = 1764$ cm$^2$.
Calculate the area of one circular design.
Area of one circle = $\pi r^2$
Area of one circle = $\frac{22}{7} \times (7)^2$
Area of one circle = $\frac{22}{7} \times 7 \times 7$
Area of one circle = $22 \times 7 = 154$ cm$^2$.
Calculate the total area of the nine circular designs.
Total area of 9 circles = $9 \times$ Area of one circle
Total area of 9 circles = $9 \times 154 = 1386$ cm$^2$.
The area of the remaining portion of the handkerchief is the area of the square minus the total area of the nine circular designs.
Area of remaining portion = Area of square - Total area of 9 circles
Area of remaining portion = $1764 - 1386$
Area of remaining portion = $378$ cm$^2$.
Hence, the area of the remaining portion of the handkerchief is 378 cm$^2$.
Question 12. In Fig. 12.30, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the
(i) quadrant OACB,
(ii) shaded region
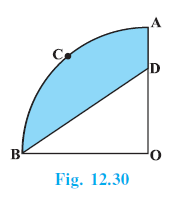
Answer:
Given:
OACB is a quadrant of a circle with centre O.
Radius of the quadrant, $r = OA = OB = 3.5$ cm.
OD = 2 cm.
To Find:
(i) Area of the quadrant OACB.
(ii) Area of the shaded region.
Solution:
(i) Area of the quadrant OACB:
A quadrant is $\frac{1}{4}$ of a circle.
The angle of a quadrant is $90^\circ$.
Area of quadrant OACB = $\frac{1}{4} \pi r^2$.
Radius $r = 3.5 \text{ cm} = \frac{35}{10} \text{ cm} = \frac{7}{2}$ cm.
Area of quadrant OACB = $\frac{1}{4} \times \frac{22}{7} \times (\frac{7}{2})^2$
Area of quadrant OACB = $\frac{1}{4} \times \frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}$
Area of quadrant OACB = $\frac{1}{\cancel{4}_1} \times \frac{\cancel{22}^{11}}{\cancel{7}_1} \times \frac{\cancel{7}^1}{\cancel{2}_1} \times \frac{7}{2}$
Area of quadrant OACB = $\frac{11 \times 7}{4 \times 2} = \frac{77}{8}$ cm$^2$.
(ii) Area of the shaded region:
The shaded region is obtained by subtracting the area of the triangle ODA from the area of the quadrant OACB.
Area of shaded region = Area of quadrant OACB - Area of $\triangle ODA$.
Since OACB is a quadrant, the angle $\angle AOB = 90^\circ$. Therefore, $\triangle ODA$ is a right-angled triangle with the right angle at O (assuming D lies on OB).
Base of $\triangle ODA = OA = r = 3.5 = \frac{7}{2}$ cm.
Height of $\triangle ODA = OD = 2$ cm (Given).
Area of $\triangle ODA = \frac{1}{2} \times \text{Base} \times \text{Height}$
Area of $\triangle ODA = \frac{1}{2} \times OA \times OD$
Area of $\triangle ODA = \frac{1}{2} \times \frac{7}{2} \times 2$
Area of $\triangle ODA = \frac{7}{2}$ cm$^2$.
Now, calculate the area of the shaded region:
Area of shaded region = Area of quadrant OACB - Area of $\triangle ODA$
Area of shaded region = $\frac{77}{8} - \frac{7}{2}$
To subtract, find a common denominator (8):
Area of shaded region = $\frac{77}{8} - \frac{7 \times 4}{2 \times 4} = \frac{77}{8} - \frac{28}{8}$
Area of shaded region = $\frac{77 - 28}{8} = \frac{49}{8}$ cm$^2$.
Hence,
(i) The area of the quadrant OACB is $\frac{77}{8}$ cm$^2$.
(ii) The area of the shaded region is $\frac{49}{8}$ cm$^2$.
Question 13. In Fig. 12.31, a square OABC is inscribed in a quadrant OPBQ. If OA = 20 cm, find the area of the shaded region. (Use π = 3.14)
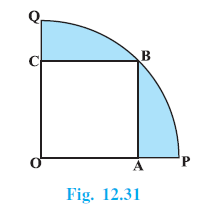
Answer:
Given:
OABC is a square inscribed in a quadrant OPBQ with centre O.
Side of the square, OA = 20 cm.
Use $\pi = 3.14$.
To Find:
The area of the shaded region.
Solution:
The shaded region is the area of the quadrant OPBQ minus the area of the square OABC.
1. Area of the square OABC:
Side of the square = OA = 20 cm.
Area of square OABC = $(\text{side})^2 = (OA)^2$
Area of square OABC = $(20)^2 = 400$ cm$^2$.
2. Radius and Area of the quadrant OPBQ:
Since OABC is a square inscribed in the quadrant OPBQ, the vertex B lies on the arc PQ.
The radius of the quadrant (R) is the distance from the centre O to the point B, which is the diagonal of the square OABC.
Consider the right-angled triangle $\triangle OAB$.
Using Pythagoras theorem:
$OB^2 = OA^2 + AB^2$
Since OABC is a square, OA = AB = 20 cm.
$OB^2 = (20)^2 + (20)^2$
$OB^2 = 400 + 400 = 800$
$OB = \sqrt{800} = \sqrt{400 \times 2} = 20\sqrt{2}$ cm.
So, the radius of the quadrant, $R = OB = 20\sqrt{2}$ cm.
Now, calculate the area of the quadrant OPBQ.
Area of quadrant = $\frac{1}{4} \pi R^2$
Area of quadrant = $\frac{1}{4} \times 3.14 \times (20\sqrt{2})^2$
Area of quadrant = $\frac{1}{4} \times 3.14 \times (400 \times 2)$
Area of quadrant = $\frac{1}{4} \times 3.14 \times 800$
Area of quadrant = $3.14 \times 200$
Area of quadrant = $628$ cm$^2$.
3. Area of the shaded region:
Area of shaded region = Area of quadrant OPBQ - Area of square OABC
Area of shaded region = $628 - 400$
Area of shaded region = $228$ cm$^2$.
Hence, the area of the shaded region is 228 cm$^2$.
Question 14. AB and CD are respectively arcs of two concentric circles of radii 21 cm and 7 cm and centre O (see Fig. 12.32). If ∠AOB = 30°, find the area of the shaded region.
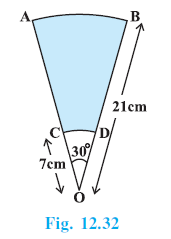
Answer:
Given:
Two concentric circles with centre O.
Radius of the outer circle (corresponding to arc AB), R = OA = OB = 21 cm.
Radius of the inner circle (corresponding to arc CD), r = OC = OD = 7 cm.
Angle subtended at the centre, $\angle AOB = \theta = 30^\circ$.
To Find:
The area of the shaded region (area between the arcs AB and CD).
Solution:
The shaded region is the area of the sector OAB (larger sector) minus the area of the sector OCD (smaller sector).
The formula for the area of a sector with angle $\theta$ and radius $R$ is $\frac{\theta}{360^\circ} \times \pi R^2$.
Area of the larger sector OAB:
Radius $R = 21$ cm, Angle $\theta = 30^\circ$.
Area(OAB) = $\frac{30^\circ}{360^\circ} \times \pi R^2$
Area(OAB) = $\frac{1}{12} \times \frac{22}{7} \times (21)^2$
Area(OAB) = $\frac{1}{12} \times \frac{22}{7} \times 21 \times 21$
Area(OAB) = $\frac{1}{\cancel{12}_2} \times \frac{\cancel{22}^{11}}{\cancel{7}_1} \times \cancel{21}^3 \times 21$
Area(OAB) = $\frac{1}{2} \times 11 \times 3 \times 7$ (Mistake in previous cancellation, let's redo)
Area(OAB) = $\frac{1}{12} \times \frac{22}{7} \times 441$
Area(OAB) = $\frac{1}{\cancel{12}_2} \times \frac{\cancel{22}^{11}}{7} \times 441$
Area(OAB) = $\frac{11}{2 \times \cancel{7}_1} \times \cancel{441}^{63}$
Area(OAB) = $\frac{11 \times 21 \times 3}{2 \times 3}$ (Re-calculating simply)
Area(OAB) = $\frac{1}{12} \times 22 \times 3 \times 21$
Area(OAB) = $\frac{1}{\cancel{12}_4} \times 22 \times \cancel{3}_1 \times 21$
Area(OAB) = $\frac{\cancel{22}^{11} \times 21}{\cancel{4}_2} = \frac{11 \times 21}{2} = \frac{231}{2}$ cm$^2$.
Area of the smaller sector OCD:
Radius $r = 7$ cm, Angle $\theta = 30^\circ$.
Area(OCD) = $\frac{30^\circ}{360^\circ} \times \pi r^2$
Area(OCD) = $\frac{1}{12} \times \frac{22}{7} \times (7)^2$
Area(OCD) = $\frac{1}{12} \times \frac{22}{7} \times 7 \times 7$
Area(OCD) = $\frac{1}{\cancel{12}_6} \times \frac{\cancel{22}^{11}}{\cancel{7}_1} \times \cancel{7}^1 \times 7$
Area(OCD) = $\frac{11 \times 7}{6} = \frac{77}{6}$ cm$^2$.
Area of the shaded region:
Area of shaded region = Area(OAB) - Area(OCD)
Area of shaded region = $\frac{231}{2} - \frac{77}{6}$
To subtract, find a common denominator (6):
Area of shaded region = $\frac{231 \times 3}{2 \times 3} - \frac{77}{6} = \frac{693}{6} - \frac{77}{6}$
Area of shaded region = $\frac{693 - 77}{6} = \frac{616}{6}$
Simplify the fraction:
Area of shaded region = $\frac{\cancel{616}^{308}}{\cancel{6}_3} = \frac{308}{3}$ cm$^2$.
Hence, the area of the shaded region is $\frac{308}{3}$ cm$^2$.
Question 15. In Fig. 12.33, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.
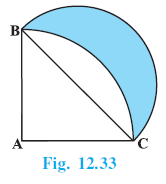
Answer:
Given:
ABC is a quadrant of a circle with centre A.
Radius of the quadrant, $R = AB = AC = 14$ cm.
A semicircle is drawn with BC as diameter.
To Find:
The area of the shaded region.
Solution:
Since ABC is a quadrant of a circle with centre A, $\angle BAC = 90^\circ$.
Consider the right-angled triangle $\triangle ABC$.
Using Pythagoras theorem to find the length of the hypotenuse BC:
$BC^2 = AB^2 + AC^2$
$BC^2 = (14)^2 + (14)^2$
$BC^2 = 196 + 196 = 2 \times 196$
$BC = \sqrt{2 \times 196} = 14\sqrt{2}$ cm.
Now, calculate the area of the different parts:
1. Area of $\triangle ABC$:
Area($\triangle ABC$) = $\frac{1}{2} \times \text{Base} \times \text{Height}$
Area($\triangle ABC$) = $\frac{1}{2} \times AC \times AB$
Area($\triangle ABC$) = $\frac{1}{2} \times 14 \times 14 = 7 \times 14 = 98$ cm$^2$.
2. Area of the quadrant ABC:
Radius of quadrant, $R = 14$ cm.
Area(Quadrant ABC) = $\frac{1}{4} \pi R^2$
Area(Quadrant ABC) = $\frac{1}{4} \times \frac{22}{7} \times (14)^2$
Area(Quadrant ABC) = $\frac{1}{4} \times \frac{22}{7} \times 196$
Area(Quadrant ABC) = $\frac{1}{4} \times 22 \times 28$
Area(Quadrant ABC) = $22 \times 7 = 154$ cm$^2$.
3. Area of the semicircle with diameter BC:
Diameter of semicircle = $BC = 14\sqrt{2}$ cm.
Radius of semicircle, $r_{\text{semi}} = \frac{BC}{2} = \frac{14\sqrt{2}}{2} = 7\sqrt{2}$ cm.
Area(Semicircle on BC) = $\frac{1}{2} \pi (r_{\text{semi}})^2$
Area(Semicircle on BC) = $\frac{1}{2} \times \frac{22}{7} \times (7\sqrt{2})^2$
Area(Semicircle on BC) = $\frac{1}{2} \times \frac{22}{7} \times (49 \times 2)$
Area(Semicircle on BC) = $\frac{1}{2} \times \frac{22}{7} \times 98$
Area(Semicircle on BC) = $11 \times 14 = 154$ cm$^2$.
4. Area of the shaded region:
The shaded region is formed by the area of the semicircle drawn on BC plus the area of the triangle ABC, minus the area of the quadrant ABC.
Area(Shaded Region) = Area($\triangle ABC$) + Area(Semicircle on BC) - Area(Quadrant ABC)
Area(Shaded Region) = $98 + 154 - 154$
Area(Shaded Region) = $98$ cm$^2$.
Hence, the area of the shaded region is 98 cm$^2$.
Question 16. Calculate the area of the designed region in Fig. 12.34 common between the two quadrants of circles of radius 8 cm each.
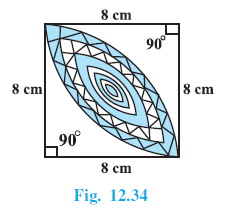
Answer:
Given:
A square with side length 8 cm.
Two quadrants of circles drawn with two opposite vertices of the square as centers.
Radius of each quadrant, $r = 8$ cm (equal to the side of the square).
The designed region is the area common to both quadrants.
To Find:
The area of the designed region.
Solution:
Let the vertices of the square be A, B, C, D. Let the quadrants be drawn with centers B and D.
The side of the square is $s = 8$ cm.
The radius of each quadrant is $r = 8$ cm.
The area of the square ABCD = $s^2 = (8)^2 = 64$ cm$^2$.
Consider the quadrant with centre B (say, quadrant ABC). Its area is:
Area(Quadrant ABC) = $\frac{1}{4} \pi r^2$
Area(Quadrant ABC) = $\frac{1}{4} \times \frac{22}{7} \times (8)^2$
Area(Quadrant ABC) = $\frac{1}{4} \times \frac{22}{7} \times 64$
Area(Quadrant ABC) = $\frac{22 \times 16}{7} = \frac{352}{7}$ cm$^2$.
Consider the quadrant with centre D (say, quadrant ADC). Its area is:
Area(Quadrant ADC) = $\frac{1}{4} \pi r^2$
Area(Quadrant ADC) = $\frac{1}{4} \times \frac{22}{7} \times (8)^2$
Area(Quadrant ADC) = $\frac{352}{7}$ cm$^2$.
The sum of the areas of the two quadrants includes the area of the square, with the common designed region counted twice.
Area(Quadrant ABC) + Area(Quadrant ADC) = Area(Square ABCD) + Area(Designed Region)
Therefore, the area of the designed region can be calculated as:
Area(Designed Region) = Area(Quadrant ABC) + Area(Quadrant ADC) - Area(Square ABCD)
Area(Designed Region) = $\frac{352}{7} + \frac{352}{7} - 64$
Area(Designed Region) = $\frac{704}{7} - 64$
Area(Designed Region) = $\frac{704}{7} - \frac{64 \times 7}{7}$
Area(Designed Region) = $\frac{704 - 448}{7}$
Area(Designed Region) = $\frac{256}{7}$ cm$^2$.
Hence, the area of the designed region is $\frac{256}{7}$ cm$^2$.

