| Non-Rationalised NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Example 1 to 7 (Before Exercise 9.1) | Exercise 9.1 | |
Chapter 9 Some Applications Of Trigonometry
Welcome to the solutions guide for Chapter 9: Some Applications of Trigonometry. Having established the fundamental definitions and identities of trigonometric ratios in the previous chapter, we now transition to their practical utility. This chapter is highly focused on application, demonstrating how the relationships between angles and side lengths in right-angled triangles can be ingeniously employed to solve real-world problems, particularly those involving the calculation of inaccessible heights and distances. It serves as a bridge between the abstract concepts of trigonometry and tangible measurements in the world around us, showcasing the power of this mathematical tool in fields like surveying, navigation, astronomy, and engineering. The core skill developed here is translating a described physical situation into a solvable geometric model using trigonometry.
A crucial first step, emphasized throughout the solutions, is the ability to visualize the problem accurately and represent it with a clear, labeled diagram. This diagram typically involves one or more right-angled triangles formed by the objects involved, the ground (or horizontal level), and lines of sight. Understanding and correctly depicting the key concepts within these diagrams is paramount:
- The Line of Sight: This is the imaginary straight line drawn from the eye of an observer to the point on the object being viewed.
- The Angle of Elevation: When the object being viewed is above the horizontal level of the observer's eye, the angle formed by the line of sight and the horizontal line is called the angle of elevation. It represents looking upwards.
- The Angle of Depression: Conversely, when the object being viewed is below the horizontal level of the observer's eye, the angle formed by the line of sight and the horizontal line is called the angle of depression. It represents looking downwards.
A key geometric insight, often utilized in the solutions, is that the angle of elevation from an observation point A to an object B is numerically equal to the angle of depression from object B back to observation point A. This equality arises because the horizontal lines at A and B are parallel, and the line of sight acts as a transversal, making these angles alternate interior angles.
The fundamental problem-solving strategy involves identifying the relevant right-angled triangle(s) within the diagram. The solutions meticulously guide users through this process: identify the known quantities (which could be an angle of elevation/depression and/or a side length representing a known distance or height) and pinpoint the unknown quantity (usually a height or distance) that needs to be calculated. The critical decision then lies in selecting the appropriate trigonometric ratio – sine ($\sin$), cosine ($\cos$), or tangent ($\tan$) – that connects the known angle(s) with the known side(s) and the required unknown side. For example, if we know an angle and the adjacent side, and need to find the opposite side, the tangent ratio ($\tan \theta = \frac{\text{Opposite}}{\text{Adjacent}}$) would be the most suitable choice.
Once the correct ratio is chosen, a trigonometric equation is set up. The solutions then demonstrate the algebraic steps required to solve this equation for the unknown variable. The types of problems addressed are diverse, commonly including:
- Finding the height of vertical objects like towers, trees, buildings, flagpoles, or mountains.
- Calculating the width of rivers or canals.
- Determining the distance between ships or other objects.
- Finding the length of slanted objects like ladders leaning against walls or the strings of kites.
More complex scenarios often involve two right triangles within the same problem setup. These might require solving the triangles sequentially (where the result from one triangle is used in the other) or setting up a system of equations. Examples include finding the height of a tower when observed from two different points on the ground, or determining the height of a cloud above a lake using its reflection. Throughout, the solutions emphasize clear diagrams, systematic calculations (often using standard angle values like $30^\circ, 45^\circ, 60^\circ$), and providing the final answer with appropriate units, reinforcing practical problem-solving discipline.
Example 1 to 7 (Before Exercise 9.1)
Example 1. A tower stands vertically on the ground. From a point on the ground, which is 15 m away from the foot of the tower, the angle of elevation of the top of the tower is found to be 60°. Find the height of the tower.
Answer:
Given
The distance from the point on the ground to the foot of the tower is 15 m.
The angle of elevation of the top of the tower from that point is 60°.
To Find
The height of the tower.
Solution
Let's represent the situation with a right-angled triangle ABC.
Let AB be the height of the tower, which we need to find. Let this be 'h' meters.
Let C be the point on the ground from where the tower is observed.
The distance from the foot of the tower (B) to the point of observation (C) is BC = 15 m.
The angle of elevation, $\angle ACB = 60^\circ$.
The tower stands vertically, so the triangle ABC is right-angled at B.
In the right-angled $\triangle ABC$, with respect to the angle C:
AB is the side opposite to the angle (Perpendicular).
BC is the side adjacent to the angle (Base).
We need to find the opposite side (h) and we are given the adjacent side (15 m). The trigonometric ratio that relates the opposite side and the adjacent side is the tangent (tan).
So, we have:
$\tan(\angle ACB) = \frac{\text{Opposite Side}}{\text{Adjacent Side}} = \frac{AB}{BC}$
Substituting the given values into the equation:
$\tan 60^\circ = \frac{h}{15}$
We know that the value of $\tan 60^\circ = \sqrt{3}$.
So, the equation becomes:
$\sqrt{3} = \frac{h}{15}$
To find 'h', we multiply both sides by 15:
$h = 15 \times \sqrt{3}$
$h = 15\sqrt{3}$ m
Hence, the height of the tower is $15\sqrt{3}$ m.
Example 2. An electrician has to repair an electric fault on a pole of height 5 m. She needs to reach a point 1.3m below the top of the pole to undertake the repair work (see Fig. 9.5). What should be the length of the ladder that she should use which, when inclined at an angle of 60° to the horizontal, would enable her to reach the required position? Also, how far from the foot of the pole should she place the foot of the ladder? (You may take $\sqrt{3}$ = 1.73)

Answer:
Given
Total height of the electric pole, AD = 5 m.
The repair point B is 1.3 m below the top of the pole, so AB = 1.3 m.
The angle of inclination of the ladder with the horizontal, $\angle BCD = 60^\circ$.
The value to be used for the square root of 3 is $\sqrt{3} = 1.73$.
To Find
1. The length of the ladder (BC).
2. The distance of the foot of the ladder from the foot of the pole (DC).
Solution
First, we need to determine the height from the ground to the point where the repair is needed. Let this height be BD.
Height BD = Total height of the pole (AD) - Distance from the top (AB)
$BD = 5 \text{ m} - 1.3 \text{ m} = 3.7 \text{ m}$
Now, we have a right-angled triangle BDC, where $\angle D = 90^\circ$.
1. Finding the length of the ladder (BC):
In the right-angled $\triangle BDC$, we know the side opposite to the angle $\angle C$ (which is BD) and we need to find the hypotenuse (BC).
We use the sine trigonometric ratio:
$\sin C = \frac{\text{Opposite Side}}{\text{Hypotenuse}} = \frac{BD}{BC}$
Substituting the known values:
$\sin 60^\circ = \frac{3.7}{BC}$
We know that $\sin 60^\circ = \frac{\sqrt{3}}{2}$.
$\frac{\sqrt{3}}{2} = \frac{3.7}{BC}$
Solving for BC:
$BC = \frac{3.7 \times 2}{\sqrt{3}} = \frac{7.4}{\sqrt{3}}$
Using the given value $\sqrt{3} = 1.73$:
$BC = \frac{7.4}{1.73} \approx 4.277$ m
Rounding to two decimal places, the length of the ladder is 4.28 m.
2. Finding the distance from the foot of the pole (DC):
In the same right-angled $\triangle BDC$, we need to find the side adjacent to $\angle C$ (which is DC).
We use the tangent trigonometric ratio:
$\tan C = \frac{\text{Opposite Side}}{\text{Adjacent Side}} = \frac{BD}{DC}$
Substituting the known values:
$\tan 60^\circ = \frac{3.7}{DC}$
We know that $\tan 60^\circ = \sqrt{3}$.
$\sqrt{3} = \frac{3.7}{DC}$
Solving for DC:
$DC = \frac{3.7}{\sqrt{3}}$
Using the given value $\sqrt{3} = 1.73$:
$DC = \frac{3.7}{1.73} \approx 2.138$ m
Rounding to two decimal places, the distance is 2.14 m.
Therefore, the length of the ladder should be 4.28 m, and she should place the foot of the ladder 2.14 m away from the foot of the pole.
Example 3. An observer 1.5 m tall is 28.5 m away from a chimney. The angle of elevation of the top of the chimney from her eyes is 45°. What is the height of the chimney?
Answer:
Given
Height of the observer = 1.5 m.
Distance of the observer from the chimney = 28.5 m.
Angle of elevation of the top of the chimney from the observer's eyes = $45^\circ$.
To Find
The height of the chimney.
Solution
Let AB be the chimney and DE be the observer. Let C be the position of the observer's eyes.
Height of the observer, DE = 1.5 m.
The distance of the observer from the chimney, BE = 28.5 m.
The angle of elevation from the eyes (C) to the top of the chimney (A) is $\angle ACD = 45^\circ$. (Here we draw a horizontal line CD from C parallel to BE).
From the figure, CD = BE = 28.5 m and BC = DE = 1.5 m.
The total height of the chimney is AB = AC + BC.
Now, consider the right-angled triangle ACD, right-angled at D.
We use the tangent ratio to find the length of AC:
$\tan(\angle ACD) = \frac{\text{Opposite Side}}{\text{Adjacent Side}} = \frac{AC}{CD}$
Substituting the values:
$\tan 45^\circ = \frac{AC}{28.5}$
Since $\tan 45^\circ = 1$:
$1 = \frac{AC}{28.5}$
$AC = 28.5$ m
Now, we can find the total height of the chimney, AB:
Height of chimney = AB = AC + BC
AB = 28.5 m + 1.5 m
AB = 30 m
Hence, the height of the chimney is 30 metres.
Example 4. From a point P on the ground the angle of elevation of the top of a 10 m tall building is 30°. A flag is hoisted at the top of the building and the angle of elevation of the top of the flagstaff from P is 45°. Find the length of the flagstaff and the distance of the building from the point P. (You may take $\sqrt{3}$ = 1.732)
Answer:
Given
Height of the building = 10 m.
Angle of elevation to the top of the building from point P = $30^\circ$.
Angle of elevation to the top of the flagstaff from point P = $45^\circ$.
To Find
1. The length of the flagstaff.
2. The distance of the building from the point P.
Solution
Let AB be the 10 m tall building. Let BC be the flagstaff on top of the building. Let P be the point of observation on the ground.
Height of the building, AB = 10 m.
Let the length of the flagstaff, BC = $h$ m.
Let the distance of the building from point P, PA = $x$ m.
We have two right-angled triangles, $\triangle PAB$ and $\triangle PAC$.
Angle of elevation to the top of the building, $\angle APB = 30^\circ$.
Angle of elevation to the top of the flagstaff, $\angle CPA = 45^\circ$.
1. Distance of the building from point P (PA):
In the right-angled triangle PAB:
$\tan(\angle APB) = \frac{AB}{PA}$
$\tan 30^\circ = \frac{10}{x}$
$\frac{1}{\sqrt{3}} = \frac{10}{x}$
$x = 10\sqrt{3}$ m.
Using $\sqrt{3} \approx 1.732$:
$x \approx 10 \times 1.732 = 17.32$ m.
2. Length of the flagstaff (BC):
In the right-angled triangle PAC, the total height is AC = AB + BC = $10 + h$.
$\tan(\angle CPA) = \frac{AC}{PA}$
$\tan 45^\circ = \frac{10 + h}{x}$
Since $\tan 45^\circ = 1$ and we found $x = 10\sqrt{3}$:
$1 = \frac{10 + h}{10\sqrt{3}}$
$10 + h = 10\sqrt{3}$
$h = 10\sqrt{3} - 10$
$h = 10(\sqrt{3} - 1)$ m.
Using $\sqrt{3} \approx 1.732$:
$h \approx 10 (1.732 - 1) = 10 (0.732) = 7.32$ m.
Thus, the length of the flagstaff is $10(\sqrt{3} - 1)$ m and the distance of the building from point P is $10\sqrt{3}$ m.
Example 5. The shadow of a tower standing on a level ground is found to be 40 m longer when the Sun’s altitude is 30° than when it is 60°. Find the height of the tower.
Answer:
Given
The shadow is 40 m longer when the Sun's altitude changes from $60^\circ$ to $30^\circ$.
To Find
The height of the tower.
Solution
Let AB be the tower of height $h$ metres.
Let C be the point where the shadow ends when the Sun's altitude is $60^\circ$ ($\angle ACB = 60^\circ$). The length of the shadow is BC.
Let D be the point where the shadow ends when the Sun's altitude is $30^\circ$ ($\angle ADB = 30^\circ$). The length of the shadow is BD.
We are given that the difference in the lengths of the shadows is 40 m, so CD = 40 m.
In the right-angled triangle ABC:
$\tan 60^\circ = \frac{AB}{BC} = \frac{h}{BC}$
$\sqrt{3} = \frac{h}{BC}$
$BC = \frac{h}{\sqrt{3}}$
$BC = \frac{h}{\sqrt{3}}$
... (i)
In the right-angled triangle ABD:
BD = BC + CD = BC + 40
$\tan 30^\circ = \frac{AB}{BD} = \frac{h}{BC + 40}$
$\frac{1}{\sqrt{3}} = \frac{h}{BC + 40}$
$BC + 40 = h\sqrt{3}$
$BC = h\sqrt{3} - 40$
... (ii)
Equating the expressions for BC from (i) and (ii):
$\frac{h}{\sqrt{3}} = h\sqrt{3} - 40$
$h = \sqrt{3}(h\sqrt{3} - 40)$
$h = 3h - 40\sqrt{3}$
$40\sqrt{3} = 3h - h$
$40\sqrt{3} = 2h$
$h = \frac{40\sqrt{3}}{2} = 20\sqrt{3}$
Hence, the height of the tower is $20\sqrt{3}$ m.
Example 6. The angles of depression of the top and the bottom of an 8 m tall building from the top of a multi-storeyed building are 30° and 45°, respectively. Find the height of the multi-storeyed building and the distance between the two buildings.
Answer:
Given
Height of the shorter building = 8 m.
Angle of depression to the top of the shorter building = $30^\circ$.
Angle of depression to the bottom of the shorter building = $45^\circ$.
To Find
1. The height of the multi-storeyed building.
2. The distance between the two buildings.
Solution
Let AB be the multi-storeyed building and CD be the 8 m tall building.
Let the height of the multi-storeyed building be AB = $H$ m.
The height of the shorter building is CD = 8 m.
Let the distance between the two buildings be BD = $x$ m.
Draw a horizontal line CE from C parallel to BD, meeting AB at E.
Then, CE = BD = $x$ m, and EB = CD = 8 m.
The height AE = AB - EB = $H - 8$ m.
The angles of depression are measured from a horizontal line through A. Let this be AX.
Angle of depression to C, $\angle XAC = 30^\circ$. Since AX || CE, $\angle ACE = 30^\circ$ (alternate interior angles).
Angle of depression to D, $\angle XAD = 45^\circ$. Since AX || BD, $\angle ADB = 45^\circ$ (alternate interior angles).
In the right-angled triangle ABD:
$\tan(\angle ADB) = \frac{AB}{BD}$
$\tan 45^\circ = \frac{H}{x}$
$1 = \frac{H}{x} \implies H = x$
$H = x$
... (i)
In the right-angled triangle ACE:
$\tan(\angle ACE) = \frac{AE}{CE}$
$\tan 30^\circ = \frac{H - 8}{x}$
$\frac{1}{\sqrt{3}} = \frac{H - 8}{x} \implies x = \sqrt{3}(H - 8)$
$x = \sqrt{3}(H - 8)$
... (ii)
Substitute $x = H$ from equation (i) into equation (ii):
$H = \sqrt{3}(H - 8)$
$H = H\sqrt{3} - 8\sqrt{3}$
$8\sqrt{3} = H\sqrt{3} - H$
$8\sqrt{3} = H(\sqrt{3} - 1)$
$H = \frac{8\sqrt{3}}{\sqrt{3} - 1}$
Rationalize the denominator:
$H = \frac{8\sqrt{3}}{\sqrt{3} - 1} \times \frac{\sqrt{3} + 1}{\sqrt{3} + 1} = \frac{8\sqrt{3}(\sqrt{3} + 1)}{(\sqrt{3})^2 - 1^2} = \frac{8(3 + \sqrt{3})}{3 - 1} = \frac{8(3 + \sqrt{3})}{2}$
$H = 4(3 + \sqrt{3})$ m.
Since $x = H$, the distance between the buildings is also $4(3 + \sqrt{3})$ m.
Thus, the height of the multi-storeyed building is $4(3 + \sqrt{3})$ m and the distance between the two buildings is $4(3 + \sqrt{3})$ m.
Example 7. From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45°, respectively. If the bridge is at a height of 3 m from the banks, find the width of the river.
Answer:
Given
Height of the bridge from the banks = 3 m.
Angles of depression of the opposite banks are $30^\circ$ and $45^\circ$.
To Find
The width of the river.
Solution
Let P be the point on the bridge, and let A and B be the points on the opposite banks of the river.
Let the height of the bridge from the banks be PD = 3 m, where D is a point on the river between A and B.
The width of the river is AB = AD + DB.
The angles of depression from P to A and B are $30^\circ$ and $45^\circ$.
Let a horizontal line be drawn through P. Then the alternate interior angles, $\angle PAD$ and $\angle PBD$, will be equal to the angles of depression.
So, $\angle PAD = 30^\circ$ and $\angle PBD = 45^\circ$.
We have two right-angled triangles, $\triangle PDA$ and $\triangle PDB$.
In the right-angled triangle PDA:
$\tan(\angle PAD) = \frac{PD}{AD}$
$\tan 30^\circ = \frac{3}{AD}$
$\frac{1}{\sqrt{3}} = \frac{3}{AD}$
$AD = 3\sqrt{3}$ m
In the right-angled triangle PDB:
$\tan(\angle PBD) = \frac{PD}{DB}$
$\tan 45^\circ = \frac{3}{DB}$
$1 = \frac{3}{DB}$
$DB = 3$ m
The width of the river is AB = AD + DB.
Width = $3\sqrt{3} + 3$
Width = $3(\sqrt{3} + 1)$ m
Hence, the width of the river is $3(\sqrt{3} + 1)$ metres.
Exercise 9.1
Question 1. A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30° (see Fig. 9.11).
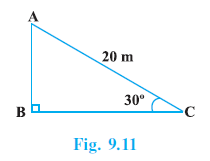
Answer:
Given:
Length of the rope = 20 m.
The rope is tied from the top of a vertical pole to the ground.
The angle made by the rope with the ground level = $30^\circ$.
To Find:
The height of the pole.
Solution:
Let AB be the vertical pole, with A being the top and B being the foot on the ground.
Let C be the point on the ground where the rope is tied.
AC is the length of the rope, AC = 20 m.
The angle made by the rope with the ground is $\angle$ACB = $30^\circ$.
We have a right-angled triangle ABC, right-angled at B (since the pole is vertical).
In $\triangle$ ABC, we need to find the height of the pole AB, which is the side opposite to the angle $\angle$ACB = $30^\circ$.
We are given the length of the hypotenuse AC = 20 m.
The trigonometric ratio that relates the opposite side and the hypotenuse is sine.
$\sin C = \frac{\text{Side opposite to } \angle \text{C}}{\text{Hypotenuse}} = \frac{AB}{AC}$
Substitute the given values:
$\sin 30^\circ = \frac{AB}{20}$
We know that the value of $\sin 30^\circ$ is $\frac{1}{2}$.
$\frac{1}{2} = \frac{AB}{20}$
Solve for AB:
$2 \times AB = 1 \times 20$
$AB = \frac{20}{2}$
$AB = 10$ m
The height of the pole is 10 metres.
Question 2. A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.
Answer:
Given
The angle made by the broken part of the tree with the ground is $30^\circ$.
The distance from the foot of the tree to the point where the top touches the ground is 8 m.
To Find
The original height of the tree.
Solution
Let AC be the original tree. Due to the storm, it breaks at point B, and the broken part BA touches the ground at point D.
So, the length of the broken part is AB = BD.
The part of the tree still standing is BC.
The total height of the tree = BC + AB = BC + BD.
We are given that the distance CD = 8 m, and the angle $\angle BDC = 30^\circ$.
The triangle BCD is a right-angled triangle, with the right angle at C.
First, we find the length of the standing part, BC.
In $\triangle BCD$, we use the tangent ratio:
$\tan(\angle BDC) = \frac{\text{Opposite Side}}{\text{Adjacent Side}} = \frac{BC}{CD}$
$\tan 30^\circ = \frac{BC}{8}$
$\frac{1}{\sqrt{3}} = \frac{BC}{8} \implies BC = \frac{8}{\sqrt{3}}$ m.
Next, we find the length of the broken part, BD.
In $\triangle BCD$, we use the cosine ratio:
$\cos(\angle BDC) = \frac{\text{Adjacent Side}}{\text{Hypotenuse}} = \frac{CD}{BD}$
$\cos 30^\circ = \frac{8}{BD}$
$\frac{\sqrt{3}}{2} = \frac{8}{BD} \implies BD = \frac{16}{\sqrt{3}}$ m.
The total height of the tree is the sum of the standing part and the broken part:
Height = BC + BD = $\frac{8}{\sqrt{3}} + \frac{16}{\sqrt{3}} = \frac{24}{\sqrt{3}}$
Rationalizing the denominator:
Height = $\frac{24}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} = \frac{24\sqrt{3}}{3} = 8\sqrt{3}$ m.
Therefore, the height of the tree is $8\sqrt{3}$ metres.
Question 3. A contractor plans to install two slides for the children to play in a park. For the children below the age of 5 years, she prefers to have a slide whose top is at a height of 1.5 m, and is inclined at an angle of 30° to the ground, whereas for elder children, she wants to have a steep slide at a height of 3m, and inclined at an angle of 60° to the ground. What should be the length of the slide in each case?
Answer:
We need to find the length of the slide in two separate cases. In each case, the slide forms the hypotenuse of a right-angled triangle.
Case 1: Slide for children below 5 years
Given:
Height (opposite side) = 1.5 m.
Angle of inclination with the ground = 30°.
To Find: Length of the slide (hypotenuse).
Let the length of the slide be $L_1$.
We use the sine ratio:
$\sin 30^\circ = \frac{\text{Opposite Side}}{\text{Hypotenuse}} = \frac{1.5}{L_1}$
Since $\sin 30^\circ = \frac{1}{2}$:
$\frac{1}{2} = \frac{1.5}{L_1} \implies L_1 = 1.5 \times 2 = 3$ m.
Case 2: Slide for elder children
Given:
Height (opposite side) = 3 m.
Angle of inclination with the ground = 60°.
To Find: Length of the slide (hypotenuse).
Let the length of the slide be $L_2$.
We use the sine ratio:
$\sin 60^\circ = \frac{\text{Opposite Side}}{\text{Hypotenuse}} = \frac{3}{L_2}$
Since $\sin 60^\circ = \frac{\sqrt{3}}{2}$:
$\frac{\sqrt{3}}{2} = \frac{3}{L_2} \implies L_2 = \frac{3 \times 2}{\sqrt{3}} = \frac{6}{\sqrt{3}}$
Rationalizing the denominator:
$L_2 = \frac{6\sqrt{3}}{3} = 2\sqrt{3}$ m.
The length of the slide for younger children should be 3 m and for elder children should be $2\sqrt{3}$ m.
Question 4. The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower, is 30°. Find the height of the tower.
Answer:
Given
Distance from the foot of the tower to the point of observation = 30 m.
Angle of elevation of the top of the tower = 30°.
To Find
The height of the tower.
Solution
Let AB be the tower of height $h$ and C be the point on the ground.
The distance BC = 30 m.
The angle of elevation, $\angle ACB = 30^\circ$.
In the right-angled triangle ABC, we need to find the opposite side (AB) and we know the adjacent side (BC).
We use the tangent ratio:
$\tan(\angle ACB) = \frac{\text{Opposite Side}}{\text{Adjacent Side}} = \frac{AB}{BC}$
$\tan 30^\circ = \frac{h}{30}$
Since $\tan 30^\circ = \frac{1}{\sqrt{3}}$:
$\frac{1}{\sqrt{3}} = \frac{h}{30}$
$h = \frac{30}{\sqrt{3}}$
Rationalizing the denominator:
$h = \frac{30\sqrt{3}}{3} = 10\sqrt{3}$ m.
Therefore, the height of the tower is $10\sqrt{3}$ m.
Question 5. A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.
Answer:
Given
Height of the kite above the ground = 60 m.
The inclination of the string with the ground = 60°.
To Find
The length of the string.
Solution
Let K be the position of the kite and G be the point on the ground where the string is tied. Let P be the point on the ground directly below the kite.
The height of the kite is KP = 60 m.
The angle of inclination is $\angle KGP = 60^\circ$.
The length of the string is the hypotenuse KG.
In the right-angled triangle KPG, we know the opposite side (KP) and need to find the hypotenuse (KG).
We use the sine ratio:
$\sin(\angle KGP) = \frac{\text{Opposite Side}}{\text{Hypotenuse}} = \frac{KP}{KG}$
$\sin 60^\circ = \frac{60}{KG}$
Since $\sin 60^\circ = \frac{\sqrt{3}}{2}$:
$\frac{\sqrt{3}}{2} = \frac{60}{KG}$
$KG = \frac{60 \times 2}{\sqrt{3}} = \frac{120}{\sqrt{3}}$
Rationalizing the denominator:
$KG = \frac{120\sqrt{3}}{3} = 40\sqrt{3}$ m.
Therefore, the length of the string is $40\sqrt{3}$ m.
Question 6. A 1.5 m tall boy is standing at some distance from a 30 m tall building. The angle of elevation from his eyes to the top of the building increases from 30° to 60° as he walks towards the building. Find the distance he walked towards the building.
Answer:
Given
Height of the building = 30 m.
Height of the boy = 1.5 m.
Initial angle of elevation = 30°.
Final angle of elevation = 60°.
To Find
The distance the boy walked towards the building.
Solution
Let AB be the 30 m tall building. Let the boy's initial position be CD and final position be FG.
The height of the boy is CD = FG = 1.5 m.
Draw a horizontal line CH from the boy's eye level to the building.
The height of the building above the eye level is AH = AB - HB = 30 - 1.5 = 28.5 m.
Let the initial position of the boy be at a distance CH from the building and the final position at a distance FH.
Initial angle of elevation $\angle ACH = 30^\circ$.
Final angle of elevation $\angle AFH = 60^\circ$.
The distance walked by the boy is CF = CH - FH.
In the right-angled triangle ACH:
$\tan 30^\circ = \frac{AH}{CH} \implies \frac{1}{\sqrt{3}} = \frac{28.5}{CH} \implies CH = 28.5\sqrt{3}$ m.
In the right-angled triangle AFH:
$\tan 60^\circ = \frac{AH}{FH} \implies \sqrt{3} = \frac{28.5}{FH} \implies FH = \frac{28.5}{\sqrt{3}}$ m.
The distance walked is:
CF = CH - FH = $28.5\sqrt{3} - \frac{28.5}{\sqrt{3}}$
= $28.5 \left( \sqrt{3} - \frac{1}{\sqrt{3}} \right) = 28.5 \left( \frac{3-1}{\sqrt{3}} \right) = 28.5 \left( \frac{2}{\sqrt{3}} \right) = \frac{57}{\sqrt{3}}$
Rationalizing the denominator:
CF = $\frac{57\sqrt{3}}{3} = 19\sqrt{3}$ m.
Therefore, the distance he walked towards the building is $19\sqrt{3}$ m.
Question 7. From a point on the ground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a 20 m high building are 45° and 60° respectively. Find the height of the tower.
Answer:
Given
Height of the building = 20 m.
Angle of elevation to the bottom of the tower = 45°.
Angle of elevation to the top of the tower = 60°.
To Find
The height of the transmission tower.
Solution
Let AB be the 20 m high building and BC be the transmission tower on top of it. Let D be the point on the ground.
Height of building, AB = 20 m.
Angle of elevation to the bottom of the tower (B), $\angle ADB = 45^\circ$.
Angle of elevation to the top of the tower (C), $\angle ADC = 60^\circ$.
Let the height of the tower be BC = $h$ m.
In the right-angled triangle ABD:
$\tan 45^\circ = \frac{AB}{AD} \implies 1 = \frac{20}{AD} \implies AD = 20$ m.
In the right-angled triangle ACD:
The total height is AC = AB + BC = 20 + $h$.
$\tan 60^\circ = \frac{AC}{AD} \implies \sqrt{3} = \frac{20 + h}{20}$
$20\sqrt{3} = 20 + h$
$h = 20\sqrt{3} - 20 = 20(\sqrt{3} - 1)$ m.
Therefore, the height of the transmission tower is $20(\sqrt{3} - 1)$ m.
Question 8. A statue, 1.6 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal.
Answer:
Given
Height of the statue = 1.6 m.
Angle of elevation to the top of the pedestal = 45°.
Angle of elevation to the top of the statue = 60°.
To Find
The height of the pedestal.
Solution
Let AB be the pedestal and BC be the statue. Let D be the point on the ground.
Height of the statue, BC = 1.6 m.
Let the height of the pedestal be AB = $h$ m.
Angle of elevation to the top of the pedestal (B), $\angle ADB = 45^\circ$.
Angle of elevation to the top of the statue (C), $\angle ADC = 60^\circ$.
In the right-angled triangle ABD:
$\tan 45^\circ = \frac{AB}{AD} \implies 1 = \frac{h}{AD} \implies AD = h$.
In the right-angled triangle ACD:
The total height is AC = AB + BC = $h + 1.6$.
$\tan 60^\circ = \frac{AC}{AD} \implies \sqrt{3} = \frac{h + 1.6}{AD}$
Since AD = h:
$\sqrt{3} = \frac{h + 1.6}{h}$
$h\sqrt{3} = h + 1.6$
$h\sqrt{3} - h = 1.6$
$h(\sqrt{3} - 1) = 1.6$
$h = \frac{1.6}{\sqrt{3} - 1}$
Rationalizing the denominator:
$h = \frac{1.6(\sqrt{3} + 1)}{(\sqrt{3} - 1)(\sqrt{3} + 1)} = \frac{1.6(\sqrt{3} + 1)}{3 - 1} = \frac{1.6(\sqrt{3} + 1)}{2} = 0.8(\sqrt{3} + 1)$ m.
Therefore, the height of the pedestal is $0.8(\sqrt{3} + 1)$ m.
Question 9. The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building.
Answer:
Given
Height of the tower = 50 m.
Angle of elevation of the building's top from the tower's foot = 30°.
Angle of elevation of the tower's top from the building's foot = 60°.
To Find
The height of the building.
Solution
Let AB be the building of height $h$ and CD be the tower of height 50 m.
Let the distance between the building and the tower be BD = $x$ m.
In the right-angled triangle CBD:
$\tan 60^\circ = \frac{CD}{BD} \implies \sqrt{3} = \frac{50}{x} \implies x = \frac{50}{\sqrt{3}}$ m.
In the right-angled triangle ABD:
$\tan 30^\circ = \frac{AB}{BD} \implies \frac{1}{\sqrt{3}} = \frac{h}{x}$
$h = \frac{x}{\sqrt{3}}$
Substitute the value of $x$ we found:
$h = \frac{50/\sqrt{3}}{\sqrt{3}} = \frac{50}{\sqrt{3} \times \sqrt{3}} = \frac{50}{3}$ m.
The height can be written as $16\frac{2}{3}$ m.
Therefore, the height of the building is $\frac{50}{3}$ m.
Question 10. Two poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60° and 30°, respectively. Find the height of the poles and the distances of the point from the poles.
Answer:
Given
Two poles of equal height.
Width of the road = 80 m.
Angles of elevation from a point on the road are 60° and 30°.
To Find
1. The height of the poles.
2. The distances of the point from the poles.
Solution
Let AB and CD be the two poles of equal height $h$. Let P be the point on the road BD.
The width of the road is BD = 80 m.
Let the distance BP = $x$ m. Then PD = (80 - $x$) m.
In the right-angled triangle ABP:
$\tan 60^\circ = \frac{AB}{BP} \implies \sqrt{3} = \frac{h}{x} \implies h = x\sqrt{3}$
$h = x\sqrt{3}$
...(i)
In the right-angled triangle CDP:
$\tan 30^\circ = \frac{CD}{PD} \implies \frac{1}{\sqrt{3}} = \frac{h}{80 - x} \implies h = \frac{80 - x}{\sqrt{3}}$
$h = \frac{80 - x}{\sqrt{3}}$
...(ii)
Equating the expressions for $h$ from (i) and (ii):
$x\sqrt{3} = \frac{80 - x}{\sqrt{3}}$
$x\sqrt{3} \times \sqrt{3} = 80 - x$
$3x = 80 - x$
$4x = 80 \implies x = 20$ m.
Now find the other distance:
PD = 80 - $x$ = 80 - 20 = 60 m.
Now find the height $h$ using equation (i):
$h = x\sqrt{3} = 20\sqrt{3}$ m.
Therefore, the height of the poles is $20\sqrt{3}$ m, and the distances of the point from the poles are 20 m and 60 m.
Question 11. A TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From another point 20 m away from this point on the line joing this point to the foot of the tower, the angle of elevation of the top of the tower is 30° (see Fig. 9.12). Find the height of the tower and the width of the canal.
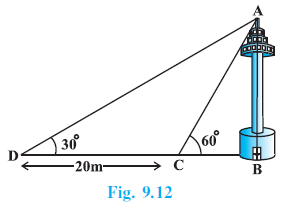
Answer:
Given
Let AB be the TV tower and BC be the width of the canal, as shown in the figure.
The angle of elevation from point C on the opposite bank is $\angle ACB = 60^\circ$.
From a point D, which is 20 m away from C, the angle of elevation is $\angle ADB = 30^\circ$.
The distance CD = 20 m.
To Find
1. The height of the tower (AB).
2. The width of the canal (BC).
Solution
Let the height of the tower, AB, be $h$ meters.
Let the width of the canal, BC, be $x$ meters.
We have two right-angled triangles: $\triangle ABC$ and $\triangle ABD$.
First, consider the right-angled triangle ABC:
$\tan(\angle ACB) = \frac{\text{Opposite Side}}{\text{Adjacent Side}} = \frac{AB}{BC}$
$\tan 60^\circ = \frac{h}{x}$
Since $\tan 60^\circ = \sqrt{3}$:
$\sqrt{3} = \frac{h}{x}$
$h = x\sqrt{3}$
...(i)
Now, consider the right-angled triangle ABD:
The base of this triangle is BD = BC + CD = $(x + 20)$ m.
$\tan(\angle ADB) = \frac{\text{Opposite Side}}{\text{Adjacent Side}} = \frac{AB}{BD}$
$\tan 30^\circ = \frac{h}{x + 20}$
Since $\tan 30^\circ = \frac{1}{\sqrt{3}}$:
$\frac{1}{\sqrt{3}} = \frac{h}{x + 20}$
...(ii)
Now we have two equations. Substitute the value of $h$ from equation (i) into equation (ii):
$\frac{1}{\sqrt{3}} = \frac{x\sqrt{3}}{x + 20}$
By cross-multiplication:
$1 \times (x + 20) = \sqrt{3} \times (x\sqrt{3})$
$x + 20 = 3x$
Rearrange the terms to solve for $x$:
$20 = 3x - x$
$20 = 2x$
$x = \frac{20}{2} = 10$ m.
So, the width of the canal is 10 m.
To find the height of the tower ($h$), substitute the value of $x$ back into equation (i):
$h = 10\sqrt{3}$ m.
Therefore, the height of the tower is $10\sqrt{3}$ m and the width of the canal is 10 m.
Question 12. From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower.
Answer:
Given
Height of the building = 7 m.
Angle of elevation of the top of a cable tower from the top of the building = 60°.
Angle of depression of the foot of the tower from the top of the building = 45°.
To Find
The height of the cable tower.
Solution
Let AB be the 7 m high building and CD be the cable tower.
Draw a horizontal line AE from A to the tower CD.
From the figure, we have a rectangle ABDE.
So, AB = ED = 7 m and BD = AE.
The height of the tower is CD = CE + ED.
The angle of elevation of C from A is $\angle CAE = 60^\circ$.
The angle of depression of D from A is equal to the alternate interior angle $\angle ADB = 45^\circ$.
First, consider the right-angled triangle ABD:
$\tan(\angle ADB) = \frac{AB}{BD}$
$\tan 45^\circ = \frac{7}{BD}$
$1 = \frac{7}{BD} \implies BD = 7$ m.
Since BD = AE, we have AE = 7 m.
Now, consider the right-angled triangle CAE:
$\tan(\angle CAE) = \frac{CE}{AE}$
$\tan 60^\circ = \frac{CE}{7}$
$\sqrt{3} = \frac{CE}{7} \implies CE = 7\sqrt{3}$ m.
The total height of the tower is CD = CE + ED.
Height of tower = $7\sqrt{3} + 7$
Height of tower = $7(\sqrt{3} + 1)$ m.
Therefore, the height of the tower is $7(\sqrt{3} + 1)$ m.
Question 13. As observed from the top of a 75 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
Answer:
Given
Height of the lighthouse = 75 m.
Angles of depression of two ships are 30° and 45°.
The ships are on the same side of the lighthouse, one behind the other.
To Find
The distance between the two ships.
Solution
Let AB be the 75 m high lighthouse. Let C and D be the positions of the two ships.
The ship with the larger angle of depression (45°) will be closer to the lighthouse. So, let the angle of depression to C be 45° and to D be 30°.
The corresponding angles of elevation from the ships to the top of the lighthouse are $\angle ACB = 45^\circ$ and $\angle ADB = 30^\circ$ (alternate interior angles).
We need to find the distance between the ships, which is CD.
First, consider the right-angled triangle ABC:
$\tan(\angle ACB) = \frac{AB}{BC}$
$\tan 45^\circ = \frac{75}{BC}$
$1 = \frac{75}{BC} \implies BC = 75$ m.
Now, consider the right-angled triangle ABD:
$\tan(\angle ADB) = \frac{AB}{BD}$
$\tan 30^\circ = \frac{75}{BD}$
$\frac{1}{\sqrt{3}} = \frac{75}{BD} \implies BD = 75\sqrt{3}$ m.
The distance between the two ships is CD = BD - BC.
CD = $75\sqrt{3} - 75$
CD = $75(\sqrt{3} - 1)$ m.
Therefore, the distance between the two ships is $75(\sqrt{3} - 1)$ m.
Question 14. A 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60°. After some time, the angle of elevation reduces to 30° (see Fig. 9.13). Find the distance travelled by the balloon during the interval.
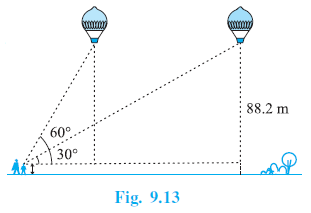
Answer:
Given
Height of the girl = 1.2 m.
Height of the balloon from the ground = 88.2 m.
The initial angle of elevation of the balloon is 60°.
The final angle of elevation of the balloon is 30°.
To Find
The distance travelled by the balloon during the interval.
Solution
Let's analyze the geometry of the problem based on the provided figure.
Let A be the initial position of the balloon and B be the final position.
Let G be the position of the girl's eyes.
The balloon is moving in a horizontal line, so its height from the ground remains constant at 88.2 m.
The height of the girl is 1.2 m.
The vertical height of the balloon from the girl's eye level is:
Height = (Height of balloon from ground) - (Height of the girl)
Height = $88.2 \text{ m} - 1.2 \text{ m} = 87 \text{ m}$.
Let C and D be the points on the horizontal line through the girl's eyes such that AC is perpendicular to GC and BD is perpendicular to GD.
So, AC = BD = 87 m.
We have two right-angled triangles: $\triangle GCA$ and $\triangle GDB$.
Initial angle of elevation, $\angle AGC = 60^\circ$.
Final angle of elevation, $\angle BGD = 30^\circ$.
First, consider the right-angled triangle GCA:
$\tan(\angle AGC) = \frac{\text{Opposite Side}}{\text{Adjacent Side}} = \frac{AC}{GC}$
$\tan 60^\circ = \frac{87}{GC}$
Since $\tan 60^\circ = \sqrt{3}$:
$\sqrt{3} = \frac{87}{GC}$
$GC = \frac{87}{\sqrt{3}}$ m.
Now, consider the right-angled triangle GDB:
$\tan(\angle BGD) = \frac{\text{Opposite Side}}{\text{Adjacent Side}} = \frac{BD}{GD}$
$\tan 30^\circ = \frac{87}{GD}$
Since $\tan 30^\circ = \frac{1}{\sqrt{3}}$:
$\frac{1}{\sqrt{3}} = \frac{87}{GD}$
$GD = 87\sqrt{3}$ m.
The distance travelled by the balloon is the distance between the initial and final positions, which is AB. Since the balloon moves horizontally, this distance is equal to CD.
Distance travelled = CD = GD - GC
Distance = $87\sqrt{3} - \frac{87}{\sqrt{3}}$
Take 87 as a common factor:
Distance = $87\left(\sqrt{3} - \frac{1}{\sqrt{3}}\right)$
Simplify the expression in the parenthesis:
Distance = $87\left(\frac{(\sqrt{3})(\sqrt{3}) - 1}{\sqrt{3}}\right) = 87\left(\frac{3 - 1}{\sqrt{3}}\right) = 87\left(\frac{2}{\sqrt{3}}\right)$
Distance = $\frac{174}{\sqrt{3}}$
Rationalize the denominator by multiplying the numerator and denominator by $\sqrt{3}$:
Distance = $\frac{174 \times \sqrt{3}}{\sqrt{3} \times \sqrt{3}} = \frac{174\sqrt{3}}{3}$
Distance = $58\sqrt{3}$ m.
Therefore, the distance travelled by the balloon during the interval is $58\sqrt{3}$ m.
Question 15. A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car at an angle of depression of 30°, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60°. Find the time taken by the car to reach the foot of the tower from this point.
Answer:
Given
A car is approaching a tower with uniform speed.
Initial angle of depression from the top of the tower is 30°.
After 6 seconds, the angle of depression is 60°.
To Find
The time taken by the car to reach the foot of the tower from the second point of observation.
Solution
Let AB be the tower of height $h$. Let the initial position of the car be C and its position after 6 seconds be D. The foot of the tower is B.
The angles of depression from A to C and D are 30° and 60° respectively. The corresponding angles of elevation from C and D are:
$\angle ACB = 30^\circ$
$\angle ADB = 60^\circ$
Let the uniform speed of the car be $v$ m/s. The distance covered in 6 seconds is CD.
Distance CD = Speed $\times$ Time = $v \times 6 = 6v$ m.
Let the distance from the second observation point D to the foot of the tower be DB = $y$ m.
In the right-angled triangle ABD:
$\tan 60^\circ = \frac{AB}{DB} = \frac{h}{y}$
$\sqrt{3} = \frac{h}{y} \implies h = y\sqrt{3}$
$h = y\sqrt{3}$
...(i)
In the right-angled triangle ABC:
The base is CB = CD + DB = $6v + y$.
$\tan 30^\circ = \frac{AB}{CB} = \frac{h}{6v + y}$
$\frac{1}{\sqrt{3}} = \frac{h}{6v + y} \implies h = \frac{6v + y}{\sqrt{3}}$
$h = \frac{6v + y}{\sqrt{3}}$
...(ii)
Equating the expressions for $h$ from equations (i) and (ii):
$y\sqrt{3} = \frac{6v + y}{\sqrt{3}}$
$y\sqrt{3} \times \sqrt{3} = 6v + y$
$3y = 6v + y$
$2y = 6v \implies y = 3v$
Now, we need to find the time taken by the car to travel the distance DB = $y$. Let this time be $t$.
Time = $\frac{\text{Distance}}{\text{Speed}}$
$t = \frac{y}{v}$
Substitute $y = 3v$ into the equation:
$t = \frac{3v}{v} = 3$ seconds.
Therefore, the time taken by the car to reach the foot of the tower from this point is 3 seconds.
Question 16. The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6 m.
Answer:
Given
Two points C and D are on the same straight line from the base of a tower B.
Distance of point C from the base, BC = 4 m.
Distance of point D from the base, BD = 9 m.
The angles of elevation from C and D to the top of the tower are complementary.
To Prove
The height of the tower is 6 m.
Proof
Let AB be the tower of height $h$ meters.
Let the angle of elevation from point C, $\angle ACB = \theta$.
Since the angles are complementary, the angle of elevation from point D is $\angle ADB = 90^\circ - \theta$.
Consider the right-angled triangle ABC:
$\tan(\angle ACB) = \frac{AB}{BC}$
$\tan \theta = \frac{h}{4}$
...(i)
Now, consider the right-angled triangle ABD:
$\tan(\angle ADB) = \frac{AB}{BD}$
$\tan(90^\circ - \theta) = \frac{h}{9}$
Using the identity $\tan(90^\circ - \theta) = \cot \theta$:
$\cot \theta = \frac{h}{9}$
...(ii)
Now, we multiply equation (i) by equation (ii):
$(\tan \theta) \times (\cot \theta) = \left( \frac{h}{4} \right) \times \left( \frac{h}{9} \right)$
Using the identity $\tan \theta \times \cot \theta = 1$:
$1 = \frac{h^2}{36}$
$h^2 = 36$
Taking the square root on both sides:
$h = \pm 6$
Since height cannot be negative, we take the positive value.
$h = 6$ m
Thus, it is proved that the height of the tower is 6 m.

