| Non-Rationalised NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Exercise 11.1 | Example 1 to 5 (Before Exercise 11.2) | Exercise 11.2 |
| Example 6 to 9 (Before Exercise 11.3) | Exercise 11.3 | Example 10 to 13 (Before Exercise 11.4) |
| Exercise 11.4 | ||
Chapter 11 Mesuration
Welcome to the comprehensive solutions guide for Chapter 11: Mensuration. This crucial chapter significantly extends your understanding of geometric measurement, moving beyond the foundational concepts of perimeter and area for basic shapes learned in earlier classes. Here, we delve deeper into calculating areas of more complex 2D figures and, importantly, venture into the three-dimensional world to explore the concepts of Surface Area and Volume for common solid shapes like cubes, cuboids, and cylinders. Mensuration is inherently practical, providing the mathematical tools needed to measure and quantify the space around us, essential skills in fields ranging from engineering, architecture, and design to everyday tasks like home renovation or packaging.
The solutions begin by consolidating and expanding upon your knowledge of 2D shapes. While revisiting perimeter and area calculations for familiar figures like rectangles, squares, triangles, and parallelograms, new formulas and techniques are introduced:
- Area of a Trapezium: Learn how to calculate the area of a quadrilateral with one pair of parallel sides using the formula $\text{Area} = \frac{1}{2} \times (\text{sum of parallel sides}) \times \text{height}$.
- Area of General Quadrilaterals: Understand methods to find the area of any four-sided figure, often by dividing it into two triangles using a diagonal and calculating the area as $\frac{1}{2} \times \text{diagonal} \times (\text{sum of perpendicular heights from opposite vertices})$.
- Area of Polygons: Approaches for finding the area of regular polygons might also be touched upon, often involving decomposition into triangles.
The solutions demonstrate applying these formulas to various problems, including calculating the area of complex shapes like pathways or shaded regions within larger figures.
The major advancement in this chapter is the exploration of 3D shapes, specifically the cube, cuboid, and cylinder. Two fundamental measures are introduced:
- Surface Area: This refers to the total area of the surfaces of a 3D object. Solutions differentiate between:
- Lateral Surface Area (LSA): The area of the sides of the object, excluding the top and bottom faces (relevant for painting walls of a room, for example).
- Total Surface Area (TSA): The sum of the areas of all surfaces of the object (relevant for wrapping a gift box).
- Cuboid (length $l$, breadth $b$, height $h$): $LSA = 2h(l+b)$; $TSA = 2(lb + bh + hl)$
- Cube (side $a$): $LSA = 4a^2$; $TSA = 6a^2$
- Cylinder (radius $r$, height $h$): $LSA = 2\pi rh$; $TSA = 2\pi r(h + r)$ (using $\pi \approx \frac{22}{7}$ or $3.14$)
- Volume: This measures the amount of space occupied by a 3D object, essentially its capacity. Solutions explain and apply the volume formulas:
- Cuboid: $Volume = l \times b \times h$
- Cube: $Volume = a^3$
- Cylinder: $Volume = \pi r^2 h$
The solutions provide meticulous guidance on a wide variety of problems: calculating LSA, TSA, and Volume given dimensions; finding unknown dimensions when area or volume is provided; and tackling complex application scenarios. These include calculating the cost of painting or plastering surfaces (based on surface area, e.g., cost in $\textsf{₹}$ per $m^2$) or determining the capacity of tanks or the amount of material needed (based on volume, e.g., in $m^3$ or litres). The importance of unit consistency and performing necessary conversions (e.g., $1m^3 = 1000$ litres, $1 L = 1000 cm^3$) is emphasized throughout these practical problems.
Exercise 11.1
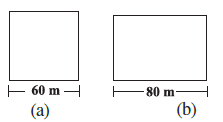
Question 1. A square and a rectangular field with measurements as given in the figure have the same perimeter. Which field has a larger area?
Answer:
Given:
Side of the square field = $60 \text{ m}$.
Length of the rectangular field = $80 \text{ m}$.
The perimeter of the square field is equal to the perimeter of the rectangular field.
To Find:
Which field has a larger area.
Solution:
First, we find the perimeter of the square field.
Perimeter of square = $4 \times \text{side}$
Perimeter of square = $4 \times 60 \text{ m} = 240 \text{ m}$.
Since the perimeter of the rectangular field is equal to the perimeter of the square field, we have:
Perimeter of rectangular field = $240 \text{ m}$.
The formula for the perimeter of a rectangle is:
Perimeter of rectangle = $2 \times (\text{length} + \text{breadth})$
Substituting the known values:
$240 \text{ m} = 2 \times (80 \text{ m} + \text{breadth})$
Divide both sides by 2:
$\frac{240}{2} \text{ m} = 80 \text{ m} + \text{breadth}$
$120 \text{ m} = 80 \text{ m} + \text{breadth}$
Subtract 80 m from both sides to find the breadth:
Breadth = $120 \text{ m} - 80 \text{ m}$
Breadth = $40 \text{ m}$.
Now we calculate the area of both fields.
Area of square field = $\text{side} \times \text{side}$
Area of square field = $60 \text{ m} \times 60 \text{ m} = 3600 \text{ m}^2$.
Area of rectangular field = $\text{length} \times \text{breadth}$
Area of rectangular field = $80 \text{ m} \times 40 \text{ m} = 3200 \text{ m}^2$.
Comparing the areas, we have $3600 \text{ m}^2$ (Area of Square) and $3200 \text{ m}^2$ (Area of Rectangle).
Since $3600 > 3200$, the area of the square field is larger than the area of the rectangular field.
Conclusion:
The square field has a larger area than the rectangular field.
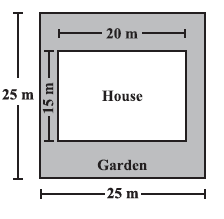
Question 2. Mrs. Kaushik has a square plot with the measurement as shown in the figure. She wants to construct a house in the middle of the plot. A garden is developed around the house. Find the total cost of developing a garden around the house at the rate of ₹ 55 per m2.
Answer:
Given:
Side of the square plot = $25 \text{ m}$.
Length of the house = $20 \text{ m}$.
Breadth of the house = $15 \text{ m}$.
Rate of developing the garden = $\textsf{₹} 55$ per $\text{m}^2$.
To Find:
The total cost of developing the garden around the house.
Solution:
First, we calculate the area of the square plot.
Area of square plot = $\text{side} \times \text{side}$
Area of square plot = $25 \text{ m} \times 25 \text{ m} = 625 \text{ m}^2$.
Next, we calculate the area of the rectangular house.
Area of house = $\text{length} \times \text{breadth}$
Area of house = $20 \text{ m} \times 15 \text{ m} = 300 \text{ m}^2$.
The area of the garden is the area of the square plot minus the area of the house.
Area of garden = Area of square plot - Area of house
Area of garden = $625 \text{ m}^2 - 300 \text{ m}^2 = 325 \text{ m}^2$.
The cost of developing the garden is the area of the garden multiplied by the rate per square metre.
Total cost = Area of garden $\times$ Rate per $\text{m}^2$
Total cost = $325 \text{ m}^2 \times \textsf{₹} 55/\text{m}^2$
Total cost = $\textsf{₹} (325 \times 55)$
Total cost = $\textsf{₹} 17875$.
Conclusion:
The total cost of developing the garden around the house is $\textsf{₹} 17875$.
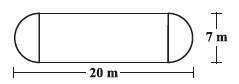
Question 3. The shape of a garden is rectangular in the middle and semi circular at the ends as shown in the diagram. Find the area and the perimeter of this garden [Length of rectangle is 20 – (3.5 + 3.5) metres].
Answer:
Given:
Total length of the garden = $20 \text{ m}$.
Width of the rectangular part (Diameter of semicircles) = $7 \text{ m}$.
Length of the rectangular part = $20 - (3.5 + 3.5)$ metres.
To Find:
The area and the perimeter of the garden.
Solution:
The garden consists of a rectangular part in the middle and two semicircular parts at the ends.
The diameter of each semicircle is equal to the width of the rectangular part, which is $7 \text{ m}$.
Radius of each semicircle, $r = \frac{\text{Diameter}}{2} = \frac{7}{2} \text{ m} = 3.5 \text{ m}$.
The length of the rectangular part is given as:
Length of rectangle, $l = 20 \text{ m} - (3.5 \text{ m} + 3.5 \text{ m})$
$l = 20 \text{ m} - 7 \text{ m}$
$l = 13 \text{ m}$.
The breadth of the rectangular part, $b = 7 \text{ m}$.
Area of the garden:
Area of the garden = Area of rectangular part + Area of two semicircular parts.
Area of rectangular part = $l \times b$
Area of rectangular part = $13 \text{ m} \times 7 \text{ m} = 91 \text{ m}^2$.
The two semicircular parts together form a complete circle with radius $r = 3.5 \text{ m}$.
Area of two semicircles = Area of circle with radius $r$
Area of two semicircles = $\pi r^2$
Using $\pi = \frac{22}{7}$:
Area of two semicircles = $\frac{22}{7} \times (3.5 \text{ m})^2$
Area of two semicircles = $\frac{22}{7} \times 3.5 \times 3.5 \text{ m}^2$
Area of two semicircles = $22 \times 0.5 \times 3.5 \text{ m}^2$
Area of two semicircles = $11 \times 3.5 \text{ m}^2$
Area of two semicircles = $38.5 \text{ m}^2$.
Total Area of garden = Area of rectangle + Area of two semicircles
Total Area = $91 \text{ m}^2 + 38.5 \text{ m}^2$
Total Area = $129.5 \text{ m}^2$.
Perimeter of the garden:
The perimeter of the garden is the sum of the lengths of the two straight sides of the rectangle and the circumferences of the two semicircular ends.
Length of straight sides = Length of rectangle = $13 \text{ m}$ each.
Circumference of a semicircle = $\frac{1}{2} \times \text{Circumference of a full circle} \ $$ = \frac{1}{2} \times 2\pi r = \pi r$.
The perimeter includes the circumference of two semicircles, which is equal to the circumference of a full circle with radius $r = 3.5 \text{ m}$.
Circumference of two semicircles = $2 \times (\pi r)$
Circumference of two semicircles = $2 \times \pi \times 3.5 \text{ m}$
Circumference of two semicircles = $\pi \times 7 \text{ m}$.
Using $\pi = \frac{22}{7}$:
Circumference of two semicircles = $\frac{22}{7} \times 7 \text{ m} = 22 \text{ m}$.
Perimeter of garden = Length of one straight side + Length of other straight side + Circumference of two semicircles
Perimeter of garden = $13 \text{ m} + 13 \text{ m} + 22 \text{ m}$
Perimeter of garden = $26 \text{ m} + 22 \text{ m}$
Perimeter of garden = $48 \text{ m}$.
Conclusion:
The area of the garden is $129.5 \text{ m}^2$ and the perimeter of the garden is $48 \text{ m}$.
Question 4. A flooring tile has the shape of a parallelogram whose base is 24 cm and the corresponding height is 10 cm. How many such tiles are required to cover a floor of area 1080 m2? (If required you can split the tiles in whatever way you want to fill up the corners).
Answer:
Given:
Shape of the tile is a parallelogram.
Base of the parallelogram tile = $24 \text{ cm}$.
Height of the parallelogram tile = $10 \text{ cm}$.
Area of the floor to be covered = $1080 \text{ m}^2$.
To Find:
The number of tiles required to cover the floor.
Solution:
First, we need to find the area of one tile.
Area of a parallelogram = base $\times$ height
Area of one tile = $24 \text{ cm} \times 10 \text{ cm} = 240 \text{ cm}^2$.
The area of the floor is given in $\text{m}^2$, so we need to convert the area of the tile to $\text{m}^2$ or the area of the floor to $\text{cm}^2$. Let's convert the area of the tile to $\text{m}^2$.
We know that $1 \text{ m} = 100 \text{ cm}$, so $1 \text{ m}^2 = (100 \text{ cm})^2 = 10000 \text{ cm}^2$.
Area of one tile in $\text{m}^2 = \frac{240}{10000} \text{ m}^2 = 0.024 \text{ m}^2$.
The area of the floor to be covered is $1080 \text{ m}^2$.
The number of tiles required is the total area of the floor divided by the area of one tile.
Number of tiles = $\frac{\text{Area of floor}}{\text{Area of one tile}}$
Number of tiles = $\frac{1080 \text{ m}^2}{0.024 \text{ m}^2}$
Number of tiles = $\frac{1080}{0.024}$
To remove the decimal, multiply the numerator and denominator by 1000:
Number of tiles = $\frac{1080 \times 1000}{0.024 \times 1000} = \frac{1080000}{24}$
Now perform the division:
$\frac{1080000}{24} = 45000$.
Conclusion:
Therefore, $45000$ tiles are required to cover the floor of area $1080 \text{ m}^2$.
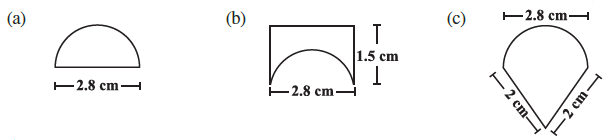
Question 5. An ant is moving around a few food pieces of different shapes scattered on the floor. For which food-piece would the ant have to take a longer round? Remember, circumference of a circle can be obtained by using the expression c = 2πr, where r is the radius of the circle.
Answer:
To find out for which food piece the ant has to take a longer round, we need to calculate the perimeter (the length of the boundary) of each of the three shapes. The ant will take the longest round for the shape with the largest perimeter.
We are given the formula for the circumference of a full circle as $C = 2\pi r$. The length of the arc of a semicircle (half a circle) would be half of the full circumference, which is $\frac{1}{2} \times 2\pi r = \pi r$.
(a) Shape (a): Semicircle
The shape is a semicircle. The ant has to travel along the curved part (arc) and the straight part (diameter).
Diameter (d) = 2.8 cm
Radius (r) = $\frac{d}{2} = \frac{2.8}{2} = 1.4$ cm
Length of the curved arc = $\pi r = \frac{22}{7} \times 1.4 = 22 \times 0.2 = 4.4$ cm
Length of the straight diameter = 2.8 cm
Total Perimeter = Length of arc + Length of diameter
Perimeter (a) = $4.4 + 2.8 = 7.2$ cm
(b) Shape (b): A shape with a semicircular arc
The ant travels along three straight sides and one semicircular arc.
The diameter of the semicircle at the bottom is 2.8 cm, so its radius (r) is 1.4 cm.
Length of the top straight side = 2.8 cm
Length of the two vertical straight sides = $1.5 + 1.5 = 3.0$ cm
Length of the curved arc = $\pi r = \frac{22}{7} \times 1.4 = 4.4$ cm
Total Perimeter = Sum of the lengths of the three straight sides and the arc.
Perimeter (b) = $2.8 + 1.5 + 1.5 + 4.4 = 10.2$ cm
(c) Shape (c): A shape made of a semicircle and two straight lines
The ant travels along a semicircular arc and two straight slant sides.
The diameter of the semicircle at the top is 2.8 cm, so its radius (r) is 1.4 cm.
Length of the curved arc = $\pi r = \frac{22}{7} \times 1.4 = 4.4$ cm
Length of the two straight sides = $2 + 2 = 4.0$ cm
Total Perimeter = Length of arc + Length of the two straight sides
Perimeter (c) = $4.4 + 4.0 = 8.4$ cm
Comparison of Perimeters:
Perimeter of shape (a) = 7.2 cm
Perimeter of shape (b) = 10.2 cm
Perimeter of shape (c) = 8.4 cm
Comparing the three perimeters, we see that $10.2$ cm is the largest value.
$10.2 \text{ cm} > 8.4 \text{ cm} > 7.2 \text{ cm}$
Conclusion:
The ant would have to take a longer round for food-piece (b), as it has the largest perimeter of 10.2 cm.
Example 1 to 5 (Before Exercise 11.2)
Example 1: Find the area of quadrilateral PQRS shown in Fig 11.11.
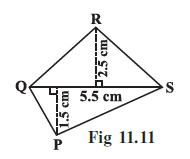
Answer:
To find the area of the quadrilateral PQRS, we can divide it into two triangles, ΔPQS and ΔRQS, using the diagonal QS. The area of the quadrilateral will be the sum of the areas of these two triangles.
Given:
In the quadrilateral PQRS:
- Length of the diagonal, $d = QS = 5.5$ cm.
- Length of the perpendicular from vertex P to the diagonal QS, $h_1 = 1.5$ cm.
- Length of the perpendicular from vertex R to the diagonal QS, $h_2 = 2.5$ cm.
To Find:
The area of the quadrilateral PQRS.
Solution:
The area of a triangle is given by the formula:
Area = $\frac{1}{2} \times \text{base} \times \text{height}$
The area of the quadrilateral PQRS can be calculated as the sum of the areas of the two triangles formed by the diagonal QS.
Area(PQRS) = Area(ΔPQS) + Area(ΔRQS)
For ΔPQS, the base is QS and the height is $h_1$.
Area(ΔPQS) = $\frac{1}{2} \times QS \times h_1$
For ΔRQS, the base is QS and the height is $h_2$.
Area(ΔRQS) = $\frac{1}{2} \times QS \times h_2$
Therefore, the total area of the quadrilateral is:
Area(PQRS) = $\left( \frac{1}{2} \times QS \times h_1 \right) + \left( \frac{1}{2} \times QS \times h_2 \right)$
We can take $\frac{1}{2} \times QS$ as a common factor:
Area(PQRS) = $\frac{1}{2} \times QS \times (h_1 + h_2)$
Now, we substitute the given values into the formula:
$d = 5.5$ cm, $h_1 = 1.5$ cm, and $h_2 = 2.5$ cm.
Area = $\frac{1}{2} \times 5.5 \times (1.5 + 2.5)$
Area = $\frac{1}{2} \times 5.5 \times (4)$
Area = $5.5 \times 2$
Area = $11$ cm2
Final Answer:
The area of the quadrilateral PQRS is 11 cm2.
Example 2: Find the area of a rhombus whose diagonals are of lengths 10 cm and 8.2 cm.
Answer:
Given:
Length of the first diagonal, $d_1 = 10 \text{ cm}$.
Length of the second diagonal, $d_2 = 8.2 \text{ cm}$.
To Find:
The area of the rhombus.
Solution:
The area of a rhombus can be calculated using the lengths of its diagonals with the formula:
Area of rhombus = $\frac{1}{2} \times d_1 \times d_2$
Substitute the given values of $d_1$ and $d_2$ into the formula:
Area = $\frac{1}{2} \times 10 \text{ cm} \times 8.2 \text{ cm}$
Area = $\frac{1}{2} \times 82 \text{ cm}^2$
Area = $41 \text{ cm}^2$.
Conclusion:
The area of the rhombus is $\boxed{41 \text{ cm}^2}$.
Example 3: The area of a trapezium shaped field is 480 m2, the distance between two parallel sides is 15 m and one of the parallel side is 20 m. Find the other parallel side.
Answer:
Given:
Area of the trapezium shaped field = $480 \text{ m}^2$.
Distance between the parallel sides (height), $h = 15 \text{ m}$.
Length of one parallel side, $a = 20 \text{ m}$.
To Find:
The length of the other parallel side.
Solution:
Let the length of the other parallel side be $b$ metres.
The formula for the area of a trapezium is given by:
Area $= \frac{1}{2} \times (\text{sum of parallel sides}) \times \text{height}$
Substituting the given values into the formula:
$480 = \frac{1}{2} \times (20 + b) \times 15$
Multiply both sides of the equation by 2:
$480 \times 2 = (20 + b) \times 15$
$960 = (20 + b) \times 15$
Divide both sides by 15:
$\frac{960}{15} = 20 + b$
$64 = 20 + b$
Subtract 20 from both sides to find the value of $b$:
$b = 64 - 20$
$b = 44$
So, the length of the other parallel side is $44$ metres.
Conclusion:
The length of the other parallel side is $44 \text{ m}$.
Example 4: The area of a rhombus is 240 cm2 and one of the diagonals is 16 cm. Find the other diagonal.
Answer:
Given:
Area of the rhombus = $240 \text{ cm}^2$.
Length of one diagonal, $d_1 = 16 \text{ cm}$.
To Find:
The length of the other diagonal ($d_2$).
Solution:
The formula for the area of a rhombus is given by:
Area $= \frac{1}{2} \times d_1 \times d_2$
Substitute the given values into the formula:
$240 = \frac{1}{2} \times 16 \times d_2$
Simplify the equation:
$240 = 8 \times d_2$
To find $d_2$, divide both sides by 8:
$d_2 = \frac{240}{8}$
$d_2 = 30$
The length of the other diagonal is $30 \text{ cm}$.
Conclusion:
The length of the other diagonal is $30 \text{ cm}$.
Example 5: There is a hexagon MNOPQR of side 5 cm (Fig 11.20). Aman and Ridhima divided it in two different ways (Fig 11.21).
Find the area of this hexagon using both ways.
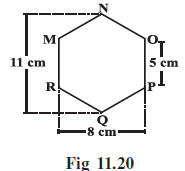
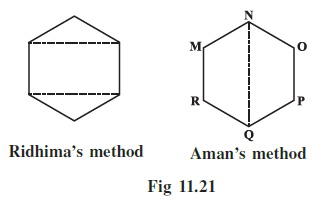
Answer:
We are asked to find the area of the hexagon MNOPQR using two different methods of division, as shown by Ridhima and Aman.
Given:
- The shape is a hexagon MNOPQR.
- The side length of the hexagon is 5 cm (e.g., OP = 5 cm).
- The total height of the hexagon (distance NQ) is 11 cm.
- The total width of the hexagon (distance between R and P) is 8 cm.
To Find:
The area of the hexagon using both Ridhima's and Aman's methods.
Solution:
We will calculate the area using each method separately.
1. Ridhima's Method
Ridhima divided the hexagon into three parts: one central rectangle and two identical triangles (one at the top and one at the bottom).
Area of Hexagon = Area of the Rectangle + 2 × Area of one Triangle
Area of the Rectangle:
From the figure, the length of the rectangle is given as 8 cm. The width of the rectangle (from M to R or O to P) is given as 5 cm.
Length ($l$) = 8 cm
Width ($w$) = 5 cm
Area of Rectangle = $l \times w = 8 \times 5 = 40$ cm2
Area of the two Triangles:
The base of each triangle is equal to the length of the rectangle, which is 8 cm.
The total height of the hexagon is 11 cm, and the height of the central rectangle is 5 cm. The remaining height is shared equally by the two triangles.
Height of one triangle ($h$) = $\frac{\text{Total height} - \text{Rectangle height}}{2} = \frac{11 - 5}{2} = \frac{6}{2} = 3$ cm
Area of one Triangle = $\frac{1}{2} \times \text{base} \times h = \frac{1}{2} \times 8 \times 3 = 12$ cm2
Area of two Triangles = $2 \times 12 = 24$ cm2
Total Area (Ridhima's Method):
Total Area = Area of Rectangle + Area of two Triangles
Total Area = $40 + 24 = 64$ cm2
2. Aman's Method
Aman divided the hexagon into two identical trapeziums: NOPQ and NMRQ.
Area of Hexagon = 2 × Area of one Trapezium
Let's find the area of trapezium NOPQ. The formula for the area of a trapezium is:
Area = $\frac{1}{2} \times (\text{sum of parallel sides}) \times \text{height}$
In trapezium NOPQ, the parallel sides are NQ and OP. The lengths of these sides are given.
Length of side NQ = 11 cm
Length of side OP = 5 cm
Sum of parallel sides = $11 + 5 = 16$ cm
The height of the trapezium is the perpendicular distance between the parallel sides. From the main diagram (Fig 11.20), the total width of the hexagon (distance from R to P) is 8 cm. Since the figure is symmetrical and divided in the middle by NQ, the height of each trapezium is half of this total width.
Height of Trapezium ($h$) = $\frac{\text{Total width RP}}{2} = \frac{8}{2} = 4$ cm
Area of Trapezium NOPQ:
Area = $\frac{1}{2} \times (16) \times 4 = 32$ cm2
Total Area (Aman's Method):
Total Area = Area of Trapezium NOPQ + Area of Trapezium NMRQ
Since the trapeziums are identical, Total Area = $2 \times 32 = 64$ cm2
Conclusion:
Both methods yield the same result.
The area of the hexagon MNOPQR is 64 cm2.
Exercise 11.2
Question 1. The shape of the top surface of a table is a trapezium. Find its area if its parallel sides are 1 m and 1.2 m and perpendicular distance between them is 0.8 m.
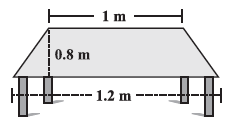
Answer:
Given:
The shape of the top surface of the table is a trapezium.
Length of the first parallel side, $a = 1 \text{ m}$.
Length of the second parallel side, $b = 1.2 \text{ m}$.
Perpendicular distance between the parallel sides (height), $h = 0.8 \text{ m}$.
To Find:
The area of the trapezium.
Solution:
The area of a trapezium is given by the formula:
Area $= \frac{1}{2} \times (\text{sum of parallel sides}) \times \text{height}$
Area $= \frac{1}{2} \times (a + b) \times h$
Substitute the given values into the formula:
Area $= \frac{1}{2} \times (1 \text{ m} + 1.2 \text{ m}) \times 0.8 \text{ m}$
Area $= \frac{1}{2} \times (2.2 \text{ m}) \times 0.8 \text{ m}$
Area $= 1.1 \text{ m} \times 0.8 \text{ m}$
Area $= 0.88 \text{ m}^2$.
Conclusion:
The area of the top surface of the table is $\boxed{0.88 \text{ m}^2}$.
Question 2. The area of a trapezium is 34 cm2 and the length of one of the parallel sides is 10 cm and its height is 4 cm. Find the length of the other parallel side.
Answer:
Given:
Area of the trapezium = $34 \text{ cm}^2$.
Length of one parallel side, $a = 10 \text{ cm}$.
Height, $h = 4 \text{ cm}$.
To Find:
The length of the other parallel side ($b$).
Solution:
The area of a trapezium is given by the formula:
Area $= \frac{1}{2} \times (\text{sum of parallel sides}) \times \text{height}$
Area $= \frac{1}{2} \times (a + b) \times h$
Substitute the given values into the formula:
$34 = \frac{1}{2} \times (10 + b) \times 4$
... (1)
Simplify equation (1):
$34 = (10 + b) \times \frac{\cancel{4}^{2}}{\cancel{2}}$
$34 = (10 + b) \times 2$
Divide both sides by 2:
$\frac{34}{2} = 10 + b$
$17 = 10 + b$
Subtract 10 from both sides to find the value of $b$:
$b = 17 - 10$
$b = 7$
So, the length of the other parallel side is $7 \text{ cm}$.
Conclusion:
The length of the other parallel side is $7 \text{ cm}$.
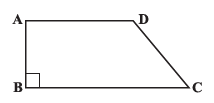
Question 3. Length of the fence of a trapezium shaped field ABCD is 120 m. If BC = 48 m, CD = 17 m and AD = 40 m, find the area of this field. Side AB is perpendicular to the parallel sides AD and BC.
Answer:
Given:
Shape of the field is a trapezium ABCD.
Length of the fence (Perimeter) = $120 \text{ m}$.
Side lengths: BC = $48 \text{ m}$, CD = $17 \text{ m}$, AD = $40 \text{ m}$.
Side AB is perpendicular to the parallel sides AD and BC.
This means AB is the height of the trapezium and AD || BC.
To Find:
The area of the trapezium field.
Solution:
The perimeter of the trapezium is the sum of the lengths of its sides:
Perimeter = AB + BC + CD + AD
$120 = \text{AB} + 48 + 17 + 40$
... (1)
Calculate the sum of the known sides:
$48 + 17 + 40 = 105 \text{ m}$.
Substitute this sum back into equation (1):
$120 = \text{AB} + 105$
Solve for AB:
AB = $120 - 105$
AB = $15 \text{ m}$.
Since AB is perpendicular to the parallel sides AD and BC, AB is the height ($h$) of the trapezium.
$h = \text{AB} = 15 \text{ m}$.
The parallel sides are AD and BC.
Let $a = \text{AD} = 40 \text{ m}$ and $b = \text{BC} = 48 \text{ m}$.
The area of a trapezium is given by the formula:
Area $= \frac{1}{2} \times (\text{sum of parallel sides}) \times \text{height}$
Area $= \frac{1}{2} \times (a + b) \times h$
Substitute the values of $a$, $b$, and $h$:
Area $= \frac{1}{2} \times (40 \text{ m} + 48 \text{ m}) \times 15 \text{ m}$
Area $= \frac{1}{2} \times (88 \text{ m}) \times 15 \text{ m}$
Area $= 44 \text{ m} \times 15 \text{ m}$
Area $= 660 \text{ m}^2$.
Conclusion:
The area of the trapezium shaped field ABCD is $660 \text{ m}^2$.
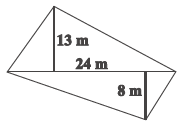
Question 4. The diagonal of a quadrilateral shaped field is 24 m and the perpendiculars dropped on it from the remaining opposite vertices are 8 m and 13 m. Find the area of the field.
Answer:
To find the area of the quadrilateral field, we can use the method of dividing the quadrilateral into two triangles along its diagonal. The area of the field will be the sum of the areas of these two triangles.
Given:
- Length of the diagonal of the quadrilateral, $d = 24$ m.
- Length of the perpendicular from one opposite vertex to the diagonal, $h_1 = 13$ m.
- Length of the perpendicular from the other opposite vertex to the diagonal, $h_2 = 8$ m.
To Find:
The total area of the field.
Solution:
The area of the quadrilateral can be calculated using the formula that sums the areas of the two triangles formed by the diagonal. The formula is:
Area of Quadrilateral = $\frac{1}{2} \times d \times (h_1 + h_2)$
where $d$ is the length of the diagonal and $h_1$ and $h_2$ are the lengths of the perpendiculars (heights) from the opposite vertices to the diagonal.
Now, we substitute the given values into the formula:
$d = 24$ m
$h_1 = 13$ m
$h_2 = 8$ m
Area = $\frac{1}{2} \times 24 \times (13 + 8)$
First, calculate the sum of the heights:
$13 + 8 = 21$ m
Now, substitute this back into the area formula:
Area = $\frac{1}{2} \times 24 \times 21$
We can simplify this by first dividing 24 by 2:
Area = $12 \times 21$
Now, we perform the multiplication:
Area = $252$ m2
Final Answer:
The area of the field is 252 m2.
Question 5. The diagonals of a rhombus are 7.5 cm and 12 cm. Find its area.
Answer:
Given:
Length of the first diagonal, $d_1 = 7.5 \text{ cm}$.
Length of the second diagonal, $d_2 = 12 \text{ cm}$.
To Find:
The area of the rhombus.
Solution:
The area of a rhombus is calculated using the formula:
Area $= \frac{1}{2} \times (\text{product of diagonals})$
Area $= \frac{1}{2} \times d_1 \times d_2$
Substitute the given values of the diagonals into the formula:
Area $= \frac{1}{2} \times 7.5 \text{ cm} \times 12 \text{ cm}$
Area $= \frac{1}{2} \times 12 \times 7.5 \text{ cm}^2$
Area $= 6 \times 7.5 \text{ cm}^2$
Area $= 45.0 \text{ cm}^2$
Area $= 45 \text{ cm}^2$.
Conclusion:
The area of the rhombus is $\boxed{45 \text{ cm}^2}$.
Question 6. Find the area of a rhombus whose side is 5 cm and whose altitude is 4.8 cm. If one of its diagonals is 8 cm long, find the length of the other diagonal.
Answer:
Given:
Side of the rhombus = $5 \text{ cm}$.
Altitude of the rhombus = $4.8 \text{ cm}$.
Length of one diagonal ($d_1$) = $8 \text{ cm}$.
To Find:
The area of the rhombus.
The length of the other diagonal ($d_2$).
Solution:
A rhombus is a special type of parallelogram. The area of a parallelogram can be calculated using its base and corresponding height (altitude).
Area of rhombus = base $\times$ altitude
Using the given side as the base and the altitude:
Area $= 5 \text{ cm} \times 4.8 \text{ cm}$
Area $= 24 \text{ cm}^2$.
We are also given the length of one diagonal and asked to find the length of the other diagonal, using the area.
The formula for the area of a rhombus using its diagonals is:
Area $= \frac{1}{2} \times d_1 \times d_2$
Substitute the calculated area ($24 \text{ cm}^2$) and the given length of one diagonal ($d_1 = 8 \text{ cm}$) into this formula:
$24 = \frac{1}{2} \times 8 \times d_2$
$24 = 4 \times d_2$
To find the value of $d_2$, divide both sides by 4:
$d_2 = \frac{24}{4}$
$d_2 = 6$
So, the length of the other diagonal is $6 \text{ cm}$.
Conclusion:
The area of the rhombus is $24 \text{ cm}^2$.
The length of the other diagonal is $6 \text{ cm}$.
Question 7. The floor of a building consists of 3000 tiles which are rhombus shaped and each of its diagonals are 45 cm and 30 cm in length. Find the total cost of polishing the floor, if the cost per m2 is ₹ 4.
Answer:
Given:
Number of rhombus shaped tiles = $3000$.
Lengths of the diagonals of each tile: $d_1 = 45 \text{ cm}$, $d_2 = 30 \text{ cm}$.
Cost of polishing per $\text{m}^2$ = $\textsf{₹} 4$.
To Find:
The total cost of polishing the floor.
Solution:
First, we need to find the area of one rhombus shaped tile.
Area of a rhombus $= \frac{1}{2} \times d_1 \times d_2$
Substitute the lengths of the diagonals:
Area of one tile $= \frac{1}{2} \times 45 \text{ cm} \times 30 \text{ cm}$
Area of one tile $= \frac{1}{2} \times 1350 \text{ cm}^2$
Area of one tile $= 675 \text{ cm}^2$.
Next, we need to find the total area of the floor covered by 3000 tiles.
Total area of floor = Number of tiles $\times$ Area of one tile
Total area of floor = $3000 \times 675 \text{ cm}^2$
Total area of floor = $2025000 \text{ cm}^2$.
The cost of polishing is given per square metre, so we need to convert the total area from $\text{cm}^2$ to $\text{m}^2$.
We know that $1 \text{ m} = 100 \text{ cm}$, so $1 \text{ m}^2 = (100 \text{ cm})^2 = 10000 \text{ cm}^2$.
To convert $\text{cm}^2$ to $\text{m}^2$, we divide by 10000.
Total area of floor in $\text{m}^2 = \frac{2025000}{10000} \text{ m}^2 = 202.5 \text{ m}^2$.
Now, we can calculate the total cost of polishing the floor.
Total cost = Total area in $\text{m}^2 \times$ Cost per $\text{m}^2$
Total cost = $202.5 \text{ m}^2 \times \textsf{₹} 4/\text{m}^2$
Total cost = $\textsf{₹} (202.5 \times 4)$
Total cost = $\textsf{₹} 810$.
Conclusion:
The total cost of polishing the floor is $\textsf{₹} 810$.
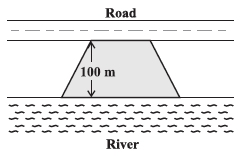
Question 8. Mohan wants to buy a trapezium shaped field. Its side along the river is parallel to and twice the side along the road. If the area of this field is 10500 m2 and the perpendicular distance between the two parallel sides is 100 m, find the length of the side along the river.
Answer:
Given:
The shape of the field is a trapezium.
The side along the river is parallel to and twice the side along the road.
Area of the trapezium field = $10500 \text{ m}^2$.
Perpendicular distance between the parallel sides (height) = $100 \text{ m}$.
To Find:
The length of the side along the river.
Solution:
Let the length of the side along the road be $x \text{ m}$.
According to the problem statement, the length of the side along the river is twice the length of the side along the road.
So, the length of the side along the river is $2x \text{ m}$.
The parallel sides of the trapezium are $a = x \text{ m}$ and $b = 2x \text{ m}$.
The height of the trapezium is $h = 100 \text{ m}$.
The area of the trapezium is given as $10500 \text{ m}^2$.
The formula for the area of a trapezium is:
Area $= \frac{1}{2} \times (\text{sum of parallel sides}) \times \text{height}$
Area $= \frac{1}{2} \times (a + b) \times h$
Substitute the known values into the formula:
$\frac{1}{2} \times (x + 2x) \times 100 = 10500$
... (1)
Simplify equation (1):
$\frac{1}{2} \times (3x) \times 100 = 10500$
$3x \times \frac{\cancel{100}^{50}}{\cancel{2}} = 10500$
$3x \times 50 = 10500$
$150x = 10500$
To solve for $x$, divide both sides by 150:
$x = \frac{10500}{150}$
$x = \frac{\cancel{10500}^{1050}}{\cancel{150}_{15}}$
$x = \frac{1050}{15}$
$x = 70$
So, the length of the side along the road is $70 \text{ m}$.
The length of the side along the river is $2x$.
Length along the river = $2 \times 70 \text{ m} = 140 \text{ m}$.
Conclusion:
The length of the side along the river is $140 \text{ m}$.
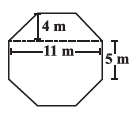
Question 9. Top surface of a raised platform is in the shape of a regular octagon as shown in the figure. Find the area of the octagonal surface.
Answer:
Given:
The top surface is a regular octagon.
Side length of the octagon = $5 \text{ cm}$.
The octagon is divided into two trapeziums and one rectangle.
For the trapeziums: Parallel sides are $5 \text{ cm}$ and $11 \text{ cm}$. Height is $4 \text{ cm}$.
For the rectangle: Length is $11 \text{ cm}$. Width is $5 \text{ cm}$.
To Find:
The area of the octagonal surface.
Solution:
The octagonal surface is composed of two identical trapeziums and one rectangle in the middle.
The total area of the octagon is the sum of the areas of these three shapes.
Area of octagon = Area of first trapezium + Area of rectangle + Area of second trapezium.
First, calculate the area of one trapezium.
The parallel sides of the trapezium are $a = 5 \text{ cm}$ and $b = 11 \text{ cm}$.
The height of the trapezium is $h = 4 \text{ cm}$.
Area of a trapezium $= \frac{1}{2} \times (\text{sum of parallel sides}) \times \text{height}$
Area of one trapezium $= \frac{1}{2} \times (5 \text{ cm} + 11 \text{ cm}) \times 4 \text{ cm}$
Area of one trapezium $= \frac{1}{2} \times 16 \text{ cm} \times 4 \text{ cm}$
Area of one trapezium $= 8 \text{ cm} \times 4 \text{ cm} = 32 \text{ cm}^2$.
Since there are two identical trapeziums, their combined area is $2 \times 32 \text{ cm}^2 = 64 \text{ cm}^2$.
Next, calculate the area of the rectangle.
The length of the rectangle is $l = 11 \text{ cm}$.
The width of the rectangle is $w = 5 \text{ cm}$.
Area of rectangle $= \text{length} \times \text{width}$
Area of rectangle $= 11 \text{ cm} \times 5 \text{ cm} = 55 \text{ cm}^2$.
Now, find the total area of the octagon:
Area of octagon = Area of two trapeziums + Area of rectangle
Area of octagon = $64 \text{ cm}^2 + 55 \text{ cm}^2$
Area of octagon = $119 \text{ cm}^2$.
Conclusion:
The area of the octagonal surface is $119 \text{ cm}^2$.
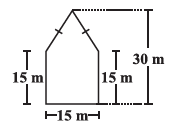
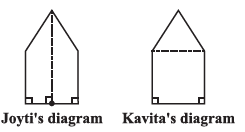
Question 10. There is a pentagonal shaped park as shown in the figure. For finding its area Jyoti and Kavita divided it in two different ways.
Find the area of this park using both ways. Can you suggest some other way of finding its area?
Answer:
To find the area of the pentagonal park, we will calculate it using the two different methods proposed by Jyoti and Kavita. We will also suggest a third method.
Given:
From the figure of the pentagonal park, we have the following dimensions:
- The shape is a pentagon which is symmetrical about the vertical line passing through its top vertex.
- The total height from the base to the top vertex is 30 m.
- The length of the base is 15 m.
- The length of the vertical sides is 15 m.
To Find:
The area of the pentagonal park using both Jyoti's and Kavita's methods, and to suggest another method.
Solution:
1. Area using Jyoti's Diagram
Jyoti divided the pentagon into two identical trapeziums by drawing a perpendicular from the top vertex to the base.
The area of the pentagon will be twice the area of one of these trapeziums.
Let's consider one trapezium. The parallel sides of the trapezium are the vertical line of symmetry and one of the vertical sides of the pentagon.
Length of one parallel side (total height) = 30 m.
Length of the other parallel side (vertical side) = 15 m.
The height of the trapezium is the perpendicular distance between the parallel sides. This is half of the length of the base of the pentagon.
Height of the trapezium = $\frac{15}{2} = 7.5$ m.
The formula for the area of a trapezium is:
Area = $\frac{1}{2} \times (\text{sum of parallel sides}) \times \text{height}$
Area of one trapezium = $\frac{1}{2} \times (30 + 15) \times 7.5$
= $\frac{1}{2} \times 45 \times 7.5$
= $22.5 \times 7.5 = 168.75$ m2
Total area of the park = $2 \times$ Area of one trapezium
= $2 \times 168.75 = 337.5$ m2
So, using Jyoti's method, the area of the park is 337.5 m2.
2. Area using Kavita's Diagram
Kavita divided the pentagon into a square at the bottom and a triangle at the top.
The area of the pentagon will be the sum of the area of the square and the area of the triangle.
Area of the Square:
The base of the pentagon is 15 m, and the vertical sides are 15 m. So, the bottom part is a square with side length 15 m.
Area of the square = side $\times$ side = $15 \times 15 = 225$ m2
Area of the Triangle:
The base of the triangle is the top side of the square, which is 15 m.
The total height of the park is 30 m, and the height of the square is 15 m.
Height of the triangle = Total height - Height of the square = $30 - 15 = 15$ m.
Area of the triangle = $\frac{1}{2} \times \text{base} \times \text{height}$
= $\frac{1}{2} \times 15 \times 15$
= $\frac{1}{2} \times 225 = 112.5$ m2
Total area of the park = Area of the square + Area of the triangle
= $225 + 112.5 = 337.5$ m2
So, using Kavita's method, the area of the park is 337.5 m2.
3. Another Way of Finding the Area
Yes, there is another way. We can divide the pentagonal park into three parts: a central rectangle and two identical triangles on its sides. Or, more simply, we can divide it into a square and two smaller right-angled triangles.
This method is a variation of Kavita's method.
- Divide the park into a square (15m x 15m) and an isosceles triangle on top.
- Draw a perpendicular from the apex of the isosceles triangle to its base. This divides the isosceles triangle into two identical right-angled triangles.
The park is now divided into one square and two right-angled triangles.
Area of the square = $15 \times 15 = 225$ m2.
For each right-angled triangle:
Height = $30 - 15 = 15$ m.
Base = $\frac{15}{2} = 7.5$ m.
Area of one right-angled triangle = $\frac{1}{2} \times \text{base} \times \text{height} \ $$ = \frac{1}{2} \times 7.5 \times 15 = 56.25$ m2.
Area of two right-angled triangles = $2 \times 56.25 = 112.5$ m2.
Total area of the park = Area of square + Area of two right-angled triangles
= $225 + 112.5 = 337.5$ m2.
This method also gives the same area.
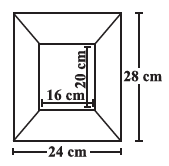
Question 11. Diagram of the adjacent picture frame has outer dimensions = 24 cm × 28 cm and inner dimensions 16 cm × 20 cm. Find the area of each section of the frame, if the width of each section is same.
Answer:
The picture frame consists of four trapezoidal sections. Since the width of each section is the same, we need to find the area of each of these four trapeziums.
Given:
- Outer dimensions of the frame: Length = 28 cm, Width = 24 cm.
- Inner dimensions of the frame: Length = 20 cm, Width = 16 cm.
To Find:
The area of each of the four sections of the frame.
Solution:
First, let's find the width of the frame. The total width of the frame along the horizontal direction is the difference between the outer width and the inner width, divided by 2.
Width of the frame = $\frac{\text{Outer width} - \text{Inner width}}{2} = \frac{24 - 16}{2} = \frac{8}{2} = 4$ cm.
Similarly, along the vertical direction:
Width of the frame = $\frac{\text{Outer length} - \text{Inner length}}{2} = \frac{28 - 20}{2} = \frac{8}{2} = 4$ cm.
So, the width of each section of the frame is 4 cm. This width acts as the height for each of the trapezoidal sections.
The frame is composed of two pairs of identical trapeziums (top & bottom, left & right).
Area of the Top and Bottom Trapeziums
These two trapeziums are identical.
The parallel sides of these trapeziums are the outer and inner widths of the frame.
Parallel side 1 ($a$) = 24 cm
Parallel side 2 ($b$) = 16 cm
The height of these trapeziums is the width of the frame, which is $h = 4$ cm.
The formula for the area of a trapezium is: Area = $\frac{1}{2} \times (a+b) \times h$.
Area of one of these sections = $\frac{1}{2} \times (24 + 16) \times 4$
= $\frac{1}{2} \times 40 \times 4$
= $20 \times 4 = 80$ cm2
So, the area of the top section is 80 cm2, and the area of the bottom section is also 80 cm2.
Area of the Left and Right Trapeziums
These two trapeziums are also identical.
The parallel sides of these trapeziums are the outer and inner lengths of the frame.
Parallel side 1 ($a$) = 28 cm
Parallel side 2 ($b$) = 20 cm
The height of these trapeziums is the width of the frame, which is $h = 4$ cm.
Area of one of these sections = $\frac{1}{2} \times (28 + 20) \times 4$
= $\frac{1}{2} \times 48 \times 4$
= $24 \times 4 = 96$ cm2
So, the area of the left section is 96 cm2, and the area of the right section is also 96 cm2.
Final Answer:
The areas of the sections of the frame are as follows:
- Area of the top section = 80 cm2
- Area of the bottom section = 80 cm2
- Area of the left section = 96 cm2
- Area of the right section = 96 cm2
Example 6 to 9 (Before Exercise 11.3)
Example 6: An aquarium is in the form of a cuboid whose external measures are 80 cm × 30 cm × 40 cm. The base, side faces and back face are to be covered with a coloured paper. Find the area of the paper needed?
Answer:
To find the area of the paper needed, we need to calculate the sum of the areas of the faces that are to be covered: the base, the two side faces, and the back face. The top face and the front face are left uncovered.
Given:
The dimensions of the cuboidal aquarium are:
- Length ($l$) = 80 cm
- Breadth ($b$) = 30 cm
- Height ($h$) = 40 cm
To Find:
The total area of the paper needed to cover the base, two side faces, and the back face.
Solution:
We will calculate the area of each required face and then add them up.
1. Area of the Base:
The base is a rectangle with dimensions length ($l$) and breadth ($b$).
Area of Base = $l \times b = 80 \text{ cm} \times 30 \text{ cm} = 2400$ cm2.
2. Area of the two Side Faces:
Each side face is a rectangle with dimensions breadth ($b$) and height ($h$). Since there are two side faces, we calculate the area of one and multiply by 2.
Area of one side face = $b \times h = 30 \text{ cm} \times 40 \text{ cm} = 1200$ cm2.
Area of two side faces = $2 \times 1200 = 2400$ cm2.
3. Area of the Back Face:
The back face is a rectangle with dimensions length ($l$) and height ($h$).
Area of Back Face = $l \times h = 80 \text{ cm} \times 40 \text{ cm} = 3200$ cm2.
4. Total Area of Paper Needed:
Total Area = Area of Base + Area of two Side Faces + Area of Back Face
Total Area = $2400 + 2400 + 3200$
Total Area = $8000$ cm2.
Final Answer:
The area of the paper needed is 8000 cm2.
Example 7: The internal measures of a cuboidal room are 12 m × 8 m × 4 m. Find the total cost of whitewashing all four walls of a room, if the cost of white washing is ₹ 5 per m2 . What will be the cost of white washing if the ceiling of the room is also whitewashed.
Answer:
This problem has two parts. First, we'll find the cost of whitewashing only the four walls. Second, we'll find the cost of whitewashing the four walls and the ceiling.
Given:
The dimensions of the cuboidal room are:
- Length ($l$) = 12 m
- Breadth ($b$) = 8 m
- Height ($h$) = 4 m
Cost of whitewashing = $\textsf{₹} \, 5$ per m2.
Part 1: Cost of whitewashing the four walls
The area of the four walls of a room is also known as the Lateral Surface Area (LSA) of the cuboid.
The formula for the LSA of a cuboid is:
LSA = $2 \times (l+b) \times h$
Substituting the given values:
Area of four walls = $2 \times (12 + 8) \times 4$
= $2 \times (20) \times 4$
= $160$ m2
Now, we calculate the cost of whitewashing this area.
Cost = Area × Rate
Cost = $160 \text{ m}^2 \times \textsf{₹} \, 5/\text{m}^2 = \textsf{₹} \, 800$
The cost of whitewashing the four walls is $\textsf{₹} \, 800$.
Part 2: Cost of whitewashing the walls and the ceiling
First, we need to find the total area to be whitewashed, which is the area of the four walls plus the area of the ceiling.
Area of the ceiling is a rectangle with dimensions length ($l$) and breadth ($b$).
Area of ceiling = $l \times b = 12 \text{ m} \times 8 \text{ m} = 96$ m2.
Total area to be whitewashed = Area of four walls + Area of ceiling
Total Area = $160 + 96 = 256$ m2.
Now, we calculate the cost for this total area.
Cost = Total Area × Rate
Cost = $256 \text{ m}^2 \times \textsf{₹} \, 5/\text{m}^2 = \textsf{₹} \, 1280$
The cost of whitewashing the four walls and the ceiling is $\textsf{₹} \, 1280$.
Example 8: In a building there are 24 cylindrical pillars. The radius of each pillaris 28 cm and height is 4 m. Find the total cost of painting the curved surface area of all pillars at the rate of ₹ 8 per m2 .
Answer:
To find the total cost of painting, we first need to calculate the total curved surface area of all 24 pillars that needs to be painted.
Given:
- Number of cylindrical pillars = 24
- Radius of each pillar ($r$) = 28 cm
- Height of each pillar ($h$) = 4 m
- Rate of painting = $\textsf{₹} \, 8$ per m2
Solution:
Step 1: Convert units to be consistent
The rate is given in per m2, and the height is in meters, but the radius is in centimeters. We need to convert the radius to meters.
Radius ($r$) = 28 cm = $\frac{28}{100}$ m = 0.28 m.
Step 2: Calculate the Curved Surface Area (CSA) of one pillar
The formula for the CSA of a cylinder is:
CSA = $2 \pi r h$
Substitute the values (using $\pi = \frac{22}{7}$):
CSA of one pillar = $2 \times \frac{22}{7} \times 0.28 \times 4$
= $2 \times 22 \times \frac{0.28}{7} \times 4$
= $2 \times 22 \times 0.04 \times 4$
= $44 \times 0.16$
= $7.04$ m2
Step 3: Calculate the total CSA of all 24 pillars
Total CSA = CSA of one pillar × Number of pillars
Total CSA = $7.04 \times 24$
Total CSA = $168.96$ m2
Step 4: Calculate the total cost of painting
Total Cost = Total CSA × Rate of painting
Total Cost = $168.96 \times 8$
Total Cost = $\textsf{₹} \, 1351.68$
Final Answer:
The total cost of painting the curved surface area of all the pillars is $\textsf{₹} \, 1351.68$.
Example 9: Find the height of a cylinder whose radius is 7 cm and the total surface area is 968 cm2.
Answer:
To find the height of the cylinder, we will use the formula for the Total Surface Area (TSA) of a cylinder and solve for the height ($h$).
Given:
- Radius of the cylinder ($r$) = 7 cm
- Total Surface Area (TSA) = 968 cm2
To Find:
The height ($h$) of the cylinder.
Solution:
The formula for the Total Surface Area (TSA) of a cylinder is:
TSA = $2 \pi r (h + r)$
We are given the TSA, radius ($r$), and we need to find the height ($h$). We will substitute the known values into the formula.
We will use the value of $\pi = \frac{22}{7}$.
$968 = 2 \times \frac{22}{7} \times 7 \times (h + 7)$
We can cancel out the 7 in the numerator and the denominator on the right side of the equation:
$968 = 2 \times 22 \times (h + 7)$
$968 = 44 \times (h + 7)$
To solve for $(h+7)$, we can divide both sides of the equation by 44:
$\frac{968}{44} = h + 7$
Let's perform the division:
$22 = h + 7$
Now, to find $h$, we subtract 7 from both sides of the equation:
$h = 22 - 7$
$h = 15$ cm
Final Answer:
The height of the cylinder is 15 cm.
Exercise 11.3
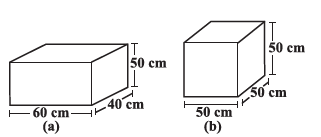
Question 1. There are two cuboidal boxes as shown in the adjoining figure. Which box requires the lesser amount of material to make?
Answer:
To determine which box requires a lesser amount of material to make, we need to calculate the total surface area (TSA) of each box. The box with the smaller TSA will require less material.
For Box (a): A Cuboid
The dimensions of the cuboidal box (a) are:
- Length ($l$) = 60 cm
- Breadth ($b$) = 40 cm
- Height ($h$) = 50 cm
The formula for the Total Surface Area (TSA) of a cuboid is:
TSA = $2(lb + bh + hl)$
Substituting the given values:
TSA of box (a) = $2((60 \times 40) + (40 \times 50) + (50 \times 60))$
= $2(2400 + 2000 + 3000)$
= $2(7400)$
= $14800$ cm2
So, the total surface area of box (a) is 14,800 cm2.
For Box (b): A Cube
The dimensions of the cubical box (b) are:
- Length ($l$) = 50 cm
- Breadth ($b$) = 50 cm
- Height ($h$) = 50 cm
Since all sides are equal, this is a cube. The formula for the Total Surface Area (TSA) of a cube is:
TSA = $6l^2$, where $l$ is the length of one side.
Substituting the given value ($l = 50$ cm):
TSA of box (b) = $6 \times (50)^2$
= $6 \times (50 \times 50)$
= $6 \times 2500$
= $15000$ cm2
So, the total surface area of box (b) is 15,000 cm2.
Comparison
Now, we compare the total surface areas of the two boxes:
- TSA of box (a) = 14,800 cm2
- TSA of box (b) = 15,000 cm2
Since $14,800 < 15,000$, the cuboidal box (a) has a smaller total surface area.
Final Answer:
The cuboidal box (a) requires the lesser amount of material to make.
Question 2. A suitcase with measures 80 cm × 48 cm × 24 cm is to be covered with a tarpaulin cloth. How many metres of tarpaulin of width 96 cm is required to cover 100 such suitcases?
Answer:
Given:
Dimensions of the suitcase (cuboid):
Length ($l$) = $80 \text{ cm}$.
Breadth ($b$) = $48 \text{ cm}$.
Height ($h$) = $24 \text{ cm}$.
Number of suitcases to be covered = $100$.
Width of the tarpaulin cloth = $96 \text{ cm}$.
To Find:
The length of tarpaulin cloth required in metres to cover 100 suitcases.
Solution:
First, we find the surface area of one suitcase. The suitcase is a cuboid, and it needs to be fully covered, so we calculate the total surface area.
Total surface area of a cuboid $= 2(lb + bh + hl)$
Substitute the dimensions of the suitcase:
TSA of one suitcase $= 2((80 \times 48) + (48 \times 24) + (24 \times 80)) \text{ cm}^2$
TSA of one suitcase $= 2((3840) + (1152) + (1920)) \text{ cm}^2$
TSA of one suitcase $= 2(3840 + 1152 + 1920) \text{ cm}^2$
TSA of one suitcase $= 2(6912) \text{ cm}^2$
TSA of one suitcase $= 13824 \text{ cm}^2$.
Next, calculate the total surface area of 100 such suitcases.
Total area to be covered = Number of suitcases $\times$ TSA of one suitcase
Total area to be covered = $100 \times 13824 \text{ cm}^2$
Total area to be covered = $1382400 \text{ cm}^2$.
The tarpaulin cloth is rectangular. Let its length be $L$. The width is given as $96 \text{ cm}$.
Area of tarpaulin cloth = Length $\times$ Width $= L \times 96 \text{ cm}^2$.
The area of the tarpaulin cloth must be equal to the total area to be covered.
Area of tarpaulin cloth = Total area to be covered
$L \times 96 = 1382400$
Solve for $L$:
$L = \frac{1382400}{96}$
$L = 14400 \text{ cm}$.
The question asks for the length in metres. We know that $1 \text{ m} = 100 \text{ cm}$. To convert centimetres to metres, we divide by 100.
Length required in metres $= \frac{14400}{100} \text{ m}$
Length required in metres $= 144 \text{ m}$.
Conclusion:
Therefore, $144 \text{ metres}$ of tarpaulin of width $96 \text{ cm}$ is required to cover 100 such suitcases.
Question 3. Find the side of a cube whose surface area is 600 cm2.
Answer:
Given:
Surface area of a cube = $600 \text{ cm}^2$.
To Find:
The length of the side of the cube.
Solution:
Let the side of the cube be $s$ cm.
The formula for the total surface area of a cube is given by:
Surface Area $= 6 \times (\text{side})^2 = 6s^2$
Substitute the given surface area into the formula:
$6s^2 = 600$
... (1)
To find $s^2$, divide both sides of equation (1) by 6:
$s^2 = \frac{600}{6}$
$s^2 = 100$
To find the side $s$, take the square root of both sides:
$s = \sqrt{100}$
$s = 10$
Since the side length must be positive, we take the positive square root.
The side of the cube is $10 \text{ cm}$.
Conclusion:
The side of the cube is $\boxed{10 \text{ cm}}$.
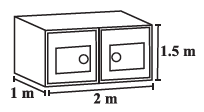
Question 4. Rukhsar painted the outside of the cabinet of measure 1 m × 2 m × 1.5 m. How much surface area did she cover if she painted all except the bottom of the cabinet.
Answer:
Given:
Dimensions of the cuboidal cabinet:
Length ($l$) = $2 \text{ m}$.
Breadth ($b$) = $1 \text{ m}$.
Height ($h$) = $1.5 \text{ m}$.
The bottom of the cabinet was not painted.
To Find:
The surface area painted by Rukhsar.
Solution:
The surface area covered by painting is the total surface area of the cabinet excluding the area of the bottom face.
The total surface area of a cuboid is given by the formula $2(lb + bh + hl)$, where $l$ is length, $b$ is breadth, and $h$ is height.
The area of the bottom face is $l \times b$.
The surface area painted = Total Surface Area - Area of Bottom Face
Surface Area Painted = $2(lb + bh + hl) - lb$
Surface Area Painted = $2lb + 2bh + 2hl - lb$
Surface Area Painted = $lb + 2bh + 2hl$
Substitute the given dimensions into the formula:
Surface Area Painted = $(2 \text{ m} \times 1 \text{ m}) + 2 \times (1 \text{ m} \times 1.5 \text{ m}) \ $$ + 2 \times (1.5 \text{ m} \times 2 \text{ m})$
Surface Area Painted = $(2 \text{ m}^2) + 2 \times (1.5 \text{ m}^2) + 2 \times (3 \text{ m}^2)$
Surface Area Painted = $2 \text{ m}^2 + 3 \text{ m}^2 + 6 \text{ m}^2$
Surface Area Painted = $11 \text{ m}^2$.
Conclusion:
Rukhsar covered a surface area of $11 \text{ m}^2$ by painting.
Question 5. Daniel is painting the walls and ceiling of a cuboidal hall with length, breadth and height of 15 m, 10 m and 7 m respectively. From each can of paint 100 m2 of area is painted. How many cans of paint will she need to paint the room?
Answer:
Given:
Dimensions of the cuboidal hall:
Length ($l$) = $15 \text{ m}$.
Breadth ($b$) = $10 \text{ m}$.
Height ($h$) = $7 \text{ m}$.
Area painted by each can = $100 \text{ m}^2$.
Daniel is painting the walls and the ceiling.
To Find:
The number of cans of paint needed.
Solution:
First, we need to find the total area that needs to be painted. This includes the area of the four walls and the area of the ceiling.
The area of the four walls is the lateral surface area of the cuboid.
Area of four walls $= 2 \times (l + b) \times h$
Area of four walls $= 2 \times (15 \text{ m} + 10 \text{ m}) \times 7 \text{ m}$
Area of four walls $= 2 \times 25 \text{ m} \times 7 \text{ m}$
Area of four walls $= 50 \text{ m} \times 7 \text{ m} = 350 \text{ m}^2$.
The area of the ceiling is the area of the top face of the cuboid.
Area of ceiling $= l \times b = 15 \text{ m} \times 10 \text{ m} = 150 \text{ m}^2$.
The total area to be painted is the sum of the area of the four walls and the area of the ceiling.
Total area to be painted = Area of four walls + Area of ceiling
Total area to be painted = $350 \text{ m}^2 + 150 \text{ m}^2 = 500 \text{ m}^2$.
Each can of paint covers an area of $100 \text{ m}^2$.
The number of cans needed is the total area to be painted divided by the area covered by one can.
Number of cans $= \frac{\text{Total area to be painted}}{\text{Area painted by each can}}$
Number of cans $= \frac{500 \text{ m}^2}{100 \text{ m}^2}$
Number of cans $= 5$.
Conclusion:
Daniel will need $5$ cans of paint to paint the room.
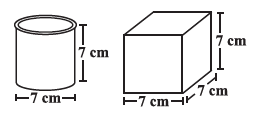
Question 6. Describe how the two figures at the right are alike and how they are different. Which box has larger lateral surface area?
Answer:
Analysis of the figures:
Figure 1 shows a cylinder with a diameter of $7 \text{ cm}$ and a height of $7 \text{ cm}$.
Figure 2 shows a cube with a side length of $7 \text{ cm}$.
How they are alike:
The two figures are alike in the following ways:
- Both are three-dimensional solid shapes.
- The height of the cylinder ($7 \text{ cm}$) is equal to the height of the cube ($7 \text{ cm}$).
- The diameter of the base of the cylinder ($7 \text{ cm}$) is equal to the side length of the cube ($7 \text{ cm}$).
How they are different:
The two figures are different in the following ways:
- The cylinder has a circular base and top, while the cube has a square base and top.
- The cylinder has a curved lateral surface, while the cube has flat rectangular lateral faces.
- The cylinder has circular edges (at the base and top), while the cube has straight edges.
To Find:
Which box has a larger lateral surface area.
Solution:
We need to calculate the lateral surface area (LSA) for both the cylinder and the cube.
For the cylinder:
Diameter = $7 \text{ cm}$. Radius, $r = \frac{7}{2} \text{ cm} = 3.5 \text{ cm}$.
Height, $h = 7 \text{ cm}$.
The formula for the lateral surface area of a cylinder is $2\pi rh$.
Using $\pi = \frac{22}{7}$:
LSA of cylinder $= 2 \times \frac{22}{7} \times 3.5 \times 7 \text{ cm}^2$
LSA of cylinder $= 2 \times 22 \times \frac{3.5 \times 7}{7} \text{ cm}^2$
LSA of cylinder $= 44 \times 3.5 \text{ cm}^2$
LSA of cylinder $= 154 \text{ cm}^2$.
For the cube:
Side length, $s = 7 \text{ cm}$.
The lateral surface area of a cube is the sum of the areas of its four side faces. Each face is a square with area $s^2$.
LSA of cube $= 4 \times s^2$
LSA of cube $= 4 \times (7 \text{ cm})^2$
LSA of cube $= 4 \times 49 \text{ cm}^2$
LSA of cube $= 196 \text{ cm}^2$.
Comparing the lateral surface areas:
LSA of cylinder $= 154 \text{ cm}^2$.
LSA of cube $= 196 \text{ cm}^2$.
Since $196 > 154$, the cube has a larger lateral surface area.
Conclusion:
The cube has a larger lateral surface area than the cylinder.
Question 7. A closed cylindrical tank of radius 7 m and height 3 m is made from a sheet of metal. How much sheet of metal is required?
Answer:
Given:
The tank is in the shape of a closed cylinder.
Radius of the cylindrical tank, $r = 7 \text{ m}$.
Height of the cylindrical tank, $h = 3 \text{ m}$.
To Find:
The amount of sheet of metal required to make the closed cylindrical tank.
Solution:
To make a closed cylindrical tank, the sheet metal is required for the base (bottom circular part), the top (top circular part), and the curved surface area.
Therefore, the total amount of metal sheet required is equal to the total surface area (TSA) of the closed cylinder.
The formula for the total surface area of a closed cylinder is:
TSA $= 2\pi r (r + h)$
Substitute the given values of the radius ($r = 7 \text{ m}$) and height ($h = 3 \text{ m}$) into the formula. Use $\pi = \frac{22}{7}$.
TSA $= 2 \times \frac{22}{7} \times 7 \text{ m} \times (7 \text{ m} + 3 \text{ m})$
TSA $= 2 \times \frac{22}{\cancel{7}} \times \cancel{7} \text{ m} \times (10 \text{ m})$
TSA $= 2 \times 22 \times 10 \text{ m}^2$
TSA $= 44 \times 10 \text{ m}^2$
TSA $= 440 \text{ m}^2$.
Conclusion:
The amount of metal sheet required to make the closed cylindrical tank is $\boxed{440 \text{ m}^2}$.
Question 8. The lateral surface area of a hollow cylinder is 4224 cm2. It is cut along its height and formed a rectangular sheet of width 33 cm. Find the perimeter of rectangular sheet?
Answer:
Given:
Lateral surface area (LSA) of the hollow cylinder = $4224 \text{ cm}^2$.
The cylinder is cut along its height and unrolled into a rectangular sheet.
Width of the rectangular sheet = $33 \text{ cm}$.
To Find:
The perimeter of the rectangular sheet.
Solution:
When a hollow cylinder is cut along its height and unrolled, it forms a rectangular sheet.
The lateral surface area of the cylinder is equal to the area of the rectangular sheet.
Area of rectangular sheet = LSA of cylinder = $4224 \text{ cm}^2$.
Let the length of the rectangular sheet be $L$ and the width be $W$.
We are given the width, $W = 33 \text{ cm}$.
The area of the rectangular sheet is given by the formula:
Area = Length $\times$ Width
Substitute the known values:
$4224 = L \times 33$
... (1)
To find the length $L$, divide both sides of equation (1) by 33:
$L = \frac{4224}{33}$
$L = 128 \text{ cm}$.
Now that we have the length ($L = 128 \text{ cm}$) and the width ($W = 33 \text{ cm}$) of the rectangular sheet, we can find its perimeter.
The formula for the perimeter of a rectangle is:
Perimeter = $2 \times (\text{Length} + \text{Width})$
Substitute the values of $L$ and $W$:
Perimeter $= 2 \times (128 \text{ cm} + 33 \text{ cm})$
Perimeter $= 2 \times (161 \text{ cm})$
Perimeter $= 322 \text{ cm}$.
Conclusion:
The perimeter of the rectangular sheet is $\boxed{322 \text{ cm}}$.
Question 9. A road roller takes 750 complete revolutions to move once over to level a road. Find the area of the road if the diameter of a road roller is 84 cm and length is 1 m.
Answer:
Given:
Number of complete revolutions taken by the road roller = $750$.
Diameter of the road roller = $84 \text{ cm}$.
Length of the road roller = $1 \text{ m}$.
To Find:
The area of the road leveled by the road roller.
Solution:
The road roller is cylindrical in shape. When it rolls, the area of the road leveled in one revolution is equal to the curved surface area (CSA) of the cylinder.
First, ensure that all units are consistent. The diameter is in centimetres (cm), and the length (which is the height of the cylinder when rolling) is in metres (m).
Convert the diameter to metres:
Diameter = $84 \text{ cm} = \frac{84}{100} \text{ m} = 0.84 \text{ m}$.
The radius of the road roller is half of the diameter:
Radius, $r = \frac{0.84}{2} \text{ m} = 0.42 \text{ m}$.
The length of the road roller is its height when rolling:
Height, $h = 1 \text{ m}$.
Calculate the curved surface area (CSA) of the road roller (cylinder).
The formula for the curved surface area of a cylinder is $2\pi rh$.
Using $\pi = \frac{22}{7}$:
CSA of road roller $= 2 \times \frac{22}{7} \times 0.42 \text{ m} \times 1 \text{ m}$
CSA of road roller $= 2 \times \frac{22}{\cancel{7}} \times \cancel{0.42}^{0.06} \times 1 \text{ m}^2$
CSA of road roller $= 2 \times 22 \times 0.06 \text{ m}^2$
CSA of road roller $= 44 \times 0.06 \text{ m}^2$
CSA of road roller $= 2.64 \text{ m}^2$.
This is the area covered in one revolution.
The road roller takes 750 revolutions to level the road.
Total area of the road leveled = Number of revolutions $\times$ Area covered in one revolution
Total area = $750 \times 2.64 \text{ m}^2$
Total area = $1980 \text{ m}^2$.
Conclusion:
The area of the road is $1980 \text{ m}^2$.
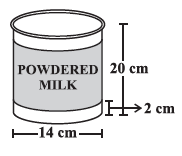
Question 10. A company packages its milk powder in cylindrical container whose base has a diameter of 14 cm and height 20 cm. Company places a label around the surface of the container (as shown in the figure). If the label is placed 2 cm from top and bottom, what is the area of the label.
Answer:
Given:
Diameter of the base of the cylindrical container = $14 \text{ cm}$.
Height of the cylindrical container = $20 \text{ cm}$.
The label is placed around the curved surface of the container.
Distance of the label from the top edge = $2 \text{ cm}$.
Distance of the label from the bottom edge = $2 \text{ cm}$.
To Find:
The area of the label.
Solution:
The label is in the shape of a cylinder's curved surface. To find the area of the label, we need the radius of the base of the label and the height of the label.
The radius of the base of the label is the same as the radius of the base of the container.
Radius of container, $r = \frac{\text{Diameter}}{2} = \frac{14 \text{ cm}}{2} = 7 \text{ cm}$.
So, the radius of the label, $r_{label} = 7 \text{ cm}$.
The height of the label is the total height of the container minus the space left at the top and the bottom.
Height of label, $h_{label} = \text{Height of container} - \text{Space at top} \ $$ - \text{Space at bottom}$
$h_{label} = 20 \text{ cm} - 2 \text{ cm} - 2 \text{ cm}$
$h_{label} = 20 \text{ cm} - 4 \text{ cm}$
$h_{label} = 16 \text{ cm}$.
The area of the label is the curved surface area of a cylinder with radius $r_{label} = 7 \text{ cm}$ and height $h_{label} = 16 \text{ cm}$.
The formula for the curved surface area (CSA) of a cylinder is $2\pi r h$.
Area of label = $2\pi r_{label} h_{label}$
Using $\pi = \frac{22}{7}$:
Area of label $= 2 \times \frac{22}{7} \times 7 \text{ cm} \times 16 \text{ cm}$
Area of label $= 2 \times \frac{22}{\cancel{7}} \times \cancel{7} \times 16 \text{ cm}^2$
Area of label $= 2 \times 22 \times 16 \text{ cm}^2$
Area of label $= 44 \times 16 \text{ cm}^2$
Area of label $= 704 \text{ cm}^2$.
Conclusion:
The area of the label is $\boxed{704 \text{ cm}^2}$.
Example 10 to 13 (Before Exercise 11.4)
Example 10: Find the height of a cuboid whose volume is 275 cm3 and base area is 25 cm2 .
Answer:
Given:
Volume of the cuboid = $275 \text{ cm}^3$.
Base area of the cuboid = $25 \text{ cm}^2$.
To Find:
The height of the cuboid.
Solution:
Let the length, breadth, and height of the cuboid be $l$, $b$, and $h$ respectively.
The volume of a cuboid is given by the formula:
Volume $= l \times b \times h$
Volume $= 275 \text{ cm}^3$
The base area of the cuboid is the area of its rectangular base, which is length $\times$ breadth.
Base Area $= l \times b$
Base Area $= 25 \text{ cm}^2$
We can rewrite the volume formula using the base area:
Volume $= (\text{Base Area}) \times \text{height}$
Substitute the given values into this formula:
$275 = 25 \times h$
... (1)
To find the height $h$, divide both sides of equation (1) by 25:
$h = \frac{275}{25}$
Performing the division:
$h = 11 \text{ cm}$.
The height of the cuboid is $11 \text{ cm}$.
Conclusion:
The height of the cuboid is $\boxed{11 \text{ cm}}$.
Example 11: A godown is in the form of a cuboid of measures 60 m × 40 m × 30 m. How many cuboidal boxes can be stored in it if the volume of one box is 0.8 m3 ?
Answer:
Given:
Dimensions of the cuboidal godown:
Length ($L$) = $60 \text{ m}$.
Breadth ($B$) = $40 \text{ m}$.
Height ($H$) = $30 \text{ m}$.
Volume of one cuboidal box = $0.8 \text{ m}^3$.
To Find:
The number of cuboidal boxes that can be stored in the godown.
Solution:
First, calculate the volume of the godown.
The volume of a cuboid is given by the formula:
Volume = Length $\times$ Breadth $\times$ Height
Volume of godown $= L \times B \times H$
Volume of godown $= 60 \text{ m} \times 40 \text{ m} \times 30 \text{ m}$
Volume of godown $= (60 \times 40 \times 30) \text{ m}^3$
Volume of godown $= 2400 \times 30 \text{ m}^3$
Volume of godown $= 72000 \text{ m}^3$.
The volume of one cuboidal box is given as $0.8 \text{ m}^3$.
To find the number of boxes that can be stored, divide the volume of the godown by the volume of one box.
Number of boxes $= \frac{\text{Volume of godown}}{\text{Volume of one box}}$
Number of boxes $= \frac{72000 \text{ m}^3}{0.8 \text{ m}^3}$
Number of boxes $= \frac{72000}{0.8}$
To remove the decimal, multiply the numerator and denominator by 10:
Number of boxes $= \frac{72000 \times 10}{0.8 \times 10} = \frac{720000}{8}$
Performing the division:
Number of boxes $= 90000$.
Conclusion:
$90000$ cuboidal boxes can be stored in the godown.
Example 12: A rectangular paper of width 14 cm is rolled along its width and a cylinder of radius 20 cm is formed. Find the volume of the cylinder (Fig 11.45). (Take $\frac{22}{7}$ for π)

Answer:
Given:
Width of the rectangular paper = $14 \text{ cm}$.
Radius of the cylinder formed, $r = 20 \text{ cm}$.
The paper is rolled along its width.
$\pi = \frac{22}{7}$.
To Find:
The volume of the cylinder.
Solution:
When a rectangular paper is rolled along its width, the width of the paper becomes the height of the cylinder, and the length of the paper becomes the circumference of the base of the cylinder.
From the given information, the height of the cylinder is the width of the rectangular paper.
Height of the cylinder, $h = 14 \text{ cm}$
(Width of the paper)
The radius of the cylinder is given as $20 \text{ cm}$.
Radius of the cylinder, $r = 20 \text{ cm}$
(Given)
The formula for the volume of a cylinder is:
Volume $= \pi r^2 h$
Substitute the values of $r$, $h$, and $\pi$ into the formula:
Volume $= \frac{22}{7} \times (20 \text{ cm})^2 \times 14 \text{ cm}$
Volume $= \frac{22}{7} \times (20 \times 20) \text{ cm}^2 \times 14 \text{ cm}$
Volume $= \frac{22}{7} \times 400 \times 14 \text{ cm}^3$
Simplify the expression by canceling out the common factor of 7:
Volume $= 22 \times 400 \times \frac{\cancel{14}^{2}}{\cancel{7}_{1}} \text{ cm}^3$
Volume $= 22 \times 400 \times 2 \text{ cm}^3$
Perform the multiplication:
Volume $= 22 \times 800 \text{ cm}^3$
Volume $= 17600 \text{ cm}^3$.
Conclusion:
The volume of the cylinder is $\boxed{17600 \text{ cm}^3}$.
Example 13: A rectangular piece of paper 11 cm × 4 cm is folded without overlapping to make a cylinder of height 4 cm. Find the volume of the cylinder.
Answer:
To find the volume of the cylinder, we first need to determine its radius. The radius can be found from the circumference of the cylinder's base, which is formed by the length of the rectangular paper.
Given:
Dimensions of the rectangular piece of paper = 11 cm × 4 cm.
The paper is folded along its length to make a cylinder. Therefore, the height of the cylinder is the width of the paper.
Height of the cylinder, $h = 4$ cm.
To Find:
The volume of the cylinder.
Solution:
When the rectangular paper is folded, the length of the paper becomes the circumference of the base of the cylinder.
So, the circumference of the base of the cylinder, $C = 11$ cm.
We know the formula for the circumference of a circle is:
$C = 2 \pi r$
(where r is the radius of the base)
Substituting the value of C and using $\pi = \frac{22}{7}$:
$11 = 2 \times \frac{22}{7} \times r$
Now, we can solve for the radius, $r$:
$r = \frac{11 \times 7}{2 \times 22}$
We can simplify the fraction:
$r = \frac{\cancel{11}^1 \times 7}{2 \times \cancel{22}_2} = \frac{7}{4}$ cm.
Now that we have the radius and the height, we can find the volume of the cylinder using the formula:
$V = \pi r^2 h$
Substituting the values of $r = \frac{7}{4}$ cm and $h = 4$ cm:
$V = \frac{22}{7} \times \left(\frac{7}{4}\right)^2 \times 4$
$V = \frac{22}{7} \times \frac{7}{4} \times \frac{7}{4} \times 4$
Now we cancel the terms to simplify the calculation:
$V = \frac{22}{\cancel{7}_1} \times \frac{\cancel{7}^1}{\cancel{4}_1} \times \frac{7}{4} \times \cancel{4}^1$
$V = 22 \times \frac{7}{4}$
$V = \frac{154}{4}$
$V = 38.5$ cm3.
Final Answer:
The volume of the cylinder is 38.5 cm3.
Exercise 11.4
Question 1. Given a cylindrical tank, in which situation will you find surface area and in which situation volume.
(a) To find how much it can hold.
(b) Number of cement bags required to plaster it.
(c) To find the number of smaller tanks that can be filled with water from it.
Answer:
When dealing with a 3-dimensional object like a cylindrical tank, we consider two main measurements: surface area and volume.
Surface Area refers to the total area of the external surfaces of the object. It is measured in square units (e.g., $\text{m}^2$, $\text{cm}^2$). We calculate surface area when we are concerned with covering the outside of the object.
Volume refers to the amount of space occupied by the object, or the capacity of the object (how much it can hold). It is measured in cubic units (e.g., $\text{m}^3$, $\text{cm}^3$, litres).
Now let's analyze each situation:
(a) To find how much it can hold.
This refers to the capacity of the tank. The capacity of a container is measured by the amount of substance it can hold, which is its volume.
Therefore, to find how much a cylindrical tank can hold, we will find its volume.
(b) Number of cement bags required to plaster it.
Plastering is done on the surface of the tank (usually the inner or outer surface, or both, depending on the context). The amount of plaster needed depends on the area of the surface to be covered.
Therefore, to find the number of cement bags required to plaster the tank, we will find its surface area.
(c) To find the number of smaller tanks that can be filled with water from it.
This situation involves transferring a quantity of water from a larger tank to smaller tanks. The quantity of water is measured by volume. The total volume of water in the large tank will be distributed among the smaller tanks.
Therefore, to find the number of smaller tanks that can be filled from the larger tank, we will compare the volume of the large tank with the volume of the smaller tanks.
Summary:
- (a) To find how much it can hold: Volume
- (b) Number of cement bags required to plaster it: Surface Area
- (c) To find the number of smaller tanks that can be filled with water from it: Volume
Question 2. Diameter of cylinder A is 7 cm, and the height is 14 cm. Diameter of cylinder B is 14 cm and height is 7 cm. Without doing any calculations can you suggest whose volume is greater? Verify it by finding the volume of both the cylinders. Check whether the cylinder with greater volume also has greater surface area?
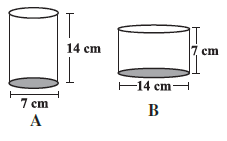
Answer:
Given:
Cylinder A: Diameter = $7 \text{ cm}$, Height, $h_A = 14 \text{ cm}$.
Cylinder B: Diameter = $14 \text{ cm}$, Height, $h_B = 7 \text{ cm}$.
Suggestion without calculations:
The volume of a cylinder is given by the formula $V = \pi r^2 h$. The radius is squared in the formula, which means a larger radius generally contributes more significantly to the volume than a larger height. Cylinder B has a much larger radius compared to Cylinder A ($r_B = 7 \text{ cm}$, $r_A = 3.5 \text{ cm}$). Although Cylinder A is taller, the effect of the larger radius in Cylinder B is likely to result in a greater volume.
Therefore, I suggest that Cylinder B has a greater volume.
Verification by calculating volumes:
First, find the radius of each cylinder.
For Cylinder A: Radius, $r_A = \frac{\text{Diameter}}{2} = \frac{7}{2} \text{ cm} = 3.5 \text{ cm}$.
For Cylinder B: Radius, $r_B = \frac{\text{Diameter}}{2} = \frac{14}{2} \text{ cm} = 7 \text{ cm}$.
Now, calculate the volume of each cylinder using the formula $V = \pi r^2 h$. Use $\pi = \frac{22}{7}$.
Volume of Cylinder A, $V_A = \pi r_A^2 h_A$
$V_A = \frac{22}{7} \times (3.5 \text{ cm})^2 \times 14 \text{ cm}$
$V_A = \frac{22}{7} \times (3.5 \times 3.5) \times 14 \text{ cm}^3$
$V_A = \frac{22}{\cancel{7}} \times 12.25 \times \cancel{14}^{2} \text{ cm}^3$
$V_A = 22 \times 12.25 \times 2 \text{ cm}^3$
$V_A = 44 \times 12.25 \text{ cm}^3$
$V_A = 539 \text{ cm}^3$.
Volume of Cylinder B, $V_B = \pi r_B^2 h_B$
$V_B = \frac{22}{7} \times (7 \text{ cm})^2 \times 7 \text{ cm}$
$V_B = \frac{22}{7} \times (7 \times 7) \times 7 \text{ cm}^3$
$V_B = \frac{22}{\cancel{7}} \times 49 \times \cancel{7}^{1} \text{ cm}^3$
$V_B = 22 \times 49 \text{ cm}^3$
$V_B = 1078 \text{ cm}^3$.
Comparing the volumes: $V_A = 539 \text{ cm}^3$ and $V_B = 1078 \text{ cm}^3$.
Since $1078 > 539$, Cylinder B has a greater volume. This verifies our initial suggestion.
Check for greater surface area:
Now, calculate the total surface area (TSA) of both cylinders using the formula TSA $= 2\pi r (r + h)$. Use $\pi = \frac{22}{7}$.
Total surface area of Cylinder A, $\text{TSA}_A = 2\pi r_A (r_A + h_A)$
$\text{TSA}_A = 2 \times \frac{22}{7} \times 3.5 \text{ cm} \times (3.5 \text{ cm} + 14 \text{ cm})$
$\text{TSA}_A = 2 \times \frac{22}{7} \times 3.5 \times (17.5) \text{ cm}^2$
$\text{TSA}_A = 2 \times 22 \times \frac{3.5 \times 17.5}{7} \text{ cm}^2$
$\text{TSA}_A = 44 \times \frac{\cancel{3.5}^{0.5} \times 17.5}{\cancel{7}_{1}} \text{ cm}^2$
$\text{TSA}_A = 44 \times (0.5 \times 17.5) \text{ cm}^2$
$\text{TSA}_A = 44 \times 8.75 \text{ cm}^2$
$\text{TSA}_A = 385 \text{ cm}^2$.
Total surface area of Cylinder B, $\text{TSA}_B = 2\pi r_B (r_B + h_B)$
$\text{TSA}_B = 2 \times \frac{22}{7} \times 7 \text{ cm} \times (7 \text{ cm} + 7 \text{ cm})$
$\text{TSA}_B = 2 \times \frac{22}{\cancel{7}} \times \cancel{7} \times (14) \text{ cm}^2$
$\text{TSA}_B = 2 \times 22 \times 14 \text{ cm}^2$
$\text{TSA}_B = 44 \times 14 \text{ cm}^2$
$\text{TSA}_B = 616 \text{ cm}^2$.
Comparing the total surface areas: $\text{TSA}_A = 385 \text{ cm}^2$ and $\text{TSA}_B = 616 \text{ cm}^2$.
Since $616 > 385$, Cylinder B has a greater surface area.
Conclusion:
Yes, the cylinder with greater volume (Cylinder B) also has greater surface area in this case.
Question 3. Find the height of a cuboid whose base area is 180 cm2 and volume is 900 cm3 ?
Answer:
To find the height of the cuboid, we can use the formula for the volume of a cuboid, which relates the volume, base area, and height.
Given:
- Base Area of the cuboid = 180 cm2
- Volume of the cuboid = 900 cm3
To Find:
The height of the cuboid.
Solution:
The formula for the volume of a cuboid is given by:
Volume = Length × Breadth × Height
We also know that the base area of a cuboid is the product of its length and breadth:
Base Area = Length × Breadth
By substituting the 'Base Area' into the volume formula, we get:
Volume = Base Area × Height
We can rearrange this formula to solve for the height:
Height = $\frac{\text{Volume}}{\text{Base Area}}$
Now, we can substitute the given values into this rearranged formula:
Volume = 900 cm3
Base Area = 180 cm2
Height = $\frac{900}{180}$
To simplify the fraction, we can cancel a zero from the numerator and the denominator:
Height = $\frac{90}{18}$
Now, we perform the division:
Height = 5 cm
Final Answer:
The height of the cuboid is 5 cm.
Question 4. A cuboid is of dimensions 60 cm × 54 cm × 30 cm. How many small cubes with side 6 cm can be placed in the given cuboid?
Answer:
Given:
Dimensions of the large cuboid:
Length ($L$) = $60 \text{ cm}$.
Breadth ($B$) = $54 \text{ cm}$.
Height ($H$) = $30 \text{ cm}$.
Side length of the small cube, $s = 6 \text{ cm}$.
To Find:
The number of small cubes that can be placed in the large cuboid.
Solution:
First, calculate the volume of the large cuboid.
Volume of cuboid = Length $\times$ Breadth $\times$ Height
Volume of large cuboid $= 60 \text{ cm} \times 54 \text{ cm} \times 30 \text{ cm}$
Volume of large cuboid $= (60 \times 54 \times 30) \text{ cm}^3$
Volume of large cuboid $= 1800 \times 54 \text{ cm}^3$
Volume of large cuboid $= 97200 \text{ cm}^3$.
Next, calculate the volume of one small cube.
Volume of cube $= (\text{side})^3$
Volume of one small cube $= (6 \text{ cm})^3$
Volume of one small cube $= 6 \times 6 \times 6 \text{ cm}^3$
Volume of one small cube $= 216 \text{ cm}^3$.
To find the number of small cubes that can be placed in the large cuboid, divide the volume of the large cuboid by the volume of one small cube.
Number of cubes $= \frac{\text{Volume of large cuboid}}{\text{Volume of one small cube}}$
Number of cubes $= \frac{97200 \text{ cm}^3}{216 \text{ cm}^3}$
Number of cubes $= \frac{97200}{216}$.
Perform the division:
$\frac{97200}{216} = 450$.
Alternatively, since the side of the small cube (6 cm) is a factor of each dimension of the cuboid (60, 54, 30), we can find how many cubes fit along each dimension:
Number of cubes along length = $\frac{60}{6} = 10$
Number of cubes along breadth = $\frac{54}{6} = 9$
Number of cubes along height = $\frac{30}{6} = 5$
Total number of cubes = (Number along length) $\times$ (Number along breadth) $\times$ (Number along height)
Total number of cubes = $10 \times 9 \times 5 = 90 \times 5 = 450$.
Both methods give the same result.
Conclusion:
$450$ small cubes with side 6 cm can be placed in the given cuboid.
Question 5. Find the height of the cylinder whose volume is 1.54 m3 and diameter of the base is 140 cm ?
Answer:
Given:
Volume of the cylinder = $1.54 \text{ m}^3$.
Diameter of the base of the cylinder = $140 \text{ cm}$.
To Find:
The height of the cylinder.
Solution:
First, ensure that all units are consistent. The volume is in cubic metres ($\text{m}^3$), and the diameter is in centimetres (cm). Convert the diameter to metres.
Diameter = $140 \text{ cm} = \frac{140}{100} \text{ m} = 1.4 \text{ m}$.
The radius of the base is half of the diameter.
Radius, $r = \frac{\text{Diameter}}{2} = \frac{1.4 \text{ m}}{2} = 0.7 \text{ m}$.
Let the height of the cylinder be $h$.
The formula for the volume of a cylinder is:
Volume $= \pi r^2 h$
Substitute the given volume and the calculated radius into the formula. Use $\pi = \frac{22}{7}$.
1.54 $\text{ m}^3 = \frac{22}{7} \times (0.7 \text{ m})^2 \times h$
... (1)
Simplify the equation:
$1.54 = \frac{22}{7} \times (0.7 \times 0.7) \times h$
$1.54 = \frac{22}{7} \times 0.49 \times h$
Cancel out the common factor of 7:
$1.54 = 22 \times \frac{\cancel{0.49}^{0.07}}{\cancel{7}_{1}} \times h$
$1.54 = 22 \times 0.07 \times h$
$1.54 = 1.54 \times h$
To find the height $h$, divide both sides by 1.54:
$h = \frac{1.54}{1.54}$
$h = 1 \text{ m}$.
The height of the cylinder is $1 \text{ m}$.
Conclusion:
The height of the cylinder is $\boxed{1 \text{ m}}$.
Question 6. A milk tank is in the form of cylinder whose radius is 1.5 m and length is 7 m. Find the quantity of milk in litres that can be stored in the tank?
Answer:
Given:
The shape of the milk tank is a cylinder.
Radius of the cylindrical tank, $r = 1.5 \text{ m}$.
Length of the cylindrical tank (Height), $h = 7 \text{ m}$.
To Find:
The quantity of milk in litres that can be stored in the tank.
Solution:
The quantity of milk that can be stored in the cylindrical tank is equal to its volume.
The formula for the volume of a cylinder is:
Volume $= \pi r^2 h$
Substitute the given values of the radius ($r = 1.5 \text{ m}$) and height ($h = 7 \text{ m}$) into the formula. Use $\pi = \frac{22}{7}$.
Volume $= \frac{22}{7} \times (1.5 \text{ m})^2 \times 7 \text{ m}$
Volume $= \frac{22}{7} \times (1.5 \times 1.5) \times 7 \text{ m}^3$
Volume $= \frac{22}{\cancel{7}} \times 2.25 \times \cancel{7}^{1} \text{ m}^3$
Volume $= 22 \times 2.25 \text{ m}^3$
Volume $= 49.5 \text{ m}^3$.
Now, we need to convert the volume from cubic metres ($\text{m}^3$) to litres.
We know the conversion factor: $1 \text{ m}^3 = 1000 \text{ litres}$.
Quantity in litres $= \text{Volume in } \text{m}^3 \times 1000$
Quantity in litres $= 49.5 \times 1000$ litres
Quantity in litres $= 49500$ litres.
Conclusion:
The quantity of milk that can be stored in the tank is $\boxed{49500 \text{ litres}}$.
Question 7. If each edge of a cube is doubled,
(i) how many times will its surface area increase?
(ii) how many times will its volume increase?
Answer:
Given:
Each edge of a cube is doubled.
To Find:
(i) How many times its surface area will increase.
(ii) How many times its volume will increase.
Solution:
Let the original edge length of the cube be $s$.
The new edge length when doubled will be $s_{new} = 2s$.
(i) Surface Area Increase:
The formula for the total surface area of a cube is $SA = 6s^2$.
Original Surface Area, $SA_{original} = 6s^2$.
New Surface Area with the doubled edge:
$SA_{new} = 6(s_{new})^2 = 6(2s)^2 = 6(4s^2)$
$SA_{new} = 24s^2$.
To find how many times the surface area increases, we divide the new surface area by the original surface area:
Increase Factor $= \frac{SA_{new}}{SA_{original}} = \frac{24s^2}{6s^2}$
Increase Factor $= \frac{24}{6} = 4$.
So, the surface area will increase by 4 times.
(ii) Volume Increase:
The formula for the volume of a cube is $V = s^3$.
Original Volume, $V_{original} = s^3$.
New Volume with the doubled edge:
$V_{new} = (s_{new})^3 = (2s)^3 = 2^3 \times s^3$
$V_{new} = 8s^3$.
To find how many times the volume increases, we divide the new volume by the original volume:
Increase Factor $= \frac{V_{new}}{V_{original}} = \frac{8s^3}{s^3}$
Increase Factor $= 8$.
So, the volume will increase by 8 times.
Conclusion:
(i) If each edge of a cube is doubled, its surface area will increase by 4 times.
(ii) If each edge of a cube is doubled, its volume will increase by 8 times.
Question 8. Water is pouring into a cubiodal reservoir at the rate of 60 litres per minute. If the volume of reservoir is 108 m3 , find the number of hours it will take to fill the reservoir.
Answer:
Given:
Rate of water pouring into the reservoir = $60$ litres per minute.
Volume of the reservoir = $108 \text{ m}^3$.
To Find:
The number of hours it will take to fill the reservoir.
Solution:
First, we need to ensure that the units of volume are consistent. The volume of the reservoir is given in cubic metres ($\text{m}^3$), while the rate is given in litres per minute. We will convert the volume of the reservoir to litres.
We know that $1 \text{ m}^3 = 1000$ litres.
Volume of reservoir in litres = Volume in $\text{m}^3 \times 1000$
Volume of reservoir = $108 \text{ m}^3 \times 1000$ litres/$\text{m}^3$
... (1)
Volume of reservoir = $108000$ litres.
The rate of water pouring is $60$ litres per minute.
The time taken to fill the reservoir is the total volume to be filled divided by the rate of pouring.
Time (in minutes) = $\frac{\text{Total Volume (in litres)}}{\text{Rate of pouring (in litres per minute)}}$
Time (in minutes) = $\frac{108000 \text{ litres}}{60 \text{ litres/minute}}$
Time (in minutes) = $\frac{108000}{60}$
Time (in minutes) = $\frac{10800}{6}$
Time (in minutes) = $1800$ minutes.
The question asks for the time in hours. We know that $1$ hour = $60$ minutes.
Time (in hours) = $\frac{\text{Time (in minutes)}}{60 \text{ minutes/hour}}$
Time (in hours) = $\frac{1800 \text{ minutes}}{60 \text{ minutes/hour}}$
Time (in hours) = $\frac{1800}{60}$
Time (in hours) = $\frac{180}{6}$
Time (in hours) = $30$ hours.
Conclusion:
It will take $\boxed{30 \text{ hours}}$ to fill the reservoir.

