| Non-Rationalised NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Exercise 5.1 | Example 1 & 2 (Before Exercise 5.2) | Exercise 5.2 |
| Example 3 (Before Exercise 5.3) | Exercise 5.3 | |
Chapter 5 Data Handling
Welcome to the solutions guide for Chapter 5: Data Handling. This chapter significantly builds upon your existing knowledge of data analysis, introducing more sophisticated techniques for organizing, visually representing, and interpreting information, as well as further exploring the concepts of chance and probability. In today's data-driven world, the ability to effectively handle and make sense of data is an increasingly vital skill. This chapter equips you with powerful tools like histograms and pie charts for visualization and refines your understanding of probability, moving beyond the basics covered in Class 7.
The first step often involves dealing with larger sets of raw data. The solutions revisit data organization, placing particular emphasis on:
- Grouping Data: For extensive datasets, grouping data into class intervals (e.g., 0-10, 10-20, 20-30) becomes essential. Solutions explain how to choose appropriate intervals and create grouped frequency distribution tables, often using tally marks (like $||||$ for 4 items or $\bcancel{||||}$ for 5) to efficiently count frequencies within each interval. This structured organization makes large amounts of data manageable and ready for analysis or representation.
Graphical representation takes center stage with the introduction of new chart types:
- Histograms: These are similar to bar graphs but are specifically used for representing continuous data or grouped data. A key difference highlighted in the solutions is that the bars in a histogram are drawn adjacent to each other, with no gaps, reflecting the continuous nature of the class intervals along the horizontal axis. Solutions provide detailed guidance on selecting suitable scales for both axes, accurately constructing the bars representing the frequency of each class interval, and interpreting the resulting graph (e.g., identifying the class interval with the highest frequency or observing the overall distribution shape).
- Pie Charts (or Circle Graphs): These are powerful tools for visualizing how a whole amount is divided into different parts or categories, representing proportions. The solutions meticulously detail the construction process:
- Calculate the proportion or percentage that each category contributes to the total.
- Determine the central angle for the sector representing each category using the formula:
$\text{Central Angle} = \left( \frac{\text{Value of the Component}}{\text{Total Value}} \right) \times 360^\circ$. - Accurately draw these sectors within a circle using a protractor.
Finally, the chapter delves deeper into Chance and Probability, building on introductory concepts:
- Key terms are revisited and clarified: random experiment (an action with uncertain outcomes), outcomes (possible results), equally likely outcomes (outcomes with the same chance of occurring), and an event (a specific outcome or collection of outcomes).
- The fundamental formula for calculating the probability of an event (E) is applied extensively:
$P(E) = \frac{\text{Number of outcomes favorable to E}}{\text{Total number of possible outcomes}}$. - Solutions tackle a variety of probability problems, commonly involving scenarios like rolling dice (e.g., probability of getting an even number, $P(\text{even}) = \frac{3}{6} = \frac{1}{2}$), tossing coins, drawing playing cards from a standard deck, or selecting items randomly from a group. Clear step-by-step calculations are provided.
By working through these detailed solutions, you will significantly enhance your data analysis toolkit, becoming proficient in organizing grouped data, constructing and interpreting histograms and pie charts, and confidently calculating basic probabilities.
Exercise 5.1
Question 1. For which of these would you use a histogram to show the data?
(a) The number of letters for different areas in a postman’s bag.
(b) The height of competitors in an athletics meet.
(c) The number of cassettes produced by 5 companies.
(d) The number of passengers boarding trains from 7:00 a.m. to 7:00 p.m. at a station.
Give reasons for each.
Answer:
A histogram is a graphical representation of the frequency distribution of continuous data or data grouped into class intervals. It uses adjacent bars to show the frequency of observations in each interval.
Based on this, the scenarios for which you would use a histogram are:
(b) The height of competitors in an athletics meet.
(d) The number of passengers boarding trains from 7:00 a.m. to 7:00 p.m. at a station.
Reasons:
(a) The number of letters for different areas in a postman’s bag:
This data represents the number of letters for distinct, discrete categories (areas). A histogram is used for continuous data or data grouped into numerical intervals. For categorical data like this, a bar graph would be more appropriate, where bars represent categories and there are gaps between bars.
(b) The height of competitors in an athletics meet:
Height is a continuous variable. The heights of competitors can be grouped into class intervals (e.g., 1.60-1.65 m, 1.65-1.70 m, etc.). The number of competitors falling into each height interval can then be represented by a histogram, where the bars are adjacent because the intervals are continuous.
(c) The number of cassettes produced by 5 companies:
This data represents the number of cassettes produced by distinct companies, which are discrete categories. Similar to option (a), this is categorical data, not suitable for a histogram. A bar graph would be appropriate here to compare production across different companies.
(d) The number of passengers boarding trains from 7:00 a.m. to 7:00 p.m. at a station:
The time period from 7:00 a.m. to 7:00 p.m. can be divided into continuous time intervals (e.g., 7:00-8:00 a.m., 8:00-9:00 a.m., etc.). The number of passengers boarding within each time interval can be grouped and represented by a histogram. This type of data, collected over sequential, continuous intervals, is suitable for a histogram.
Question 2. The shoppers who come to a departmental store are marked as: man (M), woman (W), boy (B) or girl (G). The following list gives the shoppers who came during the first hour in the morning:
| W | W | W | G | B | W | W | M | G | G |
| M | M | W | W | W | W | G | B | M | W |
| B | G | G | M | W | W | M | M | W | W |
| W | M | W | B | W | G | M | W | W | W |
| W | G | W | M | M | W | W | M | W | G |
| W | M | G | W | M | M | B | G | G | W |
Make a frequency distribution table using tally marks. Draw a bar graph to illustrate it.
Answer:
Frequency Distribution Table
To create the frequency distribution table, we go through the list of shoppers and count the occurrences of each category (W, M, B, G). We will use tally marks to keep track of the count.
The total number of shoppers is 60.
Counting each category from the given list:
- Woman (W): 28
- Man (M): 15
- Boy (B): 5
- Girl (G): 12
Total = 28 + 15 + 5 + 12 = 60.
The frequency distribution table is as follows:
| Shopper | Tally Marks | Frequency |
| Woman (W) | $\bcancel{||||}$ $\bcancel{||||}$ $\bcancel{||||}$ $\bcancel{||||}$ $\bcancel{||||}$ $|||$ | 28 |
| Man (M) | $\bcancel{||||}$ $\bcancel{||||}$ $\bcancel{||||}$ | 15 |
| Boy (B) | $\bcancel{||||}$ | 5 |
| Girl (G) | $\bcancel{||||}$ $\bcancel{||||}$ $||$ | 12 |
| Total | 60 |
Bar Graph
To illustrate the data, we can draw a bar graph. The horizontal axis (x-axis) will represent the type of shopper, and the vertical axis (y-axis) will represent the frequency (number of shoppers). The height of each bar corresponds to the frequency of that shopper type.
Question 3. The weekly wages (in ₹) of 30 workers in a factory are.
| 830 | 835 | 890 | 810 | 835 | 836 | 869 | 845 | 898 | 890 |
| 820 | 860 | 832 | 833 | 855 | 845 | 804 | 808 | 812 | 840 |
| 885 | 835 | 835 | 836 | 878 | 840 | 868 | 890 | 806 | 840 |
Using tally marks make a frequency table with intervals as 800–810, 810–820 and so on.
Answer:
Frequency Distribution Table
To create the frequency table, we will group the given data of 30 workers' weekly wages into class intervals of size 10 (e.g., 800-810, 810-820, etc.). The convention used is that the lower limit of the interval is included, and the upper limit is excluded. For example, a wage of ₹810 will be included in the 810-820 interval, not the 800-810 interval.
The frequency distribution table with tally marks is as follows:
| Class Interval (Weekly Wages in |
Tally Marks | Frequency (Number of workers) |
| 800 - 810 | $|||$ | 3 |
| 810 - 820 | $||$ | 2 |
| 820 - 830 | $|$ | 1 |
| 830 - 840 | $\bcancel{||||}$ $||||$ | 9 |
| 840 - 850 | $\bcancel{||||}$ | 5 |
| 850 - 860 | $|$ | 1 |
| 860 - 870 | $|||$ | 3 |
| 870 - 880 | $|$ | 1 |
| 880 - 890 | $|$ | 1 |
| 890 - 900 | $||||$ | 4 |
| Total | 30 |
Question 4. Draw a histogram for the frequency table made for the data in Question 3, and answer the following questions.
(i) Which group has the maximum number of workers?
(ii) How many workers earn ₹ 850 and more?
(iii) How many workers earn less than ₹ 850?
Answer:
Histogram:
A histogram for the frequency table from Question 3 is drawn below. The horizontal axis represents the weekly wages in class intervals, and the vertical axis represents the number of workers (frequency). Each bar's height corresponds to the frequency of its class interval.
Answers to the Questions:
(i) Which group has the maximum number of workers?
By observing the histogram, the tallest bar corresponds to the class interval 830–840. From the frequency table, this interval has a frequency of 9.
The group with the maximum number of workers is 830–840.
(ii) How many workers earn ₹ 850 and more?
We need to sum the frequencies for the intervals that start from 850. These are the intervals from 850–860, 860–870, 870–880, 880–890, and 890–900.
Number of workers = (Frequency of 850-860) + (Frequency of 860-870) + (Frequency of 870-880) + (Frequency of 880-890) + (Frequency of 890-900)
Number of workers = $1 + 3 + 1 + 1 + 4 = 10$.
10 workers earn ₹ 850 and more.
(iii) How many workers earn less than ₹ 850?
We need to sum the frequencies for the intervals before the 850 mark. These are the intervals 800–810, 810-820, 820-830, 830-840, and 840-850.
Number of workers = (Frequency of 800-810) + (Frequency of 810-820) + (Frequency of 820-830) + (Frequency of 830-840) + (Frequency of 840-850)
Number of workers = $3 + 2 + 1 + 9 + 5 = 20$.
20 workers earn less than ₹ 850.
Question 5. The number of hours for which students of a particular class watched television during holidays is shown through the given graph.
Answer the following.
(i) For how many hours did the maximum number of students watch TV?
(ii) How many students watched TV for less than 4 hours?
(iii) How many students spent more than 5 hours in watching TV?
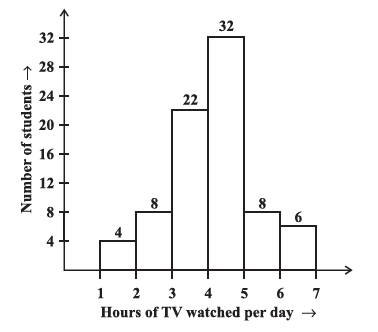
Answer:
The answers to the following questions are based on the data presented in the given histogram.
(i) For how many hours did the maximum number of students watch TV?
To find this, we look for the tallest bar in the histogram. The tallest bar represents the highest frequency of students.
The tallest bar corresponds to 32 students. Looking at the horizontal axis for this bar, it falls within the class interval of 4–5 hours.
Therefore, the maximum number of students watched TV for 4–5 hours.
(ii) How many students watched TV for less than 4 hours?
To find this, we need to add the number of students from all the class intervals that are less than 4 hours. These intervals are:
- 1–2 hours: 4 students
- 2–3 hours: 8 students
- 3–4 hours: 22 students
Total number of students who watched TV for less than 4 hours = $4 + 8 + 22 = 34$.
Therefore, 34 students watched TV for less than 4 hours.
(iii) How many students spent more than 5 hours in watching TV?
To find this, we need to add the number of students from all the class intervals that are more than 5 hours. These intervals are:
- 5–6 hours: 8 students
- 6–7 hours: 6 students
Total number of students who spent more than 5 hours watching TV = $8 + 6 = 14$.
Therefore, 14 students spent more than 5 hours watching TV.
Example 1 & 2 (Before Exercise 5.2)
Example 1: Adjoining pie chart (Fig 5.7) gives the expenditure (in percentage) on various items and savings of a family during a month.
(i) On which item, the expenditure was maximum?
(ii) Expenditure on which item is equal to the total savings of the family?
(iii) If the monthly savings of the family is ₹ 3000, what is the monthly expenditure on clothes?
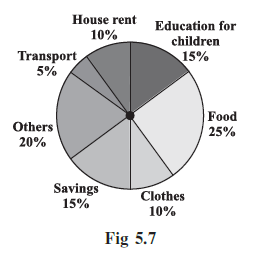
Answer:
The answers to the following questions are based on the data presented in the given pie chart.
(i) On which item, the expenditure was maximum?
To find the maximum expenditure, we need to compare the percentages of all the expenditure items shown in the pie chart.
- Food: 25%
- Education for children: 15%
- Clothes: 10%
- House rent: 10%
- Transport: 5%
- Others: 20%
The highest percentage among these is 25%, which corresponds to Food.
Therefore, the expenditure was maximum on Food.
(ii) Expenditure on which item is equal to the total savings of the family?
First, we find the percentage of total savings from the pie chart.
Total Savings = 15%.
Now, we look for an expenditure item that also has a percentage of 15%.
From the list of expenditures, we can see that the expenditure on Education for children is 15%.
Therefore, the expenditure on Education for children is equal to the total savings of the family.
(iii) If the monthly savings of the family is
From the pie chart, we know that the savings of the family represent 15% of the total monthly income.
We are given that:
15% of total monthly income =
We need to find the expenditure on clothes, which is 10% of the total monthly income.
We can find this using the unitary method:
If 15% corresponds to
$1\% = \frac{\textsf{₹} \ 3000}{15} = \textsf{₹} \ 200$
Now, we can find the value for 10% (expenditure on clothes):
$10\% = 10 \times (\text{value of } 1\%)$
$10\% = 10 \times \textsf{₹} \ 200 = \textsf{₹} \ 2000$
Therefore, the monthly expenditure on clothes is
Example 2: On a particular day, the sales (in rupees) of different items of a baker’s shop are given below.
| ordinary bread | 320 |
| fruit bread | 80 |
| cakes and pastries | 160 |
| biscuits | 120 |
| others | 40 |
| Total | 720 |
Draw a pie chart for this data.
Answer:
To draw a pie chart for the given data, we need to perform the following steps:
1. Calculate the total sales.
2. For each item, express its sales as a fraction of the total sales.
3. Calculate the central angle for each item's sector in the pie chart. The total angle of a circle is $360^\circ$, so the central angle for an item is its fraction of the total multiplied by $360^\circ$.
Central Angle for an item = $(\frac{\text{Sales of item}}{\text{Total Sales}}) \times 360^\circ$
Let's create a table to organize these calculations.
Total Sales = $320 + 80 + 160 + 120 + 40 = 720$ rupees.
Calculation Table:
| Item | Sales (in |
Fraction of Total | Central Angle |
| Ordinary bread | 320 | $\frac{320}{720} = \frac{4}{9}$ | $\frac{4}{9} \times 360^\circ = 160^\circ$ |
| Fruit bread | 80 | $\frac{80}{720} = \frac{1}{9}$ | $\frac{1}{9} \times 360^\circ = 40^\circ$ |
| Cakes and pastries | 160 | $\frac{160}{720} = \frac{2}{9}$ | $\frac{2}{9} \times 360^\circ = 80^\circ$ |
| Biscuits | 120 | $\frac{120}{720} = \frac{1}{6}$ | $\frac{1}{6} \times 360^\circ = 60^\circ$ |
| Others | 40 | $\frac{40}{720} = \frac{1}{18}$ | $\frac{1}{18} \times 360^\circ = 20^\circ$ |
| Total | 720 | 1 | $360^\circ$ |
Pie Chart Construction:
1. Draw a circle of a suitable radius.
2. Draw a horizontal radius to start.
3. Using a protractor, draw the sectors with the calculated central angles. Start with the largest angle (Ordinary bread, $160^\circ$).
4. Draw the next sector adjacent to the first one (Cakes and pastries, $80^\circ$).
5. Continue this process for all the items until the circle is completely divided.
6. Label each sector with the item it represents and its corresponding value or percentage (optional).
The resulting pie chart will look like this:
Exercise 5.2
Question 1. A survey was made to find the type of music that a certain group of young people liked in a city. Adjoining pie chart shows the findings of this survey.
From this pie chart answer the following:
(i) If 20 people liked classical music, how many young people were surveyed?
(ii) Which type of music is liked by the maximum number of people?
(iii) If a cassette company were to make 1000 CD’s, how many of each type would they make?
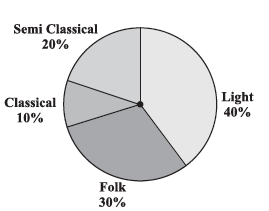
Answer:
(i) If 20 people liked classical music, how many young people were surveyed?
From the pie chart, we see that 10% of the people surveyed liked classical music.
We are given that this 10% corresponds to 20 people.
Let the total number of young people surveyed be 'x'.
Then, 10% of x = 20.
We can write this as an equation:
$\frac{10}{100} \times x = 20$
To solve for x, we can rearrange the equation:
$x = 20 \times \frac{100}{10}$
$x = 20 \times 10$
$x = 200$
Therefore, 200 young people were surveyed.
(ii) Which type of music is liked by the maximum number of people?
To find this, we look for the sector with the largest percentage in the pie chart.
- Light music: 40%
- Folk music: 30%
- Semi Classical music: 20%
- Classical music: 10%
The highest percentage is 40%, which corresponds to Light music.
Therefore, Light music is liked by the maximum number of people.
(iii) If a cassette company were to make 1000 CD’s, how many of each type would they make?
The company would likely produce CDs in proportion to the popularity of each music type. We need to calculate the number of CDs for each category based on its percentage, out of a total of 1000 CDs.
Number of Classical CDs:
10% of 1000 = $\frac{10}{100} \times 1000 = 100$ CDs.
Number of Semi Classical CDs:
20% of 1000 = $\frac{20}{100} \times 1000 = 200$ CDs.
Number of Folk CDs:
30% of 1000 = $\frac{30}{100} \times 1000 = 300$ CDs.
Number of Light music CDs:
40% of 1000 = $\frac{40}{100} \times 1000 = 400$ CDs.
Summary of CD production:
- Classical: 100 CDs
- Semi Classical: 200 CDs
- Folk: 300 CDs
- Light: 400 CDs
(Total CDs = $100 + 200 + 300 + 400 = 1000$)
Question 2. A group of 360 people were asked to vote for their favourite season from the three seasons rainy, winter and summer.
(i) Which season got the most votes?
(ii) Find the central angle of each sector.
(iii) Draw a pie chart to show this information.

Answer:
(i) Which season got the most votes?
By looking at the "No. of votes" column in the given table, we can compare the number of votes for each season:
- Summer: 90 votes
- Rainy: 120 votes
- Winter: 150 votes
The highest number of votes is 150, which was for the Winter season.
Therefore, Winter season got the most votes.
(ii) Find the central angle of each sector.
To find the central angle for each season's sector in a pie chart, we use the formula:
Central Angle = $(\frac{\text{Votes for the season}}{\text{Total number of votes}}) \times 360^\circ$
The total number of people surveyed (and thus total votes) is 360.
Let's create a table to calculate the central angle for each season.
| Season | No. of votes | Fraction of Total | Central Angle |
| Summer | 90 | $\frac{90}{360} = \frac{1}{4}$ | $\frac{1}{4} \times 360^\circ = 90^\circ$ |
| Rainy | 120 | $\frac{120}{360} = \frac{1}{3}$ | $\frac{1}{3} \times 360^\circ = 120^\circ$ |
| Winter | 150 | $\frac{150}{360} = \frac{5}{12}$ | $\frac{5}{12} \times 360^\circ = 150^\circ$ |
| Total | 360 | 1 | $360^\circ$ |
(iii) Draw a pie chart to show this information.
To draw the pie chart:
1. Draw a circle of a convenient radius.
2. Draw a radius to serve as a starting line.
3. Use a protractor to draw a sector for the Winter season with a central angle of $150^\circ$.
4. From the new line, draw an adjacent sector for the Rainy season with a central angle of $120^\circ$.
5. The remaining sector will automatically have the correct angle for the Summer season ($90^\circ$).
6. Label each sector with the name of the season.
Question 3. Draw a pie chart showing the following information. The table shows the colours preferred by a group of people.
| Colours | Number of people |
|---|---|
| Blue | 18 |
| Green | 9 |
| Red | 6 |
| Yellow | 3 |
| Total | 36 |
Find the proportion of each sector. For example, Blue is $\frac{18}{36}$ = $\frac{1}{2}$ ; Green is $\frac{9}{36}$ = $\frac{1}{4}$ and so on. Use this to find the corresponding angles.
Answer:
To draw a pie chart, we first need to calculate the central angle for each sector (colour). The central angle for a sector is calculated by finding its proportion of the total and then multiplying by $360^\circ$.
Total number of people = 36.
The formula for the central angle is:
Central Angle = $(\frac{\text{Number of people for a colour}}{\text{Total number of people}}) \times 360^\circ$
Calculation of Proportions and Central Angles:
The following table shows the calculations for each colour.
| Colours | Number of people | Proportion (Fraction) | Central Angle |
| Blue | 18 | $\frac{18}{36} = \frac{1}{2}$ | $\frac{1}{2} \times 360^\circ = 180^\circ$ |
| Green | 9 | $\frac{9}{36} = \frac{1}{4}$ | $\frac{1}{4} \times 360^\circ = 90^\circ$ |
| Red | 6 | $\frac{6}{36} = \frac{1}{6}$ | $\frac{1}{6} \times 360^\circ = 60^\circ$ |
| Yellow | 3 | $\frac{3}{36} = \frac{1}{12}$ | $\frac{1}{12} \times 360^\circ = 30^\circ$ |
| Total | 36 | 1 | $360^\circ$ |
Pie Chart Construction:
1. Draw a circle of a suitable radius.
2. Draw a horizontal diameter. The area on one side of the diameter represents the 'Blue' sector, which has a central angle of $180^\circ$.
3. From the center, use a protractor to draw the sector for 'Green' with a central angle of $90^\circ$.
4. Next, draw the sector for 'Red' with a central angle of $60^\circ$.
5. The remaining sector will be for 'Yellow', with an angle of $30^\circ$.
6. Label each sector with its corresponding colour.
Question 4. The adjoining pie chart gives the marks scored in an examination by a student in Hindi, English, Mathematics, Social Science and Science. If the total marks obtained by the students were 540, answer the following questions.
(i) In which subject did the student score 105 marks?
(Hint: for 540 marks, the central angle = 360°. So, for 105 marks, what is the central angle?)
(ii) How many more marks were obtained by the student in Mathematics than in Hindi?
(iii) Examine whether the sum of the marks obtained in Social Science and Mathematics is more than that in Science and Hindi.
(Hint: Just study the central angles).
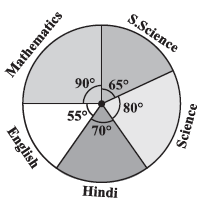
Answer:
The total marks obtained by the student are 540. The total central angle of the pie chart is $360^\circ$.
This means that 540 marks correspond to a central angle of $360^\circ$.
We can find the marks corresponding to $1^\circ$ of the central angle:
Marks per degree = $\frac{\text{Total Marks}}{\text{Total Angle}} = \frac{540}{360} = \frac{3}{2} = 1.5$ marks.
(i) In which subject did the student score 105 marks?
We are given the marks (105) and need to find the corresponding central angle to identify the subject from the pie chart.
Central Angle for 105 marks = $\frac{\text{Marks Obtained}}{\text{Total Marks}} \times 360^\circ$
Central Angle = $\frac{105}{540} \times 360^\circ$
Simplifying the fraction: $\frac{105}{540} = \frac{21}{108} = \frac{7}{36}$
Central Angle = $\frac{7}{36} \times 360^\circ = 7 \times 10^\circ = 70^\circ$
Now, we look at the pie chart to find which subject has a central angle of $70^\circ$. The subject is Hindi.
Therefore, the student scored 105 marks in Hindi.
(ii) How many more marks were obtained by the student in Mathematics than in Hindi?
First, we find the marks obtained in Mathematics and Hindi.
Marks in Hindi:
Central angle for Hindi = $70^\circ$.
Marks = $70^\circ \times 1.5$ marks/degree = 105 marks (as found in part i).
Marks in Mathematics:
Central angle for Mathematics = $90^\circ$.
Marks = $90^\circ \times 1.5$ marks/degree = 135 marks.
Difference in marks:
Difference = Marks in Mathematics - Marks in Hindi
Difference = $135 - 105 = 30$ marks.
Alternatively, we can find the difference in their central angles first:
Difference in angles = $90^\circ$ (Maths) - $70^\circ$ (Hindi) = $20^\circ$.
Difference in marks = $20^\circ \times 1.5$ marks/degree = 30 marks.
Therefore, the student obtained 30 more marks in Mathematics than in Hindi.
(iii) Examine whether the sum of the marks obtained in Social Science and Mathematics is more than that in Science and Hindi.
We can solve this by comparing the sum of the central angles for each pair of subjects. A larger sum of angles corresponds to a larger sum of marks.
Sum of angles for Social Science and Mathematics:
Angle(S.Science) + Angle(Maths) = $65^\circ + 90^\circ = 155^\circ$.
Sum of angles for Science and Hindi:
Angle(Science) + Angle(Hindi) = $80^\circ + 70^\circ = 150^\circ$.
Comparing the sums of the angles:
$155^\circ > 150^\circ$
Since the sum of the central angles for Social Science and Mathematics is greater than the sum for Science and Hindi, the sum of marks obtained in Social Science and Mathematics is also more than that in Science and Hindi.
Therefore, Yes, the sum of the marks in Social Science and Mathematics is more than in Science and Hindi.
Question 5. The number of students in a hostel, speaking different languages is given below. Display the data in a pie chart.
| Language | Hindi | English | Marathi | Tamil | Bengali | Total |
| Number of students | 40 | 12 | 9 | 7 | 4 | 72 |
Answer:
To display the given data in a pie chart, we first need to calculate the central angle for each language's sector. The central angle is found by calculating the proportion of students speaking a language out of the total and then multiplying that proportion by $360^\circ$.
Total number of students = 72.
The formula for the central angle is:
Central Angle = $(\frac{\text{Number of students for a language}}{\text{Total number of students}}) \times 360^\circ$
Calculation of Central Angles:
The following table shows the calculations for each language.
| Language | Number of students | Fraction of Total | Central Angle |
| Hindi | 40 | $\frac{40}{72} = \frac{5}{9}$ | $\frac{5}{9} \times 360^\circ = 200^\circ$ |
| English | 12 | $\frac{12}{72} = \frac{1}{6}$ | $\frac{1}{6} \times 360^\circ = 60^\circ$ |
| Marathi | 9 | $\frac{9}{72} = \frac{1}{8}$ | $\frac{1}{8} \times 360^\circ = 45^\circ$ |
| Tamil | 7 | $\frac{7}{72}$ | $\frac{7}{72} \times 360^\circ = 35^\circ$ |
| Bengali | 4 | $\frac{4}{72} = \frac{1}{18}$ | $\frac{1}{18} \times 360^\circ = 20^\circ$ |
| Total | 72 | 1 | $360^\circ$ |
Pie Chart Construction:
1. Draw a circle of a suitable radius.
2. Draw a radius to serve as a starting line.
3. Use a protractor to draw the sectors with the calculated central angles, starting with the largest angle (Hindi, $200^\circ$).
4. Draw the other sectors for English ($60^\circ$), Marathi ($45^\circ$), Tamil ($35^\circ$), and Bengali ($20^\circ$) adjacent to one another.
5. Label each sector with the corresponding language.
Example 3 (Before Exercise 5.3)
Example 3: A bag has 4 red balls and 2 yellow balls. (The balls are identical in all respects other than colour). A ball is drawn from the bag without looking into the bag. What is probability of getting a red ball? Is it more or less than getting a yellow ball?
Answer:
Given:
Number of red balls = 4
Number of yellow balls = 2
Total number of balls in the bag = Number of red balls + Number of yellow balls
Total number of balls = $4 + 2 = 6$
... (i)
We are asked to find the probability of getting a red ball and compare it with the probability of getting a yellow ball when a ball is drawn randomly from the bag.
The probability of an event is given by the formula:
$P(\text{Event}) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$
Probability of getting a red ball:
The favourable outcome is getting a red ball.
Number of favourable outcomes (getting a red ball) = Number of red balls = 4.
Total number of possible outcomes (drawing any ball) = Total number of balls = 6.
$P(\text{Red ball}) = \frac{\text{Number of red balls}}{\text{Total number of balls}}$
... (ii)
$P(\text{Red ball}) = \frac{4}{6}$
[From (ii) and Given]
$P(\text{Red ball}) = \frac{2}{3}$
Probability of getting a yellow ball:
The favourable outcome is getting a yellow ball.
Number of favourable outcomes (getting a yellow ball) = Number of yellow balls = 2.
Total number of possible outcomes (drawing any ball) = Total number of balls = 6.
$P(\text{Yellow ball}) = \frac{\text{Number of yellow balls}}{\text{Total number of balls}}$
... (iii)
$P(\text{Yellow ball}) = \frac{2}{6}$
[From (iii) and Given]
$P(\text{Yellow ball}) = \frac{1}{3}$
Comparison:
We need to compare $P(\text{Red ball}) = \frac{2}{3}$ and $P(\text{Yellow ball}) = \frac{1}{3}$.
Since $\frac{2}{3} > \frac{1}{3}$, the probability of getting a red ball is greater than the probability of getting a yellow ball.
The probability of getting a red ball is $\frac{2}{3}$.
The probability of getting a red ball is more than getting a yellow ball.
Exercise 5.3
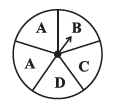
Question 1. List the outcomes you can see in these experiments.
(a) Spinning a wheel
(b) Tossing two coins together
Answer:
(a) Spinning a wheel
In this experiment, we are spinning a wheel that has a pointer. The wheel is divided into 5 sectors. The outcome of the experiment is the letter on the sector where the pointer stops.
By observing the wheel, we can see that the sectors are labeled with the letters A, B, C, and D. The letter 'A' appears in two sectors, but it represents the same outcome.
Therefore, the possible outcomes are the distinct letters on the wheel.
The list of outcomes is: A, B, C, D.
(b) Tossing two coins together
In this experiment, we are tossing two coins simultaneously. Each coin can land on either Heads (H) or Tails (T).
To list all possible outcomes, we need to consider the result of each coin for every toss. The possible combinations are:
- The first coin shows Heads (H) and the second coin shows Heads (H). Outcome: HH
- The first coin shows Heads (H) and the second coin shows Tails (T). Outcome: HT
- The first coin shows Tails (T) and the second coin shows Heads (H). Outcome: TH
- The first coin shows Tails (T) and the second coin shows Tails (T). Outcome: TT
Therefore, the complete list of possible outcomes is: HH, HT, TH, TT.
Question 2. When a die is thrown, list the outcomes of an event of getting
(i) (a) a prime number (b) not a prime number.
(ii) (a) a number greater than 5 (b) a number not greater than 5.
Answer:
When a standard six-sided die is thrown, the possible outcomes are the numbers on its faces. The set of all possible outcomes (the sample space) is $\{1, 2, 3, 4, 5, 6\}$.
(i) (a) a prime number:
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself.
From the possible outcomes $\{1, 2, 3, 4, 5, 6\}$, the prime numbers are 2, 3, and 5. (Note: 1 is not a prime number).
The outcomes of the event of getting a prime number are: 2, 3, 5.
(i) (b) not a prime number:
These are the outcomes from the sample space that are not prime numbers.
From $\{1, 2, 3, 4, 5, 6\}$, the numbers that are not prime are 1, 4, and 6.
The outcomes of the event of getting not a prime number are: 1, 4, 6.
(ii) (a) a number greater than 5:
We need to find the outcomes in $\{1, 2, 3, 4, 5, 6\}$ that are strictly greater than 5.
The only number in the set that is greater than 5 is 6.
The outcomes of the event of getting a number greater than 5 are: 6.
(ii) (b) a number not greater than 5:
These are the outcomes from the sample space that are less than or equal to 5.
From $\{1, 2, 3, 4, 5, 6\}$, the numbers that are not greater than 5 are 1, 2, 3, 4, and 5.
The outcomes of the event of getting a number not greater than 5 are: 1, 2, 3, 4, 5.
Question 3. Find the.
(a) Probability of the pointer stopping on D in (Question 1-(a))?
(b) Probability of getting an ace from a well shuffled deck of 52 playing cards?
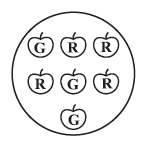
(c) Probability of getting a red apple. (See figure below)
Answer:
The probability of an event is calculated using the formula:
Probability (Event) = $\frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$
(a) Probability of the pointer stopping on D in (Question 1-(a))?
Referring to the spinning wheel from Question 1-(a), we first list the total number of possible outcomes.
The wheel is divided into 5 sectors. So, the total number of possible outcomes is 5.
Next, we find the number of favourable outcomes. A favourable outcome is the pointer stopping on the sector labeled 'D'.
By observing the wheel, we can see that there is only 1 sector labeled 'D'. So, the number of favourable outcomes is 1.
Now, we calculate the probability:
P(stopping on D) = $\frac{\text{Number of sectors with D}}{\text{Total number of sectors}} = \frac{1}{5}$
The probability of the pointer stopping on D is $\frac{1}{5}$.
(b) Probability of getting an ace from a well shuffled deck of 52 playing cards?
First, we identify the total number of possible outcomes.
A standard deck of playing cards has 52 cards. So, the total number of possible outcomes is 52.
Next, we find the number of favourable outcomes. A favourable outcome is drawing an ace.
In a standard deck, there are 4 aces (Ace of Spades, Ace of Hearts, Ace of Diamonds, and Ace of Clubs). So, the number of favourable outcomes is 4.
Now, we calculate the probability:
P(getting an ace) = $\frac{\text{Number of aces}}{\text{Total number of cards}} = \frac{4}{52}$
Simplifying the fraction:
P(getting an ace) = $\frac{1}{13}$
The probability of getting an ace is $\frac{1}{13}$.
(c) Probability of getting a red apple.
First, we count the total number of apples shown in the figure to find the total number of possible outcomes.
There are 3 green apples (G) and 4 red apples (R).
Total number of apples = 3 (Green) + 4 (Red) = 7.
So, the total number of possible outcomes is 7.
Next, we find the number of favourable outcomes. A favourable outcome is getting a red apple.
From the figure, there are 4 red apples (R). So, the number of favourable outcomes is 4.
Now, we calculate the probability:
P(getting a red apple) = $\frac{\text{Number of red apples}}{\text{Total number of apples}} = \frac{4}{7}$
The probability of getting a red apple is $\frac{4}{7}$.
Question 4. Numbers 1 to 10 are written on ten separate slips (one number on one slip), kept in a box and mixed well. One slip is chosen from the box without looking into it. What is the probability of .
(i) getting a number 6?
(ii) getting a number less than 6?
(iii) getting a number greater than 6?
(iv) getting a 1-digit number?
Answer:
Given:
Ten separate slips with numbers from 1 to 10 are kept in a box.
One slip is chosen from the box at random.
The set of all possible outcomes, or the sample space (S), is:
$S = \{1, 2, 3, 4, 5, 6, 7, 8, 9, 10\}$
The total number of possible outcomes is 10.
The probability of an event E is given by the formula:
$P(E) = \frac{\text{Number of favourable outcomes}}{\text{Total number of outcomes}}$
(i) Probability of getting a number 6
Let E be the event of getting a number 6.
The favourable outcome is the number 6 itself.
Number of favourable outcomes = 1.
Using formula (i):
$P(\text{getting a number 6}) = \frac{1}{10}$
So, the probability of getting a number 6 is $\frac{1}{10}$.
(ii) Probability of getting a number less than 6
Let E be the event of getting a number less than 6.
The numbers less than 6 in the sample space are {1, 2, 3, 4, 5}.
Number of favourable outcomes = 5.
Using formula (i):
$P(\text{getting a number less than 6}) = \frac{5}{10} = \frac{\cancel{5}^1}{\cancel{10}_2} = \frac{1}{2}$
So, the probability of getting a number less than 6 is $\frac{1}{2}$.
(iii) Probability of getting a number greater than 6
Let E be the event of getting a number greater than 6.
The numbers greater than 6 in the sample space are {7, 8, 9, 10}.
Number of favourable outcomes = 4.
Using formula (i):
$P(\text{getting a number greater than 6}) = \frac{4}{10} = \frac{\cancel{4}^2}{\cancel{10}_5} = \frac{2}{5}$
So, the probability of getting a number greater than 6 is $\frac{2}{5}$.
(iv) Probability of getting a 1-digit number
Let E be the event of getting a 1-digit number.
The 1-digit numbers in the sample space are {1, 2, 3, 4, 5, 6, 7, 8, 9}.
Number of favourable outcomes = 9.
Using formula (i):
$P(\text{getting a 1-digit number}) = \frac{9}{10}$
So, the probability of getting a 1-digit number is $\frac{9}{10}$.
Question 5. If you have a spinning wheel with 3 green sectors, 1 blue sector and 1 red sector, what is the probability of getting a green sector? What is the probability of getting a non blue sector?
Answer:
Given:
A spinning wheel has:
Number of green sectors = 3
Number of blue sectors = 1
Number of red sectors = 1
Total number of sectors = 3 + 1 + 1 = 5.
Therefore, the total number of possible outcomes is 5.
To Find:
(i) The probability of getting a green sector.
(ii) The probability of getting a non-blue sector.
Solution:
The probability of an event (E) is calculated using the formula:
$P(E) = \frac{\text{Number of favourable outcomes}}{\text{Total number of outcomes}}$
(i) Probability of getting a green sector
The event here is getting a green sector.
Number of favourable outcomes (i.e., number of green sectors) = 3.
Total number of outcomes (i.e., total number of sectors) = 5.
Using the formula (i):
$P(\text{getting a green sector}) = \frac{3}{5}$
Thus, the probability of getting a green sector is $\frac{3}{5}$.
(ii) Probability of getting a non-blue sector
A "non-blue" sector means it can be either a green sector or a red sector.
Number of favourable outcomes = (Number of green sectors) + (Number of red sectors)
Number of favourable outcomes = 3 + 1 = 4.
Total number of outcomes = 5.
Using the formula (i):
$P(\text{getting a non-blue sector}) = \frac{4}{5}$
Thus, the probability of getting a non-blue sector is $\frac{4}{5}$.
Alternate Solution for (ii):
We can also find the probability of getting a non-blue sector by using the concept of complementary events.
$P(\text{non-blue sector}) = 1 - P(\text{blue sector})$
First, let's find the probability of getting a blue sector.
Number of favourable outcomes (blue sectors) = 1.
Total number of outcomes = 5.
$P(\text{blue sector}) = \frac{1}{5}$
Now, substitute this value back into the complementary event formula:
$P(\text{non-blue sector}) = 1 - \frac{1}{5}$
$P(\text{non-blue sector}) = \frac{5}{5} - \frac{1}{5}$
$P(\text{non-blue sector}) = \frac{5-1}{5} = \frac{4}{5}$
This confirms that the probability of getting a non-blue sector is $\frac{4}{5}$.
Question 6. Find the probabilities of the events given in Question 2.
Answer:
When a die is thrown, the set of all possible outcomes, called the sample space (S), is:
$S = \{1, 2, 3, 4, 5, 6\}$
The total number of possible outcomes is 6.
The probability of any event E is calculated by the formula:
$P(E) = \frac{\text{Number of favourable outcomes}}{\text{Total number of outcomes}}$
(i) (a) Probability of getting a prime number
A prime number is a number greater than 1 that has only two factors, 1 and itself.
In the sample space {1, 2, 3, 4, 5, 6}, the prime numbers are 2, 3, and 5.
The favourable outcomes are {2, 3, 5}.
Number of favourable outcomes = 3.
Using formula (i):
$P(\text{getting a prime number}) = \frac{3}{6} = \frac{\cancel{3}^1}{\cancel{6}_2} = \frac{1}{2}$
Thus, the probability of getting a prime number is $\frac{1}{2}$.
(i) (b) Probability of getting not a prime number
The numbers in the sample space that are not prime are 1, 4, and 6.
The favourable outcomes are {1, 4, 6}.
Number of favourable outcomes = 3.
Using formula (i):
$P(\text{getting not a prime number}) = \frac{3}{6} = \frac{\cancel{3}^1}{\cancel{6}_2} = \frac{1}{2}$
Thus, the probability of getting a number that is not prime is $\frac{1}{2}$.
(ii) (a) Probability of getting a number greater than 5
In the sample space {1, 2, 3, 4, 5, 6}, the only number greater than 5 is 6.
The favourable outcome is {6}.
Number of favourable outcomes = 1.
Using formula (i):
$P(\text{getting a number greater than 5}) = \frac{1}{6}$
Thus, the probability of getting a number greater than 5 is $\frac{1}{6}$.
(ii) (b) Probability of getting a number not greater than 5
A number "not greater than 5" means the number can be 5 or less than 5.
In the sample space {1, 2, 3, 4, 5, 6}, the numbers not greater than 5 are 1, 2, 3, 4, and 5.
The favourable outcomes are {1, 2, 3, 4, 5}.
Number of favourable outcomes = 5.
Using formula (i):
$P(\text{getting a number not greater than 5}) = \frac{5}{6}$
Thus, the probability of getting a number not greater than 5 is $\frac{5}{6}$.

