| NCERT Exemplar Solutions | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
Chapter 12 Surface Areas And Volumes
Welcome to this indispensable resource offering detailed, step-by-step solutions for the Class 10 NCERT Exemplar problems focused on Surface Areas and Volumes. These Exemplar questions represent a significant leap in complexity compared to standard textbook exercises. They are specifically designed to challenge your understanding and application skills by delving into scenarios involving combinations of solids, the intricate process of conversion of solids from one shape to another, and the specific geometry of the frustum of a cone. Success with these problems often hinges on robust visualization abilities, meticulous calculation, and sophisticated geometrical reasoning.
While the foundational formulas for calculating surface areas (Lateral/Curved Surface Area - LSA/CSA, and Total Surface Area - TSA) and volumes of basic 3D shapes like cubes, cuboids, cylinders, cones, spheres, and hemispheres remain crucial, the Exemplar shifts the emphasis significantly towards more complex configurations. A major focus is on composite solids, which are formed by joining two or more basic shapes (e.g., a cylinder topped with a cone, a cube with a hemispherical depression scooped out). The solutions provided demonstrate critical strategies for tackling these:
- For Total Surface Area (TSA) of combined solids: Carefully identifying only the exposed surfaces. Internal surfaces where solids are joined are excluded from the TSA calculation.
- For Volume of combined solids: Simply summing the volumes of the individual constituent solids.
Another key area rigorously explored is the conversion of solids, typically involving melting one solid shape and recasting it into another different shape or multiple smaller shapes. The fundamental principle underpinning all such problems is the conservation of volume. The solutions consistently apply this principle, setting up equations based on $Volume_{\text{original shape}} = Volume_{\text{recast shape(s)}}$, to solve for unknown dimensions (like radius, height) or the number of smaller objects formed. This often requires careful algebraic manipulation after substituting the relevant volume formulas.
The frustum of a cone – the portion of a cone remaining after cutting off the top part with a plane parallel to the base – is a specific and important topic often emphasized in Exemplar problems. The solutions provide detailed applications of its dedicated formulas:
- Slant height: $l = \sqrt{h^2 + (r_1 - r_2)^2}$ (where $h$ is the height, $r_1$ and $r_2$ are radii of the circular bases)
- Curved Surface Area (CSA): $\text{CSA} = \pi (r_1 + r_2)l$
- Total Surface Area (TSA): $\text{TSA} = \text{CSA} + \pi r_1^2 + \pi r_2^2 = \pi l(r_1 + r_2) + \pi r_1^2 + \pi r_2^2$
- Volume: $V = \frac{1}{3}\pi h(r_1^2 + r_2^2 + r_1 r_2)$
Many Exemplar challenges manifest as intricate word problems demanding careful interpretation and multi-step solutions. Examples include calculating the capacity of buckets shaped like frustums, determining the amount of material (surface area) required for complex structures, analyzing volumes related to water flow rates (e.g., volume flowing through a pipe per unit time), comparing the capacities or surface areas of different combined shapes, or even touching upon optimization ideas implicitly. The solutions provided address all question formats (MCQs, Fill-in-the-Blanks, True/False, Short/Long Answer), offering clear diagrams, meticulous formula application, step-by-step algebraic working, careful handling of units (including conversions like $cm^3$ to litres) and $\pi$, and logical structuring, making this resource essential for mastering advanced 3D mensuration.
Sample Question 1 to 5 (Before Exercise 12.1)
Choose the correct answer from the given four options:
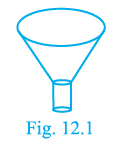
Sample Question 1: A funnel (see Fig.12.1) is the combination of
(A) a cone and a cylinder
(B) frustum of a cone and a cylinder
(C) a hemisphere and a cylinder
(D) a hemisphere and a cone
Answer:
Solution:
Upon carefully observing the shape of the funnel shown in Figure 12.1, we can identify its constituent parts.
The upper, wider part of the funnel is in the shape of a cone from which the top portion has been cut off parallel to the base. This specific geometric shape is known as a frustum of a cone.
The lower, narrower part of the funnel, which acts as the spout, is cylindrical in shape.
Therefore, the funnel is a combined solid formed by joining a frustum of a cone and a cylinder.
Comparing this observation with the given options:
- (A) a cone and a cylinder
- (B) frustum of a cone and a cylinder
- (C) a hemisphere and a cylinder
- (D) a hemisphere and a cone
Option (B) accurately describes the combination of shapes that form the funnel.
Thus, the correct answer is (B) frustum of a cone and a cylinder.
Sample Question 2: If a marble of radius 2.1 cm is put into a cylindrical cup full of water of radius 5cm and height 6 cm, then how much water flows out of the cylindrical cup?
(A) 38.8 cm3
(B) 55.4 cm3
(C) 19.4 cm3
(D) 471.4 cm3
Answer:
Solution:
When an object is fully submerged in a liquid, the volume of liquid that overflows or flows out is equal to the volume of the submerged object.
In this case, the marble is put into a cylindrical cup full of water. Assuming the marble is fully submerged (the dimensions of the cup are large enough to contain the marble completely, as $4.2 < 6$ and $4.2 < 10$), the volume of water that flows out is equal to the volume of the marble.
The marble is in the shape of a sphere with radius $r = 2.1$ cm.
The formula for the volume of a sphere is given by $V = \frac{4}{3}\pi r^3$.
Substituting the given radius $r = 2.1$ cm and using the value of $\pi \approx \frac{22}{7}$, we calculate the volume of the marble:
$V_{\text{marble}} = \frac{4}{3} \times \frac{22}{7} \times (2.1)^3$
$V_{\text{marble}} = \frac{88}{21} \times (2.1 \times 2.1 \times 2.1)$
$V_{\text{marble}} = \frac{88}{21} \times (4.41 \times 2.1)$
$V_{\text{marble}} = \frac{88}{21} \times 9.261$
$V_{\text{marble}} = \frac{88 \times 9.261}{21}$
We know that $9.261 = 2.1^3 = (21 \times 0.1)^3 = 21^3 \times 0.001$. Also, $9.261 = 21 \times 0.441$.
$V_{\text{marble}} = \frac{88}{\cancel{21}} \times \cancel{9.261}^{0.441}$ (Cancelling 21 from denominator and numerator gives $9.261 / 21 = 0.441$)
$V_{\text{marble}} = 88 \times 0.441$
Let's perform the multiplication:
$\begin{array}{cc}& & 0 & 4 & 4 & 1 \\ \times & & & & 8 & 8 \\ \hline && 3 & 5 & 2 & 8 \\ & 3 & 5 & 2 & 8 & \times \\ \hline 3 & 8 & 8 & 0 & 8 \\ \hline \end{array}$
So, $88 \times 0.441 = 38.808$.
$V_{\text{marble}} = 38.808$ cm$^3$.
The volume of water that flows out of the cylindrical cup is the volume of the marble, which is $38.808$ cm$^3$.
Comparing this value with the given options, the closest value is 38.8 cm$^3$.
Thus, the correct answer is (A) 38.8 cm$^3$.
Sample Question 3: A cubical ice cream brick of edge 22 cm is to be distributed among some children by filling ice cream cones of radius 2 cm and height 7 cm upto its brim. How many children will get the ice cream cones?
(A) 163
(B) 263
(C) 363
(D) 463
Answer:
Solution:
We are given a cubical ice cream brick and ice cream cones.
The edge length of the cubical ice cream brick is $s = 22$ cm.
The volume of the cubical brick is given by the formula $V_{\text{cube}} = s^3$.
$V_{\text{cube}} = (22 \text{ cm})^3$
$V_{\text{cube}} = 22 \times 22 \times 22 \text{ cm}^3$
$V_{\text{cube}} = 484 \times 22 \text{ cm}^3$
$V_{\text{cube}} = 10648 \text{ cm}^3$
The ice cream cones have a radius $r = 2$ cm and a height $h = 7$ cm.
The volume of a cone is given by the formula $V_{\text{cone}} = \frac{1}{3}\pi r^2 h$.
Using $\pi = \frac{22}{7}$, the volume of one ice cream cone is:
$V_{\text{cone}} = \frac{1}{3} \times \frac{22}{7} \times (2 \text{ cm})^2 \times (7 \text{ cm})$
$V_{\text{cone}} = \frac{1}{3} \times \frac{22}{\cancel{7}} \times 4 \times \cancel{7} \text{ cm}^3$
$V_{\text{cone}} = \frac{1}{3} \times 22 \times 4 \text{ cm}^3$
$V_{\text{cone}} = \frac{88}{3} \text{ cm}^3$
To find how many children will get ice cream cones, we need to divide the total volume of ice cream available (volume of the brick) by the volume of ice cream in one cone.
Number of cones = $\frac{\text{Volume of ice cream brick}}{\text{Volume of one ice cream cone}}$
Number of cones = $\frac{10648 \text{ cm}^3}{\frac{88}{3} \text{ cm}^3}$
Number of cones = $10648 \times \frac{3}{88}$
Now, we calculate the value:
Number of cones = $\frac{\cancel{10648}^{121} \times 3}{\cancel{88}^{1}}$ (Since $10648 \div 88 = 121$)
Let's show the long division for $10648 \div 88$:
$\begin{array}{r} 121\phantom{)} \\ 88{\overline{\smash{\big)}\,10648\phantom{)}}} \\ \underline{-~\phantom{(}88\downarrow\phantom{)}} \\ 184\phantom{8)} \\ \underline{-~\phantom{()}(176)\downarrow} \\ 88\phantom{)} \\ \underline{-~\phantom{()}(88)} \\ 0\phantom{)} \end{array}$
So, $10648 / 88 = 121$.
Number of cones = $121 \times 3$
Number of cones = 363
Therefore, 363 children will get the ice cream cones.
Comparing this result with the given options, we find that option (C) matches our answer.
The correct answer is (C) 363.
Sample Question 4: The radii of the ends of a frustum of a cone of height h cm are r1 cm and r2 cm. The volume in cm3 of the frustum of the cone is
(A) $\frac{1}{3}\pi$h [r12 + r22 - r1r2]
(B) $\frac{1}{3}\pi$h [r12 + r22 - r1r2]
(C) $\frac{1}{3}\pi$h [r12 - r22 + r1r2]
(D) $\frac{1}{3}\pi$h [r12 - r22 - r1r2]
Answer:
Solution:
The question asks for the formula for the volume of a frustum of a cone given its height and the radii of its ends.
Let the height of the frustum be $h$ and the radii of the two circular ends be $r_1$ and $r_2$. The formula for the volume of a frustum of a cone is a standard result in solid geometry.
The volume $V$ of the frustum of a cone is given by:
$V = \frac{1}{3}\pi h (r_1^2 + r_2^2 + r_1 r_2)$
Now, let's compare this formula with the given options:
- (A) $\frac{1}{3}\pi h [r_1^2 + r_2^2 - r_1r_2]$
- (B) $\frac{1}{3}\pi h [r_1^2 + r_2^2 + r_1r_2]$
- (C) $\frac{1}{3}\pi h [r_1^2 - r_2^2 + r_1r_2]$
- (D) $\frac{1}{3}\pi h [r_1^2 - r_2^2 - r_1r_2]$
Option (B) matches the standard formula for the volume of a frustum of a cone.
Therefore, the correct formula is $\frac{1}{3}\pi h [r_1^2 + r_2^2 + r_1r_2]$.
The correct answer is (B) $\frac{1}{3}\pi$h [r12 + r22 + r1r2].
Sample Question 5: The volume of the largest right circular cone that can be cut out from a cube of edge 4.2 cm is
(A) 9.7 cm3
(B) 77.6 cm3
(C) 58.2 cm3
(D) 19.4 cm3
Answer:
Solution:
To find the volume of the largest right circular cone that can be cut out from a cube, we need to determine the maximum possible dimensions of the cone based on the dimensions of the cube.
Let the edge of the cube be $s$. We are given that $s = 4.2$ cm.
For the cone to be the largest possible, its base must be the largest circle that can be inscribed in one face of the cube, and its height must be equal to the edge length of the cube.
The diameter of the largest circle that can be inscribed in a square face of the cube (with side $s$) is equal to the side length of the square.
So, the diameter of the base of the cone = $s = 4.2$ cm.
The radius of the base of the cone, $r$, is half of the diameter.
$r = \frac{\text{Diameter}}{2} = \frac{4.2 \text{ cm}}{2} = 2.1$ cm.
The maximum possible height of the cone, $h$, cut from the cube is limited by the dimension perpendicular to the base, which is the edge length of the cube.
$h = s = 4.2$ cm.
Now, we calculate the volume of the cone using the formula $V_{\text{cone}} = \frac{1}{3}\pi r^2 h$. We will use $\pi = \frac{22}{7}$ for this calculation.
$V_{\text{cone}} = \frac{1}{3} \times \frac{22}{7} \times (2.1 \text{ cm})^2 \times (4.2 \text{ cm})$
$V_{\text{cone}} = \frac{22}{21} \times (2.1 \times 2.1) \times 4.2$ cm$^3$
$V_{\text{cone}} = \frac{22}{21} \times 4.41 \times 4.2$ cm$^3$
We know that $4.2 = 2 \times 2.1$ and $2.1 = \frac{21}{10}$. So $4.2 = \frac{42}{10}$.
$V_{\text{cone}} = \frac{22}{21} \times (\frac{21}{10})^2 \times \frac{42}{10}$
$V_{\text{cone}} = \frac{22}{21} \times \frac{441}{100} \times \frac{42}{10}$
$V_{\text{cone}} = \frac{22}{\cancel{21}^1} \times \frac{441}{100} \times \frac{\cancel{42}^2}{10}$
$V_{\text{cone}} = 22 \times \frac{441}{100} \times \frac{2}{10}$
$V_{\text{cone}} = \frac{22 \times 441 \times 2}{1000}$
$V_{\text{cone}} = \frac{44 \times 441}{1000}$
Now let's multiply $44 \times 441$:
$\begin{array}{cc}& & 4 & 4 & 1 \\ \times & & & & 4 & 4 \\ \hline && 1 & 7 & 6 & 4 \\ & 1 & 7 & 6 & 4 & \times \\ \hline 1 & 9 & 4 & 0 & 4 \\ \hline \end{array}$
$V_{\text{cone}} = \frac{19404}{1000} = 19.404$ cm$^3$.
The volume of the largest cone that can be cut out is $19.404$ cm$^3$. We compare this with the given options:
- (A) 9.7 cm$^3$
- (B) 77.6 cm$^3$
- (C) 58.2 cm$^3$
- (D) 19.4 cm$^3$
The calculated volume $19.404$ cm$^3$ is very close to option (D) $19.4$ cm$^3$. The slight difference is likely due to rounding in the options or using $\pi \approx 22/7$.
Thus, the correct answer is (D) 19.4 cm$^3$.
Exercise 12.1
Choose the correct answer from the given four options:
Question 1. A cylindrical pencil sharpened at one edge is the combination of
(A) a cone and a cylinder
(B) frustum of a cone and a cylinder
(C) a hemisphere and a cylinder
(D) two cylinders.
Answer:
Solution:
A typical sharpened pencil has two main parts:
The main body of the pencil is cylindrical in shape. This is the part that you hold and which contains the graphite or colour core.
One end of the pencil is sharpened, forming a pointed tip. This sharpened part is conical in shape. It is essentially the part of the pencil material (wood and core) that has been removed to create a cone shape.
Therefore, a sharpened cylindrical pencil is a combination of a cylinder (the main body) and a cone (the sharpened tip).
Let's examine the given options:
- (A) a cone and a cylinder
- (B) frustum of a cone and a cylinder
- (C) a hemisphere and a cylinder
- (D) two cylinders
Option (A) matches our observation that the sharpened pencil is made up of a cone and a cylinder.
Option (B) describes a shape like a funnel, which is not a sharpened pencil.
Option (C) would mean the tip is a hemisphere, which is rounded like half a sphere, not pointed like a pencil tip.
Option (D) suggests two cylindrical parts, which does not form a sharpened point.
Thus, the correct combination is a cone and a cylinder.
The correct answer is (A) a cone and a cylinder.
Question 2. A surahi is the combination of
(A) a sphere and a cylinder
(B) a hemisphere and a cylinder
(C) two hemispheres
(D) a cylinder and a cone.
Answer:
Solution:
A surahi is a traditional Indian water pot.
Observing the typical shape of a surahi, it consists of two main parts:
The lower, wider part is usually spherical or nearly spherical in shape, designed to hold a significant volume of liquid.
The upper part is a long, narrow neck, which is cylindrical in shape, used for pouring and carrying.
Therefore, a surahi is formed by combining a sphere and a cylinder.
Let's look at the given options:
- (A) a sphere and a cylinder
- (B) a hemisphere and a cylinder
- (C) two hemispheres
- (D) a cylinder and a cone
Option (A) matches our description of the surahi's shape as a combination of a sphere and a cylinder.
Option (B) would imply the lower part is only half a sphere, which is not typical for the main body designed for volume.
Option (C) would form a complete sphere if joined at the flat surfaces, or a different shape if joined otherwise, neither of which is a surahi.
Option (D) would look like a rocket or a standing sharpened pencil, not a surahi.
Thus, the correct combination is a sphere and a cylinder.
The correct answer is (A) a sphere and a cylinder.
Question 3. A plumbline (sahul) is the combination of (see Fig. 12.2)

(A) a cone and a cylinder
(B) a hemisphere and a cone
(C) frustum of a cone and a cylinder
(D) sphere and cylinder
Answer:
Solution:
Let's examine the shape of the plumbline (sahul) shown in Figure 12.2.
The upper part of the plumbline is rounded and appears to be in the shape of a hemisphere.
The lower part of the plumbline tapers down to a point and is in the shape of a cone.
Therefore, the plumbline is a combined solid formed by joining a hemisphere and a cone.
Let's compare this observation with the given options:
- (A) a cone and a cylinder
- (B) a hemisphere and a cone
- (C) frustum of a cone and a cylinder
- (D) sphere and cylinder
Option (B) correctly describes the combination of shapes seen in the plumbline.
Thus, the correct combination is a hemisphere and a cone.
The correct answer is (B) a hemisphere and a cone.
Question 4. The shape of a glass (tumbler) (see Fig. 12.3) is usually in the form of

(A) a cone
(B) frustum of a cone
(C) a cylinder
(D) a sphere
Answer:
Solution:
We are asked to identify the shape of a glass (tumbler) as shown in Figure 12.3.
Observing the figure, the glass has a circular base and a larger circular open top. The sides are slanted, connecting the circumference of the base to the circumference of the top.
This shape is similar to a cone, but instead of tapering to a point, it has a flat, larger circular opening at the top. This is precisely the definition of a frustum of a cone, which is formed when a cone is cut by a plane parallel to its base, and the part containing the vertex is removed.
Let's compare this with the given options:
- (A) a cone - Incorrect, a cone comes to a point.
- (B) frustum of a cone - Correct, this shape matches the description.
- (C) a cylinder - Incorrect, a cylinder has parallel sides and the same radius throughout its height.
- (D) a sphere - Incorrect, a sphere is a completely round shape.
Therefore, the shape of the glass (tumbler) is usually in the form of a frustum of a cone.
The correct answer is (B) frustum of a cone.
Question 5. The shape of a gilli, in the gilli-danda game (see Fig. 12.4), is a combination of

(A) two cylinders
(B) a cone and a cylinder
(C) two cones and a cylinder
(D) two cylinders and a cone
Answer:
Solution:
We are asked to identify the shape of a gilli from the gilli-danda game as shown in Figure 12.4.
Upon observing the figure, the gilli appears to consist of three parts:
A central part which has a uniform circular cross-section along its length. This part is cylindrical in shape.
Two ends which taper to a point from the circular cross-section of the central part. These tapered ends are conical in shape.
Thus, the shape of the gilli is a combination of a cylinder in the middle and a cone at each end.
This means the gilli is a combination of two cones and a cylinder.
Let's compare this with the given options:
- (A) two cylinders - Incorrect, the ends are conical.
- (B) a cone and a cylinder - Incorrect, there are two conical ends.
- (C) two cones and a cylinder - Correct, this matches our observation.
- (D) two cylinders and a cone - Incorrect, the central part is one cylinder, and there are two cones.
Option (C) accurately describes the combination of shapes forming the gilli.
Therefore, the shape of a gilli is a combination of two cones and a cylinder.
The correct answer is (C) two cones and a cylinder.
Question 6. A shuttle cock used for playing badminton has the shape of the combination of
(A) a cylinder and a sphere
(B) a cylinder and a hemisphere
(C) a sphere and a cone
(D) frustum of a cone and a hemisphere
Answer:
Solution:
We need to identify the shapes that combine to form a badminton shuttlecock.
A typical shuttlecock consists of two main parts:
1. The base: This is the rounded part, usually made of cork or rubber. This part is in the shape of a hemisphere.
2. The skirt: This is the flared part made of feathers or synthetic material, attached to the base. The skirt tapers from a wider opening at the top down to the base. This shape is that of a cone with the top part removed parallel to the base. This geometric shape is called a frustum of a cone.
Thus, a shuttlecock is a combination of a frustum of a cone and a hemisphere.
Let's examine the given options:
- (A) a cylinder and a sphere
- (B) a cylinder and a hemisphere
- (C) a sphere and a cone
- (D) frustum of a cone and a hemisphere
Option (D) matches our analysis of the shuttlecock's shape.
Therefore, the shape of a shuttlecock is a combination of a frustum of a cone and a hemisphere.
The correct answer is (D) frustum of a cone and a hemisphere.
Question 7. A cone is cut through a plane parallel to its base and then the cone that is formed on one side of that plane is removed. The new part that is left over on the other side of the plane is called
(A) a frustum of a cone
(B) cone
(C) cylinder
(D) sphere
Answer:
Solution:
The question describes a process where a cone is cut by a plane parallel to its base. When a plane cuts a cone parallel to its base, it divides the cone into two parts: a smaller cone at the top (containing the vertex) and a shape between the cutting plane and the original base.
According to the description, the cone that is formed on one side of the plane (the smaller cone containing the vertex) is removed. The part that is left over on the other side of the plane is the remaining portion of the original cone.
This remaining part has two parallel circular bases (the original base and the circular cross-section formed by the cutting plane) and slanted sides connecting their circumferences. This geometric shape is known as a frustum of a cone.
Let's compare this with the given options:
- (A) a frustum of a cone - This matches our description of the remaining shape.
- (B) cone - Incorrect, a cone has only one base and a vertex.
- (C) cylinder - Incorrect, a cylinder has parallel sides and the same radius throughout its height.
- (D) sphere - Incorrect, a sphere is a round solid.
Option (A) accurately describes the shape that is left over.
Therefore, the new part that is left over on the other side of the plane is called a frustum of a cone.
The correct answer is (A) a frustum of a cone.
Question 8. A hollow cube of internal edge 22cm is filled with spherical marbles of diameter 0.5 cm and it is assumed that $\frac{1}{8}$ space of the cube remains unfilled. Then the number of marbles that the cube can accomodate is
(A) 142296
(B) 142396
(C) 142496
(D) 142596
Answer:
Solution:
Given:
Internal edge of the hollow cube, $s = 22$ cm.
Diameter of a spherical marble, $d = 0.5$ cm.
Radius of a spherical marble, $r = \frac{d}{2} = \frac{0.5}{2} = 0.25$ cm.
Space in the cube that remains unfilled = $\frac{1}{8}$ of the volume of the cube.
To Find:
The number of marbles that the cube can accommodate.
Calculation of Volumes:
The volume of the hollow cube is given by the formula $V_{\text{cube}} = s^3$.
$V_{\text{cube}} = (22 \text{ cm})^3$
$V_{\text{cube}} = 22 \times 22 \times 22 \text{ cm}^3$
$V_{\text{cube}} = 484 \times 22 \text{ cm}^3$
$V_{\text{cube}} = 10648 \text{ cm}^3$
The space that remains unfilled is $\frac{1}{8}$ of the cube's volume.
Unfilled Volume $= \frac{1}{8} \times V_{\text{cube}}$
Unfilled Volume $= \frac{1}{8} \times 10648 \text{ cm}^3$
Let's perform the division:
$\begin{array}{r} 1331 \\ 8{\overline{\smash{\big)}\,10648}} \\ \underline{-8\downarrow} \\ 26 \\ \underline{-24\downarrow} \\ 24 \\ \underline{-24\downarrow} \\ 08 \\ \underline{-8} \\ 0 \end{array}$
Unfilled Volume $= 1331 \text{ cm}^3$.
The volume available for the marbles is the total volume of the cube minus the unfilled space.
$V_{\text{available}} = V_{\text{cube}} - \text{Unfilled Volume}$
$V_{\text{available}} = 10648 \text{ cm}^3 - 1331 \text{ cm}^3$
$V_{\text{available}} = 9317 \text{ cm}^3$
Alternatively, the volume available for marbles is $(1 - \frac{1}{8}) = \frac{7}{8}$ of the total volume.
$V_{\text{available}} = \frac{7}{8} \times 10648 \text{ cm}^3 = 7 \times (\frac{10648}{8}) \text{ cm}^3 = 7 \times 1331 \text{ cm}^3 = 9317 \text{ cm}^3$.
The volume of one spherical marble is given by the formula $V_{\text{marble}} = \frac{4}{3}\pi r^3$.
The radius of the marble is $r = 0.25$ cm $= \frac{1}{4}$ cm.
Using the value of $\pi \approx \frac{22}{7}$, the volume of one marble is:
$V_{\text{marble}} = \frac{4}{3} \times \frac{22}{7} \times (0.25 \text{ cm})^3$
$V_{\text{marble}} = \frac{4}{3} \times \frac{22}{7} \times (\frac{1}{4})^3 \text{ cm}^3$
$V_{\text{marble}} = \frac{4}{3} \times \frac{22}{7} \times \frac{1}{64} \text{ cm}^3$
$V_{\text{marble}} = \frac{\cancel{4}^1}{3} \times \frac{22}{7} \times \frac{1}{\cancel{64}^{16}} \text{ cm}^3$
$V_{\text{marble}} = \frac{22}{3 \times 7 \times 16} \text{ cm}^3$
$V_{\text{marble}} = \frac{22}{21 \times 16} \text{ cm}^3$
$V_{\text{marble}} = \frac{22}{336} \text{ cm}^3$
Simplifying the fraction by dividing the numerator and denominator by 2:
$V_{\text{marble}} = \frac{\cancel{22}^{11}}{\cancel{336}^{168}} \text{ cm}^3 = \frac{11}{168} \text{ cm}^3$.
The number of marbles that the cube can accommodate is the ratio of the available volume to the volume of one marble.
Number of marbles $= \frac{V_{\text{available}}}{V_{\text{marble}}}$
Number of marbles $= \frac{9317 \text{ cm}^3}{\frac{11}{168} \text{ cm}^3}$
Number of marbles $= 9317 \times \frac{168}{11}$
We perform the division $9317 \div 11$.
$\begin{array}{r} 847 \\ 11{\overline{\smash{\big)}\,9317}} \\ \underline{-88\downarrow} \\ 51 \\ \underline{-44\downarrow} \\ 77 \\ \underline{-77} \\ 0 \end{array}$
So, $9317 \div 11 = 847$.
Number of marbles $= \cancel{9317}^{847} \times \frac{168}{\cancel{11}^1}$
Number of marbles $= 847 \times 168$
Now, we multiply 847 by 168:
$\begin{array}{cc}& & & 8 & 4 & 7 \\ & \times & & 1 & 6 & 8 \\ \hline &&& 6 & 7 & 7 & 6 \\ && 5 & 0 & 8 & 2 & \times \\ & 8 & 4 & 7 & \times & \times \\ \hline 1 & 4 & 2 & 2 & 9 & 6 \\ \hline \end{array}$
Number of marbles $= 142296$.
The number of marbles that the cube can accommodate is 142296.
Comparing this result with the given options, we find that option (A) matches our calculated number.
The correct answer is (A) 142296.
Question 9. A metallic spherical shell of internal and external diameters 4 cm and 8 cm, respectively is melted and recast into the form a cone of base diameter 8cm. The height of the cone is
(A) 12cm
(B) 14cm
(C) 15cm
(D) 18cm
Answer:
Solution:
Given:
A metallic spherical shell with:
Internal diameter ($D_1$) = 4 cm
External diameter ($D_2$) = 8 cm
This shell is melted and recast into a cone with:
Base diameter ($D_c$) = 8 cm
To Find:
The height of the cone ($h_c$).
Solution:
When a solid is melted and recast into another solid, the volume of the material remains the same.
First, we calculate the volume of the metallic spherical shell.
Internal radius of the shell, $r_1 = \frac{D_1}{2} = \frac{4 \text{ cm}}{2} = 2$ cm.
External radius of the shell, $r_2 = \frac{D_2}{2} = \frac{8 \text{ cm}}{2} = 4$ cm.
The volume of the spherical shell ($V_{\text{shell}}$) is the difference between the volume of the outer sphere and the volume of the inner sphere.
The formula for the volume of a sphere with radius $r$ is $\frac{4}{3}\pi r^3$.
$V_{\text{shell}} = \frac{4}{3}\pi r_2^3 - \frac{4}{3}\pi r_1^3$
$V_{\text{shell}} = \frac{4}{3}\pi (r_2^3 - r_1^3)$
$V_{\text{shell}} = \frac{4}{3}\pi (4^3 - 2^3) \text{ cm}^3$
$V_{\text{shell}} = \frac{4}{3}\pi (64 - 8) \text{ cm}^3$
$V_{\text{shell}} = \frac{4}{3}\pi (56) \text{ cm}^3$
$V_{\text{shell}} = \frac{224}{3}\pi \text{ cm}^3$
Next, we calculate the volume of the cone.
Base diameter of the cone, $D_c = 8$ cm.
Base radius of the cone, $r_c = \frac{D_c}{2} = \frac{8 \text{ cm}}{2} = 4$ cm.
Let the height of the cone be $h_c$ cm.
The formula for the volume of a cone with base radius $r_c$ and height $h_c$ is $\frac{1}{3}\pi r_c^2 h_c$.
$V_{\text{cone}} = \frac{1}{3}\pi (4)^2 h_c \text{ cm}^3$
$V_{\text{cone}} = \frac{1}{3}\pi (16) h_c \text{ cm}^3$
$V_{\text{cone}} = \frac{16}{3}\pi h_c \text{ cm}^3$
Since the metallic shell is melted and recast into the cone, their volumes are equal.
$V_{\text{shell}} = V_{\text{cone}}$
$\frac{224}{3}\pi = \frac{16}{3}\pi h_c$
Divide both sides by $\frac{16}{3}\pi$:
$h_c = \frac{\frac{224}{3}\pi}{\frac{16}{3}\pi}$
Cancel $\pi$ and $\frac{1}{3}$ from the numerator and denominator:
$h_c = \frac{224}{16}$
Now, we calculate the value of $h_c$ by dividing 224 by 16:
$h_c = \frac{\cancel{224}^{14}}{\cancel{16}^{1}}$
Let's perform the division:
$224 \div 16$
$16 \times 10 = 160$
$224 - 160 = 64$
$16 \times 4 = 64$
So, $224 = 16 \times 10 + 16 \times 4 = 16 \times (10+4) = 16 \times 14$.
$h_c = 14$ cm.
The height of the cone is 14 cm.
Comparing this result with the given options, we find that option (B) matches our calculated height.
The correct answer is (B) 14cm.
Question 10. A solid piece of iron in the form of a cuboid of dimensions 49cm × 33cm × 24cm, is moulded to form a solid sphere. The radius of the sphere is
(A) 21cm
(B) 23cm
(C) 25cm
(D) 19cm
Answer:
Solution:
Given:
Dimensions of the solid iron cuboid: length ($l$) = 49 cm, breadth ($b$) = 33 cm, height ($h$) = 24 cm.
The cuboid is melted and recast into a solid sphere.
To Find:
The radius of the sphere ($r$).
Solution:
When a solid is melted and recast into another solid, the volume of the material remains constant. Therefore, the volume of the cuboid is equal to the volume of the sphere.
The volume of the cuboid is given by the formula $V_{\text{cuboid}} = l \times b \times h$.
$V_{\text{cuboid}} = 49 \text{ cm} \times 33 \text{ cm} \times 24 \text{ cm}$
$V_{\text{cuboid}} = 38808 \text{ cm}^3$
The volume of a sphere with radius $r$ is given by the formula $V_{\text{sphere}} = \frac{4}{3}\pi r^3$.
We are given that $V_{\text{sphere}} = V_{\text{cuboid}}$.
$\frac{4}{3}\pi r^3 = 49 \times 33 \times 24$
Using the value of $\pi = \frac{22}{7}$, we have:
$\frac{4}{3} \times \frac{22}{7} \times r^3 = 49 \times 33 \times 24$
$\frac{88}{21} r^3 = 49 \times 33 \times 24$
Now, we solve for $r^3$:
$r^3 = \frac{49 \times 33 \times 24 \times 21}{88}$
Simplify the expression by cancelling out common factors:
$r^3 = \frac{49 \times \cancel{33}^{3} \times 24 \times 21}{\cancel{88}^{8}}$ (Dividing 33 by 11 and 88 by 11)
$r^3 = \frac{49 \times 3 \times \cancel{24}^{3} \times 21}{\cancel{8}^{1}}$ (Dividing 24 by 8)
$r^3 = 49 \times 3 \times 3 \times 21$
Expressing the numbers as products of their prime factors to easily find the cube root:
$49 = 7 \times 7 = 7^2$
$21 = 3 \times 7$
So, $r^3 = (7 \times 7) \times 3 \times 3 \times (3 \times 7)$
$r^3 = (7 \times 7 \times 7) \times (3 \times 3 \times 3)$
$r^3 = 7^3 \times 3^3$
$r^3 = (7 \times 3)^3$
$r^3 = 21^3$
Taking the cube root of both sides:
$r = \sqrt[3]{21^3}$
$r = 21$
The radius of the sphere is 21 cm.
Comparing this result with the given options, we find that option (A) matches our calculated radius.
The correct answer is (A) 21cm.
Question 11. A mason constructs a wall of dimensions 270cm× 300cm × 350cm with the bricks each of size 22.5cm × 11.25cm × 8.75cm and it is assumed that $\frac{1}{8}$ space is covered by the mortar. Then the number of bricks used to construct the wall is
(A) 11100
(B) 11200
(C) 11000
(D) 11300
Answer:
Solution:
Given:
Dimensions of the wall: Length ($L$) = 270 cm, Breadth ($B$) = 300 cm, Height ($H$) = 350 cm.
Dimensions of each brick: Length ($l$) = 22.5 cm, Breadth ($b$) = 11.25 cm, Height ($h$) = 8.75 cm.
Space covered by mortar = $\frac{1}{8}$ of the volume of the wall.
To Find:
The number of bricks used to construct the wall.
Solution:
First, calculate the volume of the wall:
$V_{\text{wall}} = L \times B \times H$
$V_{\text{wall}} = 270 \times 300 \times 350 \text{ cm}^3$
$V_{\text{wall}} = 28,350,000 \text{ cm}^3$
The space covered by mortar is $\frac{1}{8}$ of the wall volume.
Volume of mortar $= \frac{1}{8} \times V_{\text{wall}}$
The volume occupied by the bricks is the total volume of the wall minus the volume of the mortar.
Volume of bricks $= V_{\text{wall}} - \text{Volume of mortar}$
Volume of bricks $= V_{\text{wall}} - \frac{1}{8} V_{\text{wall}}$
Volume of bricks $= (1 - \frac{1}{8}) V_{\text{wall}}$
Volume of bricks $= \frac{7}{8} V_{\text{wall}}$
Volume of bricks $= \frac{7}{8} \times 28,350,000 \text{ cm}^3$
Volume of bricks $= 7 \times \frac{28,350,000}{8} \text{ cm}^3$
Volume of bricks $= 7 \times 3,543,750 \text{ cm}^3$
Volume of bricks $= 24,806,250 \text{ cm}^3$
Next, calculate the volume of one brick:
$V_{\text{brick}} = l \times b \times h$
$V_{\text{brick}} = 22.5 \times 11.25 \times 8.75 \text{ cm}^3$
$V_{\text{brick}} = 2204.296875 \text{ cm}^3$ (Calculating this value directly can be cumbersome and prone to errors).
Alternatively, observe the relationship between the wall dimensions and brick dimensions:
Length of wall $L = 270$ cm, Length of brick $l = 22.5$ cm. $270 / 22.5 = 12$. So, $L = 12l$.
Breadth of wall $B = 300$ cm, Breadth of brick $b = 11.25$ cm. $300 / 11.25 = 300 / (45/4) = 300 \times 4 / 45 = 1200 / 45 = 240 / 9 = 80/3$. So, $B = \frac{80}{3}b$.
Height of wall $H = 350$ cm, Height of brick $h = 8.75$ cm. $350 / 8.75 = 350 / (35/4) = 350 \times 4 / 35 = 10 \times 4 = 40$. So, $H = 40h$.
The volume of the wall can be expressed in terms of the brick dimensions:
$V_{\text{wall}} = L \times B \times H = (12l) \times (\frac{80}{3}b) \times (40h)$
$V_{\text{wall}} = (12 \times \frac{80}{3} \times 40) \times (l \times b \times h)$
$V_{\text{wall}} = (\cancel{12}^4 \times \frac{80}{\cancel{3}^1} \times 40) \times V_{\text{brick}}$
$V_{\text{wall}} = (4 \times 80 \times 40) \times V_{\text{brick}}$
$V_{\text{wall}} = (320 \times 40) \times V_{\text{brick}}$
$V_{\text{wall}} = 12800 \times V_{\text{brick}}$
The volume occupied by bricks is $\frac{7}{8}$ of the wall volume.
Volume of bricks $= \frac{7}{8} \times V_{\text{wall}}$
Volume of bricks $= \frac{7}{8} \times (12800 \times V_{\text{brick}})$
Volume of bricks $= 7 \times \frac{12800}{8} \times V_{\text{brick}}$
Volume of bricks $= 7 \times 1600 \times V_{\text{brick}}$
Volume of bricks $= 11200 \times V_{\text{brick}}$
The number of bricks is the ratio of the total volume occupied by bricks to the volume of a single brick.
Number of bricks $= \frac{\text{Volume of bricks}}{V_{\text{brick}}}$
Number of bricks $= \frac{11200 \times V_{\text{brick}}}{V_{\text{brick}}}$
Number of bricks $= 11200$
Thus, the number of bricks used to construct the wall is 11200.
Comparing this result with the given options, we find that option (B) matches our answer.
The correct answer is (B) 11200.
Question 12. Twelve solid spheres of the same size are made by melting a solid metallic cylinder of base diameter 2 cm and height 16 cm. The diameter of each sphere is
(A) 4 cm
(B) 3 cm
(C) 2 cm
(D) 6 cm
Answer:
Solution:
Given:
A solid metallic cylinder with:
Base diameter ($D_c$) = 2 cm
Height ($h_c$) = 16 cm
This cylinder is melted and recast into 12 solid spheres of the same size.
To Find:
The diameter of each sphere ($D_s$).
Solution:
When a solid is melted and recast into other solids, the total volume of the material remains constant.
First, we calculate the volume of the solid metallic cylinder.
Base radius of the cylinder, $r_c = \frac{D_c}{2} = \frac{2 \text{ cm}}{2} = 1$ cm.
The volume of the cylinder ($V_{\text{cylinder}}$) is given by the formula $V_{\text{cylinder}} = \pi r_c^2 h_c$.
$V_{\text{cylinder}} = \pi (1 \text{ cm})^2 (16 \text{ cm})$
$V_{\text{cylinder}} = \pi \times 1 \times 16 \text{ cm}^3$
$V_{\text{cylinder}} = 16\pi \text{ cm}^3$
The volume of the cylinder is melted and recast into 12 solid spheres of the same size. Let the radius of each sphere be $r_s$.
The volume of one sphere ($V_{\text{sphere}}$) is given by the formula $V_{\text{sphere}} = \frac{4}{3}\pi r_s^3$.
The total volume of the 12 spheres is equal to the volume of the cylinder.
$12 \times V_{\text{sphere}} = V_{\text{cylinder}}$
$12 \times \frac{4}{3}\pi r_s^3 = 16\pi$
Simplify the left side:
$\cancel{12}^4 \times \frac{4}{\cancel{3}^1}\pi r_s^3 = 16\pi$
$4 \times 4 \pi r_s^3 = 16\pi$
$16\pi r_s^3 = 16\pi$
Divide both sides by $16\pi$:
$\frac{16\pi r_s^3}{16\pi} = \frac{16\pi}{16\pi}$
$r_s^3 = 1$
Taking the cube root of both sides:
$r_s = \sqrt[3]{1}$
$r_s = 1$ cm.
The radius of each sphere is 1 cm. The diameter of each sphere is twice its radius.
Diameter of sphere, $D_s = 2 \times r_s$
$D_s = 2 \times 1 \text{ cm}$
$D_s = 2$ cm.
The diameter of each sphere is 2 cm.
Comparing this result with the given options, we find that option (C) matches our calculated diameter.
The correct answer is (C) 2 cm.
Question 13. The radii of the top and bottom of a bucket of slant height 45 cm are 28 cm and 7 cm, respectively. The curved surface area of the bucket is
(A) 4950 cm2
(B) 4951 cm2
(C) 4952 cm2
(D) 4953 cm2
Answer:
Solution:
Given:
Slant height of the bucket, $l = 45$ cm.
Radius of the top (larger radius), $r_1 = 28$ cm.
Radius of the bottom (smaller radius), $r_2 = 7$ cm.
To Find:
The curved surface area of the bucket.
Solution:
The shape of the bucket is a frustum of a cone.
The formula for the curved surface area (CSA) of a frustum of a cone is given by:
$CSA = \pi (r_1 + r_2) l$
Substitute the given values into the formula. We use $\pi = \frac{22}{7}$ as it is common for such problems and often leads to exact or close-to-exact integer answers when dimensions are multiples of 7.
$CSA = \frac{22}{7} \times (28 + 7) \times 45$
$CSA = \frac{22}{7} \times (35) \times 45$
Cancel out the common factor of 7:
$CSA = 22 \times \frac{\cancel{35}^{5}}{\cancel{7}^{1}} \times 45$
$CSA = 22 \times 5 \times 45$
$CSA = 110 \times 45$
Now, we perform the multiplication:
$110 \times 45 = 4950$
$\begin{array}{cc}& & 1 & 1 & 0 \\ \times & & & 4 & 5 \\ \hline && 5 & 5 & 0 \\ & 4 & 4 & 0 & \times \\ \hline 4 & 9 & 5 & 0 \\ \hline \end{array}$
$CSA = 4950$ cm$^2$.
The curved surface area of the bucket is 4950 cm$^2$.
Comparing this result with the given options, we find that option (A) matches our calculated area.
The correct answer is (A) 4950 cm$^2$.
Question 14. A medicine-capsule is in the shape of a cylinder of diameter 0.5 cm with two hemispheres stuck to each of its ends. The length of entire capsule is 2 cm. The capacity of the capsule is
(A) 0.36 cm3
(B) 0.35 cm3
(C) 0.34 cm3
(D) 0.33 cm3
Answer:
Solution:
Given:
The medicine capsule is shaped like a cylinder with two hemispheres attached to its ends.
Diameter of the cylinder and hemispheres = 0.5 cm.
Radius of the cylinder and hemispheres, $r = \frac{0.5}{2} = 0.25$ cm.
Total length of the capsule = 2 cm.
To Find:
The capacity (volume) of the capsule.
Solution:
The total length of the capsule is the sum of the height of the cylindrical part and the radii of the two hemispherical ends.
Let $h$ be the height of the cylindrical part.
Total length = Radius of hemisphere + Height of cylinder + Radius of hemisphere
$2 \text{ cm} = r + h + r$
$2 = 0.25 + h + 0.25$
$2 = 0.5 + h$
$\begin{array}{cc} & 2\ . \ 0 \\ - & 0\ . \ 5 \\ \hline & 1\ . \ 5 \\ \hline \end{array}$
$h = 2 - 0.5 = 1.5$ cm.
The capacity of the capsule is the sum of the volume of the cylindrical part and the volumes of the two hemispherical parts.
Volume of cylinder $= \pi r^2 h$
Volume of a hemisphere $= \frac{2}{3}\pi r^3$
Volume of capsule $= \text{Volume of cylinder} + 2 \times \text{Volume of hemisphere}
$V_{\text{capsule}} = \pi r^2 h + 2 \times \frac{2}{3}\pi r^3$
$V_{\text{capsule}} = \pi r^2 h + \frac{4}{3}\pi r^3$
Factor out $\pi r^2$:
$V_{\text{capsule}} = \pi r^2 (h + \frac{4}{3}r)$
Substitute the values $r = 0.25$ cm and $h = 1.5$ cm. Use $\pi = \frac{22}{7}$.
$r = 0.25 = \frac{1}{4}$
$h = 1.5 = \frac{3}{2}$
$V_{\text{capsule}} = \frac{22}{7} \times (\frac{1}{4})^2 \times (\frac{3}{2} + \frac{4}{3} \times \frac{1}{4})$
$V_{\text{capsule}} = \frac{22}{7} \times \frac{1}{16} \times (\frac{3}{2} + \frac{4}{\cancel{12}^{3}})$
$V_{\text{capsule}} = \frac{22}{7} \times \frac{1}{16} \times (\frac{3}{2} + \frac{1}{3})$
Calculate the sum inside the parenthesis:
$\frac{3}{2} + \frac{1}{3} = \frac{3 \times 3 + 1 \times 2}{6} = \frac{9 + 2}{6} = \frac{11}{6}$
$V_{\text{capsule}} = \frac{22}{7} \times \frac{1}{16} \times \frac{11}{6}$
$V_{\text{capsule}} = \frac{\cancel{22}^{11}}{7} \times \frac{1}{16} \times \frac{11}{\cancel{6}^{3}}$
$V_{\text{capsule}} = \frac{11 \times 11}{7 \times 16 \times 3}$
$V_{\text{capsule}} = \frac{121}{336}$
Now, convert the fraction to a decimal value.
$\frac{121}{336} \approx 0.35952...$
Rounding this to two decimal places gives 0.36.
The capacity of the capsule is approximately 0.36 cm$^3$.
Comparing this result with the given options, we find that option (A) matches our calculated capacity.
The correct answer is (A) 0.36 cm$^3$.
Question 15. If two solid hemispheres of same base radius r are joined together along their bases, then curved surface area of this new solid is
(A) 4πr2
(B) 6πr2
(C) 3πr2
(D) 8πr2
Answer:
Solution:
Given:
Two solid hemispheres of the same base radius $r$.
They are joined together along their bases.
To Find:
The curved surface area of the new solid formed.
Solution:
When two solid hemispheres of the same base radius $r$ are joined together along their flat circular bases, they form a complete solid sphere.
The radius of this new solid sphere is the same as the base radius of the hemispheres, which is $r$.
The surface area of the new solid (the sphere) is its curved surface area, as there are no flat surfaces remaining after joining the bases.
The formula for the curved surface area (or total surface area) of a sphere with radius $r$ is $4\pi r^2$.
Curved surface area of the new solid $= 4\pi r^2$.
Let's verify this from the components:
The curved surface area of one hemisphere is $2\pi r^2$.
When two hemispheres are joined along their bases, the two flat circular base areas ($2 \times \pi r^2$) are inside the new solid and do not contribute to the outer surface area.
The outer surface of the new solid consists only of the two curved surfaces of the original hemispheres.
Total curved surface area = Curved surface area of first hemisphere + Curved surface area of second hemisphere
Total curved surface area $= 2\pi r^2 + 2\pi r^2$
Total curved surface area $= 4\pi r^2$.
Comparing this result with the given options:
- (A) $4\pi r^2$
- (B) $6\pi r^2$
- (C) $3\pi r^2$
- (D) $8\pi r^2$
Option (A) matches the curved surface area of the resulting sphere.
The correct answer is (A) $4\pi r^2$.
Question 16. A right circular cylinder of radius r cm and height h cm (h > 2r) just encloses a sphere of diameter
(A) r cm
(B) 2r cm
(C) h cm
(D) 2h cm
Answer:
Solution:
Given:
A right circular cylinder with radius $r$ cm and height $h$ cm.
The condition $h > 2r$ is given.
The cylinder just encloses a sphere.
To Find:
The diameter of the sphere.
Solution:
When a cylinder "just encloses" a sphere, it means the sphere is the largest possible sphere that can fit inside the cylinder, and it touches the boundaries of the cylinder.
For a sphere to fit inside a right circular cylinder, its diameter must be less than or equal to both the diameter of the cylinder's base and the height of the cylinder.
Diameter of the cylinder's base = $2 \times \text{radius} = 2r$ cm.
Height of the cylinder = $h$ cm.
Let the diameter of the sphere be $D_s$. For the sphere to fit inside the cylinder, we must have:
$D_s \le 2r$
and
$D_s \le h$
For the sphere to be the *largest* possible sphere that fits inside, its diameter must be the minimum of these two dimensions:
$D_s = \min(2r, h)$
We are given that $h > 2r$.
Comparing $2r$ and $h$, since $h$ is strictly greater than $2r$, the minimum value is $2r$.
$D_s = 2r$
The largest sphere that can fit inside this cylinder has a diameter equal to $2r$ cm.
This sphere will have a diameter $2r$ (and thus a height $2r$), which is less than the cylinder's height $h$. It will touch the curved surface of the cylinder along a circle. 2r$, there will be some vertical space left above and below the sphere if it is placed centrally, but it is the largest sphere that can fit horizontally, and it does fit vertically.
Comparing this result with the given options:
- (A) r cm
- (B) 2r cm
- (C) h cm
- (D) 2h cm
Option (B) matches our calculated diameter of the sphere.
The correct answer is (B) 2r cm.
Question 17. During conversion of a solid from one shape to another, the volume of the new shape will
(A) increase
(B) decrease
(C) remain unaltered
(D) be doubled
Answer:
Solution:
When a solid is converted from one shape to another (e.g., by melting and recasting, or by moulding), the amount of material used remains the same, assuming there is no loss or addition of material during the process.
The volume of a solid represents the amount of space the material occupies. Since the quantity of the material does not change during the conversion process, the volume of the solid remains constant.
Therefore, the volume of the new shape will be equal to the volume of the original shape.
Let's consider the options:
- (A) increase - This would imply that the amount of material has increased, which is not the case in a simple conversion.
- (B) decrease - This would imply that the amount of material has decreased (e.g., due to wastage), but the standard assumption for these types of problems is conservation of volume.
- (C) remain unaltered - This is consistent with the principle of conservation of volume.
- (D) be doubled - This is incorrect; the volume should not double unless the amount of material is doubled.
Thus, during the conversion of a solid from one shape to another, the volume of the new shape remains unaltered.
The correct answer is (C) remain unaltered.
Question 18. The diameters of the two circular ends of the bucket are 44 cm and 24 cm. The height of the bucket is 35 cm. The capacity of the bucket is
(A) 32.7 litres
(B) 33.7 litres
(C) 34.7 litres
(D) 31.7 litres
Answer:
Solution:
Given:
The bucket is in the shape of a frustum of a cone.
Diameter of the top circular end ($D_1$) = 44 cm.
Diameter of the bottom circular end ($D_2$) = 24 cm.
Height of the bucket ($h$) = 35 cm.
To Find:
The capacity (volume) of the bucket in litres.
Solution:
The radii of the circular ends are:
Radius of the top end, $r_1 = \frac{D_1}{2} = \frac{44 \text{ cm}}{2} = 22$ cm.
Radius of the bottom end, $r_2 = \frac{D_2}{2} = \frac{24 \text{ cm}}{2} = 12$ cm.
The volume of a frustum of a cone (which represents the capacity of the bucket) is given by the formula:
$V = \frac{1}{3}\pi h (r_1^2 + r_2^2 + r_1 r_2)$
Substitute the given values into the formula, using $\pi = \frac{22}{7}$:
$V = \frac{1}{3} \times \frac{22}{7} \times 35 \times (22^2 + 12^2 + 22 \times 12)$
$V = \frac{22}{21} \times 35 \times (484 + 144 + 264)$
First, calculate the sum inside the parenthesis:
$484 + 144 + 264 = 628 + 264 = 892$
Now, substitute this sum back into the volume formula:
$V = \frac{22}{21} \times 35 \times 892$
We can simplify the fraction $\frac{35}{21}$ by dividing both numerator and denominator by 7:
$V = 22 \times \frac{\cancel{35}^5}{\cancel{21}^3} \times 892$
$V = \frac{22 \times 5 \times 892}{3}$
$V = \frac{110 \times 892}{3}$
Calculate $110 \times 892$:
$110 \times 892 = 98120$
$V = \frac{98120}{3}$ cm$^3$
The capacity is required in litres. We know that 1 litre = 1000 cm$^3$.
To convert cm$^3$ to litres, we divide by 1000.
Capacity in litres $= \frac{98120}{3} \div 1000$
Capacity in litres $= \frac{98120}{3 \times 1000} = \frac{98120}{3000}$
Cancel out a factor of 10 from the numerator and denominator:
Capacity in litres $= \frac{9812}{300}$
Cancel out a factor of 4 from the numerator and denominator:
$9812 \div 4 = 2453$
$300 \div 4 = 75$
Capacity in litres $= \frac{2453}{75}$ litres.
Now, perform the division to get the decimal value:
$\begin{array}{r} 32.7066... \\ 75{\overline{\smash{\big)}\,2453.0000}} \\ \underline{-225\downarrow\phantom{0000}} \\ 203\phantom{0000} \\ \underline{-150\downarrow\phantom{000}} \\ 530\phantom{000} \\ \underline{-525\downarrow\phantom{00}} \\ 50\phantom{00} \\ \underline{-0\downarrow\phantom{0}} \\ 500\phantom{0} \\ \underline{-450\downarrow} \\ 500 \\ \underline{-450} \\ 50 \end{array}$
The capacity is approximately $32.706...$ litres.
Rounding this to one decimal place, we get 32.7 litres.
The capacity of the bucket is approximately 32.7 litres.
Comparing this result with the given options, we find that option (A) matches our calculated capacity.
The correct answer is (A) 32.7 litres.
Question 19. In a right circular cone, the cross-section made by a plane parallel to the base is a
(A) circle
(B) frustum of a cone
(C) sphere
(D) hemisphere
Answer:
Solution:
We are asked to identify the shape of the cross-section formed when a right circular cone is cut by a plane parallel to its base.
Consider a right circular cone with its circular base on a horizontal plane and its vertex above the center of the base.
If we slice this cone with a plane that is also horizontal (i.e., parallel to the base), the intersection of the plane and the cone's surface will form a closed curve.
Due to the symmetry of the right circular cone and the orientation of the cutting plane (parallel to the circular base), every point on the intersection curve will be equidistant from the axis of the cone (which passes through the center of the base and the vertex).
A set of points equidistant from a central axis in a plane perpendicular to the axis forms a circle.
Therefore, the cross-section formed by a plane parallel to the base of a right circular cone is a circle.
Let's evaluate the given options:
- (A) circle - This matches our geometrical reasoning.
- (B) frustum of a cone - This is the 3D solid shape that remains after the top part (a smaller cone) is removed by the cutting plane, not the 2D cross-section itself.
- (C) sphere - A sphere is a 3D solid, not a 2D cross-section.
- (D) hemisphere - A hemisphere is a 3D solid, not a 2D cross-section.
Option (A) is the correct shape of the cross-section.
The correct answer is (A) circle.
Question 20. Volumes of two spheres are in the ratio 64:27. The ratio of their surface areas is
(A) 3 : 4
(B) 4 : 3
(C) 9 : 16
(D) 16 : 9
Answer:
Solution:
Given:
The ratio of the volumes of two spheres is 64:27.
$\frac{V_1}{V_2} = \frac{64}{27}$
To Find:
The ratio of their surface areas.
Solution:
Let the radii of the two spheres be $r_1$ and $r_2$. The volume of a sphere with radius $r$ is given by $V = \frac{4}{3}\pi r^3$.
The ratio of the volumes is:
$\frac{V_1}{V_2} = \frac{\frac{4}{3}\pi r_1^3}{\frac{4}{3}\pi r_2^3} = \frac{r_1^3}{r_2^3} = (\frac{r_1}{r_2})^3$
We are given that $\frac{V_1}{V_2} = \frac{64}{27}$.
So, $(\frac{r_1}{r_2})^3 = \frac{64}{27}$.
Taking the cube root of both sides:
$\frac{r_1}{r_2} = \sqrt[3]{\frac{64}{27}}$
$\frac{r_1}{r_2} = \frac{\sqrt[3]{64}}{\sqrt[3]{27}}$
Since $4^3 = 64$ and $3^3 = 27$, we have:
$\frac{r_1}{r_2} = \frac{4}{3}$
The surface area of a sphere with radius $r$ is given by $A = 4\pi r^2$.
The ratio of their surface areas is:
$\frac{A_1}{A_2} = \frac{4\pi r_1^2}{4\pi r_2^2} = \frac{r_1^2}{r_2^2} = (\frac{r_1}{r_2})^2$
Substitute the ratio of radii we found:
$\frac{A_1}{A_2} = (\frac{4}{3})^2$
$\frac{A_1}{A_2} = \frac{4^2}{3^2}$
$\frac{A_1}{A_2} = \frac{16}{9}$
The ratio of their surface areas is 16:9.
Comparing this result with the given options, we find that option (D) matches our calculated ratio.
The correct answer is (D) 16 : 9.
Sample Question 1 to 5 (Before Exercise 12.2)
Write ‘True’ or ‘False’ and justify your answer.
Sample Question 1: If a solid cone of base radius r and height h is placed over a solid cylinder having same base radius and height as that of the cone, then the curved surface area of the shape is $\pi r \sqrt{h^2 + r^2} + 2\pi rh$ .
Answer:
True
Justification:
The shape is formed by placing the base of the solid cone on the top face of the solid cylinder. Both the cone and the cylinder have the same base radius '$r$' and height '$h$'.
The curved surface area of this composite shape is the sum of the curved surface area of the cone and the curved surface area of the cylinder.
The curved surface area of a cone with radius '$r$' and height '$h$' is given by the formula $\pi r l$, where $l$ is the slant height. The slant height $l$ is related to the radius and height by the Pythagorean theorem: $l = \sqrt{r^2 + h^2}$.
So, the curved surface area of the cone is $\pi r \sqrt{h^2 + r^2}$.
The curved surface area of a cylinder with radius '$r$' and height '$h$' is given by the formula $2\pi r h$.
The total curved surface area of the composite shape is the sum of the curved surface area of the cone and the curved surface area of the cylinder.
Total Curved Surface Area $= (\text{Curved Surface Area of Cone}) + (\text{Curved Surface Area of Cylinder})$
Total Curved Surface Area $= \pi r \sqrt{h^2 + r^2} + 2\pi r h$.
The given statement says that the curved surface area of the shape is $\pi r \sqrt{h^2 + r^2} + 2\pi rh$.
This matches our calculated value for the curved surface area of the composite shape.
Therefore, the statement is True.
Sample Question 2: A spherical steel ball is melted to make eight new identical balls. Then, the radius of each new ball be $\frac{1}{8}$ th the radius of the original ball.
Answer:
False
Justification:
Let the radius of the original spherical ball be $R$.
The volume of the original spherical ball is given by the formula for the volume of a sphere:
$V_{original} = \frac{4}{3} \pi R^3$
Let the radius of each new identical spherical ball be $r$.
The volume of one new spherical ball is:
$V_{new} = \frac{4}{3} \pi r^3$
The original ball is melted to form eight new identical balls. This means the total volume of the eight new balls is equal to the volume of the original ball (assuming no loss of material during melting and casting).
Total volume of 8 new balls $= 8 \times V_{new} = 8 \times \frac{4}{3} \pi r^3$
By the principle of conservation of volume:
$V_{original} = \text{Total volume of 8 new balls}$
$\frac{4}{3} \pi R^3 = 8 \times \frac{4}{3} \pi r^3$
We can cancel out the common factor $\frac{4}{3} \pi$ from both sides of the equation:
$R^3 = 8 r^3$
To find the relationship between $R$ and $r$, take the cube root of both sides:
$\sqrt[3]{R^3} = \sqrt[3]{8 r^3}$
$R = \sqrt[3]{8} \times \sqrt[3]{r^3}$
$R = 2 r$
Solving for $r$, we get:
$r = \frac{R}{2}$
So, the radius of each new ball is half the radius of the original ball.
The statement claims that the radius of each new ball is $\frac{1}{8}$ th the radius of the original ball ($r = \frac{1}{8} R$). This contradicts our finding that $r = \frac{1}{2} R$.
Therefore, the statement is False.
Sample Question 3: Two identical solid cubes of side a are joined end to end. Then the total surface area of the resulting cuboid is 12a2.
Answer:
False
Justification:
When two identical solid cubes of side '$a$' are joined end to end, they form a cuboid.
Let the dimensions of the resulting cuboid be length '$l$', breadth '$b$', and height '$h$'.
The dimensions of the cuboid formed by joining two cubes of side '$a$' end to end are:
Length, $l = a + a = 2a$
Breadth, $b = a$
Height, $h = a$
The formula for the total surface area (TSA) of a cuboid is $2(lb + bh + hl)$.
Substitute the dimensions of the resulting cuboid into the formula:
TSA $= 2((2a)(a) + (a)(a) + (a)(2a))$
TSA $= 2(2a^2 + a^2 + 2a^2)$
TSA $= 2(5a^2)$
TSA $= 10a^2$
The total surface area of the resulting cuboid is $10a^2$.
The given statement claims that the total surface area is $12a^2$.
Since $10a^2 \neq 12a^2$, the statement is incorrect.
Therefore, the statement is False.
Sample Question 4: Total surface area of a lattu (top) as shown in the Fig. 12.5 is the sum of total surface area of hemisphere and the total surface area of cone.

Answer:
False
Justification:
The lattu is a composite solid formed by joining the base of a cone to the base of a hemisphere.
When the cone and the hemisphere are joined, their bases coincide and form the internal part of the composite solid. These bases are not exposed to the outside.
The total surface area of the composite lattu is the sum of the exposed surface areas of the individual components.
The exposed surface area of the cone is its curved surface area (CSA).
The exposed surface area of the hemisphere is its curved surface area (CSA).
Let $r$ be the radius of the base of the cone and also the radius of the hemisphere. Let $l$ be the slant height of the cone.
Curved Surface Area of Cone $= \pi r l$
Curved Surface Area of Hemisphere $= 2\pi r^2$
Total Surface Area of Lattu $= (\text{Curved Surface Area of Cone}) + (\text{Curved Surface Area of Hemisphere})$
Total Surface Area of Lattu $= \pi r l + 2\pi r^2$
The statement claims that the total surface area of the lattu is the sum of the total surface area (TSA) of the hemisphere and the total surface area (TSA) of the cone.
Total Surface Area of Hemisphere $= 2\pi r^2 + \pi r^2 = 3\pi r^2$ (CSA + base area)
Total Surface Area of Cone $= \pi r l + \pi r^2$ (CSA + base area)
Sum of TSA of Hemisphere and TSA of Cone $= (3\pi r^2) + (\pi r l + \pi r^2) = 4\pi r^2 + \pi r l$
Comparing the correct total surface area of the lattu ($\pi r l + 2\pi r^2$) with the sum mentioned in the statement ($4\pi r^2 + \pi r l$), we see that they are not equal.
The statement incorrectly includes the areas of the joined bases, which are hidden inside the composite solid.
Therefore, the statement is False.
Sample Question 5: Actual capacity of a vessel as shown in the Fig. 12.6 is equal to the difference of volume of the cylinder and volume of the hemisphere.

Answer:
True
Justification:
The image shows a vessel which is essentially a cylinder with a hemispherical portion removed from the bottom.
The capacity of the vessel refers to the volume of liquid it can hold. This volume is the space enclosed by the vessel's inner surface.
Let the radius of the cylindrical part and the hemisphere be '$r$' and the height of the cylindrical part be '$h$'.
The shape of the vessel can be visualized as a complete cylinder from which a hemisphere of the same radius has been scooped out from the bottom.
The volume of the complete cylinder is given by:
$V_{cylinder} = \pi r^2 h$
The volume of the hemisphere removed from the bottom is given by:
$V_{hemisphere} = \frac{2}{3} \pi r^3$
The actual capacity of the vessel is the volume of the cylinder minus the volume of the removed hemispherical part.
Capacity of Vessel $= V_{cylinder} - V_{hemisphere}$
Capacity of Vessel $= \pi r^2 h - \frac{2}{3} \pi r^3$
The statement says that the actual capacity is equal to the difference of volume of the cylinder and volume of the hemisphere. This is exactly what we found.
Therefore, the statement is True.
Exercise 12.2
Write ‘True’ or ‘False’ and justify your answer in the following:
Question 1. Two identical solid hemispheres of equal base radius r cm are stuck together along their bases. The total surface area of the combination is 6πr2 .
Answer:
False
Justification:
When two identical solid hemispheres of equal base radius '$r$' are stuck together along their bases, the resulting solid is a sphere.
The radius of this resulting sphere is equal to the base radius of the hemispheres, which is '$r$'.
The total surface area of a solid sphere with radius '$r$' is given by the formula $4\pi r^2$.
When the two hemispheres are joined, their circular bases of radius '$r$' become internal surfaces and are not part of the total external surface area of the combined solid.
The total surface area of the combination is the sum of the curved surface areas of the two hemispheres.
Curved Surface Area of one hemisphere $= 2\pi r^2$
Total Surface Area of combination $= (\text{CSA of first hemisphere}) + (\text{CSA of second hemisphere})$
Total Surface Area of combination $= 2\pi r^2 + 2\pi r^2 = 4\pi r^2$
The statement claims that the total surface area of the combination is $6\pi r^2$.
Since the correct total surface area is $4\pi r^2$ and $4\pi r^2 \neq 6\pi r^2$, the statement is incorrect.
Therefore, the statement is False.
Question 2. A solid cylinder of radius r and height h is placed over other cylinder of same height and radius. The total surface area of the shape so formed is 4πrh + 4πr2 .
Answer:
False
Justification:
When a solid cylinder of radius '$r$' and height '$h$' is placed over another identical solid cylinder of the same radius and height, the resulting shape is a single composite cylinder.
The dimensions of this composite cylinder are:
Radius = $r$
Height = $h + h = 2h$
The total surface area (TSA) of a solid cylinder with radius $R$ and height $H$ is given by the formula: $TSA = 2\pi R H + 2\pi R^2$ (Curved Surface Area + Area of two bases).
For the composite cylinder, the radius is $r$ and the height is $2h$. Substituting these values into the formula:
TSA $= 2\pi (r) (2h) + 2\pi (r)^2$
TSA $= 4\pi rh + 2\pi r^2$
When the two cylinders are stacked, the top base of the lower cylinder and the bottom base of the upper cylinder are joined together and are no longer part of the exposed total surface area. Only the curved surfaces of both cylinders, the bottom base of the lower cylinder, and the top base of the upper cylinder contribute to the total surface area of the resulting solid.
TSA $= (\text{CSA of first cylinder}) + (\text{CSA of second cylinder}) + (\text{Area of bottom base}) + (\text{Area of top base})$
TSA $= (2\pi r h) + (2\pi r h) + (\pi r^2) + (\pi r^2)$
TSA $= 4\pi rh + 2\pi r^2$
The statement claims that the total surface area of the shape so formed is $4\pi rh + 4\pi r^2$.
Our calculated total surface area is $4\pi rh + 2\pi r^2$.
Since $4\pi rh + 2\pi r^2 \neq 4\pi rh + 4\pi r^2$, the statement is incorrect.
Therefore, the statement is False.
Question 3. A solid cone of radius r and height h is placed over a solid cylinder having same base radius and height as that of a cone. The total surface area of the combined solid is $\pi r \left[ \sqrt{r^2 + h^2} + 3r + 2h \right]$ .
Answer:
False
Justification:
The composite solid is formed by placing a solid cone on the top face of a solid cylinder. Both have the same base radius '$r$' and height '$h$'.
The total surface area of the combined solid is the sum of the exposed surface areas of the individual solids.
The exposed surfaces are:
1. The curved surface area of the cone.
2. The curved surface area of the cylinder.
3. The base area of the cylinder (which is at the bottom).
The base of the cone and the top base of the cylinder are joined together and are internal to the composite solid, so they do not contribute to the total surface area.
Let $l$ be the slant height of the cone. The formula for the slant height is $l = \sqrt{r^2 + h^2}$.
Curved Surface Area of Cone $= \pi r l = \pi r \sqrt{r^2 + h^2}$
Curved Surface Area of Cylinder $= 2\pi r h$
Base Area of Cylinder (bottom) $= \pi r^2$
Total Surface Area of Combined Solid $= (\text{CSA of Cone}) + (\text{CSA of Cylinder}) + (\text{Base Area of Cylinder})$
Total Surface Area $= \pi r \sqrt{r^2 + h^2} + 2\pi r h + \pi r^2$
We can factor out $\pi r$ from the expression:
Total Surface Area $= \pi r \left( \sqrt{r^2 + h^2} + 2h + r \right)$
Total Surface Area $= \pi r \left[ \sqrt{r^2 + h^2} + r + 2h \right]$
The given statement claims the total surface area is $\pi r \left[ \sqrt{r^2 + h^2} + 3r + 2h \right]$.
Comparing our result $\pi r \left[ \sqrt{r^2 + h^2} + r + 2h \right]$ with the given expression $\pi r \left[ \sqrt{r^2 + h^2} + 3r + 2h \right]$, we see that they are different because $r \neq 3r$ (for $r \neq 0$).
Therefore, the statement is False.
Question 4. A solid ball is exactly fitted inside the cubical box of side a. The volume of the ball is $\frac{4}{3}$πa3
Answer:
False
Justification:
When a solid ball is exactly fitted inside a cubical box of side '$a$', it means the diameter of the ball is equal to the side length of the cube.
Side of the cubical box = $a$
Diameter of the ball = $a$
Radius of the ball, $r = \frac{\text{Diameter}}{2} = \frac{a}{2}$.
The volume of a solid sphere (ball) with radius '$r$' is given by the formula:
$V = \frac{4}{3}\pi r^3$
Substitute the value of the radius $r = \frac{a}{2}$ into the volume formula:
$V = \frac{4}{3}\pi \left(\frac{a}{2}\right)^3$
$V = \frac{4}{3}\pi \left(\frac{a^3}{2^3}\right)$
$V = \frac{4}{3}\pi \left(\frac{a^3}{8}\right)$
$V = \frac{4\pi a^3}{24}$
$V = \frac{1}{6}\pi a^3$
The actual volume of the ball is $\frac{1}{6}\pi a^3$.
The given statement claims the volume of the ball is $\frac{4}{3}\pi a^3$.
Since $\frac{1}{6}\pi a^3 \neq \frac{4}{3}\pi a^3$, the statement is incorrect.
Therefore, the statement is False.
Question 5. The volume of the frustum of a cone is $\frac{1}{3}$πh[r12 + r22 - r1r2] where h is vertical height of the frustum and r1 , r2 are the radii of the ends.
Answer:
False
Justification:
The formula for the volume of a frustum of a cone with vertical height '$h$' and radii of the ends '$r_1$' and '$r_2$' is given by:
$V = \frac{1}{3}\pi h(r_1^2 + r_2^2 + r_1r_2)$
The given formula for the volume of the frustum is:
$V_{given} = \frac{1}{3}\pi h[r_1^2 + r_2^2 - r_1r_2]$
Comparing the correct formula with the given formula, we see that the term inside the bracket is different ($+ r_1r_2$ in the correct formula vs. $- r_1r_2$ in the given formula).
Since the given formula is not the correct formula for the volume of a frustum of a cone, the statement is incorrect.
Therefore, the statement is False.
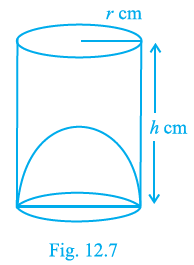
Question 6. The capacity of a cylindrical vessel with a hemispherical portion raised upward at the bottom as shown in the Fig. 12.7 is $\frac{\pi r^2}{3}\left[ 3h - 2r \right]$ .
Answer:
True
Justification:
The vessel is in the shape of a cylinder with a hemispherical portion projecting inwards from the bottom base. The radius of the cylinder is '$r$' and its height is '$h$'. The hemispherical portion has the same radius '$r$'.
The capacity of the vessel is the volume of liquid it can hold. This is equivalent to the volume of the cylinder minus the volume of the hemispherical portion that occupies space inside the cylinder.
The volume of the cylinder with radius '$r$' and height '$h$' is given by:
$V_{cylinder} = \pi r^2 h$
The volume of the hemispherical portion with radius '$r$' is given by:
$V_{hemisphere} = \frac{2}{3}\pi r^3$
The capacity of the vessel is the difference between the volume of the cylinder and the volume of the hemisphere:
Capacity $= V_{cylinder} - V_{hemisphere}$
Capacity $= \pi r^2 h - \frac{2}{3}\pi r^3$
We can factor out common terms $\pi r^2$ from the expression:
Capacity $= \pi r^2 \left( h - \frac{2}{3}r \right)$
To match the given format, we can find a common denominator inside the bracket:
Capacity $= \pi r^2 \left( \frac{3h - 2r}{3} \right)$
Capacity $= \frac{\pi r^2}{3} (3h - 2r)$
Capacity $= \frac{\pi r^2}{3} [3h - 2r]$
This calculated capacity matches the expression given in the statement.
Therefore, the statement is True.
Question 7. The curved surface area of a frustum of a cone is πl(r1 + r2), where $l = \sqrt{h^{2} + (r_{1} + r_{2})^2}$ , r1 and r2 are the radii of the two nds of the frustum and h is the vertical height.
Answer:
False
Justification:
The curved surface area (CSA) of a frustum of a cone with slant height '$l$' and radii of the two ends '$r_1$' and '$r_2$' is indeed given by the formula:
CSA $= \pi l (r_1 + r_2)$
However, the statement provides an incorrect formula for the slant height '$l$'.
Let '$h$' be the vertical height of the frustum. The correct formula for the slant height '$l$' of a frustum is given by the Pythagorean theorem applied to the right triangle formed by the height '$h$', the difference in radii $|r_1 - r_2|$, and the slant height '$l$'.
The correct formula for the slant height is:
$l = \sqrt{h^2 + (r_1 - r_2)^2}$
The statement gives the formula for the slant height as:
$l_{given} = \sqrt{h^2 + (r_1 + r_2)^2}$
Comparing the correct formula $l = \sqrt{h^2 + (r_1 - r_2)^2}$ with the given formula $l_{given} = \sqrt{h^2 + (r_1 + r_2)^2}$, we see that they are different.
Since the formula for the slant height '$l$' provided in the statement is incorrect, the entire statement is false, even though the form $\pi l (r_1 + r_2)$ for CSA is correct with the proper $l$.
Therefore, the statement is False.
Question 8. An open metallic bucket is in the shape of a frustum of a cone, mounted on a hollow cylindrical base made of the same metallic sheet. The surface area of the metallic sheet used is equal to curved surface area of frustum of a cone + area of circular base + curved surface area of cylinder
Answer:
True
Justification:
The structure is formed by a frustum of a cone placed on a hollow cylindrical base. The frustum is open at the top (the larger base) as it is a bucket.
The metallic sheet used to make this bucket comprises the following parts:
1. The curved surface area of the frustum of the cone (the side of the bucket).
2. The curved surface area of the hollow cylinder (the side of the base).
3. The area of the bottom circular base of the cylinder.
The top of the frustum is open, so its area is not included in the metallic sheet used.
The smaller base of the frustum is joined to the top of the hollow cylinder, so this area is internal and not part of the outer surface area of the metallic sheet.
The top of the hollow cylinder is where the frustum is mounted, and since the cylinder is hollow, its top edge is joined to the frustum's base and does not contribute a full circular area to the outer surface.
Therefore, the total surface area of the metallic sheet used is the sum of the exposed surfaces:
Total Surface Area of sheet = (Curved Surface Area of Frustum) + (Curved Surface Area of Cylinder) + (Area of the base of the Cylinder)
The statement says the surface area of the metallic sheet used is equal to curved surface area of frustum of a cone + area of circular base + curved surface area of cylinder.
Assuming "area of circular base" refers to the base of the cylinder (as it's the only full base exposed), the statement correctly identifies the components of the total surface area of the metallic sheet used for the open bucket with a hollow cylindrical base.
Thus, the statement is consistent with the construction of such a bucket.
Therefore, the statement is True.
Sample Question 1 to 5 (Before Exercise 12.3)
Sample Question 1: A cone of maximum size is carved out from a cube of edge 14 cm. Find the surface area of the cone and of the remaining solid left out after the cone carved out
Answer:
Given:
Edge of the cube, $a = 14$ cm.
To Find:
1. Surface area of the cone of maximum size carved out from the cube.
2. Surface area of the remaining solid.
Solution:
For a cone of maximum size to be carved out from a cube of edge '$a$', the diameter of the base of the cone must be equal to the edge of the cube, and the height of the cone must be equal to the edge of the cube.
So, the dimensions of the cone are:
Diameter of base $= a = 14$ cm
Radius of base, $r = \frac{\text{Diameter}}{2} = \frac{14}{2} = 7$ cm
Height of cone, $h = a = 14$ cm
To find the surface area of the cone, we need the slant height '$l$'. The slant height is given by the formula $l = \sqrt{r^2 + h^2}$.
$l = \sqrt{(7)^2 + (14)^2}$
$l = \sqrt{49 + 196}$
$l = \sqrt{245}$
$l = \sqrt{49 \times 5}$
$l = 7\sqrt{5}$ cm
The surface area of the cone (assuming it's a solid cone, this refers to the total surface area) is given by the formula $\pi r (r+l)$ or Curved Surface Area + Base Area.
Curved Surface Area (CSA) of cone $= \pi r l$
CSA $= \pi (7)(7\sqrt{5})$
CSA $= 49\pi\sqrt{5}$ cm$^2$
Base Area of cone $= \pi r^2$
Base Area $= \pi (7)^2$
Base Area $= 49\pi$ cm$^2$
Total Surface Area (TSA) of cone $= \text{CSA} + \text{Base Area}$
TSA of cone $= 49\pi\sqrt{5} + 49\pi$
TSA of cone $= 49\pi (\sqrt{5} + 1)$ cm$^2$
Now, let's find the surface area of the remaining solid.
The remaining solid consists of:
1. Five faces of the cube which are untouched.
2. The base face of the cube from which the cone's base area is removed.
3. The curved surface area of the cone (which is newly exposed).
Area of 5 faces of the cube $= 5 \times a^2 = 5 \times (14)^2 = 5 \times 196 = 980$ cm$^2$
Area of the base face of the cube excluding the cone base $= (\text{Area of cube face}) - (\text{Area of cone base})$
Area $= a^2 - \pi r^2 = (14)^2 - \pi (7)^2 = 196 - 49\pi$ cm$^2$
Curved Surface Area of the cone $= 49\pi\sqrt{5}$ cm$^2$ (calculated earlier)
Total Surface Area of the remaining solid $= (\text{Area of 5 faces}) + (\text{Area of base face excluding cone base}) + (\text{CSA of cone})$
TSA of remaining solid $= 980 + (196 - 49\pi) + 49\pi\sqrt{5}$
TSA of remaining solid $= 980 + 196 - 49\pi + 49\pi\sqrt{5}$
TSA of remaining solid $= 1176 - 49\pi + 49\pi\sqrt{5}$
TSA of remaining solid $= 1176 + 49\pi(\sqrt{5} - 1)$ cm$^2$
The surface area of the cone is $49\pi (\sqrt{5} + 1)$ cm$^2$.
The surface area of the remaining solid is $1176 + 49\pi(\sqrt{5} - 1)$ cm$^2$.
Sample Question 2: A solid metallic sphere of radius 10.5 cm is melted and recast into a number of smaller cones, each of radius 3.5 cm and height 3 cm. Find the number of cones so formed.
Answer:
Given:
Radius of the solid metallic sphere, $R = 10.5$ cm.
Radius of each smaller cone, $r = 3.5$ cm.
Height of each smaller cone, $h = 3$ cm.
To Find:
The number of smaller cones formed by melting and recasting the sphere.
Solution:
When a solid is melted and recast into other solids, the total volume remains conserved.
Volume of the solid metallic sphere is given by the formula $V_{sphere} = \frac{4}{3}\pi R^3$.
Substituting the given radius $R = 10.5 = \frac{21}{2}$ cm:
$V_{sphere} = \frac{4}{3} \pi \left(10.5\right)^3$
$V_{sphere} = \frac{4}{3} \pi \left(\frac{21}{2}\right)^3$
$V_{sphere} = \frac{4}{3} \pi \times \frac{21 \times 21 \times 21}{2 \times 2 \times 2}$
$V_{sphere} = \frac{4}{3} \pi \times \frac{9261}{8}$
$V_{sphere} = \frac{\pi \times 4 \times 9261}{3 \times 8}$
$V_{sphere} = \frac{\pi \times 9261}{3 \times 2}$
$V_{sphere} = \frac{3087\pi}{2}$ cm$^3$
Volume of one smaller cone is given by the formula $V_{cone} = \frac{1}{3}\pi r^2 h$.
Substituting the given radius $r = 3.5 = \frac{7}{2}$ cm and height $h = 3$ cm:
$V_{cone} = \frac{1}{3} \pi (3.5)^2 (3)$
$V_{cone} = \frac{1}{3} \pi \left(\frac{7}{2}\right)^2 (3)$
$V_{cone} = \frac{1}{3} \pi \left(\frac{49}{4}\right) (3)$
$V_{cone} = \frac{\pi \times 49 \times 3}{3 \times 4}$
$V_{cone} = \frac{49\pi}{4}$ cm$^3$
Let $n$ be the number of cones formed.
According to the conservation of volume:
Volume of sphere = Number of cones $\times$ Volume of one cone
$V_{sphere} = n \times V_{cone}$
Substitute the volumes we calculated:
$\frac{3087\pi}{2} = n \times \frac{49\pi}{4}$
To find $n$, divide the volume of the sphere by the volume of one cone:
$n = \frac{V_{sphere}}{V_{cone}}$
$n = \frac{\frac{3087\pi}{2}}{\frac{49\pi}{4}}$
$n = \frac{3087\pi}{2} \times \frac{4}{49\pi}$
Cancel out $\pi$ from numerator and denominator:
$n = \frac{3087}{2} \times \frac{4}{49}$
Simplify the expression:
$n = \frac{3087 \times \cancel{4}^2}{\cancel{2}_1 \times 49}$
$n = \frac{3087 \times 2}{49}$
Now, divide 3087 by 49. We know $49 = 7^2$. Let's check if 3087 is divisible by 7.
$3087 \div 7 = 441$. Also $441 = 21^2 = (3 \times 7)^2 = 9 \times 49$. So $3087 = 441 \times 7 = 9 \times 49 \times 7$.
Alternatively, $3087 \div 49 = (3087 \div 7) \div 7 = 441 \div 7 = 63$.
Or using fractions: $\frac{3087}{49} = \frac{21 \times 147}{7 \times 7} = \frac{3 \times 7 \times 3 \times 49}{7 \times 7} = \frac{3 \times 7 \times 3 \times 7 \times 7}{7 \times 7} = 3 \times 3 \times 7 = 63$.
So, $\frac{3087}{49} = 63$.
$n = 63 \times 2$
$n = 126$
Thus, 126 cones are formed.
Sample Question 3: A canal is 300 cm wide and 120 cm deep. The water in the canal is flowing with a speed of 20 km/h. How much area will it irrigate in 20 minutes if 8 cm of standing water is desired?
Answer:
Given:
Canal width $= 300$ cm
Canal depth $= 120$ cm
Speed of water flow $= 20$ km/h
Time duration $= 20$ minutes
Desired standing water height $= 8$ cm
To Find:
Area irrigated in 20 minutes.
Solution:
First, let's convert all the given dimensions and speed into consistent units, preferably meters and minutes.
Canal width $= 300$ cm $= \frac{300}{100}$ m $= 3$ m.
Canal depth $= 120$ cm $= \frac{120}{100}$ m $= 1.2$ m.
Speed of water flow $= 20$ km/h.
Convert speed from km/h to m/min:
$20$ km/h $= \frac{20 \text{ km}}{1 \text{ hour}}$
$= \frac{20 \times 1000 \text{ m}}{60 \text{ minutes}}$
$= \frac{20000}{60}$ m/min
$= \frac{1000}{3}$ m/min.
Time duration $= 20$ minutes.
Desired standing water height $= 8$ cm $= \frac{8}{100}$ m $= 0.08$ m.
The distance the water flows in the canal in 20 minutes represents the length of the column of water that flows out of the canal.
Distance $= \text{Speed} \times \text{Time}$
Distance $= \frac{1000}{3} \text{ m/min} \times 20 \text{ minutes}$
Distance $= \frac{20000}{3}$ m.
The volume of water that flows out of the canal in 20 minutes is the volume of a cuboid with the dimensions of the canal's cross-section (width and depth) and the distance the water travels (length).
Volume of water flow $= \text{Width} \times \text{Depth} \times \text{Distance}$
Volume $= 3 \text{ m} \times 1.2 \text{ m} \times \frac{20000}{3} \text{ m}$
Volume $= 3.6 \times \frac{20000}{3}$ m$^3$
Volume $= \frac{3.6}{3} \times 20000$ m$^3$
Volume $= 1.2 \times 20000$ m$^3$
Volume $= 24000$ m$^3$.
This volume of water is used to irrigate a certain area on the field to a desired standing height of $8$ cm ($0.08$ m).
Let the irrigated area be $A$ (in m$^2$). The volume of water on the field is given by:
Volume on field $= \text{Area} \times \text{Desired height}$
Volume on field $= A \times 0.08$ m$^3$.
By the principle of conservation of volume (assuming all water is used for irrigation), the volume of water flowing from the canal is equal to the volume of water spread over the irrigated area.
Volume of water flow = Volume on field
$24000 \text{ m}^3 = A \times 0.08 \text{ m}$
Now, we solve for the area $A$:
$A = \frac{24000}{0.08}$
$A = \frac{24000}{\frac{8}{100}}$
$A = \frac{24000 \times 100}{8}$
$A = \frac{2400000}{8}$
$A = 300000$ m$^2$.
The area that will be irrigated in 20 minutes is $300000$ m$^2$.
This area can also be expressed in hectares, where $1$ hectare $= 10000$ m$^2$.
Area in hectares $= \frac{300000}{10000}$ hectares
Area in hectares $= 30$ hectares.
The area that will be irrigated in 20 minutes is $300000$ m$^2$ (or 30 hectares).
Sample Question 4: A cone of radius 4 cm is divided into two parts by drawing a plane through the mid point of its axis and parallel to its base. Compare the volumes of the two parts.
Answer:
Given:
Radius of the original cone, $R = 4$ cm.
The cone is divided into two parts by a plane parallel to the base passing through the midpoint of its axis.
To Find:
Compare the volumes of the two parts.
Solution:
Let the height of the original cone be $H$. The radius of its base is $R = 4$ cm.
The volume of the original cone is $V_{original} = \frac{1}{3}\pi R^2 H = \frac{1}{3}\pi (4)^2 H = \frac{16}{3}\pi H$.
When a plane parallel to the base passes through the midpoint of the axis, it cuts the cone into two parts:
1. A smaller cone at the top.
2. A frustum at the bottom.
The height of the smaller cone is half the height of the original cone.
Height of smaller cone, $h_1 = \frac{H}{2}$.
The smaller cone is similar to the original cone because the cutting plane is parallel to the base.
The ratio of the radius of the smaller cone ($r_1$) to the radius of the original cone ($R$) is equal to the ratio of their heights.
$\frac{r_1}{R} = \frac{h_1}{H}$
$\frac{r_1}{4} = \frac{H/2}{H}$
$\frac{r_1}{4} = \frac{1}{2}$
$r_1 = \frac{1}{2} \times 4 = 2$ cm.
The volume of the smaller cone ($V_{cone1}$) is:
$V_{cone1} = \frac{1}{3}\pi r_1^2 h_1$
$V_{cone1} = \frac{1}{3}\pi (2)^2 \left(\frac{H}{2}\right)$
$V_{cone1} = \frac{1}{3}\pi (4) \left(\frac{H}{2}\right)$
$V_{cone1} = \frac{4\pi H}{6}$
$V_{cone1} = \frac{2}{3}\pi H$
The height of the frustum ($h_2$) is the remaining height of the original cone.
$h_2 = H - h_1 = H - \frac{H}{2} = \frac{H}{2}$.
The radii of the frustum's bases are $r_1 = 2$ cm and $R = 4$ cm.
The volume of the frustum ($V_{frustum}$) is the volume of the original cone minus the volume of the smaller cone.
$V_{frustum} = V_{original} - V_{cone1}$
$V_{frustum} = \frac{16}{3}\pi H - \frac{2}{3}\pi H$
$V_{frustum} = \frac{16\pi H - 2\pi H}{3}$
$V_{frustum} = \frac{14\pi H}{3}$
Now, we compare the volumes of the two parts, $V_{cone1}$ and $V_{frustum}$.
Ratio of volumes $= \frac{V_{cone1}}{V_{frustum}} = \frac{\frac{2}{3}\pi H}{\frac{14}{3}\pi H}$
Cancel the common terms $\frac{1}{3}\pi H$:
Ratio $= \frac{2}{14} = \frac{1}{7}$
This means the volume of the smaller cone is $\frac{1}{7}$ times the volume of the frustum.
$V_{cone1} = \frac{1}{7} V_{frustum}$
Alternatively, the volumes are in the ratio 1:7.
We can also note the relationship with the original cone's volume:
$V_{cone1} = \frac{2}{3}\pi H$. Since $V_{original} = \frac{16}{3}\pi H$, we can write $V_{cone1} = \frac{2}{16} \left(\frac{16}{3}\pi H\right) = \frac{1}{8} V_{original}$.
The volume of the smaller cone is $\frac{1}{8}$th the volume of the original cone.
The volume of the frustum is $V_{frustum} = V_{original} - V_{cone1} = V_{original} - \frac{1}{8} V_{original} = \frac{7}{8} V_{original}$.
The ratio of the volumes of the two parts (smaller cone to frustum) is $\frac{V_{cone1}}{V_{frustum}} = \frac{\frac{1}{8} V_{original}}{\frac{7}{8} V_{original}} = \frac{1}{7}$.
The volumes of the two parts are in the ratio 1 : 7.
Sample Question 5: Three cubes of a metal whose edges are in the ratio 3:4:5 are melted and converted into a single cube whose diagonal is 12$\sqrt{3}$ cm. Find the edges of the three cubes.
Answer:
Given:
Ratio of the edges of three metal cubes = $3:4:5$.
These cubes are melted and converted into a single cube.
Diagonal of the new single cube = $12\sqrt{3}$ cm.
To Find:
The lengths of the edges of the three original cubes.
Solution:
Let the edges of the three original cubes be $3x$, $4x$, and $5x$ cm, where $x$ is a positive constant.
The volumes of the three original cubes are:
$V_1 = (3x)^3 = 27x^3$ cm$^3$
$V_2 = (4x)^3 = 64x^3$ cm$^3$
$V_3 = (5x)^3 = 125x^3$ cm$^3$
When the three cubes are melted and converted into a single cube, the total volume of the metal is conserved.
Let the edge of the new single cube be $A$ cm.
The volume of the new cube is $V_{new} = A^3$ cm$^3$.
According to the problem, the total volume of the three small cubes is equal to the volume of the large cube.
$V_1 + V_2 + V_3 = V_{new}$
$27x^3 + 64x^3 + 125x^3 = A^3$
Combining the terms on the left side:
$(27 + 64 + 125)x^3 = A^3$
$216x^3 = A^3$
Take the cube root of both sides:
$\sqrt[3]{216x^3} = \sqrt[3]{A^3}$
$\sqrt[3]{216} \times \sqrt[3]{x^3} = A$
Since $6^3 = 216$, $\sqrt[3]{216} = 6$.
$6x = A$
The diagonal of a cube with edge length $A$ is given by $A\sqrt{3}$.
The diagonal of the new cube is given as $12\sqrt{3}$ cm.
Diagonal of new cube = $12\sqrt{3}$
(Given)
$A\sqrt{3} = 12\sqrt{3}$
... (i)
Divide both sides of equation (i) by $\sqrt{3}$:
$A = \frac{12\sqrt{3}}{\sqrt{3}}$
$A = 12$ cm
We have the relationship $A = 6x$. Substitute the value of $A$ into this equation:
$6x = 12$
... (ii)
Solve for $x$ from equation (ii):
$x = \frac{12}{6}$
$x = 2$
Now we can find the edges of the three original cubes using $x=2$.
Edge of the first cube = $3x = 3 \times 2 = 6$ cm.
Edge of the second cube = $4x = 4 \times 2 = 8$ cm.
Edge of the third cube = $5x = 5 \times 2 = 10$ cm.
The edges of the three original cubes are 6 cm, 8 cm, and 10 cm.
Exercise 12.3
Question 1. Three metallic solid cubes whose edges are 3 cm, 4 cm and 5 cm are melted and formed into a single cube. Find the edge of the cube so formed.
Answer:
Given:
Edges of the three metallic solid cubes are $a_1 = 3$ cm, $a_2 = 4$ cm, and $a_3 = 5$ cm.
These cubes are melted and formed into a single cube.
To Find:
The edge length of the single cube so formed.
Solution:
When solid cubes are melted and recast into a single solid, the total volume of the metal is conserved.
Volume of the first cube, $V_1 = a_1^3 = (3)^3 = 27$ cm$^3$.
Volume of the second cube, $V_2 = a_2^3 = (4)^3 = 64$ cm$^3$.
Volume of the third cube, $V_3 = a_3^3 = (5)^3 = 125$ cm$^3$.
Total volume of the three cubes $= V_1 + V_2 + V_3 = 27 + 64 + 125$ cm$^3$.
Total volume $= 91 + 125 = 216$ cm$^3$.
Let the edge of the new single cube be $A$ cm.
The volume of the new cube is $V_{new} = A^3$ cm$^3$.
According to the conservation of volume:
Volume of new cube = Total volume of the three original cubes
$A^3 = 216$
To find the edge $A$, take the cube root of both sides:
$A = \sqrt[3]{216}$
We know that $6^3 = 6 \times 6 \times 6 = 36 \times 6 = 216$.
$A = 6$ cm.
The edge of the cube so formed is 6 cm.
Question 2. How many shots each having diameter 3 cm can be made from a cuboidal lead solid of dimensions 9cm × 11cm × 12cm?
Answer:
Given:
Dimensions of the cuboidal lead solid are length $L = 12$ cm, breadth $B = 11$ cm, and height $H = 9$ cm.
Diameter of each spherical shot is $D = 3$ cm.
To Find:
The number of spherical shots that can be made from the cuboidal solid.
Solution:
When a solid is melted and recast into smaller solids, the total volume of the material remains constant.
Volume of the cuboidal lead solid is given by $V_{cuboid} = L \times B \times H$.
$V_{cuboid} = 12 \text{ cm} \times 11 \text{ cm} \times 9 \text{ cm}$
$V_{cuboid} = 132 \times 9$ cm$^3$
$V_{cuboid} = 1188$ cm$^3$.
The spherical shots are spheres. The diameter of each shot is 3 cm, so the radius is $r = \frac{\text{Diameter}}{2} = \frac{3}{2} = 1.5$ cm.
The volume of one spherical shot is given by the formula $V_{shot} = \frac{4}{3}\pi r^3$.
$V_{shot} = \frac{4}{3} \pi \left(\frac{3}{2}\right)^3$
$V_{shot} = \frac{4}{3} \pi \left(\frac{3^3}{2^3}\right)$
$V_{shot} = \frac{4}{3} \pi \left(\frac{27}{8}\right)$
$V_{shot} = \frac{\cancel{4}^1 \times \pi \times \cancel{27}^9}{\cancel{3}_1 \times \cancel{8}_2}$
$V_{shot} = \frac{9\pi}{2}$ cm$^3$.
Let $n$ be the number of shots that can be made.
The total volume of $n$ shots must be equal to the volume of the cuboidal solid.
$n \times V_{shot} = V_{cuboid}$
$n \times \frac{9\pi}{2} = 1188$
Solve for $n$:
$n = \frac{1188}{\frac{9\pi}{2}}$
$n = 1188 \times \frac{2}{9\pi}$
$n = \frac{1188 \times 2}{9\pi}$
We need to use a value for $\pi$. Assuming $\pi \approx \frac{22}{7}$ (a common approximation in such problems):
$n = \frac{1188 \times 2}{9 \times \frac{22}{7}}$
$n = \frac{1188 \times 2}{9} \times \frac{7}{22}$
Simplify the expression:
First, divide 1188 by 9:
$1188 \div 9 = 132$
So, $n = 132 \times 2 \times \frac{7}{22}$
$n = 264 \times \frac{7}{22}$
Now, divide 264 by 22:
$264 \div 22 = 12$
So, $n = 12 \times 7$
$n = 84$
Thus, 84 spherical shots can be made from the cuboidal lead solid.
Question 3. A bucket is in the form of a frustum of a cone and holds 28.490 litres of water. The radii of the top and bottom are 28 cm and 21 cm, respectively. Find the height of the bucket.
Answer:
Given:
Volume of water the bucket holds (which is the capacity of the bucket) $= 28.490$ litres.
Radius of the top (larger end) of the frustum, $r_1 = 28$ cm.
Radius of the bottom (smaller end) of the frustum, $r_2 = 21$ cm.
To Find:
The height of the bucket (frustum).
Solution:
The bucket is in the shape of a frustum of a cone. The volume of a frustum is given by the formula $V = \frac{1}{3}\pi h (r_1^2 + r_2^2 + r_1 r_2)$, where $h$ is the height and $r_1$ and $r_2$ are the radii of the two bases.
First, convert the volume from litres to cubic centimetres. We know that 1 litre $= 1000$ cm$^3$.
Volume of the bucket $= 28.490$ litres $= 28.490 \times 1000$ cm$^3$
Volume $= 28490$ cm$^3$.
Now, substitute the given values into the volume formula for a frustum:
$V = \frac{1}{3}\pi h (r_1^2 + r_2^2 + r_1 r_2)$
$28490 = \frac{1}{3}\pi h (28^2 + 21^2 + 28 \times 21)$
Calculate the terms inside the bracket:
$28^2 = 28 \times 28 = 784$
$21^2 = 21 \times 21 = 441$
$28 \times 21 = 588$
Sum of terms $= 784 + 441 + 588 = 1225 + 588 = 1813$
Substitute this back into the volume equation:
$28490 = \frac{1}{3}\pi h (1813)$
Use the value of $\pi = \frac{22}{7}$:
$28490 = \frac{1}{3} \times \frac{22}{7} \times h \times 1813$
$28490 = \frac{22 \times h \times 1813}{21}$
Now, solve for $h$:
$h = \frac{28490 \times 21}{22 \times 1813}$
Let's simplify the expression.
Divide 21 by 7 and 1813 by 7:
$1813 \div 7 = 259$.
$h = \frac{28490 \times \cancel{21}^3}{22 \times \cancel{1813}^{259}}$
$h = \frac{28490 \times 3}{22 \times 259}$
Divide 22 into 28490 or simplify with 28490.
$28490 \div 22$:
$\begin{array}{r} 1295\phantom{)} \\ 22{\overline{\smash{\big)}\,28490\phantom{)}}} \\ \underline{-~\phantom{(}(22)\phantom{000)}} \\ 64\phantom{00)} \\ \underline{-~\phantom{()}(44)\phantom{00)}} \\ 209\phantom{0)} \\ \underline{-~\phantom{()}(198)\phantom{0)}} \\ 110\phantom{)} \\ \underline{-~\phantom{()}(110)} \\ 0\phantom{)} \end{array}$So, $28490 \div 22 = 1295$.
$h = \frac{1295 \times 3}{259}$
Now, divide 1295 by 259.
Let's estimate: $259 \approx 260$. $1295 \approx 1300$. $1300 / 260 = 5$. Let's check $259 \times 5$.
$259 \times 5 = (260 - 1) \times 5 = 1300 - 5 = 1295$.
So, $1295 \div 259 = 5$.
$h = 5 \times 3$
$h = 15$ cm.
The height of the bucket is 15 cm.
Question 4. A cone of radius 8 cm and height 12 cm is divided into two parts by a plane through the mid-point of its axis parallel to its base. Find the ratio of the volumes of two parts.
Answer:
Given:
Radius of the original cone, $R = 8$ cm.
Height of the original cone, $H = 12$ cm.
The cone is divided into two parts by a plane parallel to the base passing through the midpoint of its axis.
To Find:
The ratio of the volumes of the two parts.
Solution:
The original cone has radius $R = 8$ cm and height $H = 12$ cm.
The volume of the original cone is $V_{original} = \frac{1}{3}\pi R^2 H = \frac{1}{3}\pi (8)^2 (12) = \frac{1}{3}\pi (64)(12) = \pi (64)(4) = 256\pi$ cm$^3$.
When a plane parallel to the base cuts the cone through the midpoint of its axis, it divides the cone into two parts:
1. A smaller cone at the top.
2. A frustum at the bottom.
The height of the smaller cone is half the height of the original cone.
Height of smaller cone, $h_1 = \frac{H}{2} = \frac{12}{2} = 6$ cm.
Since the cutting plane is parallel to the base, the smaller cone is similar to the original cone.
The ratio of the radius of the smaller cone ($r_1$) to the radius of the original cone ($R$) is equal to the ratio of their heights.
$\frac{r_1}{R} = \frac{h_1}{H}$
$\frac{r_1}{8} = \frac{6}{12}$
$\frac{r_1}{8} = \frac{1}{2}$
$r_1 = \frac{1}{2} \times 8 = 4$ cm.
The volume of the smaller cone ($V_{cone1}$) is:
$V_{cone1} = \frac{1}{3}\pi r_1^2 h_1$
$V_{cone1} = \frac{1}{3}\pi (4)^2 (6)$
$V_{cone1} = \frac{1}{3}\pi (16)(6)$
$V_{cone1} = \pi (16)(2)$
$V_{cone1} = 32\pi$ cm$^3$.
The second part is the frustum. The volume of the frustum ($V_{frustum}$) is the volume of the original cone minus the volume of the smaller cone.
$V_{frustum} = V_{original} - V_{cone1}$
$V_{frustum} = 256\pi - 32\pi$
$V_{frustum} = (256 - 32)\pi$
$V_{frustum} = 224\pi$ cm$^3$.
We need to find the ratio of the volumes of the two parts. Let's take the ratio of the volume of the smaller cone to the volume of the frustum.
Ratio $= \frac{V_{cone1}}{V_{frustum}}$
Ratio $= \frac{32\pi}{224\pi}$
Cancel out $\pi$ from numerator and denominator:
Ratio $= \frac{32}{224}$
Simplify the fraction. Both 32 and 224 are divisible by 32.
$32 \times 1 = 32$
$32 \times 7 = 224$ (since $30 \times 7 = 210$ and $2 \times 7 = 14$, $210+14=224$).
Ratio $= \frac{\cancel{32}^1}{\cancel{224}_7} = \frac{1}{7}$
The ratio of the volumes of the two parts (smaller cone to frustum) is $1:7$.
Alternate Method (Using Similarity):
When a cone is cut by a plane parallel to its base, the smaller cone formed is similar to the original cone.
The ratio of heights of the smaller cone to the original cone is $\frac{h_1}{H} = \frac{H/2}{H} = \frac{1}{2}$.
For similar solids, the ratio of their volumes is the cube of the ratio of their corresponding linear dimensions (like height or radius).
Ratio of volumes of smaller cone to original cone $= \left(\frac{h_1}{H}\right)^3 = \left(\frac{1}{2}\right)^3 = \frac{1}{8}$.
This means $V_{cone1} = \frac{1}{8} V_{original}$.
The volume of the frustum is the volume of the original cone minus the volume of the smaller cone.
$V_{frustum} = V_{original} - V_{cone1} = V_{original} - \frac{1}{8} V_{original} = \left(1 - \frac{1}{8}\right) V_{original} = \frac{7}{8} V_{original}$.
The two parts are the smaller cone and the frustum.
Ratio of volumes $= \frac{V_{cone1}}{V_{frustum}} = \frac{\frac{1}{8} V_{original}}{\frac{7}{8} V_{original}} = \frac{1/8}{7/8} = \frac{1}{7}$.
The ratio of the volumes of the two parts is 1 : 7.
Question 5. Two identical cubes each of volume 64 cm3 are joined together end to end. What is the surface area of the resulting cuboid?
Answer:
Given:
Volume of each of the two identical cubes $= 64$ cm$^3$.
The two cubes are joined end to end.
To Find:
The surface area of the resulting cuboid.
Solution:
Let the edge length of each identical cube be '$a$'.
The volume of a cube with edge '$a$' is $V = a^3$.
We are given that the volume of each cube is 64 cm$^3$.
$a^3 = 64$ cm$^3$
To find the edge length '$a$', take the cube root of 64:
$a = \sqrt[3]{64}$
Since $4 \times 4 \times 4 = 64$, we have $a = 4$ cm.
The edge length of each cube is 4 cm.
When two identical cubes of edge length '$a$' are joined together end to end, a cuboid is formed.
The dimensions of this resulting cuboid are:
Length, $l = a + a = 2a$
Breadth, $b = a$
Height, $h = a$
Substitute the value of $a = 4$ cm into the dimensions:
Length, $l = 2 \times 4 = 8$ cm.
Breadth, $b = 4$ cm.
Height, $h = 4$ cm.
The resulting cuboid has dimensions 8 cm $\times$ 4 cm $\times$ 4 cm.
The total surface area (TSA) of a cuboid with length $l$, breadth $b$, and height $h$ is given by the formula $TSA = 2(lb + bh + hl)$.
Substitute the dimensions of the resulting cuboid into the formula:
$TSA = 2((8)(4) + (4)(4) + (4)(8))$
$TSA = 2(32 + 16 + 32)$
$TSA = 2(48 + 32)$
$TSA = 2(80)$
$TSA = 160$
The surface area of the resulting cuboid is 160 cm$^2$.
Question 6. From a solid cube of side 7 cm, a conical cavity of height 7 cm and radius 3 cm is hollowed out. Find the volume of the remaining solid.
Answer:
Given:
Side of the solid cube, $a = 7$ cm.
A conical cavity is hollowed out from the cube.
Height of the conical cavity, $h = 7$ cm.
Radius of the conical cavity, $r = 3$ cm.
To Find:
The volume of the remaining solid.
Solution:
The volume of the remaining solid is the volume of the original cube minus the volume of the conical cavity that is hollowed out.
The volume of the solid cube with side '$a$' is $V_{cube} = a^3$.
$V_{cube} = (7 \text{ cm})^3 = 7 \times 7 \times 7 = 49 \times 7 = 343$ cm$^3$.
The volume of the conical cavity with radius '$r$' and height '$h$' is given by the formula $V_{cone} = \frac{1}{3}\pi r^2 h$.
$V_{cone} = \frac{1}{3} \pi (3 \text{ cm})^2 (7 \text{ cm})$
$V_{cone} = \frac{1}{3} \pi (9 \text{ cm}^2) (7 \text{ cm})$
$V_{cone} = \frac{1}{3} \pi (63 \text{ cm}^3)$
$V_{cone} = 21\pi$ cm$^3$.
Assuming $\pi = \frac{22}{7}$:
$V_{cone} = 21 \times \frac{22}{7}$ cm$^3$
$V_{cone} = \cancel{21}^3 \times \frac{22}{\cancel{7}_1}$ cm$^3$
$V_{cone} = 3 \times 22 = 66$ cm$^3$.
The volume of the remaining solid is $V_{remaining} = V_{cube} - V_{cone}$.
$V_{remaining} = 343 \text{ cm}^3 - 66 \text{ cm}^3$.
$V_{remaining} = 277$ cm$^3$.
The volume of the remaining solid is 277 cm$^3$.
Question 7. Two cones with same base radius 8 cm and height 15 cm are joined together along their bases. Find the surface area of the shape so formed.
Answer:
Given:
Base radius of each cone, $r = 8$ cm.
Height of each cone, $h = 15$ cm.
The two cones are joined together along their bases.
To Find:
The surface area of the shape so formed.
Solution:
When two identical solid cones are joined along their bases, the resulting shape is a double cone (like an hourglass). The bases where they are joined become internal and do not contribute to the surface area of the combined solid.
The total surface area of the combined shape is the sum of the curved surface areas (CSA) of the two individual cones.
For a cone, the curved surface area is given by the formula $\pi r l$, where $r$ is the base radius and $l$ is the slant height.
We need to find the slant height '$l$' of the cone. The slant height, radius, and height are related by the Pythagorean theorem: $l^2 = r^2 + h^2$.
Given $r = 8$ cm and $h = 15$ cm.
$l^2 = (8)^2 + (15)^2$
$l^2 = 64 + 225$
$l^2 = 289$
Taking the square root of both sides:
$l = \sqrt{289}$
$l = 17$ cm.
The slant height of each cone is 17 cm.
The curved surface area (CSA) of one cone is:
CSA $= \pi r l$
CSA $= \pi (8 \text{ cm}) (17 \text{ cm})$
CSA $= 136\pi$ cm$^2$.
The total surface area of the combined shape is the sum of the curved surface areas of the two cones.
Total Surface Area $= (\text{CSA of first cone}) + (\text{CSA of second cone})$
Since the cones are identical, their CSAs are equal.
Total Surface Area $= 136\pi + 136\pi$
Total Surface Area $= 2 \times 136\pi$
Total Surface Area $= 272\pi$ cm$^2$.
Using the value $\pi = \frac{22}{7}$ to get a numerical answer:
Total Surface Area $= 272 \times \frac{22}{7}$
Total Surface Area $= \frac{5984}{7}$ cm$^2$.
Total Surface Area $\approx 854.86$ cm$^2$.
The surface area of the shape so formed is $272\pi$ cm$^2$ or approximately 854.86 cm$^2$.
Question 8. Two solid cones A and B are placed in a cylinderical tube as shown in the Fig.12.9. The ratio of their capacities are 2:1. Find the heights and capacities of cones. Also, find the volume of the remaining portion of the cylinder.
Answer:
Given:
Cylinder height, $H = 21$ cm.
Cylinder diameter = 10 cm, so radius $R = 5$ cm.
Cones A and B have radius $r_A = r_B = R = 5$ cm.
Let heights be $h_A$ and $h_B$. $h_A + h_B = H = 21$ cm.
Ratio of volumes $V_A : V_B = 2 : 1$.
To Find:
$h_A$, $h_B$, $V_A$, $V_B$, and Volume of remaining cylinder.
Solution:
$V_A = \frac{1}{3}\pi r_A^2 h_A = \frac{1}{3}\pi (5)^2 h_A = \frac{25}{3}\pi h_A$
$V_B = \frac{1}{3}\pi r_B^2 h_B = \frac{1}{3}\pi (5)^2 h_B = \frac{25}{3}\pi h_B$
Given $V_A : V_B = 2 : 1$, so $\frac{V_A}{V_B} = 2$.
$\frac{\frac{25}{3}\pi h_A}{\frac{25}{3}\pi h_B} = 2 \implies \frac{h_A}{h_B} = 2 \implies h_A = 2h_B$.
Substitute $h_A = 2h_B$ into $h_A + h_B = 21$:
$2h_B + h_B = 21 \implies 3h_B = 21 \implies h_B = 7$ cm.
$h_A = 2 \times 7 = 14$ cm.
Heights of cones are $h_A = 14$ cm and $h_B = 7$ cm.
Capacities (Volumes): Using $\pi = \frac{22}{7}$
$V_A = \frac{25}{3}\pi h_A = \frac{25}{3} \times \frac{22}{7} \times 14 = \frac{25 \times 22 \times 14}{3 \times 7} = \frac{25 \times 22 \times 2}{3} = \frac{1100}{3}$ cm$^3$.
$V_B = \frac{25}{3}\pi h_B = \frac{25}{3} \times \frac{22}{7} \times 7 = \frac{25 \times 22}{3} = \frac{550}{3}$ cm$^3$.
Capacities are $V_A = \frac{1100}{3}$ cm$^3$ and $V_B = \frac{550}{3}$ cm$^3$.
Volume of cylinder $V_{cyl} = \pi R^2 H = \pi (5)^2 (21) = 525\pi$ cm$^3$.
Using $\pi = \frac{22}{7}$, $V_{cyl} = 525 \times \frac{22}{7} = 75 \times 22 = 1650$ cm$^3$.
Volume of remaining portion = $V_{cyl} - (V_A + V_B)$
Volume of remaining portion $= 1650 - (\frac{1100}{3} + \frac{550}{3}) = 1650 - \frac{1650}{3} = 1650 - 550 = 1100$ cm$^3$.
Volume of remaining portion is 1100 cm$^3$.
Question 9. An ice cream cone full of ice cream having radius 5 cm and height 10 cm as shown in the Fig.12.10. Calculate the volume of ice cream, provided that its $\frac{1}{6}$ part is left unfilled with ice cream.

Answer:
Given:
The ice cream cone is a composite solid consisting of a cone and a hemisphere on top.
Radius of the cone's base = Radius of the hemisphere, $r = 5$ cm.
Height of the cone, $h = 10$ cm.
Part of the total volume capacity left unfilled $= \frac{1}{6}$.
To Find:
The volume of ice cream in the cone.
Solution:
The total capacity of the ice cream cone shape is the sum of the volume of the cone part and the volume of the hemispherical part.
The volume of the cone with radius '$r$' and height '$h$' is given by the formula $V_{cone} = \frac{1}{3}\pi r^2 h$.
$V_{cone} = \frac{1}{3}\pi (5 \text{ cm})^2 (10 \text{ cm})$
$V_{cone} = \frac{1}{3}\pi (25 \text{ cm}^2) (10 \text{ cm})$
$V_{cone} = \frac{250}{3}\pi$ cm$^3$.
The volume of the hemisphere with radius '$r$' is given by the formula $V_{hemisphere} = \frac{2}{3}\pi r^3$.
$V_{hemisphere} = \frac{2}{3}\pi (5 \text{ cm})^3$
$V_{hemisphere} = \frac{2}{3}\pi (125 \text{ cm}^3)$
$V_{hemisphere} = \frac{250}{3}\pi$ cm$^3$.
The total volume capacity of the ice cream cone shape is:
$V_{total\_capacity} = V_{cone} + V_{hemisphere}$
$V_{total\_capacity} = \frac{250}{3}\pi + \frac{250}{3}\pi$
$V_{total\_capacity} = \frac{250\pi + 250\pi}{3} = \frac{500\pi}{3}$ cm$^3$.
We are given that $\frac{1}{6}$ part of the total volume capacity is left unfilled.
Volume of unfilled part $= \frac{1}{6} \times V_{total\_capacity}$
Volume of unfilled part $= \frac{1}{6} \times \frac{500\pi}{3} = \frac{500\pi}{18} = \frac{250\pi}{9}$ cm$^3$.
The volume of ice cream is the total capacity minus the unfilled part.
Volume of ice cream $= V_{total\_capacity} - \text{Volume of unfilled part}
Volume of ice cream $= \frac{500\pi}{3} - \frac{250\pi}{9}$
To subtract, find a common denominator, which is 9.
Volume of ice cream $= \frac{500\pi \times 3}{3 \times 3} - \frac{250\pi}{9} = \frac{1500\pi}{9} - \frac{250\pi}{9}$
Volume of ice cream $= \frac{1500\pi - 250\pi}{9} = \frac{1250\pi}{9}$ cm$^3$.
Alternatively, if $\frac{1}{6}$ is unfilled, then $1 - \frac{1}{6} = \frac{5}{6}$ part is filled with ice cream.
Volume of ice cream $= \frac{5}{6} \times V_{total\_capacity}$
Volume of ice cream $= \frac{5}{6} \times \frac{500\pi}{3} = \frac{2500\pi}{18} = \frac{1250\pi}{9}$ cm$^3$.
Using the value $\pi = \frac{22}{7}$ for a numerical answer:
Volume of ice cream $= \frac{1250}{9} \times \frac{22}{7}$
Volume of ice cream $= \frac{1250 \times 22}{9 \times 7} = \frac{27500}{63}$ cm$^3$.
The volume of ice cream is $\frac{1250\pi}{9}$ cm$^3$ or $\frac{27500}{63}$ cm$^3$ (approximately 436.51 cm$^3$).
Question 10. Marbles of diameter 1.4 cm are dropped into a cylindrical beaker of diameter 7 cm containing some water. Find the number of marbles that should be dropped into the beaker so that the water level rises by 5.6 cm.
Answer:
Given:
Diameter of each spherical marble, $D_m = 1.4$ cm.
Diameter of the cylindrical beaker, $D_b = 7$ cm.
Rise in water level in the beaker, $h_{rise} = 5.6$ cm.
To Find:
The number of marbles that should be dropped into the beaker.
Solution:
When marbles are dropped into the beaker, they displace a volume of water equal to the total volume of the marbles. This displaced water causes the water level to rise.
Radius of each marble, $r_m = \frac{D_m}{2} = \frac{1.4}{2} = 0.7$ cm.
Volume of one marble (sphere), $V_{marble} = \frac{4}{3}\pi r_m^3 = \frac{4}{3}\pi (0.7)^3$ cm$^3$.
Radius of the cylindrical beaker, $r_b = \frac{D_b}{2} = \frac{7}{2} = 3.5$ cm.
The rise in water level due to the marbles forms a cylindrical volume of water with radius $r_b$ and height $h_{rise}$.
Volume of displaced water (cylinder), $V_{displaced} = \pi r_b^2 h_{rise} = \pi (3.5)^2 (5.6)$ cm$^3$.
Let $n$ be the number of marbles dropped into the beaker.
The total volume of $n$ marbles is $n \times V_{marble}$.
According to the principle of volume displacement, the total volume of the marbles is equal to the volume of the displaced water.
$n \times V_{marble} = V_{displaced}$
$n \times \frac{4}{3}\pi (0.7)^3 = \pi (3.5)^2 (5.6)$
... (i)
Cancel $\pi$ from both sides of equation (i):
$n \times \frac{4}{3} (0.7)^3 = (3.5)^2 (5.6)$
Substitute the decimal values:
$0.7^3 = 0.7 \times 0.7 \times 0.7 = 0.49 \times 0.7 = 0.343$
$3.5^2 = 3.5 \times 3.5 = 12.25$
$(3.5)^2 (5.6) = 12.25 \times 5.6 = 68.6$
So, the equation becomes:
$n \times \frac{4}{3} (0.343) = 68.6$
Solve for $n$:
$n = \frac{68.6 \times 3}{4 \times 0.343}$
We can notice that $68.6 = 200 \times 0.343$.
To check: $200 \times 0.343 = 2 \times 100 \times 0.343 = 2 \times 34.3 = 68.6$.
$n = \frac{200 \times 0.343 \times 3}{4 \times 0.343}$
Cancel out 0.343 from the numerator and denominator:
$n = \frac{200 \times 3}{4}$
$n = \frac{\cancel{200}^{50} \times 3}{\cancel{4}_1}$
$n = 50 \times 3$
$n = 150$
Thus, 150 marbles should be dropped into the beaker.
Question 11. How many spherical lead shots each of diameter 4.2 cm can be obtained from a solid rectangular lead piece with dimensions 66 cm, 42 cm and 21 cm.
Answer:
Given:
Dimensions of the solid rectangular lead piece:
Length ($l$) = 66 cm
Breadth ($b$) = 42 cm
Height ($h$) = 21 cm
Diameter of each spherical lead shot = 4.2 cm
To Find:
The number of spherical lead shots that can be obtained from the rectangular lead piece.
Solution:
First, calculate the volume of the solid rectangular lead piece.
Volume of rectangular piece = $l \times b \times h$
Volume of rectangular piece = $66 \times 42 \times 21 \text{ cm}^3$
... (i)
Now, calculate the volume of one spherical lead shot.
Radius of the spherical lead shot ($r$) = $\frac{\text{Diameter}}{2} = \frac{4.2}{2} = 2.1 \text{ cm}$
Volume of a sphere = $\frac{4}{3} \pi r^3$
Using $\pi = \frac{22}{7}$:
Volume of one spherical lead shot = $\frac{4}{3} \times \frac{22}{7} \times (2.1)^3$
Volume of one spherical lead shot = $\frac{4}{3} \times \frac{22}{7} \times 2.1 \times 2.1 \times 2.1$
Volume of one spherical lead shot = $\frac{4}{3} \times \frac{22}{7} \times \frac{21}{10} \times \frac{21}{10} \times \frac{21}{10}$
... (ii)
The number of spherical lead shots obtained is the ratio of the volume of the rectangular piece to the volume of one spherical lead shot.
Number of lead shots = $\frac{\text{Volume of rectangular piece}}{\text{Volume of one spherical lead shot}}$
Number of lead shots = $\frac{66 \times 42 \times 21}{\frac{4}{3} \times \frac{22}{7} \times \frac{21}{10} \times \frac{21}{10} \times \frac{21}{10}}$
Number of lead shots = $66 \times 42 \times 21 \times \frac{3}{4} \times \frac{7}{22} \times \frac{10}{21} \times \frac{10}{21} \times \frac{10}{21}$
Number of lead shots = $66 \times 42 \times \cancel{21} \times \frac{3}{4} \times \frac{7}{22} \times \frac{10}{21} \times \frac{10}{21} \times \frac{10}{\cancel{21}}$
Number of lead shots = $66 \times 42 \times \frac{3}{4} \times \frac{7}{22} \times \frac{10}{21} \times \frac{10}{21} \times 10$
Cancel terms:
$\frac{\cancel{66}^{3}}{\cancel{22}_{1}} = 3$
$\frac{\cancel{42}^{2}}{\cancel{21}_{1}} = 2$
$\frac{\cancel{21}^{1}}{\cancel{21}_{1}} = 1$ (already cancelled one 21 from numerator with one 21 from denominator)
$\frac{42}{21 \times 21} = \frac{2}{21}$
Let's rewrite the expression after initial cancellations:
Number of lead shots = $\cancel{66} \times \cancel{42} \times 21 \times \frac{3}{4} \times \frac{7}{\cancel{22}} \times \frac{10}{\cancel{21}} \times \frac{10}{21} \times \frac{10}{21}$
Number of lead shots = $3 \times 42 \times \cancel{21} \times \frac{3}{4} \times \frac{7}{1} \times \frac{10}{\cancel{21}} \times \frac{10}{21} \times \frac{10}{21}$
Number of lead shots = $3 \times \cancel{42}^2 \times \frac{3}{4} \times 7 \times \frac{10}{\cancel{21}_1} \times \frac{10}{21} \times \frac{10}{21}$
Number of lead shots = $3 \times 2 \times \frac{3}{4} \times 7 \times 10 \times \frac{10}{21} \times \frac{10}{21}$
Number of lead shots = $\cancel{6}^{3} \times \frac{3}{\cancel{4}^2} \times 7 \times 10 \times \frac{10}{21} \times \frac{10}{21}$
Number of lead shots = $3 \times \frac{3}{2} \times 7 \times 10 \times \frac{10}{21} \times \frac{10}{21}$
Number of lead shots = $\frac{9}{2} \times 7 \times 10 \times \frac{10}{21} \times \frac{10}{21}$
Number of lead shots = $\frac{63}{2} \times 10 \times \frac{10}{21} \times \frac{10}{21}$
Number of lead shots = $\frac{630}{2} \times \frac{10}{21} \times \frac{10}{21}$
Number of lead shots = $315 \times \frac{10}{21} \times \frac{10}{21}$
Cancel 315 with 21 ($315 \div 21 = 15$):
Number of lead shots = $\cancel{315}^{15} \times \frac{10}{\cancel{21}_1} \times \frac{10}{21}$
Number of lead shots = $15 \times 10 \times \frac{10}{21}$
Number of lead shots = $150 \times \frac{10}{21}$
Cancel 150 and 21 by 3 ($150 \div 3 = 50$, $21 \div 3 = 7$):
Number of lead shots = $\cancel{150}^{50} \times \frac{10}{\cancel{21}_7}$
Number of lead shots = $50 \times \frac{10}{7}$
Let's go back and do the cancellation more systematically:
Number of lead shots = $66 \times 42 \times 21 \times \frac{3}{4} \times \frac{7}{22} \times \frac{10}{21} \times \frac{10}{21} \times \frac{10}{21}$
Number of lead shots = $\cancel{66}^{3} \times \cancel{42}^2 \times \cancel{21}^1 \times \frac{3}{\cancel{4}^2} \times \frac{7}{\cancel{22}_1} \times \frac{10}{\cancel{21}_1} \times \frac{10}{21} \times \frac{10}{21}$ (Cancelling 66 with 22, 42 with 21, one 21 with one 21)
Number of lead shots = $3 \times 2 \times 1 \times \frac{3}{2} \times 7 \times 10 \times \frac{10}{21} \times \frac{10}{21}$
Number of lead shots = $\cancel{6}^3 \times \frac{3}{\cancel{2}_1} \times 7 \times 10 \times \frac{10}{\cancel{21}_7} \times \frac{10}{21}$ (Cancelling 6 with 2, 21 with 3 and 7)
Number of lead shots = $3 \times 3 \times 7 \times 10 \times \frac{10}{7} \times \frac{10}{21}$
Number of lead shots = $9 \times \cancel{7}^1 \times 10 \times \frac{10}{\cancel{7}_1} \times \frac{10}{21}$ (Cancelling 7 with 7)
Number of lead shots = $9 \times 10 \times 10 \times \frac{10}{21}$
Number of lead shots = $900 \times \frac{10}{21}$
Number of lead shots = $\frac{9000}{21}$
Cancel 9000 and 21 by 3:
Number of lead shots = $\frac{\cancel{9000}^{3000}}{\cancel{21}_7}$
Number of lead shots = $\frac{3000}{7}$
Let's re-calculate carefully from Volume of one spherical lead shot:
Volume of one spherical lead shot = $\frac{4}{3} \times \frac{22}{7} \times (2.1)^3 = \frac{4}{3} \times \frac{22}{7} \times 9.261 \text{ cm}^3$
Volume of one spherical lead shot = $\frac{88}{21} \times 9.261 \text{ cm}^3$
$9.261 = 2.1 \times 2.1 \times 2.1$
Volume of one spherical lead shot = $\frac{88}{21} \times 2.1 \times 2.1 \times 2.1$
Volume of one spherical lead shot = $\frac{88}{\cancel{21}} \times \cancel{2.1}^{0.1} \times 2.1 \times 2.1$
Volume of one spherical lead shot = $88 \times 0.1 \times 2.1 \times 2.1$
Volume of one spherical lead shot = $8.8 \times 4.41$
$\begin{array}{cc}& & 4 & . & 4 & 1 \\ \times & & & & 8 & 8 \\ \hline && 3 & 5 & 2 & 8 \\ 3 & 5 & 2 & 8 & \times & \\ \hline 3 & 8 & . & 7 & 0 & 8 \\ \hline \end{array}$
Volume of one spherical lead shot = $38.708 \text{ cm}^3$
Volume of rectangular piece = $66 \times 42 \times 21$
$66 \times 42 = 2772$
$2772 \times 21$
$\begin{array}{cc}& & 2 & 7 & 7 & 2 \\ \times & & & & 2 & 1 \\ \hline && 2 & 7 & 7 & 2 \\ 5 & 5 & 4 & 4 & \times & \\ \hline 5 & 8 & 2 & 1 & 2 & \\ \hline \end{array}$
Volume of rectangular piece = $58212 \text{ cm}^3$
Number of lead shots = $\frac{\text{Volume of rectangular piece}}{\text{Volume of one spherical lead shot}}$
Number of lead shots = $\frac{58212}{38.708}$
Let's use the fraction form for cancellation again, being more careful.
Volume of rectangular piece = $66 \times 42 \times 21$
Volume of one spherical lead shot = $\frac{4}{3} \times \frac{22}{7} \times (2.1)^3 = \frac{4}{3} \times \frac{22}{7} \times (\frac{21}{10})^3 = \frac{4}{3} \times \frac{22}{7} \times \frac{21 \times 21 \times 21}{10 \times 10 \times 10}$
Number of lead shots = $\frac{66 \times 42 \times 21}{\frac{4}{3} \times \frac{22}{7} \times \frac{21 \times 21 \times 21}{10 \times 10 \times 10}}$
Number of lead shots = $66 \times 42 \times 21 \times \frac{3 \times 7 \times 1000}{4 \times 22 \times 21 \times 21 \times 21}$
Number of lead shots = $\cancel{66}^{3} \times \cancel{42}^2 \times \cancel{21}^1 \times \frac{3 \times \cancel{7}^1 \times 1000}{\cancel{4}^2 \times \cancel{22}_1 \times \cancel{21}_1 \times 21 \times 21}$ (Cancel 66 with 22, 42 with 21, one 21 with one 21, 7 with 7, 4 with 2)
Number of lead shots = $3 \times 2 \times 1 \times \frac{3 \times 1 \times 1000}{2 \times 1 \times 1 \times 21 \times 21}$
Number of lead shots = $6 \times \frac{3 \times 1000}{2 \times 441}$
Number of lead shots = $\cancel{6}^3 \times \frac{3000}{\cancel{2}_1 \times 441}$ (Cancel 6 with 2)
Number of lead shots = $3 \times \frac{3000}{441}$
Number of lead shots = $\frac{9000}{441}$
Cancel 9000 and 441 by 9:
$9000 \div 9 = 1000$
$441 \div 9 = 49$
Number of lead shots = $\frac{\cancel{9000}^{1000}}{\cancel{441}_{49}}$
Number of lead shots = $\frac{1000}{49}$
Let's re-check cancellations. It's possible I missed something.
Number of lead shots = $66 \times 42 \times 21 \times \frac{3}{4} \times \frac{7}{22} \times \frac{10}{21} \times \frac{10}{21} \times \frac{10}{21}$
Number of lead shots = $\frac{66 \times 42 \times 21 \times 3 \times 7 \times 10 \times 10 \times 10}{4 \times 22 \times 21 \times 21 \times 21}$
Number of lead shots = $\frac{\cancel{66}^{3} \times \cancel{42}^2 \times \cancel{21}^1 \times 3 \times \cancel{7}^1 \times 1000}{\cancel{4}^2 \times \cancel{22}_1 \times \cancel{21}_1 \times 21 \times 21}$ (66/22=3, 42/21=2, 21/21=1, 7/1=7, 4/2=2)
Number of lead shots = $\frac{3 \times 2 \times 1 \times 3 \times 1 \times 1000}{2 \times 1 \times 1 \times 21 \times 21}$
Number of lead shots = $\frac{18 \times 1000}{2 \times 441}$
Number of lead shots = $\frac{\cancel{18}^9 \times 1000}{\cancel{2}_1 \times 441}$
Number of lead shots = $\frac{9 \times 1000}{441}$
Number of lead shots = $\frac{9000}{441}$
Same result. Let's check the numbers again.
Volume of rectangular piece = $66 \times 42 \times 21 \text{ cm}^3$. Keep it in this form.
Radius $r = 2.1 = \frac{21}{10}$ cm.
Volume of sphere = $\frac{4}{3} \pi r^3 = \frac{4}{3} \times \frac{22}{7} \times (\frac{21}{10})^3 = \frac{4}{3} \times \frac{22}{7} \times \frac{21 \times 21 \times 21}{1000} \text{ cm}^3$. Keep it in this form.
Number of shots = $\frac{66 \times 42 \times 21}{\frac{4}{3} \times \frac{22}{7} \times \frac{21 \times 21 \times 21}{1000}}$
Number of shots = $66 \times 42 \times 21 \times \frac{3 \times 7 \times 1000}{4 \times 22 \times 21 \times 21 \times 21}$
Number of shots = $\frac{66 \times 42 \times 21 \times 3 \times 7 \times 1000}{4 \times 22 \times 21 \times 21 \times 21}$
Cancel a 21 from numerator and denominator:
Number of shots = $\frac{66 \times 42 \times 3 \times 7 \times 1000}{4 \times 22 \times 21 \times 21}$
Cancel 66 with 22 ($66/22 = 3$):
Number of shots = $\frac{\cancel{66}^3 \times 42 \times 3 \times 7 \times 1000}{4 \times \cancel{22}_1 \times 21 \times 21}$
Number of shots = $\frac{3 \times 42 \times 3 \times 7 \times 1000}{4 \times 21 \times 21}$
Cancel 42 with one 21 ($42/21 = 2$):
Number of shots = $\frac{3 \times \cancel{42}^2 \times 3 \times 7 \times 1000}{4 \times \cancel{21}_1 \times 21}$
Number of shots = $\frac{3 \times 2 \times 3 \times 7 \times 1000}{4 \times 21}$
Number of shots = $\frac{126 \times 1000}{84}$
Cancel 126 and 84 by 42 ($126/42 = 3$, $84/42 = 2$):
Number of shots = $\frac{\cancel{126}^3 \times 1000}{\cancel{84}_2}$
Number of shots = $\frac{3 \times 1000}{2}$
Number of shots = $\frac{3000}{2}$
Number of shots = $1500$
This seems correct. Let's verify the cancellation path.
Number of lead shots = $\frac{66 \times 42 \times 21 \times 3 \times 7 \times 1000}{4 \times 22 \times 21 \times 21 \times 21}$
Cancel 21 from top and bottom: $\frac{66 \times 42 \times 3 \times 7 \times 1000}{4 \times 22 \times 21 \times 21}$
Cancel 66 with 22: $\frac{3 \times 42 \times 3 \times 7 \times 1000}{4 \times 1 \times 21 \times 21}$
Cancel 42 with 21: $\frac{3 \times 2 \times 3 \times 7 \times 1000}{4 \times 1 \times 1 \times 21}$
Now we have $\frac{3 \times 2 \times 3 \times 7 \times 1000}{4 \times 21}$.
Numerator: $3 \times 2 \times 3 \times 7 \times 1000 = 6 \times 21 \times 1000 = 126 \times 1000 = 126000$
Denominator: $4 \times 21 = 84$
Number of shots = $\frac{126000}{84}$
Divide 126000 by 84:
$126000 \div 84 = (126 \times 1000) \div 84 = (126/84) \times 1000$
$126/84$: Divide by 6 -> $21/14$. Divide by 7 -> $3/2$. So $126/84 = 3/2$.
Number of shots = $\frac{3}{2} \times 1000 = 3 \times 500 = 1500$.
The calculation is consistent now.
The number of spherical lead shots that can be obtained is 1500.
Question 12. How many spherical lead shots of diameter 4 cm can be made out of a solid cube of lead whose edge measures 44 cm.
Answer:
Given:
Edge of the solid cube of lead ($a$) = 44 cm
Diameter of each spherical lead shot = 4 cm
To Find:
The number of spherical lead shots that can be made from the cube.
Solution:
First, calculate the volume of the solid cube.
Volume of cube = $a^3$
Volume of cube = $(44)^3 \text{ cm}^3$
... (i)
Now, calculate the volume of one spherical lead shot.
Radius of the spherical lead shot ($r$) = $\frac{\text{Diameter}}{2} = \frac{4}{2} = 2 \text{ cm}$
Volume of a sphere = $\frac{4}{3} \pi r^3$
Using $\pi = \frac{22}{7}$:
Volume of one spherical lead shot = $\frac{4}{3} \times \frac{22}{7} \times (2)^3$
Volume of one spherical lead shot = $\frac{4}{3} \times \frac{22}{7} \times 8 \text{ cm}^3$
Volume of one spherical lead shot = $\frac{4 \times 22 \times 8}{3 \times 7} = \frac{704}{21} \text{ cm}^3$
... (ii)
The number of spherical lead shots obtained is the ratio of the volume of the cube to the volume of one spherical lead shot.
Number of lead shots = $\frac{\text{Volume of cube}}{\text{Volume of one spherical lead shot}}$
Number of lead shots = $\frac{44^3}{\frac{704}{21}}$
Number of lead shots = $\frac{44 \times 44 \times 44}{\frac{704}{21}}$
Number of lead shots = $44 \times 44 \times 44 \times \frac{21}{704}$
We know that $44 = 2 \times 22$ and $704 = 32 \times 22$.
Number of lead shots = $44 \times 44 \times \cancel{44}^2 \times \frac{21}{\cancel{704}_{32}}$ (Cancelling 44 with 704 by dividing both by 22)
Number of lead shots = $44 \times 44 \times 2 \times \frac{21}{32}$
Cancel 2 with 32 ($2/32 = 1/16$):
Number of lead shots = $44 \times 44 \times \cancel{2}^1 \times \frac{21}{\cancel{32}_{16}}$
Number of lead shots = $\frac{44 \times 44 \times 21}{16}$
Cancel one 44 with 16 by dividing both by 4 ($44/4 = 11$, $16/4 = 4$):
Number of lead shots = $\frac{\cancel{44}^{11} \times 44 \times 21}{\cancel{16}_4}$
Number of lead shots = $\frac{11 \times 44 \times 21}{4}$
Cancel 44 with 4 ($44/4 = 11$):
Number of lead shots = $\frac{11 \times \cancel{44}^{11} \times 21}{\cancel{4}_1}$
Number of lead shots = $11 \times 11 \times 21$
Number of lead shots = $121 \times 21$
Performing the multiplication:
$121 \times 21 = 121 \times (20 + 1) = 121 \times 20 + 121 \times 1 = 2420 + 121 = 2541$
Alternatively:
$\begin{array}{cc}& & 1 & 2 & 1 \\ \times & & & 2 & 1 \\ \hline && 1 & 2 & 1 \\ 2 & 4 & 2 & \times & \\ \hline 2 & 5 & 4 & 1 \\ \hline \end{array}$
So, the number of lead shots is 2541.
The number of spherical lead shots that can be made is 2541.
Question 13. A wall 24 m long, 0.4 m thick and 6 m high is constructed with the bricks each of dimensions 25 cm × 16 cm × 10 cm. If the mortar occupies $\frac{1}{10}$th of the volume of the wall, then find the number of bricks used in constructing the wall.
Answer:
Given:
Dimensions of the wall:
Length ($L$) = 24 m
Thickness ($T$) = 0.4 m
Height ($H$) = 6 m
Dimensions of each brick:
Length ($l$) = 25 cm
Width ($w$) = 16 cm
Height ($h$) = 10 cm
Volume of mortar = $\frac{1}{10}$ of the volume of the wall
To Find:
The number of bricks used in constructing the wall.
Solution:
First, convert the dimensions of the wall from meters to centimeters to ensure consistent units.
$1 \text{ m} = 100 \text{ cm}$
Wall Length ($L$) = $24 \text{ m} = 24 \times 100 = 2400 \text{ cm}$
Wall Thickness ($T$) = $0.4 \text{ m} = 0.4 \times 100 = 40 \text{ cm}$
Wall Height ($H$) = $6 \text{ m} = 6 \times 100 = 600 \text{ cm}$
Now, calculate the volume of the wall.
Volume of wall = $L \times T \times H$
Volume of wall = $2400 \times 40 \times 600 \text{ cm}^3$
Volume of wall = $24 \times 4 \times 6 \times 100 \times 10 \times 100 \text{ cm}^3$
Volume of wall = $576 \times 10^5 \text{ cm}^3$
Volume of wall = $57,600,000 \text{ cm}^3$
... (i)
Calculate the volume of the mortar in the wall.
Volume of mortar = $\frac{1}{10} \times \text{Volume of wall}$
Volume of mortar = $\frac{1}{10} \times 57,600,000$
Volume of mortar = $5,760,000 \text{ cm}^3$
... (ii)
Calculate the volume of the wall occupied by bricks.
Volume of bricks in wall = Total volume of wall - Volume of mortar
Volume of bricks in wall = $57,600,000 - 5,760,000 \text{ cm}^3$
$\begin{array}{cc} & 57600000 \\ - & \phantom{0}5760000 \\ \hline & 51840000 \\ \hline \end{array}$
Volume of bricks in wall = $51,840,000 \text{ cm}^3$
... (iii)
Now, calculate the volume of one brick.
Volume of one brick = $l \times w \times h$
Volume of one brick = $25 \times 16 \times 10 \text{ cm}^3$
Volume of one brick = $400 \times 10 = 4000 \text{ cm}^3$
... (iv)
Finally, calculate the number of bricks used.
Number of bricks = $\frac{\text{Volume of bricks in wall}}{\text{Volume of one brick}}$
Number of bricks = $\frac{51,840,000}{4000}$
Number of bricks = $\frac{51840}{4}$
Number of bricks = $12960$
The number of bricks used in constructing the wall is 12960.
Question 14. Find the number of metallic circular disc with 1.5 cm base diameter and of height 0.2 cm to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm.
Answer:
Given:
For the metallic circular disc (which is a cylinder):
Base diameter ($d_{disc}$) = 1.5 cm
Height ($h_{disc}$) = 0.2 cm
For the right circular cylinder to be formed:
Height ($h_{cyl}$) = 10 cm
Diameter ($d_{cyl}$) = 4.5 cm
To Find:
The number of metallic circular discs to be melted to form the cylinder.
Solution:
First, calculate the radius of the disc and the cylinder from their respective diameters.
Radius of disc ($r_{disc}$) = $\frac{d_{disc}}{2} = \frac{1.5}{2} = 0.75 \text{ cm}$
Radius of cylinder ($r_{cyl}$) = $\frac{d_{cyl}}{2} = \frac{4.5}{2} = 2.25 \text{ cm}$
The volume of a cylinder is given by the formula $V = \pi r^2 h$.
Calculate the volume of one metallic circular disc.
Volume of one disc ($V_{disc}$) = $\pi r_{disc}^2 h_{disc}$
$V_{disc} = \pi \times (0.75)^2 \times 0.2 \text{ cm}^3$
... (i)
Calculate the volume of the right circular cylinder to be formed.
Volume of cylinder ($V_{cyl}$) = $\pi r_{cyl}^2 h_{cyl}$
$V_{cyl} = \pi \times (2.25)^2 \times 10 \text{ cm}^3$
... (ii)
The number of discs needed is the ratio of the volume of the cylinder to the volume of one disc.
Number of discs = $\frac{V_{cyl}}{V_{disc}}$
Number of discs = $\frac{\pi \times (2.25)^2 \times 10}{\pi \times (0.75)^2 \times 0.2}$
Cancel $\pi$ from the numerator and denominator:
Number of discs = $\frac{(2.25)^2 \times 10}{(0.75)^2 \times 0.2}$
Note that $2.25 = 3 \times 0.75$. Substituting this into the expression:
Number of discs = $\frac{(3 \times 0.75)^2 \times 10}{(0.75)^2 \times 0.2}$
Number of discs = $\frac{3^2 \times (0.75)^2 \times 10}{(0.75)^2 \times 0.2}$
Cancel $(0.75)^2$ from the numerator and denominator:
Number of discs = $\frac{9 \times 10}{0.2}$
Number of discs = $\frac{90}{0.2}$
To divide by a decimal, multiply the numerator and denominator by 10:
Number of discs = $\frac{90 \times 10}{0.2 \times 10} = \frac{900}{2}$
Number of discs = $450$
... (iii)
The number of metallic circular discs required is 450.
Sample Question 1 to 3 (Before Exercise 12.4)
Sample Question 1: A bucket is in the form of a frustum of a cone of height 30 cm with radii of its lower and upper ends as 10 cm and 20 cm, respectively. Find the capacity and surface area of the bucket. Also, find the cost of milk which can completely fill the container, at the rate of Rs 25 per litre ( use π = 3.14).
Answer:
Given:
Height of the frustum ($h$) = 30 cm
Radius of the lower end ($r_1$) = 10 cm
Radius of the upper end ($r_2$) = 20 cm
Cost of milk = $\textsf{₹}$ 25 per litre
Use $\pi = 3.14$
To Find:
1. Capacity (Volume) of the bucket.
2. Surface area of the bucket.
3. Cost of milk to fill the bucket.
Solution:
The bucket is in the shape of a frustum of a cone.
The formula for the volume of a frustum of a cone is $V = \frac{1}{3}\pi h (r_1^2 + r_2^2 + r_1 r_2)$.
Calculate the capacity (volume) of the bucket:
Capacity = $\frac{1}{3} \times 3.14 \times 30 \times (10^2 + 20^2 + 10 \times 20)$
Capacity = $3.14 \times 10 \times (100 + 400 + 200)$
Capacity = $31.4 \times (700)$
Capacity = $21980 \text{ cm}^3$
... (1)
To find the cost of milk, we need to convert the volume from cubic centimeters to litres.
$1 \text{ litre} = 1000 \text{ cm}^3$
Capacity in litres = $\frac{21980}{1000} = 21.98 \text{ litres}$
... (2)
Calculate the cost of milk:
Cost of milk = Capacity in litres $\times$ Rate per litre
Cost of milk = $21.98 \times 25$
Cost of milk = $\textsf{₹}$ 549.50
... (3)
Now, calculate the surface area of the bucket. The surface area consists of the curved surface area of the frustum and the area of the lower circular base (assuming the bucket is open at the top).
First, find the slant height ($l$) of the frustum.
The formula for slant height is $l = \sqrt{h^2 + (r_2 - r_1)^2}$.
Slant height $l = \sqrt{30^2 + (20 - 10)^2}$
Slant height $l = \sqrt{900 + 10^2}$
Slant height $l = \sqrt{900 + 100}$
Slant height $l = \sqrt{1000}$
Slant height $l = \sqrt{100 \times 10} = 10\sqrt{10} \text{ cm}$
For calculation with $\pi = 3.14$, it's likely expected to use an approximate value for $\sqrt{10}$. $\sqrt{9} = 3$, $\sqrt{16} = 4$. $\sqrt{10}$ is close to 3.16.
Let's assume we can proceed with $10\sqrt{10}$ or use a rounded value if needed. The problem does not specify how to handle $\sqrt{10}$. Let's calculate the curved surface area first.
The formula for the curved surface area of a frustum is $CSA = \pi (r_1 + r_2)l$.
CSA = $3.14 \times (10 + 20) \times 10\sqrt{10}$
CSA = $3.14 \times 30 \times 10\sqrt{10}$
CSA = $94.2 \times 10\sqrt{10} = 942\sqrt{10} \text{ cm}^2$
If we use $\sqrt{10} \approx 3.16$: CSA $\approx 942 \times 3.16 = 2977.52 \text{ cm}^2$.
The area of the lower base is $A_{base} = \pi r_1^2$.
A$_{base}$ = $3.14 \times (10)^2$
A$_{base}$ = $3.14 \times 100 = 314 \text{ cm}^2$
The total surface area of the bucket (open at the top) is CSA + A$_{base}$.
Total Surface Area = $942\sqrt{10} + 314 \text{ cm}^2$
... (4)
Using the approximation $\sqrt{10} \approx 3.16$:
Total Surface Area $\approx 2977.52 + 314$
Total Surface Area $\approx 3291.52 \text{ cm}^2$
... (5)
Sometimes, for simplicity, $\sqrt{10}$ is approximated to 3.16 or 3.162. Let's state the result using the approximation.
Capacity of the bucket = $21980 \text{ cm}^3$ or $21.98 \text{ litres}$.
Cost of milk = $\textsf{₹}$ 549.50.
Surface area of the bucket $\approx 3291.52 \text{ cm}^2$ (using $\sqrt{10} \approx 3.16$).
If a more precise value of $\sqrt{10}$ is used (e.g., from a calculator, $\approx 3.162277$), the surface area would be slightly different.
CSA $\approx 942 \times 3.162277 \approx 2979.06 \text{ cm}^2$
Total Surface Area $\approx 2979.06 + 314 = 3293.06 \text{ cm}^2$.
Given $\pi = 3.14$ was specified, it's likely intended to use this approximation for $\pi$ and calculate $\sqrt{10}$ if needed. The problem does not give $\sqrt{10}$ value. Let's use the value derived from the calculation $3.16$ which is a common approximation or keep the $\sqrt{10}$ form.
Final answers based on calculations:
Capacity of the bucket = $21980 \text{ cm}^3$
Capacity in litres = $21.98 \text{ litres}$
Cost of milk = $\textsf{₹}$ 549.50
Surface area of the bucket (Curved surface area + Area of lower base) = $942\sqrt{10} + 314 \text{ cm}^2$
Using $\sqrt{10} \approx 3.16$, Surface area $\approx 3291.52 \text{ cm}^2$.
Sample Question 2: A solid toy is in the form of a hemisphere surmounted by a right circular cone. The height of the cone is 4 cm and the diameter of the base is 8 cm. Determine the volume of the toy. If a cube circumscribes the toy, then find the difference of the volumes of cube and the toy. Also, find the total surface area of the toy
Answer:
Given:
The toy is a hemisphere surmounted by a cone.
Height of the cone ($h$) = 4 cm
Diameter of the base of the cone and hemisphere = 8 cm
To Find:
1. Volume of the toy.
2. Difference in volumes of the circumscribing cube and the toy.
3. Total surface area of the toy.
Solution:
The radius of the base of the cone and the radius of the hemisphere are the same.
Radius ($r$) = $\frac{\text{Diameter}}{2} = \frac{8}{2} = 4 \text{ cm}$
... (1)
The height of the cone is $h = 4 \text{ cm}$.
The volume of the toy is the sum of the volume of the cone and the volume of the hemisphere.
Volume of cone = $\frac{1}{3} \pi r^2 h$
Volume of cone = $\frac{1}{3} \pi (4)^2 (4) = \frac{1}{3} \pi (16)(4) = \frac{64}{3}\pi \text{ cm}^3$
... (2)
Volume of hemisphere = $\frac{2}{3} \pi r^3$}
Volume of hemisphere = $\frac{2}{3} \pi (4)^3 = \frac{2}{3} \pi (64) = \frac{128}{3}\pi \text{ cm}^3$
... (3)
Volume of the toy = Volume of cone + Volume of hemisphere
Volume of toy = $\frac{64}{3}\pi + \frac{128}{3}\pi = \frac{64+128}{3}\pi = \frac{192}{3}\pi = 64\pi \text{ cm}^3$
... (4)
Using $\pi \approx 3.14$:
Volume of toy $\approx 64 \times 3.14 = 200.96 \text{ cm}^3$
Next, consider the cube that circumscribes the toy.
The maximum width of the toy is the diameter of the base, which is 8 cm.
The maximum height of the toy is the height of the cone plus the radius of the hemisphere = $4 \text{ cm} + 4 \text{ cm} = 8 \text{ cm}$.
Thus, the smallest cube that can circumscribe the toy must have an edge equal to the maximum dimension, which is 8 cm.
Edge of the cube ($s$) = 8 cm
Volume of the cube = $s^3$
Volume of cube = $8^3 = 512 \text{ cm}^3$
... (5)
The difference of the volumes of the cube and the toy is:
Difference in volumes = Volume of cube - Volume of toy
Difference in volumes = $512 - 64\pi \text{ cm}^3$
... (6)
Using $\pi \approx 3.14$:
Difference in volumes $\approx 512 - 200.96 = 311.04 \text{ cm}^3$
Finally, calculate the total surface area of the toy.
The total surface area of the toy is the sum of the curved surface area of the cone and the curved surface area of the hemisphere. The base of the cone (which is also the base of the hemisphere) is internal and not part of the surface area.
First, calculate the slant height ($l$) of the cone.
The formula for slant height is $l = \sqrt{r^2 + h^2}$.
Slant height $l = \sqrt{4^2 + 4^2} = \sqrt{16 + 16} = \sqrt{32}$
Slant height $l = \sqrt{16 \times 2} = 4\sqrt{2} \text{ cm}$
... (7)
Using $\sqrt{2} \approx 1.414$:
Slant height $l \approx 4 \times 1.414 = 5.656 \text{ cm}$
Curved surface area of cone = $\pi r l$
CSA of cone = $\pi (4) (4\sqrt{2}) = 16\sqrt{2}\pi \text{ cm}^2$
Using $\pi \approx 3.14$ and $\sqrt{2} \approx 1.414$:
CSA of cone $\approx 3.14 \times 4 \times 5.656 \approx 71.05 \text{ cm}^2$
Curved surface area of hemisphere = $2 \pi r^2$
CSA of hemisphere = $2 \pi (4)^2 = 2 \pi (16) = 32\pi \text{ cm}^2$
Using $\pi \approx 3.14$:
CSA of hemisphere $\approx 2 \times 3.14 \times 16 = 6.28 \times 16 = 100.48 \text{ cm}^2$
Total surface area of toy = CSA of cone + CSA of hemisphere
Total Surface Area = $16\sqrt{2}\pi + 32\pi = (32 + 16\sqrt{2})\pi \text{ cm}^2$
... (8)
Using $\pi \approx 3.14$ and $\sqrt{2} \approx 1.414$:
Total Surface Area $\approx 71.05 + 100.48 = 171.53 \text{ cm}^2$
Volume of the toy is $64\pi \text{ cm}^3$ (or $\approx 200.96 \text{ cm}^3$).
Difference in volumes of the cube and the toy is $512 - 64\pi \text{ cm}^3$ (or $\approx 311.04 \text{ cm}^3$).
Total surface area of the toy is $(32 + 16\sqrt{2})\pi \text{ cm}^2$ (or $\approx 171.53 \text{ cm}^2$ using $\pi \approx 3.14$ and $\sqrt{2} \approx 1.414$).
Sample Question 3: A building is in the form of a cylinder surmounted by a hemispherical dome (see Fig. 12.12). The base diameter of the dome is equal to $\frac{2}{3}$ of the total height of the building. Find the height of the building, if it contains $67\frac{1}{21}$ m3 of air.

Answer:
Given:
The building is in the shape of a cylinder surmounted by a hemispherical dome.
Base diameter of the dome = $\frac{2}{3}$ of the total height of the building.
Volume of air inside the building = $67\frac{1}{21}$ m$^3$.
To Find:
The total height of the building.
Solution:
Let the total height of the building be $H$ meters.
Let the radius of the hemispherical dome and the base of the cylinder be $r$ meters.
Let the height of the cylindrical part be $h$ meters.
According to the given condition:
Diameter of dome = $\frac{2}{3} H$
$2r = \frac{2}{3} H$
$r = \frac{1}{3} H$
... (1)
The total height of the building is the sum of the height of the cylindrical part and the height of the hemispherical part.
The height of the hemispherical part is equal to its radius, $r$.
$H = h + r$
Substitute the value of $r$ from (1):
$H = h + \frac{1}{3} H$
$h = H - \frac{1}{3} H = \frac{2}{3} H$
... (2)
So, the radius of the base is $r = \frac{1}{3}H$ and the height of the cylinder is $h = \frac{2}{3}H$.
The volume of the building is the sum of the volume of the cylinder and the volume of the hemisphere.
Volume of cylinder = $\pi r^2 h$
Volume of cylinder = $\pi \left(\frac{1}{3}H\right)^2 \left(\frac{2}{3}H\right) = \pi \left(\frac{1}{9}H^2\right) \left(\frac{2}{3}H\right) = \frac{2}{27}\pi H^3$
... (3)
Volume of hemisphere = $\frac{2}{3} \pi r^3$
Volume of hemisphere = $\frac{2}{3} \pi \left(\frac{1}{3}H\right)^3 = \frac{2}{3} \pi \left(\frac{1}{27}H^3\right) = \frac{2}{81}\pi H^3$
... (4)
Total Volume of building = Volume of cylinder + Volume of hemisphere
Total Volume = $\frac{2}{27}\pi H^3 + \frac{2}{81}\pi H^3$
Total Volume = $\left(\frac{2}{27} + \frac{2}{81}\right) \pi H^3$
Total Volume = $\left(\frac{2 \times 3}{27 \times 3} + \frac{2}{81}\right) \pi H^3 = \left(\frac{6}{81} + \frac{2}{81}\right) \pi H^3 = \frac{8}{81}\pi H^3$
... (5)
The given volume of air in the building is $67\frac{1}{21}$ m$^3$.
Given Volume = $67 + \frac{1}{21} = \frac{67 \times 21 + 1}{21} = \frac{1407 + 1}{21} = \frac{1408}{21}$ m$^3$
... (6)
Equating the total volume (5) with the given volume (6):
$\frac{8}{81}\pi H^3 = \frac{1408}{21}$
Using $\pi = \frac{22}{7}$:
$\frac{8}{81} \times \frac{22}{7} \times H^3 = \frac{1408}{21}$
$\frac{176}{567} H^3 = \frac{1408}{21}$
Solve for $H^3$:
$H^3 = \frac{1408}{21} \times \frac{567}{176}$
Simplify the expression by cancelling common factors:
$H^3 = \frac{\cancel{1408}^{8}}{\cancel{21}_1} \times \frac{\cancel{567}^{27}}{\cancel{176}_1}$
$H^3 = 8 \times 27$
$H^3 = 216$
... (7)
To find $H$, take the cube root of 216.
$H = \sqrt[3]{216}$
Since $216 = 6 \times 6 \times 6 = 6^3$:
$H = 6$ meters
... (8)
The height of the building is 6 meters.
Exercise 12.4
Question 1. A solid metallic hemisphere of radius 8 cm is melted and recasted into a right circular cone of base radius 6 cm. Determine the height of the cone.
Answer:
Given:
Radius of the solid metallic hemisphere ($r_h$) = 8 cm
Radius of the base of the right circular cone ($r_c$) = 6 cm
To Find:
The height of the cone ($h_c$).
Solution:
When a solid is melted and recasted into another solid, the volume remains the same.
Volume of hemisphere = $\frac{2}{3} \pi r_h^3$
Volume of hemisphere = $\frac{2}{3} \pi (8)^3$
Volume of hemisphere = $\frac{2}{3} \pi (512) = \frac{1024}{3}\pi \text{ cm}^3$
... (i)
Volume of right circular cone = $\frac{1}{3} \pi r_c^2 h_c$
Volume of cone = $\frac{1}{3} \pi (6)^2 h_c = \frac{1}{3} \pi (36) h_c = 12\pi h_c \text{ cm}^3$
... (ii)
According to the problem, the volume of the hemisphere is equal to the volume of the cone formed.
Volume of hemisphere = Volume of cone
$\frac{1024}{3}\pi = 12\pi h_c$
Cancel $\pi$ from both sides (since $\pi \neq 0$):
$\frac{1024}{3} = 12 h_c$
Solve for $h_c$:
$h_c = \frac{1024}{3 \times 12}$
$h_c = \frac{1024}{36}$
Simplify the fraction by dividing both numerator and denominator by their greatest common divisor. Both are divisible by 4.
$\frac{\cancel{1024}^{256}}{\cancel{36}_{9}}$
$h_c = \frac{256}{9}$ cm
... (iii)
The height can also be expressed as a mixed number or decimal.
$256 \div 9$
$256 = 9 \times 28 + 4$
$h_c = 28\frac{4}{9}$ cm
As a decimal:
$256 \div 9 \approx 28.44...$
$h_c \approx 28.44$ cm (rounded to two decimal places)
The height of the cone is $\frac{256}{9}$ cm or $28\frac{4}{9}$ cm.
Question 2. A rectangular water tank of base 11 m × 6 m contains water upto a height of 5 m. If the water in the tank is transferred to a cylindrical tank of radius 3.5 m, find the height of the water level in the tank.
Answer:
Given:
Dimensions of the rectangular water tank:
Length ($l$) = 11 m
Breadth ($b$) = 6 m
Height of water level ($h_r$) = 5 m
Radius of the cylindrical tank ($r_c$) = 3.5 m
To Find:
The height of the water level in the cylindrical tank ($h_c$).
Solution:
When water is transferred from the rectangular tank to the cylindrical tank, the volume of water remains constant.
First, calculate the volume of water in the rectangular tank.
Volume of water in rectangular tank = $l \times b \times h_r$
Volume of water = $11 \times 6 \times 5 \text{ m}^3$
Volume of water = $330 \text{ m}^3$
... (i)
Now, consider the cylindrical tank. Let the height of the water level in the cylindrical tank be $h_c$.
The radius of the cylindrical tank is $r_c = 3.5$ m, which can be written as $\frac{35}{10} = \frac{7}{2}$ m.
The volume of water in the cylindrical tank is given by the formula $\pi r_c^2 h_c$.
Volume of water = $\pi (3.5)^2 h_c \text{ m}^3$
Volume of water = $\pi \left(\frac{7}{2}\right)^2 h_c = \pi \left(\frac{49}{4}\right) h_c \text{ m}^3$
... (ii)
Equating the volume of water in both tanks (from (i) and (ii)):
$330 = \pi \left(\frac{49}{4}\right) h_c$
Using the value $\pi = \frac{22}{7}$:
$330 = \frac{22}{7} \times \frac{49}{4} \times h_c$
Simplify the right side:
$330 = \frac{22}{\cancel{7}_1} \times \frac{\cancel{49}^7}{4} \times h_c$
$330 = \frac{22 \times 7}{4} \times h_c$
$330 = \frac{154}{4} \times h_c$
$330 = \frac{77}{2} h_c$
Solve for $h_c$:
$h_c = 330 \times \frac{2}{77}$
Cancel common factors. Both 330 and 77 are divisible by 11.
$h_c = \frac{\cancel{330}^{30} \times 2}{\cancel{77}_7}$
$h_c = \frac{30 \times 2}{7} = \frac{60}{7}$ meters
... (iii)
The height can also be expressed as a mixed number or decimal.
$60 \div 7$
$60 = 7 \times 8 + 4$
$h_c = 8\frac{4}{7}$ meters
As a decimal:
$60 \div 7 \approx 8.571...$
$h_c \approx 8.57$ meters (rounded to two decimal places)
The height of the water level in the cylindrical tank is $\frac{60}{7}$ meters or $8\frac{4}{7}$ meters.
Question 3. How many cubic centimetres of iron is required to construct an open box whose external dimensions are 36 cm, 25 cm and 16.5 cm provided the thickness of the iron is 1.5 cm. If one cubic cm of iron weighs 7.5 g, find the weight of the box.
Answer:
Given:
External dimensions of the open box:
External Length ($L$) = 36 cm
External Breadth ($B$) = 25 cm
External Height ($H$) = 16.5 cm
Thickness of the iron ($t$) = 1.5 cm
Weight of 1 cubic cm of iron = 7.5 g
To Find:
1. The volume of iron required to construct the box.
2. The weight of the box.
Solution:
First, calculate the external volume of the box.
External Volume = $L \times B \times H$
External Volume = $36 \times 25 \times 16.5 \text{ cm}^3$
$36 \times 25 = 900$
External Volume = $900 \times 16.5 \text{ cm}^3$
$900 \times 16.5 = 9 \times 100 \times 16.5 = 9 \times 1650$
$9 \times 1650 = 14850$
External Volume = $14850 \text{ cm}^3$
... (i)
Next, calculate the internal dimensions of the box. Since the box is open at the top, the thickness is subtracted from the length and breadth on both sides, but from the height only at the base.
Internal Length ($l$) = $L - 2t = 36 - 2(1.5) = 36 - 3 = 33 \text{ cm}$
Internal Breadth ($b$) = $B - 2t = 25 - 2(1.5) = 25 - 3 = 22 \text{ cm}$
Internal Height ($h$) = $H - t = 16.5 - 1.5 = 15 \text{ cm}$
Now, calculate the internal volume of the box.
Internal Volume = $l \times b \times h$
Internal Volume = $33 \times 22 \times 15 \text{ cm}^3$
$33 \times 22 = 726$
Internal Volume = $726 \times 15 \text{ cm}^3$
$\begin{array}{cc}& & 7 & 2 & 6 \\ \times & & & 1 & 5 \\ \hline & 3 & 6 & 3 & 0 \\ 7 & 2 & 6 & \times & \\ \hline 10 & 8 & 9 & 0 \\ \hline \end{array}$
Internal Volume = $10890 \text{ cm}^3$
... (ii)
The volume of iron required is the difference between the external volume and the internal volume.
Volume of iron = External Volume - Internal Volume
Volume of iron = $14850 - 10890 \text{ cm}^3$
$\begin{array}{cc} & 14850 \\ - & 10890 \\ \hline & \phantom{0}3960 \\ \hline \end{array}$
Volume of iron = $3960 \text{ cm}^3$
... (iii)
Now, calculate the weight of the box.
Weight of the box = Volume of iron $\times$ Weight per cubic cm
Weight of the box = $3960 \times 7.5 \text{ g}$
$3960 \times 7.5 = 3960 \times \frac{15}{2} = 1980 \times 15$
$\begin{array}{cc}& & 1 & 9 & 8 & 0 \\ \times & & & & 1 & 5 \\ \hline & 9 & 9 & 0 & 0 \\ 1 & 9 & 8 & 0 & \times & \\ \hline 2 & 9 & 7 & 0 & 0 \\ \hline \end{array}$
Weight of the box = $29700 \text{ g}$
... (iv)
The weight can also be expressed in kilograms.
Weight of the box = $\frac{29700}{1000} \text{ kg} = 29.7 \text{ kg}$
The volume of iron required is 3960 cm$^3$.
The weight of the box is 29700 g (or 29.7 kg).
Question 4. The barrel of a fountain pen, cylindrical in shape, is 7 cm long and 5 mm in diameter. A full barrel of ink in the pen is used up on writing 3300 words on an average. How many words can be written in a bottle of ink containing one fifth of a litre?
Answer:
Given:
For the cylindrical fountain pen barrel:
Length ($h$) = 7 cm
Diameter ($d$) = 5 mm
Number of words written with one barrel = 3300 words
Volume of ink in the bottle = $\frac{1}{5}$ litre
To Find:
The total number of words that can be written with the ink in the bottle.
Solution:
First, ensure all measurements are in the same unit. Convert the diameter of the barrel from millimeters to centimeters.
Diameter of barrel ($d$) = 5 mm = $\frac{5}{10} \text{ cm} = 0.5 \text{ cm}$
Calculate the radius of the barrel.
Radius of barrel ($r$) = $\frac{d}{2} = \frac{0.5}{2} = 0.25 \text{ cm}$
... (1)
Calculate the volume of ink in a full barrel (which is the volume of the cylindrical barrel).
Volume of cylinder = $\pi r^2 h$
Volume of one barrel = $\pi (0.25)^2 (7)$
Volume of one barrel = $\pi (0.0625) (7)$
Volume of one barrel = $0.4375\pi \text{ cm}^3$
... (2)
Next, calculate the total volume of ink in the bottle. Convert the volume from litres to cubic centimeters.
1 litre = 1000 cm$^3$
Volume of ink in bottle = $\frac{1}{5} \text{ litre} = \frac{1}{5} \times 1000 \text{ cm}^3 = 200 \text{ cm}^3$
... (3)
The number of words written per cubic centimeter of ink is the number of words per barrel divided by the volume of one barrel.
Words per cm$^3$ = $\frac{\text{Words per barrel}}{\text{Volume of one barrel}} = \frac{3300}{0.4375\pi}$ words/cm$^3$
... (4)
The total number of words that can be written with the ink in the bottle is the volume of ink in the bottle multiplied by the words written per cubic centimeter.
Total words = Volume of ink in bottle $\times$ Words per cm$^3$
Total words = $200 \times \frac{3300}{0.4375\pi}$
Using $\pi = \frac{22}{7}$:
Total words = $200 \times \frac{3300}{0.4375 \times \frac{22}{7}}$
Total words = $200 \times \frac{3300 \times 7}{0.4375 \times 22}$
Convert 0.4375 to a fraction: $0.4375 = \frac{4375}{10000} = \frac{875}{2000} = \frac{175}{400} = \frac{35}{80} = \frac{7}{16}$.
Total words = $200 \times \frac{3300 \times 7}{\frac{7}{16} \times 22}$
Total words = $200 \times \frac{3300 \times 7 \times 16}{7 \times 22}$
Cancel 7 from numerator and denominator:
Total words = $200 \times \frac{3300 \times \cancel{7} \times 16}{\cancel{7} \times 22}$
Total words = $200 \times \frac{3300 \times 16}{22}$
Cancel 3300 with 22. $3300 = 11 \times 300$, $22 = 11 \times 2$.
Total words = $200 \times \frac{\cancel{3300}^{300} \times 16}{\cancel{22}_2}$
Total words = $200 \times \frac{300 \times 16}{2}$
Cancel 16 with 2:
Total words = $200 \times 300 \times \cancel{16}^8 / \cancel{2}_1$
Total words = $200 \times 300 \times 8$
Total words = $60000 \times 8 = 480000$
... (5)
480000 words can be written from the bottle of ink.
Question 5. Water flows at the rate of 10m/minute through a cylindrical pipe 5 mm in diameter. How long would it take to fill a conical vessel whose diameter at the base is 40 cm and depth 24 cm?
Answer:
Given:
Rate of water flow from cylindrical pipe = 10 m/minute
Diameter of cylindrical pipe ($d_p$) = 5 mm
Diameter of conical vessel base ($d_c$) = 40 cm
Depth (height) of conical vessel ($h_c$) = 24 cm
To Find:
Time taken to fill the conical vessel.
Solution:
First, ensure all dimensions and rates are in consistent units. Let's use centimeters and minutes.
Rate of water flow = 10 m/minute = $10 \times 100 \text{ cm/minute} = 1000 \text{ cm/minute}$
Diameter of pipe ($d_p$) = 5 mm = $\frac{5}{10} \text{ cm} = 0.5 \text{ cm}$
Radius of pipe ($r_p$) = $\frac{d_p}{2} = \frac{0.5}{2} \text{ cm} = 0.25 \text{ cm}$
... (1)
Diameter of cone base ($d_c$) = 40 cm
Radius of cone base ($r_c$) = $\frac{d_c}{2} = \frac{40}{2} \text{ cm} = 20 \text{ cm}$
... (2)
Height of cone ($h_c$) = 24 cm
Calculate the volume of the conical vessel.
The formula for the volume of a cone is $V = \frac{1}{3} \pi r^2 h$.
Volume of cone ($V_c$) = $\frac{1}{3} \times \pi \times r_c^2 \times h_c$
V$_c$ = $\frac{1}{3} \times \pi \times (20)^2 \times 24 \text{ cm}^3$
V$_c$ = $\frac{1}{\cancel{3}_1} \times \pi \times 400 \times \cancel{24}^8$
V$_c$ = $3200\pi \text{ cm}^3$
... (i)
Calculate the volume of water flowing from the pipe per minute.
This is the volume of a cylinder with radius equal to the pipe's radius ($r_p$) and height equal to the flow rate (1000 cm/minute).
Volume flow rate = $\pi \times (\text{pipe radius})^2 \times \text{flow rate}$
Volume flow rate ($V_f$) = $\pi \times (0.25)^2 \times 1000 \text{ cm}^3\text{/minute}$
V$_f$ = $\pi \times (0.0625) \times 1000$
V$_f$ = $62.5\pi \text{ cm}^3\text{/minute}$
... (ii)
The time taken to fill the conical vessel is the total volume of the cone divided by the volume of water flowing per minute.
Time taken = $\frac{\text{Volume of cone (V}_c\text{)}}{\text{Volume flow rate (V}_f\text{)}}$
Time taken = $\frac{3200\pi \text{ cm}^3}{62.5\pi \text{ cm}^3\text{/minute}}$
Cancel $\pi$ from the numerator and denominator:
Time taken = $\frac{3200}{62.5}$ minutes
To perform the division, we can write $62.5$ as $\frac{125}{2}$ or multiply numerator and denominator by 10:
Time taken = $\frac{3200 \times 10}{62.5 \times 10} = \frac{32000}{625}$ minutes
Simplify the fraction by dividing both numerator and denominator by 25:
$32000 \div 25 = \frac{32000}{100} \times 4 = 320 \times 4 = 1280$
$625 \div 25 = 25$
Time taken = $\frac{\cancel{32000}^{1280}}{\cancel{625}_{25}}$ minutes
Time taken = $\frac{1280}{25}$ minutes
Divide 1280 by 25:
$1280 \div 25 = 51$ with a remainder of 5 ($25 \times 51 = 1275$).
$\frac{1280}{25} = \frac{1275 + 5}{25} = \frac{1275}{25} + \frac{5}{25} = 51 + \frac{1}{5} = 51 + 0.2 = 51.2$
Time taken = $51.2$ minutes
... (iii)
It would take 51.2 minutes to fill the conical vessel.
Question 6. A heap of rice is in the form of a cone of diameter 9 m and height 3.5 m. Find the volume of the rice. How much canvas cloth is required to just cover the heap?
Answer:
Given:
The heap of rice is in the form of a cone.
Diameter of the base of the cone ($d$) = 9 m
Height of the cone ($h$) = 3.5 m
To Find:
1. The volume of the rice (volume of the cone).
2. The amount of canvas cloth required to cover the heap (curved surface area of the cone).
Solution:
First, calculate the radius of the base from the diameter.
Radius ($r$) = $\frac{\text{Diameter}}{2} = \frac{9}{2} = 4.5 \text{ m}$
Calculate the volume of the cone using the formula $V = \frac{1}{3} \pi r^2 h$. Using $\pi = \frac{22}{7}$:
Volume = $\frac{1}{3} \pi (4.5)^2 (3.5)$
Volume = $\frac{1}{3} \times \frac{22}{7} \times (\frac{9}{2})^2 \times \frac{7}{2}$
Volume = $\frac{1}{3} \times \frac{22}{7} \times \frac{81}{4} \times \frac{7}{2}$
Volume = $\frac{1}{\cancel{3}_1} \times \frac{22}{\cancel{7}_1} \times \frac{\cancel{81}^{27}}{4} \times \frac{\cancel{7}_1}{2}$
Volume = $\frac{22 \times 27}{4 \times 2} = \frac{22 \times 27}{8}$
Volume = $\frac{\cancel{22}^{11} \times 27}{\cancel{8}_4} = \frac{11 \times 27}{4}$
Volume = $\frac{297}{4} = 74.25 \text{ m}^3$
... (i)
The volume of the rice is $74.25 \text{ m}^3$.
To find the amount of canvas cloth required to cover the heap, we need to calculate the curved surface area (CSA) of the cone. This requires the slant height ($l$).
The formula for slant height is $l = \sqrt{r^2 + h^2}$.
Slant height $l = \sqrt{(4.5)^2 + (3.5)^2}$
Slant height $l = \sqrt{(\frac{9}{2})^2 + (\frac{7}{2})^2}$
Slant height $l = \sqrt{\frac{81}{4} + \frac{49}{4}} = \sqrt{\frac{81+49}{4}} = \sqrt{\frac{130}{4}}$
Slant height $l = \frac{\sqrt{130}}{\sqrt{4}} = \frac{\sqrt{130}}{2} \text{ m}$
... (ii)
The formula for the curved surface area of a cone is $CSA = \pi r l$. Using $\pi = \frac{22}{7}$:
CSA = $\frac{22}{7} \times \frac{9}{2} \times \frac{\sqrt{130}}{2}$
CSA = $\frac{\cancel{22}^{11}}{7} \times \frac{9}{\cancel{2}_1} \times \frac{\sqrt{130}}{2} = \frac{11 \times 9 \times \sqrt{130}}{7 \times 2}$
CSA = $\frac{99\sqrt{130}}{14} \text{ m}^2$
... (iii)
For a numerical value, we use $\sqrt{130} \approx 11.40175$.
CSA $\approx \frac{99 \times 11.40175}{14} \approx \frac{1128.773}{14}$
CSA $\approx 80.6266$ m$^2$
CSA $\approx 80.63 \text{ m}^2$ (rounded to two decimal places)
... (iv)
The amount of canvas cloth required to just cover the heap is the curved surface area of the cone.
The volume of the rice is 74.25 m$^3$.
The amount of canvas cloth required to just cover the heap is $\frac{99\sqrt{130}}{14} \text{ m}^2$ or approximately 80.63 m$^2$.
Question 7. A factory manufactures 120000 pencils daily. The pencils are cylindrical in shape each of length 25 cm and circumference of base as 1.5 cm. Determine the cost of colouring the curved surfaces of the pencils manufactured in one day at Rs 0.05 per dm2 .
Answer:
Given:
Number of pencils manufactured daily = 120000
Each pencil is cylindrical in shape.
Length (height) of each pencil ($h$) = 25 cm
Circumference of the base of each pencil ($C$) = 1.5 cm
Cost of colouring = $\textsf{₹}$ 0.05 per dm$^2$
To Find:
The total cost of colouring the curved surfaces of the pencils manufactured in one day.
Solution:
The curved surface area of a cylinder is given by the formula $CSA = 2\pi r h$, where $r$ is the radius of the base and $h$ is the height.
We are given the circumference of the base, $C = 2\pi r$.
Circumference $C = 1.5$ cm
From the circumference, we can find the radius or keep it as $2\pi r$.
The curved surface area of one pencil is:
CSA of one pencil = $(2\pi r) \times h$
Substitute the given values:
CSA of one pencil = $1.5 \text{ cm} \times 25 \text{ cm}$
CSA of one pencil = $37.5 \text{ cm}^2$
... (i)
Now, calculate the total curved surface area of all pencils manufactured in one day.
Total CSA = Number of pencils $\times$ CSA of one pencil
Total CSA = $120000 \times 37.5 \text{ cm}^2$
Total CSA = $120000 \times \frac{75}{2}$
Total CSA = $60000 \times 75$
Total CSA = $4500000 \text{ cm}^2$
... (ii)
The cost of colouring is given per dm$^2$. Convert the total CSA from cm$^2$ to dm$^2$.
$1 \text{ dm} = 10 \text{ cm}$
$1 \text{ dm}^2 = (10 \text{ cm})^2 = 100 \text{ cm}^2$
Total CSA in dm$^2$ = $\frac{\text{Total CSA in cm}^2}{100}$
Total CSA in dm$^2$ = $\frac{4500000}{100} = 45000 \text{ dm}^2$
... (iii)
Calculate the total cost of colouring.
Total Cost = Total CSA in dm$^2 \times$ Cost per dm$^2$
Total Cost = $45000 \times \textsf{₹}\ 0.05$
Total Cost = $45000 \times \frac{5}{100}$
Total Cost = $450 \times 5$
Total Cost = $\textsf{₹}\ 2250$
... (iv)
The cost of colouring the curved surfaces of the pencils manufactured in one day is $\textsf{₹}\ 2250$.
Question 8. Water is flowing at the rate of 15 km/h through a pipe of diameter 14 cm into a cuboidal pond which is 50 m long and 44 m wide. In what time will the level of water in pond rise by 21 cm?
Answer:
Given:
Rate of water flow from cylindrical pipe = 15 km/h
Diameter of cylindrical pipe ($d_p$) = 14 cm
Cuboidal pond length ($L$) = 50 m
Cuboidal pond width ($B$) = 44 m
Required rise in water level ($H$) = 21 cm
To Find:
Time taken for the water level in the pond to rise by 21 cm.
Solution:
First, ensure all measurements are in consistent units. Let's convert everything to meters and hours based on the flow rate unit.
Rate of water flow = $15 \text{ km/h} = 15 \times 1000 \text{ m/h} = 15000 \text{ m/h}$
Diameter of pipe ($d_p$) = $14 \text{ cm} = \frac{14}{100} \text{ m} = 0.14 \text{ m}$
Radius of pipe ($r_p$) = $\frac{d_p}{2} = \frac{0.14}{2} \text{ m} = 0.07 \text{ m}$
Cuboidal pond length ($L$) = 50 m
Cuboidal pond width ($B$) = 44 m
Required rise in water level ($H$) = $21 \text{ cm} = \frac{21}{100} \text{ m} = 0.21 \text{ m}$
Calculate the volume of water required to raise the level in the pond by 21 cm.
Volume of water required ($V_{pond}$) = $L \times B \times H$
V$_{pond}$ = $50 \times 44 \times 0.21 \text{ m}^3$
V$_{pond}$ = $2200 \times 0.21 \text{ m}^3$
V$_{pond}$ = $462 \text{ m}^3$
... (i)
Calculate the volume of water flowing from the pipe per hour.
This volume is equal to the volume of a cylinder with radius $r_p$ and height equal to the distance water travels in one hour (flow rate).
Volume flow rate per hour ($V_{pipe/h}$) = $\pi r_p^2 \times \text{flow rate}$
V$_{pipe/h}$ = $\pi \times (0.07)^2 \times 15000 \text{ m}^3\text{/h}$
V$_{pipe/h}$ = $\pi \times (0.0049) \times 15000 \text{ m}^3\text{/h}$
Using $\pi = \frac{22}{7}$:
V$_{pipe/h}$ = $\frac{22}{7} \times 0.0049 \times 15000$
V$_{pipe/h}$ = $\frac{22}{7} \times \frac{49}{10000} \times 15000$
V$_{pipe/h}$ = $22 \times \frac{\cancel{49}^7}{\cancel{7}_1} \times \frac{\cancel{15000}^{15}}{\cancel{10000}_{10}}$
[Simplifying fractions] ... (ii)
V$_{pipe/h}$ = $22 \times 7 \times \frac{15}{10} = 22 \times 7 \times 1.5$
V$_{pipe/h}$ = $154 \times 1.5 = 231 \text{ m}^3\text{/h}$
The time taken to fill the pond by 21 cm is the ratio of the required volume in the pond to the volume flow rate from the pipe.
Time taken = $\frac{\text{Volume of water required in pond}}{\text{Volume flow rate per hour}}$
Time taken = $\frac{462 \text{ m}^3}{231 \text{ m}^3\text{/h}}$
Time taken = $\frac{462}{231}$ hours
Time taken = $2$ hours
... (iii)
It would take 2 hours for the level of water in the pond to rise by 21 cm.
Question 9. A solid iron cuboidal block of dimensions 4.4 m × 2.6 m × 1m is recast into a hollow cylindrical pipe of internal radius 30 cm and thickness 5 cm. Find the length of the pipe.
Answer:
Given:
Dimensions of the solid iron cuboidal block:
Length ($L$) = 4.4 m
Breadth ($B$) = 2.6 m
Height ($H$) = 1 m
Hollow cylindrical pipe:
Internal radius ($r_{int}$) = 30 cm
Thickness = 5 cm
To Find:
The length (height) of the pipe.
Solution:
First, ensure all dimensions are in the same unit. Let's convert all dimensions to centimeters.
Cuboid Length ($L$) = $4.4 \text{ m} = 4.4 \times 100 = 440 \text{ cm}$
Cuboid Breadth ($B$) = $2.6 \text{ m} = 2.6 \times 100 = 260 \text{ cm}$
Cuboid Height ($H$) = $1 \text{ m} = 1 \times 100 = 100 \text{ cm}$
Pipe Internal Radius ($r_{int}$) = 30 cm
Pipe Thickness = 5 cm
The external radius of the hollow pipe ($r_{ext}$) is the internal radius plus the thickness.
Pipe External Radius ($r_{ext}$) = $r_{int} + \text{Thickness} = 30 + 5 = 35 \text{ cm}$
... (1)
When the cuboidal block is recast into a hollow pipe, the volume of the material remains constant.
Calculate the volume of the solid iron cuboidal block.
Volume of cuboid = $L \times B \times H$
Volume of cuboid = $440 \times 260 \times 100 \text{ cm}^3$
Volume of cuboid = $114400 \times 100 = 11440000 \text{ cm}^3$
... (i)
Calculate the volume of the hollow cylindrical pipe. Let the length (height) of the pipe be $h_p$.
The volume of a hollow cylinder is the volume of the outer cylinder minus the volume of the inner cylinder.
Volume of hollow pipe = $\pi r_{ext}^2 h_p - \pi r_{int}^2 h_p = \pi h_p (r_{ext}^2 - r_{int}^2)$
Volume of hollow pipe = $\pi h_p (35^2 - 30^2)$
Volume of hollow pipe = $\pi h_p (1225 - 900)$
Volume of hollow pipe = $325\pi h_p \text{ cm}^3$
... (ii)
Equating the volume of the cuboid (i) and the volume of the hollow pipe (ii):
Volume of cuboid = Volume of hollow pipe
$11440000 = 325\pi h_p$
Using the value $\pi = \frac{22}{7}$:
$11440000 = 325 \times \frac{22}{7} \times h_p$
Solve for $h_p$:
$h_p = \frac{11440000 \times 7}{325 \times 22}$
Simplify the expression by cancelling common factors.
Cancel 11440000 and 22. $11440000 \div 22 = 520000$.
$h_p = \frac{\cancel{11440000}^{520000} \times 7}{325 \times \cancel{22}_1}$
$h_p = \frac{520000 \times 7}{325}$
Cancel 520000 and 325. Both are divisible by 25.
$520000 \div 25 = 20800$
$325 \div 25 = 13$
$h_p = \frac{\cancel{520000}^{20800} \times 7}{\cancel{325}_{13}}$
$h_p = \frac{20800 \times 7}{13}$
Cancel 20800 and 13. $20800 \div 13 = 1600$.
$h_p = \cancel{20800}^{1600} \times 7 / \cancel{13}_1$
$h_p = 1600 \times 7 = 11200 \text{ cm}$
... (iii)
The length of the pipe is 11200 cm.
We can convert this length back to meters if desired.
Length of pipe = $\frac{11200}{100} \text{ m} = 112 \text{ m}$
The length of the pipe is 11200 cm or 112 m.
Question 10. 500 persons are taking a dip into a cuboidal pond which is 80 m long and 50 m broad. What is the rise of water level in the pond, if the average displacement of the water by a person is 0.04m3 ?
Answer:
Given:
Number of persons = 500
Dimensions of the cuboidal pond:
Length ($L$) = 80 m
Breadth ($B$) = 50 m
Average displacement of water by a person = 0.04 m$^3$
To Find:
The rise of water level in the pond.
Solution:
When the persons take a dip into the pond, they displace a volume of water equal to the sum of their individual displacements.
Total volume of water displaced by 500 persons = Number of persons $\times$ Average displacement per person
Total displaced volume = $500 \times 0.04 \text{ m}^3$
Total displaced volume = $500 \times \frac{4}{100} \text{ m}^3$
Total displaced volume = $5 \times 4 = 20 \text{ m}^3$
... (i)
This total displaced volume of water causes the water level in the cuboidal pond to rise. Let the rise in water level be $\Delta H$ meters.
The volume of this rise in water level is the volume of a cuboid with base dimensions equal to the pond's base and height equal to the rise in level.
Volume of rise in water level = Length of pond $\times$ Breadth of pond $\times$ Rise in height
Volume of rise = $L \times B \times \Delta H$
Volume of rise = $80 \times 50 \times \Delta H \text{ m}^3$
Volume of rise = $4000 \Delta H \text{ m}^3$
... (ii)
The volume of water displaced by the persons is equal to the volume of the rise in water level.
Total displaced volume = Volume of rise in water level
$20 = 4000 \Delta H$
Solve for $\Delta H$:
$\Delta H = \frac{20}{4000}$ meters
$\Delta H = \frac{1}{200}$ meters
Convert the rise in height to centimeters:
$\Delta H = \frac{1}{200} \times 100$ cm
$\Delta H = \frac{100}{200} \text{ cm} = 0.5 \text{ cm}$
... (iii)
The rise of water level in the pond is 0.5 cm.
Question 11. 16 glass spheres each of radius 2 cm are packed into a cuboidal box of internal dimensions 16 cm × 8 cm × 8 cm and then the box is filled with water. Find the volume of water filled in the box.
Answer:
Given:
Number of glass spheres = 16
Radius of each sphere ($r_s$) = 2 cm
Internal dimensions of the cuboidal box:
Length ($L$) = 16 cm
Breadth ($B$) = 8 cm
Height ($H$) = 8 cm
To Find:
The volume of water filled in the box.
Solution:
The volume of water filled in the box is the volume of the box minus the total volume occupied by the glass spheres.
First, calculate the volume of the cuboidal box.
Volume of box ($V_{box}$) = $L \times B \times H$
V$_{box}$ = $16 \times 8 \times 8 \text{ cm}^3$
V$_{box}$ = $16 \times 64 = 1024 \text{ cm}^3$
... (i)
Next, calculate the volume of one glass sphere.
The formula for the volume of a sphere is $V = \frac{4}{3} \pi r^3$.
Volume of sphere ($V_{sphere}$) = $\frac{4}{3} \pi (2)^3$
V$_{sphere}$ = $\frac{4}{3} \pi \times 8 = \frac{32}{3}\pi \text{ cm}^3$
... (ii)
Calculate the total volume occupied by all 16 glass spheres.
Total volume of spheres ($V_{total\_spheres}$) = Number of spheres $\times$ Volume of one sphere
V$_{total\_spheres}$ = $16 \times \frac{32}{3}\pi$
V$_{total\_spheres}$ = $\frac{512}{3}\pi \text{ cm}^3$
... (iii)
The volume of water filled in the box is the volume of the box minus the total volume of the spheres.
Volume of water ($V_{water}$) = V$_{box}$ - V$_{total\_spheres}$
V$_{water}$ = $1024 - \frac{512}{3}\pi \text{ cm}^3$
... (iv)
The volume of water filled in the box is $1024 - \frac{512}{3}\pi \text{ cm}^3$.
Question 12. A milk container of height 16 cm is made of metal sheet in the form of a frustum of a cone with radii of its lower and upper ends as 8 cm and 20 cm respectively. Find the cost of milk at the rate of Rs. 22 per litre which the container can hold.
Answer:
Given:
The milk container is in the form of a frustum of a cone.
Height of the frustum ($h$) = 16 cm
Radius of the lower end ($r_1$) = 8 cm
Radius of the upper end ($r_2$) = 20 cm
Rate of milk = $\textsf{₹}\ 22$ per litre
To Find:
The cost of milk that the container can hold.
Solution:
The volume of the container (capacity) is the volume of the frustum of a cone.
The formula for the volume of a frustum is $V = \frac{1}{3}\pi h (r_1^2 + r_2^2 + r_1 r_2)$.
Using $\pi = \frac{22}{7}$:
Volume ($V$) = $\frac{1}{3} \times \frac{22}{7} \times 16 \times (8^2 + 20^2 + 8 \times 20)$
V = $\frac{22 \times 16}{21} \times (64 + 400 + 160)$
V = $\frac{352}{21} \times (624)$
Simplify the multiplication:
V = $\frac{352}{\cancel{21}_7} \times \cancel{624}^{208}$
V = $\frac{352 \times 208}{7}$
V = $\frac{73216}{7} \text{ cm}^3$
... (i)
To find the cost of milk, we need to convert the volume from cubic centimeters to litres.
$1 \text{ litre} = 1000 \text{ cm}^3$
Capacity in litres = $\frac{\text{Volume in cm}^3}{1000}$
Capacity in litres = $\frac{73216/7}{1000} = \frac{73216}{7000}$ litres
... (ii)
Calculate the cost of milk:
Cost = Capacity in litres $\times$ Rate per litre
Cost = $\frac{73216}{7000} \times 22$
Cost = $\frac{73216 \times 22}{7000}$
Simplify the fraction:
Cost = $\frac{\cancel{73216}^{9152} \times \cancel{22}^{11}}{\cancel{7000}_{875} \times \cancel{2}_1}$ (Dividing by 8 and 2)
Cost = $\frac{9152 \times 11}{875}$
Cost = $\frac{100672}{875}$
Performing the division $\frac{100672}{875}$:
$100672 \div 875 \approx 115.05$
Let's recheck the calculation $\frac{73216 \times 22}{7000}$.
Cancel 22 and 7000 by 2: $\frac{73216 \times 11}{3500}$
$73216 \times 11 = 805376$
Cost = $\frac{805376}{3500}$
Performing the division $\frac{805376}{3500}$:
$805376 \div 3500 \approx 230.1074$
Cost $\approx \textsf{₹}\ 230.11$ (rounded to two decimal places)
... (iii)
The cost of milk which the container can hold is approximately $\textsf{₹}\ 230.11$.
Question 13. A cylindrical bucket of height 32 cm and base radius 18 cm is filled with sand. This bucket is emptied on the ground and a conical heap of sand is formed. If the height of the conical heap is 24 cm, find the radius and slant height of the heap.
Answer:
Given:
For the cylindrical bucket:
Height ($h_{cyl}$) = 32 cm
Base radius ($r_{cyl}$) = 18 cm
For the conical heap:
Height ($h_{cone}$) = 24 cm
To Find:
1. The radius of the base of the conical heap ($r_{cone}$).
2. The slant height of the conical heap ($l_{cone}$).
Solution:
When the sand from the cylindrical bucket is emptied to form a conical heap, the volume of sand remains constant.
Calculate the volume of sand in the cylindrical bucket.
Volume of cylinder = $\pi r_{cyl}^2 h_{cyl}$
Volume of sand = $\pi (18)^2 (32) \text{ cm}^3$
Volume of sand = $\pi (324) (32) \text{ cm}^3$
Volume of sand = $10368\pi \text{ cm}^3$
... (i)
Now, consider the conical heap of sand. Let the radius of the base be $r_{cone}$.
The formula for the volume of a cone is $V = \frac{1}{3}\pi r^2 h$.
Volume of conical heap = $\frac{1}{3}\pi r_{cone}^2 h_{cone}$
Volume of conical heap = $\frac{1}{3}\pi r_{cone}^2 (24)$
Volume of conical heap = $8\pi r_{cone}^2 \text{ cm}^3$
... (ii)
Equate the volume of sand in the cylinder and the cone (from (i) and (ii)):
Volume of sand = Volume of conical heap
$10368\pi = 8\pi r_{cone}^2$
Cancel $\pi$ from both sides (since $\pi \neq 0$):
$10368 = 8 r_{cone}^2$
Solve for $r_{cone}^2$:
$r_{cone}^2 = \frac{10368}{8}$
$r_{cone}^2 = 1296$
... (iii)
Take the square root to find $r_{cone}$:
$r_{cone} = \sqrt{1296}$
We can find the square root by prime factorization or trial and error. $30^2 = 900$, $40^2 = 1600$. The number ends in 6, so the base digit could be 4 or 6. Let's try 36.
$36 \times 36 = 1296$.
$r_{cone} = 36$ cm
... (iv)
The radius of the conical heap is 36 cm.
Now, calculate the slant height ($l_{cone}$) of the conical heap.
The formula for slant height is $l_{cone} = \sqrt{r_{cone}^2 + h_{cone}^2}$.
$l_{cone} = \sqrt{(36)^2 + (24)^2}$
$l_{cone} = \sqrt{1296 + 576}$
Add the numbers:
$\begin{array}{cc} & 1296 \\ + & \phantom{0}576 \\ \hline & 1872 \\ \hline \end{array}$
$l_{cone} = \sqrt{1872}$
... (v)
Simplify $\sqrt{1872}$ by finding perfect square factors.
$1872 = 4 \times 468 = 4 \times 4 \times 117 = 16 \times 9 \times 13 = 144 \times 13$
$l_{cone} = \sqrt{144 \times 13} = \sqrt{144} \times \sqrt{13} = 12\sqrt{13} \text{ cm}$
... (vi)
The slant height of the conical heap is $12\sqrt{13}$ cm.
The radius of the conical heap is 36 cm.
The slant height of the conical heap is $12\sqrt{13}$ cm.
Question 14. A rocket is in the form of a right circular cylinder closed at the lower end and surmounted by a cone with the same radius as that of the cylinder. The diameter and height of the cylinder are 6 cm and 12 cm, respectively. If the the slant height of the conical portion is 5 cm, find the total surface area and volume of the rocket [Use π = 3.14].
Answer:
Given:
The rocket is a cylinder closed at the lower end, surmounted by a cone.
Diameter of the cylinder base = 6 cm
Height of the cylinder ($h_{cyl}$) = 12 cm
Slant height of the conical portion ($l_{cone}$) = 5 cm
The cone and cylinder have the same radius.
Use $\pi = 3.14$
To Find:
1. Total volume of the rocket.
2. Total surface area of the rocket.
Solution:
First, calculate the radius of the cylinder and cone from the diameter.
Radius ($r$) = $\frac{\text{Diameter}}{2} = \frac{6}{2} = 3 \text{ cm}$
... (1)
For the conical portion, we are given the radius ($r_{cone} = r = 3$ cm) and the slant height ($l_{cone} = 5$ cm). To find the volume of the cone, we need its height ($h_{cone}$).
Using the Pythagorean theorem for the cone, $l_{cone}^2 = r_{cone}^2 + h_{cone}^2$:
$(5)^2 = (3)^2 + h_{cone}^2$
$25 = 9 + h_{cone}^2$
$h_{cone}^2 = 25 - 9 = 16$
$h_{cone} = \sqrt{16} = 4 \text{ cm}$
... (2)
Calculate the volume of the cylindrical portion:
Volume of cylinder = $\pi r^2 h_{cyl}$
Volume of cylinder = $3.14 \times (3)^2 \times 12$
Volume of cylinder = $3.14 \times 9 \times 12 = 3.14 \times 108$
Volume of cylinder = $339.12 \text{ cm}^3$
... (i)
Calculate the volume of the conical portion:
Volume of cone = $\frac{1}{3} \pi r^2 h_{cone}$
Volume of cone = $\frac{1}{3} \times 3.14 \times (3)^2 \times 4$
Volume of cone = $\frac{1}{3} \times 3.14 \times 9 \times 4 = 3.14 \times 3 \times 4 = 3.14 \times 12$
Volume of cone = $37.68 \text{ cm}^3$
... (ii)
Total volume of the rocket = Volume of cylinder + Volume of cone
Total Volume = $339.12 + 37.68$
Total Volume = $376.80 \text{ cm}^3$
... (iii)
Now, calculate the total surface area of the rocket.
The total surface area consists of the area of the base of the cylinder, the curved surface area of the cylinder, and the curved surface area of the cone.
Area of the base of the cylinder = $\pi r^2$
Area of base = $3.14 \times (3)^2 = 3.14 \times 9 = 28.26 \text{ cm}^2$
... (iv)
Curved surface area of the cylinder = $2\pi r h_{cyl}$
CSA of cylinder = $2 \times 3.14 \times 3 \times 12 = 6.28 \times 36$
CSA of cylinder = $226.08 \text{ cm}^2$
... (v)
Curved surface area of the cone = $\pi r l_{cone}$
CSA of cone = $3.14 \times 3 \times 5 = 3.14 \times 15$
CSA of cone = $47.10 \text{ cm}^2$
... (vi)
Total surface area of the rocket = Area of base + CSA of cylinder + CSA of cone
Total Surface Area = $28.26 + 226.08 + 47.10$
$\begin{array}{cc} & 28.26 \\ & 226.08 \\ + & \phantom{0}47.10 \\ \hline & 301.44 \\ \hline \end{array}$
Total Surface Area = $301.44 \text{ cm}^2$
... (vii)
The total volume of the rocket is 376.80 cm$^3$.
The total surface area of the rocket is 301.44 cm$^2$.
Question 15. A building is in the form of a cylinder surmounted by a hemispherical vaulted dome and contains $41\frac{19}{21}$ m3 of air. If the internal diameter of dome is equal to its total height above the floor, find the height of the building?
Answer:
Given:
The building is in the form of a cylinder surmounted by a hemispherical dome.
Internal diameter of dome = Total height of the building.
Volume of air inside the building = $41\frac{19}{21}$ m$^3$.
To Find:
The total height of the building.
Solution:
Let the total height of the building above the floor be $H$ meters.
Let the internal diameter of the hemispherical dome be $D$ meters.
According to the given condition:
Internal diameter of dome = Total height of building
$D = H$
... (1)
Let the radius of the hemispherical dome be $r$ meters. The diameter is twice the radius.
$D = 2r$
From (1) and the definition of radius:
$2r = H$
$r = \frac{H}{2}$
... (2)
The height of the hemispherical dome is equal to its radius, which is $r = \frac{H}{2}$ meters.
The building consists of a cylindrical part and a hemispherical dome. The total height is the sum of the height of the cylindrical part ($h_{cyl}$) and the height of the dome.
Total height $H = h_{cyl} + \text{Height of dome}$
$H = h_{cyl} + r$
Substitute the value of $r$ from (2):
$H = h_{cyl} + \frac{H}{2}$
Solve for the height of the cylinder ($h_{cyl}$):
$h_{cyl} = H - \frac{H}{2} = \frac{H}{2}$
... (3)
The radius of the base of the cylinder is the same as the radius of the dome, which is $r = \frac{H}{2}$ meters.
The volume of air inside the building is the sum of the volume of the cylindrical part and the volume of the hemispherical dome.
Volume of cylinder = $\pi r^2 h_{cyl}$
Volume of cylinder = $\pi \left(\frac{H}{2}\right)^2 \left(\frac{H}{2}\right) = \pi \left(\frac{H^2}{4}\right) \left(\frac{H}{2}\right) = \frac{1}{8}\pi H^3$
... (4)
Volume of hemisphere = $\frac{2}{3} \pi r^3$
Volume of hemisphere = $\frac{2}{3} \pi \left(\frac{H}{2}\right)^3 = \frac{2}{3} \pi \left(\frac{H^3}{8}\right) = \frac{2}{24}\pi H^3 = \frac{1}{12}\pi H^3$
... (5)
Total Volume of building = Volume of cylinder + Volume of hemisphere
Total Volume = $\frac{1}{8}\pi H^3 + \frac{1}{12}\pi H^3$
Total Volume = $\left(\frac{1}{8} + \frac{1}{12}\right) \pi H^3$
Find the sum of the fractions: $\frac{1}{8} + \frac{1}{12}$. The least common multiple of 8 and 12 is 24.
$\frac{1}{8} + \frac{1}{12} = \frac{1 \times 3}{8 \times 3} + \frac{1 \times 2}{12 \times 2} = \frac{3}{24} + \frac{2}{24} = \frac{5}{24}$
Total Volume = $\frac{5}{24}\pi H^3$
... (6)
The given volume of air in the building is $41\frac{19}{21}$ m$^3$. Convert the mixed number to an improper fraction.
Given Volume = $41\frac{19}{21} = \frac{41 \times 21 + 19}{21} = \frac{861 + 19}{21} = \frac{880}{21}$ m$^3$
... (7)
Equate the total volume from (6) with the given volume from (7):
$\frac{5}{24}\pi H^3 = \frac{880}{21}$
Using the value $\pi = \frac{22}{7}$:
$\frac{5}{24} \times \frac{22}{7} \times H^3 = \frac{880}{21}$
$\frac{110}{168} H^3 = \frac{880}{21}$
$\frac{55}{84} H^3 = \frac{880}{21}$
Solve for $H^3$:
$H^3 = \frac{880}{21} \times \frac{84}{55}$
Simplify the right side:
$H^3 = \frac{880}{\cancel{21}_1} \times \frac{\cancel{84}^4}{55}$
[Cancelling 21 and 84] ... (8)
$H^3 = \frac{880 \times 4}{55}$
$H^3 = \frac{\cancel{880}^{16} \times 4}{\cancel{55}_1}$
[Cancelling 880 and 55, since $880 \div 55 = 16$] ... (9)
$H^3 = 16 \times 4 = 64$
... (10)
Take the cube root of both sides to find $H$:
$H = \sqrt[3]{64}$
$H = 4$ meters
... (11)
The height of the building is 4 meters.
Question 16. A hemispherical bowl of internal radius 9 cm is full of liquid. The liquid is to be filled into cylindrical shaped bottles each of radius 1.5 cm and height 4 cm. How many bottles are needed to empty the bowl?
Answer:
Given:
Internal radius of the hemispherical bowl ($r_b$) = 9 cm
For each cylindrical bottle:
Radius ($r_{bottle}$) = 1.5 cm
Height ($h_{bottle}$) = 4 cm
To Find:
The number of bottles needed to empty the bowl.
Solution:
The volume of liquid in the hemispherical bowl will be completely transferred to the cylindrical bottles. Therefore, the total volume of liquid in the bowl is equal to the sum of the volumes of liquid in all the filled bottles.
First, calculate the volume of the hemispherical bowl.
The formula for the volume of a hemisphere is $V = \frac{2}{3} \pi r^3$.
Volume of bowl ($V_{bowl}$) = $\frac{2}{3} \pi (9)^3$
V$_{bowl}$ = $\frac{2}{3} \pi (729) = 2 \pi \times \frac{729}{3} = 2 \pi \times 243$
V$_{bowl}$ = $486\pi \text{ cm}^3$
... (i)
Next, calculate the volume of one cylindrical bottle.
The formula for the volume of a cylinder is $V = \pi r^2 h$.
Volume of one bottle ($V_{bottle}$) = $\pi (1.5)^2 (4)$
V$_{bottle}$ = $\pi (2.25) (4)$
V$_{bottle}$ = $9\pi \text{ cm}^3$
... (ii)
Let $n$ be the number of bottles needed to empty the bowl.
The total volume of liquid in $n$ bottles is $n \times V_{bottle}$.
According to the problem:
Volume of bowl = Total volume in bottles
$V_{bowl} = n \times V_{bottle}$
Substitute the volumes from (i) and (ii):
$486\pi = n \times 9\pi$
Cancel $\pi$ from both sides (since $\pi \neq 0$):
$486 = n \times 9$
Solve for $n$:
$n = \frac{486}{9}$
Performing the division:
$\frac{486}{9} = 54$
$n = 54$
... (iii)
54 bottles are needed to empty the bowl.
Question 17. A solid right circular cone of height 120 cm and radius 60 cm is placed in a right circular cylinder full of water of height 180 cm such that it touches the bottom. Find the volume of water left in the cylinder, if the radius of the cylinder is equal to the radius of the cone.
Answer:
Given:
Dimensions of the solid right circular cone:
Height ($h_c$) = 120 cm
Radius of base ($r_c$) = 60 cm
Dimensions of the right circular cylinder:
Height ($h_{cyl}$) = 180 cm
Radius of base ($r_{cyl}$) = Radius of cone ($r_c$) = 60 cm
The cylinder is full of water and the cone is placed inside touching the bottom.
To Find:
The volume of water left in the cylinder.
Solution:
When the solid cone is placed in the cylinder full of water, the volume of water that overflows is equal to the volume of the cone, provided the cone is completely submerged. Since the height of the cone (120 cm) is less than the height of the cylinder (180 cm), the cone is indeed completely submerged.
The volume of water left in the cylinder is the volume of the cylinder minus the volume of the cone.
Calculate the volume of the cylinder:
The formula for the volume of a cylinder is $V = \pi r^2 h$.
Volume of cylinder ($V_{cyl}$) = $\pi r_{cyl}^2 h_{cyl}$
V$_{cyl}$ = $\pi (60 \text{ cm})^2 (180 \text{ cm})$
V$_{cyl}$ = $\pi (3600) (180) \text{ cm}^3$
V$_{cyl}$ = $648000\pi \text{ cm}^3$
... (i)
Calculate the volume of the cone:
The formula for the volume of a cone is $V = \frac{1}{3} \pi r^2 h$.
Volume of cone ($V_c$) = $\frac{1}{3} \pi r_c^2 h_c$
V$_c$ = $\frac{1}{3} \pi (60 \text{ cm})^2 (120 \text{ cm})$
V$_c$ = $\frac{1}{3} \pi (3600) (120) \text{ cm}^3$
V$_c$ = $\pi (3600) (\frac{120}{3}) \text{ cm}^3 = \pi (3600) (40) \text{ cm}^3$
V$_c$ = $144000\pi \text{ cm}^3$
... (ii)
The volume of water left in the cylinder is the difference between the volume of the cylinder and the volume of the cone.
Volume of water left = V$_{cyl}$ - V$_c$
Volume of water left = $648000\pi - 144000\pi \text{ cm}^3$
Volume of water left = $(648000 - 144000)\pi \text{ cm}^3$
$\begin{array}{cc} & 648000 \\ - & 144000 \\ \hline & 504000 \\ \hline \end{array}$
Volume of water left = $504000\pi \text{ cm}^3$
... (iii)
The volume of water left in the cylinder is $504000\pi \text{ cm}^3$.
Question 18. Water flows through a cylindrical pipe, whose inner radius is 1 cm, at the rate of 80 cm/sec in an empty cylindrical tank, the radius of whose base is 40 cm. What is the rise of water level in tank in half an hour?
Answer:
Given:
For the cylindrical pipe:
Inner radius ($r_p$) = 1 cm
Flow rate ($v$) = 80 cm/sec
For the cylindrical tank:
Radius of base ($r_t$) = 40 cm
Time duration ($T$) = half an hour
To Find:
The rise of water level in the tank ($h_t$) in half an hour.
Solution:
First, ensure all units are consistent. The flow rate is given in cm/sec, and dimensions are in cm. The time is given in hours, so convert it to seconds.
Time $T = 0.5 \text{ hours}$
$T = 0.5 \times 60 \text{ minutes} = 30 \text{ minutes}$
$T = 30 \times 60 \text{ seconds} = 1800 \text{ seconds}$
... (1)
The volume of water flowing out of the pipe per second is the volume of a cylinder with radius equal to the pipe's radius and height equal to the flow rate per second.
Volume flow rate = Area of pipe cross-section $\times$ Flow rate
Volume flow rate = $(\pi r_p^2) \times v$
Volume flow rate = $\pi (1 \text{ cm})^2 \times 80 \text{ cm/sec}$
Volume flow rate = $80\pi \text{ cm}^3\text{/sec}$
... (2)
The total volume of water that flows into the tank in half an hour (1800 seconds) is the volume flow rate multiplied by the total time.
Total volume of water = Volume flow rate $\times$ Time
Total volume of water = $80\pi \text{ cm}^3\text{/sec} \times 1800 \text{ seconds}$
Total volume of water = $144000\pi \text{ cm}^3$
... (i)
This volume of water causes the level in the cylindrical tank to rise. Let the rise in water level be $h_t$ centimeters.
The volume of water in the tank due to this rise is the volume of a cylinder with the tank's base radius and the height $h_t$.
Volume of water in tank = $\pi r_t^2 h_t$
Volume of water in tank = $\pi (40 \text{ cm})^2 h_t$
Volume of water in tank = $1600\pi h_t \text{ cm}^3$
... (ii)
Equating the total volume of water flowed (i) with the volume of water in the tank (ii):
Total volume of water = Volume of water in tank
$\text{144000}\pi = 1600\pi h_t$
Cancel $\pi$ from both sides (since $\pi \neq 0$):
$\text{144000} = 1600 h_t$
Solve for $h_t$:
$$h_t = \frac{144000}{1600}$$
$$h_t = \frac{1440}{16}$$
$$h_t = 90 \text{ cm}$$
... (iii)
The rise of water level in the tank in half an hour is 90 cm.
Question 19. The rain water from a roof of dimensions 22 m 20 m drains into a cylindrical vessel having diameter of base 2 m and height 3.5 m. If the rain water collected from the roof just fill the cylindrical vessel, then find the rainfall in cm.
Answer:
Given:
Dimensions of the rectangular roof:
Length ($L$) = 22 m
Width ($W$) = 20 m
Dimensions of the cylindrical vessel:
Diameter of base ($D$) = 2 m
Height ($H$) = 3.5 m
The rainwater from the roof just fills the cylindrical vessel.
To Find:
The rainfall in centimeters.
Solution:
The volume of rainwater collected on the roof is equal to the volume of water that fills the cylindrical vessel.
Let the rainfall be $h$ meters. The volume of rainwater collected on the roof is the area of the roof multiplied by the height of the rainfall.
Area of roof = $L \times W$
Area of roof = $22 \text{ m} \times 20 \text{ m} = 440 \text{ m}^2$
Volume of rainwater ($V_{rain}$) = Area of roof $\times h = 440 \times h \text{ m}^3$
... (i)
Now, calculate the volume of the cylindrical vessel. The radius of the vessel ($R$) is half of its diameter.
Radius of vessel ($R$) = $\frac{D}{2} = \frac{2}{2} = 1 \text{ m}$
The volume of a cylinder is given by the formula $V = \pi R^2 H$.
Volume of vessel ($V_{vessel}$) = $\pi (1)^2 (3.5) = 3.5\pi \text{ m}^3$
... (ii)
Since the rainwater collected just fills the vessel, the volume of rainwater is equal to the volume of the vessel.
V$_{rain}$ = V$_{vessel}$
$\text{440}h = 3.5\pi$
Solve for $h$. Using $\pi = \frac{22}{7}$:
$\text{440}h = 3.5 \times \frac{22}{7}$
$\text{440}h = \frac{7}{2} \times \frac{22}{7}$
$\text{440}h = \frac{\cancel{7}_1}{\cancel{2}_1} \times \frac{\cancel{22}^{11}}{\cancel{7}_1} = 11$
[Simplifying fractions] ... (iii)
$\text{440}h = 11$
$h = \frac{11}{440}$ meters
$h = \frac{1}{40}$ meters
... (iv)
The rainfall is in meters. Convert it to centimeters.
$1 \text{ meter} = 100 \text{ cm}$
Rainfall in cm = $h \times 100$ cm
Rainfall in cm = $\frac{1}{40} \times 100 = \frac{100}{40} = \frac{10}{4} = 2.5$ cm
... (v)
The rainfall is 2.5 cm.
Question 20. A pen stand made of wood is in the shape of a cuboid with four conical depressions and a cubical depression to hold the pens and pins, respectively. The dimension of the cuboid are 10 cm, 5 cm and 4 cm. The radius of each of the conical depressions is 0.5 cm and the depth is 2.1 cm. The edge of the cubical depression is 3 cm. Find the volume of the wood in the entire stand.
Answer:
Given:
Dimensions of the cuboidal pen stand:
Length ($L$) = 10 cm
Breadth ($B$) = 5 cm
Height ($H$) = 4 cm
For each conical depression:
Radius ($r_c$) = 0.5 cm
Depth ($h_c$) = 2.1 cm
Number of conical depressions = 4
For the cubical depression:
Edge ($s$) = 3 cm
To Find:
The volume of the wood in the entire stand.
Solution:
The volume of the wood is the volume of the cuboid minus the volume of the four conical depressions and the volume of the cubical depression.
Calculate the volume of the cuboidal pen stand.
Volume of cuboid ($V_{cuboid}$) = $L \times B \times H$
V$_{cuboid}$ = $10 \times 5 \times 4 \text{ cm}^3$
V$_{cuboid}$ = $200 \text{ cm}^3$
... (i)
Calculate the volume of one conical depression.
The formula for the volume of a cone is $V = \frac{1}{3} \pi r^2 h$. Use $\pi = \frac{22}{7}$.
Volume of one cone ($V_{cone}$) = $\frac{1}{3} \pi (0.5)^2 (2.1)$
V$_{cone}$ = $\frac{1}{3} \times \frac{22}{7} \times (0.25) \times (2.1)$
V$_{cone}$ = $\frac{1}{3} \times \frac{22}{7} \times \frac{1}{4} \times \frac{21}{10}$
[Converting decimals to fractions] ... (ii)
V$_{cone}$ = $\frac{1}{\cancel{3}} \times \frac{22}{\cancel{7}} \times \frac{1}{4} \times \frac{\cancel{3} \times \cancel{7}}{10}$
[Cancelling common factors] ... (iii)
V$_{cone}$ = $\frac{22 \times 1}{4 \times 10} = \frac{22}{40} = \frac{11}{20} = 0.55 \text{ cm}^3$
... (iv)
Calculate the total volume of the four conical depressions.
Volume of 4 cones ($V_{4cones}$) = $4 \times V_{cone}$
V$_{4cones}$ = $4 \times 0.55 \text{ cm}^3 = 2.2 \text{ cm}^3$
... (v)
Calculate the volume of the cubical depression.
The formula for the volume of a cube is $V = s^3$.
Volume of cube ($V_{cube}$) = $s^3$
V$_{cube}$ = $(3)^3 \text{ cm}^3 = 27 \text{ cm}^3$
... (vi)
The volume of the wood in the stand is the volume of the cuboid minus the combined volume of the depressions.
Volume of wood ($V_{wood}$) = V$_{cuboid}$ - V$_{4cones}$ - V$_{cube}$
V$_{wood}$ = $200 - 2.2 - 27 \text{ cm}^3$
V$_{wood}$ = $173 - 2.2 \text{ cm}^3$
V$_{wood}$ = $170.8 \text{ cm}^3$
... (vii)
The volume of the wood in the entire stand is 170.8 cm$^3$.

