| NCERT Exemplar Solutions | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Class 6th Chapters | ||
|---|---|---|
| 1. Number System | 2. Geometry | 3. Integers |
| 4. Fractions & Decimals | 5. Data Handling | 6. Mensuration |
| 7. Algebra | 8. Ratio & Proportion | 9. Symmetry & Practical Geometry |
| Content On This Page | ||
|---|---|---|
| Solved Examples (Examples 1 to 12) | Question 1 to 16 (Multiple Choice Questions) | Question 17 to 31 (Fill in the Blanks) |
| Question 32 to 41 (True or False) | Question 42 to 78 | |
Chapter 2 Geometry
Welcome to this comprehensive guide offering detailed, step-by-step solutions for the NCERT Exemplar problems pertaining to Class 6 Geometry. These solutions specifically address concepts typically covered in the NCERT chapters titled "Basic Geometrical Ideas" and "Understanding Elementary Shapes". It is crucial to recognize that the NCERT Exemplar initiative presents questions intentionally designed to be more challenging than those found in the standard textbook exercises. The primary goal is to cultivate deeper spatial reasoning abilities, reinforce the importance of precise geometric definitions, and rigorously test the application of fundamental geometric properties within more complex figures and diverse scenarios. This resource is structured to navigate students through these demanding problems effectively.
The solutions presented here encompass a wide array of foundational geometric concepts. Students will find clear guidance on questions involving:
- The fundamental building blocks: Identifying and differentiating between points, lines, line segments, and rays.
- Line relationships: Understanding the concepts of intersecting lines and parallel lines.
- Curves and Boundaries: Classifying curves as open or closed.
- Polygons: Recognizing properties such as sides, vertices, and diagonals, and classifying polygons based on the number of sides (triangles, quadrilaterals, pentagons, etc.).
- Angles: Identifying and classifying various types of angles (acute, obtuse, right, straight, reflex) and understanding their relationships, particularly adjacent angles, linear pairs, and vertically opposite angles, often within intricate diagrams.
- Triangles: Classifying triangles based on their sides (scalene, isosceles, equilateral) and their angles (acute-angled, right-angled, obtuse-angled).
- Quadrilaterals: Exploring properties and basic types of four-sided figures.
- Circles: Identifying basic parts like center, radius, diameter, chord, and circumference.
- Three-Dimensional Shapes: Recognizing and counting faces, edges, and vertices of common 3D shapes like cubes, cuboids, cones, cylinders, and spheres.
The NCERT Exemplar employs various question formats to ensure a thorough assessment of understanding. Our solutions cater specifically to each format encountered:
- Multiple Choice Questions (MCQs): Often requiring careful visual interpretation of diagrams or a precise grasp of definitions and properties.
- Fill-in-the-Blanks: Demanding the use of exact geometric terminology.
- True/False Statements: Testing the validity and application limits of geometric theorems and properties.
- Short and Long Answer Questions: These may necessitate drawing figures accurately, labeling parts correctly, applying angle sum properties (e.g., the sum of angles in a triangle is $180^\circ$), or providing logical justifications for classifications and conclusions.
Exemplar problems frequently push beyond simple recognition. For example, students might be asked to meticulously count the total number of distinct line segments or triangles embedded within a complex figure, demanding systematic observation. Other problems could involve multi-step reasoning to find unknown angles using properties of parallel lines or triangles. Determining the specific type of quadrilateral based on subtle given properties, rather than explicit statements, is another common challenge. The provided solutions feature clear diagrams where needed, emphasize the use of correct geometric terminology, demonstrate the step-by-step application of relevant theorems and properties, and articulate the logical reasoning behind each classification and conclusion. By diligently working through these elaborated solutions, students can significantly enhance their conceptual grasp of geometry, improve their ability to visualize shapes and spatial relationships, and develop the critical analytical skills essential for success in higher-level mathematics.
Solved Examples (Examples 1 to 12)
In examples 1 and 2, write the correct answer from the given four options.
Example 1: The number of diagonals of a pentagon is
(A) 3
(B) 4
(C) 5
(D) 10
Answer:
Solution:
A pentagon is a polygon with 5 sides.
Number of sides, $n = 5$.
Method 1: Using the formula
The number of diagonals of a polygon with $n$ sides is given by the formula:
Number of diagonals $= \frac{n(n-3)}{2}$
For a pentagon, $n=5$.
Substitute $n=5$ into the formula:
Number of diagonals $= \frac{5(5-3)}{2}$
$= \frac{5(2)}{2}$
$= \frac{10}{2}$
$= 5$
Method 2: Counting
A pentagon has 5 vertices.
From each vertex, we can draw a line segment to every other vertex ($5-1=4$ line segments).
These line segments include the two sides adjacent to the vertex and the diagonals.
Number of diagonals from one vertex = (Total number of vertices - 1) - (Number of adjacent vertices) $= (5-1) - 2 = 4 - 2 = 2$.
Since there are 5 vertices, the total number of such lines drawn from all vertices is $5 \times 2 = 10$.
However, each diagonal connects two vertices, so it is counted twice in this sum (once for each endpoint).
Therefore, the actual number of diagonals is half of this sum.
Number of diagonals $= \frac{10}{2} = 5$.
Thus, the number of diagonals of a pentagon is 5.
The correct option is (C) 5.
Example 2: The number of diagonals of a triangle is
(A) 0
(B) 1
(C) 2
(D) 3
Answer:
Solution:
A triangle is a polygon with 3 sides.
Number of sides, $n = 3$.
Method 1: Using the formula
The number of diagonals of a polygon with $n$ sides is given by the formula:
Number of diagonals $= \frac{n(n-3)}{2}$
For a triangle, $n=3$.
Substitute $n=3$ into the formula:
Number of diagonals $= \frac{3(3-3)}{2}$
$= \frac{3(0)}{2}$
$= \frac{0}{2}$
$= 0$
Method 2: Definition of a diagonal
A diagonal is a line segment connecting two non-adjacent vertices of a polygon.
In a triangle, any two vertices are adjacent (connected by a side).
Therefore, there are no pairs of non-adjacent vertices in a triangle.
Hence, a triangle has no diagonals.
Thus, the number of diagonals of a triangle is 0.
The correct option is (A) 0.
In examples 3 and 4, fill in the blanks to make the statements true:
Example 3: A polygon of six sides is called a ______.
Answer:
Solution:
A polygon with six sides is called a hexagon.
The completed statement is: A polygon of six sides is called a hexagon.
Example 4: A triangle with all its sides of unequal lengths is called a ______ triangle.
Answer:
Solution:
A triangle in which all three sides have different lengths is called a scalene triangle.
The completed statement is: A triangle with all its sides of unequal lengths is called a scalene triangle.
In examples 5 to 7, state whether the statements are true or false.
Example 5: Two non-parallel line segments will always intersect.
Answer:
Solution:
The statement is False.
Two lines that are non-parallel will always intersect at exactly one point.
However, the statement refers to two non-parallel line segments.
A line segment is a part of a line with two endpoints.
Even if the lines containing the two segments are non-parallel, the segments themselves might not intersect.
For example, consider a line segment $AB$ on the x-axis from $(0,0)$ to $(5,0)$ and a line segment $CD$ on the line $y=x+5$ from $(1,6)$ to $(3,8)$.
The lines containing these segments ($y=0$ and $y=x+5$) are non-parallel, as their slopes are different (0 and 1, respectively).
These two lines intersect at the point $(-5, 0)$.
However, this intersection point $(-5, 0)$ is not within the segment $AB$ (which is from $x=0$ to $x=5$) or the segment $CD$ (which has $x$ values between 1 and 3).
Therefore, the line segments $AB$ and $CD$ do not intersect, even though the lines containing them are non-parallel.
Thus, two non-parallel line segments do not necessarily intersect.
Example 6: All equilateral triangles are isosceles also.
Answer:
Solution:
The statement is True.
Let's understand the definitions:
An equilateral triangle is a triangle in which all three sides are equal in length.
An isosceles triangle is a triangle in which at least two sides are equal in length.
Consider an equilateral triangle with side lengths $a, a, a$.
Since all three sides are equal ($a=a=a$), it means that it has at least two sides equal (for example, the first two sides are equal, $a=a$).
Therefore, an equilateral triangle satisfies the condition required for a triangle to be isosceles.
Thus, all equilateral triangles are also isosceles triangles.
Example 7: Angle of 0° is an acute angle.
Answer:
Solution:
The statement is False.
Let's understand the definition of an acute angle.
An acute angle is an angle that measures greater than 0° and less than 90°.
In mathematical notation, an angle $\theta$ is acute if $0^\circ < \theta < 90^\circ$.
An angle of 0° does not satisfy the condition of being greater than 0°.
An angle of 0° is called a zero angle.
Thus, an angle of 0° is not an acute angle.
Example 8: In Fig. 2.1, PQ AB ⊥ and PO = OQ. Is PQ the perpendicular bisector of line segment AB? Why or why not?

Answer:
Solution:
Given:
1. PQ $\perp$ AB (PQ is perpendicular to AB).
2. PO = OQ (O is the midpoint of PQ).
To Determine:
Is PQ the perpendicular bisector of line segment AB?
Explanation:
A perpendicular bisector of a line segment is a line (or line segment or ray) that meets the segment at a right angle ($90^\circ$) AND passes through the midpoint of the segment.
From the given information, we know that PQ is perpendicular to AB ($\text{PQ} \perp \text{AB}$). This means the angle formed by the intersection of PQ and AB at point O is $90^\circ$.
So, the condition of being perpendicular is satisfied.
However, for PQ to be the perpendicular bisector of AB, PQ must pass through the midpoint of AB.
The given information states that PO = OQ, which means O is the midpoint of PQ.
There is no information given that states that O is the midpoint of AB, or that AO = OB.
In the figure, point O appears to be the intersection point of PQ and AB.
For PQ to be the perpendicular bisector of AB, it must bisect AB, meaning it must divide AB into two equal parts at the point of intersection O. This would require AO = OB.
Since AO = OB is not given and cannot be concluded from the given conditions, we cannot say that PQ bisects AB.
Therefore, PQ is perpendicular to AB, but it is not necessarily the bisector of AB.
For PQ to be the perpendicular bisector of AB, the condition AO = OB would also need to be given.
Answer:
No, PQ is not the perpendicular bisector of line segment AB.
It is given that PQ is perpendicular to AB ($\text{PQ} \perp \text{AB}$), which means the angle at the intersection point O is $90^\circ$.
However, for PQ to be the perpendicular bisector of AB, it must also bisect AB at O, meaning AO must be equal to OB.
The given information PO = OQ tells us that O is the midpoint of PQ, not necessarily the midpoint of AB.
Since we are not given that O is the midpoint of AB (i.e., AO = OB), PQ is only perpendicular to AB, but not necessarily its bisector.
Example 9: In Fig. 2.2, if AC BD ⊥ , then name all the right angles.

Answer:
Solution:
Given:
AC $\perp$ BD (Line segment AC is perpendicular to line segment BD).
Let the intersection point of AC and BD be O.
To Find:
Name all the right angles.
Explanation:
When two lines or line segments are perpendicular to each other, they intersect at an angle of $90^\circ$. This angle is called a right angle.
In the given figure (Fig. 2.2), the line segment AC is perpendicular to the line segment BD. They intersect at point O.
The intersection of AC and BD forms four angles around the point O.
Since AC $\perp$ BD, the angles formed at the intersection O are $90^\circ$.
These four angles are:
1. The angle formed by segment AO and segment OB is $\angle \text{AOB}$.
2. The angle formed by segment OB and segment OC is $\angle \text{BOC}$.
3. The angle formed by segment OC and segment OD is $\angle \text{COD}$.
4. The angle formed by segment OD and segment OA is $\angle \text{DOA}$.
Because AC $\perp$ BD at O, each of these four angles is a right angle.
$\angle \text{AOB} = 90^\circ$
$\angle \text{BOC} = 90^\circ$
$\angle \text{COD} = 90^\circ$
$\angle \text{DOA} = 90^\circ$
Thus, the right angles are $\angle \text{AOB}$, $\angle \text{BOC}$, $\angle \text{COD}$, and $\angle \text{DOA}$.
Example 10: Is ABCD of Fig. 2.3 a polygon? If yes, what is the special name for it?

Answer:
Solution:
Definition of a polygon:
A polygon is a simple closed curve made up entirely of line segments.
Let's examine the figure ABCD:
1. It is made up of line segments AB, BC, CD, and DA.
2. It is a closed curve, as the line segments connect to form a complete boundary.
3. It is a simple curve, meaning it does not cross itself.
Since the figure ABCD satisfies all the conditions for being a polygon, it is a polygon.
Next, we need to find its special name.
The figure ABCD has 4 line segments as its sides (AB, BC, CD, DA).
Special names for polygons based on the number of sides:
A polygon with 3 sides is a triangle.
A polygon with 4 sides is a quadrilateral.
A polygon with 5 sides is a pentagon.
A polygon with 6 sides is a hexagon, and so on.
Since the figure ABCD has 4 sides, its special name is a quadrilateral.
Answer:
Yes, ABCD is a polygon.
The special name for a polygon of four sides is a quadrilateral.
Example 11: In Fig. 2.4, BCDE is a square and a 3D shape has been formed by joining the point A in space with the vertices B, C, D and E. Name the 3D shape and also its
(i) vertices,
(ii) edges and
(iii) faces.

Answer:
Solution:
Identifying the 3D shape:
The base of the shape is given as a square BCDE. A point A in space (the apex) is connected to each vertex of this square base (B, C, D, and E).
A 3D shape formed by connecting a polygonal base to a single point (apex) is called a pyramid.
Since the base is a square, the shape is a square pyramid.
Parts of the 3D shape:
(i) Vertices:
Vertices are the corner points of the 3D shape.
These are the vertices of the base and the apex point.
The vertices are A, B, C, D, and E.
(ii) Edges:
Edges are the line segments that form the skeleton of the 3D shape.
These include the sides of the base and the segments connecting the apex to the vertices of the base.
Edges of the base: BC, CD, DE, EB.
Edges connecting the apex to the base: AB, AC, AD, AE.
The edges are AB, AC, AD, AE, BC, CD, DE, and EB.
There are 8 edges in total.
(iii) Faces:
Faces are the flat surfaces that make up the boundaries of the 3D shape.
These include the base and the triangular surfaces connecting the apex to the sides of the base.
The base face is the square BCDE.
The side faces are the triangles formed by the apex A and each side of the base: $\triangle$ABC, $\triangle$ACD, $\triangle$ADE, and $\triangle$AEB.
The faces are the square BCDE and the triangles $\triangle$ABC, $\triangle$ACD, $\triangle$ADE, $\triangle$AEB.
There are 5 faces in total (1 square base + 4 triangular sides).
Example 12: Write the measure of smaller angle formed by the hour and the minute hands of a clock at 7 O’ clock. Also, write the measure of the other angle and also state what types of angles these are.
Answer:
Solution:
At 7 O' clock, the minute hand is pointing exactly at the 12, and the hour hand is pointing exactly at the 7.
A clock face is a circle, which measures $360^\circ$.
There are 12 hour divisions on the clock face.
The angle between two consecutive hour marks is $\frac{360^\circ}{12} = 30^\circ$.
At 7 O' clock, the hour hand is at 7 and the minute hand is at 12.
The number of hour divisions between 12 and 7 (moving clockwise) is 7 (from 12 to 1, 1 to 2, ..., 6 to 7).
The angle covered by these 7 divisions is $7 \times 30^\circ = 210^\circ$.
This is the larger angle between the hands.
The smaller angle between the hands is the angle formed by the remaining part of the circle.
Smaller angle $= 360^\circ - \text{Larger angle}$
Smaller angle $= 360^\circ - 210^\circ = 150^\circ$.
Alternatively, the number of hour divisions between 7 and 12 (moving clockwise from 7 to 12) is $12 - 7 = 5$.
The angle covered by these 5 divisions is $5 \times 30^\circ = 150^\circ$.
Thus, the measure of the smaller angle is $150^\circ$.
The measure of the other (larger) angle is $210^\circ$.
Classification of angles:
An acute angle is between $0^\circ$ and $90^\circ$.
A right angle is exactly $90^\circ$.
An obtuse angle is between $90^\circ$ and $180^\circ$.
A straight angle is exactly $180^\circ$.
A reflex angle is between $180^\circ$ and $360^\circ$.
A complete angle is exactly $360^\circ$.
The smaller angle is $150^\circ$. Since $90^\circ < 150^\circ < 180^\circ$, the smaller angle is an obtuse angle.
The larger angle is $210^\circ$. Since $180^\circ < 210^\circ < 360^\circ$, the larger angle is a reflex angle.
Exercise
Question 1 to 16 (Multiple Choice Questions)
In each of the questions 1 to 16, out of four options only one is correct. Write the correct answer.
Question 1. Number of lines passing through five points such that no three of them are collinear is
(A) 10
(B) 5
(C) 20
(D) 8
Answer:
Solution:
Given:
There are five points such that no three of them are collinear.
To Find:
The number of lines passing through these five points.
Explanation:
A unique straight line can be drawn through any two distinct points.
Since no three points are collinear, every pair of points will define a distinct line.
We need to find the number of ways to choose 2 points out of the given 5 points.
The number of lines passing through $n$ points, no three of which are collinear, is given by the formula:
Number of lines $= \frac{n(n-1)}{2}$
Here, the number of points is $n=5$.
Substitute $n=5$ into the formula:
Number of lines $= \frac{5(5-1)}{2}$
$= \frac{5(4)}{2}$
$= \frac{20}{2}$
$= 10$
Thus, the number of lines passing through five points such that no three of them are collinear is 10.
The correct option is (A) 10.
Question 2. The number of diagonals in a septagon is
(A) 21
(B) 42
(C) 7
(D) 14
Answer:
Solution:
A septagon (also known as a heptagon) is a polygon with 7 sides.
Number of sides, $n = 7$.
The number of diagonals of a polygon with $n$ sides is given by the formula:
Number of diagonals $= \frac{n(n-3)}{2}$
For a septagon, substitute $n=7$ into the formula:
Number of diagonals $= \frac{7(7-3)}{2}$
$= \frac{7(4)}{2}$
$= \frac{28}{2}$
$= 14$
Thus, the number of diagonals in a septagon is 14.
The correct option is (D) 14.
Question 3. Number of line segments in Fig. 2.5 is
(A) 5
(B) 10
(C) 15
(D) 20

Answer:
Solution:
Given:
Figure 2.5 shows 5 points A, B, C, D, and E which are the vertices of a pentagon.
To Find:
The number of line segments in the figure.
Explanation:
A line segment is formed by connecting any two distinct points.
In the given figure, there are 5 points: A, B, C, D, and E.
We need to find the number of ways to choose 2 points out of these 5 points to form a line segment.
The line segments formed by connecting pairs of points are:
AB, AC, AD, AE
BC, BD, BE
CD, CE
DE
Counting these segments, we have $4 + 3 + 2 + 1 = 10$ line segments.
Alternatively, we can use the formula for the number of line segments determined by $n$ points, no three of which are collinear, which is $\frac{n(n-1)}{2}$.
Here, $n=5$ (the number of points).
Number of line segments $= \frac{5(5-1)}{2} = \frac{5(4)}{2} = \frac{20}{2} = 10$.
The line segments in the figure are the sides of the pentagon (AB, BC, CD, DE, EA) and its diagonals (AC, AD, BD, BE, CE).
Number of sides = 5
Number of diagonals = $\frac{5(5-3)}{2} = \frac{5(2)}{2} = 5$
Total number of line segments = Number of sides + Number of diagonals = $5 + 5 = 10$.
Thus, the number of line segments in Fig. 2.5 is 10.
The correct option is (B) 10.
Question 4. Measures of the two angles between hour and minute hands of a clock at 9 O’ clock are
(A) 60°, 300°
(B) 270°, 90°
(C) 75°, 285°
(D) 30°, 330°
Answer:
Solution:
At 9 O' clock, the minute hand is pointing exactly at the 12, and the hour hand is pointing exactly at the 9.
The total angle around the centre of the clock is $360^\circ$.
There are 12 hour divisions on the clock face.
The angle between consecutive hour marks is $\frac{360^\circ}{12} = 30^\circ$.
At 9 O' clock, the hour hand is at 9 and the minute hand is at 12.
Moving clockwise from 9 to 12, there are $12 - 9 = 3$ hour divisions (from 9 to 10, 10 to 11, 11 to 12).
The angle covered by these 3 divisions is $3 \times 30^\circ = 90^\circ$.
This is one of the angles between the hands, and it is the smaller angle in this case.
The other angle is the reflex angle, which is the remaining part of the circle.
Other angle $= 360^\circ - \text{Smaller angle}$
Other angle $= 360^\circ - 90^\circ = 270^\circ$.
The measures of the two angles between the hour and minute hands at 9 O' clock are $90^\circ$ and $270^\circ$.
Looking at the options, the pair of angles is $270^\circ, 90^\circ$ (the order doesn't matter for the pair).
The correct option is (B) 270°, 90°.
Question 5. If a bicycle wheel has 48 spokes, then the angle between a pair of two consecutive spokes is
(A) $\left( 5\frac{1}{2} \right)$
(B) $\left( 7\frac{1}{2} \right)$
(C) $\left( \frac{2}{11} \right)$
(D) $\left( \frac{2}{15} \right)$
Answer:
Solution:
Given:
A bicycle wheel has 48 spokes.
To Find:
The angle between a pair of two consecutive spokes.
Explanation:
The spokes of a bicycle wheel are arranged radially around the center.
These spokes divide the complete angle around the center of the wheel into equal parts.
The total angle around the center of a circle is $360^\circ$.
The number of spokes is 48.
The 48 spokes divide the $360^\circ$ into 48 equal angles between consecutive spokes.
The measure of the angle between a pair of two consecutive spokes is given by:
Angle $= \frac{\text{Total angle}}{\text{Number of spokes}}$
Angle $= \frac{360^\circ}{48}$
Now, we simplify the fraction:
$\frac{360}{48} = \frac{180 \times 2}{24 \times 2} = \frac{180}{24}$
$\frac{180}{24} = \frac{90 \times 2}{12 \times 2} = \frac{90}{12}$
$\frac{90}{12} = \frac{45 \times 2}{6 \times 2} = \frac{45}{6}$
$\frac{45}{6} = \frac{15 \times 3}{2 \times 3} = \frac{15}{2}$
Converting the improper fraction $\frac{15}{2}$ to a mixed number:
$\frac{15}{2} = 7 \frac{1}{2}$
So, the angle between a pair of two consecutive spokes is $7\frac{1}{2}^\circ$.
Comparing this result with the given options:
(A) $( 5\frac{1}{2} )^\circ$
(B) $( 7\frac{1}{2} )^\circ$
(C) $( \frac{2}{11} )^\circ$
(D) $( \frac{2}{15} )^\circ$
The calculated angle matches option (B).
The correct option is (B) $( 7\frac{1}{2} )^\circ$.
Question 6. In Fig. 2.6, ∠XYZ cannot be written as
(A) ∠Y
(B) ∠ZXY
(C) ∠ZYX
(D) ∠XYP

Answer:
Solution:
Given:
Figure 2.6 shows an angle with vertex Y and rays YX and YZ.
There is also a point P on the ray YX.
To Determine:
Which of the given options is NOT another way to write $\angle$XYZ.
Explanation:
An angle is named using three points, with the vertex in the middle, or sometimes just by its vertex if there is no ambiguity.
The angle $\angle$XYZ has its vertex at Y, and its arms are the rays YX and YZ.
Let's analyze each option:
(A) $\angle$Y: Since there is only one angle formed at the vertex Y (by the rays YX and YZ), it is acceptable to name this angle simply as $\angle$Y. So, $\angle$XYZ can be written as $\angle$Y.
(B) $\angle$ZXY: In this notation, the vertex is X. This angle is formed by the rays XZ and XY. This is a different angle from $\angle$XYZ (whose vertex is Y).
(C) $\angle$ZYX: In this notation, the vertex is Y. The rays forming the angle are YZ and YX. This is the same angle as $\angle$XYZ, just with the order of the non-vertex points reversed. So, $\angle$XYZ can be written as $\angle$ZYX.
(D) $\angle$XYP: In this notation, the vertex is Y. The rays forming the angle are YX and YP. Since P is a point on the ray YX, the ray YP is the same as the ray YX. Therefore, the angle $\angle$XYP is the same as the angle formed by the rays YX and YP. Since YX and YP are the same ray, $\angle$XYP represents the angle formed by the ray YX (or YP) and... wait, the angle should be formed by two distinct rays from the vertex. Looking at the figure, $\angle$XYP seems to refer to the angle at vertex Y formed by ray YX and the ray extending through P. However, P lies on YX. Let's re-examine the notation and the figure. The standard three-letter notation for an angle uses the vertex in the middle, and one point on each ray. $\angle$XYP refers to the angle with vertex Y, formed by ray YX and ray YP. Since P lies on the ray YX, ray YP is the same as ray YX. An angle is formed by two distinct rays originating from a common point. If P is a point on the ray YX, then $\angle$XYP doesn't represent the angle $\angle$XYZ. It represents an angle with vertex Y and arms YX and YP. If P is on the ray YX, then the rays YX and YP are the same ray. This means $\angle$XYP would technically be a 0-degree or 180-degree angle depending on the context, or it might be referring to the ray itself. However, the question is asking which notation *cannot* represent $\angle$XYZ. Let's assume P is somewhere on the ray beyond X. In that case, ray YP would be the same as ray YX. So $\angle$XYP would be referring to the angle between ray YX and ray YX, which is $0^\circ$. This is clearly not the angle $\angle$XYZ.
Let's assume P is a point distinct from X and Y such that Y-X-P or Y-P-X or X-Y-P. From the figure, P is shown on the line segment XY (or ray YX). If P is on the ray YX, then the ray YP is the same as the ray YX. In this case, $\angle$XYP would be the angle between ray YX and ray YP. If ray YP is the same as ray YX, this angle is $0^\circ$. This is not $\angle$XYZ.
Let's consider the possibility that P is simply a label for the ray YX. In some notations, an angle might be denoted by a point on one ray, the vertex, and a point on the other ray. So $\angle$XYP would mean the angle at vertex Y formed by ray YX and ray YP. If P is on ray YX, then ray YP is the same as ray YX. The angle $\angle$XYZ is formed by ray YX and ray YZ. So, if P is on ray YX, then $\angle$XYP refers to the angle between ray YX and ray YP (which is ray YX). This would be a 0 degree angle or a straight angle if P is such that X, Y, P are collinear and Y is between X and P. But from the figure, P is on the ray YX. So ray YP is the same as ray YX. Thus $\angle$XYP refers to the angle between ray YX and ray YX, which is $0^\circ$. This is not $\angle$XYZ.
Let's re-read the options carefully. The question asks which one CANNOT be written as $\angle$XYZ.
(A) $\angle$Y: Yes, possible if no other angles share vertex Y. In the figure, only one angle is shown at Y.
(C) $\angle$ZYX: Yes, this is just reversing the non-vertex letters.
(D) $\angle$XYP: This refers to the angle at vertex Y formed by ray YX and ray YP. From the figure, P lies on the ray YX. If P is distinct from Y, then ray YP is the same as ray YX. So $\angle$XYP is the angle between ray YX and ray YX, which is $0^\circ$. This is not $\angle$XYZ.
(B) $\angle$ZXY: This refers to the angle at vertex X formed by ray XZ and ray XY. This is clearly a different angle from $\angle$XYZ.
Comparing options (B) and (D), option (B) names an angle with a different vertex (X instead of Y), while option (D) names an angle with the correct vertex (Y) but uses a point P on the same ray as X, which would imply a 0-degree angle if interpreted strictly, or perhaps the notation is intended differently. However, option (B) unequivocally names an angle with a different vertex and different rays.
The standard notation $\angle$XYZ means the angle with vertex Y, formed by rays YX and YZ.
$\angle$Y is acceptable if there is only one angle at Y.
$\angle$ZYX is the same as $\angle$XYZ.
$\angle$ZXY has vertex X, not Y. So this is a different angle.
$\angle$XYP has vertex Y, formed by rays YX and YP. Since P is on the ray YX, ray YP is the same as ray YX. So $\angle$XYP represents the angle between ray YX and itself, which is $0^\circ$. This is not $\angle$XYZ unless $\angle$XYZ is $0^\circ$, which is not the case in the figure.
Both (B) and (D) cannot be equal to $\angle$XYZ unless $\angle$XYZ = $0^\circ$. However, the question asks which notation *cannot* be written as $\angle$XYZ. Option (B) names an angle at a completely different vertex (X), formed by different rays (XZ and XY). Option (D) names an angle at the correct vertex (Y) but the second ray YP is the same as the first ray YX (since P is on ray YX), resulting in a $0^\circ$ angle notation.
In standard geometry naming conventions, $\angle$XYZ is the angle at Y with arms YX and YZ. The letters X and Z lie on the respective arms.
(A) $\angle$Y refers to the angle at vertex Y. This is correct if only one angle is present at Y.
(B) $\angle$ZXY refers to the angle at vertex X with arms XZ and XY. This is different.
(C) $\angle$ZYX refers to the angle at vertex Y with arms YZ and YX. This is the same angle as $\angle$XYZ.
(D) $\angle$XYP refers to the angle at vertex Y with arms YX and YP. Since P is on ray YX, ray YP is the same as ray YX. So this notation refers to the angle between ray YX and ray YX, which is $0^\circ$.
Both (B) and (D) represent angles different from $\angle$XYZ (assuming $\angle$XYZ is non-zero).
However, the question asks which CANNOT be written as $\angle$XYZ. While (D) represents an angle of $0^\circ$ (which is different from $\angle$XYZ), the notation itself uses the vertex Y and a point on one arm (X) and another point (P) which is also on the same arm YX. This notation might be considered invalid or representing a 0 angle, but it still *could* be interpreted as referring to the angle formed by ray YX and ray YP from vertex Y. Given that P is on ray YX, ray YP is the same as ray YX. Thus, $\angle$XYP represents the angle between ray YX and ray YX, which is $0^\circ$.
Option (B), $\angle$ZXY, clearly represents an angle at a different vertex X. Therefore, it absolutely cannot be written as $\angle$XYZ, unless X and Y refer to the same point and Z also lies on the line containing XY, which is not the case in the figure.
The most straightforward interpretation is that the notation $\angle$ABC refers to the angle at vertex B formed by rays BA and BC, where A is a point on ray BA and C is a point on ray BC.
Based on this, $\angle$XYZ is the angle at Y formed by rays YX and YZ.
(A) $\angle$Y is acceptable notation.
(B) $\angle$ZXY is the angle at X formed by rays XZ and XY. This is different from the angle at Y.
(C) $\angle$ZYX is the angle at Y formed by rays YZ and YX. This is the same as $\angle$XYZ.
(D) $\angle$XYP is the angle at Y formed by rays YX and YP. Since P is on ray YX, ray YP is the same as ray YX. So $\angle$XYP refers to the angle between ray YX and itself, which is $0^\circ$. This is different from $\angle$XYZ (unless $\angle$XYZ = $0^\circ$).
Both (B) and (D) represent angles different from $\angle$XYZ. However, option (B) is a different angle based on a different vertex, which makes it definitively distinct. Option (D) might be considered an angle at the correct vertex but a degenerate case ($0^\circ$).
The question asks which CANNOT be written as $\angle$XYZ. $\angle$ZXY is an angle at vertex X, while $\angle$XYZ is an angle at vertex Y. These are clearly different angles from the figure.
Therefore, $\angle$ZXY cannot be written as $\angle$XYZ.
The correct option is (B) ∠ZXY.
Question 7. In Fig 2.7, if point A is shifted to point B along the ray PX such that PB = 2PA, then the measure of ∠BPY is
(A) greater than 45°
(B) 45°
(C) less than 45°
(D) 90°

Answer:
Solution:
Given:
Figure 2.7 shows rays PY and PX originating from the common vertex P.
The symbol at vertex P indicates that the angle formed by these rays, $\angle$XPY, is a right angle.
So, $\angle$XPY = $90^\circ$.
Point A is on the ray PX.
Point A is shifted to point B along the ray PX such that PB = 2PA.
To Find:
The measure of $\angle$BPY.
Explanation:
The angle $\angle$APY is formed by the ray PA and the ray PY, with the vertex at P.
Since point A lies on the ray PX (and is distinct from P, otherwise PA would be 0 and PB=0, which contradicts the idea of shifting a point), the ray PA is the same as the ray PX.
Therefore, the angle $\angle$APY is the angle formed by the ray PX and the ray PY, which is $\angle$XPY.
From the figure, $\angle$XPY = $90^\circ$.
So, $\angle$APY = $90^\circ$.
Point A is shifted to point B along the ray PX.
This means that point B is also located on the ray PX, which starts at P and passes through X.
The condition PB = 2PA specifies the distance of B from P along this ray, ensuring B is distinct from P (unless A=P) and further from P than A if PA > 0.
The angle $\angle$BPY is formed by the ray PB and the ray PY, with the vertex at P.
Since point B lies on the ray PX and is distinct from P (given PB = 2PA and assuming PA $\neq$ 0), the ray PB is the same as the ray PX.
Therefore, the angle $\angle$BPY is the angle formed by the ray PX and the ray PY.
This angle is the same angle as $\angle$XPY.
So, $\angle$BPY = $\angle$XPY = $90^\circ$.
The measure of an angle formed by two rays from a common vertex is determined by the relative direction of the rays, not by the position of the points used to name the angle (as long as those points lie on the respective rays and are distinct from the vertex).
Since ray PB is the same as ray PX, the angle $\angle$BPY is identical to the angle $\angle$XPY.
The measure of $\angle$BPY is $90^\circ$.
The correct option is (D) 90°.
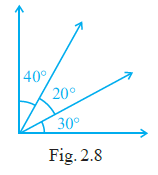
Question 8. The number of angles in Fig. 2.8 is
(A) 3
(B) 4
(C) 5
(D) 6
Answer:
Solution:
Given:
Figure 2.8 shows three rays OA, OB, and OC originating from a common point O.
To Find:
The number of angles in the figure.
Explanation:
An angle is formed by two rays having a common endpoint (vertex).
In the given figure, the common vertex is O, and the rays are OA, OB, and OC.
We can form an angle by choosing any two distinct rays from this set.
The pairs of rays originating from O are:
1. Ray OA and Ray OB, which form $\angle$AOB.
2. Ray OB and Ray OC, which form $\angle$BOC.
3. Ray OA and Ray OC, which form $\angle$AOC.
These three angles ($\angle$AOB, $\angle$BOC, and $\angle$AOC) are distinct angles shown in the figure.
The angle $\angle$AOC is the sum of $\angle$AOB and $\angle$BOC, i.e., $\angle$AOC $= \angle$AOB $+ \angle$BOC, assuming OB is between OA and OC.
Therefore, there are 3 angles in the figure.
Thus, the number of angles in Fig. 2.8 is 3.
The correct option is (A) 3.
Question 9. The number of obtuse angles in Fig. 2.9 is
(A) 2
(B) 3
(C) 4
(D) 5

Answer:
Solution:
Given:
Figure 2.9 shows five rays OA, OB, OC, OD, and OE originating from a common point O.
To Find:
The number of obtuse angles in the figure.
Explanation:
An obtuse angle is an angle whose measure is greater than $90^\circ$ and less than $180^\circ$.
In the figure, angles are formed by any two distinct rays starting from O.
There are $\binom{5}{2} = \frac{5 \times (5-1)}{2} = \frac{5 \times 4}{2} = 10$ distinct pairs of rays, each forming an angle (considering the smaller angle $\le 180^\circ$).
Let's list the angles formed by different pairs of rays from O and classify them based on their visual appearance:
1. Angles formed by adjacent rays (visually acute):
$\angle$AOB
$\angle$BOC
$\angle$COD
$\angle$DOE
$\angle$EOA
These 5 angles appear to be less than $90^\circ$, so they are acute angles.
2. Angles formed by skipping one ray (visually obtuse):
$\angle$AOC (formed by rays OA and OC)
$\angle$BOD (formed by rays OB and OD)
$\angle$COE (formed by rays OC and OE)
Visually, these three angles appear to be greater than $90^\circ$ and less than $180^\circ$, so they are obtuse angles.
3. Angles formed by skipping two rays (visually straight or reflex):
$\angle$AOD (formed by rays OA and OD). Visually, rays OA and OD appear to form a straight line. If they are collinear and opposite, the angle $\angle$AOD is $180^\circ$. A straight angle is not an obtuse angle.
$\angle$BOE (formed by rays OB and OE). Visually, rays OB and OE appear to form a straight line. If they are collinear and opposite, the angle $\angle$BOE is $180^\circ$. A straight angle is not an obtuse angle.
Other angles formed by skipping two or more rays, like $\angle$COA, $\angle$DOB, $\angle$EOC are the same as the angles already listed (e.g., $\angle$COA is the same as $\angle$AOC when considering the smaller angle).
Based on the visual appearance and the assumption that AOD and BOE are straight lines as depicted:
- There are 5 acute angles ($\angle$AOB, $\angle$BOC, $\angle$COD, $\angle$DOE, $\angle$EOA).
- There are 3 obtuse angles ($\angle$AOC, $\angle$BOD, $\angle$COE).
- There are 2 straight angles ($\angle$AOD, $\angle$BOE).
The sum of these angles is $5 + 3 + 2 = 10$, which accounts for all distinct angles $\le 180^\circ$ formed by the pairs of rays.
The number of obtuse angles is 3.
The correct option is (B) 3.
Question 10. The number of triangles in Fig. 2.10 is
(A) 10
(B) 12
(C) 13
(D) 14

Answer:
The figure shows triangle ABC with points D and E on BC, F on AC, and G on AB. Lines AD, AE, BF, and CG are drawn, and they appear to be concurrent at a single point O.
Geometrically, it is not possible for four distinct lines drawn from vertices to opposite sides (or points on them) to be concurrent at a single interior point unless there are further constraints (e.g., multiple points on a side are the same, or lines coincide). Given the options provided (10, 12, 13, 14), it is highly probable that the figure intends to represent a standard configuration that yields one of these numbers of triangles.
A common configuration involves three concurrent cevians (lines from a vertex to the opposite side). Let's assume the figure represents the case where the lines AD, BF, and CG are concurrent at O, and the point E on BC is the same as point D, making AE the same line as AD.
Under this interpretation, we are counting the number of triangles formed by the sides of $\triangle$ABC and the concurrent cevians AD, BF, and CG intersecting at O (where D is on BC, F on AC, and G on AB).
Let's systematically list the triangles formed by the segments in this configuration:
1. The large triangle:
$\triangle$ABC
(1 triangle)
2. Triangles formed by one cevian and the sides of $\triangle$ABC:
Cevian AD divides $\triangle$ABC into $\triangle$ABD and $\triangle$ACD.
Cevian BF divides $\triangle$ABC into $\triangle$ABF (degenerate, A, F, C are collinear) and $\triangle$BCF.
Cevian CG divides $\triangle$ABC into $\triangle$ACG (degenerate, A, G, B are collinear) and $\triangle$BCG.
So we have $\triangle$ABD, $\triangle$ACD, $\triangle$BCF, $\triangle$BCG.
(4 triangles)
3. Triangles formed by the intersection point O and the vertices:
The concurrent cevians divide $\triangle$ABC into 6 smaller triangles around the point of concurrency O. These are formed by O and two adjacent points among {A, B, C, D, F, G}.
Assuming the segments are OG, OA, OF, OC, OD, OB around O, the 6 small triangles are $\triangle$AOG, $\triangle$BOG, $\triangle$BOD, $\triangle$COD, $\triangle$COF, $\triangle$AOF.
(6 triangles)
4. Triangles formed by combining two adjacent small triangles around O that share a vertex of $\triangle$ABC:
$\triangle$AOB (formed by $\triangle$AOG + $\triangle$BOG)
$\triangle$BOC (formed by $\triangle$BOD + $\triangle$COD, assuming D is the point on BC met by AD passing through O)
$\triangle$COA (formed by $\triangle$COF + $\triangle$AOF)
(3 triangles)
Let's list all 14 distinct triangles obtained from the 3 concurrent cevians case:
1. $\triangle$ABC
2. $\triangle$ABD
3. $\triangle$ACD
4. $\triangle$BCF
5. $\triangle$BCG
6. $\triangle$AOB
7. $\triangle$BOC
8. $\triangle$COA
9. $\triangle$AOG
10. $\triangle$BOG
11. $\triangle$BOD
12. $\triangle$COD
13. $\triangle$COF
14. $\triangle$AOF
Total number of triangles = $1 + 4 + 6 + 3 = 14$.
Note that $\triangle$ABD is formed by segments AB, BD, AD. $\triangle$AOB is formed by segments AO, OB, AB. $\triangle$AOG is formed by segments AO, OG, AG. These are distinct triangles based on their vertices and bounding segments.
The total number of triangles is 14.
Question 11. If the sum of two angles is greater than 180°, then which of the following is not possible for the two angles?
(A) One obtuse angle and one acute angle
(B) One reflex angle and one acute angle
(C) Two obtuse angles
(D) Two right angles.
Answer:
Let's define the types of angles involved:
Acute angle: An angle $\theta$ such that $0^\circ < \theta < 90^\circ$.
Right angle: An angle $\theta$ such that $\theta = 90^\circ$.
Obtuse angle: An angle $\theta$ such that $90^\circ < \theta < 180^\circ$.
Reflex angle: An angle $\theta$ such that $180^\circ < \theta < 360^\circ$.
We are looking for the case where the sum of two angles is not possible to be greater than $180^\circ$. Let's examine each option:
(A) One obtuse angle and one acute angle
Let the obtuse angle be $\alpha$ and the acute angle be $\beta$.
We have $90^\circ < \alpha < 180^\circ$ and $0^\circ < \beta < 90^\circ$.
Adding the inequalities, we get $90^\circ + 0^\circ < \alpha + \beta < 180^\circ + 90^\circ$, which means $90^\circ < \alpha + \beta < 270^\circ$.
Since the sum can be between $90^\circ$ and $270^\circ$, it is possible for the sum to be greater than $180^\circ$. For example, an obtuse angle of $100^\circ$ and an acute angle of $85^\circ$ sum to $185^\circ$, which is greater than $180^\circ$.
(B) One reflex angle and one acute angle
Let the reflex angle be $\gamma$ and the acute angle be $\delta$.
We have $180^\circ < \gamma < 360^\circ$ and $0^\circ < \delta < 90^\circ$.
Adding the inequalities, we get $180^\circ + 0^\circ < \gamma + \delta < 360^\circ + 90^\circ$, which means $180^\circ < \gamma + \delta < 450^\circ$.
Since the minimum possible sum is greater than $180^\circ$, the sum is always greater than $180^\circ$. It is possible for the sum to be greater than $180^\circ$.
(C) Two obtuse angles
Let the two obtuse angles be $\epsilon$ and $\zeta$.
We have $90^\circ < \epsilon < 180^\circ$ and $90^\circ < \zeta < 180^\circ$.
Adding the inequalities, we get $90^\circ + 90^\circ < \epsilon + \zeta < 180^\circ + 180^\circ$, which means $180^\circ < \epsilon + \zeta < 360^\circ$.
Since the minimum possible sum is greater than $180^\circ$, the sum of two obtuse angles is always greater than $180^\circ$. It is possible for the sum to be greater than $180^\circ$.
(D) Two right angles
Let the two right angles be $\eta$ and $\iota$.
We have $\eta = 90^\circ$ and $\iota = 90^\circ$.
Their sum is $\eta + \iota = 90^\circ + 90^\circ = 180^\circ$.
The sum of two right angles is exactly $180^\circ$. It is not greater than $180^\circ$. Therefore, it is not possible for the sum of two right angles to be greater than $180^\circ$.
Based on the analysis, the only case where the sum of the two angles cannot be greater than $180^\circ$ is when both angles are right angles, as their sum is exactly $180^\circ$.
The correct option is (D) Two right angles.
Question 12. If the sum of two angles is equal to an obtuse angle, then which of the following is not possible?
(A) One obtuse angle and one acute angle.
(B) One right angle and one acute angle.
(C) Two acute angles.
(D) Two right angles.
Answer:
Let's recall the definition of an obtuse angle:
Obtuse angle: An angle $\theta$ such that $90^\circ < \theta < 180^\circ$.
We are looking for the combination of two angles whose sum cannot be an obtuse angle (i.e., cannot be between $90^\circ$ and $180^\circ$, exclusive).
Let's examine each option:
(A) One obtuse angle and one acute angle.
Let the obtuse angle be $\alpha$ ($90^\circ < \alpha < 180^\circ$) and the acute angle be $\beta$ ($0^\circ < \beta < 90^\circ$).
Their sum is $\alpha + \beta$.
The range of the sum is $90^\circ + 0^\circ < \alpha + \beta < 180^\circ + 90^\circ$, which is $90^\circ < \alpha + \beta < 270^\circ$.
It is possible for the sum to be within the obtuse angle range ($90^\circ < \text{sum} < 180^\circ$). For example, if $\alpha = 100^\circ$ and $\beta = 50^\circ$, the sum is $150^\circ$, which is an obtuse angle.
(B) One right angle and one acute angle.
Let the right angle be $\rho = 90^\circ$ and the acute angle be $\sigma$ ($0^\circ < \sigma < 90^\circ$).
Their sum is $\rho + \sigma = 90^\circ + \sigma$.
Since $0^\circ < \sigma < 90^\circ$, the sum $90^\circ + \sigma$ will be strictly between $90^\circ + 0^\circ = 90^\circ$ and $90^\circ + 90^\circ = 180^\circ$.
So, $90^\circ < 90^\circ + \sigma < 180^\circ$. This range is precisely the definition of an obtuse angle. The sum is always an obtuse angle in this case. This is possible.
(C) Two acute angles.
Let the two acute angles be $\chi$ ($0^\circ < \chi < 90^\circ$) and $\psi$ ($0^\circ < \psi < 90^\circ$).
Their sum is $\chi + \psi$.
The range of the sum is $0^\circ + 0^\circ < \chi + \psi < 90^\circ + 90^\circ$, which is $0^\circ < \chi + \psi < 180^\circ$.
It is possible for the sum to be within the obtuse angle range ($90^\circ < \text{sum} < 180^\circ$). For example, if $\chi = 50^\circ$ and $\psi = 70^\circ$, the sum is $120^\circ$, which is an obtuse angle.
(D) Two right angles.
Let the two right angles be $\eta = 90^\circ$ and $\iota = 90^\circ$.
Their sum is $\eta + \iota = 90^\circ + 90^\circ = 180^\circ$.
A sum of exactly $180^\circ$ is a straight angle. An obtuse angle must be strictly less than $180^\circ$. Therefore, the sum of two right angles cannot be an obtuse angle.
Thus, the combination of angles for which the sum cannot be equal to an obtuse angle is two right angles.
The correct option is (D) Two right angles.
Question 13. A polygon has prime number of sides. Its number of sides is equal to the sum of the two least consecutive primes. The number of diagonals of the polygon is
(A) 4
(B) 5
(C) 7
(D) 10
Answer:
Given:
A polygon has a prime number of sides.
The number of sides is equal to the sum of the two least consecutive primes.
To Find:
The number of diagonals of the polygon.
Solution:
The least prime numbers are 2, 3, 5, 7, 11, ...
The two least consecutive prime numbers are 2 and 3.
The sum of these two primes is $2 + 3 = 5$.
According to the question, the number of sides of the polygon is equal to this sum.
So, the number of sides, $n$, is 5.
We check that 5 is indeed a prime number, satisfying the condition given in the question.
The formula for the number of diagonals of a polygon with $n$ sides is given by:
Number of diagonals $= \frac{n(n-3)}{2}$
Substitute $n=5$ into the formula:
Number of diagonals $= \frac{5(5-3)}{2}$
Number of diagonals $= \frac{5(2)}{2}$
Number of diagonals $= \frac{10}{2}$
Number of diagonals $= 5$
The number of diagonals of the polygon is 5.
Comparing this result with the given options:
(A) 4
(B) 5
(C) 7
(D) 10
The calculated number of diagonals is 5, which matches option (B).
The correct answer is (B) 5.
Question 14. In Fig. 2.11, AB = BC and AD = BD = DC. The number of isoscles triangles in the figure is
(A) 1
(B) 2
(C) 3
(D) 4

Answer:
Given:
In the given figure:
AB = BC
AD = BD = DC
To Find:
The number of isosceles triangles in the figure.
Solution:
An isosceles triangle is a triangle that has at least two sides of equal length.
Let's examine the triangles in the figure based on the given conditions:
Triangle ABC:
We are given that AB = BC.
AB = BC
(Given)
Since two sides (AB and BC) are equal, triangle ABC is an isosceles triangle.
Triangle ABD:
We are given that AD = BD = DC.
AD = BD
(Given)
Since two sides (AD and BD) are equal, triangle ABD is an isosceles triangle.
Triangle BDC:
We are given that AD = BD = DC.
BD = DC
(Given)
Since two sides (BD and DC) are equal, triangle BDC is an isosceles triangle.
Triangle ADC:
We are given that AD = BD and BD = DC.
By the transitive property of equality, if AD = BD and BD = DC, then AD = DC.
AD = DC
(Derived from given conditions)
Since two sides (AD and DC) are equal, triangle ADC is an isosceles triangle.
The isosceles triangles in the figure are $\triangle$ABC, $\triangle$ABD, $\triangle$BDC, and $\triangle$ADC.
Counting these triangles, we find there are 4 isosceles triangles.
Comparing this number with the given options:
(A) 1
(B) 2
(C) 3
(D) 4
The calculated number of isosceles triangles is 4, which matches option (D).
The correct answer is (D) 4.
Question 15. In Fig. 2.12, ∠BAC = 90° and AD ⊥ BC. The number of right triangles in the figure is
(A) 1
(B) 2
(C) 3
(D) 4

Answer:
Given:
In the given figure:
$\angle$BAC = $90^\circ$
AD $\perp$ BC (AD is perpendicular to BC)
To Find:
The number of right triangles in the figure.
Solution:
A right triangle is a triangle that has one interior angle equal to $90^\circ$.
Let's examine the triangles in the figure based on the given conditions:
Triangle ABC:
We are given that $\angle$BAC = $90^\circ$.
$\angle$BAC = $90^\circ$
(Given)
Since one angle ($\angle$BAC) is $90^\circ$, triangle ABC is a right triangle.
Triangle ABD:
We are given that AD $\perp$ BC. This means that the line segment AD forms a right angle with the line segment BC at the point of intersection D.
Therefore, $\angle$ADB = $90^\circ$.
$\angle$ADB = $90^\circ$
(Since AD $\perp$ BC)
Since one angle ($\angle$ADB) is $90^\circ$, triangle ABD is a right triangle.
Triangle ADC:
We are given that AD $\perp$ BC. Similar to the previous case, the angle formed by AD and BC at D is $90^\circ$.
Therefore, $\angle$ADC = $90^\circ$.
$\angle$ADC = $90^\circ$
(Since AD $\perp$ BC)
Since one angle ($\angle$ADC) is $90^\circ$, triangle ADC is a right triangle.
The right triangles identified in the figure are $\triangle$ABC, $\triangle$ABD, and $\triangle$ADC.
Counting these triangles, we find there are 3 right triangles.
Comparing this number with the given options:
(A) 1
(B) 2
(C) 3
(D) 4
The calculated number of right triangles is 3, which matches option (C).
The correct answer is (C) 3.
Question 16. In Fig. 2.13, PQ ⊥ RQ, PQ = 5 cm and QR = 5 cm. Then ∆ PQR is
(A) a right triangle but not isosceles
(B) an isosceles right triangle
(C) isosceles but not a right triangle
(D) neither isosceles nor right triangle

Answer:
Given:
In $\triangle$ PQR:
PQ $\perp$ RQ
PQ = 5 cm
QR = 5 cm
To Determine:
The type of triangle PQR.
Solution:
The condition PQ $\perp$ RQ means that the angle formed at the vertex R between sides PQ and RQ is a right angle ($90^\circ$).
Thus, $\angle$R = $90^\circ$ (or $\angle$PRQ = $90^\circ$).
$\angle$PRQ = $90^\circ$
(Since PQ $\perp$ RQ)
Since $\triangle$ PQR has one angle equal to $90^\circ$, it is a right triangle.
We are also given that the lengths of sides PQ and QR are equal.
PQ = QR = 5 cm
(Given)
Since two sides of $\triangle$ PQR (PQ and QR) have equal lengths, it is an isosceles triangle.
Combining these two properties, $\triangle$ PQR is a triangle that is both a right triangle and an isosceles triangle.
Therefore, $\triangle$ PQR is an isosceles right triangle.
Comparing this conclusion with the given options:
(A) a right triangle but not isosceles
(B) an isosceles right triangle
(C) isosceles but not a right triangle
(D) neither isosceles nor right triangle
Our conclusion matches option (B).
The correct answer is (B) an isosceles right triangle.
Question 17 to 31 (Fill in the Blanks)
In questions 17 to 31, fill in the blanks to make the statements true:
Question 17. An angle greater than 180° and less than a complete angle is called _______.
Answer:
An angle greater than $180^\circ$ and less than a complete angle ($360^\circ$) is called a reflex angle.
Question 18. The number of diagonals in a hexagon is ________.
Answer:
A hexagon is a polygon with 6 sides.
The number of sides is $n=6$.
The formula for the number of diagonals in a polygon with $n$ sides is:
Number of diagonals $= \frac{n(n-3)}{2}$
Substituting $n=6$ for a hexagon:
Number of diagonals $= \frac{6(6-3)}{2}$
Number of diagonals $= \frac{6(3)}{2}$
Number of diagonals $= \frac{18}{2}$
Number of diagonals $= 9$
The number of diagonals in a hexagon is 9.
Question 19. A pair of opposite sides of a trapezium are ________.
Answer:
A trapezium (also known as a trapezoid) is a quadrilateral with at least one pair of parallel opposite sides.
Therefore, a pair of opposite sides of a trapezium are parallel.
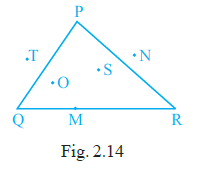
Question 20. In Fig. 2.14, points lying in the interior of the triangle PQR are ______, that in the exterior are ______ and that on the triangle itself are ______.
Answer:
Based on the figure (Fig. 2.14) and the definitions of the interior, exterior, and boundary of a triangle:
Points lying in the interior of $\triangle$PQR are those points that are inside the triangle and not on its sides or vertices. In the figure, point A is in the interior.
So, the points lying in the interior of the triangle PQR are A.
Points lying in the exterior of $\triangle$PQR are those points that are outside the triangle. In the figure, points B and C are in the exterior.
So, the points lying in the exterior of the triangle PQR are B, C.
Points lying on the triangle itself are those points that lie on the boundary of the triangle (on the vertices or on the sides). In the figure, points X and Y are on the sides PQ and QR respectively. The vertices P, Q, and R are also on the triangle itself.
So, the points lying on the triangle itself are P, Q, R, X, Y.
Question 21. In Fig. 2.15, points A, B, C, D and E are collinear such that AB = BC = CD = DE. Then
(a) AD = AB + ______
(b) AD = AC + ______
(c) mid point of AE is ______
(d) mid point of CE is ______
(e) AE = ______ × AB
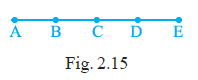
Answer:
Given:
Points A, B, C, D, and E are collinear.
AB = BC = CD = DE.
Let the common length of the segments be $x$.
So, AB = BC = CD = DE = $x$.
We can express the length of other segments in terms of $x$:
AC = AB + BC = $x + x = 2x$
AD = AB + BC + CD = $x + x + x = 3x$
AE = AB + BC + CD + DE = $x + x + x + x = 4x$
BD = BC + CD = $x + x = 2x$
BE = BC + CD + DE = $x + x + x = 3x$
CE = CD + DE = $x + x = 2x$
(a) AD = AB + ______
We know AD = AB + BD.
So, the blank is BD.
(b) AD = AC + ______
We know AD = AC + CD.
So, the blank is CD.
(c) mid point of AE is ______
The total length of AE is $4x$. The midpoint is the point at distance $\frac{4x}{2} = 2x$ from A (or E).
Starting from A, the point at distance $2x$ is C (since AC = $2x$).
Starting from E, the point at distance $2x$ is C (since EC = $2x$).
So, the midpoint of AE is C.
(d) mid point of CE is ______
The total length of CE is $2x$. The midpoint is the point at distance $\frac{2x}{2} = x$ from C (or E).
Starting from C, the point at distance $x$ is D (since CD = $x$).
Starting from E, the point at distance $x$ is D (since ED = $x$).
So, the midpoint of CE is D.
(e) AE = ______ × AB
We know AE = $4x$ and AB = $x$.
$4x = 4 \times x$
So, AE = 4 × AB.
The blank is 4.
Question 22. In Fig. 2.16,
(a) ∠AOD is a/an ______ angle
(b) ∠COA is a/an ______ angle
(c) ∠AOE is a/an ______ angle

Answer:
Based on the visual representation in Fig. 2.16 and the definitions of angle types:
(a) $\angle$AOD is formed by rays OA and OD. From the figure, it appears that this angle is greater than $90^\circ$ but less than $180^\circ$. An angle with a measure between $90^\circ$ and $180^\circ$ is called an obtuse angle.
So, $\angle$AOD is a/an obtuse angle.
(b) $\angle$COA is formed by rays OC and OA. From the figure, it appears that this angle is less than $90^\circ$. An angle with a measure between $0^\circ$ and $90^\circ$ is called an acute angle.
So, $\angle$COA is a/an acute angle.
(c) $\angle$AOE is formed by rays OA and OE. The arc shown indicates the larger angle. This angle starts from ray OA and goes around past the straight line BOD towards OE. This angle appears to be greater than $180^\circ$ but less than $360^\circ$. An angle with a measure between $180^\circ$ and $360^\circ$ is called a reflex angle.
So, $\angle$AOE is a/an reflex angle.
Question 23. The number of triangles in Fig. 2.17 is ______. Their names are ________.
Answer:
To find the number of triangles in the figure, we need to identify all combinations of three non-collinear vertices that form a triangle.
Let's list the triangles present in Fig. 2.17:
1. $\triangle$ABO
2. $\triangle$BCO
3. $\triangle$CDO
4. $\triangle$DAO
5. $\triangle$ABC (formed by sides AB, BC, and diagonal AC)
6. $\triangle$ADC (formed by sides AD, DC, and diagonal AC)
7. $\triangle$ABD (formed by sides AB, AD, and diagonal BD)
8. $\triangle$BCD (formed by sides BC, CD, and diagonal BD)
Counting the identified triangles, we find there are 8 distinct triangles in the figure.
The number of triangles in Fig. 2.17 is 8.
Their names are $\triangle$ABO, $\triangle$BCO, $\triangle$CDO, $\triangle$DAO, $\triangle$ABC, $\triangle$ADC, $\triangle$ABD, and $\triangle$BCD.
Question 24. Number of angles less than 180° in Fig. 2.17 is ______and their names are ______.
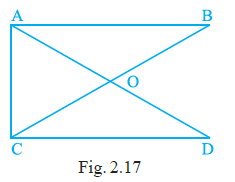
Answer:
In Fig. 2.17, we need to count all angles whose measure is less than $180^\circ$. These include the interior angles at each vertex of the quadrilateral, the angles formed by the intersection of the diagonals, and the angles formed by the sides and diagonals at each vertex.
Let's list the angles:
1. Interior angles of the quadrilateral ABCD:
$\angle$DAB (or $\angle$A)
$\angle$ABC (or $\angle$B)
$\angle$BCD (or $\angle$C)
$\angle$CDA (or $\angle$D)
There are 4 such angles.
2. Angles formed at the intersection point O of the diagonals AC and BD:
$\angle$AOB
$\angle$BOC
$\angle$COD
$\angle$DOA
These are 4 distinct angles.
3. Angles formed by the sides and diagonals at the vertices:
At vertex A: $\angle$CAB, $\angle$CAD
At vertex B: $\angle$ABD, $\angle$DBC
At vertex C: $\angle$BCA, $\angle$ACD
At vertex D: $\angle$BDA, $\angle$BDC
There are 8 such angles (2 at each of the 4 vertices).
All these angles are typically less than $180^\circ$ in a standard convex quadrilateral as shown in the figure.
The total number of distinct angles less than $180^\circ$ is the sum of the angles from these three categories: $4 + 4 + 8 = 16$.
The number of angles less than $180^\circ$ in Fig. 2.17 is 16.
Their names are $\angle$DAB, $\angle$ABC, $\angle$BCD, $\angle$CDA, $\angle$AOB, $\angle$BOC, $\angle$COD, $\angle$DOA, $\angle$CAB, $\angle$CAD, $\angle$ABD, $\angle$DBC, $\angle$BCA, $\angle$ACD, $\angle$BDA, $\angle$BDC.
Question 25. The number of straight angles in Fig. 2.17 is ______.
Answer:
A straight angle is an angle that measures exactly $180^\circ$. It is formed by a straight line.
In Fig. 2.17, the diagonals AC and BD intersect at point O. Since A, O, and C are collinear, the angle formed by the straight line segment AC is a straight angle.
This can be represented as $\angle$AOC.
$\angle$AOC = $180^\circ$
(Straight angle)
Similarly, since B, O, and D are collinear, the angle formed by the straight line segment BD is also a straight angle.
This can be represented as $\angle$BOD.
$\angle$BOD = $180^\circ$
(Straight angle)
There are no other straight lines forming angles within the figure.
The number of straight angles in Fig. 2.17 is 2.
Question 26. The number of right angles in a straight angle is ______ and that in a complete angle is ______.
Answer:
A straight angle measures $180^\circ$.
A right angle measures $90^\circ$.
To find the number of right angles in a straight angle, we divide the measure of a straight angle by the measure of a right angle:
Number of right angles = $\frac{180^\circ}{90^\circ} = 2$
The number of right angles in a straight angle is 2.
A complete angle measures $360^\circ$.
A right angle measures $90^\circ$.
To find the number of right angles in a complete angle, we divide the measure of a complete angle by the measure of a right angle:
Number of right angles = $\frac{360^\circ}{90^\circ} = 4$
The number of right angles in a complete angle is 4.
The number of right angles in a straight angle is 2 and that in a complete angle is 4.
Question 27. The number of common points in the two angles marked in Fig. 2.18 is ______.

Answer:
The two angles marked in Fig. 2.18 appear to be $\angle$AOC and $\angle$BOC.
Angle $\angle$AOC is formed by rays OA and OC, with vertex O. It consists of the vertex O, the rays OA and OC, and all points in its interior.
Angle $\angle$BOC is formed by rays OB and OC, with vertex O. It consists of the vertex O, the rays OB and OC, and all points in its interior.
Let's find the common points:
1. The vertex O is common to both angles.
2. The ray OC is common to both angles. A ray consists of infinitely many points starting from the vertex and extending in one direction.
3. The rays OA and OB are the other arms. Assuming OA and OB are distinct rays (as shown in the figure), they are not common to both angles, except for the vertex O which is already counted.
4. The interiors of the two angles are generally distinct regions (unless one angle contains the other, which is not the case here).
The common points are the vertex O and all the points on the ray OC.
Since a ray contains infinitely many points, the number of common points is infinite.
The number of common points in the two angles marked in Fig. 2.18 is infinite.
Question 28. The number of common points in the two angles marked in Fig. 2.19 is ______.

Answer:
The figure shows two angles marked. These appear to be vertical angles formed by the intersection of two lines. Let's assume the vertex is O, and the rays forming the first angle are OA and OB, and the rays forming the second angle are OC and OD, where A, O, C are collinear and B, O, D are collinear.
Let the two marked angles be $\angle$AOB and $\angle$COD.
Angle $\angle$AOB consists of:
- The vertex O.
- The ray OA.
- The ray OB.
- All points in the interior region between rays OA and OB.
Angle $\angle$COD consists of:
- The vertex O.
- The ray OC.
- The ray OD.
- All points in the interior region between rays OC and OD.
Now let's find the points that are common to both angles:
- The vertex O is the common endpoint of all four rays OA, OB, OC, and OD. Thus, O is a common point.
- The rays OA, OB, OC, and OD are distinct rays (except for the common vertex O). There are no common points on the rays themselves, other than the vertex O.
- The interior regions of $\angle$AOB and $\angle$COD are typically separate regions when they are vertical angles.
Therefore, the only point common to both angles is the vertex O.
The number of common points in the two angles marked in Fig. 2.19 is 1.
Question 29. The number of common points in the two angles marked in Fig. 2.20 ______ .

Answer:
The figure shows two angles marked as $\angle$AOB and $\angle$BOC. These angles are adjacent angles as they share a common vertex (O) and a common arm (OB).
Angle $\angle$AOB consists of the vertex O, the ray OA, the ray OB, and all points in its interior.
Angle $\angle$BOC consists of the vertex O, the ray OB, the ray OC, and all points in its interior.
Let's identify the common points:
1. The vertex O is the common endpoint of the rays OA, OB, and OC. So, O is a common point to both angles.
2. The ray OB is an arm of both $\angle$AOB and $\angle$BOC. All points lying on the ray OB (starting from O and extending infinitely) are part of both angles.
3. The rays OA and OC are the other arms. A point on ray OA (other than O) is not on ray OB or ray OC. A point on ray OC (other than O) is not on ray OA or ray OB.
4. The interiors of adjacent angles $\angle$AOB and $\angle$BOC are disjoint regions. A point in the interior of $\angle$AOB is not in the interior of $\angle$BOC, and vice versa.
The set of common points is the union of the vertex O and the ray OB. Since a ray contains infinitely many points, the number of common points is infinite.
The number of common points in the two angles marked in Fig. 2.20 is infinite.
Question 30. The number of common points in the two angles marked in Fig. 2.21 is ______.

Answer:
The two angles marked in Fig. 2.21 are adjacent angles that share a common vertex and a common arm. Let the vertex be O. The two angles are $\angle$AOB and $\angle$BOC.
Angle $\angle$AOB is formed by rays OA and OB with vertex O.
Angle $\angle$BOC is formed by rays OB and OC with vertex O.
The points common to both angles include:
1. The vertex O is the common endpoint of the rays OA, OB, and OC. So, O is common to both angles.
2. The ray OB is the common arm for both angles. All points on the ray OB, starting from O and extending infinitely, are part of both angles.
3. The interiors of the two adjacent angles $\angle$AOB and $\angle$BOC are distinct regions and do not overlap.
The common points are the points on the common ray OB, which includes the vertex O.
A ray is a part of a line that starts at a particular point and extends infinitely in one direction. Therefore, a ray contains infinitely many points.
The number of common points in the two angles marked in Fig. 2.21 is infinite.
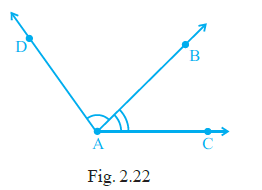
Question 31. The common part between the two angles BAC and DAB in Fig. 2.22 is ______.
Answer:
The two angles mentioned are $\angle$BAC and $\angle$DAB.
Angle $\angle$BAC is formed by the rays AB and AC, with vertex A.
Angle $\angle$DAB is formed by the rays AD and AB, with vertex A.
Both angles share the same vertex, which is point A.
Both angles share the same arm, which is the ray AB (starting from A and passing through B).
The common part between the two angles is the geometric element that is part of both angles.
The set of points that form an angle includes the vertex and the points on its arms.
The common points are the points that are on ray AB, including the vertex A.
This set of points precisely describes the ray AB.
The common part between the two angles BAC and DAB in Fig. 2.22 is the ray AB.
Question 32 to 41 (True or False)
State whether the statements given in questions 32 to 41 are true (T) or false (F):
Question 32. A horizontal line and a vertical line always intersect at right angles.
Answer:
The statement is about the intersection of a horizontal line and a vertical line.
A horizontal line extends left and right, perpendicular to the direction of gravity.
A vertical line extends up and down, parallel to the direction of gravity.
When a horizontal line and a vertical line intersect, they are perpendicular to each other. Perpendicular lines intersect at an angle of $90^\circ$.
$90^\circ$ is the definition of a right angle.
Therefore, a horizontal line and a vertical line always intersect at right angles.
The statement is True (T).
Question 33. If the arms of an angle on the paper are increased, the angle increases.
Answer:
An angle is defined by the measure of the rotation between its two rays (arms) from the common endpoint (vertex).
The length of the lines drawn on paper representing the arms of an angle does not affect the amount of rotation between the rays.
For example, if we draw a $45^\circ$ angle, it remains a $45^\circ$ angle regardless of whether the arms are drawn 1 cm long or 10 cm long.
The angle measure is independent of the visual length of its arms.
Therefore, if the arms of an angle on the paper are increased, the angle does not increase.
The statement is False (F).
Question 34. If the arms of an angle on the paper are decreased, the angle decreases.
Answer:
An angle is defined by the amount of rotation between its two rays (arms) that share a common endpoint (vertex).
The measure of an angle depends only on the relative orientation of its two arms (rays), not on the physical length drawn for the arms on a piece of paper.
Changing the length of the line segments drawn to represent the arms does not change the angle between the rays they represent.
Therefore, if the arms of an angle on the paper are decreased, the angle does not decrease.
The statement is False (F).
Question 35. If line PQ || line m, then line segment PQ || m
Answer:
Let line PQ be the infinite line passing through points P and Q.
Let line segment PQ be the part of the line PQ between points P and Q, including P and Q.
Let line m be another line.
The condition "line PQ || line m" means that the entire infinite line passing through P and Q is parallel to line m.
If a line is parallel to another line, then every part of that line, including any line segment on it, is also parallel to the other line.
This is because parallel lines maintain a constant distance between them and never intersect. If the line containing the segment PQ is parallel to line m, then all points on the segment PQ are at a constant distance from line m.
Therefore, if line PQ is parallel to line m, then the line segment PQ is also parallel to line m.
The statement is True (T).
Question 36. Two parallel lines meet each other at some point.
Answer:
Parallel lines are defined as two or more lines that lie in the same plane and never intersect each other, even if extended infinitely in both directions.
The statement says that two parallel lines meet each other at some point, which is contrary to the definition of parallel lines.
Therefore, the statement is incorrect.
The statement is False (F).
Question 37. Measures of ∠ABC and ∠CBA in Fig. 2.23 are the same.

Answer:
The angle $\angle$ABC is an angle with vertex at point B and arms being the ray BA and the ray BC.
The angle $\angle$CBA is an angle with vertex at point B and arms being the ray BC and the ray BA.
In standard geometry, the order of the non-vertex letters in the notation of an angle does not change the angle itself. Both notations, $\angle$ABC and $\angle$CBA, refer to the same geometric angle formed by the two rays originating from B and passing through A and C, respectively.
The measure of an angle is a property of the angle itself, determined by the separation between its arms. Since $\angle$ABC and $\angle$CBA represent the same angle, their measures must be equal.
Therefore, the measures of $\angle$ABC and $\angle$CBA are the same.
The statement is True (T).
Question 38. Two line segments may intersect at two points.
Answer:
A line segment is a part of a line that is bounded by two distinct endpoints.
Let's consider two line segments. For them to intersect, they must have one or more points in common.
Case 1: The two line segments lie on the same line (they are collinear).
If two collinear line segments intersect at two distinct points, say P and Q, then all the points on the segment PQ must be common to both line segments. This means they overlap along the segment PQ. In this case, they would have infinitely many common points (all points on the overlapping segment), not just two.
Case 2: The two line segments lie on different lines.
According to the postulates of Euclidean geometry, two distinct lines can intersect at most at one point. If the line segments are parts of two distinct lines, they can intersect at most at the single intersection point of those two lines. This intersection point, if it exists and lies on both segments, is a single common point.
In neither case is it possible for two line segments to intersect at exactly two distinct points.
The statement is False (F).
Question 39. Many lines can pass through two given points.
Answer:
The statement refers to the number of lines that can pass through two specific, distinct points.
A fundamental principle in geometry (often an axiom or postulate) states that through any two distinct points, there exists exactly one unique straight line.
This means that given two different points, there is only one possible line that connects them and passes through both points.
The statement "Many lines can pass through two given points" contradicts this fundamental principle, as "many" implies more than one.
Therefore, the statement is incorrect.
The statement is False (F).
Question 40. Only one line can pass through a given point.
Answer:
The statement claims that only one line can pass through a single given point.
Consider a single point in a plane.
We can draw multiple lines that all go through this one point.
Imagine drawing lines that rotate around the point. Each distinct orientation represents a different line passing through the point.
In geometry, it is a fundamental concept that infinitely many lines can pass through a single given point.
Therefore, the statement "Only one line can pass through a given point" is incorrect.
The statement is False (F).
Question 41. Two angles can have exactly five points in common.
Answer:
Let's consider the nature of an angle and its intersection with another angle.
A standard angle is formed by two rays originating from a common point (the vertex) and includes the vertex, the two rays (arms), and the region between them (the interior).
Let Angle 1 be the set of points $S_1 = R_{1a} \cup R_{1b} \cup \{V_1\} \cup I_1$, where $R_{1a}$ and $R_{1b}$ are the rays, $V_1$ is the vertex, and $I_1$ is the interior.
Let Angle 2 be the set of points $S_2 = R_{2a} \cup R_{2b} \cup \{V_2\} \cup I_2$, where $R_{2a}$ and $R_{2b}$ are the rays, $V_2$ is the vertex, and $I_2$ is the interior.
The common points are the points in the intersection $S_1 \cap S_2$.
$S_1 \cap S_2 = (R_{1a} \cup R_{1b} \cup \{V_1\} \cup I_1) \cap (R_{2a} \cup R_{2b} \cup \{V_2\} \cup I_2)$
Let's consider the possible number of common points:
1. If the angles are disjoint: The number of common points is 0.
2. If the angles intersect at only one point: This typically happens when they share only the vertex (e.g., vertical angles) or when arms intersect at a single point which is not the vertex and the interiors do not overlap. The number of common points is 1.
3. If the angles share a common ray: As seen in previous questions (like Q27, Q29, Q30), if two angles are adjacent and share a common arm, the common points include the entire ray (and the vertex). A ray consists of infinitely many points. In this case, the number of common points is infinite.
4. If the interiors overlap over a region: The intersection of two open sets (the interiors) is an open set (unless it's empty). A non-empty open set in a plane is a region containing infinitely many points. So, if the interiors overlap, there are infinitely many common points.
For the number of common points to be a finite number greater than 1, the intersection must be limited to the boundaries of the angles (the rays and the vertices), and the interiors must be disjoint or their intersection must be a finite set of points (which is generally not possible for regions). If the common points are only on the boundaries, the intersection is limited to the vertices and the intersection points of the rays.
The intersection of two rays (unless they are collinear and overlap) is at most one point.
The intersection of the boundaries of two angles (four rays from two vertices) can involve intersection points of the rays and potentially the vertices themselves if a vertex lies on the boundary of the other angle. The maximum number of distinct intersection points formed by 4 rays emanating from 2 distinct points is limited.
However, the fundamental property of geometric figures like rays and regions is that they contain infinitely many points. Any overlap beyond a single point typically results in a segment, ray, or region, all of which contain infinitely many points.
Based on the standard definitions of angles and their intersections, the number of common points between two angles is typically 0, 1, or infinite. It is not possible for two standard angles to have exactly a finite number of common points greater than 1 (like exactly 5 points).
The statement is False (F).
Question 42 to 78
Question 42. Name all the line segments in Fig. 2.24.

Answer:
In the given figure (Fig. 2.24), the points are A, B, C, and D.
A line segment is formed by connecting two distinct points.
The line segments in the figure are:
AB
AC
AD
BC
BD
CD
Thus, there are a total of 6 line segments in the given figure.
Question 43. Name the line segments shown in Fig. 2.25.

Answer:
In the given figure (Fig. 2.25), the points are P, Q, R, and S.
A line segment is a part of a line that is bounded by two distinct end points.
The line segments shown in the figure by connecting any two distinct points are:
PQ
QR
RS
PR (connecting P and R)
QS (connecting Q and S)
PS (connecting P and S)
Thus, there are a total of 6 line segments in the given figure.
Question 44. State the mid points of all the sides of Fig. 2.26.

Answer:
In the given figure (Fig. 2.26), ABCD is a quadrilateral.
The sides of the quadrilateral are AB, BC, CD, and DA.
Based on the position of the points marked on each side, we can state the midpoints:
The midpoint of side AB is P.
The midpoint of side BC is Q.
The midpoint of side CD is R.
The midpoint of side DA is S.
Therefore, the midpoints of the sides are P, Q, R, and S respectively.
Question 45. Name the vertices and the line segments in Fig. 2.27.

Answer:
In the given figure (Fig. 2.27), we need to identify the vertices and the line segments.
The vertices are the corner points or endpoints of the line segments. In the figure, the points labelled are:
A
B
C
D
E
F
G
The line segments are the straight connections between these vertices. The line segments in the figure are:
AB
BC
CD
DE
EF
FG
GA
BF
CG
DA
EB
FC
GD
AE
Question 46. Write down fifteen angles (less than 180°) involved in Fig. 2.28.

Answer:
In the given figure (Fig. 2.28), the points are P, Q, R, S, T, and U. Angles are formed at the vertices where line segments meet.
We need to list fifteen angles that are less than $180^\circ$. Based on the figure, we can identify angles formed at the vertices P, Q, R, S, and T using the line segments shown.
The line segments are PQ, QR, RS, ST, TP, PU, QU, RU, SU, and TU.
The fifteen angles less than $180^\circ$ are:
Angles at Vertex P:
$\angle$QPT
$\angle$UPQ
$\angle$UPT
Angles at Vertex Q:
$\angle$RQP
$\angle$UQR
$\angle$UQP
Angles at Vertex R:
$\angle$SRQ
$\angle$URS
$\angle$URQ
Angles at Vertex S:
$\angle$TSR
$\angle$UST
$\angle$USR
Angles at Vertex T:
$\angle$PTS
$\angle$UTP
$\angle$UTS
These are fifteen distinct angles formed by the line segments originating from the vertices P, Q, R, S, and T. All these angles, as depicted in the figure, are less than $180^\circ$.
Question 47. Name the following angles of Fig. 2.29, using three letters:
(a) ∠1
(b) ∠2
(c) ∠3
(d) ∠1 + ∠2
(e) ∠2 + ∠3
(f) ∠1 + ∠2 + ∠3
(g) ∠CBA – ∠1

Answer:
In the given figure (Fig. 2.29), the vertex of all angles is B. The angles are formed by rays originating from B.
(a) $\angle$1 is formed by rays BA and BD. So, $\angle$1 can be named as $\angle$ABD or $\angle$DBA.
(b) $\angle$2 is formed by rays BD and BE. So, $\angle$2 can be named as $\angle$DBE or $\angle$EBD.
(c) $\angle$3 is formed by rays BE and BC. So, $\angle$3 can be named as $\angle$EBC or $\angle$CBE.
(d) $\angle$1 + $\angle$2 represents the angle formed by rays BA and BE. So, $\angle$1 + $\angle$2 can be named as $\angle$ABE or $\angle$EBA.
(e) $\angle$2 + $\angle$3 represents the angle formed by rays BD and BC. So, $\angle$2 + $\angle$3 can be named as $\angle$DBC or $\angle$CBD.
(f) $\angle$1 + $\angle$2 + $\angle$3 represents the angle formed by rays BA and BC. So, $\angle$1 + $\angle$2 + $\angle$3 can be named as $\angle$ABC or $\angle$CBA.
(g) $\angle$CBA – $\angle$1 represents the angle ($\angle$1 + $\angle$2 + $\angle$3) minus $\angle$1, which is equivalent to $\angle$2 + $\angle$3. This angle is formed by rays BD and BC. So, $\angle$CBA – $\angle$1 can be named as $\angle$DBC or $\angle$CBD.
Question 48. Name the points and then the line segments in each of the following figures (Fig. 2.30):

Answer:
Let's analyse each figure in Fig. 2.30 separately.
Figure 1:
The points in this figure are the labelled dots.
The points are O, A, B, and C.
The line segments are the straight connections between any two distinct points shown in the figure.
The line segments are:
OA
OB
OC
AB
AC
BC
Figure 2:
The points in this figure are the labelled dots at the corners.
The points are P, Q, and R.
The line segments are the sides of the triangle formed by these points.
The line segments are:
PQ
QR
PR
Figure 3:
The points in this figure are the labelled dots at the vertices.
The points are W, X, Y, and Z.
The line segments are the straight connections between any two distinct points shown in the figure.
The line segments are:
WX
XY
YZ
ZW
XZ (Diagonal)
YW (Diagonal)
Question 49. Which points in Fig. 2.31, appear to be mid-points of the line segments? When you locate a mid-point, name the two equal line segments formed by it.
Answer:
In the given figure (Fig. 2.31), the points are A, B, C, D, E, F, G, H, I, and J.
A point is a midpoint of a line segment if it divides the segment into two equal parts. The double dash marks on the segments indicate that they are of equal length.
Based on the double dash markings:
Point B appears to be the midpoint of the line segment AC because the segments AB and BC are marked as equal in length.
Point D appears to be the midpoint of the line segment CE because the segments CD and DE are marked as equal in length.
Point F appears to be the midpoint of the line segment EG because the segments EF and FG are marked as equal in length.
Point H appears to be the midpoint of the line segment GI because the segments GH and HI are marked as equal in length.
Point J does not appear to be a midpoint of any labelled segment in the figure as it is the endpoint of the line shown and is not dividing a segment into two marked equal parts.
Question 50. Is it possible for the same
(a) line segment to have two different lengths?
(b) angle to have two different measures?
Answer:
(a) Is it possible for the same line segment to have two different lengths?
No, it is not possible for the same line segment to have two different lengths.
A line segment is defined by two distinct points, and its length is the unique distance between these two points.
(b) Is it possible for the same angle to have two different measures?
No, it is not possible for the same angle to have two different measures.
An angle is formed by two rays sharing a common endpoint, and its measure represents the unique amount of rotation between these two rays.
Question 51. Will the measure of ∠ABC and of ∠CBD make measure of ∠ABD in Fig. 2.32?
Answer:
In the given figure (Fig. 2.32), we have three rays BA, BC, and BD originating from the common point B.
The angle $\angle$ABD is formed by the rays BA and BD.
The angle $\angle$ABC is formed by the rays BA and BC.
The angle $\angle$CBD is formed by the rays BC and BD.
From the figure, it is clear that the ray BC lies between the rays BA and BD.
When a ray lies between the two rays forming an angle, the measure of the larger angle is equal to the sum of the measures of the two adjacent angles.
Therefore, the measure of $\angle$ABD is the sum of the measures of $\angle$ABC and $\angle$CBD.
This can be written as:
$\angle$ABD = $\angle$ABC + $\angle$CBD
Thus, the measure of $\angle$ABC and of $\angle$CBD will make the measure of $\angle$ABD in Fig. 2.32.
The answer is Yes.
Question 52. Will the lengths of line segment AB and line segment BC make the length of line segment AC in Fig. 2.33?

Answer:
In the given figure (Fig. 2.33), the points A, B, and C lie on the same straight line.
From the figure, it is clear that point B is located between point A and point C on the line segment AC.
According to the segment addition postulate, if three points A, B, and C are collinear and B is between A and C, then the length of segment AC is the sum of the lengths of segments AB and BC.
That is, Length(AC) = Length(AB) + Length(BC).
Therefore, the lengths of line segment AB and line segment BC will make the length of line segment AC in Fig. 2.33.
The answer is Yes.
Question 53. Draw two acute angles and one obtuse angle without using a protractor. Estimate the measures of the angles. Measure them with the help of a protractor and see how much accurate is your estimate.
Answer:
First, let's understand what acute and obtuse angles are.
An acute angle is an angle that measures less than $90^\circ$.
An obtuse angle is an angle that measures greater than $90^\circ$ but less than $180^\circ$.
To draw these angles without a protractor, you can start by drawing a reference line (ray).
For an acute angle, draw a second ray starting from the same endpoint that makes an opening less than what you visually perceive as a right angle ($90^\circ$). Draw two such angles with different perceived sizes (e.g., one very narrow, one wider). Let's call them $\angle$PQR and $\angle$XYZ.
For an obtuse angle, draw a second ray starting from the same endpoint that makes an opening wider than a right angle but not a straight line ($180^\circ$). Let's call this angle $\angle$LMN.
After drawing, estimate the measure of each angle in degrees based on how wide the opening is. Write down your estimated measures next to each angle.
For example, your estimate might look like:
Estimated $\angle$PQR = [Your estimate] degrees
Estimated $\angle$XYZ = [Your estimate] degrees
Estimated $\angle$LMN = [Your estimate] degrees
Now, use a protractor to measure each angle accurately. Place the protractor's center on the vertex of the angle and align the base line with one ray. Read the measure where the other ray crosses the protractor scale.
Record the measured measures:
Measured $\angle$PQR = [Measured value] degrees
Measured $\angle$XYZ = [Measured value] degrees
Measured $\angle$LMN = [Measured value] degrees
Finally, compare your estimated measures with the measured values to see how accurate your estimations were. The difference between the estimated and measured value indicates the accuracy of your estimate.
Question 54. Look at Fig. 2.34. Mark a point
(a) A which is in the interior of both ∠1 and ∠2.
(b) B which is in the interior of only ∠1.
(c) Point C in the interior of ∠1.
Now, state whether points B and C lie in the interior of ∠2 also.
Answer:
In Fig. 2.34, $\angle$1 is formed by rays OX and OY, and $\angle$2 is formed by rays OY and OZ. These are adjacent angles sharing the common ray OY and vertex O.
The interior of an angle is the region between the two rays forming the angle, excluding the rays themselves and the vertex. For adjacent angles like $\angle$1 and $\angle$2, their interiors do not overlap.
(a) Mark a point A which is in the interior of both $\angle$1 and $\angle$2.
Based on the figure and the standard definition of the interior of adjacent angles, there is no region common to the interior of both $\angle$1 and $\angle$2. Therefore, it is not possible to mark a point that is in the interior of both angles simultaneously.
(b) Mark a point B which is in the interior of only $\angle$1.
A point B in the interior of only $\angle$1 must be in the region between ray OX and ray OY, and outside the region between ray OY and ray OZ. This region is the interior of $\angle$1. So, we can place point B anywhere in the region bounded by rays OX and OY (excluding the rays and vertex).
(c) Point C in the interior of $\angle$1.
A point C in the interior of $\angle$1 must be in the region between ray OX and ray OY. This is the same region described for point B. We can place point C anywhere in the region bounded by rays OX and OY (excluding the rays and vertex).
Now, state whether points B and C lie in the interior of $\angle$2 also.
Point B was placed in the interior of $\angle$1, which is the region between rays OX and OY. The interior of $\angle$2 is the region between rays OY and OZ. Since point B is on the side of ray OY towards ray OX, and the interior of $\angle$2 is on the side of ray OY towards ray OZ, point B is not in the interior of $\angle$2.
Similarly, point C was placed in the interior of $\angle$1, which is the region between rays OX and OY. For the same reason as point B, point C is also not in the interior of $\angle$2.
Thus, points B and C lie in the interior of $\angle$1, but do not lie in the interior of $\angle$2.
Question 55. Find out the incorrect statement, if any, in the following:
An angle is formed when we have
(a) two rays with a common end-point
(b) two line segments with a common end-point
(c) a ray and a line segment with a common end-point
Answer:
Let's examine each statement based on the geometric definition of an angle.
The standard definition of an angle is the figure formed by two rays, called the sides of the angle, sharing a common endpoint, called the vertex.
(a) Two rays with a common end-point: This statement perfectly matches the definition of an angle. The two rays are the sides, and the common endpoint is the vertex. Therefore, this statement is correct.
(b) Two line segments with a common end-point: A line segment is a part of a line with two endpoints. While two line segments meeting at a common endpoint form a figure that contains an angle at that point, the sides of a geometric angle are defined as rays, which extend infinitely in one direction. Line segments are finite. Therefore, strictly speaking, an angle is not formed *by* the line segments themselves, but by the rays that contain these segments and originate from the common endpoint (vertex). This statement is incorrect based on the precise definition of the sides of an angle.
(c) A ray and a line segment with a common end-point: Similar to statement (b), while a ray and a line segment meeting at a common endpoint form a figure containing an angle, the sides of the angle are the given ray and the ray that contains the line segment and originates from the common endpoint. One side is correctly described as a ray, but the other is not directly the line segment, but the ray containing it. This statement is also technically inaccurate regarding the components that *form* the angle's sides.
Comparing the statements, statement (a) accurately describes the fundamental components that form an angle (two rays). Statements (b) and (c) describe figures that *contain* an angle but do not precisely list the rays that constitute the angle's sides. Statement (b) is the most significantly incorrect because it claims an angle is formed by two segments, neither of which is an infinite ray, which is a defining characteristic of an angle's side.
Therefore, the incorrect statement is (b) two line segments with a common end-point.
Question 56. In which of the following figures (Fig. 2.35),
(a) perpendicular bisector is shown?
(b) bisector is shown?
(c) only bisector is shown?
(d) only perpendicular is shown?

Answer:
Let's analyze each figure in Fig. 2.35:
Figure (i): This figure shows a line segment AB. A line intersects AB at point M. The marks on AM and MB indicate that AM = MB, meaning the line bisects the segment AB at M. The square symbol at M indicates that the line is perpendicular to AB at M. Thus, this figure shows a perpendicular bisector of the line segment AB.
Figure (ii): This figure shows a line segment AB. A line segment PM is drawn from a point P on AB to M. The square symbol at P indicates that PM is perpendicular to AB at point P. There are no marks indicating that P is the midpoint of AB. Thus, this figure shows a perpendicular line segment to AB, but not necessarily a bisector.
Figure (iii): This figure shows an angle $\angle$AOB. A ray OM is drawn from the vertex O in the interior of the angle. The arc marks on $\angle$AOM and $\angle$MOB indicate that $\angle$AOM = $\angle$MOB, meaning the ray OM bisects the angle $\angle$AOB. There is no symbol indicating perpendicularity. Thus, this figure shows an angle bisector.
Now, let's answer the questions:
(a) perpendicular bisector is shown?
Figure (i) shows a line that is both perpendicular to the line segment AB and bisects it. So, the perpendicular bisector is shown in Figure (i).
(b) bisector is shown?
A bisector divides something into two equal parts. Figure (i) shows a bisector of a line segment. Figure (iii) shows a bisector of an angle. Both figures show a bisector. So, bisector is shown in Figure (i) and Figure (iii).
(c) only bisector is shown?
This asks for a figure that shows a bisector but not a perpendicular (in the case of line segments) or not a perpendicular bisector. Figure (i) shows a perpendicular bisector, not *only* a bisector. Figure (iii) shows an angle bisector without perpendicularity being indicated. So, only a bisector (an angle bisector) is shown in Figure (iii).
(d) only perpendicular is shown?
This asks for a figure that shows a perpendicular but not a bisector. Figure (i) shows a perpendicular bisector, not *only* a perpendicular. Figure (ii) shows a line segment perpendicular to AB, with no indication of bisection. Figure (iii) shows a bisector, not a perpendicular. So, only perpendicular is shown in Figure (ii).
Question 57. What is common in the following figures (i) and (ii) (Fig. 2.36.)?
Is Fig. 2.36 (i) that of triangle? if not, why?
Answer:
Let's look at Figure 2.36 (i) and (ii).
Figure (i) is formed by three line segments AB, BC, and CA, joined end to end, forming a closed figure.
Figure (ii) is formed by four line segments PQ, QR, RS, and SP, joined end to end, forming a closed figure.
The common thing in both figures is that they are closed figures made up of line segments. These types of figures are called polygons.
Now let's consider the second part of the question: Is Fig. 2.36 (i) that of a triangle? if not, why?
A triangle is a closed figure formed by three line segments. It has three vertices and three sides.
In Figure 2.36 (i), we have three line segments (AB, BC, and CA) that are joined end to end to form a closed figure. The points A, B, and C are the vertices.
Yes, Figure 2.36 (i) is that of a triangle. It is a triangle because it is a polygon formed by exactly three line segments.
Question 58. If two rays intersect, will their point of intersection be the vertex of an angle of which the rays are the two sides?
Answer:
Let's consider the definition of an angle.
An angle is formed by two rays that share a common endpoint. This common endpoint is called the vertex of the angle, and the two rays are called the sides of the angle.
If two rays intersect at a point, let's call this point P. For P to be the vertex of an angle and the original two rays to be the sides of that angle, P must be the common endpoint where both rays begin.
Consider two scenarios:
1. The two rays originate from the same point P and extend in different directions. In this case, their intersection point is P, which is also their common endpoint. Here, P is the vertex, and the two rays are the sides of the angle they form.
2. The two rays originate from different points and intersect at point P. For example, a ray starting at point A passing through point B (ray AB) and a ray starting at point C passing through point D (ray CD) intersect at point P. Here, P is the intersection point, but the endpoint of ray AB is A, and the endpoint of ray CD is C. In this case, P is not the common endpoint of the original rays AB and CD. While an angle is formed at P (with sides being rays originating from P along the directions of the lines containing AB and CD), the original rays AB and CD are not the sides of the angle at P according to the strict definition.
Therefore, the point of intersection of two rays is the vertex of an angle of which the rays are the two sides only if the point of intersection is the common endpoint (origin) of both rays.
If the question implies any intersection, regardless of whether the intersection point is the origin of the rays, then the answer is generally No.
Question 59. In Fig. 2.37,
(a) name any four angles that appear to be acute angles.
(b) name any two angles that appear to be obtuse angles.

Answer:
In Fig. 2.37, angles are formed at the common vertex O by the rays OA, OB, OC, OD, OE, and OF.
We need to identify angles based on their appearance as acute (less than $90^\circ$) or obtuse (greater than $90^\circ$ and less than $180^\circ$).
(a) Name any four angles that appear to be acute angles.
Based on visual estimation, the angles that appear to have a measure less than $90^\circ$ are:
$\angle$AOB
$\angle$COD
$\angle$DOE
$\angle$FOA
These are four angles that appear to be acute.
(b) Name any two angles that appear to be obtuse angles.
Based on visual estimation, the angles that appear to have a measure greater than $90^\circ$ but less than $180^\circ$ are:
$\angle$BOC
$\angle$EOF
These are two angles that appear to be obtuse.
Question 60. In Fig. 2.38,
(a) is AC + CB = AB?
(b) is AB + AC = CB?
(c) is AB + BC = CA?

Answer:
In the given figure (Fig. 2.38), the points A, C, and B are collinear (lie on the same straight line).
From the figure, it is evident that point C lies between points A and B on the line segment AB.
According to the Segment Addition Postulate, if three points are collinear and one point is between the other two, then the length of the longest segment is equal to the sum of the lengths of the two shorter segments.
In this case, since C is between A and B, the length of the segment AB is the sum of the lengths of the segments AC and CB.
This can be expressed as:
$AC + CB = AB$
Let's evaluate the given statements:
(a) is AC + CB = AB?
Yes, this statement is consistent with the figure where C is between A and B.
(b) is AB + AC = CB?
This statement would imply that point A is located between points B and C. This contradicts the visual representation in the figure.
(c) is AB + BC = CA?
This statement would imply that point B is located between points A and C. This also contradicts the visual representation in the figure.
Therefore, based on the figure and the Segment Addition Postulate, only statement (a) is true.
Question 61. In Fig. 2.39,
(a) What is AE + EC?
(b) What is AC – EC?
(c) What is BD – BE?
(d) What is BD – DE?
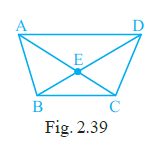
Answer:
In the given figure (Fig. 2.39), the points A, B, C, E, and D are collinear and are arranged in that order along the straight line.
We can use the Segment Addition Postulate, which states that if three points are collinear and one point is between the other two, the length of the sum of the two shorter segments equals the length of the longest segment.
(a) What is $AE + EC$?
From the figure, point E is between points A and C.
By the Segment Addition Postulate:
$AE + EC = AC$
(b) What is $AC – EC$?
From part (a), we know that $AC = AE + EC$.
Subtracting $EC$ from both sides:
$AC - EC = AE$
(c) What is $BD – BE$?
From the figure, point E is between points B and D.
By the Segment Addition Postulate:
$BE + ED = BD$
Subtracting $BE$ from both sides:
$BD - BE = ED$
(d) What is $BD – DE$?
From part (c), we know that $BD = BE + ED$.
Subtracting $DE$ (or $ED$) from both sides:
$BD - DE = BE$
Question 62. Using the information given, name the right angles in each part of Fig. 2.40:
(a) BA ⊥BD

(b) RT ⊥ ST

(c) AC⊥ BD
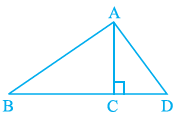
(d) RS ⊥ RW
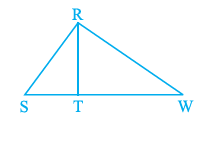
(e) AC ⊥ BD

(f) AE ⊥ CE

(g) AC ⊥ CD
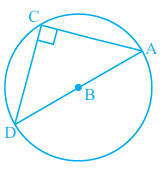
(h) OP ⊥ AB

Answer:
A right angle is an angle that measures $90^\circ$. Perpendicular lines or segments intersect to form right angles.
(a) Given BA $\perp$ BD in Fig. 2.40.
The lines BA and BD are perpendicular at point B. The angle formed is $\angle$ABD.
The right angle is $\angle$ABD.
(b) Given RT $\perp$ ST in Fig. 2.41.
The lines RT and ST are perpendicular at point T. The angle formed is $\angle$RTS.
The right angle is $\angle$RTS.
(c) Given AC $\perp$ BD in Fig. 2.42.
The lines AC and BD intersect perpendicularly at point O. The angles formed at the intersection are right angles.
The right angles are $\angle$AOB, $\angle$BOC, $\angle$COD, and $\angle$DOA.
(d) Given RS $\perp$ RW in Fig. 2.43.
The lines RS and RW are perpendicular at point R. The angle formed is $\angle$SRW.
The right angle is $\angle$SRW.
(e) Given AC $\perp$ BD in Fig. 2.44.
The lines AC and BD intersect perpendicularly at point O. The angles formed at the intersection are right angles.
The right angles are $\angle$AOB, $\angle$BOC, $\angle$COD, and $\angle$DOA.
(f) Given AE $\perp$ CE in Fig. 2.45.
The line segments AE and CE are perpendicular at point E. The angle formed is $\angle$AEC.
The right angle is $\angle$AEC.
(g) Given AC $\perp$ CD in Fig. 2.46.
The line segments AC and CD are perpendicular at point C. The angle formed is $\angle$ACD.
The right angle is $\angle$ACD.
(h) Given OP $\perp$ AB in Fig. 2.47.
The line segment OP is perpendicular to the line AB at point P. This forms right angles at P.
The right angles are $\angle$OPA and $\angle$OPB.
Question 63. What conclusion can be drawn from each part of Fig. 2.41, if
(a) DB is the bisector of ∠ADC?

(b) BD bisects ∠ABC?

(c) DC is the bisector of ∠ADB, CA ⊥ DA and CB ⊥ DB?

Answer:
Let's draw conclusions from each part of Fig. 2.41 based on the given information.
(a) Given DB is the bisector of ∠ADC in Fig. 2.48.
An angle bisector is a ray that divides an angle into two equal angles.
The angle is $\angle$ADC, with vertex D and sides DA and DC.
The ray DB is given as the bisector of this angle.
Therefore, the two angles formed by the bisector DB, namely $\angle$ADB and $\angle$CDB, must have equal measure.
Conclusion: $\angle$ADB = $\angle$CDB.
(b) Given BD bisects ∠ABC in Fig. 2.49.
An angle bisector is a ray that divides an angle into two equal angles.
The angle is $\angle$ABC, with vertex B and sides BA and BC.
The ray BD is given as the bisector of this angle.
Therefore, the two angles formed by the bisector BD, namely $\angle$ABD and $\angle$CBD, must have equal measure.
Conclusion: $\angle$ABD = $\angle$CBD.
(c) Given DC is the bisector of ∠ADB, CA ⊥ DA and CB ⊥ DB in Fig. 2.50.
We are given three conditions:
1. DC is the bisector of $\angle$ADB.
2. CA $\perp$ DA. This means that the line segment CA is perpendicular to the line containing DA. Looking at the figure, the angle formed at A is a right angle ($90^\circ$), i.e., $\angle$CAD $= 90^\circ$ (assuming CA is drawn to meet DA at A and is perpendicular). More precisely, the distance from C to the line DA is CA.
3. CB $\perp$ DB. This means that the line segment CB is perpendicular to the line containing DB. Looking at the figure, the angle formed at B is a right angle ($90^\circ$), i.e., $\angle$CBD $= 90^\circ$ (assuming CB is drawn to meet DB at B and is perpendicular). More precisely, the distance from C to the line DB is CB.
A fundamental property of an angle bisector is that any point on the angle bisector is equidistant from the sides of the angle.
Here, DC is the angle bisector of $\angle$ADB, and point C lies on this bisector.
The sides of the angle $\angle$ADB are the rays (or lines) DA and DB.
The perpendicular distance from point C to the side DA is the length of segment CA (since CA $\perp$ DA).
The perpendicular distance from point C to the side DB is the length of segment CB (since CB $\perp$ DB).
Since C is on the angle bisector DC, its distance from DA must be equal to its distance from DB.
Conclusion: $CA = CB$.
Question 64. An angle is said to be trisected, if it is divided into three equal parts. If in Fig. 2.42, ∠ BAC = ∠ CAD = ∠ DAE, how many trisectors are there for ∠BAE ?

Answer:
The question states that an angle is trisected if it is divided into three equal parts.
In the given figure (Fig. 2.51, assumed to be Fig. 2.42 as per the question), the angle under consideration is $\angle$BAE, with vertex A and sides AB and AE.
Inside $\angle$BAE, there are two rays AC and AD originating from the same vertex A.
We are given that $\angle$BAC = $\angle$CAD = $\angle$DAE.
Let the measure of each of these angles be $x$. So, $\angle$BAC = $x$, $\angle$CAD = $x$, and $\angle$DAE = $x$.
The sum of these angles forms the larger angle $\angle$BAE:
$\angle$BAE = $\angle$BAC + $\angle$CAD + $\angle$DAE
$\angle$BAE = $x + x + x$
$\angle$BAE = $3x$
The rays AC and AD divide the angle $\angle$BAE into three equal angles: $\angle$BAC, $\angle$CAD, and $\angle$DAE, as their measures are all equal ($x$).
According to the definition provided, if an angle is divided into three equal parts, the rays that perform this division are called trisectors.
In this case, the rays AC and AD are the rays that divide $\angle$BAE into three equal parts.
Therefore, the trisectors for $\angle$BAE are the rays AC and AD.
There are two such rays.
Thus, there are 2 trisectors for $\angle$BAE.
Question 65. How many points are marked in Fig. 2.43?
Answer:
Based on the figure provided alongside Question 66 (which appears to be the figure referred to in Question 65, labeled as Fig. 2.52), the marked points are the vertices of the polygon.
The marked points are P, Q, R, S, T, U, and V.
Counting these labelled points, we find there are 7 marked points.
Question 66. How many line segments are there in Fig. 2.43?

Answer:
In the figure (Fig. 2.52, which corresponds to Fig. 2.43 mentioned in the question), the marked points are P, Q, R, S, T, U, and V.
A line segment is formed by connecting any two distinct points.
To find the total number of line segments, we need to count all possible pairs of these 7 points.
The number of line segments formed by connecting 7 distinct points is given by the combination formula $\binom{n}{2} = \frac{n(n-1)}{2}$, where $n$ is the number of points.
Here, $n=7$.
Number of line segments = $\binom{7}{2} = \frac{7 \times (7-1)}{2} = \frac{7 \times 6}{2} = \frac{42}{2} = 21$.
The 21 line segments are:
PQ, PR, PS, PT, PU, PV
QR, QS, QT, QU, QV
RS, RT, RU, RV
ST, SU, SV
TU, TV
UV
Thus, there are a total of 21 line segments in Fig. 2.43.
Question 67. In Fig. 2.44, how many points are marked? Name them.

Answer:
In the figure (Fig. 2.53, corresponding to Fig. 2.44 mentioned in the question), the marked points are the labelled vertices of the figure.
Let's identify the marked points:
The points are O, A, B, C, and D.
Counting these points, we find there are 5 marked points.
The marked points are O, A, B, C, and D.
Question 68. How many line segments are there in Fig. 2.44? Name them.
Answer:
Based on the figure shown alongside Question 67 (which is Fig. 2.53, corresponding to Fig. 2.44), the marked points are O, A, B, C, and D.
A line segment is formed by connecting any two distinct points.
With 5 marked points, the number of line segments is given by the combination formula $\binom{n}{2} = \frac{n(n-1)}{2}$, where $n$ is the number of points.
Here, $n=5$.
Number of line segments = $\binom{5}{2} = \frac{5 \times (5-1)}{2} = \frac{5 \times 4}{2} = \frac{20}{2} = 10$.
The 10 line segments are:
Connecting O to other points: OA, OB, OC, OD
Connecting A to other points (excluding AO): AB, AC, AD
Connecting B to other points (excluding BO, BA): BC, BD
Connecting C to other points (excluding CO, CA, CB): CD
Segments: OA, OB, OC, OD, AB, AC, AD, BC, BD, CD.
Thus, there are a total of 10 line segments in Fig. 2.44.
The line segments are: OA, OB, OC, OD, AB, AC, AD, BC, BD, CD.
Question 69. In Fig. 2.45 how many points are marked? Name them.

Answer:
In the given figure (Fig. 2.54, corresponding to Fig. 2.45 mentioned in the question), the marked points are the labelled vertices of the polygon.
Let's identify the marked points:
The points are A, B, C, D, E, and F.
Counting these points, we find there are 6 marked points.
The marked points are A, B, C, D, E, and F.
Question 70. In Fig. 2.45 how many line segments are there? Name them.
Answer:
Based on the figure shown alongside Question 69 (which is Fig. 2.54, corresponding to Fig. 2.45 mentioned in the question), the marked points are A, B, C, D, E, and F.
A line segment is formed by connecting any two distinct points.
With 6 marked points, the number of line segments is given by the combination formula $\binom{n}{2} = \frac{n(n-1)}{2}$, where $n$ is the number of points.
Here, $n=6$.
Number of line segments = $\binom{6}{2} = \frac{6 \times (6-1)}{2} = \frac{6 \times 5}{2} = \frac{30}{2} = 15$.
The 15 line segments are:
Segments from A: AB, AC, AD, AE, AF
Segments from B (excluding BA): BC, BD, BE, BF
Segments from C (excluding CA, CB): CD, CE, CF
Segments from D (excluding DA, DB, DC): DE, DF
Segments from E (excluding EA, EB, EC, ED): EF
The line segments are: AB, AC, AD, AE, AF, BC, BD, BE, BF, CD, CE, CF, DE, DF, EF.
Thus, there are a total of 15 line segments in Fig. 2.45.
Question 71. In Fig. 2.46, how many points are marked? Name them.

Answer:
In the given figure (Fig. 2.55, corresponding to Fig. 2.46 mentioned in the question), the marked points are the labelled points on the line segments and curves.
Let's identify the marked points:
The points are O, P, Q, R, S, T, U, V, W, X, Y, and Z.
Counting these points, we find there are 12 marked points.
The marked points are O, P, Q, R, S, T, U, V, W, X, Y, and Z.
Question 72. In Fig. 2.46 how many line segments are there? Name them.
Answer:
Based on the figure (Fig. 2.55, corresponding to Fig. 2.46 mentioned in the question), the marked points are O, P, Q, R, S, T, U, V, W, X, Y, and Z.
A line segment is a straight path between two points. In the given figure, the straight lines drawn connect the central point O to each of the outer points P, Q, R, S, T, U, V, W, X, Y, and Z.
The line segments shown in the figure are:
OP
OQ
OR
OS
OT
OU
OV
OW
OX
OY
OZ
Counting these segments, there are 11 line segments in the figure.
The line segments are: OP, OQ, OR, OS, OT, OU, OV, OW, OX, OY, OZ.
Question 73. In Fig. 2.47, O is the centre of the circle.
(a) Name all chords of the circle.
(b) Name all radii of the circle.
(c) Name a chord, which is not the diameter of the circle.
(d) Shade sectors OAC and OPB.
(e) Shade the smaller segment of the circle formed by CP.

Answer:
In the given figure (Fig. 2.56, corresponding to Fig. 2.47), O is the center of the circle, and A, B, C, P are points on the circumference.
(a) Name all chords of the circle.
A chord is a line segment joining any two points on the circumference of a circle.
In the figure, the line segments joining two points on the circumference are AB, AC, and CP.
The chords are: AB, AC, CP.
(b) Name all radii of the circle.
A radius is a line segment joining the center of the circle to any point on its circumference.
The center is O, and the points on the circumference are A, B, C, and P.
The radii are: OA, OB, OC, OP.
(c) Name a chord, which is not the diameter of the circle.
A diameter is a chord that passes through the center of the circle. In the figure, the chord AB passes through the center O, so AB is a diameter.
The chords that do not pass through the center O are AC and CP.
A chord which is not a diameter is: AC (or CP).
(d) Shade sectors OAC and OPB.
A sector of a circle is the region bounded by two radii and the arc between them.
To shade sector OAC: Shade the region bounded by radii OA and OC and the arc AC.
To shade sector OPB: Shade the region bounded by radii OP and OB and the arc PB.
(e) Shade the smaller segment of the circle formed by CP.
A segment of a circle is the region bounded by a chord and the arc subtended by the chord.
The chord CP divides the circle into two segments. The smaller segment is the region bounded by the chord CP and the minor arc CP (the shorter arc between C and P).
To shade the smaller segment formed by CP: Shade the region bounded by the line segment CP and the arc CP that does not contain the center O.
Question 74. Can we have two acute angles whose sum is
(a) an acute angle? Why or why not?
(b) a right angle? Why or why not?
(c) an obtuse angle? Why or why not?
(d) a straight angle? Why or why not?
(e) a reflex angle? Why or why not?
Answer:
Let the two acute angles be $\alpha$ and $\beta$. By definition, an acute angle is an angle whose measure is greater than $0^\circ$ and less than $90^\circ$.
So, we have $0^\circ < \alpha < 90^\circ$ and $0^\circ < \beta < 90^\circ$.
The sum of these two acute angles is $\alpha + \beta$. Adding the inequalities, we get:
$0^\circ + 0^\circ < \alpha + \beta < 90^\circ + 90^\circ$
$0^\circ < \alpha + \beta < 180^\circ$
Thus, the sum of two acute angles is always greater than $0^\circ$ and less than $180^\circ$.
(a) Can their sum be an acute angle? Why or why not?
Yes, the sum of two acute angles can be an acute angle.
Reason: As long as the sum $\alpha + \beta$ is less than $90^\circ$, it will be an acute angle. This is possible if both acute angles are relatively small. For example, if $\alpha = 30^\circ$ and $\beta = 40^\circ$, then $\alpha + \beta = 70^\circ$, which is acute since $0^\circ < 70^\circ < 90^\circ$.
(b) Can their sum be a right angle? Why or why not?
Yes, the sum of two acute angles can be a right angle.
Reason: If the sum $\alpha + \beta$ equals $90^\circ$, it is a right angle. This is possible if the two acute angles are complementary. For example, if $\alpha = 30^\circ$ and $\beta = 60^\circ$, both are acute, and $\alpha + \beta = 90^\circ$.
(c) Can their sum be an obtuse angle? Why or why not?
Yes, the sum of two acute angles can be an obtuse angle.
Reason: An obtuse angle is greater than $90^\circ$ but less than $180^\circ$. Since the sum $\alpha + \beta$ is always less than $180^\circ$, it can be obtuse if it is greater than $90^\circ$. This happens if one or both acute angles are relatively large (but still less than $90^\circ$). For example, if $\alpha = 50^\circ$ and $\beta = 60^\circ$, both are acute, and $\alpha + \beta = 110^\circ$, which is obtuse since $90^\circ < 110^\circ < 180^\circ$.
(d) Can their sum be a straight angle? Why or why not?
No, the sum of two acute angles cannot be a straight angle.
Reason: A straight angle is exactly $180^\circ$. As shown earlier, the sum of two acute angles is always strictly less than $180^\circ$ ($0^\circ < \alpha + \beta < 180^\circ$). Therefore, it cannot equal $180^\circ$.
(e) Can their sum be a reflex angle? Why or why not?
No, the sum of two acute angles cannot be a reflex angle.
Reason: A reflex angle is an angle greater than $180^\circ$. As shown earlier, the sum of two acute angles is always strictly less than $180^\circ$ ($0^\circ < \alpha + \beta < 180^\circ$). Therefore, it cannot be a reflex angle.
Question 75. Can we have two obtuse angles whose sum is
(a) a reflex angle? Why or why not?
(b) a complete angle? Why or why not?
Answer:
Let the two obtuse angles be $\alpha$ and $\beta$. By definition, an obtuse angle is an angle whose measure is greater than $90^\circ$ and less than $180^\circ$.
So, we have $90^\circ < \alpha < 180^\circ$ and $90^\circ < \beta < 180^\circ$.
Let's consider the sum of these two obtuse angles, $\alpha + \beta$. Adding the inequalities, we get:
$90^\circ + 90^\circ < \alpha + \beta < 180^\circ + 180^\circ$
$180^\circ < \alpha + \beta < 360^\circ$
Thus, the sum of two obtuse angles is always greater than $180^\circ$ and less than $360^\circ$.
(a) Can their sum be a reflex angle? Why or why not?
Yes, the sum of two obtuse angles can be a reflex angle.
Reason: A reflex angle is defined as an angle greater than $180^\circ$ and less than $360^\circ$. As calculated above, the sum of two obtuse angles ($\alpha + \beta$) satisfies the condition $180^\circ < \alpha + \beta < 360^\circ$. This range is exactly the definition of a reflex angle.
For example, if $\alpha = 100^\circ$ and $\beta = 120^\circ$, both are obtuse. Their sum is $\alpha + \beta = 100^\circ + 120^\circ = 220^\circ$, which is a reflex angle ($180^\circ < 220^\circ < 360^\circ$).
(b) Can their sum be a complete angle? Why or why not?
No, the sum of two obtuse angles cannot be a complete angle.
Reason: A complete angle is an angle that measures exactly $360^\circ$. As calculated above, the sum of two obtuse angles ($\alpha + \beta$) is always strictly less than $360^\circ$ ($180^\circ < \alpha + \beta < 360^\circ$). Therefore, the sum cannot equal $360^\circ$.
Question 76. Write the name of
(a) vertices
(b) edges, and
(c) faces of the prism shown in Fig. 2.48.
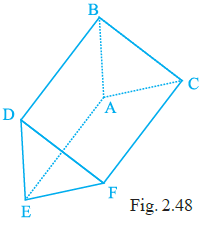
Answer:
The given figure (Fig. 2.57, corresponding to Fig. 2.48) shows a triangular prism. Let's identify its vertices, edges, and faces.
(a) Vertices: The vertices are the points where the edges meet. In the figure, these are the labelled corners.
The vertices are: A, B, C, D, E, F.
(b) Edges: The edges are the line segments forming the skeleton of the prism.
Edges on the bottom triangle: AB, BC, CA.
Edges on the top triangle: DE, EF, FD.
Edges connecting the two triangles: AD, BE, CF.
There are a total of $3 + 3 + 3 = 9$ edges.
(c) Faces: The faces are the flat surfaces of the prism.
The prism has two triangular faces (the bases) and three rectangular faces (the lateral faces).
Bottom triangular face: ABC.
Top triangular face: DEF.
Rectangular faces: ADEB, BEFC, CFDA.
There are a total of $2 + 3 = 5$ faces.
Question 77. How many edges, faces and vertices are there in a sphere?
Answer:
Let's consider the properties of a sphere in terms of edges, faces, and vertices.
A vertex is a point where three or more edges meet.
An edge is a line segment where two faces meet.
A face is a flat or curved surface of a solid object.
A sphere is a perfectly round three-dimensional object with a continuous, curved surface.
It does not have any straight line segments or flat surfaces in the way that polyhedra (like cubes or prisms) do.
Therefore, a sphere has:
Number of edges = 0
Number of faces = 0 (Conventionally, in the context of polyhedra, 'face' refers to a flat polygonal surface. While a sphere has one continuous curved surface, it is typically not counted as a 'face' in this enumeration.)
Number of vertices = 0
Question 78. Draw all the diagonals of a pentagon ABCDE and name them.
Answer:
First, let's consider a pentagon with vertices named A, B, C, D, and E in sequential order.
A diagonal of a polygon is a line segment connecting two non-adjacent vertices.
For a pentagon ABCDE, the vertices are A, B, C, D, and E.
The adjacent vertices are (A, B), (B, C), (C, D), (D, E), and (E, A). These form the sides of the pentagon.
Let's list the diagonals by connecting non-adjacent vertices:
From vertex A, the non-adjacent vertices are C and D. This gives the diagonals AC and AD.
From vertex B, the non-adjacent vertices are D and E. This gives the diagonals BD and BE.
From vertex C, the non-adjacent vertices are A and E. This gives the diagonals CA and CE. Note that CA is the same segment as AC.
From vertex D, the non-adjacent vertices are A and B. This gives the diagonals DA and DB. Note that DA is the same segment as AD, and DB is the same segment as BD.
From vertex E, the non-adjacent vertices are B and C. This gives the diagonals EB and EC. Note that EB is the same segment as BE, and EC is the same segment as CE.
The unique diagonals of the pentagon ABCDE are:
AC
AD
BD
BE
CE
There are 5 diagonals in a pentagon.
To visually represent this, draw five points A, B, C, D, E and connect them sequentially to form the pentagon. Then, draw lines connecting A to C, A to D, B to D, B to E, and C to E. These are the diagonals.

