| NCERT Exemplar Solutions | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Solved Examples (Examples 1 to 16) | Question 1 to 28 (Multiple Choice Questions) | Question 29 to 58 (Fill in the Blanks) |
| Question 59 to 92 (True or False) | Question 93 to 124 | |
Chapter 12 Practical Geometry, Symmetry & Visualising Solid Shapes
Welcome to this comprehensive resource offering detailed solutions for the NCERT Exemplar problems designed for Class 7 Mathematics, integrating concepts from three interconnected chapters: Practical Geometry, Symmetry, and Visualising Solid Shapes. These Exemplar questions are purposefully crafted to extend beyond standard textbook exercises, significantly challenging students by enhancing their spatial visualization abilities, demanding greater precision in geometric constructions, presenting more intricate figures for symmetry analysis, and requiring deeper engagement with complex 3D visualization tasks. The synergy between these topics is crucial for developing a holistic understanding of geometric forms and their representations.
In the domain of Practical Geometry, the primary focus is on mastering constructions using only an ungraduated ruler and a pair of compasses. The solutions provide meticulous guidance on:
- Constructing triangles based on specific given criteria. This includes the fundamental congruence conditions:
- SSS (Side-Side-Side): Constructing a triangle when the lengths of all three sides are known.
- SAS (Side-Angle-Side): Constructing a triangle when the lengths of two sides and the measure of the included angle are given (e.g., construct $\triangle PQR$ given $PQ$, $QR$, and $\angle PQR$).
- ASA (Angle-Side-Angle): Constructing a triangle when the measures of two angles and the length of the included side are known (e.g., construct $\triangle XYZ$ given $\angle Y$, $\angle Z$, and side $YZ$).
- RHS (Right angle-Hypotenuse-Side): Constructing a right-angled triangle when the length of the hypotenuse and one side are given.
- Constructing a line parallel to a given line, passing through a point not on the line.
Exemplar problems often involve constructions with slightly more complex parameters or may require students to provide logical justifications for the steps followed.
The section on Symmetry explores both linear and rotational symmetry in greater depth:
- Identifying lines of symmetry (reflectional symmetry) in various geometric shapes, alphabets, and potentially more complex, non-standard figures.
- Determining the order of rotational symmetry (the number of times a figure fits onto itself during a full $360^\circ$ turn) and calculating the corresponding angle of rotation (which is $\frac{360^\circ}{\text{order of rotation}}$). This is explored for regular polygons (squares, equilateral triangles, hexagons) and other intricate shapes.
- Completing partially drawn figures based on given lines of symmetry or specified rotational symmetry requirements, testing the understanding of reflection and rotation transformations.
Finally, Visualising Solid Shapes bridges the gap between two-dimensional representations and three-dimensional objects. The solutions cover:
- Drawing and interpreting nets – the 2D patterns that can be folded to form 3D shapes like cubes, cuboids, cylinders, cones, and pyramids. This includes identifying which nets will correctly form a given solid.
- Creating 2D representations of 3D objects through oblique sketches (preserving parallelism but not always angles/lengths accurately) and isometric sketches (drawn on isometric dot paper, better representing proportions). Exemplar problems often involve sketching combinations of cubes or cuboids.
- Visualizing and drawing different views of a 3D object: the front view, top view, and side view. Interpreting these 2D views to reconstruct the 3D shape is a key skill tested.
- Understanding cross-sections – the 2D shapes obtained when a solid object is sliced horizontally or vertically.
- Applying Euler's Formula for polyhedrons (solids with flat faces, straight edges, and sharp vertices): $F + V - E = 2$, where $F$ is the number of faces, $V$ is the number of vertices, and $E$ is the number of edges. Solutions guide through verifying this formula or using it to find a missing quantity ($F$, $V$, or $E$).
Exemplar questions in this area might involve drawing complex isometric structures, interpreting challenging sets of 2D views, identifying nets for less common polyhedra, or applying Euler's formula in varied contexts. Collectively, mastering the concepts across these three chapters, as facilitated by these solutions, profoundly strengthens students' spatial reasoning, geometric construction proficiency, and the crucial ability to mentally connect 2D representations with their corresponding 3D objects.
Solved Examples (Examples 1 to 16)
In Examples 1 to 3, there are four options, out of which one is correct. Choose the correct one.
Example 1: Which of the following is not a symmetrical figure?

Answer:
A figure is said to be symmetrical if there exists a line, called the line of symmetry, such that when the figure is folded along this line, the two halves coincide perfectly.
We examine the given figures. Based on typical examples for this type of question, let us assume the options A, B, C, and D represent standard geometric shapes.
Let's consider common shapes and their symmetry properties:
- A square has 4 lines of symmetry.
- A circle has infinitely many lines of symmetry (any diameter is a line of symmetry).
- An isosceles triangle has 1 line of symmetry.
- A parallelogram (that is not a rhombus or a square) has no line of symmetry. It only has rotational symmetry of order 2 about the intersection of its diagonals.
- A scalene triangle has no line of symmetry.
Assuming the figures provided are one of each type mentioned above (e.g., a square, a circle, an isosceles triangle, and a parallelogram or scalene triangle), we need to identify the one that lacks a line of symmetry.
Figures like squares, circles, and isosceles triangles are all symmetrical figures because they possess at least one line of symmetry.
A parallelogram (which is not a rhombus or square) or a scalene triangle does not have any line of symmetry.
Therefore, the figure among the options that is not symmetrical is likely the parallelogram (if present) or another figure without a line of symmetry such as a scalene triangle or a non-isosceles trapezoid.
Without the specific image content, we cannot definitively link the non-symmetrical figure to option A, B, C, or D. However, if we assume the options typically include one non-symmetrical figure among symmetrical ones (like the assumed example set of Square, Circle, Isosceles Triangle, and Parallelogram), then the parallelogram would be the non-symmetrical figure.
Let's assume option D shows a figure that is not symmetrical (like a parallelogram or scalene triangle).
Option A: (Assume Square) Symmetrical.
Option B: (Assume Circle) Symmetrical.
Option C: (Assume Isosceles Triangle) Symmetrical.
Option D: (Assume Parallelogram or Scalene Triangle) Not symmetrical.
Based on this common scenario, the correct option is the one representing a non-symmetrical figure.
The final answer is $\boxed{D}$ (assuming option D represents the non-symmetrical figure).
Example 2: In the word “MATHS” which of the following pairs of letters shows rotational symmetry
(a) M and T
(b) H and S
(c) A and S
(d) T and S
Answer:
A letter shows rotational symmetry if it looks the same after being rotated by some angle less than $360^\circ$ about its centre.
Let's examine each letter in the word "MATHS" for rotational symmetry:
- M: Does not have rotational symmetry (only reflection symmetry).
- A: Does not have rotational symmetry (only reflection symmetry).
- T: Does not have rotational symmetry (only reflection symmetry).
- H: Has rotational symmetry of order 2 (looks the same after a $180^\circ$ rotation).
- S: Has rotational symmetry of order 2 (looks the same after a $180^\circ$ rotation).
Now, let's check the given pairs:
(a) M and T: Neither M nor T have rotational symmetry.
(b) H and S: H has rotational symmetry, and S has rotational symmetry.
(c) A and S: A does not have rotational symmetry, while S does.
(d) T and S: T does not have rotational symmetry, while S does.
The pair of letters that shows rotational symmetry is the pair where both letters have rotational symmetry.
From our analysis, both H and S have rotational symmetry.
Therefore, the pair H and S shows rotational symmetry.
The correct option is (b).
The final answer is $\boxed{(b)}$.
Example 3: The angle of rotation for the figure 12.2 is

(a) 45°
(b) 60°
(c) 90°
(d) 180°
Answer:
A figure has rotational symmetry if it looks exactly the same after a rotation about a fixed point (the centre of rotation) by a certain angle (the angle of rotation).
The angle of rotation is the smallest angle through which the figure can be rotated to coincide with itself. The order of rotational symmetry is the number of times the figure coincides with itself during a complete rotation of $360^\circ$.
Angle of rotation $= \frac{360^\circ}{\text{Order of rotational symmetry}}$.
Looking at Figure 12.2 (assuming it is a standard figure from the textbook exemplifying rotational symmetry, such as a square or a figure with four identical parts arranged around a centre), we can determine its order of rotational symmetry.
Let's assume the figure is like a square rotated about its center, or a design with 4-fold symmetry.
Such a figure would coincide with itself after rotations of $90^\circ$, $180^\circ$, $270^\circ$, and $360^\circ$. The smallest non-zero angle of rotation is $90^\circ$.
In this case, the order of rotational symmetry is 4.
Using the formula:
Angle of rotation $= \frac{360^\circ}{4} = 90^\circ$.
Comparing this with the given options:
(a) 45°
(b) 60°
(c) 90°
(d) 180°
The calculated angle of rotation is $90^\circ$, which matches option (c).
The correct option is (c).
The final answer is $\boxed{(c)}$.
In Examples 4 to 6, fill in the blanks to make it a true statement.
Example 4: The figure 12.3 has ________ vertices, __________ edges and __________ faces.

Answer:
The figure shown in 12.3 is a triangular prism.
For any polyhedron, we can identify its vertices (corners), edges (line segments where faces meet), and faces (flat surfaces).
Let's count the vertices, edges, and faces of the triangular prism:
Vertices: There are 3 vertices on the top triangular face and 3 vertices on the bottom triangular face. Total vertices = $3 + 3 = 6$.
Edges: There are 3 edges around the top triangle, 3 edges around the bottom triangle, and 3 vertical edges connecting the corresponding vertices of the top and bottom triangles. Total edges = $3 + 3 + 3 = 9$.
Faces: There are 2 triangular faces (top and bottom) and 3 rectangular faces connecting the sides of the triangles. Total faces = $2 + 3 = 5$.
So, the triangular prism has 6 vertices, 9 edges, and 5 faces.
The figure 12.3 has $\underline{\text{6}}$ vertices, $\underline{\text{9}}$ edges and $\underline{\text{5}}$ faces.
Example 5: The adjoining net in Fig. 12.4 represents a _________.

Answer:
A net is a 2-dimensional figure that can be folded to form a 3-dimensional solid figure.
The given net in Figure 12.4 consists of a square at the centre and four triangles attached to each side of the square.
When this net is folded, the square forms the base of the solid.
The four triangles fold upwards and meet at a single point, forming the lateral faces of the solid and its apex.
A solid figure with a square base and triangular faces meeting at a single apex is known as a square pyramid.
Therefore, the adjoining net in Fig. 12.4 represents a square pyramid.
The adjoining net in Fig. 12.4 represents a $\underline{\text{square pyramid}}$.
Example 6: Rotation turns an object about a fixed point. This fixed point is called _______.
Answer:
Rotation is a type of transformation where an object is turned around a fixed point.
The fixed point around which an object rotates is specifically known as the centre of rotation.
Therefore, the fixed point in a rotation is called the centre of rotation.
Rotation turns an object about a fixed point. This fixed point is called $\underline{\text{centre of rotation}}$.
In Examples 7 to 9, state whether the statements are True or False.
Example 7: A net of a 3-D shape is a sort of skeleton - outline in 2-D, which, when folded results in the 3-D shape.
Answer:
A net of a 3-D shape is indeed a 2-dimensional pattern that, when folded along its edges, forms the 3-dimensional figure.
The description provided in the statement accurately defines what a net is and how it relates to a 3-D shape.
It serves as a 2-D representation or "skeleton" that allows us to construct the 3-D object.
Therefore, the statement is true.
The final answer is $\boxed{\text{True}}$.
Example 8: A regular pentagon has no lines of symmetry.
Answer:
A regular polygon with $n$ sides has $n$ lines of symmetry.
A regular pentagon is a polygon with 5 equal sides and 5 equal interior angles.
According to the property of regular polygons, a regular pentagon with $n=5$ sides has 5 lines of symmetry.
Each line of symmetry passes through a vertex and the midpoint of the opposite side.
Since a regular pentagon has 5 lines of symmetry, the statement that it has no lines of symmetry is false.
The final answer is $\boxed{\text{False}}$.
Example 9: Order of rotational symmetry for the figure 12.5 is 4.

Answer:
The order of rotational symmetry is the number of times a figure looks exactly the same during a rotation of $360^\circ$ about its centre.
Looking at Figure 12.5, we can observe that it consists of four identical parts arranged around a central point.
If we rotate this figure about its centre, it will coincide with its original position whenever each identical part moves to the position previously occupied by the next identical part.
Since there are four such identical parts, the figure will coincide with itself 4 times in a complete rotation of $360^\circ$.
The positions where it coincides are at $0^\circ$ (original position), $90^\circ$, $180^\circ$, and $270^\circ$.
The number of times it coincides is 4.
Therefore, the order of rotational symmetry for Figure 12.5 is 4.
The statement says that the order of rotational symmetry for the figure 12.5 is 4.
Our analysis shows that the order of rotational symmetry is indeed 4.
Therefore, the statement is true.
The final answer is $\boxed{\text{True}}$.
Example 10: Draw all the lines of symmetry for the following letters if they exist.
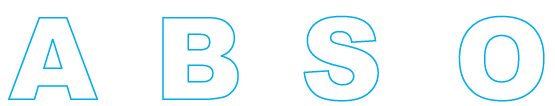
Answer:
A line of symmetry is a line that divides a figure into two mirror images. If a figure is folded along a line of symmetry, the two parts coincide exactly.
Let's examine each letter from the image (A, B, O, M):
Letter A:
The letter A has one line of symmetry.
This line is a vertical line that passes through the middle of the letter.
If you fold the letter A along this vertical line, the left half coincides with the right half.
Letter B:
The letter B has one line of symmetry.
This line is a horizontal line that passes through the middle of the letter.
If you fold the letter B along this horizontal line, the top half coincides with the bottom half.
Letter O:
Assuming 'O' is a block letter (like a circle or oval), it has multiple lines of symmetry.
It has a vertical line of symmetry passing through the centre.
It has a horizontal line of symmetry passing through the centre.
It also has infinitely many lines of symmetry passing through its centre (like a circle).
For typical block capital letters, it is often considered to have at least vertical and horizontal lines of symmetry.
Letter M:
The letter M has one line of symmetry.
This line is a vertical line that passes through the middle of the letter.
If you fold the letter M along this vertical line, the left half coincides with the right half.
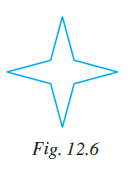
Example 11: State whether the figure 12.6 shows rotational symmetry. If yes, then what is the order of rotational symmetry?
Answer:
A figure shows rotational symmetry if it looks exactly the same after a rotation about a fixed point by an angle less than $360^\circ$.
The order of rotational symmetry is the number of times the figure coincides with itself during a complete rotation of $360^\circ$.
Looking at Figure 12.6, we can see that it is a figure with three identical components arranged symmetrically around a central point.
If we rotate this figure about its centre, it will coincide with its original position whenever one of the components moves to the position previously occupied by another identical component.
Since there are three identical components equally spaced, the figure will look the same after a rotation of $360^\circ / 3 = 120^\circ$.
In a full $360^\circ$ rotation, the figure will coincide with its original position at angles $0^\circ$, $120^\circ$, $240^\circ$, and $360^\circ$. The number of times it coincides is 3 (excluding the initial $0^\circ$ or counting $360^\circ$ as the final position back to original, typically order is the number of distinct positions of coincidence, including the original).
The distinct coinciding positions within $0^\circ$ to $360^\circ$ are $0^\circ$, $120^\circ$, and $240^\circ$. However, order is the number of times it looks the same *during* a $360^\circ$ rotation. It's common to count the number of rotations less than $360^\circ$ that result in coincidence plus the $360^\circ$ rotation returning to the original position, or simply the number of coincidences in $360^\circ$ starting from the original.
It coincides at $120^\circ$, $240^\circ$, and $360^\circ$ (which is the same as $0^\circ$). So there are 3 coincidences within a $360^\circ$ rotation interval.
Yes, the figure 12.6 shows rotational symmetry.
The order of rotational symmetry is 3.
Example 12: Identify the following figures:
Answer:
Let's identify the figures shown in the image.
The first figure appears to be perfectly round in all directions, with no flat surfaces or edges. This shape is a sphere.
The second figure appears to have six square faces of equal size. This shape is a cube.
The third figure appears to have two circular bases connected by a curved surface. This shape is a cylinder.
The fourth figure appears to have a circular base and a curved surface that tapers to a single point (apex). This shape is a cone.
The fifth figure appears to have a polygonal base (likely a square based on typical examples) and triangular faces meeting at a single point (apex). This shape is a pyramid (specifically, if the base is square, it is a square pyramid).
Therefore, the figures are, in order:
1. Sphere
2. Cube
3. Cylinder
4. Cone
5. Pyramid
Example 13: Construct a triangle PQR such that PQ = 6 cm, QR = 7 cm and PR = 4.5 cm.
Answer:
Solution:
To construct $\triangle PQR$ with the given side lengths, we use the SSS (Side-Side-Side) construction method.
Steps of Construction:
1. Draw a line segment $QR$ of length $7$ cm.
2. With Q as the centre, draw an arc of radius $PQ = 6$ cm.
3. With R as the centre, draw an arc of radius $PR = 4.5$ cm.
4. Let the two arcs intersect at point P.
5. Join P to Q and P to R.
6. The triangle PQR is the required triangle.
Example 14: Draw the top, the front and the side views of the following solid figure made up of cubes.

Answer:
To draw the top, front, and side views of a solid figure made of cubes, we need to imagine looking at the figure from directly above (Top View), from the front (Front View, usually indicated), and from the side (Side View, usually the right side if not specified).
Let's assume the "Front View" is taken from the direction the arrow points in similar textbook examples, or typically from the perspective where the figure appears as shown with the "L" shape base and stacks.
Based on a common interpretation of such figures, let's consider the solid as stacks of cubes on a 3x2 grid base (3 units wide, 2 units deep).
Let the heights of the stacks be as follows (Width, Depth):
(1,1)=2, (2,1)=1, (3,1)=2 (Front row stacks, Left to Right)
(1,2)=1, (2,2)=1, (3,2)=1 (Back row stacks, Left to Right)
Front View: Look from the front (along the Depth axis towards Depth=1). The height seen in each column of the Front view is the maximum height in that column across all depths.
Column 1 (Left): Maximum height is $\max(\text{height}(1,1), \text{height}(1,2)) = \max(2, 1) = 2$.
Column 2 (Middle): Maximum height is $\max(\text{height}(2,1), \text{height}(2,2)) = \max(1, 1) = 1$.
Column 3 (Right): Maximum height is $\max(\text{height}(3,1), \text{height}(3,2)) = \max(2, 1) = 2$.
The Front View consists of three vertical columns of heights 2, 1, and 2 squares, from left to right.
Top View: Look from directly above (along the Height axis). The Top view shows which positions on the base grid have at least one cube.
Based on our assumed heights, cubes exist at positions (1,1), (2,1), (3,1), (1,2), (2,2), and (3,2), as all have height $\geq 1$.
The Top View is a rectangular area covering all occupied base positions. It is 3 units wide and 2 units deep.
The Top View is a 3x2 rectangle of squares.
Side View (from Right): Look from the right side (along the Width axis from the right). The height seen in each column of the Side view (which correspond to Depth slices) is the maximum height in that slice across all widths.
Column 1 (Front, D=1): Maximum height is $\max(\text{height}(1,1), \text{height}(2,1), \text{height}(3,1)) = \max(2, 1, 2) = 2$.
Column 2 (Back, D=2): Maximum height is $\max(\text{height}(1,2), \text{height}(2,2), \text{height}(3,2)) = \max(1, 1, 1) = 1$.
The Side View from the Right consists of two vertical columns of heights 2 and 1 square, from front to back.
Example 15: Given a line l and a point M on it draw a perpendicular MP to l where MP = 5.2cm and a line q parallel to l through P.
Answer:
Solution:
We are given a line $l$ and a point M on it. We need to construct a line segment MP perpendicular to $l$ at M with length $5.2$ cm, and then draw a line $q$ through P parallel to $l$.
Steps of Construction:
1. Draw a line $l$ and mark a point M anywhere on it.
2. At point M, construct a perpendicular to the line $l$. This can be done by drawing a semicircle with M as the centre, intersecting $l$ at two points. From these two points, draw arcs with a radius greater than half the distance between them, intersecting above M. Draw a line through M and the intersection point of the arcs. Let's call this perpendicular line $r$.
3. On the perpendicular line $r$, cut off a line segment MP = $5.2$ cm from M.
4. Now, to draw a line $q$ through P parallel to $l$, we can construct a perpendicular to the line $r$ at point P.
5. At point P on line $r$, construct a perpendicular line $q$. This is done in the same way as step 2, but using P as the centre and line $r$. Draw a semicircle with P as the centre, intersecting $r$ at two points. From these two points, draw arcs intersecting on either side of $r$. Draw the line $q$ through P and the intersection points of these arcs.
6. The line $q$ constructed is parallel to line $l$, because both lines $l$ and $q$ are perpendicular to the same line $r$.
Example 16: Determine the number of edges, vertices and faces in the Fig. 12.12.

Answer:
The figure shown is a triangular prism.
A face is a flat surface of a 3D shape.
A vertex (plural: vertices) is a corner where edges meet.
An edge is a line segment where two faces meet.
Let's count the faces, vertices, and edges of the given triangular prism.
Faces:
A triangular prism has two triangular faces (top and bottom) and three rectangular faces (sides).
Number of faces = $2$ (triangles) $+ 3$ (rectangles) $= 5$ faces.
Vertices:
A triangular prism has vertices where the edges meet. There are 3 vertices on the top triangular face and 3 vertices on the bottom triangular face.
Number of vertices = $3$ (top) $+ 3$ (bottom) $= 6$ vertices.
Edges:
A triangular prism has edges forming the sides of the faces. There are 3 edges on the top triangle, 3 edges on the bottom triangle, and 3 vertical edges connecting the top and bottom triangles.
Number of edges = $3$ (top triangle) $+ 3$ (bottom triangle) $+ 3$ (vertical) $= 9$ edges.
So, for the given triangular prism:
Number of edges = 9
Number of vertices = 6
Number of faces = 5
We can also verify Euler's formula for polyhedra, which states that $F + V - E = 2$, where $F$ is the number of faces, $V$ is the number of vertices, and $E$ is the number of edges.
$F + V - E = 5 + 6 - 9 = 11 - 9 = 2$.
The formula holds true, confirming our counts.
Exercise
Question 1 to 28 (Multiple Choice Questions)
In each of the Questions 1 to 26, there are four options, out of which one is correct. Choose the correct one.
Question 1. A triangle can be constructed by taking its sides as:
(a) 1.8 cm, 2.6 cm, 4.4 cm
(b) 2 cm, 3 cm, 4 cm
(c) 2.4 cm, 2.4 cm, 6.4 cm
(d) 3.2 cm, 2.3 cm, 5.5 cm
Answer:
For a triangle to be constructed with side lengths $a$, $b$, and $c$, the sum of the lengths of any two sides must be greater than the length of the third side. This is known as the Triangle Inequality Theorem.
The conditions are:
$a + b > c$
$a + c > b$
$b + c > a$
Let's check each option:
(a) 1.8 cm, 2.6 cm, 4.4 cm
Let $a = 1.8$, $b = 2.6$, $c = 4.4$.
$a + b = 1.8 + 2.6 = 4.4$
Is $a + b > c$? Is $4.4 > 4.4$? No, it is equal.
Therefore, a triangle cannot be constructed with these side lengths.
(b) 2 cm, 3 cm, 4 cm
Let $a = 2$, $b = 3$, $c = 4$.
$a + b = 2 + 3 = 5$. Is $5 > 4$? Yes.
$a + c = 2 + 4 = 6$. Is $6 > 3$? Yes.
$b + c = 3 + 4 = 7$. Is $7 > 2$? Yes.
All conditions are met. Therefore, a triangle can be constructed with these side lengths.
(c) 2.4 cm, 2.4 cm, 6.4 cm
Let $a = 2.4$, $b = 2.4$, $c = 6.4$.
$a + b = 2.4 + 2.4 = 4.8$
Is $a + b > c$? Is $4.8 > 6.4$? No.
Therefore, a triangle cannot be constructed with these side lengths.
(d) 3.2 cm, 2.3 cm, 5.5 cm
Let $a = 3.2$, $b = 2.3$, $c = 5.5$.
$a + b = 3.2 + 2.3 = 5.5$
Is $a + b > c$? Is $5.5 > 5.5$? No, it is equal.
Therefore, a triangle cannot be constructed with these side lengths.
Based on the Triangle Inequality Theorem, only the side lengths in option (b) can form a triangle.
The correct option is (b) 2 cm, 3 cm, 4 cm.
Question 2. A triangle can be constructed by taking two of its angles as:
(a) 110°, 40°
(b) 70°, 115°
(c) 135°, 45°
(d) 90°, 90°
Answer:
The fundamental property of a triangle regarding its angles is that the sum of the interior angles of a triangle is always $180^\circ$. Also, each interior angle must be greater than $0^\circ$.
Let the two given angles be $\angle A$ and $\angle B$. Let the third angle be $\angle C$. For a triangle to be constructed, the following conditions must be met:
$\angle A + \angle B + \angle C = 180^\circ$
$\angle A > 0^\circ$, $\angle B > 0^\circ$, $\angle C > 0^\circ$
From the first condition, the third angle $\angle C$ must be $180^\circ - (\angle A + \angle B)$. For $\angle C$ to be a valid angle, it must be greater than $0^\circ$. This implies:
$180^\circ - (\angle A + \angle B) > 0^\circ$
Which simplifies to:
$\angle A + \angle B < 180^\circ$
So, the sum of any two angles of a triangle must be less than $180^\circ$. Also, both given angles must be less than $180^\circ$ (which is usually true for options in this type of question, but worth noting).
Let's check each option by summing the two given angles:
(a) 110°, 40°
Sum of angles = $110^\circ + 40^\circ = 150^\circ$.
Is $150^\circ < 180^\circ$? Yes.
The third angle would be $180^\circ - 150^\circ = 30^\circ$. Since $30^\circ > 0^\circ$, a triangle can be constructed with these angles.
(b) 70°, 115°
Sum of angles = $70^\circ + 115^\circ = 185^\circ$.
Is $185^\circ < 180^\circ$? No, $185^\circ > 180^\circ$.
A triangle cannot be constructed with these angles.
(c) 135°, 45°
Sum of angles = $135^\circ + 45^\circ = 180^\circ$.
Is $180^\circ < 180^\circ$? No, $180^\circ = 180^\circ$.
The third angle would be $180^\circ - 180^\circ = 0^\circ$. Since the third angle must be greater than $0^\circ$, a triangle cannot be constructed.
(d) 90°, 90°
Sum of angles = $90^\circ + 90^\circ = 180^\circ$.
Is $180^\circ < 180^\circ$? No, $180^\circ = 180^\circ$.
The third angle would be $180^\circ - 180^\circ = 0^\circ$. Since the third angle must be greater than $0^\circ$, a triangle cannot be constructed.
Only option (a) satisfies the condition that the sum of the two angles is less than $180^\circ$, allowing for a positive third angle.
The correct option is (a) 110°, 40°.
Question 3. The number of lines of symmetry in the figure given below is:

(a) 4
(b) 8
(c) 6
(d) Infinitely many
Answer:
A line of symmetry is a line that divides a figure into two identical halves that are mirror images of each other. If a figure is folded along a line of symmetry, the two halves match exactly.
The figure shown is a regular octagon. A regular octagon has 8 equal sides and 8 equal interior angles.
For a regular polygon with $n$ sides, the number of lines of symmetry is equal to $n$.
In this case, the figure is a regular octagon, so the number of sides is $n = 8$.
The lines of symmetry in a regular octagon pass through:
- The midpoints of opposite sides (4 lines).
- Opposite vertices (4 lines).
Total number of lines of symmetry = $4 + 4 = 8$.
Therefore, the number of lines of symmetry in the given figure is 8.
Comparing this with the given options:
(a) 4
(b) 8
(c) 6
(d) Infinitely many
The correct option is (b) 8.
Question 4. The number of lines of symmetry in Fig. 12.14 is

(a) 1
(b) 3
(c) 6
(d) Infinitely many
Answer:
A line of symmetry divides a figure into two halves that are mirror images of each other. The figure remains unchanged after reflection across the line of symmetry.
The given figure is derived from an equilateral triangle by removing smaller equilateral triangles from its corners. The overall shape retains the symmetry properties of the original equilateral triangle.
An equilateral triangle has 3 lines of symmetry. These lines pass through each vertex and the midpoint of the opposite side.
Let's examine if these lines are also lines of symmetry for the given figure:
1. The line passing through the top vertex and the midpoint of the base divides the figure into two symmetric halves. The removed triangles at the bottom corners are symmetric with respect to this line, and the central part is also symmetric.
2. The line passing through the bottom-left vertex and the midpoint of the opposite side (right side) also divides the figure symmetrically.
3. The line passing through the bottom-right vertex and the midpoint of the opposite side (left side) also divides the figure symmetrically.
There are no other lines of symmetry. For instance, a line connecting the midpoints of two sides would not map the removed corner regions correctly.
Thus, the number of lines of symmetry in the figure is 3.
Comparing with the given options:
(a) 1
(b) 3
(c) 6
(d) Infinitely many
The correct option is (b) 3.
Question 5. The order of rotational symmetry in the Fig. 12.15 given below is

(a) 4
(b) 8
(c) 6
(d) Infinitely many
Answer:
The order of rotational symmetry of a figure is the number of times it looks exactly the same during a full rotation of $360^\circ$ about its centre.
The given figure is a regular hexagon with a design inside that also possesses hexagonal symmetry. The design consists of six identical "petals" or segments arranged around a central point.
Consider rotating the figure about its centre. Since there are 6 identical segments, the figure will coincide with its original position after a rotation by every $\frac{360^\circ}{6} = 60^\circ$.
The positions where the figure looks the same are after rotations of $60^\circ, 120^\circ, 180^\circ, 240^\circ, 300^\circ,$ and $360^\circ$ (which is the same as $0^\circ$).
There are 6 such distinct positions (including the original position after a $360^\circ$ rotation).
Therefore, the order of rotational symmetry of the figure is 6.
Comparing with the given options:
(a) 4
(b) 8
(c) 6
(d) Infinitely many
The correct option is (c) 6.
Question 6. The order of rotational symmetry in the figure 12.16 given below is

(a) 4
(b) 2
(c) 1
(d) Infinitely many
Answer:
The order of rotational symmetry is the number of times a figure coincides with itself during a complete rotation of $360^\circ$ about its centre.
The given figure is a rectangle with a cross shape formed by two perpendicular line segments inside, intersecting at the center of the rectangle.
Let's rotate the figure about its centre:
- After a rotation of $90^\circ$, the rectangle is oriented vertically if it was originally horizontal (or vice versa). The figure does not look the same unless the rectangle is a square.
- After a rotation of $180^\circ$, the rectangle returns to its original orientation. The cross shape also looks exactly the same after a $180^\circ$ rotation.
- After a rotation of $270^\circ$, the figure is again oriented differently than the original.
- After a rotation of $360^\circ$, the figure returns to its original position, which is always a symmetry.
The angles of rotation for which the figure looks the same are $180^\circ$ and $360^\circ$ (or $0^\circ$).
The number of times the figure coincides with itself during a $360^\circ$ rotation is 2.
Therefore, the order of rotational symmetry is 2.
Comparing with the given options:
(a) 4
(b) 2
(c) 1
(d) Infinitely many
The correct option is (b) 2.
Question 7. The name of the given solid in Fig 12.17 is:
(a) triangular pyramid
(b) rectangular pyramid
(c) rectangular prism
(d) triangular prism
Answer:
Let's identify the type of solid based on its properties shown in the figure.
A pyramid is a polyhedron formed by connecting a polygonal base and a point, called the apex, by triangular faces.
- A triangular pyramid has a triangular base and three triangular faces meeting at the apex.
- A rectangular pyramid has a rectangular base and four triangular faces meeting at the apex.
The given figure has a polygon as a base, but all the other faces are triangles that meet at a single point (the apex). The base is a rectangle (or possibly a square, which is a specific type of rectangle).
A prism is a polyhedron comprising an $n$-sided polygonal base, a second base which is a translated copy of the first, and $n$ other faces (necessarily all parallelograms) joining corresponding sides of the two bases.
- A rectangular prism (also called a cuboid) has two rectangular bases and four rectangular side faces.
- A triangular prism has two triangular bases and three rectangular side faces.
Looking at the figure, the base is a four-sided polygon (a rectangle). All the faces that rise from the base are triangles and meet at a single point above the center of the base. This description matches that of a pyramid with a rectangular base.
Therefore, the solid is a rectangular pyramid.
Comparing with the given options:
(a) triangular pyramid
(b) rectangular pyramid
(c) rectangular prism
(d) triangular prism
The correct option is (b) rectangular pyramid.
Question 8. The name of the solid in Fig. 12.18 is:
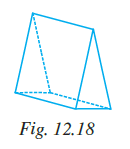
(a) triangular pyramid
(b) rectangular prism
(c) triangular prism
(d) rectangular pyramid
Answer:
Let's analyze the structure of the given solid to identify its name.
A pyramid has a polygon as a base and triangular faces that meet at a single apex.
A prism has two parallel and congruent polygonal bases, and its other faces are parallelograms (often rectangles) that connect the corresponding sides of the bases.
Looking at the figure, we can see:
- There are two faces that are congruent triangles and are parallel to each other. These are the bases.
- There are three rectangular faces connecting the corresponding sides of the two triangular bases.
This structure matches the definition of a triangular prism, where the bases are triangles and the side faces are rectangles.
Comparing with the given options:
(a) triangular pyramid (has a triangular base but triangular side faces meeting at an apex)
(b) rectangular prism (has rectangular bases)
(c) triangular prism (matches the description)
(d) rectangular pyramid (has a rectangular base and triangular side faces meeting at an apex)
The correct identification of the solid is a triangular prism.
The correct option is (c) triangular prism.
Question 9. All faces of a pyramid are always:
(a) Triangular
(b) Rectangular
(c) Congruent
(d) None of these
Answer:
Let's recall the definition and components of a pyramid.
A pyramid is a polyhedron formed by connecting a polygonal base to a point (the apex) by triangular faces.
A pyramid has one base and a set of side faces that meet at the apex.
The base can be any polygon (triangle, square, rectangle, pentagon, hexagon, etc.). The shape of the base determines the name of the pyramid (e.g., triangular pyramid, square pyramid, rectangular pyramid).
The faces connecting the base to the apex are always triangles. These are called the lateral faces.
So, a pyramid consists of one polygonal base and several triangular lateral faces.
The question asks about "All faces of a pyramid". This includes the base and the lateral faces.
Let's examine the options:
(a) Triangular: This is incorrect because a pyramid has a base which is a polygon (and can be triangular, but not always). Only the lateral faces are triangular.
(b) Rectangular: This is incorrect. The base is a polygon, and the lateral faces are triangular.
(c) Congruent: This is incorrect. The base face is generally different from the lateral faces in shape (e.g., a square base and triangular sides). Also, the lateral faces are congruent only if the base is a regular polygon and the apex is directly above the center of the base (a right pyramid with a regular base). In a general pyramid, the lateral faces might not be congruent.
(d) None of these: This option is correct because option (a), (b), and (c) are incorrect descriptions of all faces of a pyramid.
It's important to distinguish between the base and the lateral faces. While all lateral faces are triangular, the base can be any polygon. Therefore, saying "All faces" are triangular is incorrect unless it is specifically a triangular pyramid (a tetrahedron), in which case all four faces are triangles (but not necessarily congruent unless it's a regular tetrahedron).
However, the question asks about a general pyramid. For a general pyramid, only the lateral faces are triangular. The base is a polygon. So, all faces are not always triangular or rectangular or congruent.
Therefore, none of the options (a), (b), or (c) universally describe all faces of any pyramid.
The correct option is (d) None of these.
Question 10. A solid that has only one vertex is
(a) Pyramid
(b) Cube
(c) Cone
(d) Cylinder
Answer:
Let's consider the number of vertices for each of the given solid shapes.
(a) Pyramid: A pyramid has a polygonal base and triangular faces that meet at a single point called the apex. The vertices of a pyramid include the vertices of the base plus the apex. For example, a square pyramid has a square base (4 vertices) and an apex, so it has $4+1=5$ vertices. A triangular pyramid has a triangular base (3 vertices) and an apex, so it has $3+1=4$ vertices. In general, a pyramid with an $n$-sided polygon as its base has $n+1$ vertices. Since $n \geq 3$, a pyramid always has more than one vertex.
(b) Cube: A cube is a type of rectangular prism. It has 6 square faces, 12 edges, and 8 vertices.
(c) Cone: A cone has a circular base and a curved surface that tapers smoothly from the base to a single point called the vertex or apex. The circular base has no vertices, but the point at the top is the vertex. Thus, a cone has only one vertex.
(d) Cylinder: A cylinder has two parallel and congruent circular bases and a curved surface joining them. A cylinder has no vertices or edges.
Based on the analysis, the solid that has only one vertex is a cone.
The correct option is (c) Cone.
Question 11. Out of the following which is a 3-D figure?
(a) Square
(b) Sphere
(c) Triangle
(d) Circle
Answer:
Let's differentiate between 2-D (two-dimensional) and 3-D (three-dimensional) figures.
2-D figures are flat shapes that lie in a plane. They have two dimensions: length and width (or breadth). Examples include squares, triangles, circles, rectangles, polygons, etc.
3-D figures are solid shapes that occupy space. They have three dimensions: length, width (or breadth), and height (or depth). Examples include cubes, spheres, cones, cylinders, pyramids, prisms, etc.
Let's examine each option:
(a) Square: A square is a flat shape with four equal sides and four right angles. It is a 2-D figure.
(b) Sphere: A sphere is a perfectly round geometrical object in three-dimensional space that is the surface of a completely round ball. It has a radius and occupies space. It is a 3-D figure.
(c) Triangle: A triangle is a flat shape with three sides and three angles. It is a 2-D figure.
(d) Circle: A circle is a flat shape consisting of all points in a plane that are at a given distance from a central point. It is a 2-D figure.
Among the given options, only the sphere is a three-dimensional figure.
The correct option is (b) Sphere.
Question 12. Total number of edges a cylinder has
(a) 0
(b) 1
(c) 2
(d) 3
Answer:
Let's define what an edge is in the context of solid shapes and then apply it to a cylinder.
An edge is a line segment where two faces of a solid meet. This definition primarily applies to polyhedra (solids with flat faces like cubes, prisms, pyramids).
For solids with curved surfaces, like cylinders, cones, and spheres, the concept of an edge is sometimes extended to mean the boundary line where a curved surface meets a flat surface, or where two surfaces (curved or flat) meet. However, often, edges are specifically defined for polyhedra. Let's consider the common understanding used in geometry.
A cylinder has two flat circular bases and one curved lateral surface. The circular bases are connected by the curved surface.
- The boundary of each circular base is a circle.
- The curved surface meets each circular base along the circumference of the circle.
In the context of classifying the components of a solid, the boundary curves where the flat circular bases meet the curved lateral surface are considered edges. These are the lines where the faces meet.
There are two such circular boundaries.
Therefore, a cylinder has 2 edges.
Let's review the options based on this understanding:
(a) 0
(b) 1
(c) 2
(d) 3
The number of edges a cylinder has is 2.
The correct option is (c) 2.
Question 13. A solid that has two opposite identical faces and other faces as parallelograms is a
(a) prism
(b) pyramid
(c) cone
(d) sphere
Answer:
Let's analyze the properties described in the question and match them with the definitions of the given solid shapes.
The question describes a solid with two opposite identical faces and other faces as parallelograms.
Let's consider each option:
(a) Prism: A prism is a polyhedron with two parallel and congruent polygonal bases and faces joining corresponding sides of the bases. These joining faces are always parallelograms. If the prism is a right prism, these faces are rectangles (a special type of parallelogram). The two opposite identical faces are the bases.
This description perfectly matches the definition of a prism.
(b) Pyramid: A pyramid has a polygonal base and triangular faces that meet at an apex. It has only one base and the other faces are triangles, not parallelograms.
(c) Cone: A cone has a circular base and a curved surface that tapers to a single vertex. It does not have flat polygonal faces other than the base, and it only has one base.
(d) Sphere: A sphere is a round solid with no flat faces or edges. It is a single curved surface.
Based on the characteristics given ("two opposite identical faces and other faces as parallelograms"), the solid is a prism.
The correct option is (a) prism.
Question 14. The solid with one circular face, one curved surface and one vertex is known as:
(a) cone
(b) sphere
(c) cylinder
(d) prism
Answer:
We need to identify the solid that has the following properties: one circular face, one curved surface, and one vertex.
Let's examine the characteristics of each option:
(a) Cone: A cone has a flat circular base (one circular face), a curved lateral surface, and a single point at the top called the apex or vertex (one vertex). This matches all the described properties.
(b) Sphere: A sphere is a perfectly round solid with only one curved surface. It has no flat faces and no vertices.
(c) Cylinder: A cylinder has two flat circular bases (two circular faces), one curved lateral surface, and no vertices.
(d) Prism: A prism has two identical and parallel polygonal bases and flat rectangular or parallelogram faces connecting the bases. It does not have a circular face (unless the question implicitly allows approximating curved surfaces, but standard definition does not). It has multiple vertices (at least 6).
Comparing the properties with the description, the solid with one circular face, one curved surface, and one vertex is a cone.
The correct option is (a) cone.
Question 15. If three cubes each of edge 4 cm are placed end to end, then the dimensions of resulting solid are:
(a) 12 cm × 4 cm × 4 cm
(b) 4 cm × 8 cm × 4 cm
(c) 4 cm × 8 cm × 12 cm
(d) 4 cm × 6 cm × 8 cm
Answer:
We are given three cubes, each with an edge length of 4 cm. The dimensions of a single cube are 4 cm × 4 cm × 4 cm (Length × Width × Height).
When these three cubes are placed end to end, it means they are joined along one of their faces. Let's assume they are placed end to end along the length dimension.
Imagine the first cube has dimensions $4 \text{ cm} \times 4 \text{ cm} \times 4 \text{ cm}$.
When the second cube is placed end to end with the first, its 4 cm edge aligns with one face of the first cube. If placed along the length, the total length becomes $4 \text{ cm} + 4 \text{ cm} = 8 \text{ cm}$. The width and height remain 4 cm.
When the third cube is placed end to end with the resulting solid, its 4 cm edge aligns with the end face. If placed along the same dimension (length), the total length becomes $8 \text{ cm} + 4 \text{ cm} = 12 \text{ cm}$. The width and height still remain 4 cm.
So, the resulting solid will have dimensions:
Length = Sum of the lengths of the three cubes placed end to end = $4 \text{ cm} + 4 \text{ cm} + 4 \text{ cm} = 12 \text{ cm}$.
Width = Width of a single cube = $4 \text{ cm}$.
Height = Height of a single cube = $4 \text{ cm}$.
The dimensions of the resulting solid are $12 \text{ cm} \times 4 \text{ cm} \times 4 \text{ cm}$.
This new solid is a cuboid (a rectangular prism).
Comparing with the given options:
(a) 12 cm × 4 cm × 4 cm
(b) 4 cm × 8 cm × 4 cm
(c) 4 cm × 8 cm × 12 cm
(d) 4 cm × 6 cm × 8 cm
The correct option is (a) 12 cm × 4 cm × 4 cm.
Question 16. When we cut a corner of a cube as shown in the figure 12.19, we get the cutout piece as :

(a) square pyramid
(b) trapezium prism
(c) triangular pyramid
(d) a triangle
Answer:
The figure shows a cube and a plane cutting off one of its corners.
The cutout piece is the small solid removed from the cube by the cut.
Let's examine the shape of the cutout piece:
- It has one vertex which is the original corner of the cube.
- The cut is made by a plane that intersects the three edges meeting at that corner. Since the plane intersects three non-collinear points (one on each of the three edges extending from the corner), the cut surface is a triangle.
- The three faces of the cube that meet at the cut corner become triangular faces of the cutout piece. These triangular faces meet at the original cube corner (which is now the apex of the cutout piece).
- So, the cutout piece has a triangular base (the cut surface) and three triangular faces meeting at a single vertex (the original cube corner).
A solid with a polygonal base and triangular faces meeting at a single apex is a pyramid.
Since the base of the cutout piece is a triangle, it is a triangular pyramid.
Let's check the options:
(a) square pyramid: Incorrect, the base is a triangle.
(b) trapezium prism: Incorrect, it is a pyramid, not a prism, and the base is a triangle.
(c) triangular pyramid: Correct, it has a triangular base and triangular side faces meeting at an apex.
(d) a triangle: Incorrect, a triangle is a 2D shape, and the cutout piece is a 3D solid.
The cutout piece is a triangular pyramid.
The correct option is (c) triangular pyramid.
Question 17. If we rotate a right-angled triangle of height 5 cm and base 3 cm about its height a full turn, we get
(a) cone of height 5 cm, base 3 cm
(b) triangle of height 5 cm, base 3 cm
(c) cone of height 5 cm, base 6 cm
(d) triangle of height 5 cm, base 6 cm
Answer:
Consider a right-angled triangle with height $h$ and base $r$. When this triangle is rotated a full turn ($360^\circ$) about its height (the side adjacent to the right angle and along which the height is measured), the shape generated is a cone.
In the given problem, the right-angled triangle has:
Height = 5 cm
Base = 3 cm
The rotation is performed about its height (the 5 cm side).
The resulting solid will be a cone.
The height of the cone will be the height of the triangle about which it is rotated, which is 5 cm.
The radius of the circular base of the cone will be the base of the triangle (the side perpendicular to the height), which is 3 cm.
The base of the cone is a circle with radius 3 cm. The question options refer to the "base" dimension. In the context of a circle, the "base" dimension usually refers to the diameter.
Radius of the cone's base = 3 cm
Diameter of the cone's base = $2 \times \text{radius} = 2 \times 3 \text{ cm} = 6 \text{ cm}$.
So, the resulting solid is a cone with:
Height = 5 cm
Base diameter = 6 cm
Let's examine the options again, considering what "base" refers to in each option:
(a) cone of height 5 cm, base 3 cm: This suggests the base dimension is 3 cm, which would be the radius if "base" refers to radius, but usually, base refers to a linear dimension of the base shape (like diameter or side length).
(b) triangle of height 5 cm, base 3 cm: Incorrect, the result is a 3D solid, not a 2D triangle.
(c) cone of height 5 cm, base 6 cm: This option describes a cone with height 5 cm and a base dimension of 6 cm. If "base" here refers to the diameter, this is consistent with our finding (diameter = 6 cm).
(d) triangle of height 5 cm, base 6 cm: Incorrect, the result is a 3D solid.
Given the options, it is most likely that "base" in options (a) and (c) refers to the diameter of the circular base of the cone. Option (c) matches our calculated dimensions.
The correct option is (c) cone of height 5 cm, base 6 cm.
Question 18. If we rotate a right-angled triangle of height 5 cm and base 3 cm about its base, we get:
(a) cone of height 3 cm and base 3 cm
(b) cone of height 5 cm and base 5 cm
(c) cone of height 5 cm and base 3 cm
(d) cone of height 3 cm and base 5 cm
Answer:
When a right-angled triangle is rotated about one of its legs (the sides forming the right angle), the solid generated is a cone.
In this problem, we have a right-angled triangle with:
Height = 5 cm
Base = 3 cm
The rotation is performed about its base (the side of length 3 cm).
When the triangle is rotated about the side measuring 3 cm:
- The side about which the rotation occurs becomes the height of the cone. So, the height of the cone is 3 cm.
- The other leg of the right-angled triangle (the side perpendicular to the axis of rotation) becomes the radius of the circular base of the cone. So, the radius of the cone's base is 5 cm.
Thus, the resulting solid is a cone with a height of 3 cm and a base radius of 5 cm.
The diameter of the base would be $2 \times \text{radius} = 2 \times 5 \text{ cm} = 10 \text{ cm}$.
Now let's look at the options. The options describe the cone by its height and "base" dimension.
(a) cone of height 3 cm and base 3 cm
(b) cone of height 5 cm and base 5 cm
(c) cone of height 5 cm and base 3 cm
(d) cone of height 3 cm and base 5 cm
Our calculated height is 3 cm and radius is 5 cm. Option (d) states "cone of height 3 cm and base 5 cm". In this context, it appears that "base" in the options refers to the radius of the base circle, rather than the diameter or the original triangle's base length.
Therefore, based on the likely interpretation of the options, the correct description is a cone with height 3 cm and base (radius) 5 cm.
The correct option is (d) cone of height 3 cm and base 5 cm.
Question 19. When a torch is pointed towards one of the vertical edges of a cube, you get a shadow of cube in the shape of
(a) square
(b) rectangle but not a square
(c) circle
(d) triangle
Answer:
When a torch is pointed towards a solid object, the shadow formed on a surface behind the object is the projection of the object's shape from the light source onto the surface.
The shape of the shadow depends on the shape of the object, the position of the light source, and the orientation of the object relative to the light source and the surface.
For a cube, the shadow cast by a point source of light (like a torch) can be a polygon. The vertices of this polygon are the projections of the vertices of the cube that form the silhouette of the cube as seen from the light source.
Possible shapes for the shadow of a cube are a square, a rectangle, or a hexagon, depending on how the light source is positioned.
- A square shadow is formed when the light is shone perpendicular to one of the faces.
- A hexagon shadow is formed when the light is shone along a direction parallel to a space diagonal of the cube.
- A rectangle shadow is formed when the light is shone from many other angles.
In this case, the torch is pointed towards one of the vertical edges of the cube. This means the direction of light is angled relative to the faces. When the light source is positioned such that the view of the cube from the source is dominated by the two faces adjacent to the targeted vertical edge, the resulting shadow on a plane will typically be a rectangle.
Since the light is pointed towards an edge rather than perpendicular to a face, the projection will generally stretch the dimensions unevenly, resulting in a rectangle that is not a square.
Let's consider the options:
(a) square: Possible, but usually when light is perpendicular to a face.
(b) rectangle but not a square: This is a common result when the light is angled relative to the faces, such as when aimed towards an edge.
(c) circle: Impossible for a polyhedron like a cube cast by a point or directional light source.
(d) triangle: Impossible for a cube's shadow under standard conditions.
Pointing a torch towards a vertical edge creates a projection where the length and width of the shadow are typically unequal, forming a rectangle that is not a square.
The correct option is (b) rectangle but not a square.
Question 20. Which of the following sets of triangles could be the lengths of the sides of a right-angled triangle:
(a) 3 cm, 4 cm, 6 cm
(b) 9 cm, 16 cm, 26 cm
(c) 1.5 cm, 3.6 cm, 3.9 cm
(d) 7 cm, 24 cm, 26 cm
Answer:
To determine if a triangle with side lengths $a$, $b$, and $c$ is a right-angled triangle, we can use the converse of the Pythagorean theorem. If the square of the length of the longest side is equal to the sum of the squares of the lengths of the other two sides, then the triangle is a right-angled triangle.
Let the side lengths be $a$, $b$, and $c$, where $c$ is the longest side. The condition for a right-angled triangle is $a^2 + b^2 = c^2$.
Let's check each option:
(a) 3 cm, 4 cm, 6 cm
The longest side is 6 cm. Let $a = 3$, $b = 4$, $c = 6$.
Check if $a^2 + b^2 = c^2$:
$3^2 + 4^2 = 9 + 16 = 25$
$6^2 = 36$
Since $25 \neq 36$, this is not a right-angled triangle.
(b) 9 cm, 16 cm, 26 cm
The longest side is 26 cm. Let $a = 9$, $b = 16$, $c = 26$.
Check if $a^2 + b^2 = c^2$:
$9^2 + 16^2 = 81 + 256 = 337$
$26^2 = 676$
Since $337 \neq 676$, this is not a right-angled triangle.
(c) 1.5 cm, 3.6 cm, 3.9 cm
The longest side is 3.9 cm. Let $a = 1.5$, $b = 3.6$, $c = 3.9$.
Check if $a^2 + b^2 = c^2$:
$a^2 = (1.5)^2 = 2.25$
$b^2 = (3.6)^2 = 12.96$
$a^2 + b^2 = 2.25 + 12.96 = 15.21$
$c^2 = (3.9)^2 = 15.21$
Since $15.21 = 15.21$, the condition $a^2 + b^2 = c^2$ is satisfied. This set of side lengths can form a right-angled triangle.
(d) 7 cm, 24 cm, 26 cm
The longest side is 26 cm. Let $a = 7$, $b = 24$, $c = 26$.
Check if $a^2 + b^2 = c^2$:
$a^2 = 7^2 = 49$
$b^2 = 24^2 = 576$
$a^2 + b^2 = 49 + 576 = 625$
$c^2 = 26^2 = 676$
Since $625 \neq 676$, this is not a right-angled triangle.
Only the side lengths 1.5 cm, 3.6 cm, and 3.9 cm satisfy the Pythagorean theorem.
The correct option is (c) 1.5 cm, 3.6 cm, 3.9 cm.
Question 21. In which of the following cases, a unique triangle can be drawn
(a) AB = 4 cm, BC = 8 cm and CA = 2 cm
(b) BC = 5.2 cm, ∠B = 90° and ∠C = 110°
(c) XY = 5 cm, ∠X = 45° and ∠Y = 60°
(d) An isosceles triangle with the length of each equal side 6.2 cm.
Answer:
For a unique triangle to be drawn, we need sufficient and consistent information. Let's analyze each option based on triangle construction criteria:
(a) AB = 4 cm, BC = 8 cm and CA = 2 cm
This gives three side lengths (SSS criterion). We need to check the Triangle Inequality Theorem: the sum of any two sides must be greater than the third side.
Check: $4 + 2 = 6$. Is $6 > 8$? No, $6 \ngtr 8$.
Since the sum of two sides (AB + CA) is not greater than the third side (BC), a triangle cannot be constructed with these side lengths.
(b) BC = 5.2 cm, ∠B = 90° and ∠C = 110°
This gives one side and two angles (ASA or AAS criterion). The sum of the angles in a triangle must be $180^\circ$.
Sum of given angles = $90^\circ + 110^\circ = 200^\circ$.
Since the sum of two angles is already greater than $180^\circ$, the third angle would have to be negative ($180^\circ - 200^\circ = -20^\circ$), which is impossible for a triangle.
Therefore, a triangle cannot be constructed with these angles.
(c) XY = 5 cm, ∠X = 45° and ∠Y = 60°
This gives one side and the two angles adjacent to that side (ASA criterion: Angle-Side-Angle). If the sum of the given angles is less than $180^\circ$, the third angle can be determined ($180^\circ - (45^\circ + 60^\circ) = 180^\circ - 105^\circ = 75^\circ$).
The side XY connects vertices X and Y, and the angles at X and Y are given. This is the ASA condition.
According to the ASA congruence criterion (and construction principle), if two angles and the included side of one triangle are equal to two angles and the included side of another triangle, the triangles are congruent. This implies that given these conditions, only one unique triangle can be constructed.
Thus, a unique triangle can be drawn with these measurements.
(d) An isosceles triangle with the length of each equal side 6.2 cm.
An isosceles triangle has two equal sides. We are given that the length of each equal side is 6.2 cm. Let these sides be $a$ and $b$, so $a = b = 6.2$ cm.
We have the lengths of two sides. To form a unique triangle, we would need more information, such as:
- The length of the third side (SSS).
- The angle between the two equal sides (SAS: Side-Angle-Side).
- One of the base angles (AAS or ASA, depending on which angle is given in relation to the sides).
With only the lengths of the two equal sides, the third side can have any length greater than $0$ and less than the sum of the two equal sides ($6.2 + 6.2 = 12.4$ cm) and also satisfying the triangle inequality with the two equal sides (e.g., if the third side is $c$, then $6.2 + c > 6.2$, which is true for $c>0$). Any length $c$ such that $0 < c < 12.4$ can be the third side, leading to infinitely many possible isosceles triangles with equal sides of 6.2 cm (each with a different base length and angles). Therefore, a unique triangle cannot be drawn with this information alone.
Based on the analysis of each option and the triangle construction criteria, a unique triangle can only be drawn in case (c).
The correct option is (c) XY = 5 cm, ∠X = 45° and ∠Y = 60°.
Question 22. Which of the following has a line of symmetry?

Answer:
A figure has a line of symmetry if it can be folded along a straight line such that the two halves match exactly. This means the line of symmetry acts as a mirror line.
The figure shows four different shapes labeled (a), (b), (c), and (d).
Let's examine each shape to see if it has a line of symmetry:
Shape (a): This shape is an asymmetric curve. There is no straight line that can divide this figure into two mirror-image halves.
Shape (b): This shape resembles the letter 'F'. If we try to draw a horizontal or vertical line through it, or any other line, the two parts on either side of the line will not be mirror images. This shape does not have a line of symmetry.
Shape (c): This shape appears to be an arrow or a pointer. A vertical line drawn through the centre of the arrow would divide it into two identical halves that are mirror images of each other. Therefore, this shape has at least one line of symmetry (the vertical line through the centre).
Shape (d): This shape resembles the number '7'. There is no straight line that can divide this figure into two mirror-image halves.
Based on the visual inspection, only shape (c) has a line of symmetry.
The correct option is (c).
Question 23. Which of the following are reflections of each other?

Answer:
Two figures are reflections of each other if one can be obtained from the other by flipping it across a line, called the mirror line or axis of reflection. The reflected figure is the mirror image of the original figure.
Let's examine each pair of figures provided:
(a) The two irregular shapes in pair (a) do not appear to be mirror images of each other. Flipping one across any line between them would not result in the other figure.
(b) The two trapezoids in pair (b) are positioned such that if a vertical line were drawn between them, one trapezoid would be the exact mirror image of the other across that line. For example, the vertices on the left side of the first trapezoid are the same distance from the potential mirror line as the corresponding vertices on the right side of the second trapezoid, and vice versa. This pair shows reflection.
(c) The two 'L'-shaped figures in pair (c) are oriented such that one is a rotated or translated version of the other, but they are not mirror images. A reflection would flip the orientation of the figure, which is not observed here.
(d) The two irregular polygons in pair (d) do not appear to be mirror images of each other. Their shapes and orientations are not consistent with a reflection across a single line.
Based on the analysis, only the figures in pair (b) are reflections of each other.
The correct option is (b).
Question 24. Which of these nets is a net of a cube?

Answer:
A net of a solid is a 2-D pattern that can be folded to form the solid. A cube has 6 square faces. A net of a cube must consist of 6 squares arranged in a way that when folded, they form a closed cube without any overlaps or gaps.
There are 11 different possible nets of a cube. We need to examine each of the given nets to determine if it can be folded into a cube.
Let's visualize folding each net:
Net (a): This net has 6 squares. Let's consider the row of 4 squares as the 'belt' around the cube. The two remaining squares are attached to this belt. When you fold up the four squares, they form the four side walls. One of the end squares can be folded up to form the bottom base. The other end square needs to be folded up to form the top base. In net (a), the two end squares are on opposite sides of the belt and are correctly positioned to form the top and bottom faces when folded.
Net (b): This net also has 6 squares. Consider the row of 3 squares as a partial belt. If we fold this, we get three sides. The two squares above and below the middle square of the three would form the top and bottom. The remaining square is attached to the last square of the row of 3. When folding, this net would result in overlapping faces or an open solid.
Net (c): This net has 6 squares. Consider the row of 4 squares. If we fold this row, we get four sides. The two remaining squares are both attached to the second square of the row of 4, and both are on the same side of the belt. When folding this, one square can form the top/bottom, but the other square will overlap with it or another side face, or there will be a gap.
Net (d): This net has 6 squares. Consider the row of 4 squares. If we fold this row, we get four sides. The two remaining squares are attached to the first and third squares of the row, both on the same side. When folding this, one square can form the top/bottom, but the other square will either overlap or leave a gap.
The common and valid nets of a cube often have a shape like a '+' sign (four in a row, and one on each side of the second square) or variations of this shape. Net (a) fits a standard valid net configuration.
Based on the folding test or knowledge of cube nets, only net (a) can be folded into a cube.
The correct option is (a).
Question 25. Which of the following nets is a net of a cylinder?

Answer:
A cylinder is a 3-D solid shape with two parallel and congruent circular bases and a curved surface joining them.
A net of a solid is a 2-D pattern that can be folded to form the solid. To find the net of a cylinder, we need to imagine unfolding its surfaces.
When you unfold a cylinder, you get:
- Two circular faces (the top and bottom bases).
- One rectangular face (the curved surface, when unrolled).
The rectangle's length is equal to the circumference of the circular bases, and its width is equal to the height of the cylinder. The two circular bases are attached to the opposite sides of the rectangle.
Let's examine the given nets:
Net (a): This net consists of a rectangle with a circle attached to the top edge and another circle attached to the bottom edge of the rectangle. This arrangement matches the description of the net of a cylinder.
Net (b): This net has a rectangle and only one circle attached to one side. This cannot form a closed cylinder, as a cylinder requires two circular bases.
Net (c): This net has two rectangles and two circles. A cylinder only unfolds into one rectangle and two circles.
Net (d): This net has three circles and another shape. This does not match the components of a cylinder's net.
Therefore, only net (a) correctly represents the net of a cylinder.
The correct option is (a).
Question 26. Which of the following letters of English alphabets have more than 2 lines of symmetry?

Answer:
We determine the number of lines of symmetry for each letter:
- Letter A: 1 line of symmetry.
- Letter O: Has 2 lines of symmetry (horizontal and vertical) if considered an oval. If considered a perfect circle, it has infinitely many lines of symmetry.
- Letter H: Has 2 lines of symmetry (horizontal and vertical).
- Letter X: Has 4 lines of symmetry (horizontal, vertical, and two diagonal lines).
We are looking for the letter(s) with more than 2 lines of symmetry.
- A has 1 (not > 2).
- O has 2 or infinitely many. Infinitely many is > 2.
- H has 2 (not > 2).
- X has 4 (which is > 2).
Both 'O' (if a circle) and 'X' have more than 2 lines of symmetry. However, based on the typical understanding of block letters and standard multiple-choice questions expecting a single answer, 'X' with its definitive 4 lines of symmetry is the intended correct answer.
The letter X has 4 lines of symmetry, which is more than 2.
The correct option is X.
Question 27. Take a square piece of paper as shown in figure (1). Fold it along its diagonals as shown in figure (2). Again fold it as shown in figure (3). Imagine that you have cut off 3 pieces of the form of congruent isosceles right-angled triangles out of it as shown in figure 4.

On opening the piece of paper which of the following shapes will you get?

Answer:
Solution:
Let's analyse the folding process:
Figure 1: A square piece of paper.
Figure 2: The square is folded along its two diagonals. This creates 4 congruent isosceles right-angled triangles stacked on top of each other, meeting at the center of the square (let's call it O). The vertices of the square (A, B, C, D) are now aligned at the center O.
Figure 3: The folded paper (stack of 4 triangles) is folded again. The diagram shows that one of the triangles from Figure 2 (say triangle OAB, where AB is a side of the original square and O is the center) is folded along its altitude from O to the side AB. Let M be the midpoint of AB. The paper is folded along OM. This results in triangle OMA and triangle OMB being stacked. The shape now represents the triangle OMA (or OMB). Triangle OMA is a right-angled triangle with the right angle at M (midpoint of the side). Angle AOM = $45^\circ$. The stack of paper at O (the center of the original square) now consists of 8 layers (from OMA, OMB, plus their reflections across the diagonals from the first fold).
Figure 4: Three congruent isosceles right-angled triangles are cut off from the folded paper as shown. The cuts originate from the vertex corresponding to the center of the original square (vertex O in triangle OMA).
Since the folded paper represents 8 identical sections of the original square (the regions like OMA), any cut made from the center vertex O will be replicated 8 times around the center when the paper is unfolded. This means the resulting pattern will have 8-fold rotational symmetry.
The cuts shown in Figure 4 remove triangular pieces from the corner O. These removed pieces correspond to specific regions near the center of the original square. When the paper is unfolded, the areas that were cut off will become holes or empty spaces in the paper.
Let's look at the options provided, which all exhibit 8-fold symmetry:
(a) Shows a pattern with square holes at the corners, not related to cuts from the center.
(b) Shows a central octagonal hole and 8 points projecting outwards. This implies material was removed between radial lines near the center, leaving material along certain radial lines.
(c) Shows a shape with 8 "petals" projecting inwards and material removed around and between them, forming gaps. This implies material was left along certain curved/straight lines forming the petals, and removed from the areas between them.
(d) Shows a different symmetric shape.
Observing the cuts in Figure 4, the three triangular pieces cut off from the vertex O remove material along lines emanating from the center. When these removed areas are unfolded 8 times, they create the gaps or holes in the final pattern. The remaining paper in Figure 4, when unfolded, forms the solid parts of the shape.
The cuts in Figure 4 match the areas that would be removed to create the spaces between the petals shown in option (c). The white area remaining in the folded paper (Figure 4) corresponds to the shape of the petals in option (c) when unfolded.
Therefore, on opening the piece of paper, the shape obtained will be the one shown in option (c).
The correct option is (c).
Question 28. Which of the following 3-dimensional figures has the top, side and front as triangles?
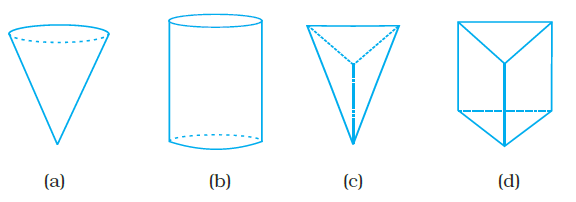
Answer:
Solution:
We need to identify the 3-dimensional figure whose Top, Side, and Front views are all triangles.
Let's consider the standard orthographic projections (views) for common 3D shapes:
- Cube or Cuboid: Top, Front, and Side views are rectangles (or squares).
- Cylinder: Top view is a circle, Front and Side views are rectangles.
- Cone: Top view is a circle (often with a dot at the center representing the apex), Front and Side views are triangles (when the base is horizontal).
- Square Pyramid: Top view is a square (with diagonals), Front and Side views are triangles (when the base is horizontal).
- Triangular Prism: Front and Back views are triangles, Top and Side views are rectangles.
- Triangular Pyramid (Tetrahedron): This shape has four triangular faces. Depending on the orientation, it is possible for the Top, Front, and Side views to all be triangles. For example, if a tetrahedron is placed such that one edge is horizontal and the opposite vertex is directly above that edge's midpoint, or if it is resting on a face and viewed from a specific angle, all three views can be triangles.
Based on the analysis of common 3D shapes and their projections, the figure that can have all three standard views (Top, Side, and Front) as triangles is a Triangular Pyramid (Tetrahedron).
Looking at the options provided in the image (which is not visible here, but assumed to represent standard geometric shapes), option (d) typically represents a Triangular Pyramid.
The other options usually represent shapes like a cube, triangular prism, or square pyramid, none of which have all three views as triangles.
Thus, the 3-dimensional figure that has the top, side and front as triangles is the Triangular Pyramid shown in option (d).
The correct option is (d).
Question 29 to 58 (Fill in the Blanks)
In Questions 29 to 58, fill in the blanks to make the statements true.
Question 29. In an isosceles right triangle, the number of lines of symmetry is ________.
Answer:
Solution:
An isosceles right triangle is a triangle with two equal sides and one right angle ($90^\circ$). The angles opposite the equal sides are also equal, and since the sum of angles in a triangle is $180^\circ$, these angles are $(180^\circ - 90^\circ)/2 = 45^\circ$ each.
A line of symmetry is a line that divides the figure into two congruent halves such that if the figure is folded along this line, the two halves coincide exactly.
For an isosceles right triangle, there is only one such line: the line segment from the vertex with the right angle to the midpoint of the hypotenuse. This line acts as the angle bisector of the right angle and is also the median and altitude to the hypotenuse, simultaneously dividing the triangle into two congruent smaller right triangles.
Therefore, the number of lines of symmetry in an isosceles right triangle is 1.
Question 30. Rhombus is a figure that has ______lines of symmetry and has a rotational symmetry of order _______.
Answer:
Solution:
A rhombus is a quadrilateral with all four sides of equal length. Key properties of a rhombus related to symmetry are:
- Its diagonals are perpendicular bisectors of each other.
- Its diagonals bisect the angles of the rhombus.
Lines of Symmetry: A line of symmetry is a line that divides the figure into two congruent halves that are mirror images of each other. For a rhombus, the lines of symmetry are its diagonals. Folding the rhombus along either diagonal will result in the two halves coinciding.
A rhombus has 2 lines of symmetry.
Rotational Symmetry: A figure has rotational symmetry if it looks the same after being rotated by a certain angle about its center. The order of rotational symmetry is the number of times the figure coincides with itself during a full rotation ($360^\circ$). For a rhombus, rotating it by $180^\circ$ about the intersection point of its diagonals makes it coincide with its original position (opposite vertices and sides swap places). Rotating it by $360^\circ$ also brings it back to its original position.
The angles of rotation for a rhombus to coincide with itself are $180^\circ$ and $360^\circ$. The number of times it coincides in a full rotation is 2.
A rhombus has a rotational symmetry of order 2.
Therefore, a rhombus is a figure that has 2 lines of symmetry and has a rotational symmetry of order 2.
Question 31. __________ triangle is a figure that has a line of symmetry but lacks rotational symmetry.
Answer:
Solution:
We need to identify a type of triangle that possesses at least one line of symmetry but has a rotational symmetry of order 1 (lacks rotational symmetry other than a $360^\circ$ rotation).
Let's consider the symmetry properties of different types of triangles:
- Scalene Triangle: No equal sides, no equal angles. It has 0 lines of symmetry and rotational symmetry of order 1. This does not fit the description as it lacks a line of symmetry.
- Isosceles Triangle (not equilateral): Two equal sides, two equal angles. It has exactly 1 line of symmetry (the line from the vertex between the equal sides to the midpoint of the opposite side). It has rotational symmetry of order 1. This fits the description.
- Equilateral Triangle: Three equal sides, three equal angles. It has 3 lines of symmetry. It has rotational symmetry of order 3 (rotations by $120^\circ$, $240^\circ$, $360^\circ$). This does not fit the description as it has rotational symmetry of order greater than 1.
Based on this analysis, an isosceles triangle (that is not equilateral) is the type of triangle that has a line of symmetry but lacks rotational symmetry (of order greater than 1).
The blank should be filled with the word "Isosceles".
Isosceles triangle is a figure that has a line of symmetry but lacks rotational symmetry.
Question 32. __________ is a figure that has neither a line of symmetry nor a rotational symmetry.
Answer:
Solution:
We are looking for a figure that has no lines of symmetry and no rotational symmetry of order greater than 1.
Let's consider different types of figures:
- Figures with high symmetry (like circles, squares, equilateral triangles) have both line and rotational symmetry.
- Figures with line symmetry but not rotational symmetry (like isosceles triangles or kites) do not fit.
- Figures with rotational symmetry but not line symmetry (like a parallelogram that is not a rhombus or rectangle) do not fit.
We need a figure with 0 lines of symmetry and rotational symmetry of order 1.
A Scalene Triangle is a triangle with all three sides of different lengths and all three angles of different measures. Due to the asymmetry, it has no line that divides it into mirror halves, and it does not coincide with itself under any rotation less than $360^\circ$.
Therefore, a Scalene Triangle is a figure that has neither a line of symmetry nor a rotational symmetry (of order greater than 1).
The blank should be filled with "Scalene Triangle".
Scalene Triangle is a figure that has neither a line of symmetry nor a rotational symmetry.
Question 33. __________ and __________ are the capital letters of English alphabets that have one line of symmetry but they interchange to each other when rotated through 180°.
Answer:
Solution:
We need to find two capital English letters that satisfy two conditions:
- Each letter has exactly one line of symmetry.
- When rotated by $180^\circ$, one letter transforms into the other, and vice-versa.
Let's consider capital letters that have exactly one line of symmetry:
- Letters with one vertical line of symmetry: A, M, T, U, V, W, Y
- Letters with one horizontal line of symmetry: B, C, D, E, K
(Note: Some letters like H, I, O, X have more than one line of symmetry, so they are excluded).
Now let's consider the effect of rotating these letters by $180^\circ$:
- A rotated $180^\circ$ is A. (Doesn't interchange with another letter)
- M rotated $180^\circ$ is W. M has a vertical line of symmetry. W has a vertical line of symmetry. This pair fits the description.
- T rotated $180^\circ$ is not T and not a letter from the list.
- U rotated $180^\circ$ is not U and not a letter from the list.
- V rotated $180^\circ$ is not V and not a letter from the list.
- W rotated $180^\circ$ is M. (Already found the pair M, W).
- Y rotated $180^\circ$ is not Y and not a letter from the list.
- B rotated $180^\circ$ is not B and not a letter from the list.
- C rotated $180^\circ$ is not C and not a letter from the list.
- D rotated $180^\circ$ is not D and not a letter from the list.
- E rotated $180^\circ$ is not E and not a letter from the list.
- K rotated $180^\circ$ is not K and not a letter from the list.
The pair of letters that satisfies both conditions is M and W.
M has one vertical line of symmetry. W has one vertical line of symmetry. Rotating M by $180^\circ$ gives W, and rotating W by $180^\circ$ gives M.
The blanks should be filled with "M" and "W".
M and W are the capital letters of English alphabets that have one line of symmetry but they interchange to each other when rotated through 180°.
Question 34. The common portion of two adjacent faces of a cuboid is called ________.
Answer:
Solution:
A cuboid is a three-dimensional solid figure bounded by six rectangular faces.
In any three-dimensional solid figure, the common portion where two faces meet is called an edge.
For example, in a cuboid like a rectangular box, two adjacent faces (like the top face and a side face) meet along a straight line segment. This line segment is an edge of the cuboid.
Therefore, the common portion of two adjacent faces of a cuboid is called an edge.
Question 35. A plane surface of a solid enclosed by edges is called __________ .
Answer:
Solution:
In the context of polyhedra (three-dimensional solids with flat faces, straight edges, and sharp corners or vertices), the boundaries are defined by these elements.
The flat surfaces of a polyhedron are called its faces.
These faces are polygons, and their boundaries are formed by the edges of the solid.
Therefore, a plane surface of a solid enclosed by edges is called a face.
Question 36. The corners of solid shapes are called its __________.
Answer:
Solution:
In geometry, a solid shape is a three-dimensional figure. The points where multiple edges meet are called the corners.
These corners are formally known as vertices (singular: vertex).
For example, in a cube or a cuboid, there are 8 corners where three edges meet. Each of these corners is a vertex.
Therefore, the corners of solid shapes are called its vertices.
Question 37. A solid with no vertex is __________.
Answer:
Solution:
Vertices are the points where edges meet. For a solid to have no vertices, it must not have any edges where distinct surfaces meet at a point.
Consider common solid shapes:
- Cube, Cuboid, Pyramids, Prisms: All have vertices.
- Cone: Has one vertex (the apex).
- Cylinder: Has no vertices (edges are circles, but they don't meet at a point). It has edges (the circular bases).
- Sphere: Has no flat faces, no straight edges, and no vertices. Its surface is completely curved.
A solid that has no vertex is one with a continuously curved surface that does not come to a point or form sharp corners where edges would typically meet.
The most common example of a solid with no vertex is a sphere.
Other solids with no vertices include tori (doughnut shapes) and ellipsoids.
Therefore, a solid with no vertex is a sphere.
Question 38. A triangular prism has __________ faces, __________ edges and __________ vertices.
Answer:
Solution:
A triangular prism is a polyhedron made of two triangular bases and three rectangular sides connecting the corresponding sides of the triangles.
Let's count the faces, edges, and vertices:
- Faces:
- There are two triangular faces (the top and bottom bases).
- There are three rectangular faces connecting the corresponding sides of the triangles.
- Total number of faces = $2$ (triangles) $+ 3$ (rectangles) $= 5$.
- Edges:
- Each triangular base has 3 edges. Since there are two bases, this gives $3 + 3 = 6$ edges.
- There are 3 edges connecting the vertices of the two triangular bases (these are the vertical edges when the prism is oriented with bases horizontal).
- Total number of edges = $6$ (base edges) $+ 3$ (connecting edges) $= 9$.
- Vertices:
- Each triangular base has 3 vertices. Since there are two bases, the total number of vertices is $3 + 3 = 6$.
We can verify this using Euler's formula for polyhedra, which states $V - E + F = 2$, where V is the number of vertices, E is the number of edges, and F is the number of faces.
$V = 6$, $E = 9$, $F = 5$.
$6 - 9 + 5 = -3 + 5 = 2$. The formula holds.
The blanks should be filled with 5, 9, and 6 respectively.
A triangular prism has 5 faces, 9 edges and 6 vertices.
Question 39. A triangular pyramid has __________ faces, __________ edges and __________vertices.
Answer:
Solution:
A triangular pyramid is a polyhedron with a triangular base and three triangular faces that meet at a single point (the apex). It is also known as a tetrahedron.
Let's count the faces, edges, and vertices:
- Faces:
- There is one triangular base.
- There are three triangular faces that rise from the edges of the base and meet at the apex.
- Total number of faces = $1$ (base) $+ 3$ (side faces) $= 4$.
- Edges:
- The triangular base has 3 edges.
- There are 3 edges connecting the vertices of the base to the apex.
- Total number of edges = $3$ (base edges) $+ 3$ (connecting edges) $= 6$.
- Vertices:
- The triangular base has 3 vertices.
- There is one vertex at the apex.
- Total number of vertices = $3$ (base vertices) $+ 1$ (apex) $= 4$.
We can verify this using Euler's formula for polyhedra, $V - E + F = 2$.
$V = 4$, $E = 6$, $F = 4$.
$4 - 6 + 4 = -2 + 4 = 2$. The formula holds.
The blanks should be filled with 4, 6, and 4 respectively.
A triangular pyramid has 4 faces, 6 edges and 4 vertices.
Question 40. A square pyramid has __________ faces, __________ edges and __________ vertices.
Answer:
Solution:
A square pyramid is a polyhedron with a square base and four triangular faces that meet at a single point (the apex).
Let's count the faces, edges, and vertices:
- Faces:
- There is one square base.
- There are four triangular faces that rise from the edges of the base and meet at the apex.
- Total number of faces = $1$ (base) $+ 4$ (side faces) $= 5$.
- Edges:
- The square base has 4 edges.
- There are 4 edges connecting the vertices of the base to the apex.
- Total number of edges = $4$ (base edges) $+ 4$ (connecting edges) $= 8$.
- Vertices:
- The square base has 4 vertices.
- There is one vertex at the apex.
- Total number of vertices = $4$ (base vertices) $+ 1$ (apex) $= 5$.
We can verify this using Euler's formula for polyhedra, $V - E + F = 2$.
$V = 5$, $E = 8$, $F = 5$.
$5 - 8 + 5 = -3 + 5 = 2$. The formula holds.
The blanks should be filled with 5, 8, and 5 respectively.
A square pyramid has 5 faces, 8 edges and 5 vertices.
Question 41. Out of __________ faces of a triangular prism, __________are rectangles and __________ are triangles.
Answer:
Solution:
From the analysis in Question 38, we know the number of faces of a triangular prism and the shapes of these faces.
A triangular prism has:
- Two triangular faces (the bases).
- Three rectangular faces (the sides).
- Total faces = $2 + 3 = 5$.
So, out of the total number of faces, some are rectangles and some are triangles.
Number of rectangular faces = 3.
Number of triangular faces = 2.
Total faces = $3 + 2 = 5$. This matches the total number of faces.
The blanks should be filled with 5, 3, and 2 respectively.
Out of 5 faces of a triangular prism, 3 are rectangles and 2 are triangles.
Question 42. The base of a triangular pyramid is a __________.
Answer:
Solution:
A pyramid is a polyhedron formed by connecting a polygonal base and a point, called the apex, where the side faces (which are triangles) meet. The name of the pyramid is determined by the shape of its base.
A triangular pyramid is specifically named because its base is a triangle.
Therefore, the base of a triangular pyramid is a triangle.
Question 43. Out of __________ faces of a square pyramid, __________ are triangles and __________ is/are squares.
Answer:
Solution:
From the analysis in Question 40, we know the number of faces of a square pyramid and the shapes of these faces.
A square pyramid has:
- One square face (the base).
- Four triangular faces (the sides).
- Total faces = $1 + 4 = 5$.
So, out of the total number of faces, some are triangles and some are squares.
Number of triangular faces = 4.
Number of square faces = 1.
Total faces = $4 + 1 = 5$. This matches the total number of faces.
The blanks should be filled with 5, 4, and 1 respectively.
Out of 5 faces of a square pyramid, 4 are triangles and 1 is/are squares.
Question 44. Out of __________ faces of a rectangular pyramid __________ are triangles and base is __________.
Answer:
Solution:
A rectangular pyramid is a pyramid with a rectangular base and four triangular faces that meet at an apex.
Let's count the faces and identify their shapes:
- Faces:
- There is one rectangular base.
- There are four triangular faces that rise from the edges of the base and meet at the apex.
- Total number of faces = $1$ (base) $+ 4$ (side faces) $= 5$.
- Triangular Faces: There are 4 triangular faces.
- Base Shape: The base is a rectangle.
The blanks should be filled with 5, 4, and "rectangle" respectively.
Out of 5 faces of a rectangular pyramid, 4 are triangles and base is rectangle.
Question 45. Each of the letters H, N, S and Z has a rotational symmetry of order __________.
Answer:
Solution:
We need to determine the order of rotational symmetry for the capital letters H, N, S, and Z.
The order of rotational symmetry is the number of times a figure coincides with itself during a rotation of $360^\circ$ about its center.
- H: Rotating H by $180^\circ$ about its center makes it look exactly the same. Rotating it by $360^\circ$ also brings it back. So, it coincides with itself at $180^\circ$ and $360^\circ$. The order of rotational symmetry is 2.
- N: Rotating N by $180^\circ$ about its center makes it look exactly the same. Rotating it by $360^\circ$ also brings it back. So, it coincides with itself at $180^\circ$ and $360^\circ$. The order of rotational symmetry is 2.
- S: Rotating S by $180^\circ$ about its center makes it look exactly the same. Rotating it by $360^\circ$ also brings it back. So, it coincides with itself at $180^\circ$ and $360^\circ$. The order of rotational symmetry is 2.
- Z: Rotating Z by $180^\circ$ about its center makes it look exactly the same. Rotating it by $360^\circ$ also brings it back. So, it coincides with itself at $180^\circ$ and $360^\circ$. The order of rotational symmetry is 2.
Each of these letters coincides with itself when rotated by $180^\circ$ and $360^\circ$ about its center. The number of times they coincide during a full rotation is 2.
Therefore, each of the letters H, N, S and Z has a rotational symmetry of order 2.
Question 46. Order of rotational symmetry of a rectangle is __________.
Answer:
Solution:
A rectangle is a quadrilateral with four right angles. Opposite sides are equal in length.
To find the order of rotational symmetry, we determine how many times the rectangle coincides with its original position during a $360^\circ$ rotation about its center (the intersection of the diagonals).
- Rotating a rectangle by $90^\circ$ does not typically make it coincide with its original position (unless it is a square).
- Rotating a rectangle by $180^\circ$ makes the top and bottom sides swap places, and the left and right sides swap places. The rectangle coincides with its original position.
- Rotating a rectangle by $270^\circ$ does not typically make it coincide with its original position.
- Rotating a rectangle by $360^\circ$ always brings it back to its original position.
The angles of rotation for a rectangle to coincide with itself are $180^\circ$ and $360^\circ$. The number of times it coincides in a full rotation is 2.
Therefore, the order of rotational symmetry of a rectangle is 2.
Question 47. Order of rotational symmetry of a circle is __________.
Answer:
Solution:
A circle is a set of points equidistant from a central point. Due to its perfect roundness, a circle looks identical after being rotated by any angle about its center.
Since it coincides with itself after rotation by any angle (infinitely many angles between $0^\circ$ and $360^\circ$), the number of times it coincides with itself during a full $360^\circ$ rotation is infinite.
Therefore, the order of rotational symmetry of a circle is infinite.
Question 48. Each face of a cuboid is a __________.
Answer:
Solution:
A cuboid is a three-dimensional shape bounded by six faces. By definition, these faces are flat surfaces that meet at right angles along edges.
Each face of a cuboid is a four-sided polygon with all interior angles equal to $90^\circ$. Opposite sides are equal in length.
This description matches the properties of a rectangle.
In the special case where all edges of the cuboid are equal in length, the cuboid is a cube, and each face is a square (which is a special type of rectangle).
Therefore, each face of a cuboid is a rectangle.
Question 49. Line of symmetry for an angle is its __________.
Answer:
Solution:
Consider an angle formed by two rays originating from a common endpoint (the vertex). A line of symmetry for this angle must divide the angle into two congruent parts such that folding along this line makes the two parts coincide.
The line that divides an angle into two equal angles is called the angle bisector.
If we fold the angle along its angle bisector, the two rays forming the angle will overlap, and the two parts of the angle will coincide.
Therefore, the line of symmetry for an angle is its angle bisector.
Question 50. A parallelogram has __________ line of symmetry.
Answer:
Solution:
A parallelogram is a quadrilateral with opposite sides parallel. Unlike special types of parallelograms like rectangles or rhombuses, a general parallelogram does not have perpendicular diagonals or equal adjacent sides.
Let's check for lines of symmetry:
- Folding a parallelogram along either of its diagonals does not generally result in the two halves coinciding.
- Folding a parallelogram along a line connecting the midpoints of opposite sides also does not generally result in the two halves coinciding.
The only case where a parallelogram has a line of symmetry is when it is a rhombus (diagonals are lines of symmetry) or a rectangle (lines joining midpoints of opposite sides are lines of symmetry). A square has both types of symmetry lines.
However, the question refers to "A parallelogram", implying a general parallelogram which is not necessarily a rhombus or a rectangle.
A general parallelogram has no lines of symmetry.
A parallelogram *does* have rotational symmetry of order 2 about the intersection of its diagonals, but the question asks about line symmetry.
Therefore, a parallelogram has no line of symmetry.
Question 51. Order of rotational symmetry of
 is _________.
is _________.
Answer:
Solution:
The image shows a figure that appears to be a stylized representation of three interconnected loops or sections, arranged symmetrically around a central point.
Let's analyze the rotational symmetry by considering rotations about the central point.
The figure has three identical parts arranged equally spaced around the center. Rotating the figure by $360^\circ / 3 = 120^\circ$ will make each part move to the position previously occupied by the next part in the sequence. This results in the figure coinciding with its original appearance.
The angles of rotation that make the figure coincide with itself are $120^\circ$, $240^\circ$, and $360^\circ$.
The number of times the figure coincides with itself during a full $360^\circ$ rotation is 3.
Therefore, the order of rotational symmetry of the given figure is 3.
Question 52. A __________ triangle has no lines of symmetry.
Answer:
Solution:
We are looking for a type of triangle that has no lines of symmetry.
From our analysis in Question 31, we know the symmetry properties of different triangles:
- Scalene Triangle: All sides and angles are different. It has 0 lines of symmetry.
- Isosceles Triangle (not equilateral): Two equal sides and angles. It has 1 line of symmetry.
- Equilateral Triangle: Three equal sides and angles. It has 3 lines of symmetry.
The triangle with no lines of symmetry is the Scalene Triangle.
The blank should be filled with "Scalene".
A Scalene triangle has no lines of symmetry.
Question 53. Cuboid is a rectangular_________ .
Answer:
Solution:
A cuboid is a three-dimensional geometric shape whose faces are all rectangles. It is a type of polyhedron.
The term often used to describe a cuboid in this context, emphasizing its rectangular nature, is "prism".
More specifically, a cuboid can be seen as a prism with a rectangular base.
Therefore, Cuboid is a rectangular prism.
Question 54. A sphere has __________vertex, __________edge and __________curved surface.
Answer:
Solution:
A sphere is a perfectly round geometrical object in three-dimensional space that is the surface of a completely round ball. It consists of all points located at a fixed distance from a given point (the center).
Let's consider the properties of a sphere:
- Vertex: A vertex is a corner where edges meet. A sphere has no corners or sharp points. It has 0 vertices.
- Edge: An edge is where two faces meet. A sphere has no flat faces, so there are no edges. It has 0 edges.
- Surface: The entire surface of a sphere is a single, continuously curved surface. It has 1 curved surface.
The blanks should be filled with 0, 0, and 1 respectively.
A sphere has 0 vertex, 0 edge and 1 curved surface.
Question 55.  is a net of a __________. Circumference of circle = ______.
is a net of a __________. Circumference of circle = ______.
Answer:
Solution:
The image shows a net consisting of a circle and a sector of a larger circle. This net can be folded to form a 3-dimensional shape.
When the sector is folded, the two straight edges are joined together, forming the curved surface of a solid shape. The circular part forms the base of this solid.
This net is the net of a cone.
The arc length of the sector is equal to the circumference of the circular base, and the radius of the sector is the slant height of the cone.
The second part of the question asks for the formula for the circumference of a circle.
The circumference of a circle is the distance around the circle. If $r$ is the radius of the circle, the circumference ($C$) is given by the formula:
$C = 2 \pi r$
... (i)
Alternatively, if $d$ is the diameter of the circle, the circumference is $C = \pi d$, since $d = 2r$.
The blanks should be filled with "cone" and "$2\pi r$ (or $\pi d$)" respectively.
 is a net of a cone. Circumference of circle = $2\pi r$.
is a net of a cone. Circumference of circle = $2\pi r$.
Question 56.  is a net of a __________.
is a net of a __________.
Answer:
Solution:
The image shows a net consisting of two circles and a rectangle. This net can be folded to form a 3-dimensional shape.
When the rectangle is curved and its opposite edges are joined, it forms the curved surface of a solid. The two circles form the top and bottom bases of this solid.
This arrangement of a rectangle forming the side and two circles forming the bases is characteristic of a cylinder.
The length of the rectangle is equal to the circumference of the circles, and the width of the rectangle is the height of the cylinder.
Therefore, the given figure is a net of a cylinder.
Question 57. Order of rotational symmetry of  is __________.
is __________.
Answer:
Solution:
The image shows a figure that appears to be a regular pentagram or a star polygon with 5 points. The central region looks like a pentagon.
This figure is constructed symmetrically around its center. It has 5 identical "points" or elements distributed equally around the center.
To find the order of rotational symmetry, we determine how many times the figure coincides with its original position during a $360^\circ$ rotation about its center.
Rotating the figure by $360^\circ / 5 = 72^\circ$ will make each point move to the position previously occupied by the next point in sequence. This results in the figure coinciding with its original appearance.
The angles of rotation that make the figure coincide with itself are $72^\circ$, $144^\circ$, $216^\circ$, $288^\circ$, and $360^\circ$.
The number of times the figure coincides with itself during a full rotation is 5.
Therefore, the order of rotational symmetry of the given figure is 5.
Question 58. Identical cubes are stacked in the corner of a room as shown below. The number of cubes that are not visible are _________.

Answer:
Solution:
The cubes are stacked in the corner of a room, meaning they form layers against two walls and the floor.
Analyzing the stack layer by layer from bottom to top:
- Bottom Layer: The base supports a $3 \times 3$ area. Total cubes in this layer = 9. We can see 3 in the front, 2 behind, and 1 in the back corner = 6 visible cubes. The number of hidden cubes = $9 - 6 = 3$.
- Middle Layer: This layer forms a $2 \times 2$ area. Total cubes in this layer = 4. We can see 2 in the front and 1 in the back corner = 3 visible cubes. The number of hidden cubes = $4 - 3 = 1$.
- Top Layer: This layer is a single $1 \times 1$ cube. Total cubes in this layer = 1. This cube is visible. The number of hidden cubes = $1 - 1 = 0$.
The total number of cubes that are not visible is the sum of the hidden cubes in each layer.
Total hidden cubes = 3 (Bottom) + 1 (Middle) + 0 (Top) = 4.
The number of cubes that are not visible are 4.
Question 59 to 92 (True or False)
In Questions from 59 to 92, state whether the statements are True or False.
Question 59. We can draw exactly one triangle whose angles are 70°, 30° and 80°.
Answer:
False
While a triangle with angles $70^\circ, 30^\circ, 80^\circ$ (summing to $180^\circ$) can be drawn, its size is not fixed by the angles alone.
Infinitely many triangles with these angles can be drawn, all of which will be similar to each other but will have different side lengths and areas.
Question 60. The distance between the two parallel lines is the same everywhere.
Answer:
True
This statement is true by the definition of parallel lines in Euclidean geometry.
Parallel lines are two straight lines that lie in the same plane and do not intersect, no matter how far they are extended.
The distance between two lines is defined as the shortest distance between any point on one line and the other line. This shortest distance is always the length of the perpendicular segment connecting the two lines.
If the distance between two lines were not the same everywhere, the lines would either get closer together or farther apart as they extend. If they got closer, they would eventually intersect, contradicting the definition of parallel lines. If they got farther apart, they wouldn't satisfy the condition of being "equidistant" from each other.
Therefore, for lines to be parallel, the perpendicular distance between them must be constant throughout their length.
Question 61. A circle has two lines of symmetry.
Answer:
False
A circle has infinitely many lines of symmetry.
Any line that passes through the center of the circle is a line of symmetry for the circle.
Question 62. An angle has two lines of symmetry.
Answer:
False
An angle typically has only one line of symmetry.
This line of symmetry is the ray that bisects the angle, dividing it into two equal angles.
Question 63. A regular hexagon has six lines of symmetry.
Answer:
True
A regular hexagon has indeed six lines of symmetry. These lines are:
1. The three lines connecting opposite vertices.
2. The three lines connecting the midpoints of opposite sides.
Question 64. An isosceles trapezium has one line of symmetry.
Answer:
True
An isosceles trapezium (or isosceles trapezoid) is a quadrilateral with one pair of parallel sides and the non-parallel sides being equal in length.
It has exactly one line of symmetry, which is the line segment connecting the midpoints of the parallel sides.
Question 65. A parallelogram has two lines of symmetry.
Answer:
False
A general parallelogram has no line of symmetry.
Special cases of parallelograms do have lines of symmetry:
A rhombus has two lines of symmetry (its diagonals).
A rectangle has two lines of symmetry (the lines joining the midpoints of opposite sides).
A square has four lines of symmetry (its diagonals and the lines joining the midpoints of opposite sides).
Since the statement refers to "a parallelogram" generally, and a general parallelogram doesn't have two lines of symmetry, the statement is false.
Question 66. Order of rotational symmetry of a rhombus is four.
Answer:
False
The order of rotational symmetry of a general rhombus is two.
A figure has rotational symmetry of order $n$ if it can be rotated by $360^\circ/n$ about its center and coincide with its original position.
A rhombus coincides with itself after a rotation of $180^\circ$ and $360^\circ$ (or $0^\circ$). Thus, the order of rotational symmetry is $360^\circ / 180^\circ = 2$.
A square, which is a special type of rhombus, has an order of rotational symmetry of four, but the statement refers to "a rhombus" generally.
Question 67. An equilateral triangle has six lines of symmetry.
Answer:
False
An equilateral triangle has exactly three lines of symmetry.
These lines of symmetry are the angle bisectors from each vertex, which are also the medians and the altitudes, and these lines also pass through the midpoint of the opposite sides.
A regular polygon with $n$ sides has $n$ lines of symmetry. An equilateral triangle is a regular polygon with $n=3$ sides, so it has 3 lines of symmetry.
Question 68. Order of rotational symmetry of a semi circle is two.
Answer:
False
The order of rotational symmetry of a semi circle is one.
Rotational symmetry is the property a shape has when it looks the same after rotation by some amount less than a full turn ($360^\circ$). The order is the number of times it looks the same during a $360^\circ$ rotation.
A semicircle consists of a straight diameter and a curved arc. If you rotate a semicircle about the midpoint of its diameter by $180^\circ$, the straight edge moves to where the curved edge was, and vice versa. The figure does not look the same as the original.
It only looks the same after a $360^\circ$ rotation (or $0^\circ$). Therefore, the order of rotational symmetry is 1.
Question 69. In oblique sketch of the solid, the measurements are kept propor_x0002_tional.
Answer:
False
In an oblique sketch, the face parallel to the plane of projection is usually drawn to scale, keeping its measurements proportional to the original object.
However, the receding edges are drawn at an angle (commonly $30^\circ$, $45^\circ$, or $60^\circ$) to the horizontal, and their lengths are often drawn either at full scale (Cavalier projection) or half scale (Cabinet projection).
Because the lengths along the receding axis are not always represented at the true scale relative to the frontal face, the overall measurements in the sketch are not kept proportional to the actual solid's dimensions everywhere.
This is a key difference between oblique sketches and isometric sketches, where all three principal axes are drawn at angles, but lengths along all three axes are typically drawn to scale, maintaining proportionality.
Question 70. An isometric sketch does not have proportional length.
Answer:
False
An isometric sketch is a drawing technique where the object is viewed from an angle such that the three principal axes appear equally foreshortened.
Crucially, lines that are parallel to these three principal axes (representing the object's length, width, and height) are drawn to scale, meaning their lengths in the sketch are proportional to their actual lengths on the object.
While angles are distorted in an isometric sketch, the measurements along the isometric axes are kept proportional to the original dimensions of the solid.
Therefore, the statement that an isometric sketch does not have proportional length is false.
Question 71. A cylinder has no vertex.
Answer:
True
A vertex is typically defined as a point where edges meet, or a corner point of a solid figure.
A cylinder has two circular bases and a curved lateral surface. It has two circular edges where the bases meet the curved surface.
However, it does not have any distinct points or corners where multiple edges converge or where the surface comes to a point. Therefore, a cylinder has no vertices.
Question 72. All the faces, except the base of a square pyramid are triangular.
Answer:
True
A square pyramid is a polyhedron with a square base and four triangular faces that meet at a point called the apex.
The base of the pyramid is a square.
The faces that rise from the sides of the square base and meet at the apex are indeed all triangles.
Therefore, all the faces, except the square base, are triangular.
Question 73. A pyramid has only one vertex.
Answer:
False
A pyramid has one vertex at the apex (where all the triangular faces meet), but it also has vertices on its base.
The number of vertices on the base depends on the shape of the base polygon. For example:
A triangular pyramid (tetrahedron) has a triangular base with 3 vertices, plus the apex, totaling $3 + 1 = 4$ vertices.
A square pyramid has a square base with 4 vertices, plus the apex, totaling $4 + 1 = 5$ vertices.
In general, a pyramid with an $n$-sided base has $n+1$ vertices.
Since a pyramid has more than one vertex (unless the base were a point, which isn't a typical pyramid), the statement is false.
Question 74. A triangular prism has 5 faces, 9 edges and 6 vertices.
Answer:
True
A triangular prism is a polyhedron with two parallel triangular bases and three rectangular faces connecting corresponding sides of the bases.
Let's count its faces, edges, and vertices:
Faces: It has 2 triangular faces (the bases) + 3 rectangular faces (the sides) = 5 faces.
Vertices: Each triangular base has 3 vertices. Since there are two bases, the total number of vertices is $3 \times 2 = 6$ vertices.
Edges: Each triangular base has 3 edges. There are 3 edges connecting the corresponding vertices of the two bases. So, total edges = $3 + 3 + 3 = 9$ edges.
The statement correctly lists the number of faces, edges, and vertices for a triangular prism as 5, 9, and 6, respectively.
We can also verify this using Euler's formula for polyhedra, $V - E + F = 2$. For a triangular prism: $6 - 9 + 5 = 2$, which is correct.
Question 75. If the base of a pyramid is a square, it is called a square pyramid.
Answer:
True
A pyramid is a polyhedron formed by connecting a polygonal base and a point (the apex) with triangular faces.
Pyramids are typically named according to the shape of their base.
If the base polygon is a triangle, it's a triangular pyramid. If the base is a pentagon, it's a pentagonal pyramid.
Therefore, if the base of a pyramid is a square, it is correctly called a square pyramid.
Question 76. A rectangular pyramid has 5 rectangular faces.
Answer:
False
Solution:
A rectangular pyramid has a base that is a rectangle.
It has four lateral faces that are triangles, as they connect the sides of the rectangular base to the apex (the single vertex at the top).
Thus, a rectangular pyramid has:
- 1 rectangular base
- 4 triangular lateral faces
The total number of faces is $1 + 4 = 5$. However, only one of these faces (the base) is rectangular. The other four faces are triangular.
Therefore, the statement that a rectangular pyramid has 5 rectangular faces is false.
Question 77. Rectangular prism and cuboid refer to the same solid.
Answer:
True.
A rectangular prism is a three-dimensional solid shape which has six faces, twelve edges, and eight vertices. All the faces of a rectangular prism are rectangles.
A cuboid is defined as a polyhedron having six faces that are quadrilaterals. In a right cuboid (which is what is typically meant unless specified otherwise), all six faces are rectangles, and adjacent faces meet at right angles.
The description of a rectangular prism perfectly matches the description of a cuboid where all faces are rectangles. Thus, the terms are interchangeable and refer to the same solid shape.
Question 78. A tetrahedron has 3 triangular faces and 1 rectangular face.
Answer:
False
A tetrahedron is a pyramid with a triangular base.
It has a triangular base and three triangular lateral faces connecting the sides of the base to the apex.
Therefore, a tetrahedron has a total of $1 + 3 = 4$ faces.
All four of these faces are triangular.
The statement claims it has 3 triangular faces and 1 rectangular face, which is incorrect.
Question 79. While rectangle is a 2-D figure, cuboid is a 3-D figure.
Answer:
True
A rectangle is a polygon (a closed shape made of straight line segments) that lies in a plane. It has length and width but no thickness, making it a two-dimensional (2-D) figure.
A cuboid is a solid (a three-dimensional object) that has volume. It has length, width, and height, making it a three-dimensional (3-D) figure.
The statement accurately distinguishes between the dimensionality of a rectangle and a cuboid.
Question 80. While sphere is a 2-D figure, circle is a 3-D figure.
Answer:
False
The statement incorrectly assigns the dimensions to both figures.
A sphere is a set of points in three-dimensional space that are equidistant from a central point. It has volume and is therefore a three-dimensional (3-D) figure.
A circle is a set of points in a two-dimensional plane that are equidistant from a central point. It has area but no thickness and is therefore a two-dimensional (2-D) figure.
The correct statement would be: While a circle is a 2-D figure, a sphere is a 3-D figure.
Question 81. Two dimensional figures are also called plane figures.
Answer:
True
Two-dimensional (2-D) figures are shapes that have dimensions only in length and width, lying entirely on a flat surface or plane.
These figures, such as squares, circles, triangles, and rectangles, are commonly referred to as plane figures because they reside within a two-dimensional plane.
The terms are often used interchangeably.
Question 82. A cone is a polyhedron.
Answer:
False
A polyhedron is a three-dimensional solid whose faces are flat polygons.
A cone has a circular base and a curved lateral surface that tapers to an apex.
Since a cone has a curved surface, and its base is a circle (which is not a polygon with straight edges in the standard definition), it does not meet the requirements of being a polyhedron.
Polyhedra include solids like cubes, prisms, and pyramids, which are made up entirely of flat polygonal faces.
Question 83. A prism has four bases.
Answer:
False
A prism is a three-dimensional solid that has two identical and parallel polygonal faces, which are called its bases.
The other faces of a prism are parallelograms (or rectangles, in the case of a right prism) that connect the corresponding sides of the two bases.
Regardless of the shape of the base polygon (triangle, square, pentagon, etc.), a prism always has exactly two bases.
Therefore, the statement that a prism has four bases is incorrect.
Question 84. The number of lines of symmetry of a regular polygon is equal to the vertices of the polygon.
Answer:
True
A regular polygon is a polygon that is both equilateral (all sides are equal) and equiangular (all angles are equal).
For a regular polygon with $n$ vertices (and $n$ sides):
If $n$ is odd, the lines of symmetry are the lines drawn from each vertex to the midpoint of the opposite side. There are $n$ such lines.
If $n$ is even, the lines of symmetry are the lines drawn from each vertex to the opposite vertex (diagonals) and the lines drawn from the midpoint of each side to the midpoint of the opposite side. There are $n/2$ of each type, totaling $n/2 + n/2 = n$ lines.
In both cases (for odd or even $n$), the number of lines of symmetry of a regular polygon is equal to its number of vertices (which is also equal to its number of sides).
Question 85. The order of rotational symmetry of a figure is 4 and the angle of rotation is 180° only.
Answer:
False
The order of rotational symmetry is the number of times a figure coincides with itself during a full $360^\circ$ rotation.
If the order of rotational symmetry is 4, it means the figure coincides with itself at 4 different angles within a $360^\circ$ rotation.
The angles of rotation for an order of symmetry $n$ are given by $\frac{360^\circ}{n} \times k$, where $k$ is an integer from 1 to $n$.
For an order of rotational symmetry of 4, the angles of rotation are:
$k=1: \frac{360^\circ}{4} \times 1 = 90^\circ$
$k=2: \frac{360^\circ}{4} \times 2 = 180^\circ$
$k=3: \frac{360^\circ}{4} \times 3 = 270^\circ$
$k=4: \frac{360^\circ}{4} \times 4 = 360^\circ$ (which is the same as the starting position)
So, if the order of rotational symmetry is 4, the figure must coincide with itself at $90^\circ, 180^\circ,$ and $270^\circ$ (in addition to $360^\circ/0^\circ$).
The statement incorrectly claims that the angle of rotation is $180^\circ$ only. While $180^\circ$ is one of the angles, it's not the only one when the order is 4.
Question 86. After rotating a figure by 120° about its centre, the figure coincides with its original position. This will happen again if the figure is rotated at an angle of 240°.
Answer:
True
If a figure coincides with its original position after a rotation of $120^\circ$, then $120^\circ$ is an angle of rotational symmetry for the figure.
Any multiple of an angle of rotational symmetry is also an angle of rotational symmetry, provided the total rotation is within $360^\circ$.
The given angle $240^\circ$ is a multiple of $120^\circ$, specifically $240^\circ = 2 \times 120^\circ$.
This means rotating the figure by $240^\circ$ is equivalent to performing the $120^\circ$ rotation twice consecutively.
Since the figure coincides with its original position after one $120^\circ$ rotation, it will also coincide after two such rotations (a total of $240^\circ$).
The order of rotational symmetry for this figure is $360^\circ / 120^\circ = 3$. The angles of rotation are $1 \times 120^\circ = 120^\circ$, $2 \times 120^\circ = 240^\circ$, and $3 \times 120^\circ = 360^\circ$ (or $0^\circ$).
Thus, the statement is correct.
Question 87. Mirror reflection leads to symmetry always.
Answer:
False
Mirror reflection itself is a transformation (a flip across a line or plane).
Symmetry, specifically reflectional symmetry (or line/mirror symmetry), exists when a figure maps onto itself after a mirror reflection across a specific line (the line of symmetry).
If you reflect a figure across a line and the resulting image is identical to the original figure, then the figure has reflectional symmetry with respect to that line.
However, if you reflect an arbitrary figure across a line, the reflected image may or may not be identical to the original figure. If it is not identical, the original figure does not have reflectional symmetry with respect to that line.
Therefore, while mirror reflection is the operation used to define reflectional symmetry, performing a mirror reflection does not automatically mean the original figure possesses that type of symmetry. It only leads to symmetry if the figure is invariant under that reflection.
Question 88. Rotation turns an object about a fixed point which is known as centre of rotation.
Answer:
True
Rotation is a type of transformation where every point of an object is turned about a fixed point.
This fixed point around which the object is rotated is precisely called the centre of rotation.
The transformation is defined by the angle of rotation and the centre of rotation.
The statement correctly describes the basic mechanism of rotation.
Question 89. Isometric sheet divides the paper into small isosceles triangles made up of dots or lines.
Answer:
True.
An isometric sheet is typically printed with a grid of dots or lines that form small equilateral triangles. An equilateral triangle is a triangle in which all three sides are equal in length. Since all three sides are equal, it follows that any two sides are equal. By definition, an isosceles triangle is a triangle that has at least two sides of equal length.
Therefore, every equilateral triangle is also an isosceles triangle. The small triangles formed by the grid on an isometric sheet are equilateral, and thus they are also isosceles triangles.
Question 90. The circle, the square, the rectangle and the triangle are examples of plane figures.
Answer:
True.
A plane figure (or two-dimensional figure) is a figure that lies entirely in a single plane. These figures have only two dimensions: length and width.
The circle, the square, the rectangle, and the triangle are all shapes that can be drawn on a flat surface (a plane) and have only length and width (or equivalent dimensions like radius for a circle, side lengths, etc.). They do not have thickness or depth.
Therefore, they are indeed examples of plane figures.
Question 91. The solid shapes are of two-dimensional.
Answer:
False.
Solid shapes (or three-dimensional shapes) are figures that occupy space. They have three dimensions: length, width, and height (or depth).
Examples of solid shapes include cubes, cuboids, spheres, cylinders, cones, pyramids, etc.
Two-dimensional shapes, on the other hand, lie in a plane and have only length and width, such as squares, circles, and triangles.
Therefore, solid shapes are three-dimensional, not two-dimensional.
Question 92. Triangle with length of sides as 5 cm, 6 cm and 11 cm can be con_x0002_structed.
Answer:
False.
To determine if a triangle can be constructed with given side lengths, we use the Triangle Inequality Theorem.
The theorem states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.
Let the given side lengths be $a=5$ cm, $b=6$ cm, and $c=11$ cm.
We check if the theorem holds for these lengths:
$a + b > c \implies 5 + 6 > 11 \implies 11 > 11$
This inequality is false.
Since the sum of two sides ($5+6=11$) is not greater than the third side ($11$), a triangle with these side lengths cannot be formed.
Question 93 to 124
Question 93. Draw the top, side and front views of the solids given below in Figures 12.21 and 12.22:

Answer:
To Find:
Draw the top, side (Right Side), and front views of the given solids in Figure 12.21 and Figure 12.22.
Solution:
The views represent the orthogonal projection of the solid onto a plane from a specific direction. Each square in the table represents a unit square face visible from that view.
Figure 12.21 Views:
Front View:
| # | ||
| # | # | # |
| # | # | # |
This view shows the silhouette and visible edges when looking directly at the front of the solid. The vertical columns have heights of 2, 3, and 2 units from left to right.
Right Side View:
| # | |
| # | |
| # | # |
This view shows the silhouette and visible edges when looking directly at the right side of the solid. The columns in the view represent the depth of the solid. The part closer to the viewer (left column in the view) has a maximum height of 3 units, and the part further away (right column in the view) has a maximum height of 1 unit.
Top View:
| # | # | # |
| # | # | # |
This view shows the silhouette and visible edges when looking directly down on the solid. The solid occupies a 3 units wide by 2 units deep rectangular area on the base plane.
Figure 12.22 Views:
Front View:
| # | # | # |
| # | # | # |
This view shows the silhouette and visible edges when looking directly at the front of the solid. The vertical columns have heights of 2, 2, and 2 units from left to right, forming a 3x2 rectangle.
Right Side View:
| # | # | # |
| # | # | # |
This view shows the silhouette and visible edges when looking directly at the right side of the solid. The columns in the view represent the depth of the solid. The maximum height is 2 units across the depth, forming a 3x2 rectangle.
Top View:
| # | ||
| # | # | # |
| # |
This view shows the silhouette and visible edges when looking directly down on the solid. The top layer forms a cross shape within the 3x3 base area.
Question 94. Draw a solid using the top. side and front views as shown below. [Use Isometric dot paper].
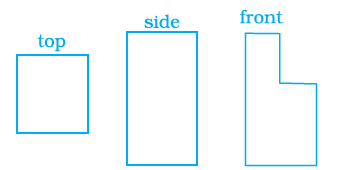
Answer:
Given:
The front, right side, and top views of a solid.
To Draw:
Draw the solid on isometric dot paper based on the given views.
Solution:
The solid is made up of unit cubes. The views provide information about the maximum height of the stack of cubes at different positions on the base and the overall shape of the solid from different directions.
Let's interpret the views:
The solid occupies a base area of $2 \times 2$ units, as suggested by the dimensions of the views. Let's denote the positions on the base grid as (width, depth), where width increases to the right in the front view, and depth increases towards the back in the side view.
The Front View is a $2 \times 2$ grid. This tells us the maximum height in the two columns (corresponding to width 1 and width 2) is 2 units.
The Right Side View is a $2 \times 2$ grid. This tells us the maximum height in the two rows (corresponding to depth 1 and depth 2 from the right side) is 2 units.
The Top View is a $2 \times 2$ grid that shows the shape of the solid when viewed from above. A shaded square indicates that there is at least one cube stacked at that position on the base. An empty square indicates there are no cubes stacked at that position.
- The top-left square in the Top View is shaded, meaning there is a stack of cubes at base position (width 1, depth 1).
- The top-right square in the Top View is shaded, meaning there is a stack of cubes at base position (width 2, depth 1).
- The bottom-left square in the Top View is empty, meaning there are no cubes stacked at base position (width 1, depth 2).
- The bottom-right square in the Top View is shaded, meaning there is a stack of cubes at base position (width 2, depth 2).
Let $h(w, d)$ be the height of the stack of cubes at base position (w, d), where $w \in \{1, 2\}$ and $d \in \{1, 2\}$.
- From the Top View: $h(1, 1) \ge 1$, $h(2, 1) \ge 1$, $h(1, 2) = 0$, $h(2, 2) \ge 1$.
- From the Front View (maximum height in width columns): $\max(h(1, 1), h(1, 2)) = 2$ and $\max(h(2, 1), h(2, 2)) = 2$.
- From the Side View (maximum height in depth rows, assuming looking from width 2 towards width 1): $\max(h(1, 1), h(2, 1)) = 2$ and $\max(h(1, 2), h(2, 2)) = 2$.
Using $h(1, 2) = 0$ and the view constraints:
- $\max(h(1, 1), 0) = 2 \implies h(1, 1) = 2$.
- $\max(0, h(2, 2)) = 2 \implies h(2, 2) = 2$.
- $\max(h(2, 1), h(2, 2)) = \max(h(2, 1), 2) = 2 \implies h(2, 1) \le 2$.
- $\max(h(1, 1), h(2, 1)) = \max(2, h(2, 1)) = 2 \implies h(2, 1) \le 2$.
- From the Top View, $h(2, 1) \ge 1$.
So, $h(1, 1) = 2$, $h(1, 2) = 0$, $h(2, 2) = 2$, and $1 \le h(2, 1) \le 2$. The simplest solid satisfying these views (often the intended answer in such problems) is one where heights are minimized while meeting the constraints and top view presence. This occurs when $h(2, 1) = 1$.
The solid is constructed by stacking unit cubes at the base grid positions with the following heights:
- Position (width 1, depth 1 - Front-Left): 2 cubes high.
- Position (width 2, depth 1 - Front-Right): 1 cube high.
- Position (width 1, depth 2 - Back-Left): 0 cubes high (empty).
- Position (width 2, depth 2 - Back-Right): 2 cubes high.
To draw this on isometric dot paper:
1. Choose a starting dot for the front-left corner of the base of the stack at (1,1).
2. From this dot, draw lines along the isometric grid to represent the base outline of the occupied positions from the top view: a $1 \times 1$ square for (1,1), a $1 \times 1$ square for (2,1) to its right, and a $1 \times 1$ square for (2,2) behind (2,1).
3. Stack the cubes vertically at each base position according to the determined heights:
- At (1,1), draw a stack of 2 cubes.
- At (2,1), draw a stack of 1 cube.
- At (1,2), draw no cubes (this position on the base should be empty).
- At (2,2), draw a stack of 2 cubes.
4. Connect the vertices to complete the visible edges of the solid.
The resulting solid will appear as two stacks of 2 cubes (front-left and back-right) with a single cube stack (front-right) in between them in the front row, and the back-left base position empty.
Question 95. Construct a right-angled triangle whose hypotenuse measures 5 cm and one of the other sides measures 3.2 cm.
Answer:
Given:
Length of hypotenuse = 5 cm.
Length of one side = 3.2 cm.
The triangle is right-angled.
To Construct:
A right-angled triangle with the given measurements.
Steps of Construction:
1. Draw a line segment BC of length 3.2 cm.
2. At point B, construct a ray BX perpendicular to BC. This will form the right angle ($\angle CBX = 90^\circ$). Use a compass and ruler to construct the perpendicular by drawing arcs, or use a protractor to mark $90^\circ$ and draw the ray.
3. With C as the center and radius 5 cm (the length of the hypotenuse), draw an arc intersecting the ray BX. Mark the point of intersection as A.
4. Join A to C.
5. $\triangle ABC$ is the required right-angled triangle, where $\angle B = 90^\circ$, $BC = 3.2$ cm, and $AC = 5$ cm.
(Note: The actual figure constructed on paper would show the triangle.)
Question 96. Construct a right-angled isosceles triangle with one side (other than hypotenuse) of length 4.5 cm.
Answer:
Given:
A right-angled isosceles triangle.
Length of one leg (side other than hypotenuse) = 4.5 cm.
To Construct:
A right-angled isosceles triangle with a leg of length 4.5 cm.
Steps of Construction:
In a right-angled isosceles triangle, the two equal sides are the legs (the sides forming the right angle). Therefore, both legs have a length of 4.5 cm.
1. Draw a line segment AB of length 4.5 cm.
2. At point B, construct a ray BX perpendicular to AB. This creates a right angle ($\angle ABX = 90^\circ$). Use a compass and ruler or a protractor for this construction.
3. With B as the center and radius 4.5 cm (since it's an isosceles triangle, the other leg is also 4.5 cm), draw an arc that intersects the ray BX. Mark the point of intersection as C.
4. Join point A to point C.
5. $\triangle ABC$ is the required right-angled isosceles triangle, where $\angle B = 90^\circ$ and $AB = BC = 4.5$ cm.
(Note: The constructed figure on paper would show the triangle $\triangle ABC$).
Question 97. Draw two parallel lines at a distance of 2.2 cm apart.
Answer:
To Construct:
Two parallel lines separated by a distance of 2.2 cm.
Steps of Construction:
1. Draw a line, let's call it line $l$.
2. Take any point P on the line $l$.
3. Construct a ray PX perpendicular to line $l$ at point P. Use a compass and ruler or a protractor to draw the perpendicular, ensuring it forms a $90^\circ$ angle with line $l$.
4. Along the ray PX, measure a distance of 2.2 cm from point P and mark the point Q.
5. At point Q, construct a line $m$ perpendicular to the ray PX. Again, use construction methods or a protractor to ensure the angle is $90^\circ$.
6. The line $m$ is parallel to line $l$, and the distance between them is 2.2 cm.
(Note: A diagram showing line $l$, point P, perpendicular PX, point Q at 2.2 cm from P, and line $m$ perpendicular to PX at Q would illustrate these steps.)
Question 98. Draw an isosceles triangle with each of equal sides of length 3 cm and the angle between them as 45°.
Answer:
Given:
Length of two equal sides = 3 cm each.
Angle between the equal sides = $45^\circ$.
To Construct:
An isosceles triangle with the given measurements.
Steps of Construction:
1. Draw a line segment AB of length 3 cm.
2. At point A, construct an angle of $45^\circ$. This can be done by constructing a $90^\circ$ angle and then bisecting it, or by using a protractor.
3. Draw a ray AX such that $\angle BAX = 45^\circ$.
4. With A as the center and radius 3 cm, draw an arc that intersects the ray AX. Mark the point of intersection as C.
5. Join point B to point C.
6. $\triangle ABC$ is the required isosceles triangle, where $AB = AC = 3$ cm and $\angle BAC = 45^\circ$.
(Note: The constructed figure on paper would show the triangle $\triangle ABC$).
Question 99. Draw a triangle whose sides are of lengths 4 cm, 5 cm and 7 cm.
Answer:
Given:
Lengths of the sides of the triangle are 4 cm, 5 cm, and 7 cm.
To Construct:
A triangle with the given side lengths.
Steps of Construction:
1. Draw a line segment BC of length 7 cm.
2. With B as the center and radius 4 cm, draw an arc.
3. With C as the center and radius 5 cm, draw another arc intersecting the previously drawn arc. Mark the point of intersection as A.
4. Join A to B and A to C.
5. $\triangle ABC$ is the required triangle with side lengths $AB = 4$ cm, $BC = 7$ cm, and $AC = 5$ cm.
(Note: The actual figure constructed on paper would show the triangle.)
Question 100. Construct an obtuse angled triangle which has a base of 5.5 cm and base angles of 30° and 120°.
Answer:
Given:
Base length = 5.5 cm.
Base angles = $30^\circ$ and $120^\circ$.
To Construct:
An obtuse-angled triangle with the given base and base angles.
Steps of Construction:
1. Draw a line segment BC of length 5.5 cm.
2. At point B, construct an angle of $30^\circ$. Draw a ray BX such that $\angle CBX = 30^\circ$. You can construct $60^\circ$ and then bisect it to get $30^\circ$, or use a protractor.
3. At point C, construct an angle of $120^\circ$. Draw a ray CY such that $\angle BCY = 120^\circ$. Use a protractor for this construction.
4. The rays BX and CY will intersect at a point. Mark this point as A.
5. $\triangle ABC$ is the required triangle. The angle $\angle ACB$ is $120^\circ$, which is greater than $90^\circ$, so it is an obtuse-angled triangle.
(Note: The constructed figure on paper would show the triangle $\triangle ABC$).
Question 101. Construct an equilateral triangle ABC of side 6 cm.
Answer:
Given:
An equilateral triangle ABC.
Side length = 6 cm.
To Construct:
An equilateral triangle with side length 6 cm.
Steps of Construction:
1. Draw a line segment AB of length 6 cm.
2. With A as the center and radius 6 cm, draw an arc.
3. With B as the center and radius 6 cm, draw another arc intersecting the previously drawn arc. Mark the point of intersection as C.
4. Join A to C and B to C.
5. $\triangle ABC$ is the required equilateral triangle with side lengths $AB = BC = AC = 6$ cm.
(Note: The constructed figure on paper would show the equilateral triangle.)
Question 102. By what minimum angle does a regular hexagon rotate so as to coincide with its origional position for the first time?
Answer:
Given:
A regular hexagon.
To Find:
The minimum angle of rotation required for the regular hexagon to coincide with its original position for the first time.
Solution:
A regular polygon has rotational symmetry. When a regular polygon is rotated about its center, it coincides with its original position multiple times during a full rotation of $360^\circ$.
The number of times a regular polygon of $n$ sides coincides with itself in a full rotation is equal to the number of sides, $n$. This is called the order of rotational symmetry.
The angles of rotation that make the polygon coincide with its original position are given by rotating through multiples of the minimum angle of rotation.
The minimum angle of rotation for a regular polygon with $n$ sides is given by the formula:
Minimum angle of rotation $= \frac{360^\circ}{\text{Number of sides}}$
Minimum angle of rotation $= \frac{360^\circ}{n}$
... (1)
For a regular hexagon, the number of sides is $n = 6$.
Substituting $n=6$ into the formula (1):
Minimum angle of rotation $= \frac{360^\circ}{6}$
Minimum angle of rotation $= 60^\circ$
This minimum angle is also known as the angle of rotation or the angle of symmetry.
Therefore, a regular hexagon rotates by a minimum angle of $60^\circ$ to coincide with its original position for the first time.
Question 103. In each of the following figures, write the number of lines of symmetry and order of rotational symmetry

[Hint: Consider these as 2-D figures not as 3-D objects.]
Answer:
To Find:
The number of lines of symmetry and the order of rotational symmetry for each figure.
Solution:
For a 2-D figure:
- Lines of Symmetry: A line of symmetry is a line such that if the figure is folded along this line, the two halves coincide exactly.
- Rotational Symmetry: A figure has rotational symmetry if it looks exactly the same after being rotated about a central point by a certain angle (less than $360^\circ$). The order of rotational symmetry is the number of times the figure coincides with itself during a full rotation of $360^\circ$. The minimum angle of rotation is $360^\circ$ divided by the order of rotational symmetry.
Figure (i) - Rectangle:
Number of lines of symmetry = 2
Order of rotational symmetry = 2
Figure (ii) - Square:
Number of lines of symmetry = 4
Order of rotational symmetry = 4
Figure (iii) - Equilateral Triangle:
Number of lines of symmetry = 3
Order of rotational symmetry = 3
Figure (iv) - Regular Pentagon:
Number of lines of symmetry = 5
Order of rotational symmetry = 5
Figure (v) - Regular Hexagon:
Number of lines of symmetry = 6
Order of rotational symmetry = 6
Question 104. In the figure 12.24 of a cube,

(i) Which edge is the intersection of faces EFGH and EFBA?
(ii) Which faces intersect at edge FB?
(iii) Which three faces form the vertex A?
(iv) Which vertex is formed by the faces ABCD, ADHE and CDHG?
(v) Give all the edges that are parallelto edge AB.
(vi) Give the edges that are neitherparallel nor perpendicular to edge BC.
(vii) Give all the edges that areperpendicular to edge AB.
(viii) Give four vertices that do not all liein one plane.
Answer:
To Identify:
Edges, faces, and vertices of the cube and their relationships based on the given figure.
Solution:
Interpreting the figure of the cube with vertices labeled A, B, C, D (bottom face) and E, F, G, H (top face), connected by vertical edges AE, BF, CG, DH.
(i) Which edge is the intersection of faces EFGH and EFBA?
Face EFGH is the top face and face EFBA is the front face. The edge common to both these faces is EF.
The edge is EF.
(ii) Which faces intersect at edge FB?
Edge FB is a vertical edge. The faces that meet at this edge are the front face (EFBA) and the right face (BCGF).
The faces are EFBA and BCGF.
(iii) Which three faces form the vertex A?
Vertex A is a corner vertex. The three faces that meet at vertex A are the bottom face (ABCD), the front face (ABFE), and the left face (ADHE).
The three faces are ABCD, ABFE, and ADHE.
(iv) Which vertex is formed by the faces ABCD, ADHE and CDHG?
Face ABCD is the bottom face.
Face ADHE is the left face.
Face CDHG connects vertices C, D, H, G. Based on the diagram's labeling, this is the back face.
The vertex common to all three faces (ABCD, ADHE, and CDHG) is the vertex D.
The vertex is D.
(v) Give all the edges that are parallel to edge AB.
Edge AB is a horizontal edge on the bottom face. Parallel edges are those running in the same direction.
The edges parallel to AB are DC (on the bottom face), EF (on the top face), and HG (on the top face).
The edges are DC, EF, and HG.
(vi) Give the edges that are neither parallel nor perpendicular to edge BC.
Edge BC is a horizontal edge on the bottom face.
Edges parallel to BC are AD, FG, EH.
Edges perpendicular to BC (either intersecting or skew) are AB, DC, BF, CG, AE, DH, EF, HG.
In a cube, every edge is either parallel or perpendicular to any other edge (in the 3D sense, considering the lines containing the edges). There are no edges that are neither parallel nor perpendicular to edge BC.
The edges are None (or the set is empty).
(vii) Give all the edges that are perpendicular to edge AB.
Edge AB is a horizontal edge. Edges perpendicular to AB are those forming a $90^\circ$ angle with AB.
Edges intersecting AB at $90^\circ$: AD, BC, AE, BF.
Edges skew to AB that are perpendicular (angle between their lines is $90^\circ$): DH (parallel to AE), CG (parallel to BF), HE (parallel to AD), FG (parallel to BC).
The edges perpendicular to edge AB are AD, BC, AE, BF, DH, CG, HE, and FG.
(viii) Give four vertices that do not all lie in one plane.
Four vertices that do not lie in the same plane are called non-coplanar vertices. We need to choose four vertices such that no single flat surface (plane) contains all of them.
Consider vertices from different faces or positions such that they don't form a single face or lie on a single diagonal plane.
For example, take the vertices of the bottom face A, B, C, D. If we pick A, B, C and one vertex from the top face not directly above A, B, or C, like H, the four vertices A, B, C, H are not coplanar.
Another common set of non-coplanar vertices is formed by taking vertices of a face diagonal and vertices of the opposite face diagonal that is not parallel to the first. For example, A, C, G, E.
Four vertices that do not all lie in one plane are A, B, C, H (or A, C, G, E, etc.).
Question 105. Draw a net of a cuboid having same breadth and height, but length double the breadth.
Answer:
Given:
A cuboid with breadth and height being equal, and length being double the breadth.
To Draw:
A net of the cuboid.
Solution:
Let the breadth of the cuboid be $b$.
Given that the height is the same as the breadth, so height $h = b$.
Given that the length is double the breadth, so length $l = 2b$.
A cuboid has 6 rectangular faces. The dimensions of these faces are determined by the length, breadth, and height.
- The top and bottom faces have dimensions length $\times$ breadth, which is $l \times b = (2b) \times b$.
- The front and back faces have dimensions length $\times$ height, which is $l \times h = (2b) \times b$.
- The left and right side faces have dimensions breadth $\times$ height, which is $b \times h = b \times b$.
So, the cuboid has four faces of size $2b \times b$ and two faces of size $b \times b$ (which are squares). A net of the cuboid is a 2-dimensional pattern that can be folded to form the cuboid.
Here is a description of one possible net for this cuboid:
1. Draw a rectangle representing one of the faces with dimensions $2b \times b$ (e.g., the Front face).
2. Attach a square face of size $b \times b$ to each of the shorter sides (which have length $b$) of the $2b \times b$ rectangle. These can be the Left and Right side faces.
3. Attach two more rectangular faces of size $2b \times b$ (e.g., the Top and Bottom faces) to the longer sides (which have length $2b$) of the central $2b \times b$ rectangle.
4. Attach the last rectangular face of size $2b \times b$ (e.g., the Back face) to the unattached longer side (length $2b$) of either the Top or the Bottom face.
A common layout based on this description is:
(Imagine a grid where each small division represents a length. Let the side of the $b \times b$ square be $b$ units, and the sides of the $2b \times b$ rectangle be $2b$ and $b$ units).
The net could be arranged as a central horizontal strip of three faces (Left Side, Front, Right Side) with the Top and Bottom faces attached above and below the Front face, and the Back face attached above the Top face.
Visual representation of the net structure (dimensions shown):
[ Back $2b \times b$ ]
[ Top $2b \times b$ ]
[Left $b \times b$][ Front $2b \times b$ ][Right $b \times b$]
[ Bottom $2b \times b$ ]
(Note: When drawing on paper, ensure the side lengths are proportional, e.g., if $b=2$ cm, then $2b=4$ cm. The $b \times b$ faces are squares, and the $2b \times b$ faces are rectangles where one side is twice the length of the other).
Question 106. Draw the nets of the following:
(i) Triangular prism
(ii) Tetrahedron
(iii) Cuboid
Answer:
To Draw:
The nets of a triangular prism, a tetrahedron, and a cuboid.
Solution:
A net is a 2-dimensional pattern of shapes that can be folded to form a 3-dimensional solid.
(i) Triangular prism:
A triangular prism has 5 faces: two congruent triangular bases and three rectangular lateral faces. The sides of the triangular bases match the widths of the rectangular faces.
A common net consists of the three rectangular faces joined along their lengths in a row, with a triangle attached to one of the longer sides of one of the central rectangles, and the second triangle attached to the opposite longer side of the same central rectangle (or an adjacent one, ensuring they fold correctly to form the bases).
Visual representation of a possible net structure:
[ Triangle ]
[ Rectangle ][ Rectangle ][ Rectangle ]
[ Triangle ]
(Each Rectangle face has dimensions $l \times w$, where $l$ is the length of the prism and $w$ is the length of a side of the triangular base. The Triangular faces are the bases of the prism, which attach to the sides of length $w$ of the rectangular faces.)
(ii) Tetrahedron:
A tetrahedron is a pyramid with a triangular base. It has 4 faces, all of which are triangles.
If it is a regular tetrahedron, all four faces are congruent equilateral triangles. A simple net is formed by arranging three triangles around a central triangle.
Visual representation of a possible net structure (for a regular tetrahedron):
[ Triangle ]
[ Triangle ][ Triangle ][ Triangle ]
(The central triangle is the base, and the other three triangles fold up to meet at the apex.)
(iii) Cuboid:
A cuboid has 6 rectangular faces. There are three pairs of identical faces (top/bottom, front/back, left/right). Let the dimensions be length ($l$), breadth ($b$), and height ($h$). The faces are $l \times b$, $l \times h$, and $b \times h$ rectangles (two of each).
A common net for a cuboid is a cross shape, consisting of four rectangular faces in a row (e.g., back, side, front, side) with the remaining two faces (top and bottom) attached to one of the rectangles in the row (typically the 'front' face).
Visual representation of a possible net structure:
[ Top $l \times b$ ]
[ Side $b \times h$ ][ Front $l \times h$ ][ Side $b \times h$ ][ Back $l \times h$ ]
[ Bottom $l \times b$ ]
(Note: Other arrangements of the faces are also possible to form a valid net, as long as they can be folded without overlap to create the cuboid. The dimensions in the visual representation show which face is which.)
Question 107. Draw a net of the solid given in the figure 12.25:

Answer:
The solid shown in the figure is a hexagonal pyramid.
A net of a solid is a 2-dimensional representation that can be folded to form the solid. For a hexagonal pyramid, the net consists of one base shape and the lateral faces.
The base of the hexagonal pyramid is a hexagon. The lateral faces are triangles that meet at the apex (vertex opposite the base). Since the base is a hexagon, there are 6 triangular faces.
To form the net, the six triangular faces are attached to the sides of the hexagonal base. When folded along the edges of the hexagon, these triangles will meet at a single point above the center of the hexagon, forming the apex of the pyramid.
A possible representation of the net would show a central hexagon with a triangle attached to each of its six sides.
Question 108. Draw an isometric view of a cuboid 6 cm × 4 cm × 2 cm.
Answer:
An isometric view is a way to represent a 3-dimensional object in two dimensions, where the lines parallel to the axes are drawn to their actual scale and the angles between the axes are $120^\circ$.
To draw an isometric view of a cuboid with dimensions 6 cm $\times$ 4 cm $\times$ 2 cm, you can follow these steps:
1. Start by drawing a vertical line segment representing one vertical edge of the cuboid. Let its length be 2 cm.
2. From the lower endpoint of this vertical line, draw two lines at an angle of $30^\circ$ to the horizontal (or $120^\circ$ to the vertical line). These represent two edges of the base. Let one line have a length of 6 cm and the other a length of 4 cm.
3. From the upper endpoint of the vertical line (2 cm long), draw two lines parallel to the 6 cm and 4 cm lines drawn in step 2. These lines should also have lengths 6 cm and 4 cm, respectively.
4. Complete the base rectangle by drawing a line parallel to the 4 cm line from the endpoint of the 6 cm line, and a line parallel to the 6 cm line from the endpoint of the 4 cm line. These two lines will meet, forming the base of the cuboid.
5. Complete the top rectangle by drawing a line parallel to the 4 cm line from the endpoint of the upper 6 cm line, and a line parallel to the 6 cm line from the endpoint of the upper 4 cm line. These two lines will meet, forming the top of the cuboid.
6. Connect the corresponding vertices of the base and the top rectangles with vertical lines. Some edges might be hidden, which can be shown using dashed lines if required.
The resulting drawing will show a 3D representation of the 6 cm $\times$ 4 cm $\times$ 2 cm cuboid, appearing as if viewed from an angle where three faces are visible.
Question 109. The net given below in Fig. 12.26 can be used to make a cube.

(i) Which edge meets AN?
(ii) Which edge meets DE?
Answer:
Question 110. Draw the net of triangular pyramid with base as equilateral triangle of side 3 cm and slant edges 5 cm.
Answer:
A net of a solid shape is a 2D pattern that can be folded to form the 3D shape.
A triangular pyramid is a polyhedron with a triangular base and three triangular faces that meet at a point called the apex. In total, a triangular pyramid has 4 faces, 6 edges, and 4 vertices.
For this specific triangular pyramid:
The base is an equilateral triangle with a side length of $3 \text{ cm}$.
The slant edges connecting the base vertices to the apex are $5 \text{ cm}$ long. The side faces are the triangles formed by one side of the base and two slant edges. Thus, each of the three side faces is an isosceles triangle with side lengths $3 \text{ cm}$, $5 \text{ cm}$, and $5 \text{ cm}$.
To draw the net of this triangular pyramid, you need to draw the base triangle and the three side triangles connected to it.
Here are the steps:
1. Draw the base triangle, which is an equilateral triangle with each side measuring $3 \text{ cm}$.
2. From each side of the base triangle, draw one of the side faces. Each side face is an isosceles triangle. The side of this isosceles triangle that is attached to the base should measure $3 \text{ cm}$. The other two sides of each isosceles triangle, which will form the slant edges when folded, should measure $5 \text{ cm}$ each.
So, the net consists of one equilateral triangle (the base) with side length $3 \text{ cm}$, and three isosceles triangles (the side faces) attached to its sides. Each isosceles triangle has side lengths $3 \text{ cm}$, $5 \text{ cm}$, and $5 \text{ cm}$.
Imagine the equilateral triangle at the center. One isosceles triangle is attached to its left side, one to its right side, and one to its bottom side (or any arrangement where each side of the base triangle has one isosceles triangle attached).
The final net will look like an equilateral triangle with an isosceles triangle joined to each of its sides. All three isosceles triangles will be identical.
Question 111. Draw the net of a square pyramid with base as square of side 4 cm and slant edges 6 cm.
Answer:
The net of a three-dimensional shape is the pattern made when the surface of the shape is laid out flat.
For a square pyramid, the net consists of a square base and four triangular faces.
Based on the given information:
The base is a square with a side length of $4$ cm.
The four triangular faces are attached to the sides of the square base. Since the slant edges are $6$ cm, each triangular face is an isosceles triangle with its base measuring $4$ cm (matching the side of the square base) and its two equal sides measuring $6$ cm (the slant edges).
To draw the net:
1. Draw a square with side length $4$ cm.
2. Attach one isosceles triangle to each side of the square. Each triangle should have a base of $4$ cm and two other sides of $6$ cm.
A typical arrangement shows the square in the center, with the four triangles unfolding outwards from each of its sides.
Question 112. Draw the net of rectangular pyramid with slant edge 6 cm and base as rectangle with length 4 cm and breadth 3 cm.
Answer:
The net of a rectangular pyramid consists of its base and its four triangular faces laid out flat.
Based on the given information:
The base is a rectangle with length $4$ cm and breadth $3$ cm.
The pyramid has four triangular faces. Since all slant edges are $6$ cm, these are all isosceles triangles. The bases of these triangles correspond to the sides of the rectangular base.
There are two triangular faces with a base of $4$ cm and two equal sides of $6$ cm (corresponding to the length of the rectangle).
There are two triangular faces with a base of $3$ cm and two equal sides of $6$ cm (corresponding to the breadth of the rectangle).
To draw the net:
1. Draw a rectangle with dimensions $4$ cm by $3$ cm.
2. Attach the four triangular faces to the sides of this rectangle. The two triangles with a $4$ cm base and $6$ cm equal sides should be attached to the $4$ cm sides of the rectangle. The two triangles with a $3$ cm base and $6$ cm equal sides should be attached to the $3$ cm sides of the rectangle.
A common way to draw this net is to place the rectangle in the center and unfold the four triangles outwards from its sides.
Question 113. Find the number of cubes in each of the following figures and in each case give the top, front, left side and right side view (arrow indicating the front view).

Answer:
Let's analyze each figure to determine the number of cubes and describe its orthogonal views (Top, Front, Left Side, Right Side).
Figure 1:
By counting the individual cubes, we find there are 5 cubes in this figure.
Number of cubes: 5
Top View: When viewed from directly above, the visible faces form an L-shape made of 3 squares.
Front View: When viewed from the direction indicated by the arrow, the visible faces form an L-shape. There are two squares in the bottom row and one square stacked on the right square of the bottom row. It is a shape made of 3 squares.
Left Side View: When viewed from the left side (relative to the front view), the visible faces form a vertical stack of 2 squares.
Right Side View: When viewed from the right side (relative to the front view), the visible faces form an L-shape. There are two squares in the bottom row and one square stacked on the left square of the bottom row. It is a shape made of 3 squares.
Figure 2:
By counting the individual cubes, considering the stacks, we find there are 6 cubes in this figure (one stack of 3 and three stacks of 1).
Number of cubes: 6
Top View: When viewed from directly above, the visible faces form a $2 \times 2$ square made of 4 squares.
Front View: When viewed from the direction indicated by the arrow, the visible faces form two vertical columns side-by-side. The left column is 3 squares high, and the right column is 1 square high.
Left Side View: When viewed from the left side (relative to the front view), the visible faces form two vertical columns side-by-side. The front column (in the left view) is 3 squares high, and the back column is 1 square high.
Right Side View: When viewed from the right side (relative to the front view), the visible faces form two vertical columns side-by-side, both are 1 square high.
Figure 3:
This figure consists of a $3 \times 3$ base (9 cubes), a $2 \times 2$ layer on the center (4 cubes), and a $1 \times 1$ layer on the center of that (1 cube). Total cubes = $9 + 4 + 1 = 14$.
Number of cubes: 14
Top View: When viewed from directly above, the visible faces form a $3 \times 3$ square made of 9 squares.
Front View: When viewed from the direction indicated by the arrow, the visible faces form three vertical columns side-by-side. From left to right, the columns are 1 square high, 3 squares high, and 2 squares high.
Left Side View: When viewed from the left side (relative to the front view), the visible faces form three vertical columns side-by-side. From left to right, the columns are 1 square high, 3 squares high, and 2 squares high.
Right Side View: When viewed from the right side (relative to the front view), the visible faces form three vertical columns side-by-side. From left to right, the columns are 2 squares high, 3 squares high, and 1 square high.
Question 114. Draw all lines of symmetry for each of the following figures as given below:

Answer:
A line of symmetry is a line that divides a figure into two mirror images.
Figure 1: Square
A square has 4 lines of symmetry.
These lines are:
1. The two lines connecting the midpoints of opposite sides (horizontal and vertical).
2. The two lines coinciding with the diagonals of the square.
Figure 2: Regular Pentagon
A regular pentagon has 5 lines of symmetry.
Each line of symmetry passes through one vertex and the midpoint of the opposite side.
Figure 3: Circle
A circle has infinitely many lines of symmetry.
Any line that passes through the center of the circle is a line of symmetry.
Figure 4: Isosceles Trapezoid
An isosceles trapezoid has 1 line of symmetry.
This line connects the midpoints of the two parallel sides.
Figure 5: Letter 'H'
The letter 'H' has 2 lines of symmetry (assuming it is a capital 'H' with equal vertical bars).
1. A horizontal line through the middle bar.
2. A vertical line midway between the two vertical bars.
Figure 6: Letter 'E'
The letter 'E' has 1 line of symmetry (assuming it is a capital 'E').
This line is a horizontal line through the middle bar.
Question 115. How many faces does Fig. 12.27 have?

Answer:
The figure shown is a triangular prism.
A prism is a polyhedron comprising an $n$-sided polygonal base, a second base which is a translated copy of the first, and $n$ other faces (necessarily all parallelograms) joining corresponding sides of the two bases.
In a triangular prism, the base is a triangle ($n=3$).
It has:
Two triangular faces (the bases).
Three rectangular faces (connecting the sides of the triangles).
Total number of faces = Number of triangular faces + Number of rectangular faces
Total number of faces = $2 + 3 = 5$
So, the figure has 5 faces.
Question 116. Trace each figure. Then draw all lines of symmetry, if it has.

Answer:
A line of symmetry is a line that divides a figure into two identical halves that are mirror images of each other.
Figure 1: Parallelogram
A general parallelogram has no lines of symmetry unless it is a rhombus or a rectangle. The figure appears to be a general parallelogram.
Number of lines of symmetry: 0
Figure 2: 5-pointed Star
This figure is a regular 5-pointed star.
It has 5 lines of symmetry. Each line passes through a vertex and the midpoint of the opposite 'valley' between two points.
Figure 3: 3-bladed figure
This figure has rotational symmetry. It also has lines of symmetry.
It has 3 lines of symmetry. Each line passes through the center of the figure and the tip of one of the 'blades'.
Figure 4: Crescent Moon
A crescent moon shape typically has one line of symmetry.
It has 1 line of symmetry. This line passes through the two pointy tips (cusps) of the crescent.
Figure 5: Cross Shape
Assuming the horizontal and vertical arms are symmetrical.
It has 4 lines of symmetry. Two lines are horizontal and vertical, passing through the center. Two more lines pass diagonally through the center (if the proportions allow).
Figure 6: Letter 'A'
Assuming a standard symmetrical capital 'A'.
It has 1 line of symmetry. This line is a vertical line passing through the center of the letter.
Question 117. Tell whether each figure has rotational symmetry or not.

Answer:
Rotational symmetry exists if a figure can be rotated about a central point by an angle between $0^\circ$ and $360^\circ$ and map onto itself (look the same as the original figure).
Figure 1: Triangle
This figure is a general triangle. It only maps onto itself after a rotation of $360^\circ$. Therefore, it does not have rotational symmetry (excluding the trivial case).
Figure 2: Square
A square can be rotated by $90^\circ$, $180^\circ$, and $270^\circ$ about its center and look the same. Therefore, it has rotational symmetry.
Figure 3: Parallelogram
A parallelogram can be rotated by $180^\circ$ about its center and look the same. Therefore, it has rotational symmetry.
Figure 4: Circle
A circle can be rotated by any angle about its center and look the same. Therefore, it has rotational symmetry.
Figure 5: Regular Pentagon
A regular pentagon can be rotated by multiples of $72^\circ$ ($360^\circ / 5$) about its center and look the same. Therefore, it has rotational symmetry.
Figure 6: 6-pointed Star
This figure appears to be a regular 6-pointed star. It can be rotated by multiples of $60^\circ$ ($360^\circ / 6$) about its center and look the same. Therefore, it has rotational symmetry.
Figure 7: Heart Shape
A heart shape only maps onto itself after a rotation of $360^\circ$. Therefore, it does not have rotational symmetry (excluding the trivial case).
Figure 8: Cross Shape
This symmetrical cross shape can be rotated by $90^\circ$, $180^\circ$, and $270^\circ$ about its center and look the same. Therefore, it has rotational symmetry.
Question 118. Draw all lines of symmetry for each of the following figures.


Answer:
A line of symmetry is a line that divides a figure into two mirror images.
Figure 1 (Top, Image 1): Rhombus
A rhombus has 2 lines of symmetry.
These lines are its two diagonals.
Figure 1 (Top, Image 2): Letter 'X'
The letter 'X' has 2 lines of symmetry (assuming it is a standard symmetrical 'X').
These lines are a horizontal line and a vertical line, both passing through the center.
Figure 1 (Top, Image 3): Regular Hexagon
A regular hexagon has 6 lines of symmetry.
Three lines pass through opposite vertices, and three lines pass through the midpoints of opposite sides.
Figure 1 (Top, Image 4): Letter 'B'
The letter 'B' has 1 line of symmetry (assuming it is a standard symmetrical capital 'B').
This line is a horizontal line passing through the middle of the letter.
Figure 2 (Bottom, Image 1): Arrow
This arrow figure has 1 line of symmetry (assuming the fins are symmetrical).
This line is a vertical line passing through the center of the arrow.
Figure 2 (Bottom, Image 2): Curved Cross Shape
This figure has 4 lines of symmetry (assuming it is symmetrical).
Two lines are horizontal and vertical, and two lines are diagonal, all passing through the center.
Figure 2 (Bottom, Image 3): Circular Design
This figure appears to have 6 lines of symmetry.
These lines pass through the center and divide the figure into 6 identical sectors.
Figure 2 (Bottom, Image 4): Swirl/Curved Shape
This figure has 0 lines of symmetry.
Question 119. Tell whether each figure has rotational symmetry. Write yes or no.
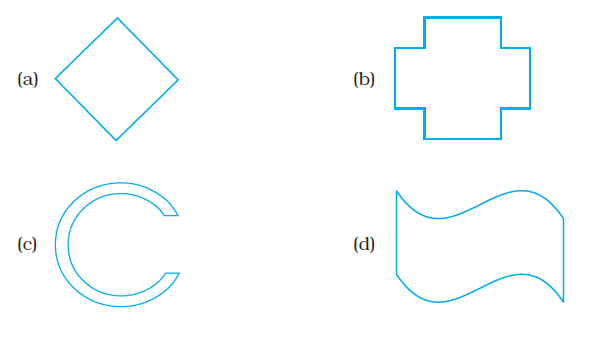
Answer:
Rotational symmetry exists if a figure can be rotated about a central point by an angle between $0^\circ$ and $360^\circ$ and map onto itself (look the same as the original figure).
Figure 1: Pinwheel
This figure has rotational symmetry. It looks the same after a certain rotation about its center.
Answer: Yes
Figure 2: Asymmetrical Shape
This figure does not appear to have rotational symmetry, as it only maps onto itself after a $360^\circ$ rotation.
Answer: No
Figure 3: Swirl
This figure does not appear to have rotational symmetry, as it only maps onto itself after a $360^\circ$ rotation.
Answer: No
Figure 4: Y Shape
This figure only maps onto itself after a $360^\circ$ rotation.
Answer: No
Figure 5: Hexagram (Star of David)
This figure has rotational symmetry. It looks the same after a rotation of $60^\circ$, $120^\circ$, etc., about its center.
Answer: Yes
Figure 6: Crosshairs / Plus Sign
This figure has rotational symmetry. it looks the same after a rotation of $90^\circ$, $180^\circ$, and $270^\circ$ about its center.
Answer: Yes
Figure 7: Curved 3-point star
This figure has rotational symmetry. It looks the same after a rotation of $120^\circ$ and $240^\circ$ about its center.
Answer: Yes
Figure 8: Arrow
This figure only maps onto itself after a $360^\circ$ rotation.
Answer: No
Figure 9: Flower/Star shape
This figure has rotational symmetry. It appears to have 8-fold rotational symmetry, looking the same after rotations of $45^\circ$, $90^\circ$, etc.
Answer: Yes
Question 120. Does the Fig. 12.28 have rotational symmetry?
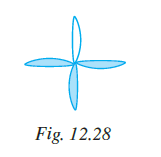
Answer:
Rotational symmetry exists if a figure can be rotated about a central point by an angle between $0^\circ$ and $360^\circ$ and map onto itself (look the same as the original figure).
The figure shown is the letter 'Z'.
If the letter 'Z' is rotated by $180^\circ$ about its center, it appears exactly the same as the original figure.
Since the figure maps onto itself for a rotation angle other than $360^\circ$, it has rotational symmetry.
Answer: Yes
Question 121. The flag of Japan is shown below. How many lines of symmetry does the flag have?
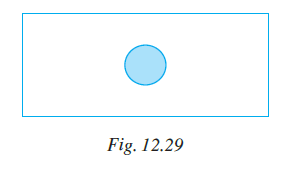
Answer:
A line of symmetry is a line that divides a figure into two identical halves that are mirror images of each other.
The flag of Japan consists of a white rectangular background with a red circle centered within it.
The center of the red circle is also the center of the rectangle.
We can check for lines of symmetry:
1. A line passing horizontally through the center of the rectangle (and thus the center of the circle) divides the flag into two identical upper and lower halves. This is a line of symmetry.
2. A line passing vertically through the center of the rectangle (and thus the center of the circle) divides the flag into two identical left and right halves. This is a line of symmetry.
Diagonal lines through the center are not lines of symmetry for a rectangle (unless it's a square), and while they pass through the center of the circle, the rectangular boundary breaks the symmetry along diagonals.
Therefore, the flag of Japan has 2 lines of symmetry.
Question 122. Which of the figures given below have both line and rotational symmetry?

Answer:
Let's examine each figure to determine if it possesses both line symmetry and rotational symmetry.
Line Symmetry: A figure has line symmetry if it can be divided into two identical mirror-image halves by a line.
Rotational Symmetry: A figure has rotational symmetry if it can be rotated by an angle between $0^\circ$ and $360^\circ$ about a central point and appear exactly the same as the original figure.
Analyzing each figure:
- Figure 1 (Square): Has 4 lines of symmetry and rotational symmetry of order 4 (rotations by $90^\circ, 180^\circ, 270^\circ$). -> Both
- Figure 2 (Regular Pentagon): Has 5 lines of symmetry and rotational symmetry of order 5 (rotations by multiples of $72^\circ$). -> Both
- Figure 3 (Circle): Has infinitely many lines of symmetry and rotational symmetry of infinite order (rotation by any angle). -> Both
- Figure 4 (Letter 'H'): Has 2 lines of symmetry (horizontal and vertical) and rotational symmetry of order 2 (rotation by $180^\circ$). -> Both
- Figure 5 (Equilateral Triangle): Has 3 lines of symmetry and rotational symmetry of order 3 (rotations by $120^\circ, 240^\circ$). -> Both
- Figure 6 (Letter 'A'): Has 1 line of symmetry (vertical) but no rotational symmetry (order 1). -> Line symmetry only
- Figure 7 (Letter 'M'): Has 1 line of symmetry (vertical) but no rotational symmetry (order 1). -> Line symmetry only
- Figure 8 (Letter 'N'): Has no line symmetry but has rotational symmetry of order 2 (rotation by $180^\circ$). -> Rotational symmetry only
- Figure 9 (Letter 'Z'): Has no line symmetry but has rotational symmetry of order 2 (rotation by $180^\circ$). -> Rotational symmetry only
- Figure 10 (Asymmetrical Triangle): Has no line symmetry and no rotational symmetry (order 1). -> Neither
The figures that have both line and rotational symmetry are:
Figure 1, Figure 2, Figure 3, Figure 4, and Figure 5.
Question 123. Which of the following figures do not have line symmetry?
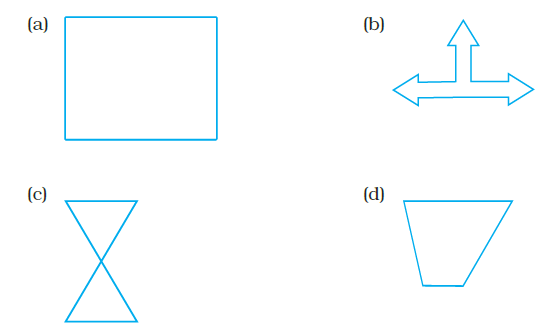
Answer:
Line symmetry exists if a figure can be divided into two identical mirror-image halves by a line.
Let's examine each figure:
- Figure 1 (Parallelogram): A general parallelogram does not have line symmetry.
- Figure 2 (Regular 5-pointed Star): This figure has line symmetry.
- Figure 3 (Curved Asymmetrical Shape): This figure does not appear to have any line of symmetry.
- Figure 4 (3-bladed Curved Shape): This figure appears to have line symmetry passing through the center and the tip of each blade.
- Figure 5 (Crescent Moon): This figure has one line of symmetry passing through its two points.
- Figure 6 (Cross Shape): This figure has line symmetry (both horizontal, vertical, and potentially diagonal depending on proportions).
- Figure 7 (Letter 'F'): The letter 'F' does not have any line of symmetry.
- Figure 8 (Heart Shape): This figure has one vertical line of symmetry.
- Figure 9 (Curved Shape): This figure does not appear to have any line of symmetry.
The figures that do not have line symmetry are:
Figure 1, Figure 3, Figure 7, and Figure 9.
Question 124. Which capital letters of English alphabet have no line of symmetry?
Answer:
A letter has line symmetry if it can be divided by a line into two identical halves that are mirror images of each other.
We need to identify the capital letters of the English alphabet that cannot be divided in this way.
Let's consider each letter from A to Z:
A: Has a vertical line of symmetry.
B: Has a horizontal line of symmetry.
C: Has a horizontal line of symmetry.
D: Has a horizontal line of symmetry.
E: Has a horizontal line of symmetry.
F: Has no line of symmetry.
G: Has no line of symmetry.
H: Has horizontal and vertical lines of symmetry.
I: Has horizontal and vertical lines of symmetry.
J: Has no line of symmetry.
K: Has a horizontal line of symmetry (assuming a standard symmetrical K).
L: Has no line of symmetry.
M: Has a vertical line of symmetry.
N: Has no line of symmetry.
O: Has infinitely many lines of symmetry (like a circle, assuming a perfect circle shape).
P: Has no line of symmetry.
Q: Has no line of symmetry (assuming a standard Q with a tail).
R: Has no line of symmetry.
S: Has no line of symmetry.
T: Has a vertical line of symmetry.
U: Has a vertical line of symmetry.
V: Has a vertical line of symmetry.
W: Has a vertical line of symmetry.
X: Has horizontal and vertical lines of symmetry.
Y: Has a vertical line of symmetry.
Z: Has no line of symmetry.
The capital letters of the English alphabet that have no line of symmetry are:
F, G, J, L, N, P, Q, R, S, Z

