| NCERT Exemplar Solutions | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
Chapter 3 Coordinate Geometry
Welcome to this comprehensive resource offering detailed answers and thorough explanations for the NCERT Exemplar problems focused on Class 9 Mathematics, Chapter 3: Coordinate Geometry. While the Class 9 syllabus introduces the foundational concepts of plotting points in a plane, these Exemplar questions are specifically designed to solidify this base significantly. They move beyond simple plotting and reading exercises, challenging students with more nuanced questions and applications that demand a careful and accurate interpretation of the Cartesian coordinate system. Mastering this chapter is crucial as it forms the bedrock for understanding graphs of linear equations and much of analytical geometry in higher classes.
The solutions provided meticulously cover the core concepts introduced at this level. This begins with a firm understanding of the Cartesian plane, defined by two perpendicular number lines: the horizontal x-axis and the vertical y-axis, intersecting at the Origin, denoted as $(0, 0)$. These axes divide the plane into four distinct regions called Quadrants, each characterized by specific sign conventions for the coordinates $(x, y)$: Quadrant I $(+, +)$, Quadrant II $(-, +)$, Quadrant III $(-, -)$, and Quadrant IV $(+, -)$. Understanding these conventions is vital for locating points correctly. The solutions thoroughly explain the process of plotting points given their coordinates $(x, y)$, where $x$ is the abscissa (distance from the y-axis) and $y$ is the ordinate (distance from the x-axis). Conversely, reading the coordinates of points already plotted on a plane is also addressed with precision.
However, the NCERT Exemplar problems frequently require students to apply this understanding in more demanding geometric contexts. Simply plotting points is often just the first step. Many problems involve:
- Identifying the type of geometric figure formed by joining a set of given points in order (e.g., determining if joining $A(x_1, y_1)$, $B(x_2, y_2)$, $C(x_3, y_3)$, and $D(x_4, y_4)$ forms a square, rectangle, parallelogram, rhombus, kite, or a general quadrilateral). This often requires careful plotting and visual inspection, implicitly using properties related to side lengths or parallel/perpendicular lines.
- Finding the coordinates of points that satisfy specific geometric conditions. For instance, finding the coordinates of a point lying on the x-axis (form $(x, 0)$) or y-axis (form $(0, y)$), points having a specific abscissa or ordinate, or determining the coordinates of the reflection of a point across the x-axis (if $(x, y)$ is the point, its reflection is $(x, -y)$) or across the y-axis (reflection is $(-x, y)$).
- Analyzing the location of points purely based on the signs of their coordinates without actually plotting them, reinforcing the understanding of quadrants.
Although the formal distance formula ($d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$) is typically introduced in Class 10, some Exemplar problems might implicitly test the concept of distance. For example, understanding that the distance of a point $(x, y)$ from the y-axis is its absolute abscissa $|x|$, and its distance from the x-axis is its absolute ordinate $|y|$, might be required. Problems could also involve identifying points equidistant from both axes (where $|x|=|y|$).
The solutions cater to the diverse question formats encountered in the Exemplar – MCQs testing understanding of quadrants or axes, Fill-in-the-Blanks requiring specific coordinates, True/False statements checking fundamental concepts, and Short/Long Answer questions demanding accurate plotting, shape identification, coordinate finding based on relationships, or graphical pattern analysis. They provide clear explanations of coordinate system rules, precise plotting instructions, logical reasoning for determining geometric properties or locations, and include helpful diagrams where necessary. Engaging with this resource ensures students develop a strong, accurate, and intuitive understanding of the Cartesian coordinate system, an absolutely essential prerequisite for future success in graphical analysis and analytical geometry.
Sample Question 1 (Before Exercise 3.1)
Write the correct answer:
Sample Question 1: The points (other than origin) for which abscissa is equal to the ordinate will lie in
(A) I quadrant only
(B) I and II quadrants
(C) I and III quadrants
(D) II and IV quadrants
Answer:
The abscissa of a point is its x-coordinate, and the ordinate is its y-coordinate.
The problem states that the abscissa is equal to the ordinate. This means that for a point $(x, y)$, we have $x = y$.
So, any point satisfying this condition will be of the form $(x, x)$.
We are asked about points other than the origin. The origin is the point $(0, 0)$, where $x=0$. So, we consider points $(x, x)$ where $x \neq 0$.
Now, let's consider the location of these points based on the sign of $x$:
If $x > 0$, then both coordinates are positive $(+, +)$. Points with positive x and positive y coordinates lie in the I quadrant.
If $x < 0$, then both coordinates are negative $(-, -)$. Points with negative x and negative y coordinates lie in the III quadrant.
Therefore, points (other than origin) where the abscissa equals the ordinate, i.e., points of the form $(x, x)$ with $x \neq 0$, lie in both the I quadrant (when $x > 0$) and the III quadrant (when $x < 0$).
Comparing this with the given options, the correct answer is (C).
The correct option is (C) I and III quadrants.
Exercise 3.1
Write the correct answer in each of the following:
Question 1. Point (–3, 5) lies in the
(A) first quadrant
(B) second quadrant
(C) third quadrant
(D) fourth quadrant
Answer:
The given point is $(-3, 5)$.
In a coordinate plane, the location of a point $(x, y)$ is determined by the signs of its x-coordinate (abscissa) and y-coordinate (ordinate).
For the point $(-3, 5)$:
The x-coordinate is $-3$, which is negative ($x < 0$).
The y-coordinate is $5$, which is positive ($y > 0$).
The quadrants are defined by the signs of the coordinates as follows:
Quadrant I: $(+, +)$ (x positive, y positive)
Quadrant II: $(-, +)$ (x negative, y positive)
Quadrant III: $(-, -)$ (x negative, y negative)
Quadrant IV: $(+, -)$ (x positive, y negative)
Since the point $(-3, 5)$ has a negative x-coordinate and a positive y-coordinate, it lies in the quadrant where x is negative and y is positive.
This corresponds to the second quadrant.
Therefore, the point $(-3, 5)$ lies in the second quadrant.
Comparing with the given options, the correct answer is (B).
The correct option is (B) second quadrant.
Question 2. Signs of the abscissa and ordinate of a point in the second quadrant are respectively
(A) +, +
(B) –, –
(C) –, +
(D) +, –
Answer:
In a coordinate system, the abscissa refers to the x-coordinate of a point, and the ordinate refers to the y-coordinate of a point.
The coordinate plane is divided into four quadrants by the x-axis and y-axis. The signs of the x and y coordinates determine which quadrant a point lies in.
The signs in each quadrant are as follows:
- First Quadrant (I): x is positive, y is positive. Signs are (+, +).
- Second Quadrant (II): x is negative, y is positive. Signs are (–, +).
- Third Quadrant (III): x is negative, y is negative. Signs are (–, –).
- Fourth Quadrant (IV): x is positive, y is negative. Signs are (+, –).
The question asks for the signs of the abscissa and ordinate of a point in the second quadrant.
In the second quadrant, the x-coordinate (abscissa) is negative (–) and the y-coordinate (ordinate) is positive (+).
Thus, the signs of the abscissa and ordinate of a point in the second quadrant are respectively –, +.
Comparing this with the given options, the correct answer is (C).
The correct option is (C) –, +.
Question 3. Point (0, –7) lies
(A) on the x –axis
(B) in the second quadrant
(C) on the y-axis
(D) in the fourth quadrant
Answer:
The given point is $(0, -7)$.
For a point $(x, y)$:
If the x-coordinate ($x$) is 0, the point lies on the y-axis.
If the y-coordinate ($y$) is 0, the point lies on the x-axis.
If both coordinates ($x$ and $y$) are non-zero, the point lies in one of the four quadrants.
In the given point $(0, -7)$, the x-coordinate is $0$.
$x = 0$
$y = -7$
Since the x-coordinate is $0$, the point must lie on the y-axis.
Furthermore, since the y-coordinate is $-7$ (which is negative), the point lies on the negative part of the y-axis.
Therefore, the point $(0, -7)$ lies on the y-axis.
Comparing with the given options, the correct answer is (C).
The correct option is (C) on the y-axis.
Question 4. Point (– 10, 0) lies
(A) on the negative direction of the x-axis
(B) on the negative direction of the y-axis
(C) in the third quadrant
(D) in the fourth quadrant
Answer:
The given point is $(-10, 0)$.
For any point $(x, y)$ in the coordinate plane:
- If the y-coordinate is $0$ ($y=0$), the point lies on the x-axis.
- If the x-coordinate is $0$ ($x=0$), the point lies on the y-axis.
- If both coordinates are non-zero ($x \neq 0$ and $y \neq 0$), the point lies in one of the four quadrants.
In the point $(-10, 0)$, the y-coordinate is $0$.
$x = -10$
$y = 0$
Since the y-coordinate is $0$, the point lies on the x-axis.
Now, we need to determine the direction on the x-axis. The x-coordinate is $-10$, which is a negative value.
Points on the x-axis with a negative x-coordinate lie on the negative direction of the x-axis.
Therefore, the point $(-10, 0)$ lies on the negative direction of the x-axis.
Comparing with the given options, the correct answer is (A).
The correct option is (A) on the negative direction of the x-axis.
Question 5. Abscissa of all the points on the x-axis is
(A) 0
(B) 1
(C) 2
(D) any number
Answer:
The abscissa of a point is its x-coordinate.
The x-axis is a horizontal line in the coordinate system. By definition, any point that lies on the x-axis has its y-coordinate equal to 0.
A general point on the x-axis can be represented in the form $(x, 0)$, where $x$ can be any real number.
Examples of points on the x-axis are $(1, 0)$, $(-5, 0)$, $(0, 0)$ (the origin), $(2.5, 0)$, etc.
In the point $(x, 0)$, the abscissa is $x$. Since $x$ can take any real value for points on the x-axis, the abscissa of points on the x-axis can be any number.
Note that the question asks for the abscissa, which is the x-coordinate, not the ordinate (y-coordinate). The ordinate of all points on the x-axis is 0.
Therefore, the abscissa of all the points on the x-axis is any number.
Comparing with the given options, the correct answer is (D).
The correct option is (D) any number.
Question 6. Ordinate of all points on the x-axis is
(A) 0
(B) 1
(C) – 1
(D) any number
Answer:
The ordinate of a point is its y-coordinate.
The x-axis is the horizontal line in the coordinate system. Any point that lies on the x-axis has a specific characteristic regarding its coordinates.
Consider any point on the x-axis. Its position is purely horizontal; it does not move up or down from the x-axis itself. This means its vertical position is at the level of the x-axis, which corresponds to a y-coordinate of 0.
A general point on the x-axis can be represented as $(x, 0)$, where $x$ is the abscissa and can be any real number, and $0$ is the ordinate.
For example, points like $(5, 0)$, $(-2, 0)$, $(0, 0)$, $(\frac{1}{2}, 0)$ all lie on the x-axis. In all these points, the y-coordinate (ordinate) is 0.
Therefore, the ordinate of all points on the x-axis is 0.
Comparing with the given options, the correct answer is (A).
The correct option is (A) 0.
Question 7. The point at which the two coordinate axes meet is called the
(A) abscissa
(B) ordinate
(C) origin
(D) quadrant
Answer:
In the Cartesian coordinate system, the two coordinate axes are the x-axis (horizontal axis) and the y-axis (vertical axis).
These two axes intersect at a specific point.
The point where the x-axis and the y-axis intersect is the central point of the coordinate system.
This point has coordinates $(0, 0)$, meaning its abscissa (x-coordinate) is 0 and its ordinate (y-coordinate) is 0.
This special point is known as the origin.
Definitions of other terms:
- Abscissa: The x-coordinate of a point.
- Ordinate: The y-coordinate of a point.
- Quadrant: One of the four regions into which the coordinate plane is divided by the axes.
Therefore, the point at which the two coordinate axes meet is called the origin.
Comparing with the given options, the correct answer is (C).
The correct option is (C) origin.
Question 8. A point both of whose coordinates are negative will lie in
(A) I quadrant
(B) II quadrant
(C) III quadrant
(D) IV quadrant
Answer:
The question asks for the quadrant in which a point lies if both of its coordinates are negative.
Let the point be $(x, y)$. We are given that both coordinates are negative, which means $x < 0$ and $y < 0$.
We need to identify the quadrant based on the signs of the coordinates:
- Quadrant I: x positive, y positive $(+, +)$
- Quadrant II: x negative, y positive $(-, +)$
- Quadrant III: x negative, y negative $(-, -)$
- Quadrant IV: x positive, y negative $(+, -)$
Since both the x-coordinate and the y-coordinate are negative for the given point $(x, y)$ where $x < 0$ and $y < 0$, the signs are $(-, -)$.
The quadrant where both coordinates are negative is the third quadrant.
Therefore, a point both of whose coordinates are negative will lie in the III quadrant.
Comparing with the given options, the correct answer is (C).
The correct option is (C) III quadrant.
Question 9. Points (1, – 1), (2, – 2), (4, – 5), (– 3, – 4)
(A) lie in II quadrant
(B) lie in III quadrant
(C) lie in IV quadrant
(D) do not lie in the same quadrant
Answer:
To determine if the given points lie in the same quadrant, we need to check the signs of the coordinates for each point and identify its quadrant.
The quadrants are defined by the signs of the x-coordinate (abscissa) and the y-coordinate (ordinate) as follows:
- Quadrant I: (+, +)
- Quadrant II: (–, +)
- Quadrant III: (–, –)
- Quadrant IV: (+, –)
Let's examine each point:
- Point 1: $(1, -1)$. The x-coordinate is $1$ (positive) and the y-coordinate is $-1$ (negative). The signs are $(+, -)$. This point lies in the IV quadrant.
- Point 2: $(2, -2)$. The x-coordinate is $2$ (positive) and the y-coordinate is $-2$ (negative). The signs are $(+, -)$. This point lies in the IV quadrant.
- Point 3: $(4, -5)$. The x-coordinate is $4$ (positive) and the y-coordinate is $-5$ (negative). The signs are $(+, -)$. This point lies in the IV quadrant.
- Point 4: $(-3, -4)$. The x-coordinate is $-3$ (negative) and the y-coordinate is $-4$ (negative). The signs are $(-, -)$. This point lies in the III quadrant.
We can see that the first three points $(1, -1)$, $(2, -2)$, and $(4, -5)$ lie in the IV quadrant. However, the fourth point $(-3, -4)$ lies in the III quadrant.
Since not all points lie in the same quadrant (specifically, points 1, 2, and 3 are in IV, while point 4 is in III), the given statement that they lie in the same quadrant is false.
Therefore, the points do not lie in the same quadrant.
Comparing with the given options, the correct answer is (D).
The correct option is (D) do not lie in the same quadrant.
Question 10. If y coordinate of a point is zero, then this point always lies
(A) in I quadrant
(B) in II quadrant
(C) on x - axis
(D) on y - axis
Answer:
The question asks about the location of a point whose y-coordinate is zero.
Let the point be $(x, y)$. We are given that the y-coordinate is zero, so $y = 0$. The point is of the form $(x, 0)$.
Let's consider the meaning of a zero y-coordinate in the Cartesian coordinate system.
The y-coordinate measures the vertical distance of a point from the x-axis. If the y-coordinate is positive, the point is above the x-axis. If the y-coordinate is negative, the point is below the x-axis. If the y-coordinate is zero, the point has no vertical distance from the x-axis; it lies precisely on the x-axis.
Points with a y-coordinate of 0 include, for example, $(5, 0)$, $(-3, 0)$, $(0, 0)$, and $(\frac{7}{2}, 0)$. All these points are located on the horizontal axis, which is the x-axis.
Points lying strictly in any of the four quadrants have non-zero x and y coordinates.
- Quadrant I: $x > 0, y > 0$
- Quadrant II: $x < 0, y > 0$
- Quadrant III: $x < 0, y < 0$
- Quadrant IV: $x > 0, y < 0$
Since $y=0$ for the given point, it cannot lie in any of the quadrants.
Therefore, a point whose y coordinate is zero always lies on the x-axis.
Comparing with the given options, the correct answer is (C).
The correct option is (C) on x - axis.
Question 11. The points (–5, 2) and (2, – 5) lie in the
(A) same quadrant
(B) II and III quadrants, respectively
(C) II and IV quadrants, respectively
(D) IV and II quadrants, respectively
Answer:
To determine the quadrant for each point, we examine the signs of their x and y coordinates.
The quadrants are defined by the signs of the coordinates as follows:
- Quadrant I: (+, +)
- Quadrant II: (–, +)
- Quadrant III: (–, –)
- Quadrant IV: (+, –)
Let's examine the first point: $(-5, 2)$.
The x-coordinate is $-5$, which is negative (–).
The y-coordinate is $2$, which is positive (+).
The signs are $(–, +)$. A point with these signs lies in the II quadrant.
Now, let's examine the second point: $(2, -5)$.
The x-coordinate is $2$, which is positive (+).
The y-coordinate is $-5$, which is negative (–).
The signs are $(+, –)$. A point with these signs lies in the IV quadrant.
So, the point $(-5, 2)$ lies in the II quadrant, and the point $(2, -5)$ lies in the IV quadrant.
The question asks where the points lie respectively. This means we state the quadrant for the first point, then the quadrant for the second point, in that order.
The points $(-5, 2)$ and $(2, -5)$ lie in the II and IV quadrants, respectively.
Comparing with the given options, the correct answer is (C).
The correct option is (C) II and IV quadrants, respectively.
Question 12. If the perpendicular distance of a point P from the x-axis is 5 units and the foot of the perpendicular lies on the negative direction of x-axis, then the point P has
(A) x coordinate = – 5
(B) y coordinate = 5 only
(C) y coordinate = – 5 only
(D) y coordinate = 5 or –5
Answer:
Let the point be P $(x, y)$.
The perpendicular distance of a point P $(x, y)$ from the x-axis is given by the absolute value of its y-coordinate, i.e., $|y|$.
We are given that this perpendicular distance is 5 units.
$|y| = 5$
... (i)
From equation (i), this means that the y-coordinate can be either $5$ or $-5$.
$y = 5$ or $y = -5$
We are also given that the foot of the perpendicular from point P to the x-axis lies on the negative direction of the x-axis.
Let F be the foot of the perpendicular from P to the x-axis. The coordinates of F are $(x, 0)$, where $x$ is the x-coordinate of P.
F $= (x, 0)$
The statement "the foot of the perpendicular lies on the negative direction of x-axis" means that the x-coordinate of F is negative and non-zero. This implies the x-coordinate of P is negative and non-zero.
$x < 0$
So, the point P has coordinates $(x, y)$ where $x < 0$ and ($y = 5$ or $y = -5$).
Let's consider the possible locations of P:
- If $y = 5$ and $x < 0$, the point P is in the II quadrant (negative x, positive y).
- If $y = -5$ and $x < 0$, the point P is in the III quadrant (negative x, negative y).
In both cases, the y-coordinate of P can be $5$ or $-5$. The information about the foot of the perpendicular being on the negative x-axis only tells us about the sign of the x-coordinate, not uniquely determining the sign of the y-coordinate. The distance from the x-axis is $|y|$, so $y$ could be positive or negative.
Therefore, the y-coordinate of point P can be $5$ or $-5$.
Comparing with the given options, the correct answer is (D).
The correct option is (D) y coordinate = 5 or –5.
Question 13. On plotting the points O (0, 0), A (3, 0), B (3, 4), C (0, 4) and joining OA, AB, BC and CO which of the following figure is obtained?
(A) Square
(B) Rectangle
(C) Trapezium
(D) Rhombus
Answer:
We are given four points: O $(0, 0)$, A $(3, 0)$, B $(3, 4)$, C $(0, 4)$. We need to determine the figure formed by joining these points in order: OA, AB, BC, and CO.
Let's find the lengths of the sides using the distance formula. The distance between two points $(x_1, y_1)$ and $(x_2, y_2)$ is $\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$.
Length of OA:
O $(0, 0)$, A $(3, 0)$
OA $= \sqrt{(3 - 0)^2 + (0 - 0)^2} = \sqrt{3^2 + 0^2} = \sqrt{9} = 3$ units.
Length of AB:
A $(3, 0)$, B $(3, 4)$
AB $= \sqrt{(3 - 3)^2 + (4 - 0)^2} = \sqrt{0^2 + 4^2} = \sqrt{16} = 4$ units.
Length of BC:
B $(3, 4)$, C $(0, 4)$
BC $= \sqrt{(0 - 3)^2 + (4 - 4)^2} = \sqrt{(-3)^2 + 0^2} = \sqrt{9} = 3$ units.
Length of CO:
C $(0, 4)$, O $(0, 0)$
CO $= \sqrt{(0 - 0)^2 + (0 - 4)^2} = \sqrt{0^2 + (-4)^2} = \sqrt{16} = 4$ units.
We have OA = BC = 3 units and AB = CO = 4 units.
This indicates that opposite sides are equal in length, which is a property of both rectangles and parallelograms.
Now let's check if adjacent sides are perpendicular, which would make it a rectangle or a square. We can do this by checking the slopes or by examining the coordinates directly.
Consider side OA, which lies on the x-axis (since the y-coordinate is 0 for both O and A).
Consider side CO, which lies on the y-axis (since the x-coordinate is 0 for both C and O).
The x-axis and y-axis are perpendicular to each other. Thus, the angle at the origin $\angle$COA is $90^\circ$.
Alternatively, consider the vector approach or visualize the points:
O (0, 0) is the origin.
A (3, 0) is on the positive x-axis, 3 units from the origin.
C (0, 4) is on the positive y-axis, 4 units from the origin.
B (3, 4) has an x-coordinate equal to that of A and a y-coordinate equal to that of C. This means B is located by moving 3 units right from the origin and then 4 units up.
The line segment OA is horizontal. The line segment CO is vertical. Since OA is on the x-axis and CO is on the y-axis, they are perpendicular at O.
The line segment AB has a constant x-coordinate (3), so it is a vertical line parallel to the y-axis.
The line segment BC has a constant y-coordinate (4), so it is a horizontal line parallel to the x-axis.
Since OA is horizontal and AB is vertical, they are perpendicular ($\angle$OAB = $90^\circ$).
Since AB is vertical and BC is horizontal, they are perpendicular ($\angle$ABC = $90^\circ$).
Since BC is horizontal and CO is vertical, they are perpendicular ($\angle$BCO = $90^\circ$).
Since CO is vertical and OA is horizontal, they are perpendicular ($\angle$COA = $90^\circ$).
The figure OABC has four sides with opposite sides equal (OA = BC, AB = CO) and all four interior angles equal to $90^\circ$. This is the definition of a rectangle.
It is not a square because the adjacent sides are not equal (OA = 3, AB = 4).
It is not a trapezium as it has two pairs of parallel sides (OA || BC, AB || CO).
It is not a rhombus as the adjacent sides are not equal (3 $\neq$ 4).
Therefore, the figure obtained is a rectangle.
Comparing with the given options, the correct answer is (B).
The correct option is (B) Rectangle.
Question 14. If P (– 1, 1), Q (3, – 4), R(1, –1), S(–2, –3) and T (– 4, 4) are plotted on the graph paper, then the point(s) in the fourth quadrant are
(A) P and T
(B) Q and R
(C) Only S
(D) P and R
Answer:
We are given five points and need to identify which of them lie in the fourth quadrant.
The fourth quadrant is defined by points $(x, y)$ where the x-coordinate is positive ($x > 0$) and the y-coordinate is negative ($y < 0$). The signs are (+, –).
Let's examine each point and determine its quadrant based on the signs of its coordinates:
- Point P: $(-1, 1)$. x is negative, y is positive. Signs are $(-, +)$. This point is in the II quadrant.
- Point Q: $(3, -4)$. x is positive, y is negative. Signs are $(+, -)$. This point is in the IV quadrant.
- Point R: $(1, -1)$. x is positive, y is negative. Signs are $(+, -)$. This point is in the IV quadrant.
- Point S: $(-2, -3)$. x is negative, y is negative. Signs are $(-, -)$. This point is in the III quadrant.
- Point T: $(-4, 4)$. x is negative, y is positive. Signs are $(-, +)$. This point is in the II quadrant.
The points that lie in the fourth quadrant (where signs are (+, –)) are Q $(3, -4)$ and R $(1, -1)$.
Comparing this finding with the given options, the correct answer is (B).
The correct option is (B) Q and R.
Question 15. If the coordinates of the two points are P (–2, 3) and Q(–3, 5), then (abscissa of P) – (abscissa of Q) is
(A) – 5
(B) 1
(C) – 1
(D) – 2
Answer:
The abscissa of a point is its x-coordinate.
The coordinates of point P are $(-2, 3)$.
Abscissa of P $= -2$
The coordinates of point Q are $(-3, 5)$.
Abscissa of Q $= -3$
We need to calculate (abscissa of P) – (abscissa of Q).
(Abscissa of P) – (Abscissa of Q) $= -2 - (-3)$
Calculating the subtraction:
$-2 - (-3) = -2 + 3 = 1$
So, (abscissa of P) – (abscissa of Q) is $1$.
Comparing with the given options, the correct answer is (B).
The correct option is (B) 1.
Question 16. If P (5, 1), Q (8, 0), R (0, 4), S (0, 5) and O (0, 0) are plotted on the graph paper, then the point(s) on the x-axis are
(A) P and R
(B) R and S
(C) Only Q
(D) Q and O
Answer:
A point lies on the x-axis if and only if its y-coordinate (ordinate) is 0.
Let's examine the y-coordinate of each given point:
- Point P: $(5, 1)$. The y-coordinate is $1$. Since $1 \neq 0$, P does not lie on the x-axis.
- Point Q: $(8, 0)$. The y-coordinate is $0$. Since the y-coordinate is $0$, Q lies on the x-axis. (It lies on the positive direction of the x-axis as x is positive).
- Point R: $(0, 4)$. The y-coordinate is $4$. Since $4 \neq 0$, R does not lie on the x-axis. (It lies on the positive direction of the y-axis as x is 0 and y is positive).
- Point S: $(0, 5)$. The y-coordinate is $5$. Since $5 \neq 0$, S does not lie on the x-axis. (It lies on the positive direction of the y-axis as x is 0 and y is positive).
- Point O: $(0, 0)$. The y-coordinate is $0$. Since the y-coordinate is $0$, O lies on the x-axis. (This is the origin, which lies on both the x-axis and the y-axis).
The points with a y-coordinate of 0 are Q $(8, 0)$ and O $(0, 0)$.
Therefore, the points on the x-axis are Q and O.
Comparing with the given options, the correct answer is (D).
The correct option is (D) Q and O.
Question 17. Abscissa of a point is positive in
(A) I and II quadrants
(B) I and IV quadrants
(C) I quadrant only
(D) II quadrant only
Answer:
The abscissa of a point is its x-coordinate.
We need to identify the quadrants where the x-coordinate of a point is positive ($x > 0$).
Let's consider the signs of the coordinates in each quadrant:
- Quadrant I: x positive, y positive $(+, +)$. Here, the abscissa is positive.
- Quadrant II: x negative, y positive $(-, +)$. Here, the abscissa is negative.
- Quadrant III: x negative, y negative $(-, -)$. Here, the abscissa is negative.
- Quadrant IV: x positive, y negative $(+, -)$. Here, the abscissa is positive.
Based on the signs, the abscissa of a point is positive in the I quadrant (where $x > 0$ and $y > 0$) and the IV quadrant (where $x > 0$ and $y < 0$).
Therefore, the abscissa of a point is positive in I and IV quadrants.
Comparing with the given options, the correct answer is (B).
The correct option is (B) I and IV quadrants.
Question 18. The points whose abscissa and ordinate have different signs will lie in
(A) I and II quadrants
(B) II and III quadrants
(C) I and III quadrants
(D) II and IV quadrants
Answer:
The abscissa is the x-coordinate, and the ordinate is the y-coordinate. We are looking for points where the signs of the x and y coordinates are different.
Let's look at the signs of $(x, y)$ in each quadrant:
- Quadrant I: $(+, +)$. The signs are the same (both positive).
- Quadrant II: $(-, +)$. The signs are different (x negative, y positive).
- Quadrant III: $(-, -)$. The signs are the same (both negative).
- Quadrant IV: $(+, -)$. The signs are different (x positive, y negative).
The quadrants where the abscissa and ordinate have different signs are the II quadrant (where x is negative and y is positive) and the IV quadrant (where x is positive and y is negative).
Therefore, the points whose abscissa and ordinate have different signs will lie in II and IV quadrants.
Comparing with the given options, the correct answer is (D).
The correct option is (D) II and IV quadrants.
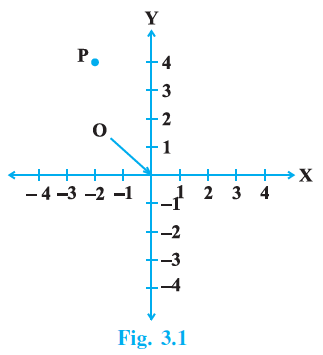
Question 19. In Fig. 3.1, coordinates of P are
(A) (– 4, 2)
(B) (–2, 4)
(C) (4, – 2)
(D) (2, – 4)
Answer:
The question asks for the coordinates of point P as shown in Fig. 3.1.
To find the coordinates of a point from a graph, we determine its position relative to the x-axis and y-axis.
The x-coordinate (abscissa) is found by drawing a vertical line from the point to the x-axis and reading the value where it intersects the x-axis.
The y-coordinate (ordinate) is found by drawing a horizontal line from the point to the y-axis and reading the value where it intersects the y-axis.
Looking at the figure, for point P:
A vertical line from P intersects the x-axis at $-2$. So, the x-coordinate of P is $-2$.
A horizontal line from P intersects the y-axis at $4$. So, the y-coordinate of P is $4$.
Therefore, the coordinates of point P are $(-2, 4)$.
Comparing these coordinates with the given options:
- (A) $(-4, 2)$
- (B) $(-2, 4)$
- (C) $(4, -2)$
- (D) $(2, -4)$
The coordinates of point P match option (B).
The correct option is (B) (–2, 4).
Question 20. In Fig. 3.2, the point identified by the coordinates (–5, 3) is

(A) T
(B) R
(C) L
(D) S
Answer:
We are asked to identify the point in Fig. 3.2 that has the coordinates $(-5, 3)$.
The coordinates of a point are given in the form $(x, y)$, where $x$ is the abscissa (distance along the x-axis) and $y$ is the ordinate (distance along the y-axis).
For the given coordinates $(-5, 3)$:
The x-coordinate is $-5$. This means we move $5$ units to the left from the origin along the x-axis.
The y-coordinate is $3$. This means we move $3$ units upwards from the point on the x-axis.
Let's locate the point in Fig. 3.2 that is situated at $x = -5$ and $y = 3$.
Starting from the origin $(0, 0)$, move left along the x-axis to the point where the x-value is $-5$. Then, from this position ($(-5, 0)$), move vertically upwards parallel to the y-axis to the point where the y-value is $3$.
Observing the graph, the point located at the intersection of the vertical line $x = -5$ and the horizontal line $y = 3$ is labeled as point T.
Let's also verify the coordinates of the other labeled points from the options for confirmation:
- Point T: The x-coordinate is $-5$, and the y-coordinate is $3$. So, T is $(-5, 3)$.
- Point R: The x-coordinate is $4$, and the y-coordinate is $-2$. So, R is $(4, -2)$.
- Point L: The x-coordinate is $-5$, and the y-coordinate is $-4$. So, L is $(-5, -4)$.
- Point S: The x-coordinate is $3$, and the y-coordinate is $-4$. So, S is $(3, -4)$.
The point with coordinates $(-5, 3)$ is indeed point T.
Comparing with the given options, the correct answer is (A).
The correct option is (A) T.
Question 21. The point whose ordinate is 4 and which lies on y-axis is
(A) (4, 0)
(B) (0, 4)
(C) (1, 4)
(D) (4, 2)
Answer:
We are looking for a point that satisfies two conditions:
1. Its ordinate is 4.
2. It lies on the y-axis.
The ordinate of a point is its y-coordinate. So, the first condition tells us that the y-coordinate of the point is 4.
y-coordinate $= 4$
A point lies on the y-axis if and only if its abscissa (x-coordinate) is 0.
x-coordinate $= 0$
So, the point must have an x-coordinate of 0 and a y-coordinate of 4.
The coordinates of the point are $(x, y) = (0, 4)$.
Let's examine the given options:
- (A) $(4, 0)$: Ordinate is 0, lies on the x-axis.
- (B) $(0, 4)$: Abscissa is 0, ordinate is 4. This point lies on the y-axis and has ordinate 4.
- (C) $(1, 4)$: Abscissa is 1, ordinate is 4. Does not lie on the y-axis.
- (D) $(4, 2)$: Abscissa is 4, ordinate is 2. Does not lie on the y-axis.
The point that satisfies both conditions is $(0, 4)$.
Comparing with the given options, the correct answer is (B).
The correct option is (B) (0, 4).
Question 22. Which of the points P(0, 3), Q(1, 0), R(0, – 1), S(–5, 0), T(1, 2) do not lie on the x-axis?
(A) P and R only
(B) Q and S only
(C) P, R and T
(D) Q, S and T
Answer:
A point lies on the x-axis if and only if its y-coordinate is 0.
We need to find the points that do not lie on the x-axis. These are the points whose y-coordinate is not 0.
Let's examine the y-coordinate of each given point:
- Point P: $(0, 3)$. The y-coordinate is $3$. Since $3 \neq 0$, P does not lie on the x-axis. (It lies on the y-axis).
- Point Q: $(1, 0)$. The y-coordinate is $0$. Since the y-coordinate is $0$, Q lies on the x-axis.
- Point R: $(0, -1)$. The y-coordinate is $-1$. Since $-1 \neq 0$, R does not lie on the x-axis. (It lies on the y-axis).
- Point S: $(-5, 0)$. The y-coordinate is $0$. Since the y-coordinate is $0$, S lies on the x-axis.
- Point T: $(1, 2)$. The y-coordinate is $2$. Since $2 \neq 0$, T does not lie on the x-axis. (It lies in the I quadrant).
The points whose y-coordinate is not 0 are P $(0, 3)$, R $(0, -1)$, and T $(1, 2)$.
Therefore, the points that do not lie on the x-axis are P, R, and T.
Comparing with the given options, the correct answer is (C).
The correct option is (C) P, R and T.
Question 23. The point which lies on y-axis at a distance of 5 units in the negative direction of y-axis is
(A) (0, 5)
(B) (5, 0)
(C) (0, – 5)
(D) (– 5, 0)
Answer:
We are looking for a point that satisfies two conditions:
1. It lies on the y-axis.
2. It is at a distance of 5 units in the negative direction of the y-axis.
A point lying on the y-axis has its x-coordinate equal to 0.
x-coordinate $= 0$
The distance of a point $(x, y)$ from the x-axis is $|y|$. This also represents the distance from the origin along the y-axis if the point is on the y-axis (i.e., $x=0$).
The point is at a distance of 5 units from the origin along the y-axis.
The direction is the negative direction of the y-axis. The y-values are negative in the negative direction of the y-axis.
So, the y-coordinate of the point is $-5$.
y-coordinate $= -5$
Combining the x and y coordinates, the point is $(0, -5)$.
Let's examine the given options:
- (A) $(0, 5)$: Lies on the y-axis, distance 5 units from origin, but in the positive direction.
- (B) $(5, 0)$: Lies on the x-axis, distance 5 units from origin.
- (C) $(0, -5)$: Lies on the y-axis (x=0), at a distance of $|-5| = 5$ units from the origin, and in the negative direction of the y-axis (y is negative).
- (D) $(-5, 0)$: Lies on the x-axis, distance 5 units from origin, in the negative direction of the x-axis.
The point that satisfies all conditions is $(0, -5)$.
Comparing with the given options, the correct answer is (C).
The correct option is (C) (0, – 5).
Question 24. The perpendicular distance of the point P (3, 4) from the y-axis is
(A) 3
(B) 4
(C) 5
(D) 7
Answer:
Let the point be P $(3, 4)$.
The perpendicular distance of a point from the y-axis is the absolute value of its x-coordinate (abscissa).
For the point P $(3, 4)$, the x-coordinate is $3$ and the y-coordinate is $4$.
The perpendicular distance from the y-axis is $|x| = |3| = 3$ units.
Think of it this way: To reach the point $(3, 4)$ from the origin $(0, 0)$, you move 3 units along the x-axis (horizontally) and then 4 units parallel to the y-axis (vertically). The horizontal movement of 3 units is the distance from the y-axis.
Note that the perpendicular distance of the point P $(3, 4)$ from the x-axis is $|y| = |4| = 4$ units.
We are asked for the distance from the y-axis, which is the absolute value of the x-coordinate.
The perpendicular distance of the point P $(3, 4)$ from the y-axis is 3.
Comparing with the given options, the correct answer is (A).
The correct option is (A) 3.
Sample Question 1 (Before Exercise 3.2)
Sample Question 1: Write whether the following statements are True or False? Justify your answer.
(i) Point (0, –2) lies on y-axis.
(ii) The perpendicular distance of the point (4, 3) from the x-axis is 4.
Answer:
(i) Point (0, –2) lies on y-axis.
For a point to lie on the y-axis, its abscissa (x-coordinate) must be $0$.
The given point is $(0, -2)$.
The x-coordinate of the point $(0, -2)$ is $0$.
Since the x-coordinate is $0$, the point $(0, -2)$ lies on the y-axis.
The statement is True.
Justification: A point $(x, y)$ lies on the y-axis if and only if $x=0$. For the point $(0, -2)$, the x-coordinate is $0$. Therefore, the point lies on the y-axis.
(ii) The perpendicular distance of the point (4, 3) from the x-axis is 4.
The perpendicular distance of a point $(x, y)$ from the x-axis is given by the absolute value of its ordinate (y-coordinate), i.e., $|y|$.
The given point is $(4, 3)$.
The x-coordinate is $4$ and the y-coordinate is $3$.
The perpendicular distance from the x-axis is the absolute value of the y-coordinate.
Distance $= |3| = 3$ units
The statement claims the perpendicular distance is 4, but we calculated it to be 3.
The statement is False.
Justification: The perpendicular distance of a point $(x, y)$ from the x-axis is $|y|$. For the point $(4, 3)$, the y-coordinate is $3$. The perpendicular distance from the x-axis is $|3| = 3$. The statement says the distance is 4, which is incorrect.
Exercise 3.2
Question 1. Write whether the following statements are True or False? Justify your answer.
(i) Point (3, 0) lies in the first quadrant.
(ii) Points (1, –1) and (–1, 1) lie in the same quadrant.
(iii) The coordinates of a point whose ordinate is $-\frac{1}{2}$ and abscissa is 1 are $-\frac{1}{2}$ , 1.
(iv) A point lies on y-axis at a distance of 2 units from the x-axis. Its coordinates are (2, 0).
(v) (-1, 7) is a point in the second quadrant.
Answer:
(i) Point (3, 0) lies in the first quadrant.
A point lies in a quadrant if both its x and y coordinates are non-zero.
The given point is $(3, 0)$. The y-coordinate is $0$.
Points with a y-coordinate of $0$ lie on the x-axis, not in any quadrant.
The first quadrant is for points with coordinates $(+, +)$. The point $(3, 0)$ has coordinates $(+, 0)$.
The statement is False.
Justification: A point $(x, y)$ lies in a quadrant if $x \neq 0$ and $y \neq 0$. If either coordinate is $0$, the point lies on an axis. For the point $(3, 0)$, the y-coordinate is $0$, so it lies on the x-axis, not in the first quadrant.
(ii) Points (1, –1) and (–1, 1) lie in the same quadrant.
Let's determine the quadrant for each point by looking at the signs of their coordinates.
For point $(1, -1)$: x is positive (+), y is negative (–). Signs are $(+, –)$. This is the IV quadrant.
For point $(-1, 1)$: x is negative (–), y is positive (+). Signs are $(–, +)$. This is the II quadrant.
Since the points lie in different quadrants (IV and II), they do not lie in the same quadrant.
The statement is False.
Justification: The point $(1, -1)$ has a positive x-coordinate and a negative y-coordinate, so it lies in the IV quadrant. The point $(-1, 1)$ has a negative x-coordinate and a positive y-coordinate, so it lies in the II quadrant. Since they are in different quadrants, the statement is false.
(iii) The coordinates of a point whose ordinate is $-\frac{1}{2}$ and abscissa is 1 are $-\frac{1}{2}$ , 1.
The coordinates of a point are always written in the form (abscissa, ordinate), or $(x, y)$.
We are given that the ordinate (y-coordinate) is $-\frac{1}{2}$ and the abscissa (x-coordinate) is $1$.
So, the x-coordinate is $1$ and the y-coordinate is $-\frac{1}{2}$.
The correct coordinates should be $(1, -\frac{1}{2})$.
The statement gives the coordinates as $(-\frac{1}{2}, 1)$, where the abscissa is $-\frac{1}{2}$ and the ordinate is $1$. This is incorrect.
The statement is False.
Justification: The coordinates of a point are written in the order (abscissa, ordinate). Given that the abscissa is $1$ and the ordinate is $-\frac{1}{2}$, the correct coordinates are $(1, -\frac{1}{2})$, not $(-\frac{1}{2}, 1)$.
(iv) A point lies on y-axis at a distance of 2 units from the x-axis. Its coordinates are (2, 0).
A point on the y-axis has an x-coordinate of $0$. The point is of the form $(0, y)$.
The distance of a point $(x, y)$ from the x-axis is $|y|$. We are given this distance is 2 units.
Distance from x-axis $= |y| = 2$
So, the y-coordinate can be $2$ or $-2$. The point could be $(0, 2)$ or $(0, -2)$. Both lie on the y-axis at a distance of 2 units from the x-axis.
The statement claims the coordinates are $(2, 0)$. This point lies on the x-axis (because the y-coordinate is 0), not the y-axis.
The statement is False.
Justification: A point on the y-axis has coordinates $(0, y)$. Its distance from the x-axis is $|y|$. If the distance is 2, then $|y|=2$, so $y=2$ or $y=-2$. The points are $(0, 2)$ or $(0, -2)$. The coordinates $(2, 0)$ represent a point on the x-axis at a distance of 2 units from the origin.
(v) (-1, 7) is a point in the second quadrant.
Let's examine the signs of the coordinates of the point $(-1, 7)$.
The x-coordinate is $-1$, which is negative (–).
The y-coordinate is $7$, which is positive (+).
The signs are $(–, +)$.
The quadrants are defined by the signs:
- I: (+, +)
- II: (–, +)
- III: (–, –)
- IV: (+, –)
A point with signs $(–, +)$ lies in the second quadrant.
The statement is True.
Justification: In the point $(-1, 7)$, the x-coordinate is negative (–) and the y-coordinate is positive (+). Points with a negative x-coordinate and a positive y-coordinate lie in the second quadrant.
Sample Question 1 & 2 (Before Exercise 3.3)
Sample Question 1: Plot the point P (– 6, 2) and from it draw PM and PN as perpendiculars to x-axis and y-axis, respectively. Write the coordinates of the points M and N.
Answer:
The given point is P $(-6, 2)$.
PM is the perpendicular drawn from point P to the x-axis.
When a perpendicular is drawn from a point $(x, y)$ to the x-axis, the foot of the perpendicular lies on the x-axis. The coordinates of the foot of the perpendicular will have the same x-coordinate as the original point, and its y-coordinate will be 0 (since it's on the x-axis).
For point P $(-6, 2)$, the x-coordinate is $-6$ and the y-coordinate is $2$.
The foot of the perpendicular M on the x-axis will have the same x-coordinate as P, which is $-6$, and its y-coordinate will be $0$.
Therefore, the coordinates of point M are $(-6, 0)$.
M $= (-6, 0)$
PN is the perpendicular drawn from point P to the y-axis.
When a perpendicular is drawn from a point $(x, y)$ to the y-axis, the foot of the perpendicular lies on the y-axis. The coordinates of the foot of the perpendicular will have the same y-coordinate as the original point, and its x-coordinate will be 0 (since it's on the y-axis).
For point P $(-6, 2)$, the x-coordinate is $-6$ and the y-coordinate is $2$.
The foot of the perpendicular N on the y-axis will have the same y-coordinate as P, which is $2$, and its x-coordinate will be $0$.
Therefore, the coordinates of point N are $(0, 2)$.
N $= (0, 2)$
The coordinates of point M are $(-6, 0)$ and the coordinates of point N are $(0, 2)$.
Sample Question 2: From the Fig. 3.4, write the following:

(i) Coordinates of B, C and E
(ii) The point identified by the coordinates (0, – 2)
(iii) The abscissa of the point H
(iv) The ordinate of the point D
Answer:
We need to find the requested information by examining the given figure (Fig. 3.4).
(i) Coordinates of B, C and E
To find the coordinates of a point, we drop a perpendicular from the point to the x-axis to find the x-coordinate (abscissa) and a perpendicular to the y-axis to find the y-coordinate (ordinate).
From the figure:
- For point B, the perpendicular to the x-axis meets at 5, and it is on the x-axis, so the y-coordinate is 0. Coordinates of B are $(5, 0)$.
- For point C, the perpendicular to the x-axis meets at 5, and the perpendicular to the y-axis meets at -5. Coordinates of C are $(5, -5)$.
- For point E, the perpendicular to the x-axis meets at -3, and the perpendicular to the y-axis meets at -4. Coordinates of E are $(-3, -4)$.
The coordinates are: B (5, 0), C (5, –5), and E (–3, –4).
(ii) The point identified by the coordinates (0, – 2)
A point with coordinates $(0, -2)$ has an x-coordinate of 0 and a y-coordinate of -2.
An x-coordinate of 0 means the point lies on the y-axis.
A y-coordinate of -2 means the point is located 2 units below the origin on the y-axis.
Looking at the figure, the point on the y-axis at $-2$ is labeled as G.
The point identified by the coordinates (0, – 2) is G.
(iii) The abscissa of the point H
The abscissa of a point is its x-coordinate.
From the figure, locate point H. Dropping a perpendicular from H to the x-axis, we see it meets the x-axis at -5.
The coordinates of H are $(-5, 3)$. The abscissa is the first value, which is $-5$.
The abscissa of the point H is –5.
(iv) The ordinate of the point D
The ordinate of a point is its y-coordinate.
From the figure, locate point D. Dropping a perpendicular from D to the y-axis, we see it meets the y-axis at 4.
The coordinates of D are $(4, 4)$. The ordinate is the second value, which is $4$.
The ordinate of the point D is 4.
Exercise 3.3
Question 1. Write the coordinates of each of the points P, Q, R, S, T and O from the Fig. 3.5.

Answer:
We need to find the coordinates of the points P, Q, R, S, T, and O from the given figure (Fig. 3.5).
The coordinates of any point in the Cartesian plane are given in the form $(x, y)$, where $x$ is the abscissa and $y$ is the ordinate. The abscissa is the perpendicular distance of the point from the y-axis (with sign), and the ordinate is the perpendicular distance of the point from the x-axis (with sign).
Let's determine the coordinates for each labeled point by observing their positions relative to the x and y axes:
For point P:
Move horizontally from P to the x-axis. It meets at $1$. So, the x-coordinate is $1$.
Move vertically from P to the y-axis. It meets at $1$. So, the y-coordinate is $1$.
Coordinates of P are (1, 1).
For point Q:
Move horizontally from Q to the x-axis. It meets at $-3$. So, the x-coordinate is $-3$.
Move vertically from Q to the y-axis. It meets at $2$. So, the y-coordinate is $2$.
Coordinates of Q are (–3, 2).
For point R:
Move horizontally from R to the x-axis. It meets at $-4$. So, the x-coordinate is $-4$.
Move vertically from R to the y-axis. It meets at $-2$. So, the y-coordinate is $-2$.
Coordinates of R are (–4, –2).
For point S:
Move horizontally from S to the x-axis. It meets at $2$. So, the x-coordinate is $2$.
Move vertically from S to the y-axis. It meets at $-4$. So, the y-coordinate is $-4$.
Coordinates of S are (2, –4).
For point T:
Point T lies on the x-axis. Any point on the x-axis has a y-coordinate of $0$.
The position of T on the x-axis is at $4$. So, the x-coordinate is $4$.
Coordinates of T are (4, 0).
For point O:
Point O is the origin, which is the intersection of the x-axis and y-axis.
The coordinates of the origin are always $(0, 0)$.
Coordinates of O are (0, 0).
Summarizing the coordinates of the points:
P: (1, 1)
Q: (–3, 2)
R: (–4, –2)
S: (2, –4)
T: (4, 0)
O: (0, 0)
Question 2. Plot the following points and write the name of the figure obtained by joining them in order:
P(– 3, 2), Q (– 7, – 3), R (6, – 3), S (2, 2)
Answer:
We are given the points P $(-3, 2)$, Q $(-7, -3)$, R $(6, -3)$, and S $(2, 2)$. We need to plot these points and identify the figure formed by joining them in the order P-Q-R-S-P.
Let's plot the points on a coordinate plane:
- Point P $(-3, 2)$: Move 3 units left from the origin, then 2 units up.
- Point Q $(-7, -3)$: Move 7 units left from the origin, then 3 units down.
- Point R $(6, -3)$: Move 6 units right from the origin, then 3 units down.
- Point S $(2, 2)$: Move 2 units right from the origin, then 2 units up.
Now, let's join the points in the given order: PQ, QR, RS, and SP.
Let's examine the sides of the figure:
- Side QR connects Q $(-7, -3)$ and R $(6, -3)$. Notice that the y-coordinate is the same for both points ($y = -3$). This means the line segment QR is a horizontal line. The length of QR is the absolute difference of the x-coordinates: $|6 - (-7)| = |6 + 7| = |13| = 13$ units.
- Side SP connects S $(2, 2)$ and P $(-3, 2)$. Notice that the y-coordinate is the same for both points ($y = 2$). This means the line segment SP is also a horizontal line. The length of SP is the absolute difference of the x-coordinates: $|-3 - 2| = |-5| = 5$ units.
Since both QR and SP are horizontal lines, they are parallel to each other and parallel to the x-axis.
Thus, we have one pair of parallel sides (QR || SP).
Now let's consider the other two sides, PQ and RS.
Side PQ connects P $(-3, 2)$ and Q $(-7, -3)$. This is not a horizontal or vertical line.
Side RS connects R $(6, -3)$ and S $(2, 2)$. This is also not a horizontal or vertical line.
A quadrilateral with exactly one pair of parallel sides is called a trapezoid (or trapezium).
In this figure, the parallel sides are QR and SP, and their lengths are different (13 and 5). The non-parallel sides are PQ and RS. Since we have exactly one pair of parallel sides, the figure PQRS is a trapezoid.
The name of the figure obtained by joining the points P, Q, R, and S in order is a Trapezoid.
Question 3. Plot the points (x, y) given by the following table:
| x | 2 | 4 | -3 | -2 | 3 | 0 |
|---|---|---|---|---|---|---|
| y | 4 | 2 | 0 | 5 | -3 | 0 |
Answer:
The table provides the x and y coordinates for six different points. We can list these points as ordered pairs $(x, y)$.
From the table, the points are:
- Point 1: x = 2, y = 4 $\implies$ (2, 4)
- Point 2: x = 4, y = 2 $\implies$ (4, 2)
- Point 3: x = -3, y = 0 $\implies$ (–3, 0)
- Point 4: x = -2, y = 5 $\implies$ (–2, 5)
- Point 5: x = 3, y = -3 $\implies$ (3, –3)
- Point 6: x = 0, y = 0 $\implies$ (0, 0)
To plot these points, we would draw a Cartesian coordinate plane with the x-axis and y-axis intersecting at the origin (0, 0).
For each point $(x, y)$, we locate the corresponding value on the x-axis and the y-axis. Then, we move horizontally from the y-axis position and vertically from the x-axis position. The intersection of these imaginary lines is the location of the point.
Specifically:
- Plot (2, 4) by moving 2 units right from the origin and 4 units up.
- Plot (4, 2) by moving 4 units right from the origin and 2 units up.
- Plot (–3, 0) by moving 3 units left from the origin along the x-axis.
- Plot (–2, 5) by moving 2 units left from the origin and 5 units up.
- Plot (3, –3) by moving 3 units right from the origin and 3 units down.
- Plot (0, 0) at the origin itself.
The question asks to plot the points. The points to be plotted are (2, 4), (4, 2), (–3, 0), (–2, 5), (3, –3), and (0, 0).
Question 4. Plot the following points and check whether they are collinear or not :
(i) (1, 3), (– 1, – 1), (– 2, – 3)
(ii) (1, 1), (2, – 3), (– 1, – 2)
(iii) (0, 0), (2, 2), (5, 5)
Answer:
Points are collinear if they lie on the same straight line. We can check for collinearity by plotting the points or by checking the slope between pairs of points.
(i) Points (1, 3), (– 1, – 1), (– 2, – 3)
Let's plot the points. We can also calculate the slope between consecutive points.
The slope between two points $(x_1, y_1)$ and $(x_2, y_2)$ is given by $m = \frac{y_2 - y_1}{x_2 - x_1}$, provided $x_1 \neq x_2$. If the slope between any two pairs of points is the same, and they share a common point, the points are collinear.
Slope between (1, 3) and (–1, –1):
$m_1 = \frac{-1 - 3}{-1 - 1} = \frac{-4}{-2} = 2$
Slope between (–1, –1) and (–2, –3):
$m_2 = \frac{-3 - (-1)}{-2 - (-1)} = \frac{-3 + 1}{-2 + 1} = \frac{-2}{-1} = 2$
Since the slope between (1, 3) and (–1, –1) is 2, and the slope between (–1, –1) and (–2, –3) is also 2, and the point (–1, –1) is common to both pairs, the three points lie on the same line.
Therefore, the points (1, 3), (– 1, – 1), (– 2, – 3) are collinear.
(ii) Points (1, 1), (2, – 3), (– 1, – 2)
Let's calculate the slopes.
Slope between (1, 1) and (2, –3):
$m_1 = \frac{-3 - 1}{2 - 1} = \frac{-4}{1} = -4$
Slope between (2, –3) and (–1, –2):
$m_2 = \frac{-2 - (-3)}{-1 - 2} = \frac{-2 + 3}{-3} = \frac{1}{-3} = -\frac{1}{3}$
Since $m_1 \neq m_2$, the slopes between the pairs of points are different. This means the three points do not lie on the same straight line.
Therefore, the points (1, 1), (2, – 3), (– 1, – 2) are not collinear.
(iii) Points (0, 0), (2, 2), (5, 5)
Let's calculate the slopes.
Slope between (0, 0) and (2, 2):
$m_1 = \frac{2 - 0}{2 - 0} = \frac{2}{2} = 1$
Slope between (2, 2) and (5, 5):
$m_2 = \frac{5 - 2}{5 - 2} = \frac{3}{3} = 1$
Since the slopes are the same ($m_1 = m_2 = 1$), and the point (2, 2) is common to both pairs, the three points lie on the same line.
The equation of the line passing through these points is $y = x$.
Therefore, the points (0, 0), (2, 2), (5, 5) are collinear.
Question 5. Without plotting the points indicate the quadrant in which they will lie, if
(i) ordinate is 5 and abscissa is – 3
(ii) abscissa is – 5 and ordinate is – 3
(iii) abscissa is – 5 and ordinate is 3
(iv) ordinate is 5 and abscissa is 3
Answer:
The quadrant in which a point $(x, y)$ lies is determined by the signs of its coordinates.
The rules for the quadrants are:
- Quadrant I: $x > 0$, $y > 0$ (abscissa positive, ordinate positive) - (+, +)
- Quadrant II: $x < 0$, $y > 0$ (abscissa negative, ordinate positive) - (–, +)
- Quadrant III: $x < 0$, $y < 0$ (abscissa negative, ordinate negative) - (–, –)
- Quadrant IV: $x > 0$, $y < 0$ (abscissa positive, ordinate negative) - (+, –)
Points on the axes (where either x or y is 0) do not lie in any quadrant.
Now let's consider each case:
(i) ordinate is 5 and abscissa is – 3
Abscissa (x-coordinate) $= -3$ (negative)
Ordinate (y-coordinate) $= 5$ (positive)
The signs are $(–, +)$. This corresponds to the II quadrant.
(ii) abscissa is – 5 and ordinate is – 3
Abscissa (x-coordinate) $= -5$ (negative)
Ordinate (y-coordinate) $= -3$ (negative)
The signs are $(–, –)$. This corresponds to the III quadrant.
(iii) abscissa is – 5 and ordinate is 3
Abscissa (x-coordinate) $= -5$ (negative)
Ordinate (y-coordinate) $= 3$ (positive)
The signs are $(–, +)$. This corresponds to the II quadrant.
(iv) ordinate is 5 and abscissa is 3
Abscissa (x-coordinate) $= 3$ (positive)
Ordinate (y-coordinate) $= 5$ (positive)
The signs are $(+, +)$. This corresponds to the I quadrant.
Summary of findings:
(i) II quadrant
(ii) III quadrant
(iii) II quadrant
(iv) I quadrant
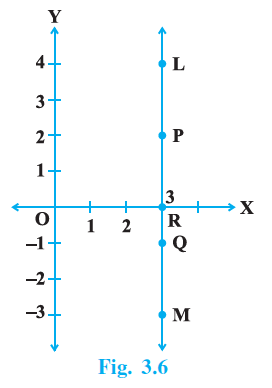
Question 6. In Fig. 3.6, LM is a line parallel to the y-axis at a distance of 3 units.
(i) What are the coordinates of the points P, R and Q?
(ii) What is the difference between the abscissa of the points L and M?
Answer:
We are given that LM is a line parallel to the y-axis at a distance of 3 units from it. Looking at the figure, the line LM is to the right of the y-axis, meaning the x-coordinate for all points on this line is positive 3.
The equation of the line LM is $x = 3$.
(i) What are the coordinates of the points P, R and Q?
All points on the line LM have an x-coordinate (abscissa) of 3.
To find the y-coordinate (ordinate) of each point, we look at where the point lies horizontally relative to the y-axis values.
- Point P is on the line $x=3$ and horizontally aligned with the y-axis value $2$. So, the coordinates of P are $(3, 2)$.
- Point R is on the line $x=3$ and horizontally aligned with the x-axis (y=0). So, the coordinates of R are $(3, 0)$.
- Point Q is on the line $x=3$ and horizontally aligned with the y-axis value $-1$. So, the coordinates of Q are $(3, -1)$.
The coordinates of the points are: P (3, 2), R (3, 0), and Q (3, –1).
(ii) What is the difference between the abscissa of the points L and M?
Points L and M lie on the line LM.
As established earlier, every point on the line LM has an x-coordinate (abscissa) of 3.
The abscissa of point L is $3$.
The abscissa of point M is $3$.
The difference between the abscissa of points L and M is the abscissa of L minus the abscissa of M (or vice versa).
Difference = Abscissa of L – Abscissa of M
Difference $= 3 - 3 = 0$
The difference between the abscissa of the points L and M is 0.
Question 7. In which quadrant or on which axis each of the following points lie?
(– 3, 5), (4, – 1), (2, 0), (2, 2), (– 3, – 6)
Answer:
To determine the quadrant or axis a point $(x, y)$ lies on, we examine the signs of its coordinates:
- If $x > 0$ and $y > 0$, the point is in Quadrant I.
- If $x < 0$ and $y > 0$, the point is in Quadrant II.
- If $x < 0$ and $y < 0$, the point is in Quadrant III.
- If $x > 0$ and $y < 0$, the point is in Quadrant IV.
- If $y = 0$ and $x \neq 0$, the point is on the x-axis.
- If $x = 0$ and $y \neq 0$, the point is on the y-axis.
- If $x = 0$ and $y = 0$, the point is the origin (lies on both axes).
Let's analyze each point:
Point (– 3, 5):
x-coordinate is $-3$ (negative).
y-coordinate is $5$ (positive).
Since $x < 0$ and $y > 0$, the point lies in the II quadrant.
Point (4, – 1):
x-coordinate is $4$ (positive).
y-coordinate is $-1$ (negative).
Since $x > 0$ and $y < 0$, the point lies in the IV quadrant.
Point (2, 0):
x-coordinate is $2$ (non-zero).
y-coordinate is $0$.
Since $y = 0$ and $x \neq 0$, the point lies on the x-axis.
Point (2, 2):
x-coordinate is $2$ (positive).
y-coordinate is $2$ (positive).
Since $x > 0$ and $y > 0$, the point lies in the I quadrant.
Point (– 3, – 6):
x-coordinate is $-3$ (negative).
y-coordinate is $-6$ (negative).
Since $x < 0$ and $y < 0$, the point lies in the III quadrant.
Summary of locations:
- (– 3, 5): II quadrant
- (4, – 1): IV quadrant
- (2, 0): on the x-axis
- (2, 2): I quadrant
- (– 3, – 6): III quadrant
Question 8. Which of the following points lie on y-axis?
A (1, 1), B (1, 0), C (0, 1), D (0, 0), E (0, – 1), F (– 1, 0), G (0, 5), H (– 7, 0), I (3, 3).
Answer:
A point lies on the y-axis if and only if its x-coordinate (abscissa) is 0.
We need to examine the x-coordinate of each given point to check if it is 0.
- Point A (1, 1): The x-coordinate is $1$. Since $1 \neq 0$, point A does not lie on the y-axis.
- Point B (1, 0): The x-coordinate is $1$. Since $1 \neq 0$, point B does not lie on the y-axis. (It lies on the x-axis).
- Point C (0, 1): The x-coordinate is $0$. Since the x-coordinate is $0$, point C lies on the y-axis.
- Point D (0, 0): The x-coordinate is $0$. Since the x-coordinate is $0$, point D lies on the y-axis. (This is the origin, which lies on both axes).
- Point E (0, – 1): The x-coordinate is $0$. Since the x-coordinate is $0$, point E lies on the y-axis.
- Point F (– 1, 0): The x-coordinate is $-1$. Since $-1 \neq 0$, point F does not lie on the y-axis. (It lies on the x-axis).
- Point G (0, 5): The x-coordinate is $0$. Since the x-coordinate is $0$, point G lies on the y-axis.
- Point H (– 7, 0): The x-coordinate is $-7$. Since $-7 \neq 0$, point H does not lie on the y-axis. (It lies on the x-axis).
- Point I (3, 3): The x-coordinate is $3$. Since $3 \neq 0$, point I does not lie on the y-axis.
The points whose x-coordinate is 0 are C (0, 1), D (0, 0), E (0, – 1), and G (0, 5).
Therefore, the points that lie on the y-axis are C, D, E, and G.
Question 9. Plot the points (x, y) given by the following table. Use scale 1 cm = 0.25 units
| x | 1.25 | 0.25 | 1.5 | -1.75 |
|---|---|---|---|---|
| y | -0.5 | 1 | 1.5 | -0.25 |
Answer:
The table provides four points with their x and y coordinates.
The points are:
- Point 1: $(1.25, -0.5)$
- Point 2: $(0.25, 1)$
- Point 3: $(1.5, 1.5)$
- Point 4: $(-1.75, -0.25)$
We are asked to plot these points using a scale of 1 cm = 0.25 units.
To plot a point $(x, y)$ with this scale, we determine the distance to move along the x-axis and y-axis from the origin. Since 1 cm represents 0.25 units, to move $x$ units along the x-axis, we need to move $x / 0.25 = 4x$ cm. Similarly, to move $y$ units along the y-axis, we need to move $y / 0.25 = 4y$ cm.
Let's calculate the distance in cm from the origin for each point using the scale:
- Point 1: (1.25, -0.5)
x-distance in cm $= 4 \times 1.25 = 5$ cm (to the right)
y-distance in cm $= 4 \times (-0.5) = -2$ cm (2 cm downwards) - Point 2: (0.25, 1)
x-distance in cm $= 4 \times 0.25 = 1$ cm (to the right)
y-distance in cm $= 4 \times 1 = 4$ cm (upwards) - Point 3: (1.5, 1.5)
x-distance in cm $= 4 \times 1.5 = 6$ cm (to the right)
y-distance in cm $= 4 \times 1.5 = 6$ cm (upwards) - Point 4: (-1.75, -0.25)
x-distance in cm $= 4 \times (-1.75) = -7$ cm (7 cm to the left)
y-distance in cm $= 4 \times (-0.25) = -1$ cm (1 cm downwards)
To plot the points, one would draw a coordinate plane. Mark the axes with a scale where each 1 cm interval represents 0.25 units (e.g., mark the axes at intervals of 0.25, 0.50, 0.75, 1.00, etc.). Then locate each point based on the calculated distances in cm or directly using the unit scale.
For example, to plot (1.25, -0.5): move 1.25 units along the positive x-axis (which is 5 cm from the origin), then move 0.5 units along the negative y-axis (which is 2 cm downwards).
The plotting process involves drawing the graph paper and marking the points accordingly. The question asks to plot the points, so listing the points and indicating how to plot them with the given scale is the appropriate response in text format.
Question 10. A point lies on the x-axis at a distance of 7 units from the y-axis. What are its coordinates? What will be the coordinates if it lies on y-axis at a distance of –7 units from x-axis?
Answer:
Let's address the first part of the question:
A point lies on the x-axis. This means its y-coordinate is 0.
The distance of a point $(x, y)$ from the y-axis is given by the absolute value of its x-coordinate, $|x|$.
We are given that the distance from the y-axis is 7 units.
Distance from y-axis $= |x| = 7$
From $|x| = 7$, the x-coordinate can be $7$ or $-7$.
$x = 7$ or $x = -7$
Since the point lies on the x-axis, its y-coordinate is 0. So the possible points are $(7, 0)$ or $(-7, 0)$.
The question states "at a distance of 7 units from the y-axis". Distance is a non-negative value. A distance of 7 units from the y-axis means the absolute value of the x-coordinate is 7.
The point could be on the positive side of the x-axis (at $x=7$) or on the negative side of the x-axis (at $x=-7$). Both points are 7 units away from the y-axis along the x-axis.
The coordinates of the point lying on the x-axis at a distance of 7 units from the y-axis are (7, 0) or (–7, 0).
Now let's address the second part of the question:
What will be the coordinates if it lies on the y-axis at a distance of –7 units from x-axis?
A point lies on the y-axis. This means its x-coordinate is 0. The point is of the form $(0, y)$.
The distance of a point $(x, y)$ from the x-axis is given by the absolute value of its y-coordinate, $|y|$.
The phrase "distance of –7 units from x-axis" is unusual because distance is typically a non-negative value. However, in the context of coordinates and axes, "distance from x-axis" often refers to the y-coordinate itself, with its sign indicating whether the point is above or below the x-axis.
If we interpret "distance of –7 units from x-axis" as meaning the y-coordinate is $-7$ (i.e., 7 units below the x-axis), then the y-coordinate is $-7$.
y-coordinate $= -7$
Since the point lies on the y-axis, its x-coordinate is 0.
The coordinates of the point are $(0, -7)$.
If we were to interpret "distance" strictly as absolute value, then the distance is $|y|$, which cannot be $-7$. The wording suggests that the 'distance' here includes direction, meaning the y-coordinate itself is -7.
The coordinates if it lies on y-axis at a "distance of –7 units from x-axis" are (0, –7).
Question 11. Find the coordinates of the point
(i) which lies on x and y axes both.
(ii) whose ordinate is – 4 and which lies on y-axis.
(iii) whose abscissa is 5 and which lies on x-axis.
Answer:
Let the coordinates of a point be $(x, y)$.
(i) which lies on x and y axes both.
A point lies on the x-axis if its y-coordinate is 0.
A point lies on the y-axis if its x-coordinate is 0.
For a point to lie on both the x-axis and the y-axis, both of these conditions must be met.
x-coordinate $= 0$
y-coordinate $= 0$
The only point with coordinates $(0, 0)$ is the origin.
The coordinates of the point which lies on x and y axes both are (0, 0).
(ii) whose ordinate is – 4 and which lies on y-axis.
The ordinate is the y-coordinate. We are given that the ordinate is $-4$.
y-coordinate $= -4$
The point lies on the y-axis. A point on the y-axis has its x-coordinate (abscissa) equal to 0.
x-coordinate $= 0$
Combining the x and y coordinates, the point is $(0, -4)$.
The coordinates of the point are (0, –4).
(iii) whose abscissa is 5 and which lies on x-axis.
The abscissa is the x-coordinate. We are given that the abscissa is $5$.
x-coordinate $= 5$
The point lies on the x-axis. A point on the x-axis has its y-coordinate (ordinate) equal to 0.
y-coordinate $= 0$
Combining the x and y coordinates, the point is $(5, 0)$.
The coordinates of the point are (5, 0).
Question 12. Taking 0.5 cm as 1 unit, plot the following points on the graph paper :
A (1, 3), B (– 3, – 1), C (1, – 4), D (– 2, 3), E (0, – 8), F (1, 0)
Answer:
We are given six points to plot on a graph paper using a specific scale: 0.5 cm = 1 unit.
The scale means that for every 1 unit distance on the coordinate axes, we should measure 0.5 cm on the graph paper. Equivalently, 1 cm on the graph paper represents $1 / 0.5 = 2$ units on the coordinate axes.
To plot a point $(x, y)$, we move $|x|$ units along the x-axis (right if $x > 0$, left if $x < 0$) and $|y|$ units along the y-axis (up if $y > 0$, down if $y < 0$). Using the scale, this corresponds to moving $|x| \times 0.5$ cm horizontally and $|y| \times 0.5$ cm vertically from the origin.
Let's determine the movement in cm from the origin for each point:
- Point A (1, 3):
x-movement: $1 \times 0.5$ cm $= 0.5$ cm (right)
y-movement: $3 \times 0.5$ cm $= 1.5$ cm (up) - Point B (– 3, – 1):
x-movement: $|-3| \times 0.5$ cm $= 3 \times 0.5$ cm $= 1.5$ cm (left)
y-movement: $|-1| \times 0.5$ cm $= 1 \times 0.5$ cm $= 0.5$ cm (down) - Point C (1, – 4):
x-movement: $1 \times 0.5$ cm $= 0.5$ cm (right)
y-movement: $|-4| \times 0.5$ cm $= 4 \times 0.5$ cm $= 2.0$ cm (down) - Point D (– 2, 3):
x-movement: $|-2| \times 0.5$ cm $= 2 \times 0.5$ cm $= 1.0$ cm (left)
y-movement: $3 \times 0.5$ cm $= 1.5$ cm (up) - Point E (0, – 8):
x-movement: $0 \times 0.5$ cm $= 0$ cm (on the y-axis)
y-movement: $|-8| \times 0.5$ cm $= 8 \times 0.5$ cm $= 4.0$ cm (down) - Point F (1, 0):
x-movement: $1 \times 0.5$ cm $= 0.5$ cm (right)
y-movement: $0 \times 0.5$ cm $= 0$ cm (on the x-axis)
To perform the plotting, draw the x and y axes on graph paper. Since 0.5 cm represents 1 unit, mark the axes with intervals of 0.5 cm, labeling them as 1, 2, 3, etc. (and -1, -2, etc.). For example, the point on the x-axis at 1 unit is 0.5 cm from the origin, at 2 units is 1 cm from the origin, etc.
Then locate each point:
- A (1, 3): Move right to the 1 unit mark on the x-axis, then up to the 3 unit mark on the y-axis. (This is 0.5 cm right and 1.5 cm up from origin).
- B (– 3, – 1): Move left to the -3 unit mark on the x-axis, then down to the -1 unit mark on the y-axis. (This is 1.5 cm left and 0.5 cm down from origin).
- C (1, – 4): Move right to the 1 unit mark on the x-axis, then down to the -4 unit mark on the y-axis. (This is 0.5 cm right and 2 cm down from origin).
- D (– 2, 3): Move left to the -2 unit mark on the x-axis, then up to the 3 unit mark on the y-axis. (This is 1 cm left and 1.5 cm up from origin).
- E (0, – 8): Stay on the y-axis, move down to the -8 unit mark. (This is 4 cm down from origin on the y-axis).
- F (1, 0): Move right to the 1 unit mark on the x-axis, stay on the x-axis. (This is 0.5 cm right from origin on the x-axis).
The process of plotting involves drawing the graph and marking these locations. This text describes the steps involved in the plotting.
Sample Question 1 (Before Exercise 3.4)
Sample Question 1: Three vertices of a rectangle are (3, 2), (– 4, 2) and (– 4, 5). Plot these points and find the coordinates of the fourth vertex.
Answer:
Let the three given vertices of the rectangle be A $(3, 2)$, B $(-4, 2)$, and C $(-4, 5)$. Let the fourth vertex be D $(x, y)$.
Let's analyze the given coordinates:
- Points A $(3, 2)$ and B $(-4, 2)$ have the same y-coordinate ($y=2$). This means the line segment AB is a horizontal line. The length of AB is the absolute difference of the x-coordinates: $|-4 - 3| = |-7| = 7$ units.
- Points B $(-4, 2)$ and C $(-4, 5)$ have the same x-coordinate ($x=-4$). This means the line segment BC is a vertical line. The length of BC is the absolute difference of the y-coordinates: $|5 - 2| = |3| = 3$ units.
In a rectangle, adjacent sides are perpendicular, and opposite sides are parallel and equal in length.
Since AB is horizontal and BC is vertical, the angle at B ($\angle$ABC) is $90^\circ$. This confirms that A, B, and C can be consecutive vertices of a rectangle.
If A, B, C are consecutive vertices, then the vertices are in the order A $\to$ B $\to$ C $\to$ D or A $\to$ B $\leftarrow$ C $\leftarrow$ D. Assuming the order A, B, C, D is consecutive (either clockwise or counterclockwise), AB is parallel to DC and BC is parallel to AD.
Since AB is parallel to the x-axis (horizontal), DC must also be parallel to the x-axis. This means the y-coordinate of D must be the same as the y-coordinate of C.
y-coordinate of D = y-coordinate of C = 5
So, D is $(x, 5)$.
Since BC is parallel to the y-axis (vertical), AD must also be parallel to the y-axis. This means the x-coordinate of D must be the same as the x-coordinate of A.
x-coordinate of D = x-coordinate of A = 3
So, D is $(3, y)$.
Combining these, the coordinates of the fourth vertex D are $(3, 5)$.
D $= (3, 5)$
Let's verify the properties of the rectangle with vertices A(3, 2), B(-4, 2), C(-4, 5), and D(3, 5):
- AB: horizontal line, length 7. CD: connects C(-4, 5) and D(3, 5). Horizontal line, length $|3 - (-4)| = 7$. AB || CD and AB = CD.
- BC: vertical line, length 3. AD: connects A(3, 2) and D(3, 5). Vertical line, length $|5 - 2| = 3$. BC || AD and BC = AD.
- Adjacent sides AB and BC are perpendicular. Adjacent sides BC and CD are perpendicular. Adjacent sides CD and DA are perpendicular. Adjacent sides DA and AB are perpendicular.
All properties of a rectangle are satisfied.
The coordinates of the fourth vertex are (3, 5).
Exercise 3.4
Question 1. Points A (5, 3), B (– 2, 3) and D (5, – 4) are three vertices of a square ABCD. Plot these points on a graph paper and hence find the coordinates of the vertex C.
Answer:
We are given three vertices of a square ABCD: A $(5, 3)$, B $(-2, 3)$, and D $(5, -4)$. We need to find the coordinates of the fourth vertex C $(x, y)$.
Let's analyze the given coordinates:
- Points A $(5, 3)$ and B $(-2, 3)$ have the same y-coordinate ($y=3$). The line segment AB is a horizontal line. Its length is the absolute difference of the x-coordinates: $|-2 - 5| = |-7| = 7$ units.
- Points A $(5, 3)$ and D $(5, -4)$ have the same x-coordinate ($x=5$). The line segment AD is a vertical line. Its length is the absolute difference of the y-coordinates: $|-4 - 3| = |-7| = 7$ units.
Since AB is horizontal and AD is vertical, the angle at A ($\angle$BAD) is $90^\circ$. Also, the lengths of AB and AD are equal (both 7 units). This confirms that A is a vertex where two sides of the square meet, and B and D are the adjacent vertices.
In a square ABCD, AB is parallel to DC, and AD is parallel to BC. The lengths of all sides are equal (7 units).
Since AB is parallel to DC, the line segment DC must be horizontal and have the same length as AB (7 units). Also, BC must be vertical and have the same length as AD (7 units).
Point C $(x, y)$ is such that BC is vertical and DC is horizontal.
Since BC is vertical, the x-coordinate of C must be the same as the x-coordinate of B.
x-coordinate of C = x-coordinate of B = –2
So, C is $(-2, y)$.
Since DC is horizontal, the y-coordinate of C must be the same as the y-coordinate of D.
y-coordinate of C = y-coordinate of D = –4
So, C is $(x, -4)$.
Combining these, the coordinates of the fourth vertex C are $(-2, -4)$.
C $= (-2, -4)$
Let's verify the side lengths with C $(-2, -4)$:
- BC: connects B $(-2, 3)$ and C $(-2, -4)$. Vertical line. Length $|-4 - 3| = |-7| = 7$ units. (Matches AD).
- DC: connects D $(5, -4)$ and C $(-2, -4)$. Horizontal line. Length $|-2 - 5| = |-7| = 7$ units. (Matches AB).
All sides have length 7, and adjacent sides are perpendicular (verified by horizontal/vertical alignment). This confirms ABCD is a square.
The coordinates of the vertex C are (–2, –4).
Question 2. Write the coordinates of the vertices of a rectangle whose length and breadth are 5 and 3 units respectively, one vertex at the origin, the longer side lies on the x-axis and one of the vertices lies in the third quadrant.
Answer:
Let the vertices of the rectangle be O, A, B, and C in order.
We are given the following information:
- One vertex is at the origin. Let this vertex be O. Coordinates of O are (0, 0).
- The length and breadth are 5 and 3 units. The longer side has length 5, and the shorter side has length 3.
- The longer side lies on the x-axis. This means one side of length 5 is along the x-axis, starting from the origin.
- One of the vertices lies in the third quadrant.
Since the longer side (length 5) lies on the x-axis and one vertex is at the origin (O(0, 0)), the adjacent vertex along the x-axis will be at a distance of 5 units from the origin on the x-axis. The third quadrant has negative x and negative y coordinates. For a vertex to be in the third quadrant, the rectangle cannot extend along the positive x and positive y axes from the origin.
Considering the vertex in the third quadrant, the rectangle must extend into the third quadrant from the origin. This means the side along the x-axis must be along the negative direction of the x-axis, and the side along the y-axis must be along the negative direction of the y-axis.
The longer side (length 5) lies on the x-axis. Starting from the origin (0, 0), the adjacent vertex along the x-axis in the direction leading to the third quadrant will be at $(-5, 0)$. Let's call this vertex A. Coordinates of A are (–5, 0).
The shorter side (length 3) is adjacent to the longer side and perpendicular to it. Since one vertex lies in the third quadrant, this shorter side must be along the negative direction of the y-axis, starting from the origin (0, 0). The adjacent vertex along the y-axis in the negative direction will be at $(0, -3)$. Let's call this vertex C. Coordinates of C are (0, –3).
Now we have three vertices: O $(0, 0)$, A $(-5, 0)$, and C $(0, -3)$. These are three vertices of the rectangle. Since OA is on the x-axis and OC is on the y-axis, $\angle$AOC = $90^\circ$, which is consistent with a rectangle at the origin.
The fourth vertex, B $(x, y)$, is opposite to the origin O. In a rectangle OABC, OA is parallel to BC and OC is parallel to AB.
Since OA is horizontal (on the x-axis), BC must be horizontal. This means the y-coordinate of B must be the same as the y-coordinate of C.
y-coordinate of B = y-coordinate of C = –3
So, B is $(x, -3)$.
Since OC is vertical (on the y-axis), AB must be vertical. This means the x-coordinate of B must be the same as the x-coordinate of A.
x-coordinate of B = x-coordinate of A = –5
So, B is $(-5, y)$.
Combining these, the coordinates of the fourth vertex B are $(-5, -3)$.
B $= (-5, -3)$
Let's check if vertex B is in the third quadrant. The coordinates are $(-5, -3)$. The x-coordinate is negative, and the y-coordinate is negative. This is indeed in the third quadrant.
The vertices of the rectangle are O $(0, 0)$, A $(-5, 0)$, B $(-5, -3)$, and C $(0, -3)$. Let's write them in alphabetical order or list them clearly.
The coordinates of the vertices of the rectangle are (0, 0), (–5, 0), (–5, –3), and (0, –3).
Question 3. Plot the points P (1, 0), Q (4, 0) and S (1, 3). Find the coordinates of the point R such that PQRS is a square.
Answer:
We are given three points P $(1, 0)$, Q $(4, 0)$, and S $(1, 3)$, which are vertices of a square PQRS. We need to find the coordinates of the fourth vertex R $(x, y)$. The order of vertices is important for a polygon.
Let's analyze the given points:
- Points P $(1, 0)$ and Q $(4, 0)$ have the same y-coordinate ($y=0$). This means the line segment PQ lies on the x-axis and is a horizontal line. The length of PQ is the absolute difference of the x-coordinates: $|4 - 1| = |3| = 3$ units.
- Points P $(1, 0)$ and S $(1, 3)$ have the same x-coordinate ($x=1$). This means the line segment PS is a vertical line. The length of PS is the absolute difference of the y-coordinates: $|3 - 0| = |3| = 3$ units.
Since PQ is horizontal and PS is vertical, the angle at P ($\angle$SPQ) is $90^\circ$. Also, the lengths of PQ and PS are equal (both 3 units). This confirms that P is a vertex where two sides of the square meet, and Q and S are the adjacent vertices.
In a square PQRS, PQ is parallel to SR, and PS is parallel to QR. All sides have the same length (3 units).
Point R $(x, y)$ is such that SR is parallel to PQ (horizontal) and QR is parallel to PS (vertical).
Since SR is horizontal, the y-coordinate of R must be the same as the y-coordinate of S.
y-coordinate of R = y-coordinate of S = 3
So, R is $(x, 3)$.
Since QR is vertical, the x-coordinate of R must be the same as the x-coordinate of Q.
x-coordinate of R = x-coordinate of Q = 4
So, R is $(4, y)$.
Combining these, the coordinates of the fourth vertex R are $(4, 3)$.
R $= (4, 3)$
Let's verify the side lengths with R $(4, 3)$:
- QR: connects Q $(4, 0)$ and R $(4, 3)$. Vertical line. Length $|3 - 0| = |3| = 3$ units. (Matches PS).
- SR: connects S $(1, 3)$ and R $(4, 3)$. Horizontal line. Length $|4 - 1| = |3| = 3$ units. (Matches PQ).
All sides have length 3, and adjacent sides are perpendicular. This confirms PQRS is a square.
The coordinates of the point R such that PQRS is a square are (4, 3).
Question 4. From the Fig. 3.8, answer the following :

(i) Write the points whose abscissa is 0.
(ii) Write the points whose ordinate is 0.
(iii) Write the points whose abscissa is – 5.
Answer:
We need to identify points from Fig. 3.8 based on their coordinates.
First, let's find the coordinates of all the labeled points in the figure:
- Point A: (-5, 4)
- Point B: (3, 4)
- Point C: (3, -1)
- Point D: (-5, -1)
- Point E: (0, -4)
- Point F: (0, 5)
- Point G: (5, 0)
- Point H: (-6, 0)
- Point I: (-5, -3)
- Point J: (3, 3)
- Point K: (5, -4)
- Point L: (-2, 0)
- Point M: (0, -2)
- Origin O: (0, 0)
Now, let's answer the questions:
(i) Write the points whose abscissa is 0.
The abscissa is the x-coordinate. We are looking for points where the x-coordinate is 0. These points lie on the y-axis.
From the list of coordinates, the points with x-coordinate 0 are:
- E (0, -4)
- F (0, 5)
- M (0, -2)
- O (0, 0)
The points whose abscissa is 0 are E, F, M, and O.
(ii) Write the points whose ordinate is 0.
The ordinate is the y-coordinate. We are looking for points where the y-coordinate is 0. These points lie on the x-axis.
From the list of coordinates, the points with y-coordinate 0 are:
- G (5, 0)
- H (-6, 0)
- L (-2, 0)
- O (0, 0)
The points whose ordinate is 0 are G, H, L, and O.
(iii) Write the points whose abscissa is – 5.
The abscissa is the x-coordinate. We are looking for points where the x-coordinate is -5.
From the list of coordinates, the points with x-coordinate -5 are:
- A (-5, 4)
- D (-5, -1)
- I (-5, -3)
The points whose abscissa is – 5 are A, D, and I.
Question 5. Plot the points A (1, – 1) and B (4, 5)
(i) Draw a line segment joining these points. Write the coordinates of a point on this line segment between the points A and B.
(ii) Extend this line segment and write the coordinates of a point on this line which lies outside the line segment AB.
Answer:
We are given two points A $(1, -1)$ and B $(4, 5)$.
(i) Draw a line segment joining these points. Write the coordinates of a point on this line segment between the points A and B.
To plot the points, draw the x and y axes. Locate point A $(1, -1)$ by moving 1 unit right and 1 unit down from the origin. Locate point B $(4, 5)$ by moving 4 units right and 5 units up from the origin.
Draw a straight line segment connecting A and B.
To find the coordinates of a point on the line segment between A and B, we can choose any point along the straight line path from A to B. A simple method is to consider the midpoint of the segment, or pick a point based on the x and y coordinates that are between those of A and B.
The x-coordinates of A and B are $1$ and $4$. Any point between A and B on the segment will have an x-coordinate between $1$ and $4$.
The y-coordinates of A and B are $-1$ and $5$. Any point between A and B on the segment will have a y-coordinate between $-1$ and $5$.
Let's find the midpoint of the segment AB. The midpoint formula for points $(x_1, y_1)$ and $(x_2, y_2)$ is $(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2})$.
Midpoint of AB $= (\frac{1 + 4}{2}, \frac{-1 + 5}{2}) = (\frac{5}{2}, \frac{4}{2}) = (2.5, 2)$
The point $(2.5, 2)$ lies on the line segment AB and is between A and B. We could choose any other point as well, for example, by choosing an x-value between 1 and 4 and finding the corresponding y-value on the line.
The coordinates of a point on this line segment between the points A and B are (2.5, 2) (or any other point on the segment excluding A and B).
(ii) Extend this line segment and write the coordinates of a point on this line which lies outside the line segment AB.
To extend the line segment AB, we continue the line in either direction beyond A or beyond B.
We can find points on the line by continuing the pattern of movement from A to B or from B to A.
The change in x from A to B is $4 - 1 = 3$. The change in y from A to B is $5 - (-1) = 6$.
The slope of the line AB is $\frac{6}{3} = 2$. The equation of the line passing through A $(1, -1)$ with slope 2 is $y - (-1) = 2(x - 1)$, which simplifies to $y + 1 = 2x - 2$, or $y = 2x - 3$.
To find a point outside the segment AB, we can choose an x-value less than the x-coordinate of A (1) or greater than the x-coordinate of B (4), and find the corresponding y-value using the equation of the line $y = 2x - 3$.
Let's choose an x-value greater than 4, say $x=5$.
For $x=5$, $y = 2(5) - 3 = 10 - 3 = 7$. The point is $(5, 7)$. This point lies on the line and is outside the segment AB (since its x-coordinate 5 is greater than 4 and its y-coordinate 7 is greater than 5). This point lies on the extension beyond B.
Alternatively, let's choose an x-value less than 1, say $x=0$.
For $x=0$, $y = 2(0) - 3 = -3$. The point is $(0, -3)$. This point lies on the line and is outside the segment AB (since its x-coordinate 0 is less than 1 and its y-coordinate -3 is less than -1). This point lies on the extension beyond A.
The coordinates of a point on this line which lies outside the line segment AB are, for example, (5, 7) (or any other point on the line $y=2x-3$ such that $x \leq 1$ or $x \geq 4$, excluding A and B). The point $(0, -3)$ is another valid example.

