Menu Top
Classwise Concept with Examples
6th 7th 8th 9th 10th 11th 12th

Class 10th Chapters
1. Real Numbers 2. Polynomials 3. Pair of Linear Equations in Two Variables
4. Quadratic Equations 5. Arithmetic Progressions 6. Triangles
7. Coordinate Geometry 8. Introduction to Trigonometry 9. Some Applications of Trigonometry
10. Circles 11. Constructions 12. Areas Related to Circles
13. Surface Areas And Volumes 14. Statistics 15. Probability

Content On This Page
Division of a Line Segment Construction of Similar Triangles Construction of Tangents to a Circle

Chapter 11 Constructions (Concepts)

Welcome to this essential chapter on Geometric Constructions, where we delve into the practical application of geometric principles using the classic tools of an unmarked ruler (straightedge) and compasses. Building significantly upon foundational constructions learned in previous classes, the focus here sharpens considerably. It's no longer sufficient to merely execute the steps accurately; a core requirement now is to provide rigorous logical justification for why each construction method works, grounding our practical skills firmly in the theoretical bedrock of theorems proven earlier. This chapter emphasizes precision, logical sequencing, and the powerful connection between doing geometry and understanding its proofs.

We will master several key constructions, each requiring careful execution and thoughtful validation. The first major technique is the Division of a Line Segment in a Given Ratio. Given a line segment $AB$ and a specific ratio $m:n$ (where $m$ and $n$ are positive integers), the task is to locate the unique point $P$ on $AB$ such that $AP:PB = m:n$. The standard construction procedure involves:

The justification for this construction elegantly relies on the Basic Proportionality Theorem (BPT or Thales Theorem) or the concept of similar triangles formed by the parallel lines.

Next, we tackle the Construction of a Triangle Similar to a Given Triangle according to a specified scale factor, say $k$. This means constructing a new triangle whose sides are $k$ times the lengths of the corresponding sides of the original triangle. Two distinct cases arise depending on the scale factor $k$:

The construction typically involves drawing a ray from one vertex of the given triangle, marking points along this ray based on the numerator and denominator of the scale factor $k$ (expressed as a fraction $\frac{m}{n}$), and then drawing lines parallel to one side of the original triangle to locate the vertices of the new, similar triangle. The justification hinges on the AA similarity criterion, ensuring corresponding angles are equal, and the BPT ensures the proportionality of sides.

Finally, we address a crucial construction involving circles: the Construction of Tangents to a Circle from a Point Outside It. Given a circle with center $O$ and a point $P$ lying outside the circle, we need to construct the two tangent lines from $P$ to the circle. The elegant procedure involves:

  1. Joining the center $O$ to the external point $P$.
  2. Constructing the perpendicular bisector of the line segment $OP$ to find its midpoint, say $M$.
  3. With $M$ as the center and $MO$ (or $MP$) as the radius, drawing a new circle (or semicircle).
  4. This new circle will intersect the given circle at two points, say $T_1$ and $T_2$. These are the points of contact.
  5. Joining $P$ to $T_1$ and $P$ to $T_2$ gives the required tangents $PT_1$ and $PT_2$.
The justification brilliantly uses the geometric property that the angle inscribed in a semicircle is a right angle ($\angle OT_1P = 90^\circ$ and $\angle OT_2P = 90^\circ$). Since $OT_1$ and $OT_2$ are radii of the original circle, this perpendicularity at the point of contact confirms, by Theorem 10.1 (Tangent is perpendicular to radius at point of contact), that $PT_1$ and $PT_2$ are indeed tangents. This chapter meticulously combines practical skill with theoretical validation.

Division of a Line Segment in a Given Ratio

Geometric constructions using only a compass and a straightedge are fundamental in geometry. One such construction involves dividing a given line segment into two parts that are in a specific ratio. This technique is useful in various geometric constructions and proofs.

To divide a line segment in a given ratio $m:n$ internally.

This construction method allows us to find a point P on a line segment AB such that the point divides the segment into two parts, AP and PB, whose lengths are in the ratio $m:n$.

Steps of Construction (General Method):

  1. Draw the line segment AB of the given length.
  2. Draw a ray AX that makes an acute angle (less than 90°) with the line segment AB.
  3. On the ray AX, use a compass to mark off $m+n$ equally spaced points. Label these points $A_1, A_2, A_3, \dots, A_{m+n}$ such that $\text{AA}_1 = \text{A}_1\text{A}_2 = \dots = \text{A}_{m+n-1}\text{A}_{m+n}$.
  4. Join the last point, $A_{m+n}$, to the endpoint B of the line segment, forming the line segment $BA_{m+n}$.
  5. From the $m$-th point on the ray, $A_m$, draw a line parallel to the segment $BA_{m+n}$. This parallel line will intersect the original line segment AB at a point. Label this point P.

The point P is the required point that divides the line segment AB in the ratio $m:n$.

Example 1. Draw a line segment of length 7.6 cm and divide it in the ratio 5:8. Measure the two parts.

Answer:

Given:

A line segment AB of length 7.6 cm.

The ratio of division is $m:n = 5:8$. Thus, $m=5$, $n=8$, and $m+n = 13$.

To Construct:

A point C on the line segment AB such that $\text{AC} : \text{CB} = 5 : 8$.

Steps of Construction:

  1. Draw a line segment AB of length 7.6 cm.
    2. Step 1: A line segment AB of length 7.6 cm is drawn.
  2. Draw a ray AX making an acute angle with AB.
    3. Step 2: A ray AX is drawn from point A, making an acute angle with AB.
  3. On ray AX, mark 13 ($=5+8$) equally spaced points, $A_1, A_2, \dots, A_{13}$.
    4. Step 3: 13 equally spaced points are marked on the ray AX.
  4. Join the last point, $A_{13}$, to B.
    5. Step 4: The last point A13 is joined to point B.
  5. From the 5th point, $A_5$, draw a line parallel to $A_{13}B$. This line intersects AB at point C.
    6. Step 5: A line parallel to A13B is drawn from A5, intersecting AB at point C. This is the final construction.

Measurement and Verification:

Upon measuring the lengths of the two parts with a ruler:

AC $\approx 2.9$ cm

CB $\approx 4.7$ cm

Verification by Calculation:

The theoretical length of AC should be:

AC = $(\frac{m}{m+n}) \times \text{AB} = \frac{5}{13} \times 7.6 = \frac{38}{13} \approx 2.92$ cm.

The theoretical length of CB should be:

CB = $(\frac{n}{m+n}) \times \text{AB} = \frac{8}{13} \times 7.6 = \frac{60.8}{13} \approx 4.68$ cm.

The measured values are consistent with the calculated values.

Result: The point C divides the line segment AB in the ratio 5:8, with lengths AC $\approx$ 2.9 cm and CB $\approx$ 4.7 cm.

Justification of Construction

We must provide a mathematical proof to show that the construction method correctly divides the line segment in the required ratio.

Proof:

Consider the triangle $\triangle \text{ABA}_{13}$. In this triangle, by construction, the line segment $A_5C$ is drawn parallel to the side $A_{13}B$.

The Basic Proportionality Theorem (BPT) states that if a line is drawn parallel to one side of a triangle to intersect the other two sides at distinct points, the other two sides are divided in the same ratio.

Applying the BPT to $\triangle \text{ABA}_{13}$, we have:

$\frac{\text{AC}}{\text{CB}} = \frac{\text{AA}_5}{\text{A}_5 \text{A}_{13}}$

(By BPT)

By construction, the points $A_1, A_2, \dots, A_{13}$ are marked such that the segments between them are equal. Let the length of each segment be $k$.

The length of $\text{AA}_5$ is the sum of the first 5 segments, so:

$\text{AA}_5 = 5 \times k$

... (i)

The length of $\text{A}_5 \text{A}_{13}$ is the sum of the remaining 8 segments, so:

$\text{A}_5 \text{A}_{13} = 8 \times k$

... (ii)

Substituting the results from (i) and (ii) into the BPT equation:

$\frac{\text{AC}}{\text{CB}} = \frac{5 \times k}{8 \times k} = \frac{5}{8}$

This shows that the point C divides the line segment AB in the ratio 5:8. Hence, the construction is justified.


Construction of Similar Triangles

In Chapter 6, we learned that two triangles are similar if their corresponding angles are equal and their corresponding sides are in the same ratio (proportional). The ratio of corresponding sides is called the scale factor. Here, we will learn how to construct a triangle similar to a given triangle with a specified scale factor using compass and straightedge.

To construct a triangle similar to a given triangle ABC with a scale factor $\frac{k}{l}$.

This construction involves creating a triangle that is similar to a given triangle, with its sides being a specific fraction (scale factor) of the corresponding sides of the original triangle. The scale factor is given as a ratio $\frac{k}{l}$, where $k$ and $l$ are positive integers. The method varies slightly depending on whether this scale factor is less than 1 or greater than 1.

Case 1: Scale factor is less than 1 ($k < l$)

When the scale factor is less than 1, the new triangle will be smaller than the original triangle.

Steps of Construction (General Method)

  1. Construct the given triangle, let's say $\triangle \text{ABC}$.
  2. From one vertex (e.g., B), draw a ray BX making an acute angle with the side BC, on the side opposite to vertex A.
  3. On the ray BX, locate a number of points equal to the larger of $k$ and $l$ (which is $l$ in this case). Mark these points $B_1, B_2, \dots, B_l$ at equal intervals.
  4. Join the last point, $B_l$, to the vertex C.
  5. From the $k$-th point, $B_k$, draw a line parallel to $B_lC$ that intersects the side BC at a new point, C'.
  6. From C', draw a line parallel to the side AC that intersects the side AB at a new point, A'.

The resulting $\triangle \text{A'BC'}$ is the required triangle, similar to $\triangle \text{ABC}$.

Example 1. Construct a triangle with sides 4 cm, 5 cm, and 6 cm and then a triangle similar to it whose sides are $\frac{2}{3}$ of the corresponding sides of the first triangle.

Answer:

Given:

A triangle ABC with sides AB = 4 cm, BC = 5 cm, and AC = 6 cm.

The scale factor is $\frac{k}{l} = \frac{2}{3}$. Here, $k=2$ and $l=3$. Since $k < l$, the new triangle will be smaller.

To Construct:

A triangle A'BC' such that $\triangle \text{A'BC'} \sim \triangle \text{ABC}$ and $\frac{\text{A'B}}{\text{AB}} = \frac{\text{BC'}}{\text{BC}} = \frac{\text{A'C'}}{\text{AC}} = \frac{2}{3}$.

Steps of Construction:

  1. Construct $\triangle \text{ABC}$ by drawing a line segment BC = 5 cm. With B as centre and radius 4 cm, draw an arc. With C as centre and radius 6 cm, draw another arc to intersect the first one at A. Join AB and AC.
    2. Step 1: The original triangle ABC is constructed with sides 4 cm, 5 cm, and 6 cm.
  2. Draw a ray BX starting from B, making an acute angle with BC.
    3. Step 2: A ray BX is drawn from vertex B.
  3. Since the larger number in the ratio is 3, locate 3 points ($B_1, B_2, B_3$) on ray BX such that $BB_1 = B_1B_2 = B_2B_3$.
    4. Step 3: Three equally spaced points B1, B2, B3 are marked on ray BX.
  4. Join the last point, $B_3$, to vertex C to form the line segment $CB_3$.
    5. Step 4: The point B3 is joined to C.
  5. From the 2nd point, $B_2$, draw a line parallel to $CB_3$, which intersects BC at C'.
    6. Step 5: A line parallel to CB3 is drawn from B2, intersecting BC at C'.
  6. From C', draw a line parallel to AC, which intersects AB at A'.
    7. Step 6: A line parallel to AC is drawn from C', intersecting AB at A'. The required triangle A'BC' is formed.

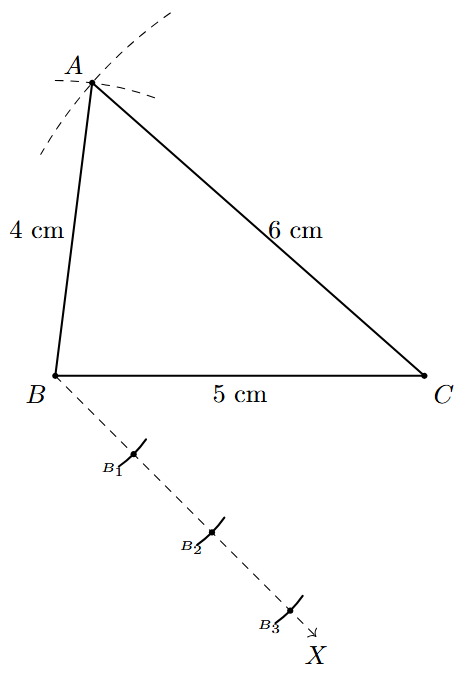
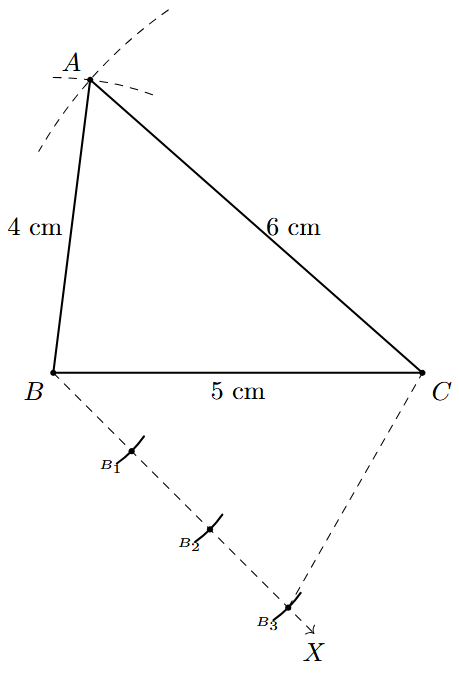
The triangle $\triangle \text{A'BC'}$ is the required similar triangle.

Justification for Case 1

Proof:

We need to prove that $\triangle \text{A'BC'} \sim \triangle \text{ABC}$ and that its sides are $\frac{k}{l}$ times the corresponding sides of $\triangle \text{ABC}$.

In $\triangle \text{BCB}_l$, by construction, $B_kC'$ is parallel to $B_lC$. By the Basic Proportionality Theorem, this divides the sides BC and BB$_l$ in the same ratio:

$\frac{\text{BC'}}{\text{C'C}} = \frac{\text{BB}_k}{\text{B}_k\text{B}_l}$

However, it is more direct to use similar triangles. Since $B_kC' \parallel B_lC$, $\triangle \text{BB}_k\text{C'} \sim \triangle \text{BB}_l\text{C}$ (by AA similarity, as $\angle B$ is common and $\angle \text{BB}_k\text{C'} = \angle \text{BB}_l\text{C}$ are corresponding angles).

Therefore, the ratio of corresponding sides is equal:

$\frac{\text{BC'}}{\text{BC}} = \frac{\text{BB}_k}{\text{BB}_l}$

By construction, $\text{BB}_k = k \times (\text{unit length})$ and $\text{BB}_l = l \times (\text{unit length})$.

$\frac{\text{BC'}}{\text{BC}} = \frac{k}{l}$

... (i)

Now, consider $\triangle \text{ABC}$. By construction, $A'C' \parallel AC$. Therefore, $\triangle \text{A'BC'} \sim \triangle \text{ABC}$ (by AA similarity, as $\angle B$ is common and $\angle \text{BC'A'} = \angle \text{BCA}$ are corresponding angles).

The ratio of corresponding sides of similar triangles is equal:

$\frac{\text{A'B}}{\text{AB}} = \frac{\text{BC'}}{\text{BC}} = \frac{\text{A'C'}}{\text{AC}}$

... (ii)

Combining equations (i) and (ii), we get:

$\frac{\text{A'B}}{\text{AB}} = \frac{\text{BC'}}{\text{BC}} = \frac{\text{A'C'}}{\text{AC}} = \frac{k}{l}$

Thus, the construction is justified.

Case 2: Scale factor is greater than 1 ($k > l$)

When the scale factor is greater than 1, the new triangle will be larger than the original triangle.

Steps of Construction (General Method)

  1. Construct the given triangle, $\triangle \text{ABC}$.
  2. Extend the sides AB and BC from the common vertex B.
  3. From vertex B, draw a ray BX making an acute angle with side BC.
  4. On the ray BX, locate a number of points equal to the larger of $k$ and $l$ (which is $k$ in this case). Mark these points $B_1, B_2, \dots, B_k$ at equal intervals.
  5. Join the $l$-th point, $B_l$, to vertex C.
  6. From the $k$-th point, $B_k$, draw a line parallel to $B_lC$ that intersects the extended line segment BC at a new point, C'.
  7. From C', draw a line parallel to the side AC that intersects the extended line segment BA at a new point, A'.

The resulting $\triangle \text{A'BC'}$ is the required triangle, similar to $\triangle \text{ABC}$.

Example 2. Construct a triangle with sides 4 cm, 5 cm, and 6 cm and then a triangle similar to it whose sides are $\frac{5}{3}$ of the corresponding sides of the first triangle.

Answer:

Given:

A triangle ABC with sides AB = 4 cm, BC = 5 cm, and AC = 6 cm.

The scale factor is $\frac{k}{l} = \frac{5}{3}$. Here, $k=5$ and $l=3$. Since $k > l$, the new triangle will be larger.

To Construct:

A triangle A'BC' such that $\triangle \text{A'BC'} \sim \triangle \text{ABC}$ and $\frac{\text{A'B}}{\text{AB}} = \frac{\text{BC'}}{\text{BC}} = \frac{\text{A'C'}}{\text{AC}} = \frac{5}{3}$.

Steps of Construction:

  1. Construct $\triangle \text{ABC}$ with sides AB = 4 cm, BC = 5 cm, and AC = 6 cm.
    2. Step 1: The original triangle ABC is constructed.
  2. Extend the line segments BA and BC from vertex B. Draw a ray BX making an acute angle with BC.
    3. Step 2: Sides BA and BC are extended, and a ray BX is drawn.
  3. Since the larger number in the ratio is 5, locate 5 points ($B_1, B_2, \dots, B_5$) on ray BX at equal intervals.
    4. Step 3: Five equally spaced points are marked on ray BX.
  4. Join the 3rd point, $B_3$, to vertex C.
    5. Step 4: The point B3 is joined to C.
  5. From the 5th point, $B_5$, draw a line parallel to $CB_3$, which intersects the extended line segment BC at C'.
    6. Step 5: A line parallel to CB3 is drawn from B5, intersecting the extended side BC at C'.
  6. From C', draw a line parallel to AC, which intersects the extended line segment BA at A'.
    7. Step 6: A line parallel to AC is drawn from C', intersecting the extended side BA at A'. The required triangle A'BC' is formed.

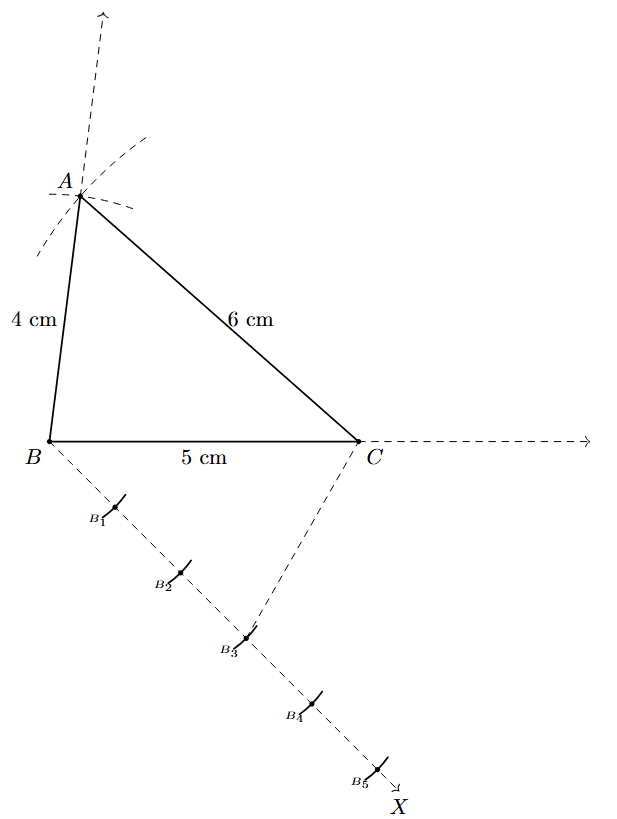
The triangle $\triangle \text{A'BC'}$ is the required similar triangle.

Justification for Case 2

Proof:

The justification is analogous to Case 1.

By construction, $B_kC' \parallel B_lC$. This implies that $\triangle \text{BB}_k\text{C'} \sim \triangle \text{BB}_l\text{C}$ (by AA similarity).

Therefore, the ratio of corresponding sides is equal:

$\frac{\text{BC'}}{\text{BC}} = \frac{\text{BB}_k}{\text{BB}_l} = \frac{k}{l}$

... (iii)

Also by construction, $A'C' \parallel AC$. This implies that $\triangle \text{A'BC'} \sim \triangle \text{ABC}$ (by AA similarity).

The ratio of corresponding sides of these similar triangles is equal:

$\frac{\text{A'B}}{\text{AB}} = \frac{\text{BC'}}{\text{BC}} = \frac{\text{A'C'}}{\text{AC}}$

... (iv)

Combining equations (iii) and (iv), we get:

$\frac{\text{A'B}}{\text{AB}} = \frac{\text{BC'}}{\text{BC}} = \frac{\text{A'C'}}{\text{AC}} = \frac{k}{l}$

Thus, the construction is justified.


Construction of Tangents to a Circle

This construction provides a method to draw the two possible tangents from a single point located outside a given circle. The method relies on the geometric properties of circles, particularly the fact that the angle in a semicircle is a right angle, which helps establish the perpendicular relationship between a tangent and a radius.

To construct the tangents to a circle from a point outside it.

Steps of Construction (General Method)

  1. Draw the circle with a given centre (O) and radius, and mark the position of the external point (P).
  2. Join the centre of the circle O to the external point P to form the line segment OP.
  3. Construct the perpendicular bisector of the line segment OP. The point where the bisector intersects OP is the midpoint of OP. Let this midpoint be M.
  4. With M as the centre and the length MO (or MP) as the radius, draw a new circle. This circle will pass through both O and P.
  5. This new circle will intersect the original circle at two points. Label these points of intersection A and B.
  6. Join the external point P to the intersection points A and B.

The line segments PA and PB are the two required tangents to the circle from the external point P.

Example. Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths.

Answer:

Given:

Radius of the circle = 6 cm.

Distance of the external point from the centre, OP = 10 cm.

To Construct:

A pair of tangents from the external point P to the circle and measure their lengths.

Steps of Construction:

  1. Draw a circle with centre O and radius 6 cm. Mark a point P such that OP = 10 cm. Join OP.
    2. Step 1: A circle with center O, radius 6 cm, and an external point P, 10 cm away, are drawn. The line segment OP is also drawn.
  2. Construct the perpendicular bisector of the line segment OP. Let M be the midpoint of OP.
    3. Step 2: The perpendicular bisector of OP is constructed, and its midpoint M is found.
  3. With M as the centre and MO as the radius, draw a new circle.
    4. Step 3: A second circle is drawn with center M and radius MO, passing through O and P.
  4. This new circle intersects the original circle at two points. Label these points A and B.
    5. Step 4: The intersection points of the two circles are marked as A and B. These are the points of contact.
  5. Join PA and PB. These are the required tangents.
    6. Step 5: The final construction showing the two tangents PA and PB from point P to the circle.

Verification by Calculation:

To find the length of the tangents, we join the radius OA. The radius at the point of contact is perpendicular to the tangent as $\angle$ OAP is an angle in the semicircle with center M. Therefore, $\triangle \text{OAP}$ is a right-angled triangle with the right angle at A.

We have:

OA = 6 cm (Radius of the circle)

OP = 10 cm (Given distance)

In the right-angled $\triangle \text{OAP}$, by applying the Pythagorean theorem:

$\text{OP}^2 = \text{OA}^2 + \text{PA}^2$

(Pythagorean Theorem)

Substituting the values:

$10^2 = 6^2 + \text{PA}^2$

$100 = 36 + \text{PA}^2$

$\text{PA}^2 = 100 - 36$

$\text{PA}^2 = 64$

$\text{PA} = \sqrt{64}$

$\text{PA} = 8$ cm

Similarly, in $\triangle \text{OBP}$, PB = 8 cm. Thus, the length of each tangent is 8 cm.

Justification of Construction

Proof:

We must prove that the constructed lines PA and PB are indeed tangents to the circle with centre O.

Let's join OA. Consider the circle drawn with diameter OP.

Diagram for justification, showing the radius OA and the line segment PA forming a right angle.

The point A lies on the circumference of the circle with diameter OP. The angle $\angle \text{OAP}$ is an angle subtended by the diameter at a point on the circumference.

A well-known geometric theorem states that the angle in a semicircle is a right angle.

$\angle \text{OAP} = 90^\circ$

(Angle in a semicircle)

This implies that $OA \perp PA$.

Since OA is the radius of the original circle and PA is a line perpendicular to the radius at its endpoint (point of contact A), PA must be a tangent to the circle.

Similarly, by joining OB, we can show that $\angle \text{OBP} = 90^\circ$, which proves that PB is also a tangent to the circle at point B.

Hence, the construction is mathematically justified.