| Latest Maths NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Example 1 to 3 (Before Exercise 10.1) | Exercise 10.1 | |
Chapter 10 Heron's Formula
Welcome to the focused solutions guide for Chapter 10, "Heron's Formula," from the latest Class 9 NCERT mathematics textbook for the academic session 2024-25. This chapter introduces a remarkably useful formula attributed to Heron of Alexandria, providing a powerful method to calculate the area of a triangle when only the lengths of its three sides are known. This is particularly advantageous when the height (altitude) of the triangle is not given or is difficult to determine, offering an alternative to the standard Area = $\frac{1}{2} \times \text{base} \times \text{height}$ formula. These solutions provide comprehensive, step-by-step assistance in applying Heron's formula accurately and effectively to various problems.
The core of this chapter revolves around understanding and applying Heron's Formula. The solutions clearly introduce the formula itself. For a triangle with side lengths $a$, $b$, and $c$, the area ($A$) is calculated as follows:
- First, calculate the semi-perimeter ($s$) of the triangle: $s = \frac{a+b+c}{2}$.
- Then, apply Heron's Formula: $A = \sqrt{s(s-a)(s-b)(s-c)}$.
A key application highlighted in the solutions is using Heron's formula to find the area of quadrilaterals or other polygons. This is achieved by dividing the polygon into constituent triangles using one or more diagonals. If the side lengths of these resulting triangles are known (or can be determined – perhaps using the Pythagorean theorem if a right-angled triangle is formed within the quadrilateral), Heron's formula can be applied to each triangle individually. The total area of the polygon is then found by summing the areas of these triangles. The solutions provide clear illustrations of this strategy, breaking down the process into manageable steps.
Furthermore, the solutions address practical word problems that often involve finding the area of triangular fields, plots of land, or other real-world shapes where side lengths are the primary information provided. These problems test the student's ability to extract the side lengths from the problem description and apply Heron's formula correctly, sometimes involving calculations with units (like $m^2$) or costs associated with the area (e.g., cost of leveling a field at a certain rate per square meter, potentially using $\textsf{₹}$).
Regarding the rationalized syllabus for 2024-25, Chapter 10, "Heron's Formula" (formerly Chapter 12), has been retained in the Class 9 NCERT curriculum. Its focus remains squarely on the introduction and application of Heron's formula for finding the area of triangles and its use in calculating the area of quadrilaterals by division into triangles. The rationalization process primarily involved ensuring the exercises focus directly on these core applications without excessive complexity in calculations or contexts. By diligently working through these detailed solutions, students can master the precise application of Heron's formula, perform the calculations accurately, and confidently solve problems involving the area of triangles and related composite shapes based on given side lengths.
Example 1 to 3 (Before Exercise 10.1)
Example 1. Find the area of a triangle, two sides of which are 8 cm and 11 cm and the perimeter is 32 cm (see Fig. 10.3).

Answer:
Given:
Two sides of the triangle are $a = 8$ cm and $b = 11$ cm.
Perimeter of the triangle = 32 cm.
To Find:
Area of the triangle.
Solution:
Let the third side of the triangle be $c$ cm.
The perimeter of a triangle is the sum of its three sides.
Perimeter = $a + b + c$
Substitute the given values:
$32 = 8 + 11 + c$
$32 = 19 + c$
Subtract 19 from both sides to find $c$:
$c = 32 - 19$
$c = 13$ cm
The third side of the triangle is 13 cm.
Now, we calculate the semi-perimeter ($s$).
$s = \frac{\text{Perimeter}}{2}$
$s = \frac{32}{2}$
$s = 16$ cm
Using Heron's formula, the area of a triangle with sides a, b, c and semi-perimeter s is given by:
$\text{Area} = \sqrt{s(s-a)(s-b)(s-c)}$
Substitute the values of s, a, b, and c:
$\text{Area} = \sqrt{16(16-8)(16-11)(16-13)}$
$\text{Area} = \sqrt{16(8)(5)(3)}$
$\text{Area} = \sqrt{16 \times 8 \times 5 \times 3}$
$\text{Area} = \sqrt{16 \times 120}$
$\text{Area} = \sqrt{1920}$
$\text{Area} = \sqrt{64 \times 30}$
$\text{Area} = \sqrt{64} \times \sqrt{30}$
$\text{Area} = 8 \times \sqrt{30}$
$\text{Area} = 8\sqrt{30}$ cm$^2$
The area of the triangle is $8\sqrt{30}$ cm$^2$.
The final answer is $8\sqrt{30}$ cm$^2$.
Example 2. A triangular park ABC has sides 120m, 80m and 50m (see Fig. 10.4). A gardener Dhania has to put a fence all around it and also plant grass inside. How much area does she need to plant? Find the cost of fencing it with barbed wire at the rate of ₹ 20 per metre leaving a space 3m wide for a gate on one side.
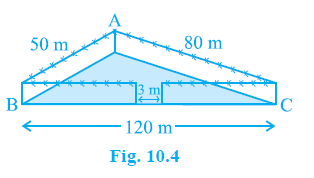
Answer:
Given:
The sides of the triangular park ABC are $a = 120$ m, $b = 80$ m, and $c = 50$ m.
Rate of fencing = $\textsf{₹}$ 20 per metre.
Space left for a gate = 3 m.
To Find:
The area required to plant grass.
The cost of fencing.
Solution:
To find the area required to plant grass, we use Heron's formula.
First, calculate the semi-perimeter ($s$) of the triangular park.
$s = \frac{a + b + c}{2}$
$s = \frac{120 + 80 + 50}{2}$
$s = \frac{250}{2}$
$s = 125$ m
Now, calculate $s-a$, $s-b$, and $s-c$:
$s - a = 125 - 120 = 5$ m
$s - b = 125 - 80 = 45$ m
$s - c = 125 - 50 = 75$ m
Using Heron's formula for the area of the triangle:
$\text{Area} = \sqrt{s(s-a)(s-b)(s-c)}$
Substitute the values:
$\text{Area} = \sqrt{125 \times 5 \times 45 \times 75}$
$\text{Area} = \sqrt{(5^3) \times 5 \times (3^2 \times 5) \times (3 \times 5^2)}$
$\text{Area} = \sqrt{3^2 \times 3 \times 5^3 \times 5^1 \times 5^1 \times 5^2}$
$\text{Area} = \sqrt{3^3 \times 5^7}$
$\text{Area} = \sqrt{3^2 \times 3 \times 5^6 \times 5}$
$\text{Area} = \sqrt{3^2} \times \sqrt{5^6} \times \sqrt{3 \times 5}$
$\text{Area} = 3 \times 5^3 \times \sqrt{15}$
$\text{Area} = 3 \times 125 \times \sqrt{15}$
$\text{Area} = 375\sqrt{15}$ m$^2$
The area needed to plant grass is $375\sqrt{15}$ m$^2$.
To find the cost of fencing, we first find the total perimeter.
Total Perimeter = $a + b + c$
Total Perimeter = $120 + 80 + 50$
Total Perimeter = $250$ m
A space of 3m is left for a gate, so the length of the fence required is:
Length of fence = Total Perimeter - Gate space
Length of fence = $250$ m - $3$ m
Length of fence = $247$ m
The cost of fencing is the length of the fence multiplied by the rate per metre.
Cost of fencing = Length of fence $\times$ Rate
Cost of fencing = $247 \times \textsf{₹} 20$
Cost of fencing = $\textsf{₹} 4940$
Final Answer:
The area needed to plant grass is $375\sqrt{15}$ m$^2$.
The cost of fencing is $\textsf{₹} 4940$.
Example 3. The sides of a triangular plot are in the ratio of 3 : 5 : 7 and its perimeter is 300 m. Find its area.
Answer:
Given:
The ratio of the sides of the triangular plot $= 3 : 5 : 7$.
Perimeter of the plot $= 300$ m.
To Find:
Area of the triangular plot.
Solution:
Let the sides of the triangle be $a = 3x$, $b = 5x$, and $c = 7x$.
$3x + 5x + 7x = 300$
(Sum of sides = Perimeter)
$15x = 300$
$x = \frac{\cancel{300}^{20}}{\cancel{15}_{1}}$
$x = 20$
... (i)
Substituting the value of $x$ from equation (i) to find the sides:
$a = 3 \times 20 = 60$ m
$b = 5 \times 20 = 100$ m
$c = 7 \times 20 = 140$ m
The semi-perimeter ($s$) is calculated as:
$s = \frac{a+b+c}{2} = \frac{300}{2} = 150$ m
Using Heron's Formula:
Area of triangle $= \sqrt{s(s-a)(s-b)(s-c)}$
Area $= \sqrt{150(150-60)(150-100)(150-140)}$
Area $= \sqrt{150 \times 90 \times 50 \times 10}$
Area $= \sqrt{(15 \times 10) \times (9 \times 10) \times (5 \times 10) \times 10}$
Area $= \sqrt{15 \times 9 \times 5 \times 10,000}$
Area $= \sqrt{75 \times 9 \times 100^2}$
Area $= \sqrt{25 \times 3 \times 3^2 \times 100^2}$
Area $= 5 \times 3 \times 100 \sqrt{3}$
Area $= 1500\sqrt{3}$ m$^2$
Exercise 10.1
Question 1. A traffic signal board, indicating ‘SCHOOL AHEAD’, is an equilateral triangle with side ‘a’. Find the area of the signal board, using Heron’s formula. If its perimeter is 180 cm, what will be the area of the signal board?
Answer:
Given:
Side of the equilateral triangle $= a$.
Perimeter $= 180$ cm.
To Find:
1. Area of the signal board using Heron's formula.
2. Area when perimeter is $180$ cm.
Solution:
For an equilateral triangle with side $a$, the semi-perimeter $s = \frac{a+a+a}{2} = \frac{3a}{2}$.
Using Heron's Formula:
Area $= \sqrt{s(s-a)(s-b)(s-c)}$
Since $a = b = c$:
Area $= \sqrt{\frac{3a}{2}\left(\frac{3a}{2}-a\right)\left(\frac{3a}{2}-a\right)\left(\frac{3a}{2}-a\right)}$
Area $= \sqrt{\frac{3a}{2} \times \frac{a}{2} \times \frac{a}{2} \times \frac{a}{2}}$
$\text{Area} = \frac{\sqrt{3}}{4} a^2$
... (i)
Now, given Perimeter $= 180$ cm.
$3a = 180$
$a = \frac{180}{3} = 60$ cm
Substituting $a = 60$ in equation (i):
$\text{Area} = \frac{\sqrt{3}}{4} (60)^2$
$\text{Area} = \frac{\sqrt{3}}{4} \times 3600$
$\text{Area} = 900\sqrt{3}$ cm$^2$
Question 2. The triangular side walls of a flyover have been used for advertisements. The sides of the walls are 122 m, 22 m and 120 m (see Fig. 10.6). The advertisements yield an earning of ₹ 5000 per m2 per year. A company hired one of its walls for 3 months. How much rent did it pay?

Answer:
Given:
Sides of the wall: $a = 122$ m, $b = 22$ m, $c = 120$ m.
Earning rate $= \textsf{₹} \ 5000$ per m$^2$ per year.
Time period $= 3$ months.
To Find:
Total rent paid by the company.
Solution:
Calculate semi-perimeter $s$:
$s = \frac{122 + 22 + 120}{2} = \frac{264}{2} = 132$ m
Using Heron's Formula:
Area $= \sqrt{132(132-122)(132-22)(132-120)}$
Area $= \sqrt{132 \times 10 \times 110 \times 12}$
Area $= \sqrt{(11 \times 12) \times 10 \times (11 \times 10) \times 12}$
Area $= \sqrt{11^2 \times 12^2 \times 10^2} = 11 \times 12 \times 10$
$\text{Area} = 1320$ m$^2$
... (i)
Rent for 1 year per m$^2 = \textsf{₹} \ 5000$.
Rent for 3 months (i.e., $\frac{3}{12}$ year) for $1320$ m$^2$:
$\text{Total Rent} = 1320 \times 5000 \times \frac{3}{12}$
$\text{Total Rent} = 1320 \times 5000 \times \frac{1}{4}$
$\text{Total Rent} = 330 \times 5000$
Total Rent $= \textsf{₹} \ 16,50,000$.
Question 3. There is a slide in a park. One of its side walls has been painted in some colour with a message “KEEP THE PARK GREEN AND CLEAN” (see Fig. 10.7). If the sides of the wall are 15 m, 11 m and 6 m, find the area painted in colour.

Answer:
Given:
Sides of the wall: $a = 15$ m, $b = 11$ m, $c = 6$ m.
To Find:
Area painted in colour.
Solution:
Calculate semi-perimeter $s$:
$s = \frac{15 + 11 + 6}{2} = \frac{32}{2} = 16$ m
Using Heron's Formula:
Area $= \sqrt{16(16-15)(16-11)(16-6)}$
Area $= \sqrt{16 \times 1 \times 5 \times 10}$
Area $= \sqrt{16 \times 50}$
Area $= \sqrt{16 \times 25 \times 2}$
Area $= 4 \times 5 \times \sqrt{2}$
Area $= 20\sqrt{2}$ m$^2$.
Final Answer:
The area painted in colour is $20\sqrt{2}$ m$^2$.
Question 4. Find the area of a triangle two sides of which are 18 cm and 10 cm and the perimeter is 42 cm.
Answer:
Given:
Let the sides of the triangle be $a$, $b$, and $c$.
Two sides are $a = 18$ cm and $b = 10$ cm.
Perimeter $P = 42$ cm.
To Find:
The area of the triangle.
Solution:
The perimeter of a triangle is the sum of its three sides.
$P = a + b + c$
We are given $P = 42$ cm, $a = 18$ cm, and $b = 10$ cm.
Substituting the given values:
$42 = 18 + 10 + c$
... (i)
$42 = 28 + c$
Now, we can find the third side $c$:
$c = 42 - 28$
$c = 14$ cm
Next, we find the semi-perimeter ($s$) of the triangle, which is half of the perimeter.
$s = \frac{P}{2}$
$s = \frac{42}{2}$
$s = 21$ cm
We can find the area of the triangle using Heron's formula, which is given by:
Area $= \sqrt{s(s-a)(s-b)(s-c)}$
Calculate the terms $(s-a)$, $(s-b)$, and $(s-c)$:
$s - a = 21 - 18 = 3$ cm
$s - b = 21 - 10 = 11$ cm
$s - c = 21 - 14 = 7$ cm
Substitute these values into Heron's formula:
Area $= \sqrt{21 \times 3 \times 11 \times 7}$
Factorize the numbers inside the square root:
Area $= \sqrt{(3 \times 7) \times 3 \times 11 \times 7}$
Group the common factors:
Area $= \sqrt{3^2 \times 7^2 \times 11}$
Take the terms with squares out of the square root:
Area $= 3 \times 7 \times \sqrt{11}$
Area $= 21\sqrt{11}$ cm$^2$
The area of the triangle is $21\sqrt{11}$ cm$^2$.
Question 5. Sides of a triangle are in the ratio of 12 : 17 : 25 and its perimeter is 540 cm. Find its area.
Answer:
Given:
Ratio of the sides of the triangle $= 12 : 17 : 25$.
Perimeter of the triangle $= 540$ cm.
To Find:
The area of the triangle.
Solution:
Let the sides of the triangle be $a$, $b$, and $c$.
According to the given ratio, let the sides be:
$a = 12x$
$b = 17x$
$c = 25x$
We know that the perimeter of a triangle is the sum of its sides.
$12x + 17x + 25x = 540$
(Sum of sides = Perimeter)
$54x = 540$
$x = \frac{\cancel{540}^{10}}{\cancel{54}_{1}}$
$x = 10$
... (i)
Now, substitute the value of $x$ from equation (i) to find the actual lengths of the sides:
$a = 12 \times 10 = 120$ cm
$b = 17 \times 10 = 170$ cm
$c = 25 \times 10 = 250$ cm
Next, we calculate the semi-perimeter ($s$) of the triangle:
$s = \frac{\text{Perimeter}}{2}$
$s = \frac{540}{2}$
$s = 270$ cm
... (ii)
Now, calculate the values of $(s-a)$, $(s-b)$, and $(s-c)$:
$(s-a) = 270 - 120 = 150$ cm
$(s-b) = 270 - 170 = 100$ cm
$(s-c) = 270 - 250 = 20$ cm
Using Heron's Formula to find the area of the triangle:
Area $= \sqrt{s(s-a)(s-b)(s-c)}$
Substitute the values from equation (ii) and the calculated differences:
Area $= \sqrt{270 \times 150 \times 100 \times 20}$
To simplify the square root, we can factorize the terms:
Area $= \sqrt{(3 \times 3 \times 3 \times 10) \times (3 \times 5 \times 10) \times (10 \times 10) \times (2 \times 10)}$
Area $= \sqrt{3^4 \times 5 \times 2 \times 10^5}$
Let's use a simpler grouping:
Area $= \sqrt{(270 \times 150 \times 20) \times 100}$
Area $= \sqrt{8,10,000 \times 100}$
Area $= \sqrt{8,10,00,000}$
Area $= \sqrt{9000^2}$
Area $= 9000$ cm$^2$
Final Answer:
The area of the triangle is $9000$ cm$^2$.
Question 6. An isosceles triangle has perimeter 30 cm and each of the equal sides is 12 cm. Find the area of the triangle.
Answer:
Given:
The perimeter of an isosceles triangle is $30$ cm.
Each of the equal sides is $12$ cm.
To Find:
The area of the triangle.
Solution:
Let the equal sides of the isosceles triangle be $a = 12$ cm and $b = 12$ cm. Let the third side be $c$ cm.
The perimeter of the triangle is the sum of its sides.
Perimeter $= a + b + c$
We are given the perimeter is $30$ cm, and $a = 12$, $b = 12$.
$30 = 12 + 12 + c$
... (i)
$30 = 24 + c$
To find the length of the third side $c$:
$c = 30 - 24$
$c = 6$ cm
The lengths of the sides of the triangle are $12$ cm, $12$ cm, and $6$ cm.
Next, we calculate the semi-perimeter ($s$), which is half the perimeter.
$s = \frac{\text{Perimeter}}{2}$
$s = \frac{30}{2}$
$s = 15$ cm
To find the area of the triangle, we use Heron's formula:
Area $= \sqrt{s(s-a)(s-b)(s-c)}$
First, calculate $(s-a)$, $(s-b)$, and $(s-c)$:
$s - a = 15 - 12 = 3$ cm
$s - b = 15 - 12 = 3$ cm
$s - c = 15 - 6 = 9$ cm
Now, substitute these values into Heron's formula:
Area $= \sqrt{15 \times 3 \times 3 \times 9}$
Area $= \sqrt{(3 \times 5) \times 3^2 \times 3^2}$
Area $= \sqrt{3 \times 5 \times 9 \times 9}$
Area $= \sqrt{3 \times 5 \times 81}$
Area $= \sqrt{81 \times 15}$
Area $= \sqrt{81} \times \sqrt{15}$
Area $= 9\sqrt{15}$ cm$^2$
The area of the isosceles triangle is $9\sqrt{15}$ cm$^2$.

