| Non-Rationalised NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
Chapter 13 Surface Areas And Volumes
Welcome to the solutions guide for Chapter 13: Surface Areas And Volumes. This chapter significantly elevates our study of three-dimensional geometry, moving beyond the analysis of individual, standard solids like the cube, cuboid, cylinder, cone, sphere, and hemisphere. Here, we tackle more intricate scenarios involving the calculation of surface areas and volumes for objects constructed by combinations of these basic solid shapes. Imagine toys constructed from cones and hemispheres, medicinal capsules formed by cylinders capped with hemispheres, or tents combining cylindrical bases with conical tops – these composite structures require careful consideration of how surfaces join and volumes aggregate. Furthermore, this chapter explores the dynamic process of transforming solids from one shape into another, such as when metal is melted and recast, introducing the fundamental principle of volume conservation. Additionally, for syllabi that include it, we delve into a specific derived shape: the frustum of a cone, the shape resembling a bucket or a lampshade, which results from slicing off the top portion of a cone with a plane parallel to its base. Successfully navigating this chapter demands strong spatial visualization skills, precise application of surface area and volume formulas, and adept algebraic manipulation.
A primary focus is calculating the surface area and volume of combinations of solids. The solutions emphasize distinct strategies for each calculation:
- Surface Area: When calculating the total surface area of a combined solid, the key is to identify and sum only the areas of the surfaces that are exposed or visible externally. Importantly, the areas where the constituent solids are joined together are not included in the total surface area. For instance, the surface area of a tent composed of a cylinder topped by a cone would be the sum of the Curved Surface Area (CSA) of the cylinder and the CSA of the cone (assuming the base is open or on the ground).
- Volume: Calculating the volume of a combined solid is generally more straightforward. It simply involves summing the individual volumes of the basic shapes that make up the composite object. For example, the volume of a toy shaped like a cone mounted on a hemisphere is the sum of the volume of the cone and the volume of the hemisphere.
Examples explored include toys, architectural structures like pillars with hemispherical domes, industrial objects like tanks, and medical items like capsules.
The chapter also addresses problems involving the conversion of solids. This typically involves scenarios where a solid of one shape (e.g., a large metallic sphere) is melted down and recast into one or more solids of another shape (e.g., smaller spheres, a cylindrical wire, or numerous small cubes). The unwavering physical principle governing these transformations is that of Volume Conservation: the volume of the material remains constant throughout the process. Therefore, the core strategy is to equate the volume of the original solid to the total volume of the solid(s) formed after recasting ($\text{Volume}_{\text{original}} = \text{Volume}_{\text{final}}$). Solutions demonstrate using this principle to find unknown dimensions (like the radius of a new sphere or the length of a wire) or to determine the number of smaller objects that can be created.
Lastly, the concept of the Frustum of a Cone is introduced (note: this may be excluded in rationalised syllabi). A frustum is the portion of a cone remaining when its top part is cut off by a plane parallel to the base. Let $\mathbf{r_1}$ and $\mathbf{r_2}$ be the radii of the larger and smaller circular ends, respectively, $\mathbf{h}$ be the perpendicular height, and $\mathbf{l}$ be the slant height. The solutions provide and apply the specific formulas for the frustum:
- Slant Height: $\mathbf{l} = \sqrt{\mathbf{h}^2 + (\mathbf{r_1} - \mathbf{r_2})^2}$
- Curved Surface Area (CSA): $CSA = \pi(\mathbf{r_1} + \mathbf{r_2})\mathbf{l}$
- Total Surface Area (TSA): $TSA = \pi(\mathbf{r_1} + \mathbf{r_2})\mathbf{l} + \pi \mathbf{r_1}^2 + \pi \mathbf{r_2}^2$
- Volume: $V = \frac{1}{3}\pi \mathbf{h}(\mathbf{r_1}^2 + \mathbf{r_2}^2 + \mathbf{r_1}\mathbf{r_2})$
Applications involve calculating the capacity (volume) and surface area of objects commonly shaped like frustums, such as buckets, drinking glasses, or lampshades. Mastery of this chapter hinges on careful interpretation of problems, accurate visualization, correct formula selection, and precise calculations.
Example 1 to 4 (Before Exercise 13.1)
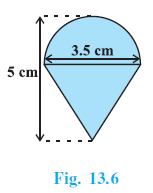
Example 1. Rasheed got a playing top (lattu) as his birthday present, which surprisingly had no colour on it. He wanted to colour it with his crayons. The top is shaped like a cone surmounted by a hemisphere (see Fig 13.6). The entire top is 5 cm in height and the diameter of the top is 3.5 cm. Find the area he has to colour. (Take π = $\frac{22}{7}$ )
Answer:
Given:
The playing top is shaped like a cone surmounted by a hemisphere.
Total height of the top = 5 cm.
Diameter of the top = 3.5 cm.
Value of $\pi = \frac{22}{7}$.
To Find:
The total surface area of the top that needs to be coloured.
Solution:
The total surface area (TSA) of the top to be coloured is the sum of the curved surface area (CSA) of the hemisphere and the curved surface area (CSA) of the cone.
Diameter of the top = 3.5 cm.
Radius of the hemisphere (and base of the cone), $r = \frac{\text{Diameter}}{2} = \frac{3.5}{2} = 1.75$ cm.
Height of the hemispherical part = Radius = $r = 1.75$ cm.
Height of the conical part, $h = \text{Total height} - \text{Height of hemisphere}$
$h = 5 - 1.75 = 3.25$ cm.
Now, we need to find the slant height ($l$) of the cone.
The formula for slant height is $l = \sqrt{r^2 + h^2}$.
$l = \sqrt{(1.75)^2 + (3.25)^2}$
$l = \sqrt{3.0625 + 10.5625}$
$l = \sqrt{13.625}$
$l \approx 3.69$ cm. We can approximate this to $l \approx 3.7$ cm (as commonly done in textbook examples for this value).
Calculate the CSA of the hemisphere.
CSA of hemisphere = $2 \pi r^2$
CSA of hemisphere = $2 \times \frac{22}{7} \times (1.75)^2$
CSA of hemisphere = $2 \times \frac{22}{7} \times 1.75 \times 1.75$
CSA of hemisphere = $2 \times \frac{22}{7} \times \frac{175}{100} \times \frac{175}{100}$
CSA of hemisphere = $2 \times \frac{22}{1} \times \frac{25}{100} \times \frac{175}{100}$
CSA of hemisphere = $2 \times 22 \times \frac{1}{4} \times 1.75$
CSA of hemisphere = $11 \times 1.75 = 19.25$ cm$^2$.
Calculate the CSA of the cone.
CSA of cone = $\pi r l$
CSA of cone = $\frac{22}{7} \times 1.75 \times 3.7$ (using the approximate value of $l$)
CSA of cone = $\frac{22}{7} \times \frac{175}{100} \times 3.7$
CSA of cone = $\frac{22}{1} \times \frac{25}{100} \times 3.7$
CSA of cone = $22 \times \frac{1}{4} \times 3.7$
CSA of cone = $5.5 \times 3.7 = 20.35$ cm$^2$.
Total Surface Area of the top = CSA of hemisphere + CSA of cone
TSA = $19.25 + 20.35$
TSA = $39.6$ cm$^2$.
Hence, the area Rasheed has to colour is 39.6 cm$^2$.
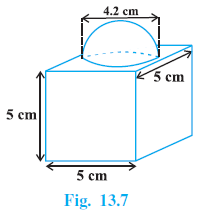
Example 2. The decorative block shown in Fig. 13.7 is made of two solids — a cube and a hemisphere. The base of the block is a cube with edge 5 cm, and the hemisphere fixed on the top has a diameter of 4.2 cm. Find the total surface area of the block. (Take π = $\frac{22}{7}$ )
Answer:
Given:
A decorative block made of a cube and a hemisphere.
Edge length of the cube, $s = 5$ cm.
Diameter of the hemisphere fixed on top = 4.2 cm.
Value of $\pi = \frac{22}{7}$.
To Find:
The total surface area (TSA) of the block.
Solution:
The total surface area of the block consists of:
1. The total surface area of the cube.
2. The curved surface area (CSA) of the hemisphere.
3. We need to subtract the area of the base of the hemisphere because it covers a part of the top face of the cube.
TSA of block = (TSA of cube) - (Base area of hemisphere) + (CSA of hemisphere)
Calculate the TSA of the cube:
TSA of cube = $6 \times (\text{edge})^2 = 6s^2$
TSA of cube = $6 \times (5)^2 = 6 \times 25 = 150$ cm$^2$.
Calculate the dimensions and areas related to the hemisphere:
Diameter of hemisphere = 4.2 cm.
Radius of hemisphere, $r = \frac{\text{Diameter}}{2} = \frac{4.2}{2} = 2.1$ cm.
Base area of hemisphere = $\pi r^2$
Base area = $\frac{22}{7} \times (2.1)^2 = \frac{22}{7} \times 2.1 \times 2.1$
Base area = $22 \times 0.3 \times 2.1 = 6.6 \times 2.1 = 13.86$ cm$^2$.
Curved Surface Area (CSA) of hemisphere = $2 \pi r^2$
CSA of hemisphere = $2 \times (\text{Base area}) = 2 \times 13.86 = 27.72$ cm$^2$.
Calculate the total surface area of the block:
TSA of block = (TSA of cube) - (Base area of hemisphere) + (CSA of hemisphere)
TSA of block = $150 - 13.86 + 27.72$
TSA of block = $150 + (27.72 - 13.86)$
TSA of block = $150 + 13.86$
TSA of block = $163.86$ cm$^2$.
Alternatively, using the simplified formula TSA = $6s^2 + \pi r^2$:
TSA = $150 + 13.86 = 163.86$ cm$^2$.
Hence, the total surface area of the block is 163.86 cm$^2$.
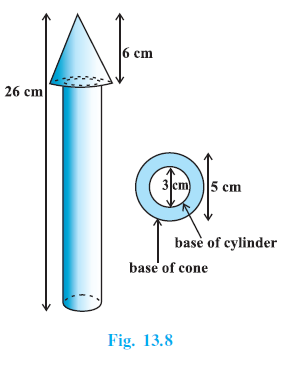
Example 3. A wooden toy rocket is in the shape of a cone mounted on a cylinder, as shown in Fig. 13.8. The height of the entire rocket is 26 cm, while the height of the conical part is 6 cm. The base of the conical portion has a diameter of 5 cm, while the base diameter of the cylindrical portion is 3 cm. If the conical portion is to be painted orange and the cylindrical portion yellow, find the area of the rocket painted with each of these colours. (Take π = 3.14)
Answer:
Given:
A toy rocket shaped like a cone mounted on a cylinder.
Total height of the rocket = 26 cm.
Height of the conical part, $h_{cone} = 6$ cm.
Diameter of the base of the cone, $d_{cone} = 5$ cm.
Diameter of the base of the cylinder, $d_{cyl} = 3$ cm.
Conical portion is painted orange.
Cylindrical portion is painted yellow.
Value of $\pi = 3.14$.
To Find:
1. The area painted orange.
2. The area painted yellow.
Solution:
Dimensions:
Radius of the conical part, $r_{cone} = \frac{d_{cone}}{2} = \frac{5}{2} = 2.5$ cm.
Radius of the cylindrical part, $r_{cyl} = \frac{d_{cyl}}{2} = \frac{3}{2} = 1.5$ cm.
Height of the conical part, $h_{cone} = 6$ cm.
Height of the cylindrical part, $h_{cyl} = \text{Total height} - h_{cone} = 26 - 6 = 20$ cm.
Slant height of the conical part ($l_{cone}$):
$l_{cone} = \sqrt{r_{cone}^2 + h_{cone}^2}$
$l_{cone} = \sqrt{(2.5)^2 + (6)^2}$
$l_{cone} = \sqrt{6.25 + 36} = \sqrt{42.25}$
$l_{cone} = 6.5$ cm.
Area painted Orange:
The orange area includes the Curved Surface Area (CSA) of the cone and the area of the base ring of the cone (Base area of cone - Base area of cylinder).
CSA of cone = $\pi r_{cone} l_{cone}$
CSA of cone = $3.14 \times 2.5 \times 6.5$
CSA of cone = $3.14 \times 16.25 = 51.025$ cm$^2$.
Base area of cone = $\pi r_{cone}^2$
Base area of cone = $3.14 \times (2.5)^2 = 3.14 \times 6.25 = 19.625$ cm$^2$.
Base area of cylinder = $\pi r_{cyl}^2$
Base area of cylinder = $3.14 \times (1.5)^2 = 3.14 \times 2.25 = 7.065$ cm$^2$.
Area of the base ring of the cone = Base area of cone - Base area of cylinder
Area of base ring = $19.625 - 7.065 = 12.56$ cm$^2$.
Total area painted orange = CSA of cone + Area of base ring
Area (Orange) = $51.025 + 12.56 = 63.585$ cm$^2$.
Area painted Yellow:
The yellow area includes the Curved Surface Area (CSA) of the cylinder and the area of the bottom base of the cylinder.
CSA of cylinder = $2 \pi r_{cyl} h_{cyl}$
CSA of cylinder = $2 \times 3.14 \times 1.5 \times 20$
CSA of cylinder = $6.28 \times 30 = 188.4$ cm$^2$.
Area of the bottom base of cylinder = $\pi r_{cyl}^2 = 7.065$ cm$^2$ (calculated previously).
Total area painted yellow = CSA of cylinder + Area of bottom base
Area (Yellow) = $188.4 + 7.065 = 195.465$ cm$^2$.
Hence,
The area of the rocket painted orange is 63.585 cm$^2$.
The area of the rocket painted yellow is 195.465 cm$^2$.
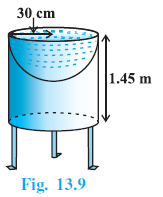
Example 4. Mayank made a bird-bath for his garden in the shape of a cylinder with a hemispherical depression at one end (see Fig. 13.9). The height of the cylinder is 1.45 m and its radius is 30 cm. Find the total surface area of the bird-bath. (Take π = $\frac{22}{7}$ )
Answer:
Given:
Shape of the bird-bath: Cylinder with a hemispherical depression at one end.
Height of the cylinder, $h = 1.45$ m.
Radius of the cylinder (and hemisphere), $r = 30$ cm.
Value of $\pi = \frac{22}{7}$.
To Find:
The total surface area (TSA) of the bird-bath.
Solution:
First, ensure the units are consistent. Convert the height to centimeters.
Height $h = 1.45 \text{ m} = 1.45 \times 100 \text{ cm} = 145$ cm.
Radius $r = 30$ cm.
The total surface area of the bird-bath includes the Curved Surface Area (CSA) of the cylinder and the inner surface area of the hemispherical depression (which is the CSA of the hemisphere).
The base of the cylinder is usually considered part of the TSA, but in the context of a bird-bath, often the calculation focuses on the area exposed to water or the environment, which is the outer wall and the inner depression. Let's calculate based on this interpretation (CSA of cylinder + CSA of hemisphere).
Calculate the CSA of the cylinder:
CSA$_{cylinder}$ = $2 \pi r h$
CSA$_{cylinder}$ = $2 \times \frac{22}{7} \times 30 \times 145$
CSA$_{cylinder}$ = $\frac{44 \times 4350}{7} = \frac{191400}{7}$ cm$^2$.
Calculate the CSA of the hemisphere:
CSA$_{hemisphere}$ = $2 \pi r^2$
CSA$_{hemisphere}$ = $2 \times \frac{22}{7} \times (30)^2$
CSA$_{hemisphere}$ = $2 \times \frac{22}{7} \times 900$
CSA$_{hemisphere}$ = $\frac{44 \times 900}{7} = \frac{39600}{7}$ cm$^2$.
Calculate the Total Surface Area (TSA) of the bird-bath:
TSA = CSA$_{cylinder}$ + CSA$_{hemisphere}$
TSA = $\frac{191400}{7} + \frac{39600}{7}$
TSA = $\frac{191400 + 39600}{7} = \frac{231000}{7}$
TSA = $33000$ cm$^2$.
Converting the area to square meters:
TSA = $33000 \text{ cm}^2 = \frac{33000}{100 \times 100} \text{ m}^2 = 3.3 \text{ m}^2$.
Hence, the total surface area of the bird-bath is 33000 cm$^2$ or 3.3 m$^2$.
Exercise 13.1
Unless stated otherwise, take π = $\frac{22}{7}$
Question 1. 2 cubes each of volume 64 cm3 are joined end to end. Find the surface area of the resulting cuboid.
Answer:
Given
Two cubes are joined end to end.
Volume of each cube = 64 cm3.
To Find
The surface area of the resulting cuboid.
Solution
Let the side length of each cube be 's'.
The volume of a cube is given by the formula $V = s^3$.
Given, Volume = 64 cm3.
$s^3 = 64$
$s = \sqrt[3]{64}$
$s = 4$ cm.
So, the edge of each cube is 4 cm.
When two such cubes are joined end to end, they form a cuboid.
The dimensions of the resulting cuboid will be:
Length (L) = Side of first cube + Side of second cube = $s + s = 4 + 4 = 8$ cm.
Breadth (B) = Side of cube = $s = 4$ cm.
Height (H) = Side of cube = $s = 4$ cm.
The surface area of a cuboid is given by the formula:
Surface Area = $2(LB + BH + HL)$
Substitute the values of L, B, and H:
Surface Area = $2 \times ((8 \times 4) + (4 \times 4) + (4 \times 8))$
Surface Area = $2 \times (32 + 16 + 32)$
Surface Area = $2 \times (80)$
Surface Area = $160$ cm2.
Hence, the surface area of the resulting cuboid is 160 cm2.
Question 2. A vessel is in the form of a hollow hemisphere mounted by a hollow cylinder. The diameter of the hemisphere is 14 cm and the total height of the vessel is 13 cm. Find the inner surface area of the vessel.
Answer:
Given
A vessel in the form of a hollow hemisphere mounted by a hollow cylinder.
Diameter of the hemisphere = 14 cm.
Total height of the vessel = 13 cm.
To Find
The inner surface area of the vessel.
Solution
The inner surface area of the vessel is the sum of the inner curved surface area of the cylinder and the inner curved surface area of the hemisphere.
Diameter of the hemisphere = 14 cm.
Radius of the hemisphere, $r = \frac{14}{2} = 7$ cm.
Since the cylinder is mounted on the hemisphere, the radius of the cylinder is the same as the radius of the hemisphere.
Radius of cylinder, $r = 7$ cm.
The height of the hemispherical part is equal to its radius, so height of hemisphere = 7 cm.
Height of the cylindrical part, $h$ = Total height of vessel - Height of hemisphere
$h = 13 - 7 = 6$ cm.
Inner surface area of vessel = (Inner CSA of cylinder) + (Inner CSA of hemisphere)
Inner surface area = $(2\pi rh) + (2\pi r^2)$
Inner surface area = $2\pi r(h + r)$
Substitute the values $r=7$ and $h=6$:
Inner surface area = $2 \times \frac{22}{7} \times 7 \times (6 + 7)$
= $2 \times 22 \times 13$
= $44 \times 13$
= $572$ cm2.
The inner surface area of the vessel is 572 cm2.
Question 3. A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius. The total height of the toy is 15.5 cm. Find the total surface area of the toy.
Answer:
Given
A toy in the form of a cone mounted on a hemisphere.
Radius of the cone and hemisphere, $r = 3.5$ cm.
Total height of the toy = 15.5 cm.
To Find
The total surface area of the toy.
Solution
The total surface area of the toy is the sum of the curved surface area (CSA) of the cone and the curved surface area (CSA) of the hemisphere.
Radius of hemisphere and cone, $r = 3.5$ cm.
Height of the hemispherical part = radius = 3.5 cm.
Height of the conical part, $h$ = Total height of toy - Height of hemisphere
$h = 15.5 - 3.5 = 12$ cm.
To find the CSA of the cone, we first need to find its slant height, $l$.
$l = \sqrt{r^2 + h^2}$
$l = \sqrt{(3.5)^2 + (12)^2} = \sqrt{12.25 + 144} = \sqrt{156.25}$
$l = 12.5$ cm.
Total Surface Area (TSA) of toy = (CSA of cone) + (CSA of hemisphere)
TSA = $\pi r l + 2\pi r^2 = \pi r(l + 2r)$
Substitute the values $r = 3.5$, $l = 12.5$, and $\pi = \frac{22}{7}$:
TSA = $\frac{22}{7} \times 3.5 \times (12.5 + 2 \times 3.5)$
= $\frac{22}{7} \times \frac{7}{2} \times (12.5 + 7)$
= $11 \times (19.5)$
= $214.5$ cm2.
The total surface area of the toy is 214.5 cm2.
Question 4. A cubical block of side 7 cm is surmounted by a hemisphere. What is the greatest diameter the hemisphere can have? Find the surface area of the solid.
Answer:
Given
A cubical block of side 7 cm is surmounted by a hemisphere.
To Find
1. The greatest diameter the hemisphere can have.
2. The surface area of the solid.
Solution
1. Greatest Diameter of the Hemisphere:
For the hemisphere to be surmounted on the cube, its base must lie on one of the faces of the cube. The greatest possible diameter for the hemisphere is equal to the side length of the cube.
Side of the cube = 7 cm.
Therefore, the greatest diameter the hemisphere can have is 7 cm.
Radius of the hemisphere, $r = \frac{7}{2} = 3.5$ cm.
2. Surface Area of the Solid:
The total surface area of the solid is the sum of the total surface area of the cube and the curved surface area of the hemisphere, minus the area of the base of the hemisphere (since it is covered).
Surface Area = (TSA of cube) - (Area of base of hemisphere) + (CSA of hemisphere)
TSA of cube = $6 \times (\text{side})^2 = 6 \times (7)^2 = 6 \times 49 = 294$ cm2.
Area of base of hemisphere = $\pi r^2 = \frac{22}{7} \times (3.5)^2 = \frac{22}{7} \times 12.25 = 38.5$ cm2.
CSA of hemisphere = $2\pi r^2 = 2 \times 38.5 = 77$ cm2.
Surface Area of solid = $294 - 38.5 + 77$
= $294 + 38.5 = 332.5$ cm2.
The greatest diameter the hemisphere can have is 7 cm.
The surface area of the solid is 332.5 cm2.
Question 5. A hemispherical depression is cut out from one face of a cubical wooden block such that the diameter l of the hemisphere is equal to the edge of the cube. Determine the surface area of the remaining solid.
Answer:
Given
A cubical wooden block with edge length $l$.
A hemispherical depression is cut out from one face.
The diameter of the hemisphere is equal to the edge of the cube, $l$.
To Find
The surface area of the remaining solid.
Solution
The surface area of the remaining solid is the sum of the total surface area of the cube plus the inner curved surface area of the hemispherical depression, minus the area of the circular opening on the face of the cube.
Edge of the cube = $l$.
Diameter of the hemisphere = $l$.
Radius of the hemisphere, $r = \frac{l}{2}$.
Surface Area = (TSA of cube) - (Area of circular opening) + (Inner CSA of hemisphere)
TSA of cube = $6 \times (\text{edge})^2 = 6l^2$.
Area of circular opening = $\pi r^2 = \pi \left(\frac{l}{2}\right)^2 = \frac{\pi l^2}{4}$.
Inner CSA of hemisphere = $2\pi r^2 = 2\pi \left(\frac{l}{2}\right)^2 = \frac{2\pi l^2}{4} = \frac{\pi l^2}{2}$.
Surface Area of remaining solid = $6l^2 - \frac{\pi l^2}{4} + \frac{\pi l^2}{2}$
= $6l^2 + \left(\frac{\pi l^2}{2} - \frac{\pi l^2}{4}\right)$
= $6l^2 + \frac{2\pi l^2 - \pi l^2}{4}$
= $6l^2 + \frac{\pi l^2}{4}$
We can factor out $l^2$ to get:
Surface Area = $l^2 \left(6 + \frac{\pi}{4}\right)$
Alternatively, we can take $\frac{1}{4}$ common as well:
Surface Area = $\frac{l^2}{4}(24 + \pi)$.
The surface area of the remaining solid is $\frac{l^2}{4}(24 + \pi)$ square units.
Question 6. A medicine capsule is in the shape of a cylinder with two hemispheres stuck to each of its ends (see Fig. 13.10). The length of the entire capsule is 14 mm and the diameter of the capsule is 5 mm. Find its surface area.
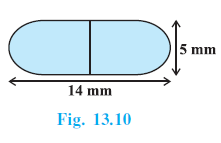
Answer:
Given:
Medicine capsule shape: cylinder with two hemispheres stuck to each end.
Total length of the capsule = 14 mm
Diameter of the capsule = 5 mm
To Find:
The surface area of the capsule.
Solution:
The capsule is composed of a cylinder and two hemispheres of the same diameter.
The diameter of the capsule is 5 mm.
The radius of the capsule (hemisphere and cylinder) is half of the diameter.
Radius, $r = \frac{\text{Diameter}}{2} = \frac{5}{2} = 2.5$ mm.
Radius, $r = 2.5$ mm.
... (i)
The total length of the capsule is 14 mm.
The length of each hemispherical part is equal to its radius, which is 2.5 mm.
The length of the cylindrical part is the total length minus the lengths of the two hemispheres.
Height of the cylindrical part, $h$ = Total length - (Radius of one hemisphere) - (Radius of the other hemisphere)
$h = 14 \text{ mm} - 2.5 \text{ mm} - 2.5 \text{ mm}$
$h = 14 \text{ mm} - 5 \text{ mm}$
Height of cylinder, $h = 9$ mm.
... (ii)
The surface area of the capsule is the sum of the curved surface area (CSA) of the two hemispheres and the curved surface area of the cylinder.
CSA of one hemisphere $= 2\pi r^2$.
CSA of two hemispheres $= 2 \times (2\pi r^2) = 4\pi r^2$.
CSA of cylinder $= 2\pi r h$.
Total Surface Area of capsule = (CSA of two hemispheres) + (CSA of cylinder)
Total Area $= 4\pi r^2 + 2\pi r h$
We can factor out $2\pi r$ from the expression:
Total Area $= 2\pi r (2r + h)$
Substitute the values of $r$ and $h$ from (i) and (ii):
Total Area $= 2\pi (2.5 \text{ mm}) (2 \times 2.5 \text{ mm} + 9 \text{ mm})$
Total Area $= 2\pi (2.5) (5 + 9)$
Total Area $= 5\pi (14)$
Total Area $= 70\pi$ mm$^2$.
Using the value $\pi = \frac{22}{7}$:
Total Area $= 70 \times \frac{22}{7}$
Total Area $= \frac{\cancel{70}^{10} \times 22}{\cancel{7}_{1}}$
Total Area $= 10 \times 22$
Total Area $= 220$
So, the surface area of the medicine capsule is 220 mm$^2$.
Final Answer:
The surface area of the medicine capsule is $220 \text{ mm}^2$.
Question 7. A tent is in the shape of a cylinder surmounted by a conical top. If the height and diameter of the cylindrical part are 2.1 m and 4 m respectively, and the slant height of the top is 2.8 m, find the area of the canvas used for making the tent. Also, find the cost of the canvas of the tent at the rate of ₹ 500 per m2 . (Note that the base of the tent will not be covered with canvas.)
Answer:
Given
Shape of the tent: Cylinder surmounted by a cone.
Height of the cylindrical part, $h_{cyl} = 2.1$ m.
Diameter of the cylindrical part = 4 m.
Slant height of the conical part, $l = 2.8$ m.
Cost of canvas =
To Find
1. The area of the canvas used.
2. The total cost of the canvas.
Solution
The total area of canvas required is the sum of the curved surface area (CSA) of the cylindrical part and the curved surface area of the conical part. The base is not covered.
1. Calculate dimensions:
Diameter = 4 m, so the radius of both the cylinder and the cone is $r = \frac{4}{2} = 2$ m.
Height of cylinder, $h_{cyl} = 2.1$ m.
Slant height of cone, $l = 2.8$ m.
2. Calculate the area of canvas:
Area of canvas = (CSA of cylinder) + (CSA of cone)
Area = $(2\pi r h_{cyl}) + (\pi r l)$
Area = $\pi r (2h_{cyl} + l)$
Substitute the values:
Area = $\frac{22}{7} \times 2 \times (2 \times 2.1 + 2.8)$
= $\frac{44}{7} \times (4.2 + 2.8)$
= $\frac{44}{7} \times (7.0)$
= $44$ m2.
3. Calculate the cost of the canvas:
Cost = Total Area $\times$ Rate per m2
Cost = $44 \times 500$
Cost =
The area of the canvas used is 44 m2 and the cost of the canvas is
Question 8. From a solid cylinder whose height is 2.4 cm and diameter 1.4 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid to the nearest cm2 .
Answer:
Given
A solid cylinder with height $h = 2.4$ cm and diameter $d = 1.4$ cm.
A conical cavity of the same height and diameter is hollowed out.
To Find
The total surface area of the remaining solid to the nearest cm2.
Solution
The total surface area of the remaining solid is the sum of the curved surface area (CSA) of the cylinder, the area of the base of the cylinder, and the inner curved surface area of the conical cavity.
1. Calculate dimensions:
Height of cylinder and cone, $h = 2.4$ cm.
Diameter = 1.4 cm, so the radius of both is $r = \frac{1.4}{2} = 0.7$ cm.
2. Calculate the slant height of the cone:
Slant height, $l = \sqrt{r^2 + h^2}$
$l = \sqrt{(0.7)^2 + (2.4)^2} = \sqrt{0.49 + 5.76} = \sqrt{6.25}$
$l = 2.5$ cm.
3. Calculate the total surface area:
Total Surface Area (TSA) = (CSA of cylinder) + (Area of cylinder base) + (CSA of cone)
TSA = $(2\pi r h) + (\pi r^2) + (\pi r l)$
TSA = $\pi r (2h + r + l)$
Substitute the values:
TSA = $\frac{22}{7} \times 0.7 \times (2 \times 2.4 + 0.7 + 2.5)$
= $2.2 \times (4.8 + 0.7 + 2.5)$
= $2.2 \times (8.0)$
= $17.6$ cm2.
The question asks for the answer to the nearest cm2.
Rounding 17.6 to the nearest whole number gives 18.
The total surface area of the remaining solid is approximately 18 cm2.
Question 9. A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in Fig. 13.11. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the total surface area of the article.
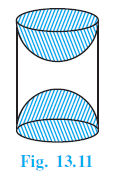
Answer:
Given
A solid cylinder with a hemisphere scooped out from each end.
Height of the cylinder, $h = 10$ cm.
Radius of the base, $r = 3.5$ cm.
To Find
The total surface area of the article.
Solution
The total surface area of the article is the sum of the curved surface area (CSA) of the cylinder and the inner curved surface areas of the two hemispherical depressions.
Radius of the cylinder and hemispheres, $r = 3.5$ cm.
Height of the cylinder, $h = 10$ cm.
Total Surface Area (TSA) = (CSA of cylinder) + 2 $\times$ (CSA of hemisphere)
TSA = $(2\pi r h) + 2 \times (2\pi r^2)$
TSA = $2\pi r h + 4\pi r^2 = 2\pi r(h + 2r)$
Substitute the values:
TSA = $2 \times \frac{22}{7} \times 3.5 \times (10 + 2 \times 3.5)$
= $2 \times \frac{22}{7} \times \frac{7}{2} \times (10 + 7)$
= $22 \times (17)$
= $374$ cm2.
The total surface area of the article is 374 cm2.
Example 5 to 7 (Before Exercise 13.2)
Example 5. Shanta runs an industry in a shed which is in the shape of a cuboid surmounted by a half cylinder (see Fig. 13.12). If the base of the shed is of dimension 7 m × 15 m, and the height of the cuboidal portion is 8 m, find the volume of air that the shed can hold. Further, suppose the machinery in the shed occupies a total space of 300 m3 , and there are 20 workers, each of whom occupy about 0.08 m3 space on an average. Then, how much air is in the shed? (Take π = $\frac{22}{7}$ )
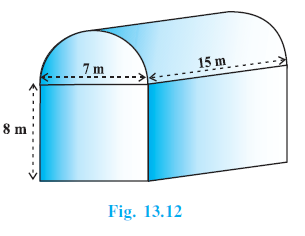
Answer:
Given
Shape of the shed: a cuboid surmounted by a half cylinder.
Dimensions of the cuboidal base: length = 15 m, breadth = 7 m.
Height of the cuboidal portion = 8 m.
Volume of machinery = 300 m3.
Number of workers = 20.
Volume occupied by one worker = 0.08 m3.
To Find
1. Total volume of air the shed can hold.
2. Actual volume of air in the shed after accounting for machinery and workers.
Solution
The total volume of the shed is the sum of the volume of the cuboidal part and the volume of the half-cylindrical part.
1. Volume of the cuboidal part:
Volume = length $\times$ breadth $\times$ height
$V_{cuboid} = 15 \times 7 \times 8 = 840$ m3.
2. Volume of the half-cylindrical part:
The half cylinder is placed on the 7m x 15m top face. The diameter of the half-cylinder is the breadth of the cuboid, so diameter = 7 m.
Radius of the half-cylinder, $r = \frac{7}{2} = 3.5$ m.
The length of the half-cylinder is the length of the cuboid, which is 15 m. This acts as the height ($h_{cyl}$) of the half-cylinder.
Volume of a half-cylinder = $\frac{1}{2} \times \pi r^2 h_{cyl}$
$V_{half-cyl} = \frac{1}{2} \times \frac{22}{7} \times (3.5)^2 \times 15$
= $\frac{1}{2} \times \frac{22}{7} \times 12.25 \times 15$
= $11 \times 1.75 \times 15 = 11 \times 26.25 = 288.75$ m3.
3. Total volume of the shed:
Total Volume = $V_{cuboid} + V_{half-cyl}$
Total Volume = $840 + 288.75 = 1128.75$ m3.
4. Actual volume of air in the shed:
First, calculate the total volume occupied by objects and people inside.
Volume of machinery = 300 m3.
Volume of workers = $20 \times 0.08 = 1.6$ m3.
Total occupied volume = $300 + 1.6 = 301.6$ m3.
Now, find the volume of air remaining:
Volume of air = Total volume of shed - Total occupied volume
Volume of air = $1128.75 - 301.6 = 827.15$ m3.
The volume of air that the shed can hold is 1128.75 m3.
After accounting for machinery and workers, the amount of air in the shed is 827.15 m3.
Example 6. A juice seller was serving his customers using glasses as shown in Fig. 13.13. The inner diameter of the cylindrical glass was 5 cm, but the bottom of the glass had a hemispherical raised portion which reduced the capacity of the glass. If the height of a glass was 10 cm, find the apparent capacity of the glass and its actual capacity. (Use π = 3.14.)
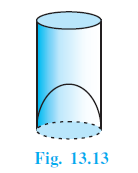
Answer:
Given
A cylindrical glass with a hemispherical raised bottom.
Inner diameter of the glass = 5 cm.
Height of the glass = 10 cm.
Use $\pi = 3.14$.
To Find
1. The apparent capacity of the glass.
2. The actual capacity of the glass.
Solution
1. Apparent Capacity:
The apparent capacity is the volume of the cylinder as if it had a flat bottom.
Diameter = 5 cm, so radius, $r = \frac{5}{2} = 2.5$ cm.
Height, $h = 10$ cm.
Apparent Capacity = Volume of cylinder = $\pi r^2 h$
= $3.14 \times (2.5)^2 \times 10$
= $3.14 \times 6.25 \times 10$
= $3.14 \times 62.5 = 196.25$ cm3.
2. Actual Capacity:
The actual capacity is the apparent capacity minus the volume of the hemispherical raised portion.
The hemisphere has the same radius as the cylinder, $r = 2.5$ cm.
Volume of hemisphere = $\frac{2}{3} \pi r^3$
= $\frac{2}{3} \times 3.14 \times (2.5)^3$
= $\frac{2}{3} \times 3.14 \times 15.625$
= $\frac{2}{3} \times 49.0625 \approx 32.71$ cm3.
Actual Capacity = Apparent Capacity - Volume of hemisphere
= $196.25 - 32.71$
= $163.54$ cm3.
The apparent capacity of the glass is 196.25 cm3.
The actual capacity of the glass is 163.54 cm3.
Example 7. A solid toy is in the form of a hemisphere surmounted by a right circular cone. The height of the cone is 2 cm and the diameter of the base is 4 cm. Determine the volume of the toy. If a right circular cylinder circumscribes the toy, find the difference of the volumes of the cylinder and the toy. (Take π = 3.14)
Answer:
Given
A solid toy: a cone on top of a hemisphere.
Height of the cone, $h_{cone} = 2$ cm.
Diameter of the base = 4 cm.
A right circular cylinder circumscribes the toy.
Use $\pi = 3.14$.
To Find
1. The volume of the toy.
2. The difference in volumes between the cylinder and the toy.
Solution
1. Volume of the Toy:
The volume of the toy is the sum of the volume of the cone and the volume of the hemisphere.
Diameter = 4 cm, so radius of both cone and hemisphere is $r = \frac{4}{2} = 2$ cm.
Height of cone, $h_{cone} = 2$ cm.
Volume of cone = $\frac{1}{3} \pi r^2 h_{cone} = \frac{1}{3} \times 3.14 \times (2)^2 \times 2 \ $$ = \frac{1}{3} \times 3.14 \times 8 \ $$ = \frac{25.12}{3}$ cm3.
Volume of hemisphere = $\frac{2}{3} \pi r^3 = \frac{2}{3} \times 3.14 \times (2)^3 = \frac{2}{3} \times 3.14 \times 8 = \frac{50.24}{3}$ cm3.
Volume of toy = Volume of cone + Volume of hemisphere
= $\frac{25.12}{3} + \frac{50.24}{3} = \frac{75.36}{3} = 25.12$ cm3.
2. Difference in Volumes:
First, find the volume of the circumscribing cylinder.
The cylinder has the same radius as the toy, so radius of cylinder, $R = 2$ cm.
The height of the cylinder is the total height of the toy.
Total height of toy = Height of cone + Height of hemisphere (which is its radius)
Height of cylinder, $H = h_{cone} + r = 2 + 2 = 4$ cm.
Volume of cylinder = $\pi R^2 H = 3.14 \times (2)^2 \times 4 = 3.14 \times 16 = 50.24$ cm3.
Now, find the difference in volumes:
Difference = Volume of cylinder - Volume of toy
= $50.24 - 25.12 = 25.12$ cm3.
The volume of the toy is 25.12 cm3.
The difference in the volumes of the cylinder and the toy is 25.12 cm3.
Exercise 13.2
Unless stated otherwise, take π = $\frac{22}{7}$
Question 1. A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid in terms of π.
Answer:
Given
A solid composed of a cone standing on a hemisphere.
Radius of the hemisphere = 1 cm.
Radius of the cone = 1 cm.
Height of the cone = radius of the cone = 1 cm.
To Find
The volume of the solid in terms of π.
Solution
The total volume of the solid is the sum of the volume of the cone and the volume of the hemisphere.
Radius of cone and hemisphere, $r = 1$ cm.
Height of cone, $h = 1$ cm.
Volume of the solid = (Volume of cone) + (Volume of hemisphere)
Volume = $\left(\frac{1}{3} \pi r^2 h\right) + \left(\frac{2}{3} \pi r^3\right)$
Substitute the values of $r$ and $h$:
Volume = $\left(\frac{1}{3} \pi (1)^2 (1)\right) + \left(\frac{2}{3} \pi (1)^3\right)$
Volume = $\left(\frac{1}{3} \pi\right) + \left(\frac{2}{3} \pi\right)$
Volume = $\left(\frac{1}{3} + \frac{2}{3}\right) \pi$
Volume = $\left(\frac{3}{3}\right) \pi = 1\pi$
Volume = $\pi$ cm3.
The volume of the solid is $\pi$ cm3.
Question 2. Rachel, an engineering student, was asked to make a model shaped like a cylinder with two cones attached at its two ends by using a thin aluminium sheet. The diameter of the model is 3 cm and its length is 12 cm. If each cone has a height of 2 cm, find the volume of air contained in the model that Rachel made. (Assume the outer and inner dimensions of the model to be nearly the same.)
Answer:
Given
Shape of the model: A cylinder with two cones at its ends.
Diameter of the model = 3 cm.
Total length (height) of the model = 12 cm.
Height of each cone = 2 cm.
To Find
The volume of air contained in the model.
Solution
The total volume of the model is the sum of the volume of the central cylindrical part and the volumes of the two identical cones at the ends.
1. Calculate the dimensions:
Diameter = 3 cm, so the radius of the cylinder and cones is $r = \frac{3}{2} = 1.5$ cm.
Height of each cone, $h_{cone} = 2$ cm.
Total length of the model = 12 cm.
Height of the cylindrical part, $h_{cyl}$ = Total length - (Height of cone 1 + Height of cone 2)
$h_{cyl} = 12 - (2 + 2) = 12 - 4 = 8$ cm.
2. Calculate the volumes:
Volume of the cylindrical part = $\pi r^2 h_{cyl}$
= $\pi (1.5)^2 \times 8 = \pi \times 2.25 \times 8 = 18\pi$ cm3.
Volume of one cone = $\frac{1}{3} \pi r^2 h_{cone}$
= $\frac{1}{3} \pi (1.5)^2 \times 2 = \frac{1}{3} \pi \times 2.25 \times 2 = \frac{4.5\pi}{3} = 1.5\pi$ cm3.
Volume of two cones = $2 \times 1.5\pi = 3\pi$ cm3.
3. Calculate the total volume of the model:
Total Volume = Volume of cylinder + Volume of two cones
Total Volume = $18\pi + 3\pi = 21\pi$ cm3.
Using $\pi = \frac{22}{7}$:
Total Volume = $21 \times \frac{22}{7} = 3 \times 22 = 66$ cm3.
The volume of air contained in the model is 66 cm3.
Question 3. A gulab jamun,contains sugar syrup up to about 30% of its volume. Find approximately how much syrup would be found in 45 gulab jamuns,each shaped like a cylinder with two hemispherical ends with length 5 cm and diameter 2.8 cm (see Fig. 13.15).
Answer:
Given
Shape of one gulab jamun: a cylinder with two hemispherical ends.
Total length of one gulab jamun = 5 cm.
Diameter of the gulab jamun = 2.8 cm.
Number of gulab jamuns = 45.
Sugar syrup content = 30% of the total volume of the gulab jamuns.
To Find
The approximate volume of syrup in 45 gulab jamuns.
Solution
First, we need to find the volume of a single gulab jamun.
The volume of one gulab jamun is the sum of the volume of the central cylindrical part and the volumes of the two hemispherical ends.
1. Calculate the dimensions:
Diameter = 2.8 cm.
Radius of the cylinder and the hemispheres, $r = \frac{2.8}{2} = 1.4$ cm.
The two hemispherical ends together form a sphere of radius 1.4 cm. The length of these two ends is $2 \times r = 2 \times 1.4 = 2.8$ cm.
Total length of the gulab jamun = 5 cm.
Length (height) of the cylindrical part, $h_{cyl}$ = Total length - Length of two hemispherical ends
$h_{cyl} = 5 - 2.8 = 2.2$ cm.
2. Calculate the volume of one gulab jamun:
Volume of one gulab jamun = (Volume of cylinder) + (Volume of two hemispheres)
The volume of two hemispheres is equal to the volume of one sphere with the same radius.
Volume = $(\pi r^2 h_{cyl}) + (\frac{4}{3} \pi r^3)$
Volume = $\pi r^2 (h_{cyl} + \frac{4}{3} r)$
Substitute the values, using $\pi = \frac{22}{7}$:
Volume = $\frac{22}{7} \times (1.4)^2 \times \left(2.2 + \frac{4}{3} \times 1.4\right)$
= $\frac{22}{7} \times 1.96 \times \left(2.2 + \frac{5.6}{3}\right)$
= $22 \times 0.28 \times \left(\frac{6.6 + 5.6}{3}\right)$
= $6.16 \times \frac{12.2}{3}$
= $\frac{75.152}{3}$ cm3.
3. Calculate the total volume of 45 gulab jamuns:
Total volume = $45 \times$ (Volume of one gulab jamun)
Total volume = $45 \times \frac{75.152}{3}$
= $15 \times 75.152 = 1127.28$ cm3.
4. Calculate the volume of the sugar syrup:
The syrup is 30% of the total volume of the gulab jamuns.
Volume of syrup = $30\%$ of Total volume
= $\frac{30}{100} \times 1127.28$
= $0.3 \times 1127.28$
= $338.184$ cm3.
The question asks for the approximate amount, so we can round the result.
Approximate volume of syrup $\approx 338$ cm3.
Therefore, approximately 338 cm3 of syrup would be found in 45 gulab jamuns.
Question 4. A pen stand made of wood is in the shape of a cuboid with four conical depressions to hold pens. The dimensions of the cuboid are 15 cm by 10 cm by 3.5 cm. The radius of each of the depressions is 0.5 cm and the depth is 1.4 cm. Find the volume of wood in the entire stand (see Fig. 13.16).
Answer:
Given
A wooden pen stand in the shape of a cuboid.
Dimensions of the cuboid (length, breadth, height): $L = 15$ cm, $B = 10$ cm, $H = 3.5$ cm.
There are 4 conical depressions.
Radius of each conical depression, $r = 0.5$ cm.
Depth (height) of each conical depression, $h = 1.4$ cm.
To Find
The volume of wood in the entire stand.
Solution
The volume of the wood in the pen stand is the volume of the original cuboid minus the volume of the wood removed to create the four conical depressions.
Volume of wood = Volume of cuboid - 4 $\times$ (Volume of one cone).
1. Calculate the Volume of the Cuboid:
Volume of cuboid = $L \times B \times H$
= $15 \times 10 \times 3.5$
= $150 \times 3.5$
= $525$ cm3.
2. Calculate the Volume of one Conical Depression:
The formula for the volume of a cone is $V = \frac{1}{3} \pi r^2 h$.
Substitute the values $r = 0.5$ cm, $h = 1.4$ cm, and $\pi = \frac{22}{7}$:
Volume of one cone = $\frac{1}{3} \times \frac{22}{7} \times (0.5)^2 \times 1.4$
= $\frac{1}{3} \times \frac{22}{7} \times 0.25 \times 1.4$
= $\frac{1}{3} \times 22 \times 0.25 \times 0.2$
= $\frac{1}{3} \times 22 \times 0.05$
= $\frac{1.1}{3}$ cm3.
3. Calculate the Total Volume of the Four Conical Depressions:
Total volume of 4 cones = $4 \times$ (Volume of one cone)
= $4 \times \frac{1.1}{3} = \frac{4.4}{3}$ cm3.
As a decimal, this is approximately $1.467$ cm3.
4. Calculate the Volume of Wood in the Stand:
Volume of wood = Volume of cuboid - Total volume of 4 cones
= $525 - \frac{4.4}{3}$
= $\frac{1575 - 4.4}{3} = \frac{1570.6}{3}$
$\approx 523.533$ cm3.
Therefore, the volume of wood in the entire stand is approximately 523.53 cm3.
Question 5. A vessel is in the form of an inverted cone. Its height is 8 cm and the radius of its top, which is open, is 5 cm. It is filled with water up to the brim. When lead shots, each of which is a sphere of radius 0.5 cm are dropped into the vessel, one-fourth of the water flows out. Find the number of lead shots dropped in the vessel.
Answer:
Given
An inverted conical vessel.
Height of the cone, $H = 8$ cm.
Radius of the cone's top, $R = 5$ cm.
Spherical lead shots of radius, $r = 0.5$ cm.
When lead shots are dropped, $\frac{1}{4}$ of the water flows out.
To Find
The number of lead shots dropped in the vessel.
Solution
The volume of water that flows out is equal to the total volume of the lead shots dropped into the vessel.
1. Calculate the volume of water in the cone:
Volume of the cone, $V_{cone} = \frac{1}{3}\pi R^2 H$
$V_{cone} = \frac{1}{3} \pi (5)^2 (8) = \frac{1}{3} \pi \times 25 \times 8 = \frac{200\pi}{3}$ cm3.
2. Calculate the volume of water that flows out:
Volume of water flowed out = $\frac{1}{4} \times V_{cone}$
= $\frac{1}{4} \times \frac{200\pi}{3} = \frac{50\pi}{3}$ cm3.
3. Calculate the volume of a single lead shot:
Radius of a lead shot (sphere), $r = 0.5$ cm = $\frac{1}{2}$ cm.
Volume of a sphere, $V_{shot} = \frac{4}{3}\pi r^3$
$V_{shot} = \frac{4}{3}\pi \left(\frac{1}{2}\right)^3 = \frac{4}{3}\pi \left(\frac{1}{8}\right) = \frac{\pi}{6}$ cm3.
4. Find the number of lead shots:
Let $n$ be the number of lead shots dropped.
Total volume of lead shots = Volume of water flowed out
$n \times V_{shot} = \frac{50\pi}{3}$
$n \times \frac{\pi}{6} = \frac{50\pi}{3}$
$n = \frac{50\pi}{3} \times \frac{6}{\pi}$
$n = 50 \times 2 = 100$.
The number of lead shots dropped in the vessel is 100.
Question 6. A solid iron pole consists of a cylinder of height 220 cm and base diameter 24 cm, which is surmounted by another cylinder of height 60 cm and radius 8 cm. Find the mass of the pole, given that 1 cm3 of iron has approximately 8g mass. (Use π = 3.14)
Answer:
Given
A solid iron pole made of two cylinders.
Lower cylinder: height $H = 220$ cm, diameter = 24 cm.
Upper cylinder: height $h = 60$ cm, radius $r = 8$ cm.
Density of iron = 8 g/cm3.
Use $\pi = 3.14$.
To Find
The mass of the pole.
Solution
To find the mass, we first need to calculate the total volume of the iron pole.
Total Volume = Volume of lower cylinder + Volume of upper cylinder.
1. Volume of the lower cylinder:
Diameter = 24 cm, so radius, $R = \frac{24}{2} = 12$ cm.
Height, $H = 220$ cm.
Volume, $V_{lower} = \pi R^2 H = 3.14 \times (12)^2 \times 220$
= $3.14 \times 144 \times 220 = 3.14 \times 31680 = 99475.2$ cm3.
2. Volume of the upper cylinder:
Radius, $r = 8$ cm.
Height, $h = 60$ cm.
Volume, $V_{upper} = \pi r^2 h = 3.14 \times (8)^2 \times 60$
= $3.14 \times 64 \times 60 = 3.14 \times 3840 = 12057.6$ cm3.
3. Total Volume of the pole:
Total Volume = $V_{lower} + V_{upper}$
= $99475.2 + 12057.6 = 111532.8$ cm3.
4. Mass of the pole:
Mass = Total Volume $\times$ Density
Mass = $111532.8 \text{ cm}^3 \times 8 \text{ g/cm}^3 = 892262.4$ g.
To convert the mass to kilograms (kg), we divide by 1000.
Mass = $\frac{892262.4}{1000} = 892.2624$ kg.
The mass of the pole is approximately 892.26 kg.
Question 7. A solid consisting of a right circular cone of height 120 cm and radius 60 cm standing on a hemisphere of radius 60 cm is placed upright in a right circular cylinder full of water such that it touches the bottom. Find the volume of water left in the cylinder, if the radius of the cylinder is 60 cm and its height is 180 cm.
Answer:
Given
A solid composed of a cone standing on a hemisphere.
Radius of cone and hemisphere, $r_{solid} = 60$ cm.
Height of cone, $h_{cone} = 120$ cm.
The solid is placed in a cylinder full of water.
Radius of cylinder, $r_{cyl} = 60$ cm.
Height of cylinder, $h_{cyl} = 180$ cm.
To Find
The volume of water left in the cylinder.
Solution
The volume of water left in the cylinder is the initial volume of water (which is the volume of the cylinder) minus the volume of water displaced (which is the volume of the solid).
Volume of water left = Volume of cylinder - Volume of solid.
1. Volume of the Cylinder:
$V_{cyl} = \pi r_{cyl}^2 h_{cyl} = \pi \times (60)^2 \times 180$
= $\pi \times 3600 \times 180 = 648000\pi$ cm3.
2. Volume of the Solid:
The solid consists of a cone and a hemisphere.
Volume of cone = $\frac{1}{3} \pi r_{solid}^2 h_{cone} = \frac{1}{3} \pi \times (60)^2 \times 120$
= $\frac{1}{3} \pi \times 3600 \times 120 = \pi \times 1200 \times 120 = 144000\pi$ cm3.
Volume of hemisphere = $\frac{2}{3} \pi r_{solid}^3 = \frac{2}{3} \pi \times (60)^3$
= $\frac{2}{3} \pi \times 216000 = 2\pi \times 72000 = 144000\pi$ cm3.
Total volume of solid, $V_{solid} = 144000\pi + 144000\pi = 288000\pi$ cm3.
3. Volume of Water Left:
Volume left = $V_{cyl} - V_{solid}$
= $648000\pi - 288000\pi = 360000\pi$ cm3.
To convert this to a numerical value, we can use $\pi = \frac{22}{7}$ and also convert to m3 (1 m3 = 1,000,000 cm3).
Volume left = $360000 \times \frac{22}{7} \approx 1131428.57$ cm3.
In m3, Volume left $\approx \frac{1131428.57}{1000000} \approx 1.131$ m3.
The volume of water left in the cylinder is $360000\pi$ cm3 (or approximately 1.131 m3).
Question 8. A spherical glass vessel has a cylindrical neck 8 cm long, 2 cm in diameter; the diameter of the spherical part is 8.5 cm. By measuring the amount of water it holds, a child finds its volume to be 345 cm3 . Check whether she is correct, taking the above as the inside measurements, and π= 3.14.
Answer:
Given
A glass vessel with a spherical body and a cylindrical neck.
Cylindrical neck: height $h = 8$ cm, diameter = 2 cm.
Spherical part: diameter = 8.5 cm.
Child's measured volume = 345 cm3.
Use $\pi = 3.14$.
To Check
Whether the child's measurement of the volume is correct.
Solution
We need to calculate the actual volume of the vessel and compare it with the child's measurement.
Total Volume = Volume of spherical part + Volume of cylindrical neck.
1. Volume of the spherical part:
Diameter = 8.5 cm, so radius, $R = \frac{8.5}{2} = 4.25$ cm.
Volume, $V_{sphere} = \frac{4}{3}\pi R^3 = \frac{4}{3} \times 3.14 \times (4.25)^3$
= $\frac{4}{3} \times 3.14 \times 76.765625 \approx \frac{4}{3} \times 241.025 \approx 321.367$ cm3.
Let's re-calculate more accurately: $V_{sphere} = \frac{4}{3} \times 3.14 \times 76.765625 = \frac{964.135}{3} \approx 321.39$ cm3.
2. Volume of the cylindrical neck:
Diameter = 2 cm, so radius, $r = \frac{2}{2} = 1$ cm.
Height, $h = 8$ cm.
Volume, $V_{cyl} = \pi r^2 h = 3.14 \times (1)^2 \times 8 = 3.14 \times 8 = 25.12$ cm3.
3. Total Volume of the vessel:
Total Volume = $V_{sphere} + V_{cyl}$
$\approx 321.39 + 25.12 = 346.51$ cm3.
4. Comparison:
The calculated volume is approximately 346.51 cm3.
The child's measured volume is 345 cm3.
Since the calculated volume (346.51 cm3) is not equal to the measured volume (345 cm3), the child's measurement is incorrect.
The calculated volume is 346.51 cm3. Therefore, the child is not correct.
Example 8 to 11 (Before Exercise 13.3)
Example 8. A cone of height 24 cm and radius of base 6 cm is made up of modelling clay. A child reshapes it in the form of a sphere. Find the radius of the sphere.
Answer:
Given
A cone made of modelling clay.
Height of the cone, $h_{cone} = 24$ cm.
Radius of the cone's base, $r_{cone} = 6$ cm.
The cone is reshaped into a sphere.
To Find
The radius of the sphere.
Solution
When an object is reshaped from one form to another, its volume remains constant. Therefore, the volume of the cone will be equal to the volume of the sphere.
1. Calculate the volume of the cone:
Volume of a cone, $V_{cone} = \frac{1}{3} \pi r_{cone}^2 h_{cone}$
$V_{cone} = \frac{1}{3} \pi (6)^2 (24)$
= $\frac{1}{3} \pi \times 36 \times 24$
= $\pi \times 12 \times 24 = 288\pi$ cm3.
2. Equate the volumes and find the radius of the sphere:
Let the radius of the sphere be $r_{sphere}$.
Volume of a sphere, $V_{sphere} = \frac{4}{3} \pi r_{sphere}^3$.
Set the volumes equal:
$V_{sphere} = V_{cone}$
$\frac{4}{3} \pi r_{sphere}^3 = 288\pi$
Divide both sides by $\pi$:
$\frac{4}{3} r_{sphere}^3 = 288$
$r_{sphere}^3 = 288 \times \frac{3}{4}$
$r_{sphere}^3 = 72 \times 3 = 216$
$r_{sphere} = \sqrt[3]{216}$
Since $6 \times 6 \times 6 = 216$, the cube root of 216 is 6.
$r_{sphere} = 6$ cm.
The radius of the sphere is 6 cm.
Example 9. Selvi’s house has an overhead tank in the shape of a cylinder. This is filled by pumping water from a sump (an underground tank) which is in the shape of a cuboid. The sump has dimensions 1.57 m × 1.44 m × 95cm. The overhead tank has its radius 60 cm and height 95 cm. Find the height of the water left in the sump after the overhead tank has been completely filled with water from the sump which had been full. Compare the capacity of the tank with that of the sump. (Use π = 3.14)
Answer:
Given
Sump (cuboid): length $l = 1.57$ m, breadth $b = 1.44$ m, height $h_{sump} = 95$ cm.
Overhead tank (cylinder): radius $r_{tank} = 60$ cm, height $h_{tank} = 95$ cm.
The sump was initially full, and water from it is used to fill the overhead tank completely.
Use $\pi = 3.14$.
To Find
1. Height of the water left in the sump.
2. Comparison of the capacities of the tank and the sump.
Solution
First, ensure all units are consistent. Let's use centimeters (cm).
Dimensions in cm:
Sump: $l = 157$ cm, $b = 144$ cm, $h_{sump} = 95$ cm.
Tank: $r_{tank} = 60$ cm, $h_{tank} = 95$ cm.
1. Calculate the volumes (capacities):
Volume of the sump (initial water volume) = $l \times b \times h_{sump}$
$V_{sump} = 157 \times 144 \times 95 = 2147760$ cm3.
Volume of the overhead tank (water removed from sump) = $\pi r_{tank}^2 h_{tank}$
$V_{tank} = 3.14 \times (60)^2 \times 95 = 3.14 \times 3600 \times 95 = 1073880$ cm3.
2. Calculate the volume of water left in the sump:
Volume left = $V_{sump} - V_{tank}$
= $2147760 - 1073880 = 1073880$ cm3.
3. Find the height of the water left in the sump:
The water left in the sump has a volume of 1073880 cm3 and occupies the base of the sump, which is $157 \times 144$ cm2.
Let the new height be $h_{left}$.
Volume left = $l \times b \times h_{left}$
$1073880 = 157 \times 144 \times h_{left}$
$1073880 = 22608 \times h_{left}$
$h_{left} = \frac{1073880}{22608} = 47.5$ cm.
4. Compare the capacities:
Ratio = $\frac{\text{Capacity of tank}}{\text{Capacity of sump}} = \frac{V_{tank}}{V_{sump}} = \frac{1073880}{2147760} = \frac{1}{2}$.
This shows that the capacity of the tank is half the capacity of the sump.
The height of the water left in the sump is 47.5 cm.
The capacity of the tank is half the capacity of the sump.
Example 10. A copper rod of diameter 1 cm and length 8 cm is drawn into a wire of length 18 m of uniform thickness. Find the thickness of the wire.
Answer:
Given
Copper rod (cylinder): diameter = 1 cm, length = 8 cm.
It is drawn into a wire (cylinder) of length 18 m.
To Find
The thickness (diameter) of the wire.
Solution
When the rod is drawn into a wire, the volume of copper remains the same.
Volume of rod = Volume of wire.
1. Calculate the volume of the rod:
Diameter of rod = 1 cm, so radius, $r_{rod} = \frac{1}{2} = 0.5$ cm.
Length (height) of rod, $h_{rod} = 8$ cm.
Volume of rod = $\pi r_{rod}^2 h_{rod} = \pi \times (0.5)^2 \times 8 = \pi \times 0.25 \times 8 = 2\pi$ cm3.
2. Equate volumes to find the wire's thickness:
Let the radius of the wire be $r_{wire}$.
Length (height) of wire, $h_{wire} = 18$ m = $18 \times 100 = 1800$ cm.
Volume of wire = $\pi r_{wire}^2 h_{wire} = \pi \times r_{wire}^2 \times 1800$.
Set the volumes equal:
$2\pi = \pi \times r_{wire}^2 \times 1800$
Divide by $\pi$:
$2 = 1800 \times r_{wire}^2$
$r_{wire}^2 = \frac{2}{1800} = \frac{1}{900}$
$r_{wire} = \sqrt{\frac{1}{900}} = \frac{1}{30}$ cm.
The thickness of the wire is its diameter.
Thickness = $2 \times r_{wire} = 2 \times \frac{1}{30} = \frac{1}{15}$ cm.
In millimeters, this is $\frac{1}{15} \times 10 = \frac{2}{3} \approx 0.67$ mm.
The thickness of the wire is $\frac{1}{15}$ cm (or approximately 0.67 mm).
Example 11. A hemispherical tank full of water is emptied by a pipe at the rate of $3\frac{4}{7}$ litres per second. How much time will it take to empty half the tank, if it is 3m in diameter? (Take π = $\frac{22}{7}$ )
Answer:
Given
A hemispherical tank with a diameter of 3 m.
The tank is emptied at a rate of $3\frac{4}{7}$ litres per second.
To Find
The time it will take to empty half the tank.
Solution
1. Calculate the volume of water to be emptied:
Diameter of the tank = 3 m, so radius, $r = \frac{3}{2} = 1.5$ m.
Volume of the full hemispherical tank = $\frac{2}{3}\pi r^3$
$V_{full} = \frac{2}{3} \times \frac{22}{7} \times (1.5)^3 = \frac{2}{3} \times \frac{22}{7} \times 3.375 = \frac{99}{14}$ m3.
We need to empty half the tank, so the volume of water to be emptied is:
$V_{empty} = \frac{1}{2} \times V_{full} = \frac{1}{2} \times \frac{99}{14} = \frac{99}{28}$ m3.
2. Convert the volume to litres:
Since 1 m3 = 1000 litres:
$V_{empty} = \frac{99}{28} \times 1000 = \frac{99000}{28} = \frac{24750}{7}$ litres.
3. Calculate the rate of emptying:
Rate = $3\frac{4}{7} = \frac{25}{7}$ litres per second.
4. Calculate the time taken:
Time = $\frac{\text{Total Volume to Empty}}{\text{Rate of Emptying}}$
Time = $\frac{24750/7}{25/7}$ seconds
Time = $\frac{24750}{7} \times \frac{7}{25} = \frac{24750}{25} = 990$ seconds.
5. Convert the time to minutes:
Time in minutes = $\frac{990}{60} = \frac{99}{6} = \frac{33}{2} = 16.5$ minutes.
16.5 minutes is equal to 16 minutes and 30 seconds.
It will take 16.5 minutes (or 16 minutes and 30 seconds) to empty half the tank.
Exercise 13.3
Take π = $\frac{22}{7}$ ,unless stated otherwise.
Question 1. A metallic sphere of radius 4.2 cm is melted and recast into the shape of a cylinder of radius 6 cm. Find the height of the cylinder.
Answer:
Given
A metallic sphere is melted and recast into a cylinder.
Radius of the sphere, $r_{sphere} = 4.2$ cm.
Radius of the cylinder, $r_{cyl} = 6$ cm.
To Find
The height of the cylinder, $h_{cyl}$.
Solution
When an object is melted and recast into a different shape, its volume remains constant.
Therefore, the volume of the sphere is equal to the volume of the cylinder.
Volume of Sphere = Volume of Cylinder
$\frac{4}{3}\pi r_{sphere}^3 = \pi r_{cyl}^2 h_{cyl}$
We can cancel $\pi$ from both sides:
$\frac{4}{3} r_{sphere}^3 = r_{cyl}^2 h_{cyl}$
Substitute the given values for the radii:
$\frac{4}{3} (4.2)^3 = (6)^2 h_{cyl}$
$\frac{4}{3} \times (4.2 \times 4.2 \times 4.2) = 36 \times h_{cyl}$
$\frac{4}{3} \times 74.088 = 36 \times h_{cyl}$
$4 \times 24.696 = 36 \times h_{cyl}$
$98.784 = 36 \times h_{cyl}$
Now, solve for the height of the cylinder:
$h_{cyl} = \frac{98.784}{36}$
$h_{cyl} = 2.744$ cm.
The height of the cylinder is 2.744 cm.
Question 2. Metallic spheres of radii 6 cm, 8 cm and 10 cm, respectively, are melted to form a single solid sphere. Find the radius of the resulting sphere.
Answer:
Given
Three metallic spheres with radii $r_1 = 6$ cm, $r_2 = 8$ cm, and $r_3 = 10$ cm.
These spheres are melted to form a single solid sphere.
To Find
The radius of the resulting single sphere (let's call it R).
Solution
When the spheres are melted and recast, the total volume of the metal is conserved.
Volume of the resulting sphere = Sum of the volumes of the three smaller spheres.
$\frac{4}{3}\pi R^3 = \frac{4}{3}\pi r_1^3 + \frac{4}{3}\pi r_2^3 + \frac{4}{3}\pi r_3^3$
We can factor out and cancel the term $\frac{4}{3}\pi$ from both sides:
$R^3 = r_1^3 + r_2^3 + r_3^3$
Substitute the given radii:
$R^3 = (6)^3 + (8)^3 + (10)^3$
$R^3 = 216 + 512 + 1000$
$R^3 = 1728$
To find R, take the cube root of 1728:
$R = \sqrt[3]{1728}$
Since $12 \times 12 \times 12 = 1728$,
$R = 12$ cm.
The radius of the resulting sphere is 12 cm.
Question 3. A 20 m deep well with diameter 7 m is dug and the earth from digging is evenly spread out to form a platform 22 m by 14 m. Find the height of the platform.
Answer:
Given
A cylindrical well with depth (height) $h_{well} = 20$ m and diameter = 7 m.
The excavated earth is spread to form a cuboidal platform with length $L = 22$ m and breadth $B = 14$ m.
To Find
The height of the platform, $H_{platform}$.
Solution
The volume of the earth dug from the well is equal to the volume of the platform.
Volume of well (cylinder) = Volume of platform (cuboid).
1. Calculate the volume of the earth dug out (Volume of the well):
Radius of the well, $r_{well} = \frac{\text{Diameter}}{2} = \frac{7}{2}$ m.
Height of the well, $h_{well} = 20$ m.
Volume of well = $\pi r_{well}^2 h_{well}$
= $\frac{22}{7} \times \left(\frac{7}{2}\right)^2 \times 20$
= $\frac{22}{7} \times \frac{49}{4} \times 20$
= $22 \times 7 \times 5 = 770$ m3.
2. Equate volumes to find the height of the platform:
Volume of platform = $L \times B \times H_{platform}$
Volume of platform = $22 \times 14 \times H_{platform}$.
Set the volumes equal:
$770 = 22 \times 14 \times H_{platform}$
$770 = 308 \times H_{platform}$
$H_{platform} = \frac{770}{308}$
Simplify the fraction:
$H_{platform} = \frac{77 \times 10}{77 \times 4} = \frac{10}{4} = 2.5$ m.
The height of the platform is 2.5 m.
Question 4. A well of diameter 3 m is dug 14 m deep. The earth taken out of it has been spread evenly all around it in the shape of a circular ring of width 4 m to form an embankment. Find the height of the embankment.
Answer:
Given
A cylindrical well with diameter = 3 m and depth (height) = 14 m.
The excavated earth forms a circular ring (embankment) of width 4 m around the well.
To Find
The height of the embankment.
Solution
The volume of the earth dug out from the well is equal to the volume of the embankment.
1. Calculate the volume of the earth dug out:
Radius of the well, $r_{well} = \frac{3}{2}$ m.
Height of the well, $h_{well} = 14$ m.
Volume of earth = $\pi r_{well}^2 h_{well} = \frac{22}{7} \times \left(\frac{3}{2}\right)^2 \times 14$
= $\frac{22}{7} \times \frac{9}{4} \times 14 = 22 \times \frac{9}{4} \times 2 = 11 \times 9 = 99$ m3.
2. Calculate the height of the embankment:
The embankment is a hollow cylinder. Let its height be $H$.
The inner radius of the embankment is the radius of the well, $r_{inner} = \frac{3}{2}$ m.
The width of the embankment is 4 m.
The outer radius of the embankment, $r_{outer} = r_{inner} + \text{width} = \frac{3}{2} + 4 = \frac{3+8}{2} = \frac{11}{2}$ m.
Volume of the embankment = $\pi (r_{outer}^2 - r_{inner}^2) H$
$99 = \frac{22}{7} \times \left[ \left(\frac{11}{2}\right)^2 - \left(\frac{3}{2}\right)^2 \right] \times H$
$99 = \frac{22}{7} \times \left[ \frac{121}{4} - \frac{9}{4} \right] \times H$
$99 = \frac{22}{7} \times \frac{112}{4} \times H$
$99 = \frac{22}{7} \times 28 \times H$
$99 = 22 \times 4 \times H$
$99 = 88 \times H$
$H = \frac{99}{88} = \frac{9}{8} = 1.125$ m.
The height of the embankment is 1.125 m.
Question 5. A container shaped like a right circular cylinder having diameter 12 cm and height 15 cm is full of ice cream. The ice cream is to be filled into cones of height 12 cm and diameter 6 cm, having a hemispherical shape on the top. Find the number of such cones which can be filled with ice cream.
Answer:
Given
A cylindrical container: diameter = 12 cm, height = 15 cm.
Ice cream cones: conical part with height = 12 cm, diameter = 6 cm, and a hemispherical top.
To Find
The number of ice cream cones that can be filled.
Solution
Total volume of ice cream available = Volume of 'n' ice cream cones.
1. Calculate the volume of the cylindrical container:
Radius of cylinder, $R = \frac{12}{2} = 6$ cm.
Height of cylinder, $H = 15$ cm.
Volume of cylinder, $V_{cyl} = \pi R^2 H = \pi \times (6)^2 \times 15 = 540\pi$ cm3.
2. Calculate the volume of one ice cream cone:
Radius of cone and hemisphere, $r = \frac{6}{2} = 3$ cm.
Height of cone, $h = 12$ cm.
Volume of one cone = (Volume of conical part) + (Volume of hemispherical top)
$V_{cone} = \frac{1}{3}\pi r^2 h + \frac{2}{3}\pi r^3 = \frac{1}{3}\pi r^2 (h + 2r)$
$V_{cone} = \frac{1}{3}\pi (3)^2 (12 + 2 \times 3) = \frac{1}{3}\pi \times 9 \times (18) = 3\pi \times 18 = 54\pi$ cm3.
3. Find the number of cones (n):
$n = \frac{\text{Volume of cylinder}}{\text{Volume of one cone}} = \frac{V_{cyl}}{V_{cone}}$
$n = \frac{540\pi}{54\pi} = 10$.
10 such cones can be filled with ice cream.
Question 6. How many silver coins, 1.75 cm in diameter and of thickness 2 mm, must be melted to form a cuboid of dimensions 5.5 cm × 10 cm × 3.5 cm?
Answer:
Given
Silver coins (cylinders): diameter = 1.75 cm, thickness (height) = 2 mm.
Resulting cuboid: dimensions 5.5 cm $\times$ 10 cm $\times$ 3.5 cm.
To Find
The number of silver coins to be melted.
Solution
Let 'n' be the number of coins. The total volume of 'n' coins equals the volume of the cuboid.
$n \times (\text{Volume of one coin}) = \text{Volume of cuboid}$.
1. Calculate the volume of one coin:
Diameter = 1.75 cm, so radius, $r = \frac{1.75}{2}$ cm.
Thickness (height), $h = 2$ mm = 0.2 cm.
Volume of one coin = $\pi r^2 h = \frac{22}{7} \times \left(\frac{1.75}{2}\right)^2 \times 0.2$
= $\frac{22}{7} \times \frac{1.75 \times 1.75}{4} \times 0.2 = \frac{22}{7} \times 0.25 \times 1.75 \times 0.2 = 0.48125$ cm3.
2. Calculate the volume of the cuboid:
Volume = $5.5 \times 10 \times 3.5 = 55 \times 3.5 = 192.5$ cm3.
3. Find the number of coins (n):
$n = \frac{\text{Volume of cuboid}}{\text{Volume of one coin}} = \frac{192.5}{0.48125}$
$n = 400$.
400 silver coins must be melted.
Question 7. A cylindrical bucket, 32 cm high and with radius of base 18 cm, is filled with sand. This bucket is emptied on the ground and a conical heap of sand is formed. If the height of the conical heap is 24 cm, find the radius and slant height of the heap.
Answer:
Given
Cylindrical bucket: height $h_{cyl} = 32$ cm, radius $r_{cyl} = 18$ cm.
The sand is formed into a conical heap of height $h_{cone} = 24$ cm.
To Find
1. Radius of the conical heap ($r_{cone}$).
2. Slant height of the conical heap ($l_{cone}$).
Solution
The volume of sand remains the same.
Volume of cylinder = Volume of cone.
1. Equate volumes to find the radius of the cone:
$\pi r_{cyl}^2 h_{cyl} = \frac{1}{3}\pi r_{cone}^2 h_{cone}$
$(18)^2 \times 32 = \frac{1}{3} \times r_{cone}^2 \times 24$
$324 \times 32 = 8 \times r_{cone}^2$
$10368 = 8 \times r_{cone}^2$
$r_{cone}^2 = \frac{10368}{8} = 1296$
$r_{cone} = \sqrt{1296} = 36$ cm.
2. Find the slant height of the cone:
$l_{cone} = \sqrt{r_{cone}^2 + h_{cone}^2}$
$l_{cone} = \sqrt{(36)^2 + (24)^2} = \sqrt{1296 + 576} = \sqrt{1872}$
To simplify $\sqrt{1872}$: $1872 = 144 \times 13$.
$l_{cone} = \sqrt{144 \times 13} = 12\sqrt{13}$ cm.
The radius of the conical heap is 36 cm and the slant height is $12\sqrt{13}$ cm.
Question 8. Water in a canal, 6 m wide and 1.5 m deep, is flowing with a speed of 10 km/h. How much area will it irrigate in 30 minutes, if 8 cm of standing water is needed?
Answer:
Given
Canal: width = 6 m, depth = 1.5 m.
Speed of water = 10 km/h.
Time for irrigation = 30 minutes.
Required height of standing water = 8 cm.
To Find
The area that can be irrigated.
Solution
1. Calculate the volume of water flowing from the canal in 30 minutes:
Speed of water = 10 km/h = 10000 m/h.
Time = 30 minutes = 0.5 hours.
Length of water column that flows in 30 minutes = Speed $\times$ Time = $10000 \times 0.5 = 5000$ m.
Volume of water = Length $\times$ Width $\times$ Depth
$V_{water} = 5000 \times 6 \times 1.5 = 45000$ m3.
2. Calculate the irrigated area:
The volume of water from the canal is spread over the field to a certain height.
Volume of water = Area of field $\times$ Height of standing water.
Height of standing water = 8 cm = 0.08 m.
$45000 = \text{Area} \times 0.08$
Area = $\frac{45000}{0.08} = \frac{4500000}{8} = 562500$ m2.
To convert to hectares (1 hectare = 10000 m2):
Area = $\frac{562500}{10000} = 56.25$ hectares.
The area it will irrigate is 562,500 m2 (or 56.25 hectares).
Question 9. A farmer connects a pipe of internal diameter 20 cm from a canal into a cylindrical tank in her field, which is 10 m in diameter and 2 m deep. If water flows through the pipe at the rate of 3 km/h, in how much time will the tank be filled?
Answer:
Given
Pipe: internal diameter = 20 cm.
Rate of water flow = 3 km/h.
Cylindrical tank: diameter = 10 m, depth (height) = 2 m.
To Find
The time required to fill the tank.
Solution
Let's use meters and hours as our units.
1. Calculate the volume of water flowing through the pipe per hour:
Radius of pipe, $r_{pipe} = \frac{\text{diameter}}{2} = \frac{20 \text{ cm}}{2} = 10$ cm = 0.1 m.
Speed of water = 3 km/h = 3000 m/h. This is the length of the water column flowing in one hour.
Volume flow rate = (Cross-sectional area of pipe) $\times$ (Speed)
= $\pi r_{pipe}^2 \times 3000 = \pi \times (0.1)^2 \times 3000 = \pi \times 0.01 \times 3000 = 30\pi$ m3/h.
2. Calculate the volume of the tank:
Radius of tank, $R_{tank} = \frac{10 \text{ m}}{2} = 5$ m.
Height of tank, $H_{tank} = 2$ m.
Volume of tank = $\pi R_{tank}^2 H_{tank} = \pi \times (5)^2 \times 2 = 50\pi$ m3.
3. Calculate the time to fill the tank:
Time = $\frac{\text{Total Volume to Fill}}{\text{Volume Flow Rate}}$
Time = $\frac{50\pi \text{ m}^3}{30\pi \text{ m}^3/\text{h}} = \frac{50}{30} = \frac{5}{3}$ hours.
To convert this to minutes:
Time = $\frac{5}{3} \times 60 = 100$ minutes.
The tank will be filled in 100 minutes (or 1 hour and 40 minutes).
Example 12 to 14 (Before Exercise 13.4)
Example 12. The radii of the ends of a frustum of a cone 45 cm high are 28 cm and 7 cm (see Fig. 13.21). Find its volume, the curved surface area and the total suface area (Take π = $\frac{22}{7}$ )
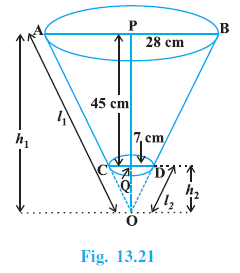
Answer:
Given:
A frustum of a cone.
Height of the frustum ($h$) = 45 cm.
Radius of the larger circular end ($R$) = 28 cm.
Radius of the smaller circular end ($r$) = 7 cm.
Value of $\pi = \frac{22}{7}$.
To Find:
1. Volume of the frustum ($V$).
2. Curved Surface Area (CSA) of the frustum.
3. Total Surface Area (TSA) of the frustum.
Solution:
1. Volume of the Frustum:
The formula for the volume of a frustum of a cone is:
$V = \frac{1}{3}\pi h (R^2 + r^2 + Rr)$
Substitute the given values:
$V = \frac{1}{3} \times \frac{22}{7} \times 45 \times (28^2 + 7^2 + 28 \times 7)$
Calculate the terms inside the parenthesis:
$28^2 = 784$
$7^2 = 49$
$28 \times 7 = 196$
$R^2 + r^2 + Rr = 784 + 49 + 196 = 1029$
Now substitute this back into the volume formula:
$V = \frac{1}{3} \times \frac{22}{7} \times 45 \times 1029$
Simplify the expression:
$V = \frac{1}{\cancel{3}} \times \frac{22}{\cancel{7}} \times \cancel{45}^{15} \times \cancel{1029}^{147}$
$V = 22 \times 15 \times 147$
$V = 330 \times 147$
$V = 48510$ cm³
So, the volume of the frustum is 48510 cm³.
2. Curved Surface Area (CSA) of the Frustum:
First, we need to find the slant height ($l$) of the frustum. The formula is:
$l = \sqrt{h^2 + (R-r)^2}$
$l = \sqrt{45^2 + (28-7)^2}$
$l = \sqrt{45^2 + 21^2}$
$l = \sqrt{2025 + 441}$
$l = \sqrt{2466}$ cm
The formula for the Curved Surface Area (CSA) of a frustum is:
$\text{CSA} = \pi l (R + r)$
Substitute the values:
$\text{CSA} = \frac{22}{7} \times \sqrt{2466} \times (28 + 7)$
$\text{CSA} = \frac{22}{7} \times \sqrt{2466} \times 35$
$\text{CSA} = 22 \times \sqrt{2466} \times \frac{35}{7}$
$\text{CSA} = 22 \times \sqrt{2466} \times 5$
$\text{CSA} = 110\sqrt{2466}$ cm²
So, the Curved Surface Area of the frustum is $110\sqrt{2466}$ cm².
(Note: $\sqrt{2466} \approx 49.659$. If an approximate value is needed, CSA $\approx 110 \times 49.659 \approx 5462.5$ cm².)
3. Total Surface Area (TSA) of the Frustum:
The Total Surface Area (TSA) is the sum of the CSA and the areas of the two circular ends.
Area of the top circular end (smaller base) = $\pi r^2$
Area$_{top} = \frac{22}{7} \times (7)^2 = \frac{22}{7} \times 49 = 22 \times 7 = 154$ cm²
Area of the bottom circular end (larger base) = $\pi R^2$
Area$_{bottom} = \frac{22}{7} \times (28)^2 = \frac{22}{7} \times 784 = 22 \times 112 = 2464$ cm²
The formula for TSA is:
$\text{TSA} = \text{CSA} + \text{Area}_{top} + \text{Area}_{bottom}$
$\text{TSA} = 110\sqrt{2466} + 154 + 2464$
$\text{TSA} = 110\sqrt{2466} + 2618$ cm²
So, the Total Surface Area of the frustum is $(110\sqrt{2466} + 2618)$ cm².
(Note: Using the approximation CSA $\approx 5462.5$ cm², TSA $\approx 5462.5 + 2618 = 8080.5$ cm².)
Example 13. Hanumappa and his wife Gangamma are busy making jaggery out of sugarcane juice. They have processed the sugarcane juice to make the molasses, which is poured into moulds in the shape of a frustum of a cone having the diameters of its two circular faces as 30 cm and 35 cm and the vertical height of the mould is 14 cm (see Fig. 13.22). If each cm3 of molasses has mass about 1.2 g, find the mass of the molasses that can be poured into each mould.(Take π = $\frac{22}{7}$ )
Answer:
Given:
Shape of the mould: Frustum of a cone.
Diameter of the larger circular face = 35 cm.
Diameter of the smaller circular face = 30 cm.
Vertical height of the mould ($h$) = 14 cm.
Density of molasses = 1.2 g/cm³.
Value of $\pi = \frac{22}{7}$.
To Find:
The mass of the molasses that can be poured into each mould.
Solution:
First, find the radii of the two circular faces of the frustum:
Radius of the larger face ($R$) = $\frac{\text{Diameter}}{2} = \frac{35}{2}$ cm = 17.5 cm.
Radius of the smaller face ($r$) = $\frac{\text{Diameter}}{2} = \frac{30}{2}$ cm = 15 cm.
Next, calculate the volume of the frustum-shaped mould using the formula:
$V = \frac{1}{3}\pi h (R^2 + r^2 + Rr)$
Substitute the given values:
$V = \frac{1}{3} \times \frac{22}{7} \times 14 \times ((17.5)^2 + (15)^2 + (17.5 \times 15))$
Calculate the terms inside the parenthesis:
$(17.5)^2 = 306.25$
$(15)^2 = 225$
$17.5 \times 15 = 262.5$
$R^2 + r^2 + Rr = 306.25 + 225 + 262.5 = 793.75$
Now substitute this back into the volume formula:
$V = \frac{1}{3} \times \frac{22}{7} \times 14 \times 793.75$
Simplify the expression:
$V = \frac{1}{3} \times 22 \times (\frac{14}{7}) \times 793.75$
$V = \frac{1}{3} \times 22 \times 2 \times 793.75$
$V = \frac{44}{3} \times 793.75$
$V = \frac{44}{3} \times \frac{79375}{100}$
$V = \frac{\cancel{44}^{11}}{3} \times \frac{79375}{\cancel{100}_{25}}$
$V = \frac{11}{3} \times \frac{79375}{25}$
$V = \frac{11}{3} \times 3175$
$V = \frac{34925}{3}$ cm³
As a decimal, $V \approx 11641.67$ cm³
Now, find the mass of the molasses that can be poured into the mould.
Mass = Volume × Density
Mass = $V \times 1.2$ g
Mass = $\frac{34925}{3} \times 1.2$ g
Mass = $\frac{34925}{3} \times \frac{12}{10}$ g
Mass = $\frac{34925}{\cancel{3}} \times \frac{\cancel{12}^4}{10}$ g
Mass = $\frac{34925 \times 4}{10}$ g
Mass = $\frac{139700}{10}$ g
Mass = $13970$ g
The mass can also be expressed in kilograms.
Since 1 kg = 1000 g,
Mass = $\frac{13970}{1000}$ kg = 13.97 kg.
Therefore, the mass of the molasses that can be poured into each mould is 13970 g or 13.97 kg (approximately).
Example 14. An open metal bucket is in the shape of a frustum of a cone, mounted on a hollow cylindrical base made of the same metallic sheet (see Fig. 13.23). The diameters of the two circular ends of the bucket are 45 cm and 25 cm, the total vertical height of the bucket is 40 cm and that of the cylindrical base is 6 cm. Find the area of the metallic sheet used to make the bucket, where we do not take into account the handle of the bucket. Also, find the volume of water the bucket can hold (Take π = $\frac{22}{7}$ )

Answer:
Given:
The bucket consists of a frustum of a cone mounted on a hollow cylindrical base.
Diameter of the top circular end of the frustum = 45 cm.
Diameter of the bottom circular end of the frustum (and the cylinder) = 25 cm.
Total vertical height of the bucket = 40 cm.
Height of the cylindrical base ($h_{cyl}$) = 6 cm.
The bucket is open at the top.
Value of $\pi = \frac{22}{7}$.
To Find:
1. The area of the metallic sheet used to make the bucket (excluding the handle).
2. The volume of water the bucket can hold.
Solution:
First, determine the dimensions (radii and heights) for the frustum and cylindrical parts.
Radius of the top end of the frustum ($R$) = $\frac{45}{2} = 22.5$ cm.
Radius of the bottom end of the frustum ($r$) = $\frac{25}{2} = 12.5$ cm.
Radius of the cylindrical base ($r_{cyl}$) = $r = 12.5$ cm.
Height of the frustum ($h_{frustum}$) = Total height - Height of cylinder = $40 - 6 = 34$ cm.
Height of the cylinder ($h_{cyl}$) = 6 cm.
1. Area of the Metallic Sheet:
The area of the metallic sheet used is the sum of:
(i) Curved Surface Area (CSA) of the frustum.
(ii) Area of the circular base (bottom of frustum / top of cylinder).
(iii) Curved Surface Area (CSA) of the cylindrical base.
(i) CSA of the Frustum:
First, calculate the slant height ($l$) of the frustum:
$l = \sqrt{h_{frustum}^2 + (R-r)^2}$
$l = \sqrt{34^2 + (22.5 - 12.5)^2}$
$l = \sqrt{34^2 + 10^2}$
$l = \sqrt{1156 + 100} = \sqrt{1256}$ cm.
Now, calculate the CSA of the frustum:
$\text{CSA}_{frustum} = \pi l (R + r)$
$\text{CSA}_{frustum} = \frac{22}{7} \times \sqrt{1256} \times (22.5 + 12.5)$
$\text{CSA}_{frustum} = \frac{22}{7} \times \sqrt{1256} \times 35$
$\text{CSA}_{frustum} = 22 \times \sqrt{1256} \times \frac{35}{7} = 22 \times \sqrt{1256} \times 5$
$\text{CSA}_{frustum} = 110\sqrt{1256}$ cm²
(ii) Area of the Circular Base:
$\text{Area}_{base} = \pi r^2$
$\text{Area}_{base} = \frac{22}{7} \times (12.5)^2$
$\text{Area}_{base} = \frac{22}{7} \times 156.25 = \frac{3437.5}{7}$ cm²
(iii) CSA of the Cylindrical Base:
$\text{CSA}_{cyl} = 2 \pi r h_{cyl}$
$\text{CSA}_{cyl} = 2 \times \frac{22}{7} \times 12.5 \times 6$
$\text{CSA}_{cyl} = \frac{44}{7} \times 75 = \frac{3300}{7}$ cm²
Total Area of Sheet:
Total Area = $\text{CSA}_{frustum} + \text{Area}_{base} + \text{CSA}_{cyl}$
Total Area = $110\sqrt{1256} + \frac{3437.5}{7} + \frac{3300}{7}$
Total Area = $110\sqrt{1256} + \frac{3437.5 + 3300}{7}$
Total Area = $110\sqrt{1256} + \frac{6737.5}{7}$ cm²
Using the approximation $\sqrt{1256} \approx 35.44$ cm:
Total Area $\approx 110 \times 35.44 + \frac{6737.5}{7}$
Total Area $\approx 3898.4 + 962.5$
Total Area $\approx 4860.9$ cm²
The area of the metallic sheet used is $(110\sqrt{1256} + \frac{6737.5}{7})$ cm², or approximately 4860.9 cm².
2. Volume of Water the Bucket Can Hold:
The volume of water the bucket can hold is the volume of the frustum part.
$V_{frustum} = \frac{1}{3}\pi h_{frustum} (R^2 + r^2 + Rr)$
$V_{frustum} = \frac{1}{3} \times \frac{22}{7} \times 34 \times ((22.5)^2 + (12.5)^2 + (22.5 \times 12.5))$
$V_{frustum} = \frac{1}{3} \times \frac{22}{7} \times 34 \times (506.25 + 156.25 + 281.25)$
$V_{frustum} = \frac{1}{3} \times \frac{22}{7} \times 34 \times (943.75)$
$V_{frustum} = \frac{22 \times 34 \times 943.75}{21}$
$V_{frustum} = \frac{748 \times 943.75}{21} = \frac{705925}{21}$ cm³
$V_{frustum} \approx 33615.48$ cm³
To express the volume in litres (1 L = 1000 cm³):
Volume in litres = $\frac{33615.48}{1000} \approx 33.615$ L
The volume of water the bucket can hold is $\frac{705925}{21}$ cm³, or approximately 33.62 litres.
Exercise 13.4
Use π = $\frac{22}{7}$ unless stated otherwise.
Question 1. A drinking glass is in the shape of a frustum of a cone of height 14 cm. The diameters of its two circular ends are 4 cm and 2 cm. Find the capacity of the glass.
Answer:
Given
A drinking glass in the shape of a frustum of a cone.
Height of the frustum, $h = 14$ cm.
Diameter of the top circular end, $D_1 = 4$ cm.
Diameter of the bottom circular end, $D_2 = 2$ cm.
To Find
The capacity (volume) of the glass.
Solution
First, we find the radii of the two circular ends.
Radius of the top end, $r_1 = \frac{D_1}{2} = \frac{4}{2} = 2$ cm.
Radius of the bottom end, $r_2 = \frac{D_2}{2} = \frac{2}{2} = 1$ cm.
The capacity of the glass is the volume of the frustum. The formula for the volume of a frustum of a cone is:
$V = \frac{1}{3}\pi h (r_1^2 + r_2^2 + r_1 r_2)$
Substitute the given values into the formula, using $\pi = \frac{22}{7}$:
$V = \frac{1}{3} \times \frac{22}{7} \times 14 \times (2^2 + 1^2 + (2 \times 1))$
$V = \frac{1}{3} \times \frac{22}{\cancel{7}_1} \times \cancel{14}^2 \times (4 + 1 + 2)$
$V = \frac{1}{3} \times 22 \times 2 \times (7)$
$V = \frac{44 \times 7}{3} = \frac{308}{3}$ cm³.
As a mixed fraction, this is $102\frac{2}{3}$ cm³.
As a decimal, this is approximately $102.67$ cm³.
The capacity of the glass is $\frac{308}{3}$ cm³.
Question 2. The slant height of a frustum of a cone is 4 cm and the perimeters (circumference) of its circular ends are 18 cm and 6 cm. Find the curved surface area of the frustum.
Answer:
Given
A frustum of a cone.
Slant height, $l = 4$ cm.
Circumference of the larger end, $C_1 = 18$ cm.
Circumference of the smaller end, $C_2 = 6$ cm.
To Find
The Curved Surface Area (CSA) of the frustum.
Solution
Let the radii of the larger and smaller circular ends be $r_1$ and $r_2$ respectively.
We are given the circumferences:
$C_1 = 2\pi r_1 = 18$ cm.
$C_2 = 2\pi r_2 = 6$ cm.
From these, we can find the radii:
$r_1 = \frac{18}{2\pi} = \frac{9}{\pi}$ cm.
$r_2 = \frac{6}{2\pi} = \frac{3}{\pi}$ cm.
The formula for the Curved Surface Area (CSA) of a frustum of a cone is:
$\text{CSA} = \pi l (r_1 + r_2)$
Substitute the expressions for the radii:
$\text{CSA} = \pi \times 4 \times \left(\frac{9}{\pi} + \frac{3}{\pi}\right)$
$\text{CSA} = 4\pi \times \left(\frac{9+3}{\pi}\right)$
$\text{CSA} = 4\pi \times \frac{12}{\pi}$
Cancel $\pi$ from the expression:
$\text{CSA} = 4 \times 12 = 48$ cm².
Alternate Method
The CSA formula can also be expressed in terms of the circumferences.
$\text{CSA} = \pi l (r_1 + r_2) = l (\pi r_1 + \pi r_2)$
Since $C_1 = 2\pi r_1$ and $C_2 = 2\pi r_2$, we have $\pi r_1 = \frac{C_1}{2}$ and $\pi r_2 = \frac{C_2}{2}$.
$\text{CSA} = l \left(\frac{C_1}{2} + \frac{C_2}{2}\right) = \frac{l}{2}(C_1 + C_2)$
Substitute the given values:
$\text{CSA} = \frac{4}{2}(18 + 6) = 2(24) = 48$ cm².
The curved surface area of the frustum is 48 cm².
Question 3. A fez, the cap used by the Turks, is shaped like the frustum of a cone (see Fig. 13.24). If its radius on the open side is 10 cm, radius at the upper base is 4 cm and its slant height is 15 cm, find the area of material used for making it.
Answer:
Given
A fez cap in the shape of a frustum of a cone.
Radius of the open side (larger base), $r_1 = 10$ cm.
Radius of the upper base (smaller, closed side), $r_2 = 4$ cm.
Slant height of the frustum, $l = 15$ cm.
To Find
The area of the material used for making the fez.
Solution
The area of the material used to make the fez will be the sum of the curved surface area (CSA) of the frustum and the area of the closed upper base.
Area of material = (CSA of the frustum) + (Area of the upper circular base).
1. Calculate the Curved Surface Area (CSA) of the frustum:
The formula for the CSA of a frustum is:
CSA = $\pi l (r_1 + r_2)$
Substitute the given values, using $\pi = \frac{22}{7}$:
CSA = $\frac{22}{7} \times 15 \times (10 + 4)$
= $\frac{22}{7} \times 15 \times 14$
= $\frac{22}{\cancel{7}_1} \times 15 \times \cancel{14}^2$
= $22 \times 15 \times 2 = 22 \times 30 = 660$ cm2.
2. Calculate the Area of the upper circular base:
The upper base is a circle with radius $r_2 = 4$ cm.
Area of upper base = $\pi r_2^2$
= $\frac{22}{7} \times (4)^2 = \frac{22}{7} \times 16 = \frac{352}{7}$ cm2.
As a decimal, this is approximately $50.2857$ cm2.
3. Calculate the total area of the material:
Total Area = CSA + Area of upper base
= $660 + \frac{352}{7}$
= $\frac{660 \times 7 + 352}{7} = \frac{4620 + 352}{7}$
= $\frac{4972}{7}$ cm2.
As a mixed fraction, this is $710\frac{2}{7}$ cm2.
As a decimal, this is approximately $710.2857$ cm2.
Therefore, the area of the material used for making the fez is $\frac{4972}{7}$ cm2 or $710\frac{2}{7}$ cm2.
Question 4. A container, opened from the top and made up of a metal sheet, is in the form of a frustum of a cone of height 16 cm with radii of its lower and upper ends as 8 cm and 20 cm, respectively. Find the cost of the milk which can completely fill the container, at the rate of ₹ 20 per litre. Also find the cost of metal sheet used to make the container, if it costs ₹ 8 per 100 cm2 . (Take π = 3.14)
Answer:
Given:
The container is in the shape of a frustum of a cone, open at the top.
Height of the frustum ($h$) = 16 cm.
Radius of the upper end (open end, R) = 20 cm.
Radius of the lower end (closed base, r) = 8 cm.
Cost of milk =
Cost of metal sheet =
Value of $\pi = 3.14$.
To Find:
1. Cost of the milk to completely fill the container.
2. Cost of the metal sheet used to make the container.
Solution:
Part 1: Cost of Milk
First, find the capacity (volume) of the container (frustum).
The formula for the volume of a frustum of a cone is:
$V = \frac{1}{3}\pi h (R^2 + r^2 + Rr)$
Substitute the given values:
$V = \frac{1}{3} \times 3.14 \times 16 \times (20^2 + 8^2 + (20 \times 8))$
$V = \frac{1}{3} \times 3.14 \times 16 \times (400 + 64 + 160)$
$V = \frac{1}{3} \times 3.14 \times 16 \times (624)$
$V = 3.14 \times 16 \times (\frac{624}{3})$
$V = 3.14 \times 16 \times 208$
$V = 3.14 \times 3328$
$V = 10449.92$ cm³
Now, convert the volume from cm³ to litres (since 1 litre = 1000 cm³):
Volume in litres = $\frac{10449.92}{1000} = 10.44992$ litres
Calculate the cost of the milk:
Cost of milk = Volume in litres × Rate per litre
Cost of milk = $10.44992 \times 20$
Cost of milk =
Rounding to two decimal places, the cost of milk is
Part 2: Cost of Metal Sheet
The area of the metal sheet used includes the Curved Surface Area (CSA) of the frustum and the area of the lower circular base (since the container is open at the top).
Area of sheet = CSA of frustum + Area of lower base
First, calculate the slant height ($l$) of the frustum:
$l = \sqrt{h^2 + (R-r)^2}$
$l = \sqrt{16^2 + (20-8)^2}$
$l = \sqrt{16^2 + 12^2}$
$l = \sqrt{256 + 144} = \sqrt{400}$
$l = 20$ cm
Next, calculate the CSA of the frustum:
CSA = $\pi l (R + r)$
CSA = $3.14 \times 20 \times (20 + 8)$
CSA = $3.14 \times 20 \times 28$
CSA = $3.14 \times 560$
CSA = $1758.4$ cm²
Now, calculate the area of the lower circular base:
Area$_{base}$ = $\pi r^2$
Area$_{base}$ = $3.14 \times (8)^2$
Area$_{base}$ = $3.14 \times 64$
Area$_{base}$ = $200.96$ cm²
Calculate the total area of the metal sheet:
Total Area = CSA + Area$_{base}$
Total Area = $1758.4 + 200.96$
Total Area = $1959.36$ cm²
Finally, calculate the cost of the metal sheet:
Cost of sheet = $\frac{\text{Total Area}}{100} \times \text{Rate per 100 cm}^2$
Cost of sheet = $\frac{1959.36}{100} \times 8$
Cost of sheet = $19.5936 \times 8$
Cost of sheet =
Rounding to two decimal places, the cost of the metal sheet is
Summary:
The cost of the milk which can completely fill the container is
The cost of the metal sheet used to make the container is
Question 5. A metallic right circular cone 20 cm high and whose vertical angle is 60° is cut into two parts at the middle of its height by a plane parallel to its base. If the frustum so obtained be drawn into a wire of diameter $\frac{1}{16}$ cm, find the length of the wire.
Answer:
Given
A metallic right circular cone with height $H = 20$ cm and vertical angle $60^\circ$.
The cone is cut into a smaller cone and a frustum at the middle of its height.
The frustum is drawn into a cylindrical wire of diameter $\frac{1}{16}$ cm.
To Find
The length of the wire.
Solution
First, we need to find the dimensions and volume of the frustum.
Let the original cone be represented by $\triangle VAB$, where V is the vertex, and AB is the diameter of the base. Let O be the center of the base.
The height of the cone is $VO = H = 20$ cm.
The vertical angle is $\angle AVB = 60^\circ$, so the semi-vertical angle is $\angle AVO = 30^\circ$.
The radius of the base of the original cone is $R = OA$.
In the right-angled triangle $\triangle VOA$:
$\tan(\angle AVO) = \frac{OA}{VO} \implies \tan 30^\circ = \frac{R}{20}$
$\frac{1}{\sqrt{3}} = \frac{R}{20} \implies R = \frac{20}{\sqrt{3}}$ cm.
The cone is cut at the middle of its height. Let the cutting plane be at C'D', where O' is the center.
Height of the smaller cone, $h_1 = VO' = \frac{20}{2} = 10$ cm.
Height of the frustum, $h_2 = O'O = 20 - 10 = 10$ cm.
Let the radius of the top circular end of the frustum be $r = O'C'$.
The smaller cone VC'D' is similar to the original cone VAB.
By similarity of triangles ($\triangle VO'C' \sim \triangle VOA$):
$\frac{VO'}{VO} = \frac{O'C'}{OA} \implies \frac{10}{20} = \frac{r}{R} \implies r = \frac{R}{2} = \frac{1}{2} \times \frac{20}{\sqrt{3}} = \frac{10}{\sqrt{3}}$ cm.
Now, we can calculate the volume of the frustum.
Volume of frustum, $V_{frustum} = \frac{1}{3} \pi h_2 (R^2 + r^2 + Rr)$
= $\frac{1}{3} \pi (10) \left[ \left(\frac{20}{\sqrt{3}}\right)^2 + \left(\frac{10}{\sqrt{3}}\right)^2 + \left(\frac{20}{\sqrt{3}}\right)\left(\frac{10}{\sqrt{3}}\right) \right]$
= $\frac{10\pi}{3} \left[ \frac{400}{3} + \frac{100}{3} + \frac{200}{3} \right]$
= $\frac{10\pi}{3} \left[ \frac{400 + 100 + 200}{3} \right]$
= $\frac{10\pi}{3} \left[ \frac{700}{3} \right] = \frac{7000\pi}{9}$ cm3.
The frustum is drawn into a wire, which is a cylinder. The volume of the metal remains constant.
Volume of wire = Volume of frustum.
Diameter of the wire = $\frac{1}{16}$ cm.
Radius of the wire, $r_{wire} = \frac{1}{2} \times \frac{1}{16} = \frac{1}{32}$ cm.
Let the length of the wire be $L$.
Volume of wire, $V_{wire} = \pi r_{wire}^2 L = \pi \left(\frac{1}{32}\right)^2 L = \frac{\pi L}{1024}$.
Equating the volumes:
$\frac{\pi L}{1024} = \frac{7000\pi}{9}$
Cancel $\pi$ from both sides:
$\frac{L}{1024} = \frac{7000}{9}$
$L = \frac{7000 \times 1024}{9} = \frac{7168000}{9}$ cm.
$L \approx 796444.44$ cm.
To convert this length to meters, we divide by 100:
$L \approx \frac{796444.44}{100} \approx 7964.44$ m.
The length of the wire is $\frac{7168000}{9}$ cm or approximately 7964.44 m.
Exercise 13.5 (Optional)
Question 1. A copper wire, 3 mm in diameter, is wound about a cylinder whose length is 12 cm, and diameter 10 cm, so as to cover the curved surface of the cylinder. Find the length and mass of the wire, assuming the density of copper to be 8.88 g per cm3 .
Answer:
Given
Diameter of the copper wire = 3 mm.
Length of the cylinder, $H = 12$ cm.
Diameter of the cylinder = 10 cm.
Density of copper = 8.88 g/cm3.
To Find
1. The length of the copper wire.
2. The mass of the copper wire.
Solution
1. Finding the Length of the Wire:
The wire is wound around the cylinder. The thickness of the wire is its diameter, which is 3 mm or 0.3 cm.
Each turn of the wire covers a height of 0.3 cm on the cylinder.
Total height of the cylinder to be covered = 12 cm.
Number of turns = $\frac{\text{Height of cylinder}}{\text{Diameter of wire}} = \frac{12}{0.3} = \frac{120}{3} = 40$ turns.
The length of the wire in one turn is equal to the circumference of the cylinder.
Radius of the cylinder, $R = \frac{10}{2} = 5$ cm.
Length of wire in one turn = $2\pi R = 2\pi(5) = 10\pi$ cm.
Total length of the wire = Number of turns $\times$ Length per turn
Total Length = $40 \times 10\pi = 400\pi$ cm.
Using $\pi = 3.14$:
Total Length = $400 \times 3.14 = 1256$ cm.
2. Finding the Mass of the Wire:
First, we need the volume of the wire. The wire itself is a very long, thin cylinder.
Radius of the wire, $r = \frac{3 \text{ mm}}{2} = 1.5$ mm = 0.15 cm.
Length of the wire, $L = 1256$ cm.
Volume of the wire = $\pi r^2 L = 3.14 \times (0.15)^2 \times 1256$
= $3.14 \times 0.0225 \times 1256$
= $0.07065 \times 1256 \approx 88.7364$ cm3.
Now, we find the mass using the density.
Mass = Volume $\times$ Density
Mass = $88.7364 \times 8.88 \approx 787.97$ g.
The length of the wire is 1256 cm (or 12.56 m) and its mass is approximately 788 g.
Question 2. A right triangle, whose sides are 3 cm and 4 cm (other than hypotenuse) is made to revolve about its hypotenuse. Find the volume and surface area of the double cone so formed. (Choose value of π as found appropriate.)
Answer:
Given
A right-angled triangle with perpendicular sides 3 cm and 4 cm.
The triangle is revolved about its hypotenuse.
To Find
1. The volume of the double cone formed.
2. The surface area of the double cone.
Solution
Let the right triangle be ABC, right-angled at B, with AB = 3 cm and BC = 4 cm.
Step 1: Find the dimensions of the double cone.
First, find the hypotenuse AC using the Pythagorean theorem:
$AC = \sqrt{AB^2 + BC^2} = \sqrt{3^2 + 4^2} = \sqrt{9+16} = \sqrt{25} = 5$ cm.
When revolved about AC, a double cone is formed. The common radius ($r$) of the two cones is the altitude from B to AC. Let's call this altitude BD.
Area of $\triangle ABC = \frac{1}{2} \times AB \times BC = \frac{1}{2} \times 3 \times 4 = 6$ cm2.
Also, Area of $\triangle ABC = \frac{1}{2} \times AC \times BD$.
$6 = \frac{1}{2} \times 5 \times r \implies r = \frac{12}{5} = 2.4$ cm.
The two cones have heights AD ($h_1$) and CD ($h_2$). $h_1 + h_2 = AC = 5$ cm.
In $\triangle ABD$, $h_1 = \sqrt{AB^2 - r^2} = \sqrt{3^2 - (2.4)^2} = \sqrt{9 - 5.76} = \sqrt{3.24} \ $$ = 1.8$ cm.
$h_2 = AC - h_1 = 5 - 1.8 = 3.2$ cm.
Step 2: Calculate the Volume.
Volume of double cone = Volume of cone 1 + Volume of cone 2
$V = \frac{1}{3}\pi r^2 h_1 + \frac{1}{3}\pi r^2 h_2 = \frac{1}{3}\pi r^2 (h_1 + h_2)$
$V = \frac{1}{3}\pi (2.4)^2 (5) = \frac{1}{3} \times 3.14 \times 5.76 \times 5 = 30.144$ cm3.
Step 3: Calculate the Surface Area.
The surface area is the sum of the curved surface areas (CSA) of the two cones.
The slant heights of the two cones are the sides of the original triangle, $l_1 = AB = 3$ cm and $l_2 = BC = 4$ cm.
Surface Area = $\pi r l_1 + \pi r l_2 = \pi r (l_1 + l_2)$
Surface Area = $\pi \times 2.4 \times (3 + 4) = \pi \times 2.4 \times 7 = 16.8\pi$ cm2.
Using $\pi = 3.14$, Surface Area = $16.8 \times 3.14 = 52.752$ cm2.
The volume of the double cone is 30.144 cm3.
The surface area of the double cone is 52.752 cm2.
Question 3. A cistern, internally measuring 150 cm × 120 cm × 110 cm, has 129600 cm3 of water in it. Porous bricks are placed in the water until the cistern is full to the brim. Each brick absorbs one-seventeenth of its own volume of water. How many bricks can be put in without overflowing the water, each brick being 22.5 cm × 7.5 cm × 6.5 cm?
Answer:
Given
Cistern dimensions: 150 cm $\times$ 120 cm $\times$ 110 cm.
Initial volume of water = 129600 cm3.
Brick dimensions: 22.5 cm $\times$ 7.5 cm $\times$ 6.5 cm.
Water absorption by each brick = $\frac{1}{17}$ of its own volume.
To Find
The number of bricks that can be put in without water overflowing.
Solution
Step 1: Calculate volumes.
Volume of the cistern = $150 \times 120 \times 110 = 1,980,000$ cm3.
Volume of the cistern to be filled (empty space) = $1,980,000 - 129,600 = 1,850,400$ cm3.
Volume of one brick = $22.5 \times 7.5 \times 6.5 = 1096.875$ cm3.
Step 2: Calculate the net volume displaced by one brick.
When a brick is placed in water, it displaces its full volume. However, it also absorbs some water, reducing the water level. The net effect on the water level is due to the volume of the solid part of the brick that remains after absorption.
Volume of water absorbed by one brick = $\frac{1}{17} \times 1096.875 = 64.522$ cm3.
The volume of space that one brick effectively fills up = (Volume of brick) - (Volume of water it absorbs).
Net volume increase per brick = $1096.875 - 64.522 = 1032.353$ cm3.
Alternatively, the net volume increase is $\frac{16}{17}$ of the brick's volume: $\frac{16}{17} \times 1096.875 \approx 1032.353$ cm3.
Step 3: Find the number of bricks.
Let 'n' be the number of bricks.
Total net volume increase = $n \times (\text{Net volume increase per brick})$.
This must be equal to the empty space in the cistern.
$n \times 1032.353 = 1,850,400$
$n = \frac{1,850,400}{1032.353} \approx 1792.41$
Since the number of bricks must be a whole number, we cannot place the 1793rd brick without overflow.
Therefore, the maximum number of bricks is 1792.
1792 bricks can be put into the cistern without water overflowing.
Question 4. In one fortnight of a given month, there was a rainfall of 10 cm in a river valley. If the area of the valley is 7280 km2 , show that the total rainfall was approximately equivalent to the addition to the normal water of three rivers each 1072 km long, 75 m wide and 3 m deep.
Answer:
Given
Rainfall in a river valley: Depth = 10 cm, Area = 7280 km2.
Dimensions of one river: Length = 1072 km, Width = 75 m, Depth = 3 m.
To Show
Volume of rainfall $\approx$ Total volume of 3 such rivers.
Proof
Let's calculate both volumes in cubic meters (m3) for consistency.
1. Calculate the volume of rainfall:
Area of the valley = 7280 km2.
Since 1 km = 1000 m, 1 km2 = $(1000 \text{ m})^2 = 1,000,000$ m2.
Area = $7280 \times 1,000,000 = 7,280,000,000$ m2.
Depth of rainfall = 10 cm = 0.1 m.
Volume of rainfall = Area $\times$ Depth
$V_{rainfall} = 7,280,000,000 \times 0.1 = 728,000,000$ m3.
2. Calculate the total volume of the three rivers:
Length of one river = 1072 km = $1072 \times 1000 = 1,072,000$ m.
Width of one river = 75 m.
Depth of one river = 3 m.
Volume of one river = Length $\times$ Width $\times$ Depth
$V_{river} = 1,072,000 \times 75 \times 3 = 1,072,000 \times 225 = 241,200,000$ m3.
Total volume of three rivers = $3 \times V_{river}$
$V_{3rivers} = 3 \times 241,200,000 = 723,600,000$ m3.
3. Compare the volumes:
Volume of rainfall $\approx 728,000,000$ m3.
Total volume of three rivers $\approx 723,600,000$ m3.
The two values are very close to each other. The difference is only about 0.6%.
Hence, it is shown that the total rainfall was approximately equivalent to the addition to the normal water of the three rivers.
Question 5. An oil funnel made of tin sheet consists of a 10 cm long cylindrical portion attached to a frustum of a cone. If the total height is 22 cm, diameter of the cylindrical portion is 8 cm and the diameter of the top of the funnel is 18 cm, find the area of the tin sheet required to make the funnel (see Fig. 13.25).
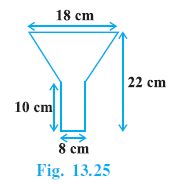
Answer:
Given
An oil funnel made of a cylindrical portion and a frustum of a cone.
Height of the cylindrical portion, $h_{cyl} = 10$ cm.
Total height of the funnel, $H_{total} = 22$ cm.
Diameter of the cylindrical portion = 8 cm.
Diameter of the top of the funnel (top of the frustum) = 18 cm.
To Find
The area of the tin sheet required to make the funnel.
Solution
The area of the tin sheet required is the sum of the curved surface area (CSA) of the frustum and the curved surface area (CSA) of the cylindrical portion.
1. Dimensions and Area of the Cylindrical Portion:
Diameter of the cylinder = 8 cm.
Radius of the cylinder, $r_2 = \frac{8}{2} = 4$ cm.
Height of the cylinder, $h_{cyl} = 10$ cm.
CSA of cylinder = $2\pi r_2 h_{cyl}$
= $2\pi \times 4 \times 10 = 80\pi$ cm2.
2. Dimensions and Area of the Frustum Portion:
Diameter of the top of the frustum = 18 cm.
Radius of the top end, $r_1 = \frac{18}{2} = 9$ cm.
The bottom end of the frustum is attached to the cylinder, so its radius is the same as the cylinder's radius.
Radius of the bottom end, $r_2 = 4$ cm.
Height of the frustum, $h_{frustum} = H_{total} - h_{cyl} = 22 - 10 = 12$ cm.
To find the CSA of the frustum, we first need its slant height, $l$.
The formula for slant height is $l = \sqrt{h_{frustum}^2 + (r_1 - r_2)^2}$.
$l = \sqrt{(12)^2 + (9 - 4)^2}$
$l = \sqrt{144 + (5)^2} = \sqrt{144 + 25} = \sqrt{169}$
$l = 13$ cm.
Now, calculate the CSA of the frustum:
CSA of frustum = $\pi l (r_1 + r_2)$
= $\pi \times 13 \times (9 + 4)$
= $\pi \times 13 \times 13 = 169\pi$ cm2.
3. Total Area of the Tin Sheet:
Total Area = (CSA of cylinder) + (CSA of frustum)
= $80\pi + 169\pi$
= $249\pi$ cm2.
Using $\pi = \frac{22}{7}$:
Total Area = $249 \times \frac{22}{7} = \frac{5478}{7}$ cm2.
As a decimal, this is approximately $782.57$ cm2.
Therefore, the area of the tin sheet required to make the funnel is $\frac{5478}{7}$ cm2 (or approximately 782.57 cm2).
Question 6. Derive the formula for the curved surface area and total surface area of the frustum of a cone, given to you in Section 13.5, using the symbols as explained.
Answer:
To Derive
1. Formula for the Curved Surface Area (CSA) of a frustum of a cone.
2. Formula for the Total Surface Area (TSA) of a frustum of a cone.
Setup and Symbols
Let's consider a right circular cone that is cut by a plane parallel to its base. This divides the cone into a smaller cone at the top and a frustum at the bottom.
- Let $h$ be the height of the frustum.
- Let $l$ be the slant height of the frustum.
- Let $r_1$ and $r_2$ be the radii of the two circular bases of the frustum, with $r_1 > r_2$.
- Let the original cone have a total height $H = h_1$ and a total slant height $L = l_1$.
- The smaller cone that is removed has a height $h_2 = h_1 - h$ and a slant height $l_2 = l_1 - l$.
By similarity of triangles (consider the cross-section), we have the following relationship:
$\frac{h_2}{h_1} = \frac{r_2}{r_1} = \frac{l_2}{l_1}$
Derivation of Curved Surface Area (CSA)
The CSA of the frustum is the CSA of the large cone minus the CSA of the small cone.
$CSA_{frustum} = CSA_{large} - CSA_{small}$
$CSA_{frustum} = \pi r_1 l_1 - \pi r_2 l_2$
From the similarity relation, we have $\frac{r_2}{r_1} = \frac{l_2}{l_1}$, which gives $l_2 = \frac{r_2 l_1}{r_1}$.
Substitute this into the CSA equation:
$CSA_{frustum} = \pi r_1 l_1 - \pi r_2 \left(\frac{r_2 l_1}{r_1}\right) = \pi l_1 \left(r_1 - \frac{r_2^2}{r_1}\right) = \pi l_1 \left(\frac{r_1^2 - r_2^2}{r_1}\right)$
$CSA_{frustum} = \pi l_1 \frac{(r_1 - r_2)(r_1 + r_2)}{r_1}$
Now, we need to express $l_1$ in terms of the frustum's slant height $l$. We know $l = l_1 - l_2$.
From the similarity relation again, $\frac{l_2}{l_1} = \frac{r_2}{r_1} \ $$ \implies l_1 r_2 = l_2 r_1 = (l_1 - l)r_1 = l_1 r_1 - l r_1$.
$l r_1 = l_1 r_1 - l_1 r_2 = l_1(r_1 - r_2)$.
So, $l_1 = \frac{l r_1}{r_1 - r_2}$.
Substitute this expression for $l_1$ back into our CSA formula:
$CSA_{frustum} = \pi \left(\frac{l r_1}{r_1 - r_2}\right) \frac{(r_1 - r_2)(r_1 + r_2)}{r_1}$
Cancel out the common terms $(r_1 - r_2)$ and $r_1$:
$CSA_{frustum} = \pi l (r_1 + r_2)$
This is the formula for the curved surface area of the frustum.
Derivation of Total Surface Area (TSA)
The total surface area of the frustum is its curved surface area plus the area of its two circular bases.
Area of the top circular base = $\pi r_2^2$.
Area of the bottom circular base = $\pi r_1^2$.
$TSA_{frustum} = CSA_{frustum} + (\text{Area of top base}) \ $$ + (\text{Area of bottom base})$
$TSA_{frustum} = \pi l (r_1 + r_2) + \pi r_1^2 + \pi r_2^2$
This is the formula for the total surface area of the frustum.
Question 7. Derive the formula for the volume of the frustum of a cone, given to you in Section 13.5, using the symbols as explained.
Answer:
To Derive
The formula for the Volume (V) of a frustum of a cone.
Setup and Symbols
Let's use the same setup as in the previous derivation:
- Height of the frustum: $h$
- Radii of the bases: $r_1$ and $r_2$ (with $r_1 > r_2$)
- Height of the large (original) cone: $h_1$
- Height of the small (removed) cone: $h_2$
The height of the frustum is $h = h_1 - h_2$.
By similarity of triangles (from the cross-section), we have:
$\frac{h_2}{h_1} = \frac{r_2}{r_1} \implies h_1 r_2 = h_2 r_1$
Derivation of Volume
The volume of the frustum is the volume of the large cone minus the volume of the small cone.
$V_{frustum} = V_{large} - V_{small}$
$V_{frustum} = \frac{1}{3}\pi r_1^2 h_1 - \frac{1}{3}\pi r_2^2 h_2$
$V_{frustum} = \frac{1}{3}\pi (r_1^2 h_1 - r_2^2 h_2)$
We need to express this formula in terms of $h, r_1,$ and $r_2$. From the similarity relation, we have $h_2 = \frac{h_1 r_2}{r_1}$.
Also, $h = h_1 - h_2 = h_1 - \frac{h_1 r_2}{r_1} = h_1 \left(1 - \frac{r_2}{r_1}\right) = h_1 \left(\frac{r_1 - r_2}{r_1}\right)$.
From this, we can express the height of the large cone, $h_1$, in terms of the frustum's dimensions:
$h_1 = \frac{h r_1}{r_1 - r_2}$.
And the height of the small cone, $h_2 = h_1 - h = \frac{h r_1}{r_1 - r_2} - h = \frac{h r_1 - h(r_1 - r_2)}{r_1 - r_2} = \frac{h r_2}{r_1 - r_2}$.
Now substitute these expressions for $h_1$ and $h_2$ into the volume equation:
$V_{frustum} = \frac{1}{3}\pi \left[ r_1^2 \left(\frac{h r_1}{r_1 - r_2}\right) - r_2^2 \left(\frac{h r_2}{r_1 - r_2}\right) \right]$
$V_{frustum} = \frac{1}{3}\pi h \left[ \frac{r_1^3}{r_1 - r_2} - \frac{r_2^3}{r_1 - r_2} \right]$
$V_{frustum} = \frac{1}{3}\pi h \left( \frac{r_1^3 - r_2^3}{r_1 - r_2} \right)$
Using the algebraic identity for the difference of cubes, $a^3 - b^3 = (a-b)(a^2+ab+b^2)$:
$V_{frustum} = \frac{1}{3}\pi h \left( \frac{(r_1 - r_2)(r_1^2 + r_1 r_2 + r_2^2)}{r_1 - r_2} \right)$
Cancel the term $(r_1 - r_2)$:
$V_{frustum} = \frac{1}{3}\pi h (r_1^2 + r_2^2 + r_1 r_2)$
This is the derived formula for the volume of the frustum of a cone.

