| Latest Maths NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
Chapter 1 Patterns in Mathematics
Welcome to this dedicated resource focusing on the solutions for the exercises within the inaugural chapter, "Patterns in Mathematics", featured in the latest Class 6 Ganita Prakash textbook published by NCERT for the academic year 2024-25. This solution guide is meticulously crafted to serve as a comprehensive companion for students navigating the fascinating world of mathematical patterns. It aims to provide clear, step-by-step assistance, ensuring that learners can confidently approach problems involving the identification, thorough analysis, logical extension, and even creation of diverse mathematical patterns presented in their textbook.
Students who find themselves challenged by the task of discerning the underlying rule or logic governing a sequence will find these solutions particularly beneficial. The exercises in "Patterns in Mathematics" explore various forms, and these solutions address them all systematically. The types of patterns encountered include:
- Numerical Sequences: Such as arithmetic progressions (e.g., $4, 9, 14, 19, ...$ where a constant value, $5$, is added) or geometric progressions (e.g., $2, 6, 18, 54, ...$ where each term is multiplied by a constant value, $3$).
- Visual and Geometric Patterns: Sequences involving shapes that might grow, shrink, rotate, or change in arrangement following a predictable logic.
- Repeating Patterns: Sequences of numbers, shapes, or symbols that cycle through a specific set order.
- Simple Algebraic Patterns: Introductory instances where a pattern can be described using a basic variable expression, like the sequence $3, 5, 7, 9, ...$ potentially being represented by a rule related to $2n+1$.
The core strength of this resource lies in its methodical approach. For numerical patterns, the solutions explicitly demonstrate how to determine the relationship between consecutive terms – calculating the constant difference (like $a_{n+1} - a_n$) in arithmetic sequences or the constant ratio (like $\frac{a_{n+1}}{a_n}$) in geometric ones. Once this fundamental rule is established, the solutions illustrate its application to predict subsequent terms or identify missing elements within a given sequence. When tackling visual or geometric patterns, the provided explanations carefully break down the transformation from one step to the next. Changes in critical attributes such as shape components, overall size, orientation, or the quantity of elements are highlighted, empowering students to accurately forecast the next figure or stage in the pattern's evolution.
Furthermore, these solutions guide students through problems requiring the formulation of a pattern's rule, expressed either descriptively in words or using introductory mathematical notation. By engaging with these detailed walkthroughs, students are expected to gain more than just the correct answers. The primary objective is to foster a deeper understanding of the logical reasoning and observational skills that are essential for mastering pattern recognition. This is not merely about solving Chapter 1 exercises; it's about building a foundational skill crucial for grasping more advanced concepts in algebra, geometry, and logical thinking encountered later in their mathematical education using the NCERT Class 6 Ganita Prakash (2024-25) syllabus. The emphasis is firmly placed on clarity and structured thinking, ensuring students grasp why a pattern functions as it does.
Figure it Out (Page 2)
Question 1. Can you think of other examples where mathematics helps us in our everyday lives?
Answer:
Yes, mathematics is used in many parts of our everyday lives, often without us noticing. It is a practical tool for solving common problems.
Here are some examples:
1. Managing Money: Mathematics is used for budgeting pocket money, calculating discounts at a store to see the final price, and checking if you have received the correct change after buying something. It helps in saving money for a future purchase.
2. Cooking and Baking: Recipes involve mathematical concepts. Measuring ingredients in grams or millilitres, understanding ratios (like two parts water for one part rice), and scaling a recipe to make more or less food all require basic math skills.
3. Playing Games and Sports: Board games, video games, and sports rely on mathematics. Keeping score, calculating statistics like batting averages or run rates, and understanding probabilities to make strategic moves all involve math.
4. Art and Construction: Creating symmetrical patterns in art, drawing geometric shapes, and building models require an understanding of geometry. Measuring lengths and angles is crucial to ensure that different parts fit together correctly.
5. Telling Time and Planning: Reading a clock or a calendar, calculating the duration of an event, and planning a schedule for the day or week are all practical applications of mathematics.
6. Technology: All modern gadgets, such as mobile phones, computers, and tablets, are fundamentally based on mathematical principles. The algorithms that run apps, games, and video streaming services are complex mathematical instructions.
Question 2. How has mathematics helped propel humanity forward? (You might think of examples involving: carrying out scientific experiments; running our economy and democracy; building bridges, houses or other complex structures; making TVs, mobile phones, computers, bicycles, trains, cars, planes, calendars, clocks, etc.)
Answer:
Mathematics has been a fundamental tool for human progress and the development of civilization. It provides the language and methods for science, engineering, and technology.
Science and Exploration: Scientists use mathematics to model physical phenomena, analyse experimental data, and make predictions. For example, the laws of physics, which govern everything from planetary motion to the behaviour of atoms, are expressed in mathematical equations. Space exploration, including launching satellites and sending rovers to other planets, is entirely dependent on precise mathematical calculations.
Engineering and Construction: The design and construction of complex structures like bridges, dams, and skyscrapers rely on mathematics. Engineers use principles from geometry, trigonometry, and calculus to calculate loads, stresses, and material strengths, ensuring that these structures are safe and stable.
Technology and Communication: Modern digital technology is built on a mathematical foundation. Computers, mobile phones, and the internet function based on binary logic and algorithms. Data encryption, which keeps our online information secure, uses advanced number theory. Signal processing, a branch of mathematics, is essential for creating and transmitting images and sounds on TVs and phones.
Health and Safety: In medicine, mathematics is used to analyse clinical trial data, model the spread of diseases (epidemiology), and develop medical imaging technologies like MRI and CT scans. Weather forecasting relies on complex mathematical models run on supercomputers to predict storms and other natural disasters, helping to save lives.
Organizing Society: Mathematics is crucial for running economies and democracies. Economics uses mathematical models to understand markets and predict financial trends. Statistics are used to conduct censuses and opinion polls, and fair voting systems are designed using mathematical principles. Our systems for keeping track of time, such as calendars and clocks, were developed by using mathematics to observe and predict astronomical cycles.
Figure it Out (Page 3)
| Table 1 Examples of number sequences | |
|---|---|
| 1, 1, 1, 1, 1, 1, 1, ... | (All 1’s) |
| 1, 2, 3, 4, 5, 6, 7, ... | (Counting numbers) |
| 1, 3, 5, 7, 9, 11, 13, ... | (Odd numbers) |
| 2, 4, 6, 8, 10, 12, 14, ... | (Even numbers) |
| 1, 3, 6, 10, 15, 21, 28, ... | (Triangular numbers) |
| 1, 4, 9, 16, 25, 36, 49, ... | (Squares) |
| 1, 8, 27, 64, 125, 216, ... | (Cubes) |
| 1, 2, 3, 5, 8, 13, 21, ... | (Virahānka numbers) |
| 1, 2, 4, 8, 16, 32, 64, ... | (Powers of 2) |
| 1, 3, 9, 27, 81, 243, 729, ... | (Powers of 3) |
Question 1. Can you recognize the pattern in each of the sequences in Table 1?
Answer:
Yes, we can find the pattern in each list of numbers in Table 1.
1. 1, 1, 1, 1, 1, 1, 1, ...
Pattern: The pattern is very simple! Every number in the list is the same, always 1.
$\checkmark$ Pattern Recognized.
2. 1, 2, 3, 4, 5, 6, 7, ...
Pattern: This is the list of counting numbers, starting from 1. Each number is just 1 more than the number before it.
$1 + 1 = 2$, $2 + 1 = 3$, and so on.
$\checkmark$ Pattern Recognized.
3. 1, 3, 5, 7, 9, 11, 13, ...
Pattern: This is the list of odd numbers. Each number is found by adding 2 to the number before it.
$1 + 2 = 3$, $3 + 2 = 5$, and so on.
$\checkmark$ Pattern Recognized.
4. 2, 4, 6, 8, 10, 12, 14, ...
Pattern: This is the list of even numbers. Each number is found by adding 2 to the number before it.
$2 + 2 = 4$, $4 + 2 = 6$, and so on.
$\checkmark$ Pattern Recognized.
5. 1, 3, 6, 10, 15, 21, 28, ...
Pattern: To get the next number, you add an increasing number each time. You add 2, then 3, then 4, then 5, and so on.
$1 + 2 = 3$, $3 + 3 = 6$, $6 + 4 = 10$, $10 + 5 = 15$, etc.
These are called triangular numbers.
$\checkmark$ Pattern Recognized.
6. 1, 4, 9, 16, 25, 36, 49, ...
Pattern: These are the square numbers. To get a number in the list, you take its position number (1st, 2nd, 3rd, etc.) and multiply it by itself.
1st number: $1 \times 1 = 1$
2nd number: $2 \times 2 = 4$
3rd number: $3 \times 3 = 9$
And so on.
$\checkmark$ Pattern Recognized.
7. 1, 8, 27, 64, 125, 216, ...
Pattern: These are the cube numbers. To get a number in the list, you take its position number (1st, 2nd, 3rd, etc.) and multiply it by itself three times.
1st number: $1 \times 1 \times 1 = 1$
2nd number: $2 \times 2 \times 2 = 8$
3rd number: $3 \times 3 \times 3 = 27$
And so on.
$\checkmark$ Pattern Recognized.
8. 1, 2, 3, 5, 8, 13, 21, ...
Pattern: Starting from the third number, each number is the sum of the two numbers right before it.
$1 + 2 = 3$
$2 + 3 = 5$
$3 + 5 = 8$
And so on. These are called Virahānka numbers (like Fibonacci numbers).
$\checkmark$ Pattern Recognized.
9. 1, 2, 4, 8, 16, 32, 64, ...
Pattern: To get the next number, you multiply the number before it by 2.
$1 \times 2 = 2$
$2 \times 2 = 4$
$4 \times 2 = 8$
And so on. These are called powers of 2.
$\checkmark$ Pattern Recognized.
10. 1, 3, 9, 27, 81, 243, 729, ...
Pattern: To get the next number, you multiply the number before it by 3.
$1 \times 3 = 3$
$3 \times 3 = 9$
$9 \times 3 = 27$
And so on. These are called powers of 3.
$\checkmark$ Pattern Recognized.
Question 2. Rewrite each sequence of Table 1 in your notebook, along with the next three numbers in each sequence! After each sequence, write in your own words what is the rule for forming the numbers in the sequence.
Answer:
Here are the lists of numbers with the next three numbers added, and the rule explained in simple words:
1. Sequence: 1, 1, 1, 1, 1, 1, 1, 1, 1, 1
Rule: The rule is simple: the number is always 1. It never changes.
2. Sequence: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
Rule: Start at 1 and add 1 each time to get the next number. (These are the counting numbers).
3. Sequence: 1, 3, 5, 7, 9, 11, 13, 15, 17, 19
Rule: Start at 1 and add 2 each time to get the next number. (These are the odd numbers).
Next numbers: $13+2 = 15$, $15+2 = 17$, $17+2 = 19$.
4. Sequence: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20
Rule: Start at 2 and add 2 each time to get the next number. (These are the even numbers).
Next numbers: $14+2 = 16$, $16+2 = 18$, $18+2 = 20$.
5. Sequence: 1, 3, 6, 10, 15, 21, 28, 36, 45, 55
Rule: Add a number to the last term, but the number you add goes up by 1 each time: add 2, then add 3, then add 4, and so on.
Next numbers: $28 + 8 = 36$, $36 + 9 = 45$, $45 + 10 = 55$.
6. Sequence: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100
Rule: Multiply the position number of the term by itself. (1st term: $1 \times 1$; 2nd term: $2 \times 2$; etc.).
Next numbers: 8th term is $8 \times 8 = 64$, 9th term is $9 \times 9 = 81$, 10th term is $10 \times 10 = 100$.
7. Sequence: 1, 8, 27, 64, 125, 216, 343, 512, 729
Rule: Multiply the position number of the term by itself three times. (1st term: $1 \times 1 \times 1$; 2nd term: $2 \times 2 \times 2$; etc.).
Next numbers: 7th term is $7 \times 7 \times 7 = 343$, 8th term is $8 \times 8 \times 8 = 512$, 9th term is $9 \times 9 \times 9 = 729$.
8. Sequence: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89
Rule: Start with 1 and 2. From the third number onwards, add the two numbers that came just before it.
Next numbers: $13 + 21 = 34$, $21 + 34 = 55$, $34 + 55 = 89$.
9. Sequence: 1, 2, 4, 8, 16, 32, 64, 128, 256, 512
Rule: Start at 1 and multiply by 2 each time to get the next number.
Next numbers: $64 \times 2 = 128$, $128 \times 2 = 256$, $256 \times 2 = 512$.
10. Sequence: 1, 3, 9, 27, 81, 243, 729, 2187, 6561, 19683
Rule: Start at 1 and multiply by 3 each time to get the next number.
Next numbers: $729 \times 3 = 2187$, $2187 \times 3 = 6561$, $6561 \times 3 = 19683$.
Figure it Out (Page 5 - 6)
| Table 2 Pictorial representation of some number sequences | |
|---|---|
.jpg)
|
(All 1’s) |
.jpg)
|
(Counting numbers) |
.jpg)
|
(Odd numbers) |
.jpg)
|
(Even numbers) |
.jpg)
|
(Triangular numbers) |
.jpg)
|
(Squares) |
.jpg)
|
(Cubes) |
Question 1. Copy the pictorial representations of the number sequences in Table 2 in your notebook, and draw the next picture for each sequence!
Answer:
| Next Picture (6th term) in Each Sequence | |
|---|---|

|
(All 1’s) |
|
(Counting numbers) |
|
(Odd numbers) |

|
(Even numbers) |

|
(Triangular numbers) |

|
(Squares) |

|
(Cubes) |
Below is the description of each sequence and how to draw the next picture (the 6th term):
1. Sequence: All 1's
Pattern: Each picture represents the number 1. The sequence is $1, 1, 1, 1, 1, 1, \dots$ The last picture shown in the table is the 5th term, which is 1.
How to draw the next picture: The next picture (the 6th term) is simply the representation of the number 1. Draw just one dot.
2. Sequence: Counting numbers
Pattern: The pictures represent the counting numbers $1, 2, 3, 4, 5, 6, \dots$ Each picture has one more dot than the previous one. The last picture shown in the table is the 5th term, which is 5 dots.
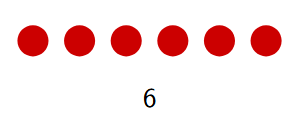
How to draw the next picture: The next number in the sequence is the 6th term, which is 6. Draw a group of 6 dots. You can arrange them in two rows of three dots to continue the pattern.
3. Sequence: Odd numbers
Pattern: The pictures represent the odd numbers $1, 3, 5, 7, 9, 11, \dots$ Each picture has two more dots than the previous one. The last picture shown in the table is the 5th term, which is 9 dots.
How to draw the next picture: The next number in the sequence is the 6th term, $9+2=11$. Draw a picture with 11 dots, for example by making a rectangle of 2 rows of 5 dots and adding one extra dot on top.
4. Sequence: Even numbers
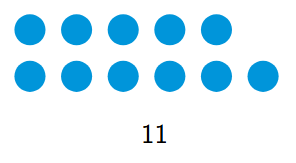
Pattern: The pictures represent the even numbers $2, 4, 6, 8, 10, 12, \dots$ Each picture has two more dots than the previous one. The last picture shown in the table is the 5th term, which is 10 dots.
How to draw the next picture: The next number in the sequence is the 6th term, $10+2=12$. Draw a picture with 12 dots, for example by making a rectangle of 2 rows of 6 dots.
5. Sequence: Triangular numbers
Pattern: The pictures form triangles. The sequence is $1, 3, 6, 10, 15, 21, \dots$ The $n$-th triangular number is obtained by adding $n$ dots to the previous term. The 5th term is $10+5=15$.
How to draw the next picture: The next number is the 6th triangular number, which is $15 + 6 = 21$. Draw a triangle of dots with 6 rows. The rows will have $1, 2, 3, 4, 5,$ and $6$ dots from top to bottom.
6. Sequence: Squares
Pattern: The pictures form squares. The sequence is $1, 4, 9, 16, 25, 36, \dots$ The $n$-th square number is $n \times n$. The 5th term is $5 \times 5=25$.
How to draw the next picture: The next number is the 6th square number, which is $6 \times 6 = 36$. Draw a $6 \times 6$ square grid of dots.
7. Sequence: Cubes
Pattern: The pictures represent cubes. The sequence is $1, 8, 27, 64, 125, 216, \dots$ The $n$-th cube number is $n \times n \times n$. The 5th term is $5^3=125$.
How to draw the next picture: The next number is the 6th cube number, which is $6 \times 6 \times 6 = 216$. Draw a picture that looks like a $6 \times 6 \times 6$ cube made of smaller blocks.
Question 2. Why are 1, 3, 6, 10, 15, … called triangular numbers? Why are 1, 4, 9, 16, 25, … called square numbers or squares? Why are 1, 8, 27, 64, 125, … called cubes?
This shows that the same number can be represented differently, and play different roles, depending on the context. Try representing some other numbers pictorially in different ways!
Answer:
The names of these number lists come from the geometric shapes that can be formed by arranging that many objects, like dots or blocks.
The numbers 1, 3, 6, 10, 15, ... are called triangular numbers because this many dots can be arranged to form filled-in triangles. For example, 6 dots form a triangle with 3 rows ($1+2+3$), and 10 dots form a triangle with 4 rows ($1+2+3+4$).
The numbers 1, 4, 9, 16, 25, ... are called square numbers because this many dots can be arranged to form perfect square shapes. For example, 4 dots form a $2 \times 2$ square, and 9 dots form a $3 \times 3$ square. These numbers are the result of multiplying a whole number by itself.
The numbers 1, 8, 27, 64, 125, ... are called cubes because this many small blocks can be arranged to form solid, three-dimensional cube shapes. For example, 8 blocks form a $2 \times 2 \times 2$ cube, and 27 blocks form a $3 \times 3 \times 3$ cube.
Yes, the same number can be shown in different ways, highlighting its different properties.
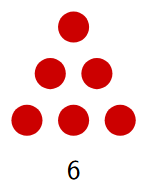
Let's try representing the number 6 in different ways:
-
As a single group (showing its value):
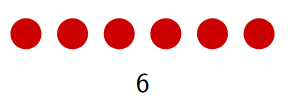
-
As a rectangle (showing its factors $2 \times 3$):

-
As another rectangle (showing its factors $3 \times 2$):

-
As a triangle (showing it is a triangular number):
Let's try representing the number 12 in different ways:
-
As a single group (showing its value):
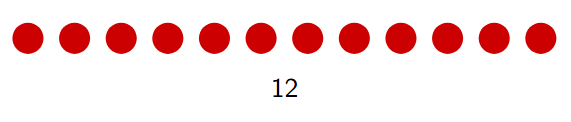
-
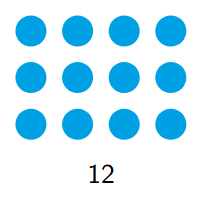
As a rectangle (showing its factors $3 \times 4$):
-
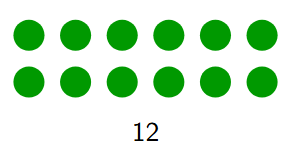
As another rectangle (showing its factors $2 \times 6$):
These examples show how pictorial representations can reveal different mathematical properties of a number.
Question 3. You will have noticed that 36 is both a triangular number and a square number! That is, 36 dots can be arranged perfectly both in a triangle and in a square. Make pictures in your notebook illustrating this!
This shows that the same number can be represented differently, and play different roles, depending on the context. Try representing some other numbers pictorially in different ways!
Answer:
Yes, the number 36 is a special type of number known as a "square triangular number" because it can be represented pictorially as both a perfect triangle and a perfect square.
Why 36 is a Triangular Number:
A number is triangular if it is the sum of consecutive whole numbers starting from 1. To get 36, you add the first 8 whole numbers:
$1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = 36$
This means 36 dots can be arranged to form a triangle with 8 rows.
Here is the pictorial representation:

Why 36 is a Square Number:
A number is a square number if it is the result of multiplying a whole number by itself. To get 36, you multiply 6 by itself:
$6 \times 6 = 36$
This means 36 dots can be arranged to form a perfect $6 \times 6$ square.
Here is the pictorial representation:

Same Number, Different Pictures:
So, 36 dots can be arranged to make both a triangle and a square! This clearly shows that the same number (36) can be represented pictorially in different ways, which helps us see different properties or roles it can play in number patterns and shapes.
Representing Other Numbers Differently:
We can show other numbers in different picture ways too!
A number like 12 can be shown as different rectangles, illustrating its factors:
A $2 \times 6$ rectangle:

A $3 \times 4$ rectangle:
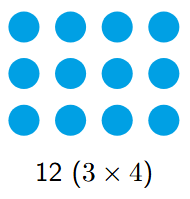
An even number like 10 can be shown as a rectangle with 2 rows, which highlights that it is divisible by 2:

A prime number like 7 can only be arranged in a single row (a $1 \times 7$ rectangle), showing that its only factors are 1 and itself.

These examples show how using pictures can help us understand different things about numbers, like what factors they have or what kind of number pattern they belong to.
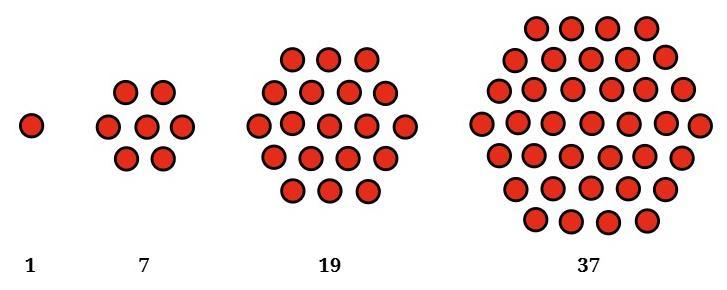
That’s right, they are called hexagonal numbers! Draw these in your notebook. What is the next number in the sequence?
Answer:
The sequence of numbers shown in the picture, 1, 7, 19, 37, ..., are called hexagonal numbers.
They are given this name because the dots representing each number can be arranged to form the shape of a regular hexagon, with each new number forming a larger hexagon by adding a new layer of dots around the previous one.
To find the next number in the sequence, let's look at the pattern:
- The first number is 1.
- The second number is $7 = 1 + 6$.
- The third number is $19 = 7 + 12$.
- The fourth number is $37 = 19 + 18$.
We can see that to get the next number, we are adding multiples of 6. The numbers we are adding are 6, 12, and 18.
The next multiple of 6 after 18 is $18 + 6 = 24$.
So, to find the next number in the sequence, we add 24 to the last number, 37:
$37 + 24 = 61$
The next number in the sequence is 61.
The next picture in the sequence would be a larger hexagon representing the number 61. It would be formed by adding a new layer of 24 dots around the hexagon of 37 dots.

Here is one possible way of thinking about Powers of 2:
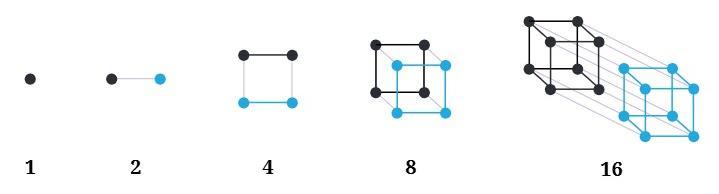
Answer:
Yes, there are many creative pictorial ways to visualize number sequences. The one shown for the powers of 2 is a very interesting way that uses dimensions!
Visualising the Sequence of Powers of 2
The picture you have shows one way to think about the powers of 2 ($1, 2, 4, 8, 16, \dots$) by building shapes in higher dimensions. Here is how it works:
- You start with a point (0 dimensions). It has 1 vertex ($2^0$).
- You take that point, make a copy of it, and connect them. You get a line segment (1 dimension). It has 2 vertices ($2^1$).
- You take that line segment, make a copy of it, and connect the matching vertices. You get a square (2 dimensions). It has 4 vertices ($2^2$).
- You take that square, make a copy of it, and connect the matching vertices. You get a cube (3 dimensions). It has 8 vertices ($2^3$).
- You take that cube, make a copy of it, and connect the matching vertices. You get a tesseract or hypercube (a 4-dimensional shape!). It has 16 vertices ($2^4$).
At each step, you are doubling the number of points (vertices) by copying the shape and connecting it to the original.
Another way to visualize the powers of 2 is by using a branching tree, which shows how things double at each step.
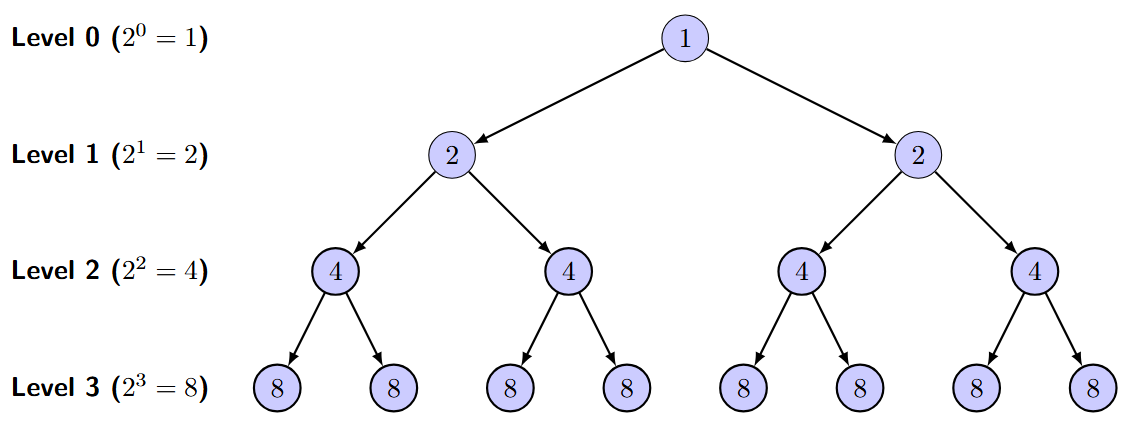
- Level 0: Start with 1 trunk ($2^0=1$).
- Level 1: The trunk splits into 2 branches ($2^1=2$).
- Level 2: Each of those branches splits into 2 more, for a total of 4 branches ($2^2=4$).
- Level 3: Each of those splits into 2 more, for a total of 8 branches ($2^3=8$), and so on.
Visualising the Sequence of Powers of 3
We can use similar ideas to visualize the powers of 3 ($1, 3, 9, 27, 81, \dots$).
Method 1: Using Grids in Different Dimensions
This is like the squares and cubes we have seen before, but focusing on the number of points.
- $3^0 = 1$: Start with a single point.
- $3^1 = 3$: Arrange 3 points in a line.
- $3^2 = 9$: Arrange 9 points in a $3 \times 3$ square grid.
- $3^3 = 27$: Arrange 27 points in a $3 \times 3 \times 3$ cubic grid.
This shows how the sequence grows in space.
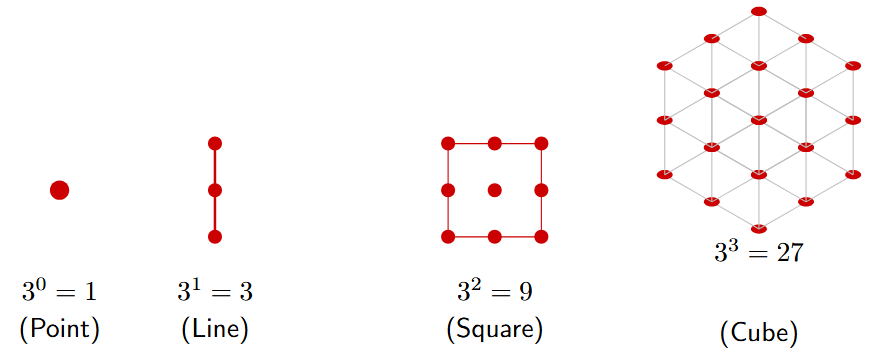
Method 2: Using a Branching Tree
Just like with the powers of 2, we can make a tree. But this time, every branch splits into three new branches.
- Level 0: Start with 1 trunk ($3^0=1$).
- Level 1: The trunk splits into 3 branches ($3^1=3$).
- Level 2: Each of those 3 branches splits into 3 more, for a total of 9 branches ($3^2=9$).
- Level 3: Each of those 9 splits into 3 more, for a total of 27 branches ($3^3=27$), and so on.

These pictures help us "see" how fast these number sequences grow!
Intext Questions (Page 7)
Adding Odd Numbers: Consider adding the first few odd numbers:
1 = 1
1 + 3 = 4
1 + 3 + 5 = 9
1 + 3 + 5 + 7 = 16
1 + 3 + 5 + 7 + 9 = 25
1 + 3 + 5 + 7 + 9 + 11 = 36
It appears that the sum of the first n odd numbers is equal to n2 , a perfect square.

Question 1: By drawing a similar picture, can you say what is the sum of the first 10 odd numbers?
Answer:
The pattern established in the text and the picture is that the sum of the first $n$ odd numbers is equal to $n^2$.
To find the sum of the first 10 odd numbers, we use this pattern with $n = 10$.
The sum will be $10^2$.
Calculation:
$10^2 = 10 \times 10 = 100$
Therefore, the sum of the first 10 odd numbers is 100.
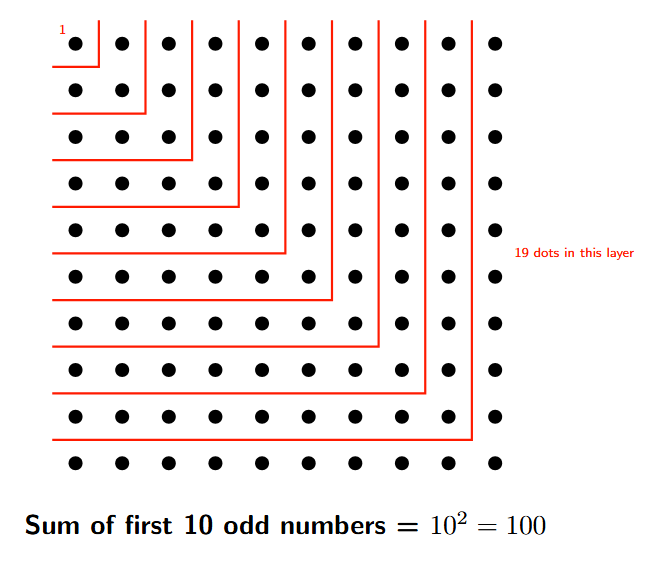
Drawing a similar picture:
To represent this visually, we would draw a square grid of dots with 10 rows and 10 columns. The total number of dots in this grid would be $10 \times 10 = 100$.
Just like the picture provided, this $10 \times 10$ square can be built by starting with 1 dot and successively adding L-shaped layers of dots representing the next odd numbers:
$1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 = 100$
The final picture would be a $10 \times 10$ square grid.
Question 2: Now by imagining a similar picture, or by drawing it partially, as needed, can you say what is the sum of the first 100 odd numbers?
Answer:
We use the same pattern: the sum of the first $n$ odd numbers is equal to $n^2$.
In this case, we want to find the sum of the first 100 odd numbers, so $n = 100$.
According to the pattern, the sum will be $100^2$.
Calculation:
$100^2 = 100 \times 100 = 10000$
Therefore, the sum of the first 100 odd numbers is 10000.
To imagine a similar picture, we would think of a very large square grid of dots. This grid would have 100 rows and 100 columns. The total number of dots in such a square would be $100 \times 100$, which is 10,000. This visual concept confirms that the sum of the first 100 odd numbers is 10,000.
Intext Questions (Page 8)
Adding up and down: Let’s examine another interesting sequence that leads to square numbers:
1 = 1
1 + 2 + 1 = 4
1 + 2 + 3 + 2 + 1 = 9
1 + 2 + 3 + 4 + 3 + 2 + 1 = 16
1 + 2 + 3 + 4 + 5 + 4 + 3 + 2 + 1 = 25
1 + 2 + 3 + 4 + 5 + 6 + 5 + 4 + 3 + 2 + 1 = 36
Here, we are adding the numbers in a symmetrical fashion—first increasing, then decreasing. The total sum still results in a square number.

Answer:
Yes, there is a clear pictorial explanation for why adding numbers symmetrically (e.g., $1+2+3+2+1$) results in a perfect square.
The pattern is that the sum of the sequence $1 + 2 + \dots + n + \dots + 2 + 1$ is always equal to $n^2$, where $n$ is the largest number in the sequence.
The pictorial explanation involves arranging the dots in a diamond or tilted square shape. Let's see how this works for the sum $1+2+3+2+1=9$.
1. Start with the middle number, 3, and draw a diagonal line of 3 dots.

2. Add the next numbers, 2, as diagonals on either side of the main diagonal.
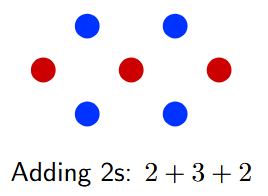
3. Add the final numbers, 1, as single dots at the corners.
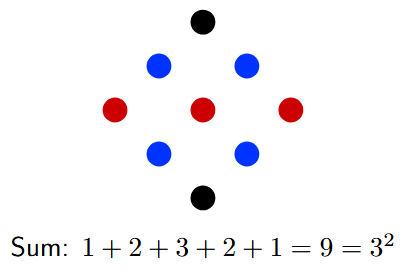
When you look at the final arrangement, the dots form a tilted $3 \times 3$ square. The total number of dots is 9, which is equal to $3^2$.
Let's do the same for the sum $1+2+3+4+3+2+1 = 16$.
We would arrange the dots in diagonal rows of length 1, 2, 3, 4, 3, 2, and 1. This arrangement perfectly forms a tilted $4 \times 4$ square, containing a total of 16 dots ($4^2$).

This visual method shows that arranging the numbers in a sequence "up and down" as diagonal rows creates a perfect square. The size of the square ($n \times n$) is determined by the largest number in the sequence ($n$).
Figure it Out (Page 8 - 9)
Question 1. Can you find a similar pictorial explanation for why adding counting numbers up and down, i.e., 1, 1 + 2 + 1, 1 + 2 + 3 + 2 + 1, …, gives square numbers?
Answer:
Yes, there is a clear pictorial explanation for why this "adding up and down" sequence creates square numbers. The key is to arrange the rows of dots diagonally to form a tilted square.
The pattern is that the sum of the sequence $1 + 2 + \dots + n + \dots + 2 + 1$ is always equal to $n^2$, where $n$ is the largest number in the sequence.
Let's take the example for n=3, where the sum is 1 + 2 + 3 + 2 + 1 = 9.
We can arrange the dots in diagonal rows. The middle diagonal has 3 dots, the diagonals next to it have 2 dots each, and the corner diagonals have 1 dot each. When put together, they form a perfect $3 \times 3$ square.

Similarly, for n=4, the sum is 1 + 2 + 3 + 4 + 3 + 2 + 1 = 16.
Arranging these dots in diagonal rows of lengths 1, 2, 3, 4, 3, 2, and 1 forms a tilted $4 \times 4$ square, which contains a total of 16 dots ($4^2$).
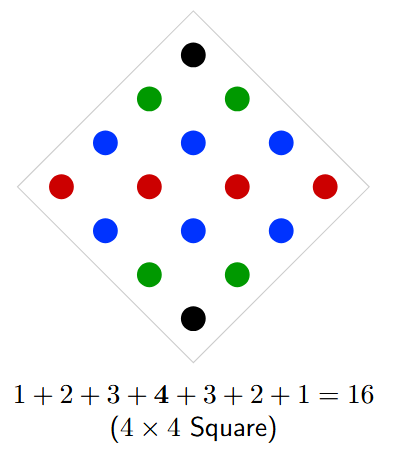
This visual arrangement shows that for any peak number 'n', the sum of the sequence $1+2+...+n+...+2+1$ will always form an $n \times n$ square, which is why the sum is always $n^2$.
Question 2. By imagining a large version of your picture, or drawing it partially, as needed, can you see what will be tha value of 1 + 2 + 3 + ... + 99 + 100 + 99 + ... + 3 + 2 + 1?
Answer:
The sequence of sums $1$, $1+2+1$, $1+2+3+2+1$, etc., follows the pattern where the sum of numbers increasing up to $n$ and decreasing back to 1 is equal to $n^2$.
The given sum is $1 + 2 + 3 + ... + 99 + 100 + 99 + ... + 3 + 2 + 1$.
In this sequence, the peak number (the largest number reached before decreasing) is 100.
According to the pattern, the sum is the square of the peak number, which is $n^2$ where $n = 100$.
Therefore, the value of the sum is $100^2$.
Calculation:
$100^2 = 100 \times 100 = 10000$
By imagining the pictorial representation, this sum corresponds to the total number of dots in a $100 \times 100$ square grid. The number of dots in such a grid is $100 \times 100 = 10000$.
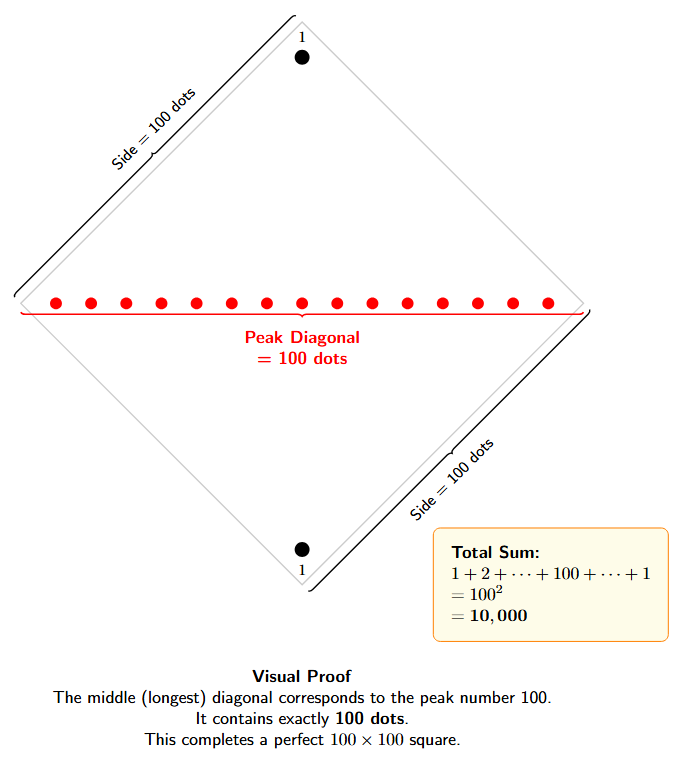
The value of $1 + 2 + 3 + ... + 99 + 100 + 99 + ... + 3 + 2 + 1$ is 10000.
Question 3. Which sequence do you get when you start to add the All 1’s sequence up? What sequence do you get when you add the All 1’s sequence up and down?
Answer:
Let the "All 1's" sequence be denoted by $a_n = 1$ for $n = 1, 2, 3, \dots$. The sequence is 1, 1, 1, 1, ...
Part 1: Adding the All 1’s sequence up
Adding the sequence up means finding the cumulative sum of the terms. Let $S_n$ be the sum of the first $n$ terms of the sequence.
The first term is 1.
Sum of the first 2 terms: $1 + 1 = 2$.
Sum of the first 3 terms: $1 + 1 + 1 = 3$.
Sum of the first 4 terms: $1 + 1 + 1 + 1 = 4$.
In general, the sum of the first $n$ terms is $1 \times n = n$.
The sequence of sums is 1, 2, 3, 4, 5, 6, ...
This is the sequence of counting numbers (or natural numbers).
Part 2: Adding the All 1’s sequence up and down
The "adding up and down" pattern means taking symmetrical sums like $a_1$, $a_1+a_2+a_1$, $a_1+a_2+a_3+a_2+a_1$. Since every term in the "All 1's" sequence is just 1, this is the same as adding 1 a certain number of times.
Let's form the sums based on a peak number of terms $n$. The total number of terms will be $2n-1$.
For $n=1$: The sum is just 1.
For $n=2$: The sum is $1 + 1 + 1 = 3$.
For $n=3$: The sum is $1 + 1 + 1 + 1 + 1 = 5$.
For $n=4$: The sum is $1 + 1 + 1 + 1 + 1 + 1 + 1 = 7$.
The sum for a peak of $n$ terms results in the sum of $2n-1$ ones, which is just $2n-1$.
The sequence of sums is 1, 3, 5, 7, 9, 11, ...
This is the sequence of odd numbers.
Question 4. Which sequence do you get when you start to add the Counting numbers up? Can you give a smaller pictorial explanation?
Answer:
The sequence of Counting numbers is 1, 2, 3, 4, 5, ...
When we start to add the Counting numbers up, we are calculating the cumulative sum at each step:
- Sum of the first 1 counting number: $1 = 1$
- Sum of the first 2 counting numbers: $1 + 2 = 3$
- Sum of the first 3 counting numbers: $1 + 2 + 3 = 6$
- Sum of the first 4 counting numbers: $1 + 2 + 3 + 4 = 10$
The sequence we get by adding the Counting numbers up is 1, 3, 6, 10, 15, 21, ...
This sequence is known as the sequence of triangular numbers.
Pictorial Explanation:
The name "triangular numbers" comes from the fact that each sum can be represented by dots arranged in the shape of a triangle. Each new number in the counting sequence adds a new row to the triangle.
For example, to get the 4th triangular number (10), we add the first 4 counting numbers:
$1 + 2 + 3 + 4 = 10$
This can be pictured as a triangle with 4 rows:

This visual representation clearly shows why adding counting numbers up results in the sequence of triangular numbers.
Question 5. What happens when you add up pairs of consecutive triangular numbers? That is, take 1 + 3, 3 + 6, 6 + 10, 10 + 15, … ? Which sequence do you get? Why? Can you explain it with a picture?
Answer:
When you add two consecutive triangular numbers together, you get a Square Number!
Let's check this by adding them up:
- $1 + 3 = 4$ (This is $2^2$)
- $3 + 6 = 9$ (This is $3^2$)
- $6 + 10 = 16$ (This is $4^2$)
- $10 + 15 = 25$ (This is $5^2$)
Why does this happen?
Think of it like a puzzle. A "Triangular Number" makes a triangle shape.
If you take two triangles that are next to each other in the sequence (like 6 and 10), you can turn the smaller triangle upside down and fit it perfectly on top of the bigger triangle.
Together, they fill up the gaps to make a perfect Square.
Pictorial Explanation:
Let's look at $6 + 10 = 16$.
- Take the triangular number 10 (shown in Red below). It has 4 rows.
- Take the previous triangular number 6 (shown in Blue). It has 3 rows.
- Fit them together, and they create a $4 \times 4$ Square.

Question 6. What happens when you start to add up powers of 2 starting with 1, i.e., take 1, 1 + 2, 1 + 2 + 4, 1 + 2 + 4 + 8, … ? Now add 1 to each of these numbers — what numbers do you get? Why does this happen?
Answer:
Let's play with the "Powers of 2" numbers: 1, 2, 4, 8, 16, 32...
Step 1: Add them up!
- Start with 1: 1
- 1 + 2 = 3
- 1 + 2 + 4 = 7
- 1 + 2 + 4 + 8 = 15
- 1 + 2 + 4 + 8 + 16 = 31
Step 2: Add 1 to your answer.
- $1 + 1 =$ 2
- $3 + 1 =$ 4
- $7 + 1 =$ 8
- $15 + 1 =$ 16
- $31 + 1 =$ 32
What do you notice?
When we add 1, we get the sequence 2, 4, 8, 16, 32.... These are the Powers of 2 again!
Why does this happen?
Think of it like money. If you have a 1 rupee coin, a 2 rupee coin, and a 4 rupee coin, you have 7 rupees. You are exactly 1 rupee short of having 8 rupees.
The sum of all the smaller powers is always just 1 less than the next power of 2. So, when you add that missing "1", you jump up to the next level!
Question 7. What happens when you multiply the triangular numbers by 6 and add 1? Which sequence do you get? Can you explain it with a picture?
Answer:
Let's use the formula: $( \text{Triangular Number} \times 6 ) + 1$.
Recall the Triangular Numbers: 1, 3, 6, 10...
- For 1: $(1 \times 6) + 1 = $ 7
- For 3: $(3 \times 6) + 1 = $ 19
- For 6: $(6 \times 6) + 1 = $ 37
- For 10: $(10 \times 6) + 1 = $ 61
The Result:
The sequence 7, 19, 37, 61... is the sequence of Hexagonal Numbers!
Pictorial Explanation:
Why does multiplying by 6 and adding 1 make a hexagon?
Imagine a hexagon like a flower with a center and petals.
- The "+ 1" is the single dot in the Center (Black).
- The "$\times 6$" means we have 6 petals around the center.
- Each "petal" is actually a Triangular Number!
For example, to get 19, we take the center dot (1) and surround it with 6 small triangles of 3 dots each (the 2nd triangular number).
$1 + (6 \times 3) = 19$

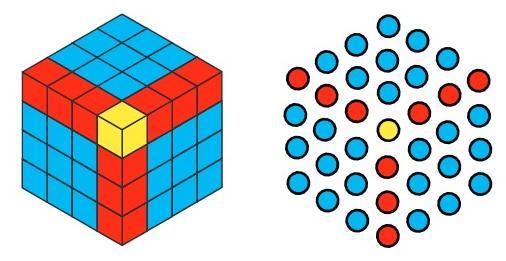
Answer:
Let's first find the sequence that we get when we add up the hexagonal numbers.
The sequence of hexagonal numbers is 1, 7, 19, 37, ...
Now, let's find the sum at each step:
- Sum of the first term: $1$
- Sum of the first 2 terms: $1 + 7 = 8$
- Sum of the first 3 terms: $1 + 7 + 19 = 27$
- Sum of the first 4 terms: $1 + 7 + 19 + 37 = 64$
The sequence we get is 1, 8, 27, 64, ...
This is the sequence of cube numbers! ($1^3, 2^3, 3^3, 4^3, \dots$)
Pictorial Explanation using a Cube:
The pictures help us understand why adding hexagonal numbers creates cube numbers. We can think of building a large cube by adding layers around a single, central cube, like an onion.
- Step 1 (The first sum is 1): We start with a single, central cube. This represents the number 1, which is the first hexagonal number and also the first cube number ($1^3$).
- Step 2 (The second sum is 1 + 7 = 8): To build a $2 \times 2 \times 2$ cube, we add a layer of cubes around the first central cube. This new layer requires 7 more cubes to complete the $2 \times 2 \times 2$ shape. The total is now $1+7 = 8$ cubes, which is $2^3$. The number of cubes in this new layer (7) is the second hexagonal number.
- Step 3 (The third sum is 1 + 7 + 19 = 27): To build a $3 \times 3 \times 3$ cube, we add another layer around the $2 \times 2 \times 2$ cube. This new layer requires 19 more cubes. The total is now $1+7+19 = 27$ cubes, which is $3^3$. The number of cubes in this layer (19) is the third hexagonal number.
- Step 4 (The fourth sum is 1 + 7 + 19 + 37 = 64): To build a $4 \times 4 \times 4$ cube (like the one in the picture), we add a final layer around the $3 \times 3 \times 3$ cube. This outermost layer requires 37 cubes. The total is now $1+7+19+37 = 64$ cubes, which is $4^3$. The number of cubes in this layer (37) is the fourth hexagonal number.
The image of the hexagon with 37 dots shows you what one of these "layers" looks like if you lay it flat. The image of the $4 \times 4 \times 4$ cube shows the final result of adding up all four layers.
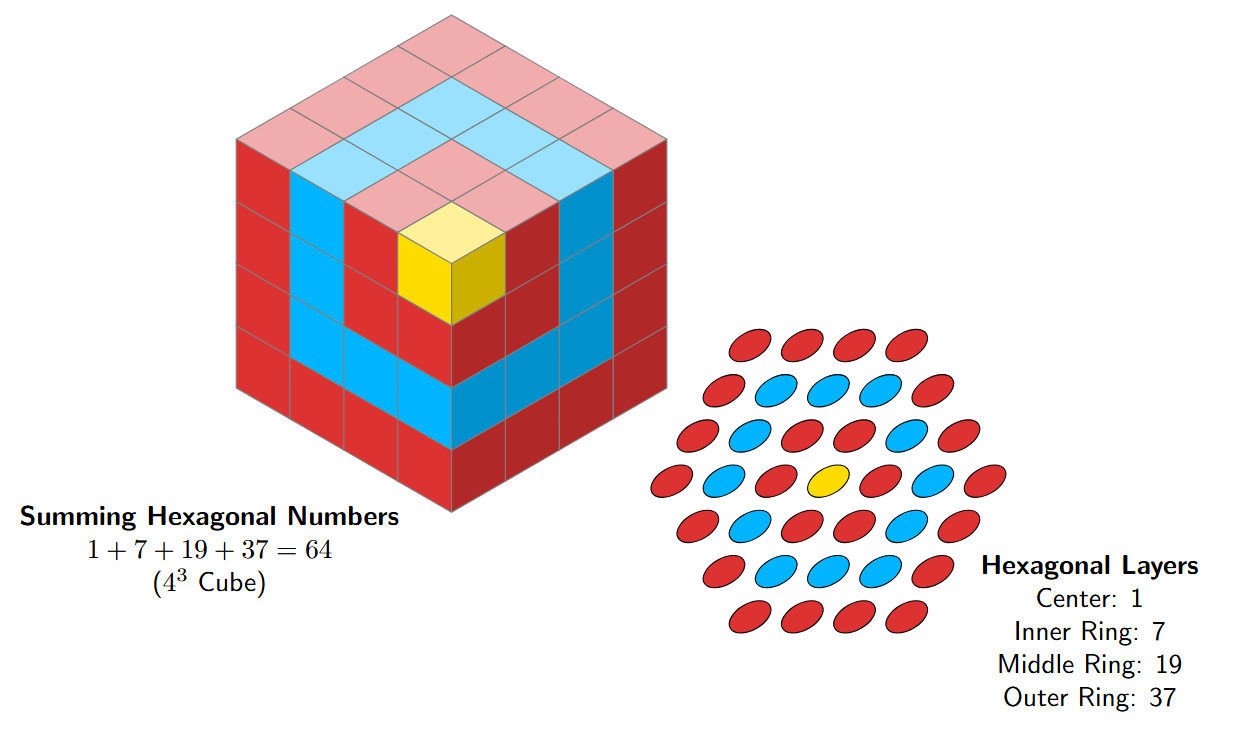
Therefore, the sum of the first n hexagonal numbers is equal to n3, the n-th cube number.
| Table 1 Examples of number sequences | |
|---|---|
| 1, 1, 1, 1, 1, 1, 1, ... | (All 1’s) |
| 1, 2, 3, 4, 5, 6, 7, ... | (Counting numbers) |
| 1, 3, 5, 7, 9, 11, 13, ... | (Odd numbers) |
| 2, 4, 6, 8, 10, 12, 14, ... | (Even numbers) |
| 1, 3, 6, 10, 15, 21, 28, ... | (Triangular numbers) |
| 1, 4, 9, 16, 25, 36, 49, ... | (Squares) |
| 1, 8, 27, 64, 125, 216, ... | (Cubes) |
| 1, 2, 3, 5, 8, 13, 21, ... | (Virahānka numbers) |
| 1, 2, 4, 8, 16, 32, 64, ... | (Powers of 2) |
| 1, 3, 9, 27, 81, 243, 729, ... | (Powers of 3) |
Answer:
There are many "magic tricks" hidden in these numbers! Here are three patterns you can find, with pictures to explain them.
Pattern 1: Adding Odd Numbers builds Squares
If you start with 1 and add the odd numbers ($1, 3, 5, 7 \dots$) one by one, the answer is always a Square Number!
- $1 = \mathbf{1}$ ($1 \times 1$)
- $1 + 3 = \mathbf{4}$ ($2 \times 2$)
- $1 + 3 + 5 = \mathbf{9}$ ($3 \times 3$)
- $1 + 3 + 5 + 7 = \mathbf{16}$ ($4 \times 4$)
The Picture Explanation:
Think of it as growing a square. You start with 1 dot. To make it bigger, you wrap an "L-shape" of dots around it. Each new "L-shape" is the next odd number!

Pattern 2: Two Neighbors make a Square
If you take any two Triangular Numbers that are next to each other in the list and add them, you get a Square Number.
Let's try the 2nd and 3rd triangular numbers (3 and 6):
$\mathbf{3} + \mathbf{6} = \mathbf{9}$ (which is a Square!)
The Picture Explanation:
A square is just two triangles sitting together! If you draw a square of 9 dots, you can draw a diagonal line to split it into a triangle of 6 dots and a smaller triangle of 3 dots.
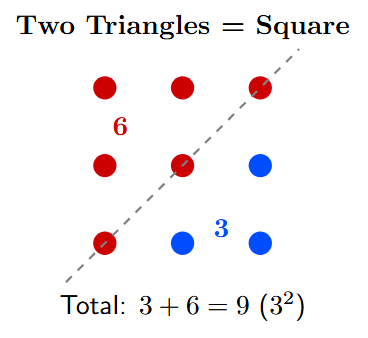
Pattern 3: The Rectangle Trick
If you take two copies of the same Triangular Number, you can fit them together to make a Rectangle.
Let's take the triangular number 10. If we have two of them, the total is 20.
$\mathbf{10} + \mathbf{10} = \mathbf{20}$
The Picture Explanation:
Take one triangle of 10 dots. Take another identical triangle and flip it upside down. They fit together perfectly to make a rectangle with 4 rows and 5 columns ($4 \times 5 = 20$).

Figure it Out (Page 11)
| Table 3 Examples of Shape Sequences | |
|---|---|
| Regular Polygons | .jpg)
|
| Complete Graphs | .jpg)
|
| Stacked Squares | .jpg)
|
| Stacked Triangles | .jpg)
|
| Koch Snowflake | .jpg)
|
Question 1. Can you recognise the pattern in each of the sequences in Table 3?
Answer:
Yes, the pattern in each sequence can be recognised as follows:
1. Regular Polygons
The sequence consists of polygons where all sides and angles are equal. The pattern is based on the number of sides.
Pattern: The number of sides increases by $1$ in each successive shape. It starts with a Triangle ($3$ sides), followed by a Quadrilateral ($4$ sides), Pentagon ($5$ sides), Hexagon ($6$ sides), and so on up to a Decagon ($10$ sides).
2. Complete Graphs
This sequence represents graphs denoted by $K_n$, where $n$ represents the number of vertices (points).
Pattern: In each shape, there are $n$ points, and every point is connected to every other point by a line segment. The number of points ($n$) increases by $1$ in each step, starting from $K_2$ ($2$ points) to $K_6$ ($6$ points).
3. Stacked Squares
This sequence shows larger squares constructed using unit squares.
Pattern: The side length of the square increases by $1$ unit at each step.
- Step 1: $1 \times 1$ grid ($1^2 = 1$ square)
- Step 2: $2 \times 2$ grid ($2^2 = 4$ squares)
- Step 3: $3 \times 3$ grid ($3^2 = 9$ squares)
4. Stacked Triangles
This sequence displays larger equilateral triangles formed by stacking smaller unit triangles.
Pattern: The number of rows of small triangles increases by $1$ in each subsequent shape. Alternatively, the side length of the large triangle increases by $1$ unit at each step. The total number of small triangles in the $n$-th shape follows the square numbers sequence ($1, 4, 9, 16, \dots$).
5. Koch Snowflake
This sequence illustrates a fractal curve known as the Koch Snowflake.
Pattern: The sequence starts with an equilateral triangle. In each subsequent step, the middle third of every side is removed and replaced with two sides of a smaller equilateral triangle pointing outwards. This process increases the complexity and perimeter of the shape infinitely while enclosing a finite area.
Question 2. Try and redraw each sequence in Table 3 in your notebook. Can you draw the next shape in each sequence? Why or why not? After each sequence, describe in your own words what is the rule or pattern for forming the shapes in the sequence.
Answer:
Yes, it is possible to redraw these sequences and determine the next shape for most of them, though the complexity increases. Here is the detailed explanation for each sequence:
1. Regular Polygons
Can you draw the next shape? Yes.
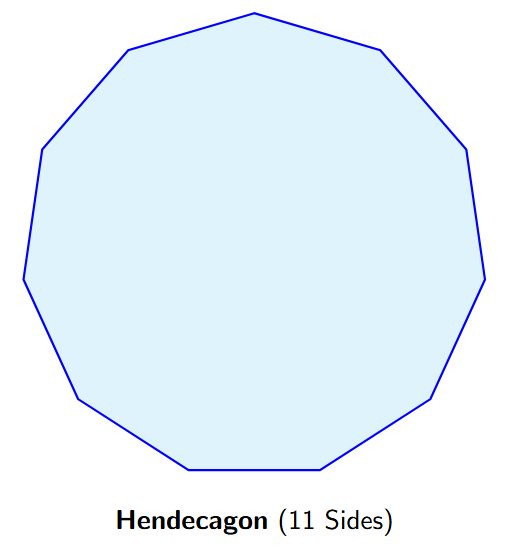
Description of the next shape: The last shape in the table is a Decagon ($10$ sides). The next shape will have $11$ equal sides and $11$ equal angles. This is known as a Hendecagon.
Rule/Pattern: The rule is to increase the number of sides by $1$ in each subsequent step. The sequence progresses as $3, 4, 5, \dots, n, n+1$ sides.
2. Complete Graphs
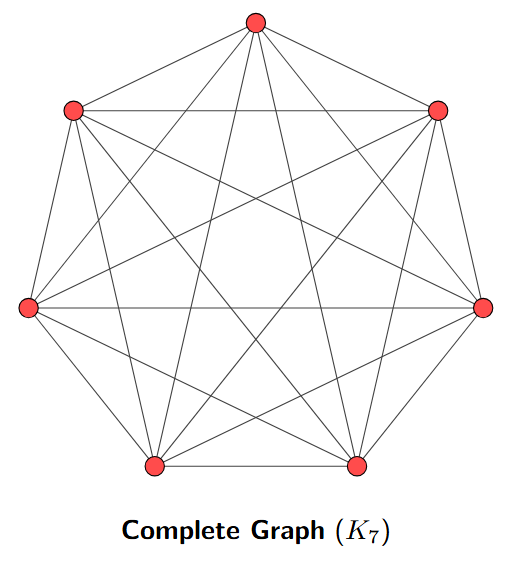
Can you draw the next shape? Yes.
Description of the next shape: The last shape shown is $K_6$ ($6$ points). The next shape will be $K_7$. It consists of $7$ distinct points arranged in a circle (or polygon), where every point is connected to every other point by a straight line.
Rule/Pattern: Add one new vertex (point) to the graph and draw a line connecting this new point to all existing points. The number of lines increases significantly with each step.
3. Stacked Squares
Can you draw the next shape? Yes.
Description of the next shape: The sequence ends at a $5 \times 5$ grid. The next shape will be a $6 \times 6$ square grid. It will contain a total of $36$ small unit squares ($6 \times 6 = 36$).
Rule/Pattern: The side length of the large square increases by $1$ unit at each step. If the current square is $n \times n$, the next shape is $(n+1) \times (n+1)$.

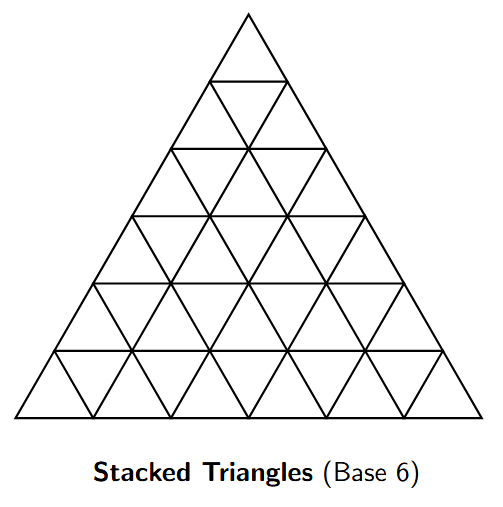
4. Stacked Triangles
Can you draw the next shape? Yes.
Description of the next shape: The last triangle has a base of $5$ units. The next shape will be a large equilateral triangle with a base of $6$ units. It will consist of $36$ small unit triangles.
Rule/Pattern: Add a new row of small triangles at the bottom of the previous shape. The number of small triangles follows the sequence of square numbers: $1, 4, 9, 16, 25, 36, \dots$
5. Koch Snowflake
Can you draw the next shape? Yes, but it is difficult.
Reason: The Koch Snowflake is a fractal. With each step, the details become smaller and more intricate. Drawing the next iteration by hand requires high precision to draw the tiny triangular "bumps" on every existing small side.
Description of the next shape: The next shape will look similar to the previous one but with a "fuzzier" or more jagged outline, as every straight line segment is broken again to form a new outward-pointing triangle.
Rule/Pattern: Take every straight line segment in the current shape, divide it into three equal parts, remove the middle part, and replace it with two sides of an equilateral triangle pointing outwards.
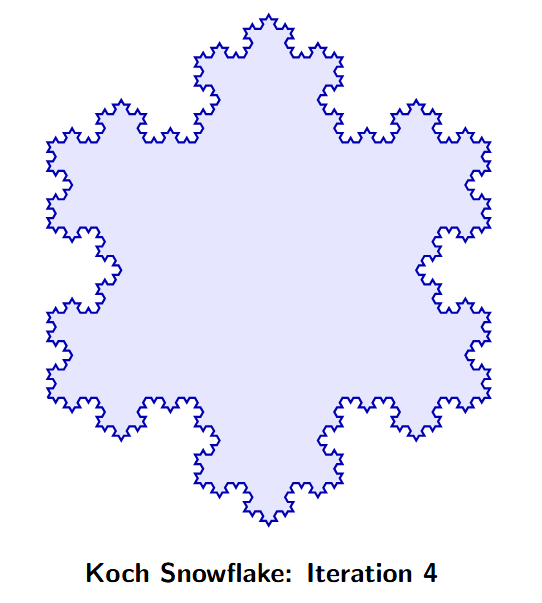
Figure it Out (Page 11 - 12)
Question 1. Count the number of sides in each shape in the sequence of Regular Polygons. Which number sequence do you get? What about the number of corners in each shape in the sequence of Regular Polygons? Do you get the same number sequence? Can you explain why this happens?
Answer:
Let's count the number of sides for the first few shapes in the Regular Polygons sequence:
- Triangle: 3 sides
- Quadrilateral (Square): 4 sides
- Pentagon: 5 sides
- Hexagon: 6 sides
The sequence of the number of sides is 3, 4, 5, 6, ...
Now, let's count the number of corners (vertices) for each shape:
- Triangle: 3 corners
- Quadrilateral (Square): 4 corners
- Pentagon: 5 corners
- Hexagon: 6 corners
The sequence of the number of corners is also 3, 4, 5, 6, ...
Yes, we get the exact same number sequence for both sides and corners.
Explanation:
This happens because for any simple closed polygon, a side is a line segment that connects two corners, and a corner is a point where two sides meet. In any such shape, the number of sides must always be equal to the number of corners. If you have 'n' corners, you will need 'n' sides to connect them all in a closed loop.
Question 2. Count the number of lines in each shape in the sequence of Complete Graphs. Which number sequence do you get? Can you explain why?
Answer:
Let's count the number of lines (edges) for each shape in the Complete Graphs sequence.
- K2 (2 points): 1 line
- K3 (3 points): 3 lines
- K4 (4 points): 6 lines
- K5 (5 points): 10 lines
- K6 (6 points): 15 lines
The number sequence we get is 1, 3, 6, 10, 15, ...
This is the sequence of triangular numbers.
Explanation:
A complete graph is a shape where every point is connected to every other point. When we add a new point to the graph, we must draw new lines from this new point to all the points that were already there.
- To go from K2 to K3, we add 1 point and connect it to the 2 existing points, adding 2 new lines. Total lines = $1+2=3$.
- To go from K3 to K4, we add 1 point and connect it to the 3 existing points, adding 3 new lines. Total lines = $3+3=6$.
- To go from K4 to K5, we add 1 point and connect it to the 4 existing points, adding 4 new lines. Total lines = $6+4=10$.
The total number of lines is the sum of the counting numbers: $1$, $1+2$, $1+2+3$, $1+2+3+4$, and so on. This process of summing the counting numbers is exactly how triangular numbers are generated.
Question 3. How many little squares are there in each shape of the sequence of Stacked Squares? Which number sequence does this give? Can you explain why?
Answer:
Let's count the number of small squares in each shape of the Stacked Squares sequence.
- 1st shape ($1 \times 1$): 1 small square.
- 2nd shape ($2 \times 2$): 4 small squares.
- 3rd shape ($3 \times 3$): 9 small squares.
- 4th shape ($4 \times 4$): 16 small squares.
- 5th shape ($5 \times 5$): 25 small squares.
The number sequence we get is 1, 4, 9, 16, 25, ...
This is the sequence of square numbers.
Explanation:
This happens because the $n$-th shape in the sequence is an $n \times n$ square grid. The total number of small squares in such a grid is found by multiplying its length by its width. Since both the length and width are $n$, the total number of small squares is $n \times n = n^2$. This is the definition of a square number.
Question 4. How many little triangles are there in each shape of the sequence of Stacked Triangles? Which number sequence does this give? Can you explain why?
(Hint: In each shape in the sequence, how many triangles are there in each row?)
Answer:
Let's count the number of small triangles in each shape of the Stacked Triangles sequence.
- 1st shape (side length 1): 1 small triangle.
- 2nd shape (side length 2): 4 small triangles.
- 3rd shape (side length 3): 9 small triangles.
- 4th shape (side length 4): 16 small triangles.
- 5th shape (side length 5): 25 small triangles.
The number sequence we get is 1, 4, 9, 16, 25, ...
This is the sequence of square numbers.
Explanation:
The hint in the original image might be misleading for this particular sequence of stacked triangles. Let's re-examine the picture. The number of small triangles in each row (from the top) is 1, 3, 5, 7, ... which are the odd numbers. The total number of triangles is the sum of consecutive odd numbers.
- 1st shape: 1 = 1
- 2nd shape: $1 + 3 = 4$
- 3rd shape: $1 + 3 + 5 = 9$
- 4th shape: $1 + 3 + 5 + 7 = 16$
We know that the sum of the first $n$ odd numbers is always $n^2$. Since the $n$-th triangle in the sequence is built from the first $n$ odd numbers of small triangles, the total number of small triangles is $n^2$. This is why the sequence gives square numbers.
Question 5. To get from one shape to the next shape in the Koch Snowflake sequence, one replaces each line segment ‘—’ by a ‘speed bump’ __⋀__ . As one does this more and more times, the changes become tinier and tinier with very very small line segments. How many total line segments are there in each shape of the Koch Snowflake? What is the corresponding number sequence? (The answer is 3, 12, 48, ..., i.e. 3 times Powers of 4; this sequence is not shown in Table 1)
Answer:
Let's count the total number of line segments at each step of the Koch Snowflake sequence.
The rule is that every one line segment is replaced by four smaller line segments.
Let's count the segments:
- Step 0 (Initial shape): The starting shape is an equilateral triangle. It has 3 line segments.
- Step 1: Each of the 3 segments is replaced by 4 new segments. Total segments = $3 \times 4 = 12$.
- Step 2: Each of the 12 segments from the previous step is replaced by 4 new segments. Total segments = $12 \times 4 = 48$.
- Step 3: Each of the 48 segments is replaced by 4. Total segments = $48 \times 4 = 192$.
The number of segments is multiplied by 4 at each step.
The corresponding number sequence is: 3, 12, 48, 192, ...
This can be written as 3 times the powers of 4:
- $3 = 3 \times 4^0$
- $12 = 3 \times 4^1$
- $48 = 3 \times 4^2$
- $192 = 3 \times 4^3$
The formula for the number of segments at step $n$ (starting with $n=0$) is $3 \times 4^n$.

