| Latest Maths NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
Chapter 7 Fractions
This solutions page provides comprehensive guidance for Chapter 7, "Fractions," a fundamental topic within the Class 6 Ganita Prakash textbook mandated by NCERT for the 2024-25 academic session. Fractions represent a crucial step beyond whole numbers, introducing the concept of parts of a whole or elements within a collection. Mastering fractions is essential for building a robust mathematical foundation. These solutions are meticulously designed to demystify fractional concepts and operations, offering clear, step-by-step explanations for every exercise presented in the chapter.
The journey begins with understanding the very essence of a fraction. The solutions vividly illustrate how fractions, typically written in the form $\frac{a}{b}$ where $b \neq 0$, represent a portion. This is often visualized using diagrams, such as shaded parts of a circle or rectangle, reinforcing the idea of a fraction as 'parts out of a total number of equal parts'. Furthermore, the solutions demonstrate how fractions find their place on the number line, nestled between whole numbers, helping students visualize their magnitude and order relative to integers and other fractions. Accurate representation, both visually and numerically, is emphasized as the first step towards confidence with fractions.
Understanding the different types of fractions is critical. The solutions clearly differentiate between:
- Proper Fractions: Where the numerator is smaller than the denominator (i.e., $\text{numerator} < \text{denominator}$), representing a quantity less than one whole, like $\frac{3}{5}$.
- Improper Fractions: Where the numerator is greater than or equal to the denominator (i.e., $\text{numerator} \ge \text{denominator}$), representing a quantity equal to or greater than one whole, such as $\frac{7}{4}$ or $\frac{5}{5}$.
- Mixed Numbers (or Mixed Fractions): Which combine a whole number and a proper fraction, like $2\frac{1}{3}$.
A significant focus is placed on the concept of equivalent fractions – different fractions that represent the same value (e.g., $\frac{1}{2} = \frac{2}{4} = \frac{3}{6}$). The solutions demonstrate the principle that multiplying or dividing both the numerator and the denominator of a fraction by the same non-zero number results in an equivalent fraction. Related to this is the essential skill of simplifying fractions to their lowest terms or simplest form. This is achieved by dividing both the numerator and the denominator by their Highest Common Factor (HCF), and the solutions illustrate this process clearly.
Comparing and ordering fractions is another vital skill addressed thoroughly. The solutions present robust strategies for determining which fraction is larger or smaller. For unlike fractions (fractions with different denominators), the primary method involves finding a common denominator, typically the Lowest Common Multiple (LCM) of the original denominators. Each fraction is then converted into an equivalent fraction with this common denominator, allowing for direct comparison of the numerators. The alternative method of cross-multiplication is also often explained. Accurate comparison is fundamental for ordering a set of fractions.
Finally, the solutions provide meticulous, step-by-step procedures for performing arithmetic operations: addition and subtraction of fractions. For like fractions (same denominator), the process is straightforward: add or subtract the numerators and keep the common denominator (e.g., $\frac{a}{c} + \frac{b}{c} = \frac{a+b}{c}$). For unlike fractions, the solutions reiterate finding the $\text{LCM}$ of the denominators, converting to equivalent fractions with that $\text{LCM}$ as the new denominator, and then performing the operation on the numerators (e.g., finding $\frac{a}{b} + \frac{c}{d}$ requires finding $\text{LCM}(b,d)$). Operations involving mixed numbers are also carefully explained, usually by converting them to improper fractions first. By diligently working through these solutions for Chapter 7 of the Class 6 Ganita Prakash (NCERT 2024-25), students will gain the necessary skills and confidence to handle fractions effectively, preparing them for subsequent mathematical challenges in algebra and beyond.
Figure it Out (Page 152 - 153)
Fill in the blanks with fractions.
Question 1. Three guavas together weigh 1 kg. If they are roughly of the same size, each guava will roughly weigh ____kg.
Answer:
Given:
Total weight of 3 guavas = $1 \text{ kg}$.
The guavas are of the same size, meaning they have equal weight.
To Find:
The weight of each guava.
Solution:
To find the weight of one guava, we need to divide the total weight equally among the three guavas.
This can be represented as:
Weight of each guava = $\frac{\text{Total weight}}{\text{Number of guavas}}$
Substituting the given values:
Weight of each guava = $\frac{1 \text{ kg}}{3}$
Therefore, each guava weighs $\frac{1}{3} \text{ kg}$.
Each guava will roughly weigh $\frac{1}{3}$ kg.
Question 2. A wholesale merchant packed 1 kg of rice in four packets of equal weight. The weight of each packet is ___ kg.
Answer:
Given:
Total weight of rice = $1 \text{ kg}$.
Number of packets = $4$.
All packets are of equal weight.
To Find:
The weight of each packet.
Solution:
To find the weight of a single packet, we must divide the total weight of the rice by the number of packets it is packed into.
This can be represented as:
Weight of each packet = $\frac{\text{Total weight of rice}}{\text{Number of packets}}$
Substituting the given values:
Weight of each packet = $\frac{1 \text{ kg}}{4}$
Therefore, each packet weighs $\frac{1}{4} \text{ kg}$.
The weight of each packet is $\frac{1}{4}$ kg.
Question 3. Four friends ordered 3 glasses of sugarcane juice and shared it equally among themselves. Each one drank ____ glass of sugarcane juice
Answer:
Given:
Total number of glasses of sugarcane juice = $3$.
Total number of friends sharing the juice = $4$.
To Find:
The amount of juice each friend drank.
Solution:
To find the share for each friend, we need to divide the total amount of juice by the number of friends.
This can be represented as:
Share per friend = $\frac{\text{Total glasses of juice}}{\text{Number of friends}}$
Substituting the given values:
Share per friend = $\frac{3}{4}$ glasses
This means each friend gets three-fourths of a glass of juice.
Each one drank $\frac{3}{4}$ glass of sugarcane juice.
Question 4.
The big fish weighs $\frac{1}{2}$ kg. The small one weighs $\frac{1}{4}$ kg. Together they weigh ____ kg.
Find out and discuss the words for fractions that are used in the
different languages spoken in your home, city, or state. Ask your
grandparents, parents, teachers, and classmates what words they use
for different fractions, such as for one and a half, three quarters, one
and a quarter, half, quarter, and two and a half, and write them here:
Answer:
Part 1: Combined Weight of Fish
Given:
Weight of the big fish = $\frac{1}{2} \text{ kg}$.
Weight of the small fish = $\frac{1}{4} \text{ kg}$.
To Find:
The total weight of both fish combined.
Solution:
To find the combined weight, we must add the weights of the two fish.
Total weight = $\frac{1}{2} + \frac{1}{4}$
To add fractions, they need to have a common denominator. The least common multiple (LCM) of the denominators 2 and 4 is 4.
The fraction $\frac{1}{4}$ already has this denominator. We convert $\frac{1}{2}$ to an equivalent fraction with a denominator of 4:
$\frac{1}{2} = \frac{1 \times 2}{2 \times 2} = \frac{2}{4}$
Now we can add the two fractions:
Total weight = $\frac{2}{4} + \frac{1}{4} = \frac{2+1}{4} = \frac{3}{4} \text{ kg}$
Together they weigh $\frac{3}{4}$ kg.
Part 2: Words for Fractions in Different Languages
This question is an activity for you to explore how fractions are expressed in the languages spoken around you. The answers will vary depending on your location and community. You should ask your family, friends, and teachers as suggested. Here is a sample table showing how you could organize your findings for Hindi and English:
| Fraction | Numerical Form | Word in English | Word in Hindi |
| $\frac{1}{4}$ | 0.25 | Quarter | Paav (पाव) |
| $\frac{1}{2}$ | 0.5 | Half | Aadha (आधा) |
| $\frac{3}{4}$ | 0.75 | Three quarters | Pauna (पौना) |
| $1\frac{1}{4}$ | 1.25 | One and a quarter | Sava (सवा) |
| $1\frac{1}{2}$ | 1.5 | One and a half | Dedh (डेढ़) |
| $2\frac{1}{2}$ | 2.5 | Two and a half | Dhai (ढाई) |
You can create a similar table for the languages spoken in your area.
Question 5.
Arrange these fraction words in order of size from the smallest to the biggest in the empty box below:
One and a half, three quarters, one and a quarter, half, quarter, two and a half.
Answer:
Given:
A list of fraction words: One and a half, three quarters, one and a quarter, half, quarter, two and a half.
To Do:
Arrange these fraction words in increasing order of their value (from smallest to biggest).
Solution:
Step 1: Convert the words to numerical fractions.
- Quarter → $\frac{1}{4}$
- Half → $\frac{1}{2}$
- Three quarters → $\frac{3}{4}$
- One and a quarter → $1\frac{1}{4}$
- One and a half → $1\frac{1}{2}$
- Two and a half → $2\frac{1}{2}$
Step 2: Convert the numerical fractions to decimals to make comparison easier.
- $\frac{1}{4} = 0.25$
- $\frac{1}{2} = 0.5$
- $\frac{3}{4} = 0.75$
- $1\frac{1}{4} = 1.25$
- $1\frac{1}{2} = 1.5$
- $2\frac{1}{2} = 2.5$
Step 3: Arrange the decimal values in order from smallest to biggest.
$0.25 < 0.5 < 0.75 < 1.25 < 1.5 < 2.5$
Step 4: Match the ordered decimals back to their original fraction words.
$0.25 \rightarrow$ Quarter
$0.5 \rightarrow$ Half
$0.75 \rightarrow$ Three quarters
$1.25 \rightarrow$ One and a quarter
$1.5 \rightarrow$ One and a half
$2.5 \rightarrow$ Two and a half
The correct order from smallest to biggest is:
Quarter, Half, Three quarters, One and a quarter, One and a half, Two and a half.
Intext Question (Page 154 - 155)
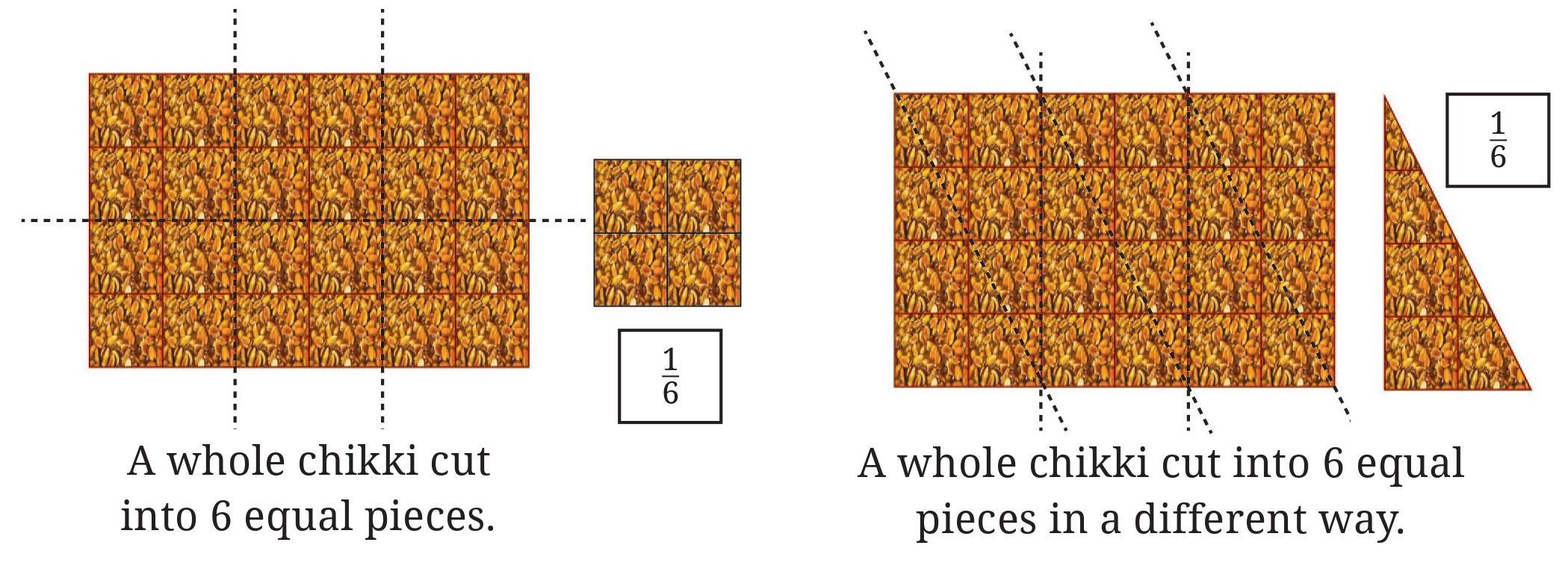
Answer:
Given:
A whole chikki is divided into 6 equal parts in two different ways, as shown in the image.
The first method produces rectangular pieces, and the second method produces triangular pieces.
Each piece represents the fraction $\frac{1}{6}$ of the whole chikki.
To Determine:
Whether the pieces, despite having different shapes (rectangle vs. triangle), are of the same size.
Solution:
The key to understanding this is the phrase "6 equal parts".
When a whole object is divided into a number of equal parts, each part must have the same measure. In the case of a flat object like a chikki, this measure is its area.
The fraction $\frac{1}{6}$ represents one part of a whole that has been divided into six equal parts.
- In the first case, the whole chikki is divided into 6 equal rectangles. The size (area) of each rectangular piece is exactly one-sixth of the total area of the whole chikki.
- In the second case, the whole chikki is divided into 6 equal triangles. The size (area) of each triangular piece is also exactly one-sixth of the total area of the whole chikki.
Therefore, even though the shapes are different, the amount of chikki in each piece is the same. They both have an area equal to $\frac{1}{6}$ of the original chikki.
Answer:
Yes, they are of the same size.
Because the whole chikki was divided into six equal parts in both scenarios, each resulting piece must have the same size (area), regardless of its shape.
Figure it Out (Page 155)
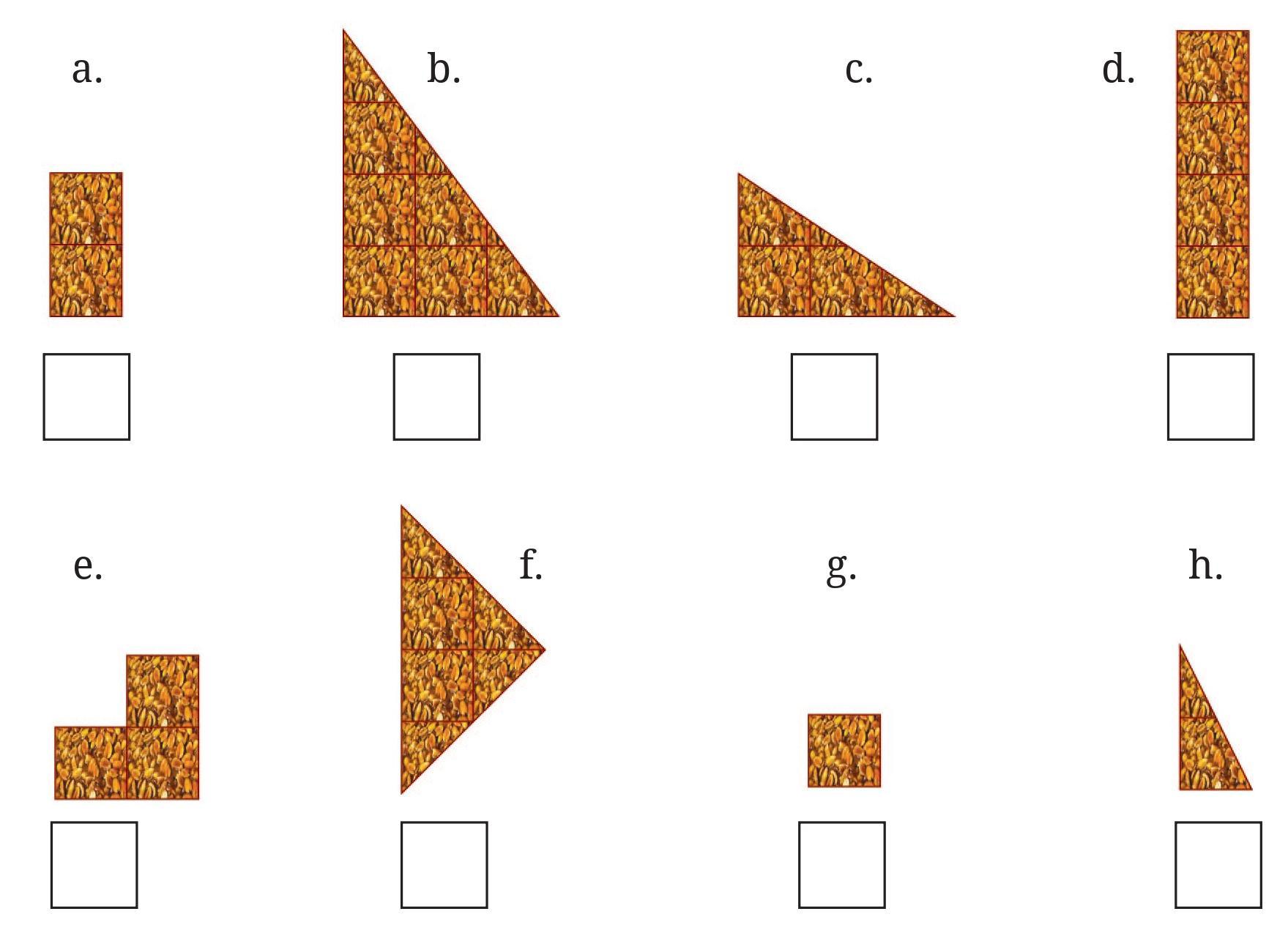
Answer:
Given:
A whole chikki is composed of 24 equal square pieces (arranged in a 6x4 grid).
To Find:
The fraction of the whole chikki that each piece represents.
Solution:
The total number of square units in one whole chikki is 24. The fraction for each piece is calculated by dividing the number of square units in that piece by the total number of units in the whole.
Fraction = $\frac{\text{Number of square units in the piece}}{\text{Total number of square units in a whole chikki}} = \frac{\text{Area of the piece}}{24}$
The area for rectangles is $length \times breadth$, and for triangles is $\frac{1}{2} \times base \times height$.
Calculations for Each Piece:
a. This piece is a rectangle with area = $1 \times 2 = 2$ square units.
Fraction = $\frac{2}{24} = \frac{\cancel{2}^{1}}{\cancel{24}_{12}} = \frac{1}{12}$
Answer for (a): $\mathbf{\frac{1}{12}}$
b. This piece is a right-angled triangle with area = $\frac{1}{2} \times 3 \times 4 = 6$ square units.
Fraction = $\frac{6}{24} = \frac{\cancel{6}^{1}}{\cancel{24}_{4}} = \frac{1}{4}$
Answer for (b): $\mathbf{\frac{1}{4}}$
c. This piece is a right-angled triangle with area = $\frac{1}{2} \times 3 \times 2 = 3$ square units.
Fraction = $\frac{3}{24} = \frac{\cancel{3}^{1}}{\cancel{24}_{8}} = \frac{1}{8}$
Answer for (c): $\mathbf{\frac{1}{8}}$
d. This piece is a rectangle with area = $1 \times 4 = 4$ square units.
Fraction = $\frac{4}{24} = \frac{\cancel{4}^{1}}{\cancel{24}_{6}} = \frac{1}{6}$
Answer for (d): $\mathbf{\frac{1}{6}}$
e. This L-shaped piece is made of 3 square units.
Fraction = $\frac{3}{24} = \frac{\cancel{3}^{1}}{\cancel{24}_{8}} = \frac{1}{8}$
Answer for (e): $\mathbf{\frac{1}{8}}$
f. This piece is an isosceles triangle with area = $\frac{1}{2} \times 4 \times 2 = 4$ square units.
Fraction = $\frac{4}{24} = \frac{\cancel{4}^{1}}{\cancel{24}_{6}} = \frac{1}{6}$
Answer for (f): $\mathbf{\frac{1}{6}}$
g. This piece is a single square unit, so its area is 1.
Fraction = $\frac{1}{24}$
Answer for (g): $\mathbf{\frac{1}{24}}$
h. This piece is a right-angled triangle with area = $\frac{1}{2} \times 1 \times 2 = 1$ square unit.
Fraction = $\frac{1}{24}$
Answer for (h): $\mathbf{\frac{1}{24}}$
Figure it Out (Page 158)
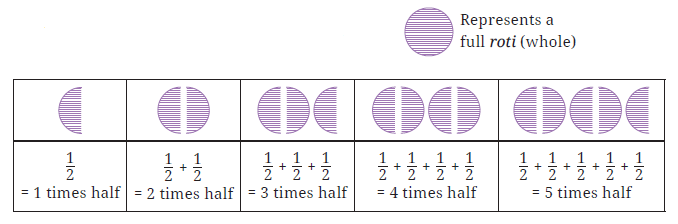
Question 1. Continue this table of $\frac{1}{2}$ for 2 more steps.
Answer:
Given:
A table showing the repeated addition of $\frac{1}{2}$ from 1 to 5 times, with corresponding visual representations using rotis.
To Do:
Continue the table for two more steps, which correspond to 6 times half and 7 times half.
Solution:
We need to follow the pattern established in the table. Each step adds another $\frac{1}{2}$.
Step 1: 6 times half
This is the sum of $\frac{1}{2}$ added to itself six times.
$6 \times \frac{1}{2} = \frac{1}{2} + \frac{1}{2} + \frac{1}{2} + \frac{1}{2} + \frac{1}{2} + \frac{1}{2} = \frac{6}{2} = 3$
Visually, this is represented by 3 full rotis.
Step 2: 7 times half
This is the sum of $\frac{1}{2}$ added to itself seven times.
$7 \times \frac{1}{2} = \frac{1}{2} + \frac{1}{2} + \frac{1}{2} + \frac{1}{2} + \frac{1}{2} + \frac{1}{2} + \frac{1}{2} = \frac{7}{2} = 3\frac{1}{2}$
Visually, this is represented by 3 full rotis and one half roti.
Answer:
The continuation of the table for 2 more steps is shown below:
| 6 times half | 7 times half |
|
3 full rotis 
|
3 full rotis and 1 half roti 
|
| $ 6 \times \frac{1}{2} = \frac{6}{2} = 3$ | $7 \times \frac{1}{2} = \frac{7}{2} = 3\frac{1}{2}$ |
Question 2. Can you create a similar table for $\frac{1}{4}$?
Answer:
To Do:
Create a table showing the repeated addition of the fraction $\frac{1}{4}$, similar to the example provided for $\frac{1}{2}$.
Solution:
Yes, a similar table can be created for the fraction $\frac{1}{4}$. We will show the results of taking $\frac{1}{4}$ one time, two times, three times, and so on. Each step involves adding another $\frac{1}{4}$. The visual representation will use a circle (roti) divided into four equal parts (quarters).
Answer:
Here is a table for $\frac{1}{4}$ showing the first five steps:
| Description | Visual Representation | Mathematical Calculation |
| 1 time quarter |

|
$1 \times \frac{1}{4} = \frac{1}{4}$ |
| 2 times quarter |
|
$\frac{1}{4}+\frac{1}{4} = \frac{2}{4} = \frac{1}{2}$ |
| 3 times quarter |

|
$\frac{1}{4}+\frac{1}{4}+\frac{1}{4} = \frac{3}{4}$ |
| 4 times quarter |
|
$\frac{1}{4}+\frac{1}{4}+\frac{1}{4}+\frac{1}{4} = \frac{4}{4} = 1$ |
| 5 times quarter |
|
$\frac{1}{4}+\frac{1}{4}+\frac{1}{4}+\frac{1}{4}+\frac{1}{4} = \frac{5}{4} = 1\frac{1}{4}$ |
Question 3. Make $\frac{1}{3}$ using a paper strip. Can you use this to also make $\frac{1}{6}$?
Answer:
Part 1: Making $\frac{1}{3}$ using a paper strip
To represent the fraction $\frac{1}{3}$, a whole object (in this case, a paper strip) must be divided into 3 equal parts. This can be achieved by folding:
1. Take a rectangular strip of paper which represents the 'whole'.
2. Carefully fold the strip to create three sections that are of equal length. A common method is to make a 'Z' fold, ensuring the edges of the strip align perfectly before making the creases sharp.
3. Unfold the paper. The two creases will divide the strip into three equal sections. Each of these sections represents $\frac{1}{3}$ of the whole paper strip.
Part 2: Using the strip to make $\frac{1}{6}$
Yes, it is possible to use the paper strip that is already divided into thirds to make sixths.
1. Take the strip that you have already marked into three equal parts (thirds).
2. Now, fold the entire strip of paper exactly in half along its length. Press down to make a new, sharp crease.
3. Unfold the strip. You will see that the new crease has divided each of the original $\frac{1}{3}$ sections into two smaller, equal parts.
4. The strip is now divided into a total of $3 \times 2 = 6$ equal sections. Each of these new, smaller sections represents $\frac{1}{6}$ of the original whole strip.
This works because dividing a third in half gives a sixth: $\frac{1}{3} \div 2 = \frac{1}{6}$.
Answer:
You can make $\frac{1}{3}$ by folding a paper strip into three equal parts.
Yes, you can then use this strip to make $\frac{1}{6}$ by folding the entire strip in half. This action divides each third into two equal parts, resulting in six equal parts for the whole strip.
Question 4. Draw a picture and write an addition statement as above to show:
a. 5 times $\frac{1}{4}$ of a roti
b. 9 times $\frac{1}{4}$ of a roti
Answer:
a. 5 times $\frac{1}{4}$ of a roti
Picture:
To show 5 times $\frac{1}{4}$, we need 5 quarter pieces. Since 4 quarters make a whole roti, this is equal to one whole roti and one extra quarter piece.
Addition Statement:
"5 times $\frac{1}{4}$" means adding $\frac{1}{4}$ to itself 5 times.
$\frac{1}{4} + \frac{1}{4} + \frac{1}{4} + \frac{1}{4} + \frac{1}{4} = \frac{1+1+1+1+1}{4} = \frac{5}{4}$
The result is $\frac{5}{4}$, which can also be written as the mixed number $\mathbf{1\frac{1}{4}}$.
b. 9 times $\frac{1}{4}$ of a roti
Picture:
To show 9 times $\frac{1}{4}$, we need 9 quarter pieces. Since 4 quarters make a whole roti, this is equal to two whole rotis (which use 8 quarters) and one extra quarter piece.
Addition Statement:
"9 times $\frac{1}{4}$" means adding $\frac{1}{4}$ to itself 9 times.
$\frac{1}{4} + \frac{1}{4} + \frac{1}{4} + \frac{1}{4} + \frac{1}{4} + \frac{1}{4} + \frac{1}{4} + \frac{1}{4} + \frac{1}{4} = \frac{9}{4}$
The result is $\frac{9}{4}$, which can also be written as the mixed number $\mathbf{2\frac{1}{4}}$.
Answer:
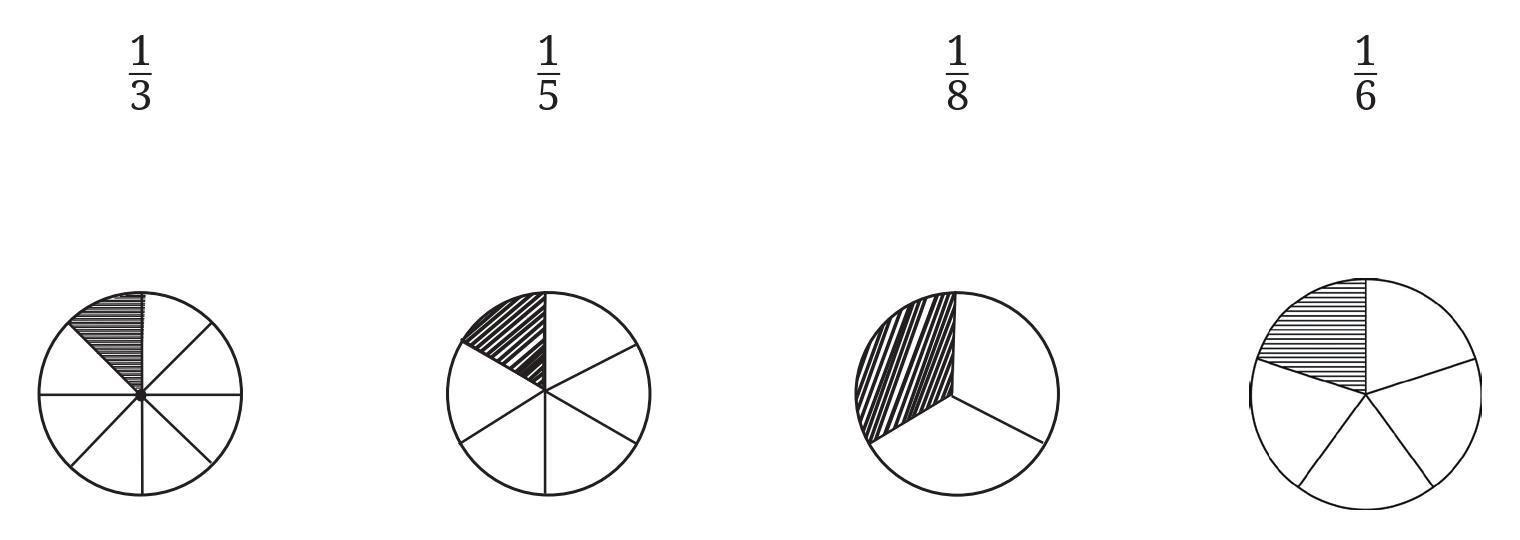
To Do:
Match each fraction from the set {$\frac{1}{3}$, $\frac{1}{5}$, $\frac{1}{8}$, $\frac{1}{6}$} with the correct circular diagram that visually represents it.
Solution:
To match the fractions, we need to count the total number of equal parts each circle is divided into. The fraction $\frac{1}{n}$ corresponds to the circle that is divided into 'n' equal parts with one part shaded.
- The fraction $\frac{1}{3}$ matches the circle divided into 3 equal parts with 1 part shaded. This is the third picture from the left.
- The fraction $\frac{1}{5}$ matches the circle divided into 5 equal parts with 1 part shaded. This is the fourth picture from the left.
- The fraction $\frac{1}{8}$ matches the circle divided into 8 equal parts with 1 part shaded. This is the first picture from the left.
- The fraction $\frac{1}{6}$ matches the circle divided into 6 equal parts with 1 part shaded. This is the second picture from the left.
Answer:
The correct matches are shown in the table below:
| Fractional Unit | Matching Picture (Description) |
| $\frac{1}{3}$ | The circle with 1 of 3 equal parts shaded (Third picture). |
| $\frac{1}{5}$ | The circle with 1 of 5 equal parts shaded (Fourth picture). |
| $\frac{1}{8}$ | The circle with 1 of 8 equal parts shaded (First picture). |
| $\frac{1}{6}$ | The circle with 1 of 6 equal parts shaded (Second picture). |
Intext Question (Page 159)
Question: Now, can you find the lengths of the various blue lines shown below? Fill in the boxes as well.
1. Here, the fractional unit is dividing a length of 1 unit into three equal parts. Write the fraction that gives the length of the blue line in the box or in your notebook.

2. Here, a unit is divided into 5 equal parts. Write the fraction that gives the length of the blue lines in the respective boxes or in your notebook.

3. Now, a unit is divided into 8 equal parts. Write the appropriate fractions in your notebook.
Answer:
1. Number Line Divided into Three Parts
Analysis: The segment on the number line from 0 to 1 is divided into 3 equal parts. This means that each mark represents a multiple of $\frac{1}{3}$. The sequence of marks is $\frac{0}{3}$ (which is 0), $\frac{1}{3}$, $\frac{2}{3}$, and $\frac{3}{3}$ (which is 1).
Filling the Box: The empty box is located at the second mark after 0, so the fraction that belongs in the box is $\frac{2}{3}$.
Length of the Blue Line: The blue line starts at 0 and ends at the position of the box. Therefore, the length of the blue line is also $\frac{2}{3}$.
Answer: The fraction in the box is $\mathbf{\frac{2}{3}}$. The length of the blue line is $\mathbf{\frac{2}{3}}$.
2. Number Line Divided into Five Parts
Analysis: The segment on the number line from 0 to 1 is divided into 5 equal parts. This means that each mark represents a multiple of $\frac{1}{5}$. The sequence of marks is $\frac{0}{5}, \frac{1}{5}, \frac{2}{5}, \frac{3}{5}, \frac{4}{5}$, and $\frac{5}{5}$ (which is 1).
Filling the Boxes:
- The first empty box is at the second mark, which corresponds to the fraction $\frac{2}{5}$.
- The second empty box is at the fourth mark, which corresponds to the fraction $\frac{4}{5}$.
Length of the Blue Lines:
- The shorter blue line starts at 0 and ends at the first box. Its length is $\frac{2}{5}$.
- The longer blue line starts at 0 and ends at the second box. Its length is $\frac{4}{5}$.
Answer: The first box is $\mathbf{\frac{2}{5}}$ and the second box is $\mathbf{\frac{4}{5}}$. The lengths of the blue lines are $\mathbf{\frac{2}{5}}$ and $\mathbf{\frac{4}{5}}$ respectively.
3. Number Line Divided into Eight Parts
Analysis: If a unit length from 0 to 1 is divided into 8 equal parts, each part represents a length of $\frac{1}{8}$.
Writing the Fractions: The fractions that would mark the divisions on the number line are multiples of $\frac{1}{8}$, starting from 0.
Answer: The appropriate fractions for a unit divided into 8 equal parts are $\mathbf{\frac{0}{8} \text{ (or 0)}, \frac{1}{8}, \frac{2}{8}, \frac{3}{8}, \frac{4}{8}, \frac{5}{8}, \frac{6}{8}, \frac{7}{8}, \text{ and } \frac{8}{8} \text{ (or 1)}}$.
Some of these fractions can be simplified: $\frac{2}{8} = \frac{1}{4}$, $\frac{4}{8} = \frac{1}{2}$, and $\frac{6}{8} = \frac{3}{4}$.
Figure it Out (Page 160)
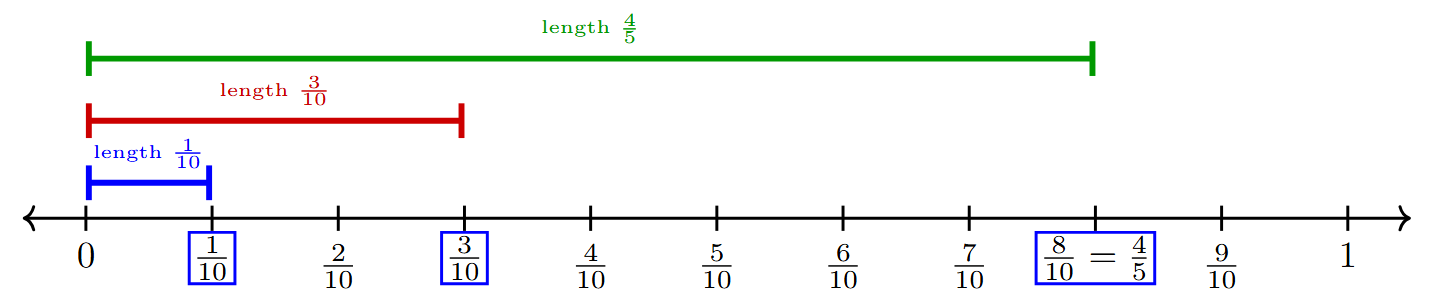
Question 1. On a number line, draw lines of lengths $\frac{1}{10}$ , $\frac{3}{10}$ , and $\frac{4}{5}$.
Answer:
To Do:
Represent the lengths $\frac{1}{10}$, $\frac{3}{10}$, and $\frac{4}{5}$ on a number line.
Solution:
Step 1: Find a common denominator.
To place these fractions on the same number line easily, we should express them with a common denominator. The denominators are 10 and 5. The least common multiple (LCM) of 10 and 5 is 10.
The fractions $\frac{1}{10}$ and $\frac{3}{10}$ already have this denominator.
We convert $\frac{4}{5}$ to an equivalent fraction with a denominator of 10:
$\frac{4}{5} = \frac{4 \times 2}{5 \times 2} = \frac{8}{10}$
So, the lengths we need to draw are $\frac{1}{10}$, $\frac{3}{10}$, and $\frac{8}{10}$.
Step 2: Prepare the number line.
Draw a number line. Since all fractions are between 0 and 1, we can focus on the segment from 0 to 1. Based on our common denominator, we will divide the length from 0 to 1 into 10 equal parts. Each part will represent a length of $\frac{1}{10}$.
Step 3: Draw the lines.
Draw a line segment starting from 0 for each fraction:
- For $\frac{1}{10}$: Draw a line from 0 to the first mark after 0.
- For $\frac{3}{10}$: Draw a line from 0 to the third mark after 0.
- For $\frac{4}{5}$ (or $\frac{8}{10}$): Draw a line from 0 to the eighth mark after 0.
Answer:
The image below represents the number line with the required lengths shown.
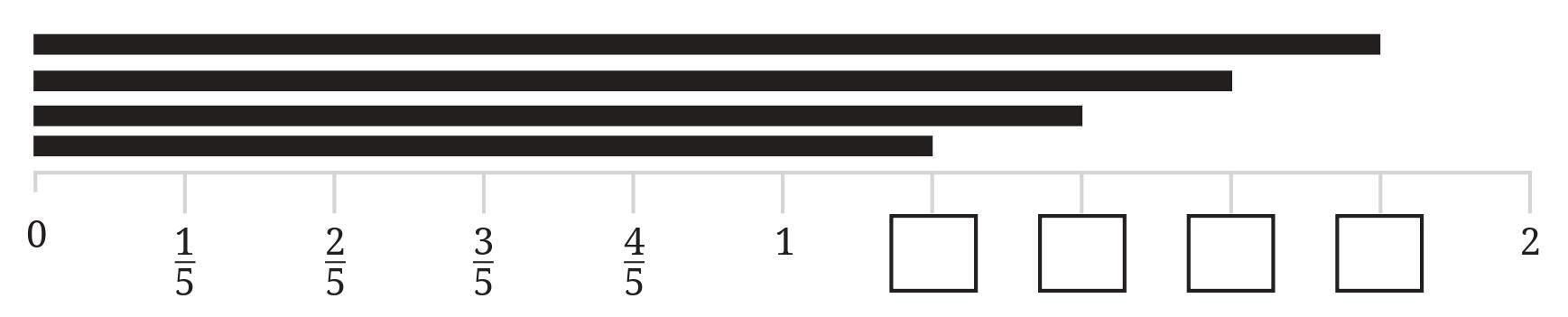
Question 2. Write five more fractions of your choice and mark them on the number line.
Answer:
To Do:
Choose five different fractions and show their positions on a number line.
Solution:
Step 1: Choose five fractions.
Let's choose a mix of proper and improper fractions:
$\frac{3}{4}$, $\frac{1}{3}$, $\frac{7}{5}$, $\frac{1}{8}$, $\frac{5}{2}$
Step 2: Understand the position of each fraction.
It is helpful to convert improper fractions to mixed numbers to find their position easily.
- $\frac{3}{4}$ is between 0 and 1.
- $\frac{1}{3}$ is between 0 and 1.
- $\frac{7}{5} = 1\frac{2}{5}$. This is between 1 and 2.
- $\frac{1}{8}$ is between 0 and 1.
- $\frac{5}{2} = 2\frac{1}{2}$. This is between 2 and 3.
Step 3: Mark the fractions on a number line.
Draw a number line that extends from 0 to 3 to accommodate all the fractions.
- To mark $\frac{1}{8}$ and $\frac{3}{4}$: Divide the segment from 0 to 1 into 8 equal parts. The first mark is $\frac{1}{8}$. The sixth mark is $\frac{6}{8}$, which simplifies to $\frac{3}{4}$.
- To mark $\frac{1}{3}$: Divide the segment from 0 to 1 into 3 equal parts. The first mark is $\frac{1}{3}$.
- To mark $\frac{7}{5}$: Go to 1. Divide the segment from 1 to 2 into 5 equal parts. The second mark after 1 is $1\frac{2}{5}$ or $\frac{7}{5}$.
- To mark $\frac{5}{2}$: Go to 2. Divide the segment from 2 to 3 into 2 equal parts. The first mark after 2 is $2\frac{1}{2}$ or $\frac{5}{2}$.
Answer:
Five chosen fractions are $\frac{3}{4}, \frac{1}{3}, \frac{7}{5}, \frac{1}{8}$, and $\frac{5}{2}$. Their positions on a number line are shown in the conceptual image below.

Question 3. How many fractions lie between 0 and 1? Think, discuss with your classmates, and write your answer.
Answer:
Question:
How many fractions are there between 0 and 1?
Reasoning and Discussion:
To answer this, let's explore how fractions are created.
Argument 1: Using Different Denominators
We can create fractions between 0 and 1 by choosing a denominator and then a numerator that is smaller than the denominator.
- If we divide the space between 0 and 1 into two parts (denominator 2), we get the fraction $\frac{1}{2}$.
- If we divide it into three parts (denominator 3), we get $\frac{1}{3}$ and $\frac{2}{3}$.
- If we divide it into ten parts (denominator 10), we get $\frac{1}{10}, \frac{2}{10}, \dots, \frac{9}{10}$.
- If we divide it into one thousand parts (denominator 1000), we get 999 different fractions between 0 and 1.
Since we can choose any whole number as a denominator (2, 3, 4, 5, ..., 1 million, 1 billion, and so on), and there is no largest whole number, we can create an unlimited number of new fractions. This suggests there are infinitely many.
Argument 2: Finding a Fraction Between Any Two Fractions
Let's pick any two different fractions between 0 and 1, for example, $\frac{1}{3}$ and $\frac{1}{2}$. Can we find a fraction between them? Yes. A simple way is to find their average:
Average = $\frac{\frac{1}{3} + \frac{1}{2}}{2} = \frac{\frac{2}{6} + \frac{3}{6}}{2} = \frac{\frac{5}{6}}{2} = \frac{5}{12}$
The fraction $\frac{5}{12}$ is between $\frac{1}{3}$ (which is $\frac{4}{12}$) and $\frac{1}{2}$ (which is $\frac{6}{12}$).
We could now find a fraction between $\frac{1}{3}$ and $\frac{5}{12}$, and so on. This process can be repeated forever. Because we can always find a new fraction between any two existing fractions, there cannot be a finite number of them.
Answer:
There are infinitely many fractions that lie between 0 and 1.

Answer:
Given:
A number line is shown where the distance from 0 to 1 is one unit.
The unit length is divided into two equal parts, so each part has a length of $\frac{1}{2}$.
The length of the blue line is given as $\frac{1}{2}$ units.
The black line starts at 0 and ends at a point halfway between 1 and 2.
To Find:
The fraction that gives the length of the black line and should be written in the empty box.
Solution:
The number line is marked in units of "halves" or $\frac{1}{2}$.
We can identify the value of each major point on the number line in terms of this fraction:
- The starting point is $0 = \frac{0}{2}$.
- The first mark (end of the blue line) is $\frac{1}{2}$.
- The point marked '1' can be written as $\frac{2}{2}$.
The black line ends at the next mark after '1'. Following the pattern, this mark would be $\frac{3}{2}$.
The point marked '2' can be written as $\frac{4}{2}$. The mark $\frac{3}{2}$ is exactly halfway between $\frac{2}{2}$ (which is 1) and $\frac{4}{2}$ (which is 2), which matches the position in the diagram.
Alternate Solution (Using Mixed Numbers):
The point where the black line ends is located 1 full unit from 0, plus an additional half unit.
This can be written as the mixed number $1\frac{1}{2}$.
To convert this mixed number to an improper fraction, we calculate:
$1\frac{1}{2} = \frac{(1 \times 2) + 1}{2} = \frac{2+1}{2} = \frac{3}{2}$
The length of the black line is its distance from 0, which is $\frac{3}{2}$. This is the fraction that goes in the box.
The fraction that gives the length of the black line in the box is $\frac{3}{2}$.
Answer:
Given:
A number line is shown where the distance from 0 to 1 is one unit.
The unit length is divided into five equal parts, so each part has a length of $\frac{1}{5}$.
Four black lines of different lengths are shown, all starting from 0.
To Find:
The fraction that gives the length of each black line and the values for the empty boxes on the number line.
Solution:
The number line is marked in units of "fifths" or $\frac{1}{5}$. We can determine the value of each mark by counting in steps of $\frac{1}{5}$ from 0.
The marked points are:
$0 = \frac{0}{5}$, $\frac{1}{5}$, $\frac{2}{5}$, $\frac{3}{5}$, $\frac{4}{5}$, $1 = \frac{5}{5}$
The points after 1 continue this pattern:
The first point after 1 is $\frac{5}{5} + \frac{1}{5} = \frac{6}{5}$.
The second point after 1 is $\frac{6}{5} + \frac{1}{5} = \frac{7}{5}$.
The third point after 1 is $\frac{7}{5} + \frac{1}{5} = \frac{8}{5}$.
The fourth point after 1 is $\frac{8}{5} + \frac{1}{5} = \frac{9}{5}$.
The point marked '2' is $\frac{10}{5}$.
Lengths of the Black Lines and Values for the Boxes:
Now we match the end of each black line to the corresponding mark on the number line.
- Shortest black line: This line ends at the mark $\frac{3}{5}$. Its length is $\mathbf{\frac{3}{5}}$.
- Second shortest black line: This line ends at the mark $\frac{4}{5}$. Its length is $\mathbf{\frac{4}{5}}$.
- Second longest black line: This line ends at the mark $\frac{7}{5}$. Its length is $\mathbf{\frac{7}{5}}$. This can also be written as $1\frac{2}{5}$.
- Longest black line: This line ends at the mark $\frac{9}{5}$. Its length is $\mathbf{\frac{9}{5}}$. This can also be written as $1\frac{4}{5}$.
The empty boxes on the number line correspond to the marks after 1. From our calculations above:
- First box: $\mathbf{\frac{6}{5}}$ (or $1\frac{1}{5}$)
- Second box: $\mathbf{\frac{7}{5}}$ (or $1\frac{2}{5}$)
- Third box: $\mathbf{\frac{8}{5}}$ (or $1\frac{3}{5}$)
- Fourth box: $\mathbf{\frac{9}{5}}$ (or $1\frac{4}{5}$)
Intext Question (Page 161)
Now, let us classify these in two groups:

Answer:
To Do:
First, we will classify some of the fractions from the previous exercises into two groups: those less than 1 and those more than 1. Then, we will identify the common property of the fractions that are greater than 1.
Classification of Fractions:
Let's take the fractions we have worked with, such as $\frac{1}{10}, \frac{2}{5}, \frac{3}{5}, \frac{4}{5}, \frac{1}{2}, \frac{3}{2}, \frac{6}{5}, \frac{7}{5}, \frac{9}{5}$.
| Lengths less than 1 unit | Lengths more than 1 unit |
| $\frac{1}{10}, \frac{2}{5}, \frac{3}{5}, \frac{4}{5}, \frac{1}{2}$ | $\frac{3}{2}, \frac{6}{5}, \frac{7}{5}, \frac{9}{5}$ |
Observation and Answer to the Question:
Yes, there is a common property among all the fractions that are greater than 1.
Let's examine the fractions in the "Lengths more than 1 unit" column:
- In $\frac{3}{2}$, the numerator (3) is greater than the denominator (2).
- In $\frac{6}{5}$, the numerator (6) is greater than the denominator (5).
- In $\frac{7}{5}$, the numerator (7) is greater than the denominator (5).
- In $\frac{9}{5}$, the numerator (9) is greater than the denominator (5).
The common characteristic is that for every fraction greater than 1, the numerator is greater than the denominator.
Fractions where the numerator is greater than the denominator are called improper fractions. Fractions where the numerator is less than the denominator (those in the first column) are called proper fractions.
Figure it Out (Page 162)
Question 1. How many whole units are there in $\frac{7}{2}$?
Answer:
Given:
The improper fraction $\frac{7}{2}$.
To Find:
The number of whole units contained in $\frac{7}{2}$.
Solution:
To find the number of whole units, we need to convert the improper fraction into a mixed number. A mixed number has a whole number part and a proper fraction part.
The fraction $\frac{7}{2}$ can be interpreted as "7 halves". We know that 2 halves ($\frac{2}{2}$) make one whole unit.
We can find how many groups of 2 are in 7 by dividing the numerator by the denominator.
We perform the division $7 \div 2$.
$\begin{array}{r} 3\phantom{2)} \\ 2{\overline{\smash{\big)}\,7\phantom{)}}} \\ \underline{-~\phantom{(}6} \\ 1\phantom{)} \end{array}$
The result of the division is:
- Quotient: 3
- Remainder: 1
The quotient represents the number of full whole units. The remainder represents the number of parts left over.
So, $\frac{7}{2}$ is equal to 3 whole units and 1 part of size $\frac{1}{2}$ left over.
As a mixed number, this is written as $3\frac{1}{2}$.
The whole number part is 3.
Answer:
There are 3 whole units in $\frac{7}{2}$.
Question 2. How many whole units are there in $\frac{4}{3}$ and in $\frac{7}{3}$?
Answer:
To Find:
The number of whole units in the fractions $\frac{4}{3}$ and $\frac{7}{3}$.
Solution for $\frac{4}{3}$:
The fraction $\frac{4}{3}$ means "4 thirds". Since 3 thirds ($\frac{3}{3}$) make one whole unit, we divide the numerator (4) by the denominator (3) to find the number of whole units.
$4 \div 3 = 1$ with a remainder of $1$.
The quotient, 1, is the number of whole units.
As a mixed number, $\frac{4}{3} = 1\frac{1}{3}$.
So, there is 1 whole unit in $\frac{4}{3}$.
Solution for $\frac{7}{3}$:
The fraction $\frac{7}{3}$ means "7 thirds". Again, we divide the numerator (7) by the denominator (3).
$7 \div 3 = 2$ with a remainder of $1$.
The quotient, 2, is the number of whole units.
As a mixed number, $\frac{7}{3} = 2\frac{1}{3}$.
So, there are 2 whole units in $\frac{7}{3}$.
Answer:
There is 1 whole unit in $\frac{4}{3}$ and there are 2 whole units in $\frac{7}{3}$.
Figure it Out (Page 162 - 163)
Question 1. Figure out the number of whole units in each of the following fractions:
a. $\frac{8}{3}$
b. $\frac{11}{5}$
c. $\frac{9}{4}$
Answer:
To Find:
The number of whole units in each given improper fraction.
Method:
To find the number of whole units in an improper fraction, we divide the numerator by the denominator. The quotient of this division gives the number of whole units.
a. $\frac{8}{3}$
We divide 8 by 3.
$8 \div 3 = 2$ with a remainder of 2.
The quotient is 2. This means $\frac{8}{3}$ can be written as the mixed number $2\frac{2}{3}$.
Therefore, there are 2 whole units in $\frac{8}{3}$.
b. $\frac{11}{5}$
We divide 11 by 5.
$11 \div 5 = 2$ with a remainder of 1.
The quotient is 2. This means $\frac{11}{5}$ can be written as the mixed number $2\frac{1}{5}$.
Therefore, there are 2 whole units in $\frac{11}{5}$.
c. $\frac{9}{4}$
We divide 9 by 4.
$9 \div 4 = 2$ with a remainder of 1.
The quotient is 2. This means $\frac{9}{4}$ can be written as the mixed number $2\frac{1}{4}$.
Therefore, there are 2 whole units in $\frac{9}{4}$.
Question 2.
Can all fractions greater than 1 be written as such mixed numbers?
A mixed number / mixed fraction contains a whole number (called the whole part) and a fraction that is less than 1 (called the fractional part).
Answer:
Yes, all fractions greater than 1 can be written as mixed numbers.
Explanation:
A fraction is greater than 1 if its numerator is larger than its denominator. Such fractions are called improper fractions.
The definition of a mixed number is a number consisting of a whole number and a proper fraction (a fraction where the numerator is smaller than the denominator, making it less than 1).
To convert any improper fraction, say $\frac{p}{q}$ (where $p > q$), into a mixed number, we perform the division $p \div q$.
Let the result of this division be a quotient, $Q$, and a remainder, $R$.
Then the improper fraction can be expressed as:
$\frac{p}{q} = Q\frac{R}{q}$
Here:
- $Q$ is the whole number part. Since $p > q$, the quotient $Q$ will always be at least 1.
- $\frac{R}{q}$ is the fractional part. By the rules of division, the remainder $R$ is always less than the divisor $q$. This ensures that $\frac{R}{q}$ is always a proper fraction (a fraction less than 1).
Since this process works for any improper fraction, we can conclude that all fractions greater than 1 can be written as mixed numbers.
Question 3. Write the following fractions as mixed fractions $(e.g., \frac{9}{2} = 4\frac{1}{2})$:
a. $\frac{9}{2}$
b. $\frac{9}{5}$
c. $\frac{21}{19}$
d. $\frac{47}{9}$
e. $\frac{12}{11}$
f. $\frac{19}{6}$
Answer:
To Do:
Convert the given improper fractions into mixed fractions.
Method:
Divide the numerator by the denominator. The quotient becomes the whole number, the remainder becomes the new numerator, and the denominator stays the same.
a. $\frac{9}{2}$
Divide 9 by 2: $9 \div 2 = 4$ with a remainder of 1.
Mixed fraction: $4\frac{1}{2}$
b. $\frac{9}{5}$
Divide 9 by 5: $9 \div 5 = 1$ with a remainder of 4.
Mixed fraction: $1\frac{4}{5}$
c. $\frac{21}{19}$
Divide 21 by 19: $21 \div 19 = 1$ with a remainder of 2.
Mixed fraction: $1\frac{2}{19}$
d. $\frac{47}{9}$
Divide 47 by 9: $47 \div 9 = 5$ with a remainder of 2.
Mixed fraction: $5\frac{2}{9}$
e. $\frac{12}{11}$
Divide 12 by 11: $12 \div 11 = 1$ with a remainder of 1.
Mixed fraction: $1\frac{1}{11}$
f. $\frac{19}{6}$
Divide 19 by 6: $19 \div 6 = 3$ with a remainder of 1.
Mixed fraction: $3\frac{1}{6}$
Figure it Out (Page 163)
Write the following mixed numbers as fractions:
a. $3\frac{1}{4}$
b. $7\frac{2}{3}$
c. $9\frac{4}{9}$
d. $3\frac{1}{6}$
e. $2\frac{3}{11}$
f. $3\frac{9}{10}$
Answer:
To Do:
Convert the given mixed numbers into improper fractions.
Method:
To convert a mixed number into an improper fraction, we use the following formula:
Improper Fraction = $\frac{(\text{Whole Number} \times \text{Denominator}) + \text{Numerator}}{\text{Denominator}}$
a. $3\frac{1}{4}$
Using the formula:
$3\frac{1}{4} = \frac{(3 \times 4) + 1}{4} = \frac{12 + 1}{4} = \frac{13}{4}$
So, the fraction is $\frac{13}{4}$.
b. $7\frac{2}{3}$
Using the formula:
$7\frac{2}{3} = \frac{(7 \times 3) + 2}{3} = \frac{21 + 2}{3} = \frac{23}{3}$
So, the fraction is $\frac{23}{3}$.
c. $9\frac{4}{9}$
Using the formula:
$9\frac{4}{9} = \frac{(9 \times 9) + 4}{9} = \frac{81 + 4}{9} = \frac{85}{9}$
So, the fraction is $\frac{85}{9}$.
d. $3\frac{1}{6}$
Using the formula:
$3\frac{1}{6} = \frac{(3 \times 6) + 1}{6} = \frac{18 + 1}{6} = \frac{19}{6}$
So, the fraction is $\frac{19}{6}$.
e. $2\frac{3}{11}$
Using the formula:
$2\frac{3}{11} = \frac{(2 \times 11) + 3}{11} = \frac{22 + 3}{11} = \frac{25}{11}$
So, the fraction is $\frac{25}{11}$.
f. $3\frac{9}{10}$
Using the formula:
$3\frac{9}{10} = \frac{(3 \times 10) + 9}{10} = \frac{30 + 9}{10} = \frac{39}{10}$
So, the fraction is $\frac{39}{10}$.
Intext Question (Page 164 - 165)

Question: Answer the following questions after looking at the fraction wall:
1. Are the lengths $\frac{1}{2}$ and $\frac{3}{6}$ equal?
2. Are $\frac{2}{3}$ and $\frac{4}{6}$ equivalent fractions? Why?
3. How many pieces of length $\frac{1}{6}$ will make a length of $\frac{1}{2}$ ?
4. How many pieces of length $\frac{1}{6}$ will make a length of $\frac{1}{3}$ ?
Answer:
Question 1: Are the lengths $\frac{1}{2}$ and $\frac{3}{6}$ equal?
Answer: Yes, the lengths $\frac{1}{2}$ and $\frac{3}{6}$ are equal.
Reasoning from the Fraction Wall: If you look at the fraction wall, the vertical line marking the end of the $\frac{1}{2}$ block aligns perfectly with the vertical line marking the end of the third $\frac{1}{6}$ block (which represents the length $\frac{3}{6}$). This visual alignment shows they represent the same length or value.
Question 2: Are $\frac{2}{3}$ and $\frac{4}{6}$ equivalent fractions? Why?
Answer: Yes, $\frac{2}{3}$ and $\frac{4}{6}$ are equivalent fractions.
Reasoning from the Fraction Wall: The vertical line at the end of the second $\frac{1}{3}$ block (representing $\frac{2}{3}$) is in the exact same position as the vertical line at the end of the fourth $\frac{1}{6}$ block (representing $\frac{4}{6}$). Because they cover the same portion of the whole unit, they are equivalent.
Mathematical Reasoning: We can obtain $\frac{4}{6}$ by multiplying the numerator and denominator of $\frac{2}{3}$ by the same number (2): $\frac{2 \times 2}{3 \times 2} = \frac{4}{6}$.
Question 3: How many pieces of length $\frac{1}{6}$ will make a length of $\frac{1}{2}$?
Answer: 3 pieces of length $\frac{1}{6}$ will make a length of $\frac{1}{2}$.
Reasoning from the Fraction Wall: Looking at the row for sixths, you can see that three of the $\frac{1}{6}$ blocks are needed to cover the same length as one of the $\frac{1}{2}$ blocks.
Mathematical Reasoning: We are asking to find 'x' such that $x \times \frac{1}{6} = \frac{1}{2}$. This is the same as asking $\frac{1}{2} \div \frac{1}{6} = \frac{1}{2} \times \frac{6}{1} = \frac{6}{2} = 3$.
Question 4: How many pieces of length $\frac{1}{6}$ will make a length of $\frac{1}{3}$?
Answer: 2 pieces of length $\frac{1}{6}$ will make a length of $\frac{1}{3}$.
Reasoning from the Fraction Wall: By observing the fraction wall, we can see that two of the $\frac{1}{6}$ blocks fit perfectly under one of the $\frac{1}{3}$ blocks.
Mathematical Reasoning: We need to find 'x' such that $x \times \frac{1}{6} = \frac{1}{3}$. This is equivalent to calculating $\frac{1}{3} \div \frac{1}{6} = \frac{1}{3} \times \frac{6}{1} = \frac{6}{3} = 2$.
Figure it Out (Page 165)
Question 1. Are $\frac{3}{6}$, $\frac{4}{8}$, $\frac{5}{10}$ equivalent fractions? Why?
Answer:
To Determine:
If the fractions $\frac{3}{6}$, $\frac{4}{8}$, and $\frac{5}{10}$ are equivalent.
Reasoning:
Equivalent fractions are fractions that represent the same value or proportion of a whole. A common way to check for equivalence is to simplify each fraction to its simplest form. If all fractions simplify to the same value, they are equivalent.
Step 1: Simplify $\frac{3}{6}$
The greatest common divisor (GCD) of the numerator (3) and the denominator (6) is 3. We divide both by 3.
$\frac{3}{6} = \frac{3 \div 3}{6 \div 3} = \frac{1}{2}$
Step 2: Simplify $\frac{4}{8}$
The GCD of the numerator (4) and the denominator (8) is 4. We divide both by 4.
$\frac{4}{8} = \frac{4 \div 4}{8 \div 4} = \frac{1}{2}$
Step 3: Simplify $\frac{5}{10}$
The GCD of the numerator (5) and the denominator (10) is 5. We divide both by 5.
$\frac{5}{10} = \frac{5 \div 5}{10 \div 5} = \frac{1}{2}$
Conclusion:
Yes, the fractions $\frac{3}{6}$, $\frac{4}{8}$, and $\frac{5}{10}$ are equivalent.
Why? Because all three fractions simplify to the same fraction, $\frac{1}{2}$, which means they all represent the same value (one half).
Question 2. Write two equivalent fractions for $\frac{2}{6}$ .
Answer:
Given Fraction:
$\frac{2}{6}$
Method:
To find equivalent fractions, we can either multiply or divide both the numerator and the denominator by the same non-zero number.
Method 1: Simplification (Division)
We can simplify $\frac{2}{6}$ by dividing the numerator and denominator by their greatest common divisor, which is 2.
$\frac{2 \div 2}{6 \div 2} = \frac{1}{3}$
So, $\frac{1}{3}$ is one equivalent fraction.
Method 2: Expansion (Multiplication)
We can find another equivalent fraction by multiplying the numerator and denominator by any whole number, for example, 2.
$\frac{2 \times 2}{6 \times 2} = \frac{4}{12}$
So, $\frac{4}{12}$ is another equivalent fraction.
Answer:
Two equivalent fractions for $\frac{2}{6}$ are $\frac{1}{3}$ and $\frac{4}{12}$.
(Other possible answers include $\frac{6}{18}$, $\frac{8}{24}$, etc.)
Question 3. $\frac{4}{6}$ = $\frac{-}{-}$ = $\frac{-}{-}$ = $\frac{-}{-}$ = ............ (Write as many as you can)
Answer:
Given Fraction:
$\frac{4}{6}$
Method:
We can generate an infinite number of equivalent fractions for $\frac{4}{6}$. It is best to first simplify the fraction to its lowest terms and then generate other fractions from the simplified form.
Step 1: Simplify the fraction.
Divide the numerator and denominator by their GCD, which is 2.
$\frac{4 \div 2}{6 \div 2} = \frac{2}{3}$
Step 2: Generate other equivalent fractions from the simplified form $\frac{2}{3}$.
Multiply the numerator and denominator of $\frac{2}{3}$ by 2, 3, 4, 5, etc.
$\frac{2 \times 2}{3 \times 2} = \frac{4}{6}$ (the original fraction)
$\frac{2 \times 3}{3 \times 3} = \frac{6}{9}$
$\frac{2 \times 4}{3 \times 4} = \frac{8}{12}$
$\frac{2 \times 5}{3 \times 5} = \frac{10}{15}$
$\frac{2 \times 10}{3 \times 10} = \frac{20}{30}$
Answer:
Here are some equivalent fractions for $\frac{4}{6}$:
$\frac{4}{6} = \mathbf{\frac{2}{3}} = \mathbf{\frac{6}{9}} = \mathbf{\frac{8}{12}} = \mathbf{\frac{10}{15}} = \mathbf{\frac{12}{18}} = \mathbf{\frac{20}{30}} = \dots$
Figure it Out (Page 166)

Question 1. Three rotis are shared equally by four children. Show the division in the picture and write a fraction for how much each child gets. Also, write the corresponding division facts, addition facts, and, multiplication facts.
Fraction of roti each child gets is ______.
Division fact:
Addition fact:
Multiplication fact:
Compare your picture and answers with your classmates!
Answer:
Given:
Number of rotis = 3
Number of children = 4
The rotis are shared equally.
Solution:
To share 3 rotis equally among 4 children, we can divide each of the 3 rotis into 4 equal pieces (quarters). This gives a total of $3 \times 4 = 12$ pieces.
Now, these 12 pieces can be distributed equally among the 4 children.
Number of pieces each child gets = $\frac{\text{Total pieces}}{\text{Number of children}} = \frac{12}{4} = 3$ pieces.
Each piece is a quarter ($\frac{1}{4}$) of a roti. So, each child gets 3 quarter-pieces.
The fraction of roti each child gets is the sum of the fractions of these 3 pieces:
$\frac{1}{4} + \frac{1}{4} + \frac{1}{4} = \frac{3}{4}$
So, each child gets $\frac{3}{4}$ of a roti.
Fraction of roti each child gets is $\mathbf{\frac{3}{4}}$.
Division fact:
The total amount (3 rotis) is divided by the number of people (4). This directly gives the share per person.
$3 \div 4 = \frac{3}{4}$
Addition fact:
The sum of the shares of all four children must equal the total number of rotis.
$\frac{3}{4} + \frac{3}{4} + \frac{3}{4} + \frac{3}{4} = \frac{12}{4} = 3$
Multiplication fact:
The number of children multiplied by the share of each child equals the total number of rotis.
$4 \times \frac{3}{4} = \frac{12}{4} = 3$
Question 2. Draw a picture to show how much each child gets when 2 rotis are shared equally by 4 children. Also, write the corresponding division facts, addition facts, and multiplication facts.
Answer:
Given:
Number of rotis = 2
Number of children = 4
Amount Each Child Gets:
To find the share for each child, we divide the total number of rotis by the number of children.
Share per child = $\frac{\text{Total rotis}}{\text{Number of children}} = \frac{2}{4}$
Simplifying this fraction, we get:
$\frac{2}{4} = \frac{2 \div 2}{4 \div 2} = \frac{1}{2}$
So, each child gets $\frac{1}{2}$ of a roti.
Picture Representation:
We can show this by dividing each of the 2 rotis into 2 equal halves. This gives a total of 4 half-roti pieces. Each of the 4 children can then take one of these pieces.

Division fact:
The division of 2 rotis among 4 children gives each child a share of $\frac{1}{2}$.
$2 \div 4 = \frac{2}{4} = \frac{1}{2}$
Addition fact:
Adding the shares of all 4 children together gives the total number of rotis.
$\frac{1}{2} + \frac{1}{2} + \frac{1}{2} + \frac{1}{2} = \frac{4}{2} = 2$
Multiplication fact:
Multiplying the number of children by the share each one gets gives the total number of rotis.
$4 \times \frac{1}{2} = \frac{4}{2} = 2$
Question 3. Anil was in a group where 2 cakes were divided equally among 5 children. How much cake would Anil get?
Answer:
Given:
Total number of cakes = 2
Total number of children = 5
The cakes are divided equally.
To Find:
The fraction of a cake that Anil gets.
Solution:
To find the share for one person when a quantity is divided equally among a group, we set up a fraction where the total quantity is the numerator and the number of people is the denominator.
Share per child = $\frac{\text{Total number of cakes}}{\text{Total number of children}}$
Substituting the given values:
Share per child = $\frac{2}{5}$
Since Anil is one of the children in the group, he will receive an equal share.
Answer:
Anil would get $\frac{2}{5}$ of a cake.
Figure it Out (Page 168 - 169)
Find the missing numbers:
a. 5 glasses of juice shared equally among 4 friends is the same as ____ glasses of juice shared equally among 8 friends. So, $\frac{5}{4}$ = $\frac{-}{8}$ .
b. 4 kg of potatoes divided equally in 3 bags is the same as 12 kgs of potatoes divided equally in ___ bags. So, $\frac{4}{3}$ = $\frac{12}{-}$
c. 7 rotis divided among 5 children is the same as____rotis divided among _____ children. So, $\frac{7}{5}$ = $\frac{-}{-}$ .
Answer:
a. 5 glasses of juice shared equally among 4 friends...
The amount of juice each friend gets is represented by the fraction $\frac{5}{4}$.
We need to find an equivalent fraction with a denominator of 8.
$\frac{5}{4} = \frac{?}{8}$
To change the denominator from 4 to 8, we multiply by 2 ($4 \times 2 = 8$). To keep the fraction equivalent, we must also multiply the numerator by 2.
$5 \times 2 = 10$
So, the equivalent fraction is $\frac{10}{8}$.
Answer: 5 glasses of juice shared equally among 4 friends is the same as 10 glasses of juice shared equally among 8 friends. So, $\frac{5}{4} = \frac{10}{8}$.
b. 4 kg of potatoes divided equally in 3 bags...
The amount of potatoes in each bag is represented by the fraction $\frac{4}{3}$.
We need to find an equivalent fraction with a numerator of 12.
$\frac{4}{3} = \frac{12}{?}$
To change the numerator from 4 to 12, we multiply by 3 ($4 \times 3 = 12$). To keep the fraction equivalent, we must also multiply the denominator by 3.
$3 \times 3 = 9$
So, the equivalent fraction is $\frac{12}{9}$.
Answer: 4 kg of potatoes divided equally in 3 bags is the same as 12 kgs of potatoes divided equally in 9 bags. So, $\frac{4}{3} = \frac{12}{9}$.
c. 7 rotis divided among 5 children...
The amount of roti each child gets is represented by the fraction $\frac{7}{5}$.
We need to find an equivalent fraction. We can do this by multiplying the numerator and denominator by the same whole number. Let's choose to multiply by 2.
Multiply the numerator by 2: $7 \times 2 = 14$.
Multiply the denominator by 2: $5 \times 2 = 10$.
So, an equivalent fraction is $\frac{14}{10}$. This represents 14 rotis divided among 10 children.
Answer: 7 rotis divided among 5 children is the same as 14 rotis divided among 10 children. So, $\frac{7}{5} = \frac{14}{10}$. (Note: Other answers are possible, such as $\frac{21}{15}$ by multiplying by 3.)
Intext Question (Page 169)
Question: In which group will each child get more chikki?
1 chikki divided between 2 children or 5 chikkis divided among 8 children.
Answer:
To Find:
Which situation provides a larger share of chikki per child: 1 chikki for 2 children, or 5 chikkis for 8 children.
Solution:
First, we need to represent the share each child gets in both scenarios as a fraction.
Scenario 1: 1 chikki divided between 2 children.
The fraction of chikki each child gets is $\frac{\text{Number of chikkis}}{\text{Number of children}} = \frac{1}{2}$.
Scenario 2: 5 chikkis divided among 8 children.
The fraction of chikki each child gets is $\frac{\text{Number of chikkis}}{\text{Number of children}} = \frac{5}{8}$.
Now, we need to compare the two fractions: $\frac{1}{2}$ and $\frac{5}{8}$.
To compare them, we can find a common denominator. The least common multiple (LCM) of the denominators 2 and 8 is 8.
The fraction $\frac{5}{8}$ already has the denominator 8. We need to convert $\frac{1}{2}$ to an equivalent fraction with a denominator of 8.
$\frac{1}{2} = \frac{1 \times 4}{2 \times 4} = \frac{4}{8}$
Now we compare the two fractions: $\frac{4}{8}$ and $\frac{5}{8}$.
Since the denominators are the same, we can compare the numerators. We see that $5 > 4$.
Therefore, $\frac{5}{8} > \frac{4}{8}$
This means that the share in the second scenario is larger.
Alternate Solution (Using Decimals):
We can convert both fractions to decimals and compare them.
For Scenario 1: $\frac{1}{2} = 1 \div 2 = 0.5$
For Scenario 2: $\frac{5}{8} = 5 \div 8 = 0.625$
Comparing the decimals, we see that $0.625 > 0.5$.
This confirms that the share in the second scenario is larger.
Answer:
Each child will get more chikki in the group where 5 chikkis are divided among 8 children.
Intext Question (Page 169)
Question: What about the following groups? In which group will each child get more?
1 chikki divided between 2 children or 4 chikkis divided among 7 children.
Answer:
To Find:
Which scenario provides a larger share of chikki per child: 1 chikki for 2 children, or 4 chikkis for 7 children.
Solution:
First, we write the fraction representing the share each child gets in both groups.
Group 1: 1 chikki divided between 2 children.
The share per child is $\frac{\text{Number of chikkis}}{\text{Number of children}} = \frac{1}{2}$.
Group 2: 4 chikkis divided among 7 children.
The share per child is $\frac{\text{Number of chikkis}}{\text{Number of children}} = \frac{4}{7}$.
Now, we need to compare the fractions $\frac{1}{2}$ and $\frac{4}{7}$.
To compare these fractions, we can convert them to equivalent fractions with a common denominator. The least common multiple (LCM) of the denominators 2 and 7 is 14.
Convert $\frac{1}{2}$ to an equivalent fraction with a denominator of 14:
$\frac{1}{2} = \frac{1 \times 7}{2 \times 7} = \frac{7}{14}$
Convert $\frac{4}{7}$ to an equivalent fraction with a denominator of 14:
$\frac{4}{7} = \frac{4 \times 2}{7 \times 2} = \frac{8}{14}$
Now we compare the numerators of $\frac{7}{14}$ and $\frac{8}{14}$.
Since $8 > 7$, it means that $\frac{8}{14}$ is greater than $\frac{7}{14}$.
Therefore, $\frac{4}{7} > \frac{1}{2}$.
Alternate Solution (Cross-Multiplication):
We can compare $\frac{1}{2}$ and $\frac{4}{7}$ by cross-multiplying.
Multiply the numerator of the first fraction by the denominator of the second: $1 \times 7 = 7$.
Multiply the numerator of the second fraction by the denominator of the first: $4 \times 2 = 8$.
Since the second product (8) is greater than the first product (7), the second fraction ($\frac{4}{7}$) is the larger one.
Answer:
Each child will get more chikki in the group where 4 chikkis are divided among 7 children.
Intext Question (Page 170)
Question: Suppose the number of children is kept the same, but the number of units that are being shared is increased? What can you say about each child’s share now? Why? Discuss how your reasoning explains
$\frac{1}{5}$ < $\frac{2}{5}$ , $\frac{3}{7}$ < $\frac{4}{7}$ , and $\frac{1}{2}$ < $\frac{5}{8}$ .
Answer:
The General Principle
If the number of children is kept the same, but the number of units being shared is increased, then each child’s share will increase.
Why?
In fractions, the number of children represents the denominator (the number of equal parts a whole is divided into), and the number of units being shared represents the numerator (the number of those parts being considered).
When the denominator is kept the same, the size of each individual part does not change. If we increase the numerator, we are simply giving each person more of those same-sized parts. Therefore, the total share for each person becomes larger.
Applying the Reasoning to the Examples
1. Explaining $\frac{1}{5} < \frac{2}{5}$
This comparison represents sharing among 5 children (the denominator is 5 in both fractions). The first case shares 1 unit, and the second case shares 2 units. Since the number of units increased from 1 to 2 while the number of children remained 5, each child gets a larger share in the second case. This is why $\frac{1}{5}$ is less than $\frac{2}{5}$.
2. Explaining $\frac{3}{7} < \frac{4}{7}$
This comparison represents sharing among 7 children (the denominator is 7 in both fractions). The number of units being shared increases from 3 to 4. Because more units are being shared among the same number of children, each child's share is larger. This explains why $\frac{3}{7}$ is less than $\frac{4}{7}$.
3. Explaining $\frac{1}{2} < \frac{5}{8}$
In this case, our initial reasoning does not apply directly because both the number of units (numerator) and the number of children (denominator) are different.
However, we can use our reasoning after we make the number of children (the denominator) the same. To do this, we find a common denominator for $\frac{1}{2}$ and $\frac{5}{8}$. The common denominator is 8.
We convert $\frac{1}{2}$ to an equivalent fraction with a denominator of 8:
$\frac{1}{2} = \frac{1 \times 4}{2 \times 4} = \frac{4}{8}$
Now, the original comparison $\frac{1}{2} < \frac{5}{8}$ becomes a comparison between $\frac{4}{8}$ and $\frac{5}{8}$.
At this point, our reasoning applies perfectly: we are comparing a situation where 4 units are shared among 8 children ($\frac{4}{8}$) with a situation where 5 units are shared among the same 8 children ($\frac{5}{8}$). Since the number of units increased from 4 to 5, the share is larger. Thus, $\frac{4}{8} < \frac{5}{8}$, which confirms that the original statement $\frac{1}{2} < \frac{5}{8}$ is correct.
Intext Question (Page 170)
Question: Now, decide in which of the two groups will each child get a larger share:
1. Group 1: 3 glasses of sugarcane juice divided equally among 4 children.
Group 2: 7 glasses of sugarcane juice divided equally among 10 children.
2. Group 1: 4 glasses of sugarcane juice divided equally among 7 children.
Group 2: 5 glasses of sugarcane juice divided equally among 7 children.
Answer:
Problem 1:
Group 1: 3 glasses of juice for 4 children. The share per child is $\frac{3}{4}$.
Group 2: 7 glasses of juice for 10 children. The share per child is $\frac{7}{10}$.
Comparison: We need to compare $\frac{3}{4}$ and $\frac{7}{10}$.
To compare, we find a common denominator. The least common multiple (LCM) of 4 and 10 is 20.
Convert $\frac{3}{4}$ to an equivalent fraction with a denominator of 20:
$\frac{3}{4} = \frac{3 \times 5}{4 \times 5} = \frac{15}{20}$
Convert $\frac{7}{10}$ to an equivalent fraction with a denominator of 20:
$\frac{7}{10} = \frac{7 \times 2}{10 \times 2} = \frac{14}{20}$
Since $15 > 14$, we have $\frac{15}{20} > \frac{14}{20}$. Therefore, $\frac{3}{4} > \frac{7}{10}$.
Conclusion for Problem 1: Each child will get a larger share in Group 1.
Problem 2:
Group 1: 4 glasses of juice for 7 children. The share per child is $\frac{4}{7}$.
Group 2: 5 glasses of juice for 7 children. The share per child is $\frac{5}{7}$.
Comparison: We need to compare $\frac{4}{7}$ and $\frac{5}{7}$.
In this case, the denominators are the same (the number of children is 7 in both groups). When the denominators are the same, the fraction with the larger numerator is the greater fraction.
Since $5 > 4$, we have $\frac{5}{7} > \frac{4}{7}$.
This is because more glasses of juice are being shared among the same number of children, so each child's share is larger.
Conclusion for Problem 2: Each child will get a larger share in Group 2.
Intext Question (Page 172)
Question: Find equivalent fractions for the given pairs of fractions such that the fractional units are the same.
a. $\frac{7}{2}$ and $\frac{3}{5}$
b. $\frac{8}{3}$ and $\frac{5}{6}$
c. $\frac{3}{4}$ and $\frac{3}{5}$
d. $\frac{6}{7}$ and $\frac{8}{5}$
e. $\frac{9}{4}$ and $\frac{5}{2}$
f. $\frac{1}{10}$ and $\frac{2}{9}$
g. $\frac{8}{3}$ and $\frac{11}{4}$
h. $\frac{13}{6}$ and $\frac{1}{9}$
Answer:
To find equivalent fractions with the same fractional unit, we need to rewrite the fractions with a common denominator. The least common denominator (LCD) is the least common multiple (LCM) of the denominators.
a. Given fractions are $\frac{7}{2}$ and $\frac{3}{5}$.
Denominators are 2 and 5.
LCM(2, 5) = 10.
Convert $\frac{7}{2}$ to an equivalent fraction with denominator 10:
$\frac{7}{2} = \frac{7 \times 5}{2 \times 5} = \frac{35}{10}$
Convert $\frac{3}{5}$ to an equivalent fraction with denominator 10:
$\frac{3}{5} = \frac{3 \times 2}{5 \times 2} = \frac{6}{10}$
The equivalent fractions with the same fractional unit are $\frac{35}{10}$ and $\frac{6}{10}$.
b. Given fractions are $\frac{8}{3}$ and $\frac{5}{6}$.
Denominators are 3 and 6.
LCM(3, 6) = 6.
Convert $\frac{8}{3}$ to an equivalent fraction with denominator 6:
$\frac{8}{3} = \frac{8 \times 2}{3 \times 2} = \frac{16}{6}$
The fraction $\frac{5}{6}$ already has the denominator 6.
The equivalent fractions with the same fractional unit are $\frac{16}{6}$ and $\frac{5}{6}$.
c. Given fractions are $\frac{3}{4}$ and $\frac{3}{5}$.
Denominators are 4 and 5.
LCM(4, 5) = 20.
Convert $\frac{3}{4}$ to an equivalent fraction with denominator 20:
$\frac{3}{4} = \frac{3 \times 5}{4 \times 5} = \frac{15}{20}$
Convert $\frac{3}{5}$ to an equivalent fraction with denominator 20:
$\frac{3}{5} = \frac{3 \times 4}{5 \times 4} = \frac{12}{20}$
The equivalent fractions with the same fractional unit are $\frac{15}{20}$ and $\frac{12}{20}$.
d. Given fractions are $\frac{6}{7}$ and $\frac{8}{5}$.
Denominators are 7 and 5.
LCM(7, 5) = 35.
Convert $\frac{6}{7}$ to an equivalent fraction with denominator 35:
$\frac{6}{7} = \frac{6 \times 5}{7 \times 5} = \frac{30}{35}$
Convert $\frac{8}{5}$ to an equivalent fraction with denominator 35:
$\frac{8}{5} = \frac{8 \times 7}{5 \times 7} = \frac{56}{35}$
The equivalent fractions with the same fractional unit are $\frac{30}{35}$ and $\frac{56}{35}$.
e. Given fractions are $\frac{9}{4}$ and $\frac{5}{2}$.
Denominators are 4 and 2.
LCM(4, 2) = 4.
The fraction $\frac{9}{4}$ already has the denominator 4.
Convert $\frac{5}{2}$ to an equivalent fraction with denominator 4:
$\frac{5}{2} = \frac{5 \times 2}{2 \times 2} = \frac{10}{4}$
The equivalent fractions with the same fractional unit are $\frac{9}{4}$ and $\frac{10}{4}$.
f. Given fractions are $\frac{1}{10}$ and $\frac{2}{9}$.
Denominators are 10 and 9.
LCM(10, 9) = 90.
Convert $\frac{1}{10}$ to an equivalent fraction with denominator 90:
$\frac{1}{10} = \frac{1 \times 9}{10 \times 9} = \frac{9}{90}$
Convert $\frac{2}{9}$ to an equivalent fraction with denominator 90:
$\frac{2}{9} = \frac{2 \times 10}{9 \times 10} = \frac{20}{90}$
The equivalent fractions with the same fractional unit are $\frac{9}{90}$ and $\frac{20}{90}$.
g. Given fractions are $\frac{8}{3}$ and $\frac{11}{4}$.
Denominators are 3 and 4.
LCM(3, 4) = 12.
Convert $\frac{8}{3}$ to an equivalent fraction with denominator 12:
$\frac{8}{3} = \frac{8 \times 4}{3 \times 4} = \frac{32}{12}$
Convert $\frac{11}{4}$ to an equivalent fraction with denominator 12:
$\frac{11}{4} = \frac{11 \times 3}{4 \times 3} = \frac{33}{12}$
The equivalent fractions with the same fractional unit are $\frac{32}{12}$ and $\frac{33}{12}$.
h. Given fractions are $\frac{13}{6}$ and $\frac{1}{9}$.
Denominators are 6 and 9.
LCM(6, 9) = 18.
Convert $\frac{13}{6}$ to an equivalent fraction with denominator 18:
$\frac{13}{6} = \frac{13 \times 3}{6 \times 3} = \frac{39}{18}$
Convert $\frac{1}{9}$ to an equivalent fraction with denominator 18:
$\frac{1}{9} = \frac{1 \times 2}{9 \times 2} = \frac{2}{18}$
The equivalent fractions with the same fractional unit are $\frac{39}{18}$ and $\frac{2}{18}$.
Figure it Out (Page 173)
Express the following fractions in lowest terms:
a. $\frac{17}{51}$
b. $\frac{64}{144}$
c. $\frac{126}{147}$
d. $\frac{525}{112}$
Answer:
To express a fraction in its lowest terms, we divide both the numerator and the denominator by their greatest common divisor (GCD).
a. Given fraction is $\frac{17}{51}$.
We find the GCD of the numerator 17 and the denominator 51.
17 is a prime number.
We check if 51 is divisible by 17: $51 = 17 \times 3$.
So, the GCD(17, 51) = 17.
Divide the numerator and denominator by 17:
$\frac{17 \div 17}{51 \div 17} = \frac{1}{3}$
The lowest term of $\frac{17}{51}$ is $\frac{1}{3}$.
b. Given fraction is $\frac{64}{144}$.
We find the GCD of 64 and 144.
Using prime factorization:
$64 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 = 2^6$
$144 = 2 \times 72 = 2 \times 2 \times 36 = 2 \times 2 \times 2 \times 18 = 2 \times 2 \times 2 \times 2 \times 9 \ $$ = 2^4 \times 3^2$
GCD(64, 144) = $2^4 = 16$.
Divide the numerator and denominator by 16:
$\frac{64 \div 16}{144 \div 16} = \frac{4}{9}$
The lowest term of $\frac{64}{144}$ is $\frac{4}{9}$.
c. Given fraction is $\frac{126}{147}$.
We find the GCD of 126 and 147.
Using prime factorization:
$126 = 2 \times 63 = 2 \times 3 \times 21 = 2 \times 3 \times 3 \times 7 = 2 \times 3^2 \times 7$
$147 = 3 \times 49 = 3 \times 7 \times 7 = 3 \times 7^2$
GCD(126, 147) = $3 \times 7 = 21$.
Divide the numerator and denominator by 21:
$\frac{126 \div 21}{147 \div 21} = \frac{6}{7}$
The lowest term of $\frac{126}{147}$ is $\frac{6}{7}$.
d. Given fraction is $\frac{525}{112}$.
We find the GCD of 525 and 112.
Using prime factorization:
$525 = 5 \times 105 = 5 \times 5 \times 21 = 3 \times 5^2 \times 7$
$112 = 2 \times 56 = 2 \times 2 \times 28 = 2 \times 2 \times 2 \times 14 = 2 \times 2 \times 2 \times 2 \times 7 \ $$ = 2^4 \times 7$
GCD(525, 112) = $7$.
Divide the numerator and denominator by 7:
$\frac{525 \div 7}{112 \div 7} = \frac{75}{16}$
The lowest term of $\frac{525}{112}$ is $\frac{75}{16}$.
Figure it Out (Page 174)
Question 1. Compare the following fractions and justify your answers:
a. $\frac{8}{3}$ , $\frac{5}{2}$
b. $\frac{4}{9}$ , $\frac{3}{7}$
c. $\frac{7}{10}$ , $\frac{9}{14}$
d. $\frac{12}{5}$ , $\frac{8}{5}$
e. $\frac{9}{4}$ , $\frac{5}{2}$
Answer:
To compare fractions, we can find a common denominator and then compare the numerators, or if the denominators are already the same, we just compare the numerators directly.
a. Compare $\frac{8}{3}$ and $\frac{5}{2}$.
The denominators are 3 and 2. The least common multiple (LCM) of 3 and 2 is 6.
Convert $\frac{8}{3}$ to an equivalent fraction with denominator 6:
$\frac{8}{3} = \frac{8 \times 2}{3 \times 2} = \frac{16}{6}$
Convert $\frac{5}{2}$ to an equivalent fraction with denominator 6:
$\frac{5}{2} = \frac{5 \times 3}{2 \times 3} = \frac{15}{6}$
Now compare $\frac{16}{6}$ and $\frac{15}{6}$. Since the denominators are the same, we compare the numerators. $16 > 15$.
Therefore, $\frac{16}{6} > \frac{15}{6}$, which means $\frac{8}{3} > \frac{5}{2}$.
Justification: We converted both fractions to equivalent fractions with a common denominator (6) and compared their numerators. $16 > 15$, so $\frac{8}{3}$ is greater than $\frac{5}{2}$.
b. Compare $\frac{4}{9}$ and $\frac{3}{7}$.
The denominators are 9 and 7. The LCM of 9 and 7 is 63.
Convert $\frac{4}{9}$ to an equivalent fraction with denominator 63:
$\frac{4}{9} = \frac{4 \times 7}{9 \times 7} = \frac{28}{63}$
Convert $\frac{3}{7}$ to an equivalent fraction with denominator 63:
$\frac{3}{7} = \frac{3 \times 9}{7 \times 9} = \frac{27}{63}$
Now compare $\frac{28}{63}$ and $\frac{27}{63}$. Since the denominators are the same, we compare the numerators. $28 > 27$.
Therefore, $\frac{28}{63} > \frac{27}{63}$, which means $\frac{4}{9} > \frac{3}{7}$.
Justification: We converted both fractions to equivalent fractions with a common denominator (63) and compared their numerators. $28 > 27$, so $\frac{4}{9}$ is greater than $\frac{3}{7}$.
c. Compare $\frac{7}{10}$ and $\frac{9}{14}$.
The denominators are 10 and 14. The LCM of 10 and 14 is 70.
Convert $\frac{7}{10}$ to an equivalent fraction with denominator 70:
$\frac{7}{10} = \frac{7 \times 7}{10 \times 7} = \frac{49}{70}$
Convert $\frac{9}{14}$ to an equivalent fraction with denominator 70:
$\frac{9}{14} = \frac{9 \times 5}{14 \times 5} = \frac{45}{70}$
Now compare $\frac{49}{70}$ and $\frac{45}{70}$. Since the denominators are the same, we compare the numerators. $49 > 45$.
Therefore, $\frac{49}{70} > \frac{45}{70}$, which means $\frac{7}{10} > \frac{9}{14}$.
Justification: We converted both fractions to equivalent fractions with a common denominator (70) and compared their numerators. $49 > 45$, so $\frac{7}{10}$ is greater than $\frac{9}{14}$.
d. Compare $\frac{12}{5}$ and $\frac{8}{5}$.
The denominators are 5 and 5. They are the same.
Compare the numerators: 12 and 8. $12 > 8$.
Therefore, $\frac{12}{5} > \frac{8}{5}$.
Justification: Since the fractions have the same denominator, the fraction with the larger numerator is greater. $12 > 8$, so $\frac{12}{5}$ is greater than $\frac{8}{5}$.
e. Compare $\frac{9}{4}$ and $\frac{5}{2}$.
The denominators are 4 and 2. The LCM of 4 and 2 is 4.
The fraction $\frac{9}{4}$ already has the denominator 4.
Convert $\frac{5}{2}$ to an equivalent fraction with denominator 4:
$\frac{5}{2} = \frac{5 \times 2}{2 \times 2} = \frac{10}{4}$
Now compare $\frac{9}{4}$ and $\frac{10}{4}$. Since the denominators are the same, we compare the numerators. $9 < 10$.
Therefore, $\frac{9}{4} < \frac{10}{4}$, which means $\frac{9}{4} < \frac{5}{2}$.
Justification: We converted $\frac{5}{2}$ to an equivalent fraction with a common denominator (4) and compared the numerators. $9 < 10$, so $\frac{9}{4}$ is less than $\frac{5}{2}$.
Question 2. Write the following fractions in ascending order.
a. $\frac{7}{10}$ , $\frac{11}{15}$ , $\frac{2}{5}$
b. $\frac{19}{24}$ , $\frac{5}{6}$ , $\frac{7}{12}$
Answer:
To write fractions in ascending order, we first find a common denominator for all the fractions and then compare their numerators.
a. Given fractions are $\frac{7}{10}$, $\frac{11}{15}$, and $\frac{2}{5}$.
The denominators are 10, 15, and 5.
The least common multiple (LCM) of 10, 15, and 5 is 30.
Convert each fraction to an equivalent fraction with denominator 30:
For $\frac{7}{10}$: $\frac{7}{10} = \frac{7 \times 3}{10 \times 3} = \frac{21}{30}$
For $\frac{11}{15}$: $\frac{11}{15} = \frac{11 \times 2}{15 \times 2} = \frac{22}{30}$
For $\frac{2}{5}$: $\frac{2}{5} = \frac{2 \times 6}{5 \times 6} = \frac{12}{30}$
Now we compare the numerators of the equivalent fractions: 21, 22, and 12.
Arranging the numerators in ascending order: $12 < 21 < 22$.
This corresponds to the fractions: $\frac{12}{30} < \frac{21}{30} < \frac{22}{30}$.
Replacing with the original fractions:
$\frac{2}{5} < \frac{7}{10} < \frac{11}{15}$.
The fractions in ascending order are $\frac{2}{5}$, $\frac{7}{10}$, $\frac{11}{15}$.
b. Given fractions are $\frac{19}{24}$, $\frac{5}{6}$, and $\frac{7}{12}$.
The denominators are 24, 6, and 12.
The least common multiple (LCM) of 24, 6, and 12 is 24.
Convert each fraction to an equivalent fraction with denominator 24:
The fraction $\frac{19}{24}$ already has the denominator 24.
For $\frac{5}{6}$: $\frac{5}{6} = \frac{5 \times 4}{6 \times 4} = \frac{20}{24}$
For $\frac{7}{12}$: $\frac{7}{12} = \frac{7 \times 2}{12 \times 2} = \frac{14}{24}$
Now we compare the numerators of the equivalent fractions: 19, 20, and 14.
Arranging the numerators in ascending order: $14 < 19 < 20$.
This corresponds to the fractions: $\frac{14}{24} < \frac{19}{24} < \frac{20}{24}$.
Replacing with the original fractions:
$\frac{7}{12} < \frac{19}{24} < \frac{5}{6}$.
The fractions in ascending order are $\frac{7}{12}$, $\frac{19}{24}$, $\frac{5}{6}$.
Question 3. Write the following fractions in descending order.
a. $\frac{25}{16}$ , $\frac{7}{8}$ , $\frac{13}{4}$ , $\frac{17}{32}$
b. $\frac{3}{4}$ , $\frac{12}{5}$ , $\frac{7}{12}$ , $\frac{5}{4}$
Answer:
To write fractions in descending order, we need to find a common denominator for all the fractions and then compare their numerators.
a. Given fractions are $\frac{25}{16}$, $\frac{7}{8}$, $\frac{13}{4}$, and $\frac{17}{32}$.
The denominators are 16, 8, 4, and 32.
The least common multiple (LCM) of 16, 8, 4, and 32 is 32.
Convert each fraction to an equivalent fraction with a denominator of 32:
For $\frac{25}{16}$: $\frac{25}{16} = \frac{25 \times 2}{16 \times 2} = \frac{50}{32}$
For $\frac{7}{8}$: $\frac{7}{8} = \frac{7 \times 4}{8 \times 4} = \frac{28}{32}$
For $\frac{13}{4}$: $\frac{13}{4} = \frac{13 \times 8}{4 \times 8} = \frac{104}{32}$
For $\frac{17}{32}$: This fraction already has the denominator 32.
The equivalent fractions are $\frac{50}{32}$, $\frac{28}{32}$, $\frac{104}{32}$, and $\frac{17}{32}$.
Now we compare the numerators: 50, 28, 104, and 17.
Arranging the numerators in descending order: $104 > 50 > 28 > 17$.
This corresponds to the fractions in descending order:
$\frac{104}{32} > \frac{50}{32} > \frac{28}{32} > \frac{17}{32}$
Replacing with the original fractions:
$\frac{13}{4} > \frac{25}{16} > \frac{7}{8} > \frac{17}{32}$.
The fractions in descending order are $\frac{13}{4}$, $\frac{25}{16}$, $\frac{7}{8}$, $\frac{17}{32}$.
b. Given fractions are $\frac{3}{4}$, $\frac{12}{5}$, $\frac{7}{12}$, and $\frac{5}{4}$.
The denominators are 4, 5, 12, and 4. The unique denominators are 4, 5, and 12.
The least common multiple (LCM) of 4, 5, and 12 is 60.
$\begin{array}{c|cc} 2 & 4 \;, & 5 \;, & 12 \\ \hline 2 & 2 \; , & 5 \; , & 6 \\ \hline 3 & 1 \; , & 5 \; , & 3 \\ \hline 5 & 1 \; , & 1 \; , & 1 \\ \hline & 1 \; , & 1 \; , & 1 \end{array}$
LCM = $2 \times 2 \times 3 \times 5 = 60$.
Convert each fraction to an equivalent fraction with a denominator of 60:
For $\frac{3}{4}$: $\frac{3}{4} = \frac{3 \times 15}{4 \times 15} = \frac{45}{60}$
For $\frac{12}{5}$: $\frac{12}{5} = \frac{12 \times 12}{5 \times 12} = \frac{144}{60}$
For $\frac{7}{12}$: $\frac{7}{12} = \frac{7 \times 5}{12 \times 5} = \frac{35}{60}$
For $\frac{5}{4}$: $\frac{5}{4} = \frac{5 \times 15}{4 \times 15} = \frac{75}{60}$
The equivalent fractions are $\frac{45}{60}$, $\frac{144}{60}$, $\frac{35}{60}$, and $\frac{75}{60}$.
Now we compare the numerators: 45, 144, 35, and 75.
Arranging the numerators in descending order: $144 > 75 > 45 > 35$.
This corresponds to the fractions in descending order:
$\frac{144}{60} > \frac{75}{60} > \frac{45}{60} > \frac{35}{60}$
Replacing with the original fractions:
$\frac{12}{5} > \frac{5}{4} > \frac{3}{4} > \frac{7}{12}$.
The fractions in descending order are $\frac{12}{5}$, $\frac{5}{4}$, $\frac{3}{4}$, $\frac{7}{12}$.
Intext Question (Page 177)
Question: Try adding $\frac{4}{7}$ + $\frac{6}{7}$ using a number line. Do you get the same answer?
Answer:
To Do:
1. Add the fractions $\frac{4}{7}$ and $\frac{6}{7}$ using a number line.
2. Compare this result with the answer from the standard method of adding fractions.
Solution using a Number Line:
Step 1: Set up the Number Line
The fractions have a denominator of 7, so we need to divide our number line into units of $\frac{1}{7}$. Since the sum will be $\frac{4+6}{7} = \frac{10}{7}$, which is greater than 1, our number line should extend past 1, for example, up to 2.
We draw a number line and mark whole numbers 0, 1, and 2. Then, we divide the segment between 0 and 1 into 7 equal parts, and the segment between 1 and 2 also into 7 equal parts. The marks will represent fractions $\frac{1}{7}, \frac{2}{7}, \frac{3}{7}, \dots, \frac{7}{7} (=1), \frac{8}{7}, \frac{9}{7}, \dots, \frac{14}{7} (=2)$.
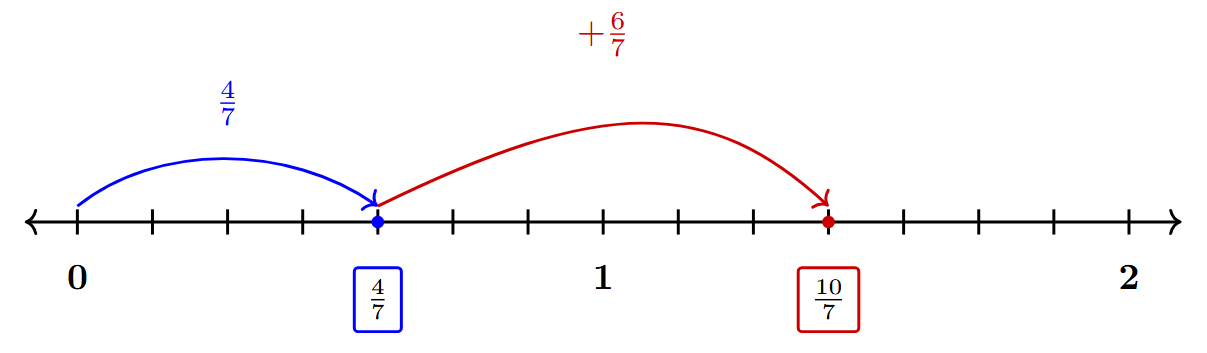
Step 2: Perform the Addition
1. To represent the first fraction, $\frac{4}{7}$, we start at 0 and move 4 units to the right. This lands us on the point marked $\frac{4}{7}$.
2. To add $\frac{6}{7}$, we start from our current position, $\frac{4}{7}$, and move another 6 units to the right.
3. Counting these 6 steps from $\frac{4}{7}$, we land on the points $\frac{5}{7}, \frac{6}{7}, \frac{7}{7}, \frac{8}{7}, \frac{9}{7}$, and finally $\frac{10}{7}$.
The final point on the number line is $\frac{10}{7}$.
Standard Calculation:
When adding fractions with the same denominator, we add their numerators and keep the denominator unchanged.
$\frac{4}{7} + \frac{6}{7} = \frac{4+6}{7} = \frac{10}{7}$
Conclusion:
Yes, you get the same answer. Both the number line method and the standard calculation give the result $\frac{10}{7}$.
This improper fraction can also be written as a mixed number: $1\frac{3}{7}$.
Figure it Out (Page 179)
Question 1. Add the following fractions using Brahmagupta’s method:
a. $\frac{2}{7}$ + $\frac{5}{7}$ + $\frac{6}{7}$
b. $\frac{3}{4}$ + $\frac{1}{3}$
c. $\frac{2}{3}$ + $\frac{5}{6}$
d. $\frac{2}{3}$ + $\frac{2}{7}$
e. $\frac{3}{4}$ + $\frac{1}{3}$ + $\frac{1}{5}$
f. $\frac{2}{3}$ + $\frac{4}{5}$
g. $\frac{4}{5}$ + $\frac{2}{3}$
h. $\frac{3}{5}$ + $\frac{5}{8}$
i. $\frac{9}{2}$ + $\frac{5}{4}$
j. $\frac{8}{3}$ + $\frac{2}{7}$
k. $\frac{3}{4}$ + $\frac{1}{3}$ + $\frac{1}{5}$
l. $\frac{2}{3}$ + $\frac{4}{5}$ + $\frac{3}{7}$
m. $\frac{9}{2}$ + $\frac{5}{4}$ + $\frac{7}{6}$
Answer:
Brahmagupta's method for adding fractions $\frac{a}{b}$ and $\frac{c}{d}$ gives the sum as $\frac{ad + bc}{bd}$. This method relies on finding a common denominator, which is the product of the denominators or their least common multiple (LCM). We will use the general method of finding the LCM of the denominators, which is equivalent to Brahmagupta's principle.
a. Add $\frac{2}{7}$ + $\frac{5}{7}$ + $\frac{6}{7}$.
The fractions have the same denominator (7).
Add the numerators and keep the common denominator:
$\frac{2}{7} + \frac{5}{7} + \frac{6}{7} = \frac{2+5+6}{7} = \frac{13}{7}$
The sum is $\frac{13}{7}$.
b. Add $\frac{3}{4}$ + $\frac{1}{3}$.
The denominators are 4 and 3. The LCM(4, 3) = 12.
Convert fractions to equivalent fractions with denominator 12:
$\frac{3}{4} = \frac{3 \times 3}{4 \times 3} = \frac{9}{12}$
$\frac{1}{3} = \frac{1 \times 4}{3 \times 4} = \frac{4}{12}$
Add the equivalent fractions:
$\frac{9}{12} + \frac{4}{12} = \frac{9+4}{12} = \frac{13}{12}$
The sum is $\frac{13}{12}$.
c. Add $\frac{2}{3}$ + $\frac{5}{6}$.
The denominators are 3 and 6. The LCM(3, 6) = 6.
Convert fractions to equivalent fractions with denominator 6:
$\frac{2}{3} = \frac{2 \times 2}{3 \times 2} = \frac{4}{6}$
The fraction $\frac{5}{6}$ already has the denominator 6.
Add the equivalent fractions:
$\frac{4}{6} + \frac{5}{6} = \frac{4+5}{6} = \frac{9}{6}$
Simplify the result:
$\frac{9}{6} = \frac{\cancel{9}^{3}}{\cancel{6}_{2}} = \frac{3}{2}$
The sum is $\frac{3}{2}$.
d. Add $\frac{2}{3}$ + $\frac{2}{7}$.
The denominators are 3 and 7. The LCM(3, 7) = 21.
Convert fractions to equivalent fractions with denominator 21:
$\frac{2}{3} = \frac{2 \times 7}{3 \times 7} = \frac{14}{21}$
$\frac{2}{7} = \frac{2 \times 3}{7 \times 3} = \frac{6}{21}$
Add the equivalent fractions:
$\frac{14}{21} + \frac{6}{21} = \frac{14+6}{21} = \frac{20}{21}$
The sum is $\frac{20}{21}$.
e. Add $\frac{3}{4}$ + $\frac{1}{3}$ + $\frac{1}{5}$.
The denominators are 4, 3, and 5. The LCM(4, 3, 5) = 60.
Convert fractions to equivalent fractions with denominator 60:
$\frac{3}{4} = \frac{3 \times 15}{4 \times 15} = \frac{45}{60}$
$\frac{1}{3} = \frac{1 \times 20}{3 \times 20} = \frac{20}{60}$
$\frac{1}{5} = \frac{1 \times 12}{5 \times 12} = \frac{12}{60}$
Add the equivalent fractions:
$\frac{45}{60} + \frac{20}{60} + \frac{12}{60} = \frac{45+20+12}{60} = \frac{77}{60}$
The sum is $\frac{77}{60}$.
f. Add $\frac{2}{3}$ + $\frac{4}{5}$.
The denominators are 3 and 5. The LCM(3, 5) = 15.
Convert fractions to equivalent fractions with denominator 15:
$\frac{2}{3} = \frac{2 \times 5}{3 \times 5} = \frac{10}{15}$
$\frac{4}{5} = \frac{4 \times 3}{5 \times 3} = \frac{12}{15}$
Add the equivalent fractions:
$\frac{10}{15} + \frac{12}{15} = \frac{10+12}{15} = \frac{22}{15}$
The sum is $\frac{22}{15}$.
g. Add $\frac{4}{5}$ + $\frac{2}{3}$.
This is the same addition problem as in part f, just with the fractions in a different order. Addition is commutative.
The sum is $\frac{22}{15}$.
h. Add $\frac{3}{5}$ + $\frac{5}{8}$.
The denominators are 5 and 8. The LCM(5, 8) = 40.
Convert fractions to equivalent fractions with denominator 40:
$\frac{3}{5} = \frac{3 \times 8}{5 \times 8} = \frac{24}{40}$
$\frac{5}{8} = \frac{5 \times 5}{8 \times 5} = \frac{25}{40}$
Add the equivalent fractions:
$\frac{24}{40} + \frac{25}{40} = \frac{24+25}{40} = \frac{49}{40}$
The sum is $\frac{49}{40}$.
i. Add $\frac{9}{2}$ + $\frac{5}{4}$.
The denominators are 2 and 4. The LCM(2, 4) = 4.
Convert fractions to equivalent fractions with denominator 4:
$\frac{9}{2} = \frac{9 \times 2}{2 \times 2} = \frac{18}{4}$
The fraction $\frac{5}{4}$ already has the denominator 4.
Add the equivalent fractions:
$\frac{18}{4} + \frac{5}{4} = \frac{18+5}{4} = \frac{23}{4}$
The sum is $\frac{23}{4}$.
j. Add $\frac{8}{3}$ + $\frac{2}{7}$.
The denominators are 3 and 7. The LCM(3, 7) = 21.
Convert fractions to equivalent fractions with denominator 21:
$\frac{8}{3} = \frac{8 \times 7}{3 \times 7} = \frac{56}{21}$
$\frac{2}{7} = \frac{2 \times 3}{7 \times 3} = \frac{6}{21}$
Add the equivalent fractions:
$\frac{56}{21} + \frac{6}{21} = \frac{56+6}{21} = \frac{62}{21}$
The sum is $\frac{62}{21}$.
k. Add $\frac{3}{4}$ + $\frac{1}{3}$ + $\frac{1}{5}$.
This is the same addition problem as in part e.
The denominators are 4, 3, and 5. The LCM(4, 3, 5) = 60.
Equivalent fractions: $\frac{45}{60}$, $\frac{20}{60}$, $\frac{12}{60}$.
Add the equivalent fractions:
$\frac{45}{60} + \frac{20}{60} + \frac{12}{60} = \frac{45+20+12}{60} = \frac{77}{60}$
The sum is $\frac{77}{60}$.
l. Add $\frac{2}{3}$ + $\frac{4}{5}$ + $\frac{3}{7}$.
The denominators are 3, 5, and 7. The LCM(3, 5, 7) = $3 \times 5 \times 7 = 105$.
Convert fractions to equivalent fractions with denominator 105:
$\frac{2}{3} = \frac{2 \times 35}{3 \times 35} = \frac{70}{105}$
$\frac{4}{5} = \frac{4 \times 21}{5 \times 21} = \frac{84}{105}$
$\frac{3}{7} = \frac{3 \times 15}{7 \times 15} = \frac{45}{105}$
Add the equivalent fractions:
$\frac{70}{105} + \frac{84}{105} + \frac{45}{105} = \frac{70+84+45}{105} = \frac{199}{105}$
The sum is $\frac{199}{105}$.
m. Add $\frac{9}{2}$ + $\frac{5}{4}$ + $\frac{7}{6}$.
The denominators are 2, 4, and 6.
Find the LCM(2, 4, 6):
$\begin{array}{c|cc} 2 & 2 \;, & 4 \;, & 6 \\ \hline 2 & 1 \; , & 2 \; , & 3 \\ \hline 3 & 1 \; , & 1 \; , & 3 \\ \hline & 1 \; , & 1 \; , & 1 \end{array}$
LCM = $2 \times 2 \times 3 = 12$.
Convert fractions to equivalent fractions with denominator 12:
$\frac{9}{2} = \frac{9 \times 6}{2 \times 6} = \frac{54}{12}$
$\frac{5}{4} = \frac{5 \times 3}{4 \times 3} = \frac{15}{12}$
$\frac{7}{6} = \frac{7 \times 2}{6 \times 2} = \frac{14}{12}$
Add the equivalent fractions:
$\frac{54}{12} + \frac{15}{12} + \frac{14}{12} = \frac{54+15+14}{12} = \frac{83}{12}$
The sum is $\frac{83}{12}$.
Question 2. Rahim mixes $\frac{2}{3}$ litres of yellow paint with $\frac{3}{4}$ litres of blue paint to make green paint. What is the volume of green paint he has made?
Answer:
Given:
Volume of yellow paint = $\frac{2}{3}$ litres
Volume of blue paint = $\frac{3}{4}$ litres
To Find:
The total volume of green paint made.
Solution:
To find the total volume of green paint, we need to add the volume of yellow paint and the volume of blue paint.
Total volume = Volume of yellow paint + Volume of blue paint
Total volume = $\frac{2}{3} + \frac{3}{4}$
To add these fractions, we need to find a common denominator. The denominators are 3 and 4. The least common multiple (LCM) of 3 and 4 is 12.
Convert each fraction to an equivalent fraction with a denominator of 12:
$\frac{2}{3} = \frac{2 \times 4}{3 \times 4} = \frac{8}{12}$
$\frac{3}{4} = \frac{3 \times 3}{4 \times 3} = \frac{9}{12}$
Now, add the equivalent fractions:
Total volume = $\frac{8}{12} + \frac{9}{12}$
Add the numerators and keep the common denominator:
Total volume = $\frac{8 + 9}{12} = \frac{17}{12}$
The total volume of green paint made is $\frac{17}{12}$ litres.
This can also be expressed as a mixed number:
$\frac{17}{12} = 1 \frac{5}{12}$
Answer: Rahim has made $\frac{17}{12}$ litres (or $1 \frac{5}{12}$ litres) of green paint.
Question 3. Geeta bought $\frac{2}{5}$ meter of lace and Shamim bought $\frac{3}{4}$ meter of the same lace to put a complete border on a table cloth whose perimeter is 1 meter long. Find the total length of the lace they both have bought. Will the lace be sufficient to cover the whole border?
Answer:
Given:
Length of lace Geeta bought = $\frac{2}{5}$ meter
Length of lace Shamim bought = $\frac{3}{4}$ meter
Perimeter of the table cloth = 1 meter
To Find:
1. Total length of lace they both have bought.
2. Whether the lace is sufficient to cover the whole border.
Solution:
1. To find the total length of lace they both have bought, we need to add the length of lace Geeta bought and the length of lace Shamim bought.
Total length of lace = Length Geeta bought + Length Shamim bought
Total length of lace = $\frac{2}{5} + \frac{3}{4}$
To add these fractions, we need to find a common denominator. The denominators are 5 and 4. The least common multiple (LCM) of 5 and 4 is 20.
Convert each fraction to an equivalent fraction with a denominator of 20:
$\frac{2}{5} = \frac{2 \times 4}{5 \times 4} = \frac{8}{20}$
$\frac{3}{4} = \frac{3 \times 5}{4 \times 5} = \frac{15}{20}$
Now, add the equivalent fractions:
Total length of lace = $\frac{8}{20} + \frac{15}{20}$
Total length of lace = $\frac{8+15}{20} = \frac{23}{20}$ meters.
2. To determine if the lace is sufficient, we compare the total length of lace with the perimeter of the table cloth.
Total length of lace = $\frac{23}{20}$ meters
Perimeter of table cloth = 1 meter
We can write 1 meter as a fraction with denominator 20: $1 = \frac{20}{20}$.
Now compare $\frac{23}{20}$ and $\frac{20}{20}$.
Since the denominators are the same, we compare the numerators. $23 > 20$.
Therefore, $\frac{23}{20} > \frac{20}{20}$.
This means the total length of lace is greater than the perimeter of the table cloth.
So, the lace will be sufficient to cover the whole border.
Answer:
The total length of lace they both have bought is $\frac{23}{20}$ meters.
The lace will be sufficient to cover the whole border because $\frac{23}{20} \text{ meters} > 1 \text{ meter}$.
Figure it Out (Page 181)
Question 1. $\frac{5}{8}$ – $\frac{3}{8}$
Answer:
Given:
Subtraction problem: $\frac{5}{8} - \frac{3}{8}$
To Find:
The difference between the given fractions.
Solution:
The given fractions $\frac{5}{8}$ and $\frac{3}{8}$ have the same denominator, which is 8. These are like fractions.
To subtract like fractions, we subtract the numerators and keep the denominator the same.
$\frac{5}{8} - \frac{3}{8} = \frac{5 - 3}{8}$
Subtracting the numerators:
$5 - 3 = 2$
So, the difference is:
$\frac{2}{8}$
The resulting fraction can be simplified by dividing both the numerator and the denominator by their greatest common divisor (GCD).
The GCD of 2 and 8 is 2.
$\frac{2}{8} = \frac{2 \div 2}{8 \div 2} = \frac{1}{4}$
The difference is $\frac{1}{4}$.
Question 2. $\frac{7}{9}$ – $\frac{5}{9}$
Answer:
Given:
Subtraction problem: $\frac{7}{9} - \frac{5}{9}$
To Find:
The difference between the given fractions.
Solution:
The given fractions $\frac{7}{9}$ and $\frac{5}{9}$ have the same denominator, which is 9. These are like fractions.
To subtract like fractions, we subtract the numerators and keep the denominator the same.
$\frac{7}{9} - \frac{5}{9} = \frac{7 - 5}{9}$
Subtracting the numerators:
$7 - 5 = 2$
So, the difference is:
$\frac{2}{9}$
The fraction $\frac{2}{9}$ is already in its lowest terms because the greatest common divisor (GCD) of 2 and 9 is 1.
The difference is $\frac{2}{9}$.
Question 3. $\frac{10}{27}$ – $\frac{1}{27}$
Answer:
Given:
Subtraction problem: $\frac{10}{27} - \frac{1}{27}$
To Find:
The difference between the given fractions.
Solution:
The given fractions $\frac{10}{27}$ and $\frac{1}{27}$ have the same denominator, which is 27. These are like fractions.
To subtract like fractions, we subtract the numerators and keep the denominator the same.
$\frac{10}{27} - \frac{1}{27} = \frac{10 - 1}{27}$
Subtracting the numerators:
$10 - 1 = 9$
So, the difference is:
$\frac{9}{27}$
The resulting fraction can be simplified by dividing both the numerator and the denominator by their greatest common divisor (GCD).
The GCD of 9 and 27 is 9, since $27 = 3 \times 9$.
$\frac{9}{27} = \frac{9 \div 9}{27 \div 9} = \frac{1}{3}$
The difference is $\frac{1}{3}$.
Figure it Out (Page 182)
Question 1. Carry out the following subtractions using Brahmagupta’s method:
a. $\frac{8}{15}$ – $\frac{3}{15}$
b. $\frac{2}{5}$ – $\frac{4}{15}$
c. $\frac{5}{6}$ – $\frac{4}{9}$
d. $\frac{2}{3}$ – $\frac{1}{2}$
Answer:
Brahmagupta's method for subtracting $\frac{c}{d}$ from $\frac{a}{b}$ is given by $\frac{ad - bc}{bd}$. This is equivalent to finding a common denominator and subtracting the numerators. We will use the method of finding the least common multiple (LCM) of the denominators to perform the subtraction.
a. Subtract $\frac{3}{15}$ from $\frac{8}{15}$.
The fractions have the same denominator (15). These are like fractions.
Subtract the numerators and keep the common denominator:
$\frac{8}{15} - \frac{3}{15} = \frac{8-3}{15} = \frac{5}{15}$
Simplify the result by dividing the numerator and denominator by their GCD, which is 5:
$\frac{5}{15} = \frac{\cancel{5}^{1}}{\cancel{15}_{3}} = \frac{1}{3}$
The difference is $\frac{1}{3}$.
b. Subtract $\frac{4}{15}$ from $\frac{2}{5}$.
The denominators are 5 and 15. The LCM(5, 15) = 15.
Convert $\frac{2}{5}$ to an equivalent fraction with denominator 15:
$\frac{2}{5} = \frac{2 \times 3}{5 \times 3} = \frac{6}{15}$
The fraction $\frac{4}{15}$ already has the denominator 15.
Subtract the equivalent fractions:
$\frac{6}{15} - \frac{4}{15} = \frac{6-4}{15} = \frac{2}{15}$
The fraction $\frac{2}{15}$ is in its lowest terms as the GCD(2, 15) = 1.
The difference is $\frac{2}{15}$.
c. Subtract $\frac{4}{9}$ from $\frac{5}{6}$.
The denominators are 6 and 9. The LCM(6, 9) = 18.
Convert fractions to equivalent fractions with denominator 18:
$\frac{5}{6} = \frac{5 \times 3}{6 \times 3} = \frac{15}{18}$
$\frac{4}{9} = \frac{4 \times 2}{9 \times 2} = \frac{8}{18}$
Subtract the equivalent fractions:
$\frac{15}{18} - \frac{8}{18} = \frac{15-8}{18} = \frac{7}{18}$
The fraction $\frac{7}{18}$ is in its lowest terms as the GCD(7, 18) = 1.
The difference is $\frac{7}{18}$.
d. Subtract $\frac{1}{2}$ from $\frac{2}{3}$.
The denominators are 3 and 2. The LCM(3, 2) = 6.
Convert fractions to equivalent fractions with denominator 6:
$\frac{2}{3} = \frac{2 \times 2}{3 \times 2} = \frac{4}{6}$
$\frac{1}{2} = \frac{1 \times 3}{2 \times 3} = \frac{3}{6}$
Subtract the equivalent fractions:
$\frac{4}{6} - \frac{3}{6} = \frac{4-3}{6} = \frac{1}{6}$
The fraction $\frac{1}{6}$ is in its lowest terms as the GCD(1, 6) = 1.
The difference is $\frac{1}{6}$.
Question 2. Subtract as indicated:
a. $\frac{13}{4}$ from $\frac{10}{3}$
b. $\frac{18}{5}$ from $\frac{23}{3}$
c. $\frac{29}{7}$ from $\frac{45}{7}$
Answer:
To subtract fractions, we first find a common denominator if needed, then subtract the numerators and keep the common denominator.
a. Subtract $\frac{13}{4}$ from $\frac{10}{3}$. This means calculating $\frac{10}{3} - \frac{13}{4}$.
The denominators are 3 and 4. The least common multiple (LCM) of 3 and 4 is 12.
Convert fractions to equivalent fractions with denominator 12:
$\frac{10}{3} = \frac{10 \times 4}{3 \times 4} = \frac{40}{12}$
$\frac{13}{4} = \frac{13 \times 3}{4 \times 3} = \frac{39}{12}$
Now subtract the equivalent fractions:
$\frac{40}{12} - \frac{39}{12} = \frac{40 - 39}{12} = \frac{1}{12}$
The difference is $\frac{1}{12}$.
b. Subtract $\frac{18}{5}$ from $\frac{23}{3}$. This means calculating $\frac{23}{3} - \frac{18}{5}$.
The denominators are 3 and 5. The LCM of 3 and 5 is 15.
Convert fractions to equivalent fractions with denominator 15:
$\frac{23}{3} = \frac{23 \times 5}{3 \times 5} = \frac{115}{15}$
$\frac{18}{5} = \frac{18 \times 3}{5 \times 3} = \frac{54}{15}$
Now subtract the equivalent fractions:
$\frac{115}{15} - \frac{54}{15} = \frac{115 - 54}{15}$
Performing the subtraction:
$\begin{array}{cc} & 1 & 1 & 5 \\ - & & 5 & 4 \\ \hline & & 6 & 1 \\ \hline \end{array}$
The difference is $\frac{61}{15}$.
c. Subtract $\frac{29}{7}$ from $\frac{45}{7}$. This means calculating $\frac{45}{7} - \frac{29}{7}$.
The fractions have the same denominator (7). These are like fractions.
Subtract the numerators and keep the common denominator:
$\frac{45}{7} - \frac{29}{7} = \frac{45 - 29}{7}$
Performing the subtraction:
$\begin{array}{cc} & 4 & 5 \\ - & 2 & 9 \\ \hline & 1 & 6 \\ \hline \end{array}$
The difference is $\frac{16}{7}$.
Question 3. Solve the following problems:
a. Jaya’s school is $\frac{7}{10}$ km from her home. She takes an auto for $\frac{1}{2}$ km from her home daily, and then walks the remaining distance to reach her school. How much does she walk daily to reach the school?
b. Jeevika takes $\frac{10}{3}$ minutes to take a complete round of the park and her friend Namit takes $\frac{13}{4}$ minutes to do the same. Who takes less time and by how much?
Answer:
a.
Given:
Total distance to school = $\frac{7}{10}$ km
Distance covered by auto = $\frac{1}{2}$ km
To Find:
The distance Jaya walks daily.
Solution:
The distance Jaya walks is the total distance minus the distance covered by auto.
Distance walked = Total distance - Distance by auto
Distance walked = $\frac{7}{10} - \frac{1}{2}$
To subtract these fractions, we need a common denominator. The denominators are 10 and 2. The least common multiple (LCM) of 10 and 2 is 10.
Convert $\frac{1}{2}$ to an equivalent fraction with denominator 10:
$\frac{1}{2} = \frac{1 \times 5}{2 \times 5} = \frac{5}{10}$
Now, perform the subtraction:
Distance walked = $\frac{7}{10} - \frac{5}{10} = \frac{7 - 5}{10} = \frac{2}{10}$
Simplify the result:
$\frac{2}{10} = \frac{\cancel{2}^{1}}{\cancel{10}_{5}} = \frac{1}{5}$
Jaya walks $\frac{1}{5}$ km daily to reach the school.
Answer: Jaya walks $\frac{1}{5}$ km daily.
b.
Given:
Jeevika's time = $\frac{10}{3}$ minutes
Namit's time = $\frac{13}{4}$ minutes
To Find:
Who takes less time and by how much.
Solution:
To find who takes less time, we need to compare the two fractions $\frac{10}{3}$ and $\frac{13}{4}$.
To compare these fractions, we find a common denominator. The denominators are 3 and 4. The least common multiple (LCM) of 3 and 4 is 12.
Convert both fractions to equivalent fractions with denominator 12:
Jeevika's time: $\frac{10}{3} = \frac{10 \times 4}{3 \times 4} = \frac{40}{12}$ minutes
Namit's time: $\frac{13}{4} = \frac{13 \times 3}{4 \times 3} = \frac{39}{12}$ minutes
Now compare the equivalent fractions $\frac{40}{12}$ and $\frac{39}{12}$. Since the denominators are the same, we compare the numerators: $40 > 39$.
So, $\frac{40}{12} > \frac{39}{12}$. This means $\frac{10}{3} > \frac{13}{4}$.
Namit takes less time than Jeevika.
To find out by how much less time Namit takes, we subtract Namit's time from Jeevika's time:
Difference in time = Jeevika's time - Namit's time
Difference in time = $\frac{10}{3} - \frac{13}{4}$
We already converted these fractions to have a common denominator of 12:
Difference in time = $\frac{40}{12} - \frac{39}{12} = \frac{40 - 39}{12} = \frac{1}{12}$ minutes.
Namit takes $\frac{1}{12}$ minutes less than Jeevika.
Answer: Namit takes less time by $\frac{1}{12}$ minutes.
Intext Question (Page 184 - 185)
Question: Puzzle!
It is easy to add up fractional units to obtain the sum 1, if one uses the same fractional unit, e.g.,
$\frac{1}{2}$ + $\frac{1}{2}$ = 1, $\frac{1}{3}$ + $\frac{1}{3}$ + $\frac{1}{3}$ = 1, $\frac{1}{4}$ + $\frac{1}{4}$ + $\frac{1}{4}$ + $\frac{1}{4}$ = 1, etc.
1. Can you find three different fractional units that add up to 1?
It turns out there is only one solution to this problem (up to changing the order of the 3 fractions)! Can you find it? Try to find it before reading further.
2. Can you find four different fractional units that add up to 1?
It turns out that this problem has six solutions! Can you find at least one of them? Can you find them all? You can try using similar reasoning as in the cases of two and three fractional units – or find your own method!
Answer:
This is a classic puzzle involving unit fractions (fractions with a numerator of 1).
1. Three different fractional units that add up to 1
We are looking for three different whole numbers, let's call them $a$, $b$, and $c$, such that:
$\frac{1}{a} + \frac{1}{b} + \frac{1}{c} = 1$
To solve this, let's assume an order, say $a < b < c$. This means $\frac{1}{a}$ must be the largest of the three fractions.
The largest fraction, $\frac{1}{a}$, must be greater than $\frac{1}{3}$ (because if all three fractions were $\frac{1}{3}$, they would add up to 1, but since they are different, one must be larger).
The only unit fraction larger than $\frac{1}{3}$ but less than 1 is $\frac{1}{2}$. So, we can conclude that the largest fraction must be $\frac{1}{2}$. Let $a=2$.
Our equation now becomes:
$\frac{1}{2} + \frac{1}{b} + \frac{1}{c} = 1$
Subtracting $\frac{1}{2}$ from both sides, we get:
$\frac{1}{b} + \frac{1}{c} = 1 - \frac{1}{2} = \frac{1}{2}$
Now we need to find two different numbers, $b$ and $c$ (where $2 < b < c$), whose unit fractions add up to $\frac{1}{2}$. Using the same logic, $\frac{1}{b}$ must be the larger fraction, so it must be greater than $\frac{1}{4}$ (since $\frac{1}{4}+\frac{1}{4}=\frac{1}{2}$). The only unit fraction that fits this and is smaller than $\frac{1}{2}$ is $\frac{1}{3}$. So, let $b=3$.
Our equation is now:
$\frac{1}{3} + \frac{1}{c} = \frac{1}{2}$
Solving for $\frac{1}{c}$:
$\frac{1}{c} = \frac{1}{2} - \frac{1}{3} = \frac{3}{6} - \frac{2}{6} = \frac{1}{6}$
This gives us $c=6$.
The three different fractional units are $\frac{1}{2}$, $\frac{1}{3}$, and $\frac{1}{6}$. Let's check:
$\frac{1}{2} + \frac{1}{3} + \frac{1}{6} = \frac{3}{6} + \frac{2}{6} + \frac{1}{6} = \frac{6}{6} = 1$
The only solution is $\mathbf{\frac{1}{2} + \frac{1}{3} + \frac{1}{6} = 1}$.
2. Four different fractional units that add up to 1
We are looking for four different whole numbers, $a, b, c, d$, such that:
$\frac{1}{a} + \frac{1}{b} + \frac{1}{c} + \frac{1}{d} = 1$
There are six possible solutions, but we only need to find one. We can use a similar strategy.
Let's again assume $a < b < c < d$. The largest fraction, $\frac{1}{a}$, must be greater than $\frac{1}{4}$. So, $a$ can be 2 or 3. Let's start with $a=2$.
This gives us $\frac{1}{b} + \frac{1}{c} + \frac{1}{d} = \frac{1}{2}$.
Now we have the same problem as in the first part, but for the sum $\frac{1}{2}$. The largest fraction, $\frac{1}{b}$, must be greater than $\frac{1}{6}$ (since $\frac{1}{6}+\frac{1}{6}+\frac{1}{6}=\frac{1}{2}$). Let's try $b=3$.
This gives us $\frac{1}{c} + \frac{1}{d} = \frac{1}{2} - \frac{1}{3} = \frac{1}{6}$.
We need to find two different numbers $c$ and $d$ (where $3 < c < d$) whose unit fractions add to $\frac{1}{6}$. The larger fraction, $\frac{1}{c}$, must be greater than $\frac{1}{12}$ (since $\frac{1}{12}+\frac{1}{12}=\frac{1}{6}$). Let's try the next possible value, $c=7$.
This gives us $\frac{1}{d} = \frac{1}{6} - \frac{1}{7} = \frac{7}{42} - \frac{6}{42} = \frac{1}{42}$. So, $d=42$.
This gives us a set of four different fractional units: $\frac{1}{2}, \frac{1}{3}, \frac{1}{7}, \frac{1}{42}$. Let's check:
$\frac{1}{2} + \frac{1}{3} + \frac{1}{7} + \frac{1}{42} = \frac{21}{42} + \frac{14}{42} + \frac{6}{42} + \frac{1}{42} = \frac{21+14+6+1}{42} = \frac{42}{42} = 1$
One solution is $\mathbf{\frac{1}{2} + \frac{1}{3} + \frac{1}{7} + \frac{1}{42} = 1}$.
Another possible solution that you might find is:
$\mathbf{\frac{1}{2} + \frac{1}{4} + \frac{1}{6} + \frac{1}{12} = 1}$

