| Latest Maths NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
Chapter 8 Playing with Constructions
Welcome to the solutions guide for Chapter 8, "Playing with Constructions," a hands-on exploration of practical geometry featured in the Class 6 Ganita Prakash textbook (NCERT, 2024-25 session). This chapter shifts the focus from theoretical understanding to the precise art of drawing geometric figures using fundamental tools. These solutions are designed to provide highly detailed, sequential instructions, acting as a virtual tutor guiding students through the essential techniques of using a ruler (straightedge) and a pair of compasses to create accurate geometric constructions.
The essence of this chapter lies in appreciating the power and precision offered by these simple instruments. Unlike freehand sketching, geometric constructions demand accuracy, achieved through the careful use of a ruler for drawing straight line segments and measuring lengths, and compasses for drawing arcs and circles, and crucially, for transferring lengths accurately without direct measurement. The solutions emphasize the correct handling of these tools – maintaining a sharp pencil point in the compasses, setting the radius accurately, and drawing clear arcs – as foundational to successful construction. This chapter builds spatial reasoning and an understanding of geometric properties through action.
These solutions meticulously detail the steps required for several fundamental constructions involving lines and angles. Key constructions covered include:
- Constructing a line segment of a precisely given length.
- Copying a given line segment accurately onto another position without measuring its length directly, using only compasses and a ruler.
- Constructing a line perpendicular to a given line, addressing two scenarios: through a point situated on the line itself, and from a point located outside the line.
- Constructing the perpendicular bisector of a given line segment. The solutions highlight how this construction simultaneously finds the midpoint of the segment and creates a line at a perfect $90^\circ$ angle to it.
Furthermore, the solutions provide comprehensive guidance on constructions related to angles:
- Copying a given angle: Transferring an angle of unknown measure to a different location using only compass and ruler techniques.
- Bisecting a given angle: Dividing an angle into two angles of exactly equal measure (finding $\frac{\theta}{2}$ if the original angle is $\theta$).
- Constructing specific angles using only ruler and compasses (without a protractor). This often involves leveraging properties of equilateral triangles (for $60^\circ$) and bisection techniques. Common constructions explained include: $60^\circ$, $120^\circ$ (as $2 \times 60^\circ$), $90^\circ$ (often by bisecting a straight angle, $180^\circ$, or constructing a perpendicular), $30^\circ$ (by bisecting a $60^\circ$ angle), and $45^\circ$ (by bisecting a $90^\circ$ angle).
The emphasis throughout these solutions for Chapter 8 of the Class 6 Ganita Prakash (NCERT 2024-25) is not just on achieving the final figure, but on understanding the process and the underlying geometric principles that make these constructions work. By carefully following these detailed, step-by-step solutions, students will develop essential dexterity with geometric tools, enhance their fine motor skills and spatial awareness, and gain a deeper appreciation for how precise geometric figures can be created based purely on logical steps and the properties of shapes, laying a strong foundation for future geometry studies.
Construct (Page 190 - 191)
Question 1. A Person
How will you draw this?

This figure has two components.

You might have figured out a way of drawing the first part. For drawing the second part, see this.

The challenge here is to find out where to place the tip of the compass and the radius to be taken for drawing this curve. You can fix a radius in the compass and try placing the tip of the compass in different locations to see which point works for getting the curve. Use your Estimate where to keep the tip.
Answer:
To Construct:
The figure of a person as shown, which is composed of a circle for the head, a line for the neck, and a rectangular shape with a curved top for the body.

Steps of Construction:
The figure can be constructed in two main parts: (A) The head and neck, and (B) The body.
Part A: Constructing the Head and Neck
1. Draw the Head: Choose a point on your paper and mark it as 'O'. Using a compass, draw a circle with center 'O' and a suitable radius. This circle represents the head.
2. Draw the Neck: From the center 'O', draw a vertical line downwards that passes through the circle. The part of the line below the circle will serve as the neck. Let the bottom end of the neck be point 'P'.
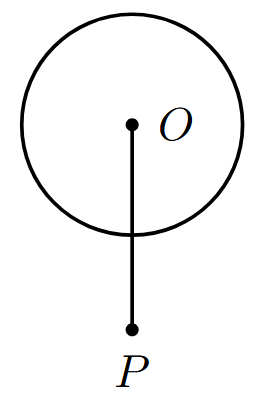
Part B: Constructing the Body
1. Draw the Sides: From point 'P' (the bottom of the neck), draw a horizontal line. On this line, mark two points, 'A' and 'B', such that 'P' is the midpoint of AB (i.e., PA = PB). Now, from points A and B, draw two vertical line segments of equal length downwards. Let these be AC and BD.
2. Draw the Base: Join points C and D with a straight horizontal line segment using a ruler. This completes the three straight sides of the body.
3. Draw the Curved Top: The top of the body is a concave arc connecting the two shoulder points, A and B.
- To draw this arc, we need to find a center point for the compass. As suggested in the problem, we can find this point by estimation.
- The center of this arc must be on the vertical line that contains the neck, somewhere above the points A and B. A convenient point to choose is the center of the head, point 'O'.
- Place the metal tip of the compass at point 'O'.
- Adjust the compass width so that the pencil tip is at point A. The radius is now OA.
- Keeping the compass tip at O, draw an arc from point A to point B. This will create the curved shoulder line.
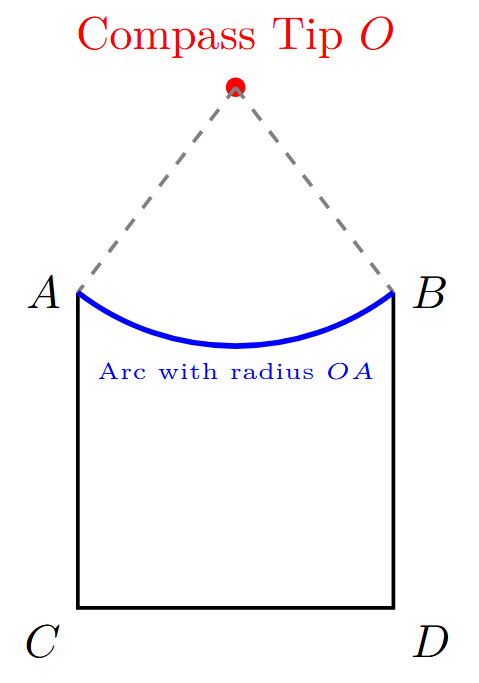
By following these steps, you will have constructed the complete figure of the person.
Question 2. Wavy Wave
Construct this.

As the length of the central line is not specified, we can take it to be of any length.
Let us take AB to be the central line such that the length of AB is 8 cm. We write this as AB = 8 cm.
Here, the first wave is drawn as a half circle.

Answer:
To Construct:
The "Wavy Wave" pattern as shown in the figure, using a line segment of length 8 cm as the base.
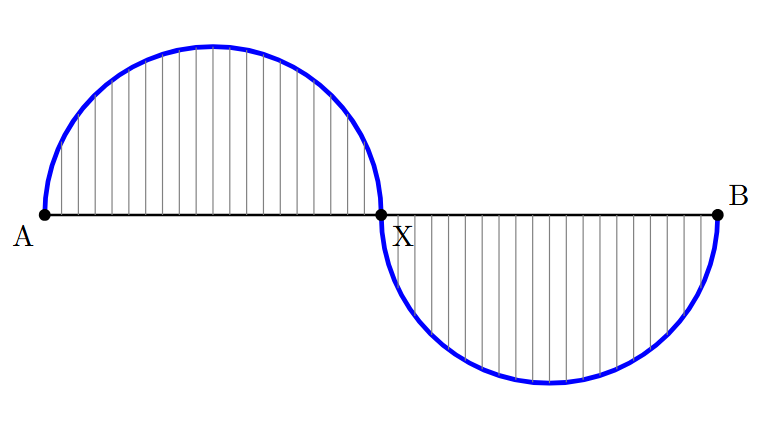
Steps of Construction:
1. First, draw a line segment AB with a length of 8 cm using a ruler. This will be the central line for our pattern.

2. The wavy pattern consists of two identical waves (semicircles) on opposite sides. This means we need to divide the line segment AB into two equal halves. Find the midpoint of AB and label it X. Thus, we have AX = XB = $\frac{8}{2} = 4$ cm.
3. The first wave is a semicircle with AX as its diameter. To draw this semicircle, we first need to find the midpoint of the segment AX. Let's call this midpoint O. The radius of the semicircle will be half the diameter, so the radius is OA = OX = $\frac{4}{2} = 2$ cm.
4. Now, place the metal tip of the compass on point O and the pencil tip on point A (or X). Rotate the compass to draw a semicircle on one side of the line AB (for example, above it).
5. The second wave is a semicircle with XB as its diameter. Similarly, find the midpoint of the segment XB. Let's call this midpoint P. The radius of this second semicircle will be PX = PB = $\frac{4}{2} = 2$ cm.
6. Place the metal tip of the compass on point P and the pencil tip on point X (or B). Rotate the compass to draw another semicircle, this time on the opposite side of the line AB (below it).
7. The basic outline of the wavy wave is now constructed. To complete the figure as shown in the question, you can draw a series of parallel vertical lines inside both semicircles using a ruler.
How do you draw these eyes with a compass?

Answer:
Given:
A figure representing a pair of eyes, where each eye consists of an outer boundary formed by two intersecting arcs and an inner solid circle representing the pupil.
To Construct:
A pair of identical eye shapes using a compass and a ruler.
Steps of Construction:
1. Draw the Base Line: Use a ruler to draw a horizontal line segment. Mark two points $A$ and $B$ on this line which will represent the corners of the first eye.
2. Mark the Midpoint: Find the midpoint $M$ of the segment $AB$. This point $M$ will serve as the center for the inner pupil.
$AM = MB$
(Midpoint of the eye length)
3. Draw the Pupil: Place the metal pointer of the compass at $M$ and draw a small circle with a suitable radius. This forms the central part of the eye.
4. Construct the Perpendicular Bisector: Draw a perpendicular line passing through point $M$. This line will help us locate the centers for the upper and lower arcs (the eyelids).

5. Draw the Upper Arc: Place the compass pointer at a point $P$ on the perpendicular bisector (below the line $AB$). Adjust the compass width so the pencil touches point $A$. Draw an arc from $A$ to $B$ passing above the pupil.
6. Draw the Lower Arc: Place the compass pointer at a point $Q$ on the perpendicular bisector (above the line $AB$), ensuring the distance $MQ$ is equal to $MP$. Draw an arc from $A$ to $B$ passing below the pupil.
$MP = MQ$
[For symmetry of the eye] ... (i)
7. Construct the Second Eye: Repeat the same steps at a distance to the right of the first eye to complete the pair.

Figure it Out (Page 191)
Question 1. What radius should be taken in the compass to get this half circle? What should be the length of AX?
Answer:
Given:
The figure from the "Wavy Wave" construction shows a line segment AB of length 8 cm, which is divided into two parts. A semicircle is drawn on the first part, labeled AX in the diagram.

To Find:
1. The radius that should be taken in the compass to get the semicircle.
2. The length of AX.
Solution:
The "Wavy Wave" pattern consists of two identical semicircles on the central line AB = 8 cm. This means the line segment AB is divided into two equal parts at point X.
The segment AX serves as the diameter for the first semicircle.
Therefore, the length of AX is half the length of AB.
Length of AX = $\frac{\text{Length of AB}}{2} = \frac{8 \text{ cm}}{2} = 4 \text{ cm}$.
1. The radius of a semicircle is half of its diameter.
Diameter = Length of AX = 4 cm.
Radius = $\frac{1}{2} \times \text{Diameter}$
Radius = $\frac{1}{2} \times 4 \text{ cm} = 2 \text{ cm}$.
2. As calculated above, the point X is the midpoint of the line segment AB.
Length of AX = $4 \text{ cm}$.
Answer:
The radius that should be taken in the compass is $2 \text{ cm}$.
The length of AX should be $4 \text{ cm}$.
Question 2. Take a central line of a different length and try to draw the wave on it.
Answer:
We will construct the "Wavy Wave" pattern on a central line of a new length. Let's choose the length of the central line AB to be 10 cm.
Steps for Construction:
1. Draw the Central Line: Using a ruler, draw a line segment AB of length 10 cm.
2. Divide the Line Segment: The pattern consists of two equal waves (semicircles). Therefore, we need to divide the line segment AB into two equal parts. Find the midpoint of AB and label it X.
Length of each part (diameter) = $\frac{\text{Total length}}{2} = \frac{10 \text{ cm}}{2} = 5 \text{ cm}$.
So, AX = XB = 5 cm. Each of these segments will be the diameter for one semicircle.
3. Determine the Radius and Centers:
The radius of each semicircle is half of its diameter.
Radius = $\frac{1}{2} \times \text{Diameter} = \frac{1}{2} \times 5 \text{ cm} = 2.5 \text{ cm}$.
The center of the first semicircle (on diameter AX) will be the midpoint of AX. Let's call this center O.
The center of the second semicircle (on diameter XB) will be the midpoint of XB. Let's call this center P.
4. Draw the Semicircles:
- Set the compass radius to 2.5 cm.
- Place the compass tip on the first center point O. Draw a semicircle above the line AB, starting from A and ending at X.
- Place the compass tip on the second center point P. Draw a semicircle below the line AB, starting from X and ending at B.
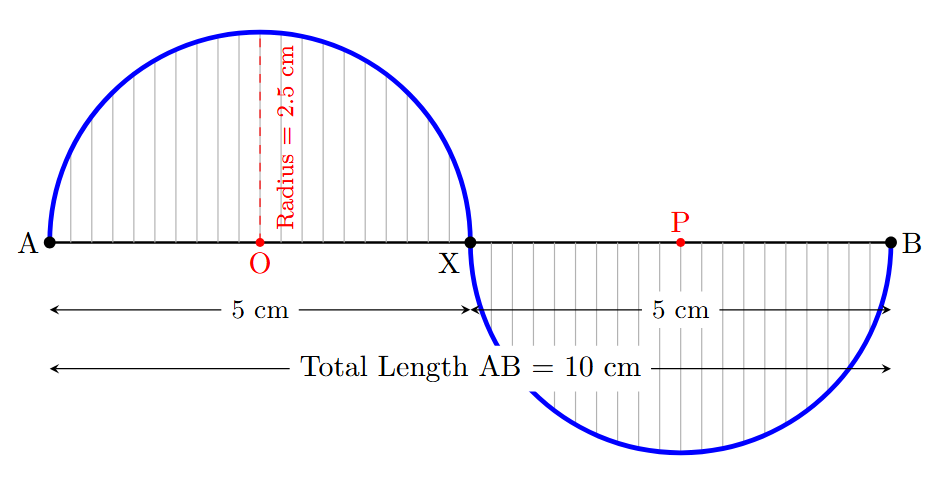
By following these steps, the "Wavy Wave" pattern can be successfully constructed on any central line.
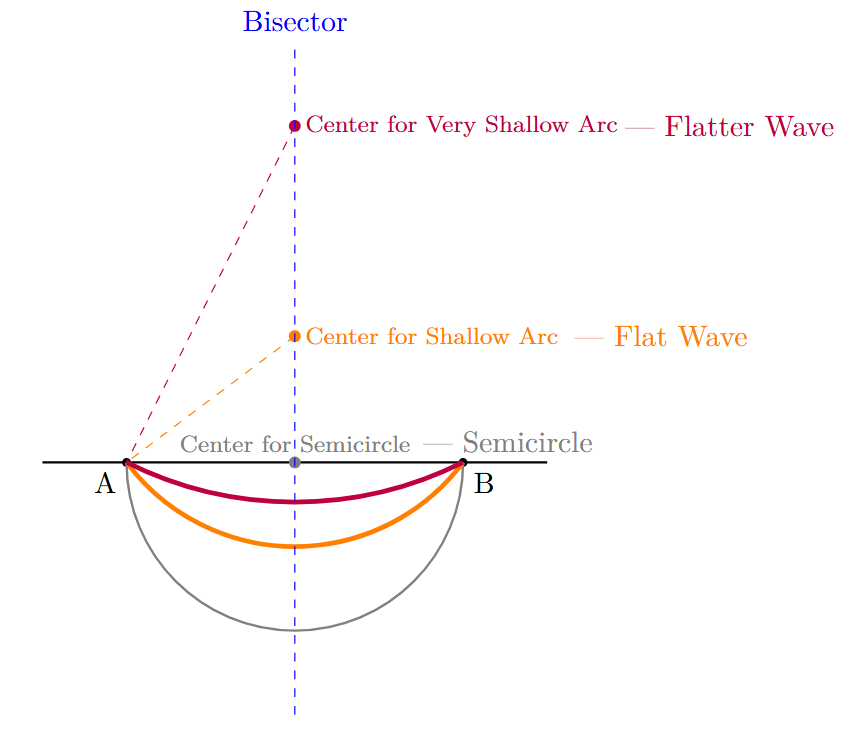
Question 3. Try to recreate the figure where the waves are smaller than a half circle (as appearing in the neck of the figure ‘A Person’). The challenge here is to get both the waves to be identical. This may be tricky!
Answer:
Given:
Two diagrams are provided: one of 'A Person' with shallow shoulder curves (waves) and another of a standard wave consisting of semicircles. The objective is to recreate the shallow waves seen in the neck/shoulder area of the person, ensuring both waves are perfectly identical.
To Find/Construct:
A method to draw two identical waves that are smaller than a half-circle (shallow arcs) using a compass and a ruler.
Steps of Construction:
1. Draw the Base Line: Use a ruler to draw a horizontal line. Mark three points $A$, $B$, and $C$ such that $B$ is exactly in the middle of $A$ and $C$. The segments $AB$ and $BC$ represent the width of each wave.
$AB = BC$
(Equal width for identical waves) ... (i)
2. Construct Perpendicular Bisectors: Draw perpendicular bisectors for both segments $AB$ and $BC$. These vertical lines will act as the "center lines" for our compass placement.
3. Identify the Center for Shallow Waves: To make the wave smaller than a half-circle, the center must be placed further away from the segment than the radius of a semicircle. Mark a point $O_1$ on the first bisector and $O_2$ on the second bisector at the same vertical distance from the base line.
$Distance \ (O_1, AB) = Distance \ (O_2, BC)$
[Ensures identical curvature] ... (ii)
4. Set the Compass Radius: Place the metal tip of the compass at $O_1$. Extend the pencil tip to touch point $A$. This distance $O_1A$ is our radius $r$. To ensure the arc is flatter than a semicircle, the center $O_1$ must be chosen such that:
$r > \frac{1}{2}AB$
... (iii)
5. Draw the Arcs: Draw an arc from $A$ to $B$ with center $O_1$. Keeping the same radius, move the compass tip to $O_2$ and draw the second arc from $B$ to $C$.
6. Result: This creates two identical, shallow waves. In the 'A Person' figure, these arcs are concave (curving inward), which is achieved by placing the centers $O_1$ and $O_2$ above the base line.

Comparison between Waves:
| Feature | Standard Wave (Image 2) | Shoulder Wave (Person) |
| Shape | Semicircle | Shallow Arc |
| Center Point | On the base line (Midpoint) | Above or Below the base line |
| Radius ($r$) | $r = \frac{1}{2} \times Width$ | $r > \frac{1}{2} \times Width$ |
Key Observations for Symmetry:
1. Horizontal Alignment: The starting, middle, and ending points ($A, B, C$) must be collinear.
2. Vertical Alignment: The centers of the circles from which the arcs are carved must be at the same "height" relative to the base line. If one center is higher than the other, the waves will not be identical.
3. Fixed Radius: Crucially, the compass setting must not be adjusted between drawing the first wave and the second wave.
Alternate Solution:
For a quick recreation, one can use a Tracing Paper. Draw one shallow arc (wave) perfectly using a compass. Fold the paper along the vertical line passing through point $B$ and trace the first wave onto the second segment. This ensures 100% identical "waves" as seen in the neck of the 'A Person' figure.
Figure it Out (Page 194)

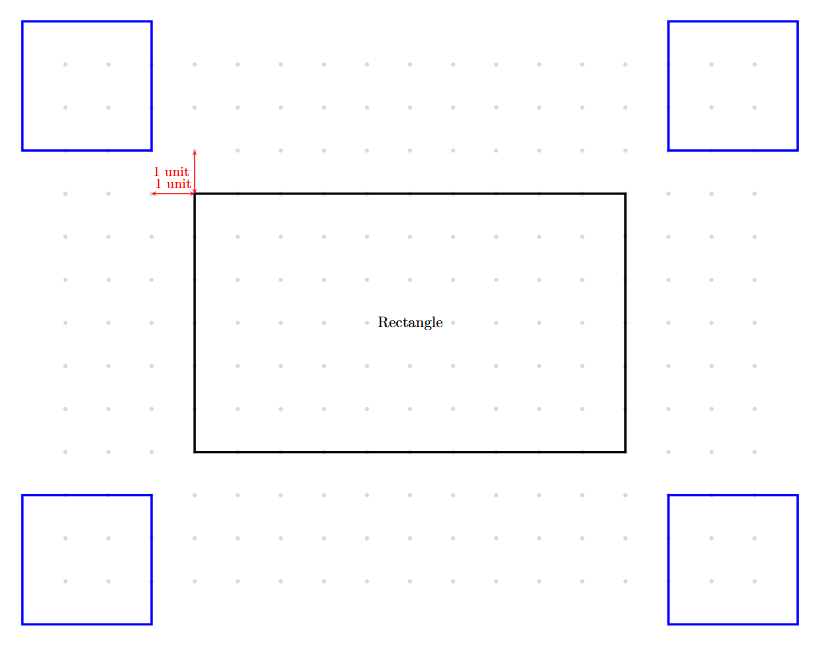
What did you do to recreate this figure so that the four squares are placed symmetrically around the rectangle? Discuss with your classmates.
Answer:
Given:
A configuration (Fig. 8.3) consisting of a central rectangle and four squares located near its corners.
To Construct:
Recreate the given figure on dot paper such that the four squares are placed symmetrically around the rectangle.
Solution:
The use of dot paper (or grid paper) allows us to maintain symmetry by simply counting the number of dots between shapes. Symmetry ensures that the figure looks balanced and that each square is positioned identically relative to the central rectangle.
Steps for Construction on Dot Paper:
1. Draw the Central Rectangle: Choose a central location on the dot paper. Draw a rectangle by connecting dots. For example, let the length be $10$ units and the breadth be $6$ units.
2. Define the Offset (Gap): To maintain symmetry, choose a fixed horizontal gap $x$ and a fixed vertical gap $y$ from the corners of the rectangle. For example, let $x = 2$ dots and $y = 2$ dots.
$x = 2 \ dots, \ y = 2 \ dots$
(Fixed gap for symmetry)
3. Place the Squares: Starting from each corner of the rectangle, move $x$ units horizontally outward and $y$ units vertically outward to mark the starting corner for each square.
4. Draw Identical Squares: Draw four squares, each of the same size (e.g., $3 \times 3$ dots). Because we started from symmetrical points and used the same size for all squares, the final figure is perfectly symmetrical.
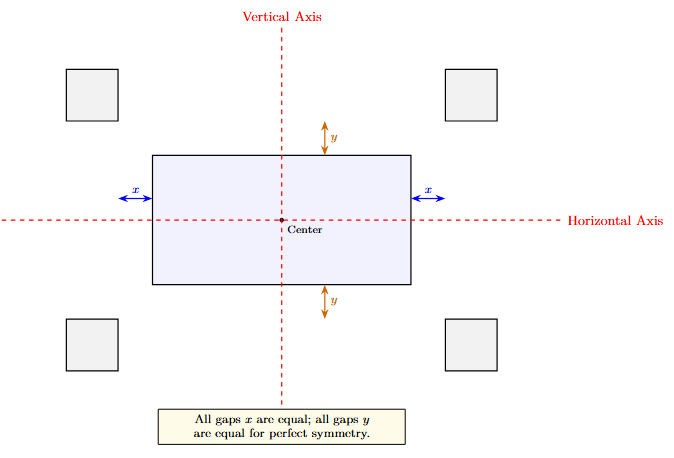
Discussion on Achieving Symmetry:
To ensure the four squares are placed symmetrically, we must satisfy three conditions:
1. Equality of Size: All four squares must have the same side length $s$. If one square is larger than the others, the symmetry is broken.
2. Horizontal Symmetry: The distance from the left edge of the rectangle to the left squares must be equal to the distance from the right edge to the right squares.
$Distance_{Left} = Distance_{Right}$
[Horizontal Symmetry] ... (i)
3. Vertical Symmetry: The distance from the top edge of the rectangle to the top squares must be equal to the distance from the bottom edge to the bottom squares.
$Distance_{Top} = Distance_{Bottom}$
[Vertical Symmetry] ... (ii)
By following these constraints on dot paper, the figure will have both reflective symmetry (across horizontal and vertical axes) and rotational symmetry (if the rectangle were a square).
Alternate Solution:
Instead of drawing the rectangle first, you can find the center dot of the paper. Mark four points at equal diagonal distances from this center to serve as the centers of the four squares. Then, draw the rectangle such that its center coincides with the center of the paper. This "Center-Out" approach often leads to a more balanced placement on the sheet.

Think: Is it possible to reason out if the sides are equal or not, and if the angles are right or not without using any measuring instruments in the above figure? Can we do this by only looking at the position of corners in the dot grid?
Answer:
Given. Four shapes labelled A, B, C and D drawn on a dot grid (see picture).
To Find. Which of these shapes are squares?
Idea:
On a dot grid you can check two things without a ruler:
- If all four sides look the same length by counting the dots or steps between corners.
- If the corners look like right angles (they should look like the corner of a book or a box).
Check each shape (by looking at the grid):
| Shape | What we see | So it is a... |
| A | All four sides look equal and corners look like right angles. | Square |
| B | All four sides look about equal but the corners are not right angles (two are sharp, two are wide). | Rhombus (not a square) |
| C | All four sides look about equal but angles are not right angles. | Rhombus (not a square) |
| D | Opposite sides are equal and corners look like right angles, but adjacent sides are not equal. | Rectangle (not a square) |
Simple explanation:
A is a square because its four sides are equal and every corner looks like a right angle. You can count the dots between corners to see the sides match, and the corner points form a box shape.
B and C have all sides equal, but their corners are not right angles (they look slanted). That makes them rhombuses, not squares.
D has right corners but two sides are longer than the other two, so it is a rectangle, not a square.
Only A is a square. B and C are rhombuses (they are slanted), and D is a rectangle but not a square.
Question 3. Draw at least 3 rotated squares and rectangles on a dot grid. Draw them such that their corners are on the dots. Verify if the squares and rectangles that you have drawn satisfy their respective properties.
Answer:
Here are three different rotated squares and three different rotated rectangles drawn on a dot grid. The corners of each shape land exactly on the dots. Let's check if they follow the rules for being squares and rectangles.
Rotated Squares
A square must have two important properties:
- All four of its sides must be the exact same length.
- All four of its corners must be perfect right angles (like the corner of a square tile).
Square 1
Verification:
- Checking the Sides: We can check the length by counting how we move from one dot to the next.
- To draw the first side, we move 2 dots across and 1 dot up.
- To draw the next side, we move 1 dot across and 2 dots up.
- For every side of this square, the movement is a combination of '2 dots' and '1 dot'. This means all four sides are the exact same length.
- Checking the Corners: Notice how for the first side we move '2 across, 1 up', and for the next side, the numbers are swapped to '1 across, 2 up'. On a dot grid, whenever you swap the "across" and "up" movements for the next side, you create a perfect right angle. This works for all four corners.
Since all sides are equal and all corners are right angles, this is a square.
Square 2
Verification:
- Checking the Sides: Let's look at the movement pattern for this square.
- To draw a side, we move 3 dots across and 2 dots up.
- Since every side is made using a '3 dot' and '2 dot' movement, all four sides are equal in length.
- Checking the Corners: Just like the first square, the movement numbers are swapped for adjacent sides (from '3 across, 2 up' to '2 across, 3 up'). This creates four perfect right angles.
Therefore, this is also a square.
Square 3
Verification:
- Checking the Sides: This square is long and skinny, but it's still a square!
- Each side is made by moving 4 dots across and 1 dot up.
- Because every side follows the same '4 and 1' dot pattern, all four sides are equal.
- Checking the Corners: The movement numbers are swapped for the next side ('1 across and 4 up'), which confirms that all corners are perfect right angles.
So, this shape is a square too.
Rotated Rectangles
A rectangle must have two important properties:
- Its opposite sides must be equal in length.
- All four of its corners must be perfect right angles.
Rectangle 1
Verification:
- Checking the Sides:
- The two longer sides are made by moving 3 dots across and 1 dot up. Since they have the same pattern, they are equal.
- The two shorter sides are made by moving 1 dot across and 3 dots up. They are also equal to each other.
The opposite sides are equal, so the first rule is satisfied.
- Checking the Corners: The longer side has a '3 and 1' pattern, and the shorter side has a '1 and 3' pattern. Since the numbers are swapped, the corners where they meet are all perfect right angles.
Because its opposite sides are equal and its corners are right angles, this is a rectangle.
Rectangle 2
Verification:
- Checking the Sides:
- The two opposite long sides are made by moving 4 dots across and 2 dots up. They are equal.
- The two opposite short sides are made by moving 2 dots across and 4 dots up. They are equal.
- Checking the Corners: The adjacent sides have swapped movement patterns ('4 and 2' becomes '2 and 4'), so all four corners are right angles.
This shape satisfies all the rules, so it is a rectangle.
Rectangle 3
Verification:
- Checking the Sides:
- The two long opposite sides are made by a '5 dots across, 2 dots up' movement.
- The two short opposite sides are made by a '2 dots across, 5 dots up' movement.
The opposite sides match, so they are equal in length.
- Checking the Corners: The movement patterns for adjacent sides are '5 and 2' and '2 and 5'. The numbers are swapped, which means the corners are all perfect right angles.
Therefore, this shape is also a rectangle.
Construct (Page 197)
Question 1. Draw a rectangle with sides of length 4 cm and 6 cm. After drawing, check if it satisfies both the rectangle properties.
Answer:
Here are the steps to draw a rectangle with sides of 4 cm and 6 cm, and then check if it satisfies the properties of a rectangle.
Steps for Drawing the Rectangle:
- First, take a ruler and draw a straight line segment. Measure and mark a length of 6 cm. Let's name the endpoints A and B. This is the first side of our rectangle.
- Now, place a protractor or a set square at point A and draw a line that is exactly perpendicular to the line AB. This means the angle at A should be 90°.
- Measure 4 cm along this new line from point A and mark the endpoint as D. This is the second side of our rectangle.
- Next, place the protractor at point B and draw another line that is perpendicular to AB, making a 90° angle.
- Measure 4 cm along this line from point B and mark the endpoint as C. This is the third side.
- Finally, use your ruler to join the points C and D. This will be the fourth side of the rectangle.
AB = 6 cm
AD = 4 cm
BC = 4 cm
You have now drawn a rectangle ABCD.
Verification of Rectangle Properties
A shape is a rectangle only if it satisfies two important properties:
Property 1: The opposite sides must be equal in length.
Property 2: All four angles must be right angles (exactly $90^\circ$).
Let's check our drawing against these properties.
Checking Property 1 (Opposite sides are equal):
- We drew the side AB to be 6 cm long. Now, take your ruler and measure the side opposite to it, which is CD. You will find that the length of CD is also 6 cm.
- We drew the side AD to be 4 cm long. Now, measure its opposite side, BC. You will find that the length of BC is also 4 cm.
So, AB = CD = 6 cm.
So, AD = BC = 4 cm.
Since both pairs of opposite sides are equal, the first property is satisfied.
Checking Property 2 (All angles are right angles):
- When we were drawing, we made sure that the angle at A ($\angle A$) and the angle at B ($\angle B$) were exactly $90^\circ$ using a protractor.
- Now, take your protractor and measure the other two angles, $\angle C$ and $\angle D$.
- You will find that $\angle C = 90^\circ$ and $\angle D = 90^\circ$.
Since all four angles are $90^\circ$, the second property is also satisfied.
Conclusion:
Because the figure we drew has equal opposite sides and all four angles are $90^\circ$, we can confirm that it is indeed a rectangle.
Question 2. Draw a rectangle of sides 2 cm and 10 cm. After drawing, check if it satisfies both the rectangle properties.
Answer:
Here are the instructions to draw a rectangle with side lengths of 2 cm and 10 cm. Afterwards, we will check if the drawing follows the properties of a rectangle.
Steps for Drawing the Rectangle:
- Start by using a ruler to draw a straight line segment with a length of 10 cm. Label the endpoints A and B. This will be the longer side of the rectangle.
- Place a protractor (or a set square) at point A. Draw a line that makes a perfect 90° angle with the line segment AB.
- On this new line, measure a length of 2 cm from point A. Mark this new point as D. This is the shorter side of the rectangle.
- Now, move the protractor to point B. Draw another line that is perpendicular to AB, ensuring the angle is 90°.
- Measure 2 cm along this line from point B and label the endpoint as C.
- The last step is to connect the points D and C using a ruler. This forms the final side of the rectangle.
AB = 10 cm
AD = 2 cm
BC = 2 cm
You have now constructed a rectangle ABCD.
Verification of Rectangle Properties
For a shape to be a true rectangle, it must satisfy two conditions:
Property 1: The opposite sides must be equal in length.
Property 2: All four interior angles must be right angles (exactly $90^\circ$).
Let's check our drawing to see if it meets these conditions.
Checking Property 1 (Opposite sides are equal):
- We drew the side AB with a length of 10 cm. Now, take your ruler and measure the side opposite to it, which is DC. You will find that the length of DC is also 10 cm.
- We drew the side AD with a length of 2 cm. Now, measure its opposite side, BC. You will find that the length of BC is also 2 cm.
So, AB = DC = 10 cm.
So, AD = BC = 2 cm.
Since both pairs of opposite sides are equal, the first property is satisfied.
Checking Property 2 (All angles are right angles):
- During the construction, we used a protractor to ensure that $\angle A$ and $\angle B$ were both exactly $90^\circ$.
- Now, to verify, place your protractor at corners C and D.
- When you measure these angles, you will find that $\angle C = 90^\circ$ and $\angle D = 90^\circ$.
Since all four angles measure $90^\circ$, the second property is also satisfied.
Conclusion:
Our drawn figure has opposite sides of equal length (10 cm and 2 cm) and four right angles. Therefore, it successfully satisfies both properties and is confirmed to be a rectangle.
Question 3. Is it possible to construct a 4-sided figure in which—
- all the angles are equal to 90º but
- opposite sides are not equal?
Answer:
No, it is not possible to construct such a 4-sided figure.
Explanation:
Let's break down the two conditions given in the question.
Condition 1: All the angles are equal to 90º.
Any 4-sided figure (a quadrilateral) that has all four of its angles equal to 90º is, by definition, a rectangle. A square is also a special type of rectangle.
Property of a Rectangle:
A fundamental and necessary property of every rectangle is that its opposite sides must be equal in length. If the opposite sides are not equal, the shape cannot be a rectangle.
Condition 2: Opposite sides are not equal.
This condition directly contradicts the property of a rectangle. You cannot have a rectangle where the opposite sides are unequal.
Conclusion:
The question is asking for a shape that is a rectangle (because all angles are 90º) but at the same time is not a rectangle (because opposite sides are not equal). This is a contradiction.
Think about it like this: It's like asking someone to draw a circle that is also a square. It's impossible because the properties of a circle and a square are different and cannot exist in the same shape.
Therefore, it is impossible to construct a 4-sided figure where all angles are 90º but the opposite sides are not equal.
Construct (Page 199)

Construct a rectangle that can be divided into 3 identical squares as shown in the figure.
Answer:
To construct a rectangle that can be divided into 3 identical squares, we first need to understand the relationship between its sides. If we place three identical squares side-by-side, the length of the resulting rectangle will be three times its width.
So, we need to draw a rectangle where one side is three times the length of the other. Let's choose some simple measurements.
Let's choose the side of the square to be 3 cm.
- The width of our rectangle will be 3 cm.
- The length of our rectangle will be $3 \times 3 \text{ cm} = 9 \text{ cm}$.
Steps for Construction
Part 1: Drawing the Main Rectangle (9 cm x 3 cm)
- Take a ruler and draw a line segment AB of length 9 cm.
- Place a protractor or set square at point A and draw a line perpendicular to AB. Measure 3 cm along this line and mark the point D.
- Now, place the protractor at point B and draw another line perpendicular to AB. Measure 3 cm along this line and mark the point C.
- Join the points D and C with your ruler. The line segment DC should also measure 9 cm.
You now have a large rectangle ABCD with sides 9 cm and 3 cm.
Part 2: Dividing the Rectangle into 3 Squares
- Place your ruler along the length AB, starting from A. Make a mark at 3 cm and another mark at 6 cm. Let's call these points P and Q.
- Now, do the same on the opposite side DC. Place your ruler at D and make marks at 3 cm and 6 cm. Let's call these points R and S.
- Use your ruler to draw a straight line connecting point P on the top to point R on the bottom.
- Draw another straight line connecting point Q to point S.
Result and Verification
You have successfully constructed the figure. Let's check it.
- The overall shape is a rectangle of 9 cm by 3 cm.
- It has been divided into three smaller parts.
- Measure the sides of the first part (APRD). Its length AP is 3 cm and its width AD is 3 cm. So, it's a square.
- Measure the sides of the middle part (PQSR). Its length PQ is 3 cm and its width is 3 cm. It's also a square.
- Measure the sides of the last part (QBCS). Its length QB is 3 cm and its width BC is 3 cm. This is also a square.
Since the rectangle is divided into three identical squares, the construction is correct.
Question 2. Give the lengths of the sides of a rectangle that cannot be divided into —
- two identical squares;
- three identical squares.
Answer:
To answer this, let's first understand when a rectangle can be divided into identical squares.
- A rectangle can be divided into two identical squares only if its length is exactly double its width. For example, a rectangle of 8 cm by 4 cm can be split into two 4x4 cm squares.
- A rectangle can be divided into three identical squares only if its length is exactly triple its width. For example, a rectangle of 12 cm by 4 cm can be split into three 4x4 cm squares.
The question asks for the dimensions of a single rectangle that fails both of these conditions.
We need to find a pair of lengths where one side is not double the other, and also not triple the other.
Let's pick a width for our rectangle, for instance, 5 cm.
-
For the first condition: The rectangle cannot be divided into two identical squares.
This means the length cannot be double the width. So, the length cannot be $2 \times 5 = 10$ cm.
-
For the second condition: The rectangle cannot be divided into three identical squares.
This means the length cannot be triple the width. So, the length cannot be $3 \times 5 = 15$ cm.
So, we can choose any length for our 5 cm wide rectangle, as long as the length is not 10 cm and not 15 cm. A simple choice would be 7 cm.
Answer:
A rectangle with sides of 5 cm and 7 cm.
Verification:
- Is 7 cm double 5 cm? No. Therefore, it cannot be divided into two identical squares.
- Is 7 cm triple 5 cm? No. Therefore, it cannot be divided into three identical squares.
Note: There are many other correct answers. For example, a square with sides of 4 cm and 4 cm would also work, as would a rectangle with sides of 3 cm and 5 cm.
Construct (Page 201 - 203)
Question 1. A Square within a Rectangle

Construct a rectangle of sides 8 cm and 4 cm. How will you construct a square inside, as shown in the figure, such that the centre of the square is the same as the centre of the rectangle ?
Hint: Draw a rough figure. What will be the sidelength of the square? What will be the distance between the corners of the square and the outer rectangle?
Answer:
Here is how you can construct the rectangle and the square inside it, making sure their centers are the same.
First, let's use the hint to figure out the dimensions and position of the inner square.
Analysis (Finding the size and position of the square)
- The rectangle has a width of 4 cm. As you can see from the figure, the top and bottom sides of the square touch the top and bottom sides of the rectangle. This means the side length of the square must be equal to the width of the rectangle.
- The rectangle has a total length of 8 cm. The square, with its side of 4 cm, sits in the middle of this length.
- Since the square is in the exact center, this leftover 4 cm space must be divided equally between the left and right sides.
So, the side length of the square will be 4 cm.
The space left over on both sides of the square is: $8 \text{ cm (total length)} - 4 \text{ cm (square's length)} = 4 \text{ cm}$.
The distance (or margin) on each side will be: $4 \text{ cm} \div 2 = 2 \text{ cm}$.
So, we need to draw a 4 cm x 4 cm square inside the 8 cm x 4 cm rectangle, with a 2 cm gap on the left and right sides.
Steps for Construction
Part 1: Construct the outer rectangle (8 cm x 4 cm)
- Use a ruler to draw a line segment AB of length 8 cm.
- At point A, use a protractor or set square to draw a line AD of length 4 cm, making a 90° angle with AB.
- At point B, draw a line BC of length 4 cm, also at a 90° angle to AB.
- Join the points D and C with a straight line. You now have the rectangle ABCD.
Part 2: Construct the inner square (4 cm x 4 cm)
- On the top line AB, measure 2 cm from point A and make a mark. Call this point P.
- On the bottom line DC, measure 2 cm from point D and make a mark. Call this point S.
- Use your ruler to join the points P and S with a straight vertical line. This line will be 4 cm long.
- Now, go back to the top line AB. From point P, measure 4 cm towards B and make a mark. Call this point Q. (You will notice that Q is 2 cm away from B).
- Similarly, on the bottom line DC, measure 4 cm from point S towards C and make a mark. Call this point R.
- Join the points Q and R with a straight vertical line.
Result and Verification
You have now completed the construction. The figure PQRS inside the rectangle is the required square.
- The outer shape ABCD is a rectangle of 8 cm and 4 cm.
- The inner shape PQRS has all sides equal to 4 cm, so it is a square.
- The distance from the left side of the rectangle to the square (AP) is 2 cm.
- The distance from the right side of the rectangle to the square (QB) is 2 cm.
Since the square is placed with equal spacing on both sides, its centre is the same as the centre of the rectangle.


Answer:
Here are the step-by-step instructions to construct the "Falling Squares" patterns as shown in the two figures.
Construction for Figure 1: Three Identical Squares
This figure is made of three identical squares, each with a side length of 4 cm.
Steps:
- Draw the Bottom Square: Start by using a ruler and a set square (or protractor) to draw the first square at the bottom. Make sure each side is exactly 4 cm long and all corners are perfect right angles (90°).
- Locate the Shared Corner: Find the top-left corner of the square you just drew. This point will also be the bottom-right corner of the middle square.
- Draw the Middle Square: From this shared corner point, draw a 4 cm line straight up and another 4 cm line straight to the right. Then, complete the second square using these new lines.
- Locate the Next Shared Corner: Now, find the top-left corner of this middle square. This point will be the bottom-right corner of the top square.
- Draw the Top Square: Repeat the process. From the new shared corner, draw a 4 cm line straight up and a 4 cm line straight to the right. Complete the third square.
Construction for Figure 2: Three Different Squares
This figure is made of three squares of different sizes: a 7 cm square at the bottom, a 5 cm square in the middle, and a 3 cm square at the top.
Steps:
- Draw the Bottom Square (7 cm): Begin by drawing the largest square. Use your ruler to make each side 7 cm long. Use a set square or protractor to ensure all corners are 90°.
- Locate the First Shared Corner: Find the top-left corner of the 7 cm square. This will be the bottom-right corner for the next square.
- Draw the Middle Square (5 cm): From this shared corner, draw a 5 cm line straight up and a 5 cm line straight to the right. Complete this second square.
- Locate the Second Shared Corner: Now, find the top-left corner of the 5 cm square you just drew. This will be the bottom-right corner for the smallest square.
- Draw the Top Square (3 cm): From this new shared corner, draw a 3 cm line straight up and a 3 cm line straight to the right. Complete the final, smallest square.

Construct this. Choose measurements of your choice. Note that the larger 4-sided figure is a square and so are the smaller ones.
Answer:
This is a fun pattern made of squares within a larger square. The question allows us to choose our own measurements to construct it. Let's pick some simple numbers to make it easy to draw.
Choosing our Measurements
Let's look at the smallest squares in the pattern. We will decide that the side length of these smallest squares will be 2 cm.
- The entire figure is a large square. If you count across the top, there are four of the smallest squares.
- So, the side length of the large outer square will be $4 \times 2 \text{ cm} = \textbf{8 cm}$.
- The large blank square at the bottom-left is made of two small squares across and two small squares down. Its side length will be $2 \times 2 \text{ cm} = \textbf{4 cm}$.
Steps for Construction
Part 1: Draw the Main Grid
- Start by drawing the large outer square. Using a ruler and a set square, draw an 8 cm by 8 cm square. Let's call its corners A, B, C, and D.
- Find the middle point of each side of this large square. This will be at the 4 cm mark on each side.
- Draw a straight horizontal line and a straight vertical line connecting these midpoints. This will divide your 8x8 cm square into four equal 4x4 cm quadrants.
- Now, you have a large blank 4x4 cm square in the bottom-left. Leave this one as it is.
- For the other three 4x4 cm quadrants (top-left, top-right, and bottom-right), you need to divide each one into four smaller squares. Find the midpoints of their sides (at the 2 cm mark) and draw lines to divide them. You will end up with a grid of 2x2 cm squares in these three sections.
Part 2: Add the Diagonals and Shading
- Now we need to add the details. We will be drawing a diagonal line from the top-left corner to the bottom-right corner in some of the 2x2 cm squares.
- In the top-left quadrant: Draw this diagonal in all four of the 2x2 cm squares.
- In the top-right quadrant: Draw this diagonal in all four of the 2x2 cm squares.
- In the bottom-right quadrant: Draw this diagonal in the top-left, top-right, and bottom-right squares. Leave the bottom-left square in this section blank.
- Finally, in every square where you drew a diagonal, carefully shade the upper triangle with parallel lines.
Result
After following all the steps, your drawing should look exactly like the figure in the question. You have successfully constructed the pattern.
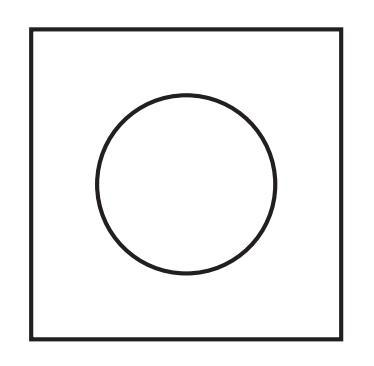
Hint: Think where the centre of the circle should be.
Answer:
To construct a square with a perfectly centered circular hole, we need to follow a few simple steps. The key, as the hint suggests, is to first find the exact center of the square. This point will also be the center for our circle.
Let's choose some easy measurements to work with. We will construct a square with a side length of 6 cm.
Analysis Before Drawing:
- If the square has a side length of 6 cm, the circle that fits perfectly inside (touching all four sides) must have a diameter equal to the side length of the square.
- The radius of a circle is half of its diameter.
So, the Diameter of the circle = 6 cm.
So, the Radius of the circle will be $6 \text{ cm} \div 2 = \textbf{3 cm}$.
Steps for Construction
Part 1: Draw the Square
- Use a ruler to draw a line segment AB of length 6 cm.
- Using a protractor or a set square, draw a line segment AD of length 6 cm at a perfect 90° angle from point A.
- Do the same at point B, drawing a 6 cm line segment BC at a 90° angle.
- Join the points D and C to complete the square ABCD.
Part 2: Find the Center of the Square
- The center of the square is the point where its diagonals intersect. Use your ruler to lightly draw the two diagonals: one line from corner A to corner C, and another from corner B to corner D.
- The point where these two lines cross is the exact center of the square. Mark this point and label it O.
Part 3: Draw the Circle
- Take your compass. Place the metal point firmly on the center point O.
- Adjust the width of the compass so that the pencil tip is 3 cm away from the metal point (this is the radius we calculated).
- Keeping the metal point on O, carefully rotate the compass to draw a complete circle.
Result and Verification
You have now constructed a square with a circular hole. If you have drawn it correctly, the edge of the circle will perfectly touch the middle of each of the four sides of the square.
The construction is correct because the center of the circle is the same as the center of the square, and its radius is exactly half the side length of the square, making it touch all sides.

Answer:
This construction involves drawing a large square, dividing it into four smaller, equal squares, and then drawing a perfectly centered circle inside each of these smaller squares.
Let's choose some convenient measurements to make the construction straightforward. We will start by drawing a large square with a side length of 8 cm.
Analysis Before Drawing:
- If the large square is 8 cm by 8 cm, dividing it into four equal smaller squares means each small square will have a side length of $8 \text{ cm} \div 2 = \textbf{4 cm}$.
- Each circle must fit perfectly inside one of these 4 cm by 4 cm squares. This means the diameter of each circle must be 4 cm.
- The radius of each circle is half of its diameter. Therefore, the radius for each circle will be $4 \text{ cm} \div 2 = \textbf{2 cm}$.
Steps for Construction
Part 1: Draw the Large Square and Divide It
- Use a ruler and a set square to draw a large square with sides of 8 cm. Label the corners A, B, C, and D.
- Find the midpoint of each side of this square by measuring 4 cm from a corner along each side. Mark these midpoints.
- Draw a straight horizontal line connecting the midpoints of the left and right sides.
- Draw a straight vertical line connecting the midpoints of the top and bottom sides.
You now have a large square perfectly divided into four smaller, identical squares, each with sides of 4 cm.
Part 2: Find the Center of Each Small Square
- To draw a circle in the center of each small square, we first need to find their exact centers.
- For the top-left square, lightly draw its two diagonals (from corner to corner). The point where they cross is the center. Mark this point O1.
- Repeat this process for the other three squares, marking their centers as O2, O3, and O4.
Part 3: Draw the Four Circles
- Take your compass and set its width to the radius we calculated, which is 2 cm.
- Place the metal point of the compass firmly on the first center point, O1.
- Carefully rotate the compass to draw a complete circle. It should touch the four sides of the small square it's in.
- Without changing the compass width, move the compass point to O2 and draw the second circle.
- Repeat this for the centers O3 and O4.
Result
You have now completed the construction. Your drawing should show a large square containing four smaller squares, each with a perfectly centered circular hole.
Question 6. Square with Curves
This is a square with 8 cm sidelengths.
Hint: Think where the tip of the compass can be placed to get all the 4 arcs to bulge uniformly from each of the sides. Try it out!

Answer:
This construction creates a beautiful curved shape inside a square. The key to drawing this is to understand where to place the compass and what radius to use, as the hint suggests.
Understanding the Hint and the Method
The pattern is made by drawing four large, identical arcs. To make the curves symmetrical, each arc is drawn by placing the compass point on one of the corners of the square. The radius of the compass should be equal to the side length of the square (8 cm).
When you draw an arc from a corner, it will connect the two adjacent corners. By doing this from all four corners, the arcs will overlap to create the shape in the middle.
Steps for Construction
Part 1: Draw the Square
- Using a ruler and a set square (or protractor), draw a perfect square with sides of 8 cm.
- Label the corners of the square as A, B, C, and D in a clockwise direction, starting from the top-left.
Part 2: Draw the Four Arcs
- First Arc: Place the metal point of your compass at corner A. Open the compass so that the pencil tip is exactly on corner B (or D). The radius will be 8 cm. Now, draw a smooth arc that connects point B to point D.
- Second Arc: Move the compass point to corner B. Without changing the radius (it should still be 8 cm), draw an arc that connects point A to point C.
- Third Arc: Move the compass point to corner C. With the same 8 cm radius, draw an arc that connects point B to point D.
- Fourth Arc: Finally, place the compass point on corner D. With the 8 cm radius, draw the last arc connecting point C to point A.
Result
After you have drawn all four arcs, the central area formed by the innermost edges of these curves will look exactly like the shape in the question.
Construct (Page 211)
Question 1. Construct a rectangle in which one of the diagonals divides the opposite angles into 50° and 40°.
Answer:
To construct this rectangle, we can start by constructing a right-angled triangle that will make up one-half of the rectangle. In any rectangle, all four corners are 90°. Since a diagonal splits one corner into 50° and 40°, the angles of the triangle formed by the diagonal will be 90°, 50°, and 40°.
Steps for Construction:
- Draw a straight line segment AB of any length you choose (for example, 6 cm).
- Place your protractor at point B and draw a line that makes a perfect 90° angle with AB. Make this line long enough to work with.
- Now, place your protractor at point A. Measure and draw a line from A that makes a 40° angle with the line AB. Extend this line until it crosses the 90° line you drew from point B.
- The point where the lines from A and B cross is the third corner of our rectangle. Label this point C. You have now created a triangle ABC with angles 90°, 40°, and 50° (at corner C).
- To complete the rectangle, we need to find the fourth corner, D. Place your protractor at point A and draw a line at a 90° angle to AB.
- Measure the length of the side BC with your ruler. Now, measure the same length along the 90° line from A and mark the point D.
- Join point D to point C with a ruler.
The figure ABCD is the required rectangle.
Why this works:
We started by building a right-angled triangle ABC. By construction, $\angle$B is 90° and $\angle$BAC is 40°. Since the sum of angles in a triangle is 180°, $\angle$BCA must be 50°.
When we complete the rectangle, the diagonal AC splits the corner A into $\angle$BAC = 40° and $\angle$CAD = 50° (since $\angle$A must be 90° in total). Similarly, it splits corner C into $\angle$BCA = 50° and $\angle$ACD = 40°.
Therefore, we have a rectangle where the diagonal divides the opposite angles into 50° and 40°.
Question 2. Construct a rectangle in which one of the diagonals divides the opposite angles into 45° and 45°. What do you observe about the sides?
Answer:
We are asked to construct a special rectangle where the diagonal cuts the corner angles exactly in half (since 45° + 45° = 90°). Let's construct it and see what kind of shape it is.
Steps for Construction:
- Draw a line segment AB. Let's make its length 5 cm.
- At point B, use a protractor or a set square to draw a line that is perpendicular (at a 90° angle) to AB.
- At point A, use your protractor to draw a line that makes a 45° angle with AB. Extend this line until it intersects the perpendicular line from B. Label the intersection point C.
- Now, we will complete the rectangle. At point A, draw a line perpendicular to AB.
- Measure the length of the side BC. Use your ruler to mark the same length on the perpendicular line from A. Label this point D.
- Join points C and D with a straight line.
The figure ABCD is the required rectangle.
Observation about the sides:
Now that the construction is complete, take your ruler and measure all four sides of the figure ABCD.
- We drew side AB to be 5 cm.
- If you measure side BC, you will find it is also 5 cm long.
- Side CD will be 5 cm, and side DA will be 5 cm.
AB = BC = CD = DA = 5 cm
Conclusion: We observe that all four sides of the rectangle are equal. A rectangle with all four sides of equal length is called a square.
Question 3. Construct a rectangle one of whose sides is 4 cm and the diagonal is of length 8 cm.
Answer:
We will construct the rectangle by first drawing a right-angled triangle formed by one side, the other side, and the diagonal.
Given:
Length of one side = 4 cm.
Length of the diagonal = 8 cm.
Steps for Construction:
- Draw a line segment AB of length 4 cm. This will be one side of the rectangle.
- At point B, use a protractor or set square to draw a long line that is perpendicular to AB (at a 90° angle). The side BC will be on this line.
- Now, take your compass and open it to a width of 8 cm (the length of the diagonal).
- Place the metal point of the compass at point A and draw an arc that cuts the perpendicular line you drew from B. The point where the arc intersects the line is corner C.
- To find the last corner D, you can do one of two things:
Method 1: From point A, draw a line perpendicular to AB. Measure the length of BC and mark that length from A to find D. Join C and D.
Method 2: Set your compass to the length of BC. From point A, draw an arc. Then, set your compass to 4 cm (the length of AB). From point C, draw another arc that crosses the first one. This intersection is point D. Join A to D and C to D.
ABCD is the required rectangle.
Why this works:
In any rectangle, the corner angles are 90°. This means that a diagonal splits the rectangle into two identical right-angled triangles. By constructing the triangle ABC with a right angle at B, a side AB of 4 cm, and a diagonal (hypotenuse) AC of 8 cm, we have created one half of the rectangle correctly. Completing the shape by making the opposite sides equal and parallel ensures we get the desired rectangle.
Question 4. Construct a rectangle one of whose sides is 3 cm and the diagonal is of length 7 cm.
Answer:
We can construct this rectangle by first creating a right-angled triangle using the given side and the diagonal.
Given:
Length of one side = 3 cm.
Length of the diagonal = 7 cm.
Steps for Construction:
- Draw a line segment AB of length 3 cm.
- At point B, use a protractor or a set square to draw a line perpendicular to AB (at a 90° angle).
- Set the width of your compass to 7 cm (the length of the diagonal).
- Place the metal tip of the compass on point A and draw an arc so that it intersects the perpendicular line from B. This point of intersection is corner C.
- Now, to find the fourth corner, D, set your compass to the length of side AB (3 cm). Place the compass tip at C and draw an arc.
- Next, set your compass to the length of side BC. Place the compass tip at A and draw another arc that crosses the one you just made. The intersection point is corner D.
- Join the points A to D and C to D to complete the rectangle.
ABCD is the required rectangle.
Why this works:
A rectangle is made up of two right-angled triangles joined along their longest side (the diagonal). We first constructed one of these triangles, $\triangle$ABC, with a 90° angle at B. We then constructed the second triangle, $\triangle$ADC, by making its sides equal to the opposite sides of the first triangle. This ensures that the final four-sided shape has equal opposite sides and four right angles, making it a rectangle.
Construct (Page 215)

Answer:
We need to construct a larger version of the house shown in the figure. In the original house, all the main sides (the square base and the triangle roof) are 5 cm long. In our new, bigger house, all these main sides will be 7 cm long.
You will need a ruler, a compass, and a protractor (or a set square) for this construction.
Steps for Construction
Part 1: Draw the Square Body of the House
- Start by drawing a horizontal line segment at the bottom. Use your ruler to make it exactly 7 cm long. Label the endpoints D and E.
- Place your protractor at point D and draw a line straight up, making a 90° angle with DE. Measure 7 cm along this line and mark the point B.
- Do the same thing at point E. Draw a 7 cm line straight up at a 90° angle and mark the point C.
- Join the points B and C with your ruler. You have now drawn the 7 cm by 7 cm square body of the house.
Part 2: Draw the Triangle Roof
- The top side of the square, BC, will be the base of our triangle roof. It is already 7 cm long.
- Take your compass and set its width to 7 cm using your ruler.
- Place the metal point of the compass on corner B and draw a large arc above the square.
- Now, place the compass point on corner C (without changing the 7 cm width) and draw another arc that crosses the first one.
- The point where the two arcs intersect is the peak of the roof. Label this point A.
- Use your ruler to draw straight lines connecting A to B and A to C. The roof is now complete.
Part 3: Draw the Curved Arc
- To draw the decorative curve below the roof, keep your compass set to 7 cm.
- Place the metal point of the compass on the peak of the roof, point A.
- Carefully draw an arc that starts at point B and swings down to point C.
Part 4: Draw the Door
- Find the center of the bottom line DE. Since DE is 7 cm long, the center is at 3.5 cm from either D or E. Mark this point lightly.
- Let's make the door 2 cm wide and 3 cm high. From the center point, measure 1 cm to the left and 1 cm to the right. Make two marks for the bottom corners of the door.
- From these two marks, draw vertical lines straight up, each 3 cm long.
- Join the tops of these two vertical lines to finish the door.
Result
You have now constructed a bigger house where the square body and the triangle roof all have sides of 7 cm.
Question 2. Try to recreate ‘A Person’, ‘Wavy Wave’ and ‘Eyes’ from the section Artwork, using ideas involved in the ‘House’ construction.
Answer:
The construction of the 'House' involved using a ruler to draw straight lines of specific lengths, a protractor or set square for right angles, and a compass to draw arcs and find intersection points. We can use these same basic techniques to create the other figures.
Recreating 'A Person'
The 'Person' can be drawn by combining simple shapes like a rectangle for the body, a circle for the head, and straight lines for the arms and legs. We can choose our own measurements.
Construction Steps:
- Body: Draw a rectangle that is 2 cm wide and 4 cm tall.
- Head: Find the midpoint of the top side of the rectangle. From this midpoint, measure up 0.5 cm to find the center for the head. Place your compass here and draw a circle with a radius of 1.5 cm.
- Legs: From the bottom two corners of the rectangle, draw two straight lines going downwards, each 4 cm long.
- Arms: From the top two corners of the rectangle, draw two straight lines going outwards and slightly downwards, each 3 cm long.
Recreating 'Wavy Wave'
The 'Wavy Wave' is a series of connected, smooth curves. We can create this using a compass to draw arcs, similar to how we drew the curved part of the house roof.
Construction Steps:
- Draw a light, straight horizontal line to guide you. Mark points along this line every 3 cm.
- Set your compass to a width of 3 cm.
- First Arc (Upwards): Place the compass point on the second mark and draw an arc from the first mark to the third mark.
- Second Arc (Downwards): Move the compass point to the fourth mark and draw an arc from the third mark down to the fifth mark.
- Continue this pattern, alternating between drawing arcs from above and below the guideline, to create a continuous wavy line.
Recreating 'Eyes'
The 'Eyes' can be constructed using two overlapping circles to create a classic eye shape, with a smaller circle inside for the pupil.
Construction Steps:
- First Eye: Draw a horizontal line segment that is 3 cm long. Mark its endpoints A and B.
- Set your compass to a width of 3 cm. Place the point on A and draw a large arc that passes through B. Then, place the point on B and draw another large arc that passes through A. The space where these two arcs overlap forms the eye shape.
- Pupil: Inside this eye shape, find a central point and draw a small circle with a radius of 0.5 cm.
- Second Eye: Leave a small gap (e.g., 2 cm) and repeat the entire process to draw a second, identical eye.
Question 3. Is there a 4-sided figure in which all the sides are equal in length but is not a square? If such a figure exists, can you construct it?
Answer:
Yes, such a 4-sided figure does exist. It is called a rhombus.
A square is a special kind of rhombus where all the corner angles are perfect 90° right angles. A non-square rhombus still has four equal sides, but its corners are not 90°. Instead, its opposite angles are equal (two are sharp, or acute, and two are wide, or obtuse).
How to Construct a Rhombus
We can construct a rhombus by choosing a side length and an angle that is not 90°. Let's choose a side length of 6 cm and an angle of 60°.
Construction Steps:
- Draw a line segment AB of length 6 cm.
- Place your protractor at point A and measure a 60° angle. Draw a line from A at this angle.
- Measure 6 cm along this new line from point A and mark the point D. You now have two sides of the rhombus.
- Now, take your compass and set its width to 6 cm (the side length).
- Place the metal point of the compass at point B and draw an arc.
- Next, place the metal point at point D and draw another arc that crosses the first one. The point where the arcs intersect is the last corner, C.
- Join points B to C and D to C with your ruler.
Verification:
By construction, all four sides (AB, AD, BC, and DC) are 6 cm long. The angle at corner A is 60°, which is not 90°. Therefore, the figure ABCD is a rhombus but not a square.

