| Latest Maths NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
Chapter 4 Data Handling and Presentation
Welcome to the solutions resource for Chapter 4, "Data Handling and Presentation," derived from the Class 6 Ganita Prakash textbook published by NCERT for the 2024-25 academic session. This chapter introduces students to the fundamental principles of managing information, a skill that is increasingly vital in our modern world. These meticulously prepared solutions aim to provide clear, comprehensive guidance on the essential techniques for organizing raw data, representing it visually, and extracting meaningful insights from it. This journey into data handling is crucial for developing analytical thinking and making informed interpretations based on collected information.
The initial phase of data handling often involves dealing with raw, unorganized information. These solutions will expertly guide students through the systematic process of bringing order to this data. A primary technique covered is the use of tally marks for efficiently counting occurrences within a dataset. Students will learn the standard method of grouping counts, for instance, representing a count of four as $||||$ and a count of five as $\bcancel{||||}$. Following the tallying process, the solutions demonstrate how to translate these counts into structured frequency distribution tables. This involves listing the different categories or values observed and recording their corresponding frequencies (the number of times each occurs), ensuring accuracy and clarity in the initial organization of data.
A major focus of this chapter, and consequently these solutions, lies in the graphical representation of data. Visual formats make data easier to understand at a glance. The solutions provide detailed, step-by-step instructions for constructing two key types of graphs suitable for this level:
- Pictographs: Guidance covers selecting an appropriate symbol to represent the data, crucially defining a key or scale (e.g., one symbol representing 10 items), and accurately drawing the correct number or fraction of symbols for each category based on the frequency and the chosen scale.
- Bar Graphs: The solutions walk through the entire process, emphasizing critical elements such as choosing a suitable numerical scale for the vertical axis, clearly labeling both the horizontal and vertical axes (including titles and units, if any), drawing rectangular bars of uniform width whose heights accurately correspond to the data values, and maintaining equal spacing between consecutive bars for clarity and correct visual comparison.
Beyond merely constructing these visual representations, a significant emphasis is placed on data interpretation. The solutions demonstrate how to effectively read and analyze information presented in pre-existing pictographs and bar graphs. Students will learn to answer specific questions by extracting information directly from the graphs – for example, identifying the category with the highest frequency (tallest bar or most symbols) or the lowest frequency, calculating total counts by summing up values, determining the difference between the values of two categories, and drawing simple yet valid conclusions based on the visual evidence. By engaging with these solutions for Chapter 4 of the Class 6 Ganita Prakash (NCERT 2024-25), students will cultivate practical skills in data management and visualization, appreciate the significance of accuracy and clarity in presenting information, and develop the analytical prowess needed to interpret data effectively in various academic and real-life contexts.
Figure it Out (Page 75 - 76)
Naresh and Navya decided to go to each student in the class and ask what their favourite game is. Then they prepared a list.
Navya is showing the list:

Question 1. What would you do to find the most popular game among Naresh’s and Navya’s classmates?
Answer:
To find the most popular game, I would systematically count how many students chose each game and then identify which game has the highest count.
The process involves these steps:
1. Identify all the unique games from the list: Kabaddi, Hockey, Satoliya (Pittu), Cricket, Badminton, and Football.
2. Create a frequency distribution table to organize the data. This table helps in systematically counting the preferences.
3. Tally the data. I would go through the original list and for each student's choice, I would place a tally mark next to the corresponding game. Applying this method to the given list results in the following completed table:
| Game | Tally Marks | Number of Students (Frequency) |
| Kabaddi | $\bcancel{||||} |$ | 6 |
| Hockey | $\bcancel{||||} |||$ | 8 |
| Satoliya (Pittu) | $\bcancel{||||}$ | 5 |
| Cricket | $\bcancel{||||} |$ | 6 |
| Badminton | $||$ | 2 |
| Football | $||||$ | 4 |
4. Analyze the table. After completing the table, I would compare the final counts in the "Number of Students (Frequency)" column.
5. The game with the highest frequency is the most popular game. From the table, we can see the highest frequency is 8, which corresponds to Hockey.
Question 2. What is the most popular game in their class?
Answer:
To find the most popular game, we first need to count the number of students who chose each game from the list. We can organize this information in a frequency distribution table.
By tallying the choices from the image, we get the following table:
| Game | Tally Marks | Number of Students (Frequency) |
| Kabaddi | $\bcancel{||||} |$ | 6 |
| Hockey | $\bcancel{||||} |||$ | 8 |
| Satoliya (Pittu) | $\bcancel{||||}$ | 5 |
| Cricket | $\bcancel{||||} |$ | 6 |
| Badminton | $||$ | 2 |
| Football | $||||$ | 4 |
By comparing the frequencies in the last column, we see that the highest number is 8, which corresponds to the game of Hockey.
Therefore, the most popular game in their class is Hockey.
Question 3. Try to find out the most popular game among your classmates.
Answer:
You can find the most popular game among your classmates by following these steps:
Step 1: Collect Data
Ask each of your classmates the question, "What is your favourite game?". Write down each person's answer to create a list.
Step 2: Organize the Data
Create a frequency table to organize the responses. Your table should have columns for the Game, Tally Marks, and the total Number of Students.
Here is a template you can use:
| Game | Tally Marks | Number of Students |
| Cricket | ||
| Football | ||
| Badminton | ||
| (Add more rows for other games) |
Step 3: Analyze the Results
After you have tallied all the answers, look at the 'Number of Students' column. The game with the highest count is the most popular game in your class.
a. What is the most popular TV show among her classmates?
b. When did India get independence?
c. How much water is getting wasted in her locality?
d. What is the capital of India?
Answer:
Data collection is required when the answer depends on specific people, places, or situations and is not a universally known fact.
a. What is the most popular TV show among her classmates?
To find this, Pari must ask her classmates for their preferences. This requires gathering new information directly from the source.
Answer: ✔
b. When did India get independence?
This is a fixed historical fact. The answer can be found in books or online and does not change. No new data is needed.
Answer: ✗
c. How much water is getting wasted in her locality?
This information is specific to her locality. To find the answer, she would need to observe, measure, or survey the area. This requires data collection.
Answer: ✔
d. What is the capital of India?
This is a well-established geographical fact. The answer is fixed and can be looked up easily. It does not require collecting data.
Answer: ✗
Figure it Out (Page 76 - 77)
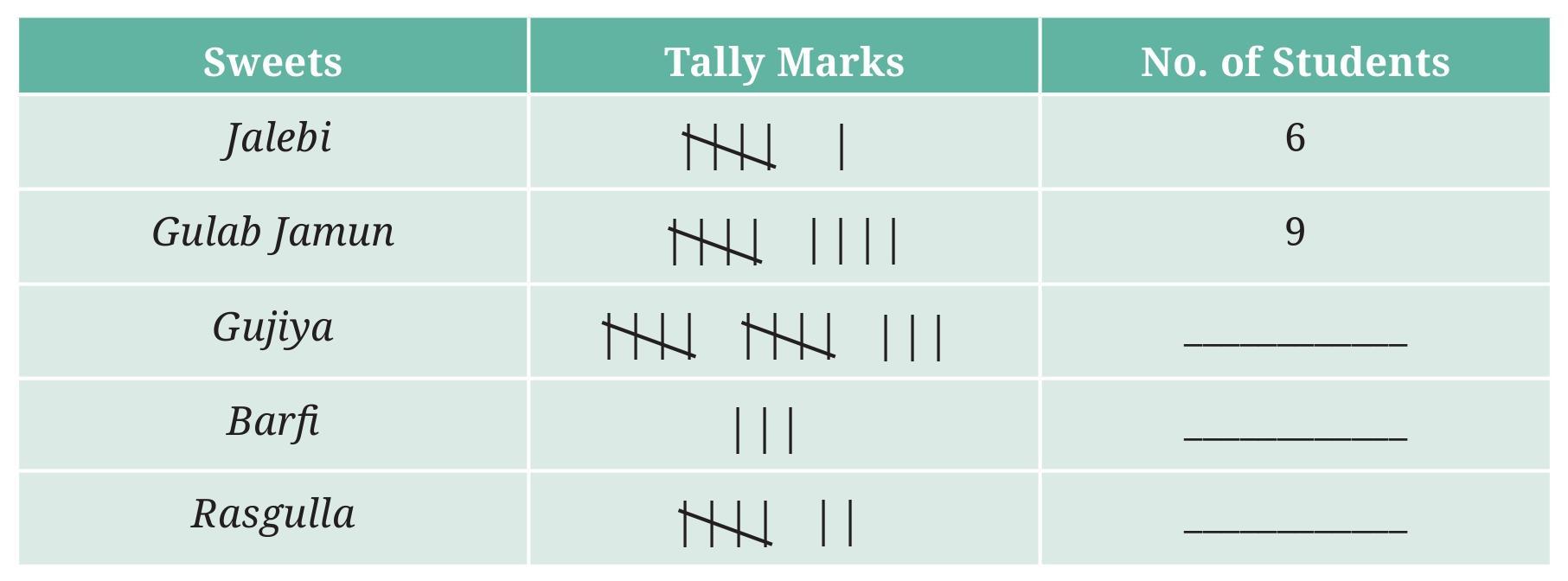
- How many students chose jalebi? ______
- Barfi was chosen by ______ students?
- How many students chose gujiya? _______
- Rasgulla was chosen by ______ students?
- How many students chose gulab jamun? _______
Answer:
To answer the questions, we first need to complete the table by counting the tally marks for each sweet and filling in the "No. of Students" column.
We know that $\bcancel{||||}$ represents a group of 5, and each individual line $|$ represents 1.
- Gujiya: $\bcancel{||||} \bcancel{||||} ||| = 5 + 5 + 3 = 13$ students.
- Barfi: $||| = 3$ students.
- Rasgulla: $\bcancel{||||} || = 5 + 2 = 7$ students.
The completed table is as follows:
| Sweets | Tally Marks | No. of Students |
| Jalebi | $\bcancel{||||} |$ | 6 |
| Gulab Jamun | $\bcancel{||||} ||||$ | 9 |
| Gujiya | $\bcancel{||||} \bcancel{||||} |||$ | 13 |
| Barfi | $|||$ | 3 |
| Rasgulla | $\bcancel{||||} ||$ | 7 |
Now we can answer the specific questions based on the completed table:
How many students chose jalebi? 6
Barfi was chosen by 3 students.
How many students chose gujiya? 13
Rasgulla was chosen by 7 students.
How many students chose gulab jamun? 9
Question 2. Is the above table sufficient to distribute each type of sweet to the correct student? Explain. If it is not sufficient, what is the alternative?
Answer:
No, the table provided is not sufficient to distribute each type of sweet to the correct student.
Explanation:
The table is a summary of the data, showing only the frequency (the total number) of students who prefer each sweet. For example, it tells Shri Nilesh that he needs 6 Jalebis and 9 Gulab Jamuns, but it does not tell him which specific students chose Jalebi or Gulab Jamun. Without the names of the students linked to their choices, he cannot perform the correct distribution.
Alternative:
To solve this problem, the data needs to be recorded in a way that links each student to their preference. The best alternative would be to create a list or a table with two columns: one for the student's name and one for their chosen sweet.
An example of such a table would be:
| Student Name | Favourite Sweet |
| (e.g., Priya) | Gulab Jamun |
| (e.g., Rohan) | Jalebi |
| (e.g., Simran) | Gujiya |
| ... and so on for all students. |
This format provides the necessary information to ensure that every student receives the exact sweet they chose.
Figure it Out (Page 77 - 79)

3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 6, 6, 6, 6, 7
- The largest shoe size in the class is _________
- The smallest shoe size in the class is _________
- There are _________ students who wear shoe size 5.
- There are _________ students who wear shoe sizes larger than 4.
Answer:
We can find the answers by carefully observing the list of shoe sizes that Sushri Sandhya arranged in ascending order:
3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 6, 6, 6, 6, 7
- The largest shoe size is the last number in the sorted list. Therefore, the largest shoe size in the class is 7.
- The smallest shoe size is the first number in the sorted list. Therefore, the smallest shoe size in the class is 3.
- To find the number of students who wear shoe size 5, we count the number of times '5' appears in the list. There are 10 students who wear shoe size 5.
- To find the number of students who wear shoe sizes larger than 4, we need to count all the students who wear sizes 5, 6, and 7.
Number of students with size 5 = 10
Number of students with size 6 = 4
Number of students with size 7 = 1
Total students = $10 + 4 + 1 = 15$.
Therefore, there are 15 students who wear shoe sizes larger than 4.
Question 2. How did arranging the data in ascending order help to answer these questions?
Answer:
Arranging the data in ascending order (from smallest to largest) is a crucial step in data organization that makes answering these questions significantly easier, faster, and more accurate.
Here’s how it helped for each specific task:
1. Finding the Largest and Smallest Shoe Size:
In a sorted list, the smallest value is always the first number and the largest value is always the last number. This allows for immediate identification without needing to scan the entire set of random numbers.
2. Counting Students with Shoe Size 5:
Sorting groups all the identical values together. All the '5's are placed consecutively in the list. This makes it very easy to count them quickly and accurately, without the risk of missing any, which is a common error when counting from a jumbled list.
3. Counting Students with Shoe Sizes Larger than 4:
In an ascending list, once you locate the first number greater than 4 (which is the first '5'), you know that all subsequent numbers in the list will also be greater than 4. You can simply count from that point to the end, instead of having to check every single number in the entire dataset individually.
In summary, sorting transforms a chaotic set of numbers into an organized structure, which streamlines the process of finding key information like minimums, maximums, and frequencies, thereby making the data analysis much more efficient.
Question 3. Are there other ways to arrange the data?
Answer:
Yes, there are several other effective ways to arrange the data besides ascending order. Each method has its own advantages for understanding the information.
1. Descending Order
This is the direct opposite of ascending order. The data can be arranged from the largest value to the smallest value.
For this data, it would look like: 7, 6, 6, 6, 6, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 4, 4, 4, 4, 4, 4, 4, 4, 4, 3, 3, 3.
This method is equally effective for quickly finding the largest and smallest sizes.
2. Frequency Distribution Table
This is a very powerful and common method in statistics. Instead of listing every single data point, you list each unique shoe size and then count how many times it appears (its frequency). This is often done using tally marks.
Here is how it would look for the shoe size data:
| Shoe Size | Tally Marks | Number of Students (Frequency) |
| 3 | $|||$ | 3 |
| 4 | $\bcancel{||||} ||||$ | 9 |
| 5 | $\bcancel{||||} \bcancel{||||}$ | 10 |
| 6 | $||||$ | 4 |
| 7 | $|$ | 1 |
This table condenses the data and makes it very easy to see which shoe size is the most or least common at a glance.
3. Visual Arrangements (Graphs and Plots)
The data can also be arranged into a visual format, which can make patterns even clearer.
- A Bar Graph could be used, where each shoe size is a bar, and the height of the bar shows the number of students.
- A Line Plot (or Dot Plot) could be made. This involves drawing a number line and placing an 'X' or a dot above a shoe size for each student who wears it.
a. Which tree was found in the greatest number?
b. Which tree was found in the smallest number?
c. Were there any two trees found in the same numbers?
Answer:
This is an activity for you to do by observing your surroundings. The answers will be based on what you see. Here is an example to help you understand how to do it.
Let's pretend that on my way to school, I counted the different trees and filled my table like this:
| Tree | No. of Trees |
| Peepal | 8 |
| Neem | 12 |
| Banyan | 5 |
| Mango | 12 |
| Gulmohar | 7 |
Now, based on this example table, let's answer the questions.
a. Which tree was found in the greatest number?
To find this, we look for the biggest number in the 'No. of Trees' column. The biggest number is 12. Two trees have this number: Neem and Mango. So, the Neem and Mango trees were found the most.
b. Which tree was found in the smallest number?
To find this, we look for the smallest number in the 'No. of Trees' column. The smallest number is 5, which is for the Banyan tree. So, the Banyan tree was found the least.
c. Were there any two trees found in the same numbers?
Yes. If we look at the table, we can see that both the Neem tree and the Mango tree were found 12 times. They have the same number.
Important Note: Remember, this is just an example. You should go out, count the trees you see, fill in your own table, and then write your own answers!
a. The letter found the most number of times is ________
b. The letter found the least number of times is ________
c. List the five letters ‘c’, ‘e’, ‘i’, ‘r’, ‘x’ in ascending order of frequency. Now, compare the order of your list with that of your classmates. Is your order the same or nearly the same as theirs? (Almost everyone is likely to get the order ‘x, c, r, i, e’.) Why do you think this is the case?
d. Write the process you followed to complete this task.
e. Discuss with your friends the processes they followed.
f. If you do this task with another news item, what process would you follow?
Answer:
This is a fun activity where your answers will depend on the news article you choose. Here is an example to show you how to complete it.
Example Activity
First, I chose a short news item. Let's pretend my news item says:
"The city experienced extreme rainfall yesterday. Rescue crews are working to clear the roads. Experts advise citizens to exercise caution and remain indoors."
Next, I chose 'a' as my "other letter of your choice". Now, I will count how many times each letter appears in the article.
- c: city, crews, exercise, caution, citizens = 5 times
- e: experienced, extreme, yesterday, Rescue, crews, clear, Experts, exercise, citizens, remain = 10 times
- i: city, experienced, rainfall, citizens = 4 times
- r: experienced, extreme, rainfall, Rescue, crews, are, working, clear, roads, Experts = 10 times
- x: experienced, extreme, Experts, exercise = 4 times
- a: rainfall, are, roads, advise, caution, remain = 6 times
Now, I will fill in the table with my results:
| Letter | c | e | i | r | x | Any other letter of your choice: a |
| Number of times found in the news item | 5 | 10 | 4 | 10 | 4 | 6 |
Answering the Questions (Based on my example)
a. The letter found the most number of times is ________
In my example, the highest number is 10. Two letters, ‘e’ and ‘r’, were found 10 times.
b. The letter found the least number of times is ________
The smallest number is 4. The letters ‘i’ and ‘x’ were found 4 times.
c. List the five letters ‘c’, ‘e’, ‘i’, ‘r’, ‘x’ in ascending order of frequency. Now, compare the order of your list with that of your classmates. Is your order the same or nearly the same as theirs? (Almost everyone is likely to get the order ‘x, c, r, i, e’.) Why do you think this is the case?
My counts are: i=4, x=4, c=5, e=10, r=10.
Ascending order of frequency: i, x, c, e, r (since i and x are tied, and e and r are tied).
This order is a little different from the expected ‘x, c, r, i, e’. This is because my news item was very short. If we take a very long article or a whole book, we will find a similar pattern. This happens because in the English language, some letters are used much more often than others. The letter 'e' is the most common of all, while 'x' is one of the rarest. That's why most students will find 'x' very few times and 'e' very frequently.
d. Write the process you followed to complete this task.
The process I followed was:
1. I chose a small news article to work with.
2. I decided which extra letter I wanted to count (I chose 'a').
3. I read the article slowly and carefully, focusing on one letter at a time. For example, I first went through the whole article just to count all the 'c's.
4. I repeated this step for each of the letters: 'e', 'i', 'r', 'x', and 'a'.
5. I wrote down the final count for each letter in the table.
e. Discuss with your friends the processes they followed.
This is a good idea. You can ask your friends how they made sure their counting was correct. Maybe some of them used a highlighter pen to mark the letters as they counted, or maybe they used tally marks on a separate paper to keep track.
f. If you do this task with another news item, what process would you follow?
I would follow the exact same process as described in part (d). It is a good, systematic method that helps to avoid mistakes and ensures that the counting is accurate. The process works for any piece of text.
Intext Question (Page 80)

Question: Which mode of travel is used by the most number of students?
Answer:
To find the mode of travel used by the most number of students, we will use the provided data to see which category has the highest count.
The number of students for each mode of travel is as follows:
- Private car: 4 students.
- Public bus: 5 students.
- School bus: 11 students.
- Cycle: 3 students.
- Walking: 7 students.
Now, we compare these numbers to find the largest value:
4 (Private car), 5 (Public bus), 11 (School bus), 3 (Cycle), 7 (Walking).
The largest number in this set is 11.
The number 11 corresponds to the School bus. Therefore, the mode of travel used by the most number of students is the School bus.
Question: Which mode of travel is used by the least number of students?
Answer:
To find the mode of travel used by the least number of students, we need to find the category with the smallest number of students.
Let's look at the number of students for each mode of travel:
- Private car: 4 students.
- Public bus: 5 students.
- School bus: 11 students.
- Cycle: 3 students.
- Walking: 7 students.
Now, we compare these numbers to find the smallest value:
4 (Private car), 5 (Public bus), 11 (School bus), 3 (Cycle), 7 (Walking).
The smallest number in this list is 3.
The number 3 corresponds to the Cycle. Therefore, the mode of travel used by the least number of students is the Cycle.
Figure it Out (Page 83 - 85)

a. On which day were the minimum number of books borrowed?
b. What was the total number of books borrowed during the week?
c. On which day were the maximum number of books borrowed? What may be the possible reason?
Answer:
On the basis of the above data, let's list the number of books borrowed each day:
- Monday: 5 books
- Tuesday: 4 books
- Wednesday: 2 books
- Thursday: 0 books
- Friday: 5 books
- Saturday: 8 books
a. On which day were the minimum number of books borrowed?
By looking at the numbers, the smallest number of books borrowed is 0. This occurred on Thursday.
b. What was the total number of books borrowed during the week?
To find the total, we add the number of books borrowed each day:
$5 + 4 + 2 + 0 + 5 + 8 = 24$
A total of 24 books were borrowed during the week.
c. On which day were the maximum number of books borrowed? What may be the possible reason?
The largest number of books borrowed is 8. This happened on Saturday.
Possible Reason: Students often borrow more books on Saturday because it is the beginning of the weekend. They have more free time on Saturday and Sunday to read the books they borrow.

Prepare a pictograph using the symbol 🪁 to represent 100 kites. Answer the following questions:
a. How many symbols represent the kites that Rani purchased?
b. Who purchased the maximum number of kites?
c. Who purchased more kites, Jasmeet or Chaman?
d. Rukhsana says Poonam Ben purchased more than double the number of kites that Rani purchased. Is she correct? Why?
Answer:
First, we will prepare a pictograph based on the new data. The key is that one full symbol 🪁 represents 100 kites. This means a half symbol, representing 50 kites, will be shown as 🪁.
Here is the pictograph:
| Shopkeeper | Number of Kites Sold ( 🪁 = 100 Kites) |
| Chaman (250) | 🪁🪁🪁 |
| Rani (300) | 🪁🪁🪁 |
| Rukhsana (100) | 🪁 |
| Jasmeet (450) | 🪁🪁🪁🪁🪁 |
| Jetha Lal (250) | 🪁🪁🪁 |
| Poonam Ben (700) | 🪁🪁🪁🪁🪁🪁🪁 |
a. How many symbols represent the kites that Rani purchased?
Rani purchased 300 kites. Since one symbol represents 100 kites, we divide 300 by 100.
$300 \div 100 = 3$.
So, 3 full symbols represent the kites Rani purchased.
b. Who purchased the maximum number of kites?
By looking at the table of data or the pictograph, we can see that the highest number of kites sold is 700. This corresponds to Poonam Ben.
c. Who purchased more kites, Jasmeet or Chaman?
Jasmeet purchased 450 kites, and Chaman purchased 250 kites. Since 450 is greater than 250, Jasmeet purchased more kites.
d. Rukhsana says Poonam Ben purchased more than double the number of kites that Rani purchased. Is she correct? Why?
Yes, Rukhsana is correct.
Reason:
Number of kites Rani purchased = 300.
Double the number of kites Rani purchased = $2 \times 300 = 600$.
Number of kites Poonam Ben purchased = 700.
Since 700 is greater than 600, Poonam Ben did purchase more than double the number of kites that Rani purchased.
Intext Question (Page 86)

1. In Class 2, ___________ students were absent that day.
2. In which class were the maximum number of students absent?___________
3. Which class had full attendance that day? ___________
Answer:
To answer these questions, we need to read the information from the bar graph. The height of each bar tells us the number of students who were absent in that class.
By looking at the graph, we can find the number of absent students for each class:
- Class 1: 3 students were absent.
- Class 2: 5 students were absent.
- Class 3: 4 students were absent.
- Class 4: 2 students were absent.
- Class 5: 0 students were absent (there is no bar).
- Class 6: 1 student was absent.
- Class 7: 5 students were absent.
- Class 8: 7 students were absent.
1. In Class 2, ___________ students were absent that day.
We look at the bar for "Class 2". The top of the bar lines up with the number 5 on the "Number of students" axis. Therefore, in Class 2, 5 students were absent that day.
2. In which class were the maximum number of students absent?___________
The maximum number means the highest number. We need to find the tallest bar. The tallest bar is for "Class 8", which reaches the number 7. Therefore, Class 8 had the maximum number of students absent.
3. Which class had full attendance that day? ___________
Full attendance means zero students were absent. We look for a class that has no bar. "Class 5" has no bar, which means 0 students were absent. Therefore, Class 5 had full attendance that day.
Figure it Out (Page 88)
The number of vehicles passing through the crossing each hour from 6 am to 12:00 noon is shown in the bar graph. One unit of length stands for 100 vehicles.

Question 1. How many total cars passed through the crossing between 6 am and noon?
Answer:
To find the total number of cars that passed through the crossing, we first need to read the number of vehicles for each one-hour time interval from the horizontal bar graph.
By reading the length of each bar against the 'Number of vehicles' axis, we get the following data:
- 6–7 am: The bar ends halfway between 100 and 200, which represents 150 vehicles.
- 7–8 am: The bar ends at 1200, representing 1200 vehicles.
- 8–9 am: The bar ends at 1000, representing 1000 vehicles.
- 9–10 am: The bar ends halfway between 800 and 900, which represents 850 vehicles.
- 10–11 am: The bar ends at 700, representing 700 vehicles.
- 11–12 am: The bar ends at 600, representing 600 vehicles.
Now, to find the total number of cars, we add the number of vehicles from all the time intervals:
Total cars = $150 + 1200 + 1000 + 850 + 700 + 600$
Adding these numbers together:
$150 + 1200 + 1000 + 850 + 700 + 600 = 4500$
Therefore, a total of 4500 cars passed through the crossing between 6 am and noon.
Question 2. Why do you think so little traffic occurred during the hour of 6–7 am, as compared to the other hours from 7 am-noon?
Answer:
The bar graph shows very little traffic between 6 am and 7 am.
The traffic is much heavier in the later hours.
This is because 6 am to 7 am is very early in the morning.
Most people are still at home during this time.
They are getting ready for their day.
Schools and offices usually start after 8 am.
So, most people start traveling after 7 am.
This is why there are fewer cars on the road so early.
Question 3. Why do you think the traffic was the heaviest between 7 am and 8 am?
Answer:
The graph shows the traffic was heaviest between 7 am and 8 am.
This time is called the morning rush hour.
Most schools and offices open around 8 am or 9 am.
A very large number of people travel at this time.
They all need to reach their destinations on time.
So, many cars, buses, and other vehicles are on the road together.
This is why the traffic is the heaviest during this hour.
Question 4. Why do you think the traffic was lesser and lesser each hour after 8am all the way until noon?
Answer:
The graph shows that after 8 am, the traffic starts to decrease.
It becomes less and less with each hour until noon.
This happens because the morning rush hour is over.
By 9 am, most people have already reached their school or office.
They are no longer driving on the roads.
With fewer people commuting, the number of cars on the road goes down.
This makes the traffic lighter during the later morning hours.
Intext Question (Page 93)

Use the bar graph to answer the following questions:
Question 1. On which item does Imran’s family spend the most and the second most?
Answer:
To answer this question, we will use the corrected data provided for Imran's family's expenditure.
The expenditure on each item is as follows:
| Item | Expenditure (in |
| House rent | 3000 |
| Food | 3400 |
| Education | 800 |
| Electricity | 400 |
| Transport | 600 |
| Miscellaneous | 1200 |
First, let's find the item with the highest expenditure. By comparing all the amounts, we can see that
Next, we find the second-highest expenditure. The second largest amount in the table is
Therefore, Imran's family spends the most on Food and the second most on House rent.
Question 2. Is the cost of electricity about one-half the cost of education?
Answer:
To answer this, we first need to find the expenditure on Electricity and Education from the given data.
Expenditure on Electricity =
Expenditure on Education =
Now, we need to calculate one-half the cost of education.
One-half the cost of education = $\frac{1}{2} \times \textsf{₹}800$
=
Now we compare the cost of electricity with one-half the cost of education.
The cost of electricity is
One-half the cost of education is also
The two amounts are exactly the same.
Yes, the cost of electricity is not just "about" one-half, it is exactly one-half the cost of education.
Question 3. Is the cost of education less than one-fourth the cost of food?
Answer:
To answer this, we need to find the expenditure on Education and Food from the given data.
Expenditure on Education =
Expenditure on Food =
Now, let's calculate one-fourth the cost of food.
One-fourth the cost of food = $\frac{1}{4} \times \textsf{₹}3400$
= $\frac{3400}{4}$
=
Now we check if the cost of education is less than one-fourth the cost of food.
Is
The statement is true.
Yes, the cost of education (
Figure it Out (Page 93 - 100)

Help her prepare a bar graph representing this data.
Answer:
To help Samantha prepare a bar graph, we will use the data she collected. A bar graph will help to show the number of each insect and critter in a way that is easy to see and compare.
Steps to Prepare the Bar Graph:
1. Draw the Axes: First, we need to draw two lines, one horizontal and one vertical, that meet at a corner. The horizontal line is the X-axis, and the vertical line is the Y-axis.
2. Label the Axes:
- On the horizontal line (X-axis), we will write the names of the insects and critters. We should leave equal space between each name. Let's label this axis "Insects and Critters".
- On the vertical line (Y-axis), we will mark numbers to show the count of the insects. Since the highest number is 10, we can mark from 0 to 10. Let's label this axis "Number Found".
3. Choose a Scale: For the Y-axis, we can decide that a height of 1 unit will represent 1 insect. This is a simple and clear scale (Scale: 1 unit = 1 insect).
4. Draw the Bars: Now, we draw a rectangular bar above the name of each insect. The height of the bar will match the number of insects found.
- Mites: The number is 6, so we draw a bar up to the mark '6' on the Y-axis.
- Caterpillars: The number is 10, so we draw a bar up to the mark '10'.
- Beetles: The number is 5, so we draw a bar up to the mark '5'.
- Butterflies: The number is 3, so we draw a bar up to the mark '3'.
- Grasshoppers: The number is 2, so we draw a bar up to the mark '2'.
5. Add a Title: At the top of the graph, we should write a title, for example, "Insects and Critters Found in a Tea Garden".
The final bar graph would look like this:


She used this data and prepared a bar graph on the board to discuss the data with her students, but someone erased a portion of the graph.

a. Write the number of tickets sold for Vidisha above the bar.
b. Write the number of tickets sold for Jabalpur above the bar.
c. The bar for Vidisha is 6 unit lengths and the bar for Jabalpur is 5 unit lengths. What is the scale for this graph?
d. Draw the correct bar for Sagar.
e. Add the scale of the bar graph placing the correct numbers on the vertical axis.
f. Are the bars for Seoni and Indore correct in this graph? If not, draw the correct bar(s).
Answer:
Let's solve this step by step using the given data table and the incomplete bar graph.
Data from the table:
- Vidisha: 24 tickets
- Jabalpur: 20 tickets
- Seoni: 16 tickets
- Indore: 28 tickets
- Sagar: 16 tickets
a. Write the number of tickets sold for Vidisha above the bar.
The number of tickets sold for Vidisha is 24.
b. Write the number of tickets sold for Jabalpur above the bar.
The number of tickets sold for Jabalpur is 20.
c. The bar for Vidisha is 6 unit lengths and the bar for Jabalpur is 5 unit lengths. What is the scale for this graph?
To find the scale, we can see how many tickets one unit length represents.
For Vidisha: 24 tickets are represented by 6 units. So, 1 unit = $24 \div 6 = 4$ tickets.
For Jabalpur: 20 tickets are represented by 5 units. So, 1 unit = $20 \div 5 = 4$ tickets.
The scale is consistent. Therefore, the scale for this graph is 1 unit length = 4 tickets.
d. Draw the correct bar for Sagar.
Sagar has 16 tickets sold. Using our scale (1 unit = 4 tickets), the height of the bar for Sagar should be $16 \div 4 = 4$ unit lengths.
e. Add the scale of the bar graph placing the correct numbers on the vertical axis.
Since 1 unit = 4 tickets, the marks on the vertical axis (Y-axis) should go up in multiples of 4. Starting from the bottom, the marks would be 0, 4, 8, 12, 16, 20, 24, 28, etc.
f. Are the bars for Seoni and Indore correct in this graph? If not, draw the correct bar(s).
Let's check the existing bars for Seoni and the missing bar for Indore based on our scale.
For Seoni:
- Data: 16 tickets
- Required bar height: $16 \div 4 = 4$ units.
- The bar in the graph is 4 units high. So, the bar for Seoni is correct.
For Indore:
- Data: 28 tickets
- Required bar height: $28 \div 4 = 7$ units.
- The bar for Indore is missing in the incomplete graph. We need to draw a bar that is 7 units high.
Here is the completed bar graph with all the corrections and additions:


a. Prepare a frequency distribution table for the data.
b. Which means of transport was used the most?
c. If you were there to collect this data, how could you do it? Write the steps or process.
Answer:
a. Prepare a frequency distribution table for the data.
Based on the corrected counts of the vehicles in Chinu's list, here is the frequency distribution table:
| Means of Transport | Tally Marks | Frequency (Number of Vehicles) |
| Bike | $\bcancel{||||} \bcancel{||||} |||$ | 13 |
| Car | $\bcancel{||||} |$ | 6 |
| Bicycle | $\bcancel{||||} |||$ | 8 |
| Bus | $||||$ | 4 |
| Auto | $\bcancel{||||} |||$ | 8 |
| Scooter | $\bcancel{||||} ||||$ | 9 |
| Bullock cart | $||$ | 2 |
b. Which means of transport was used the most?
To find the most used means of transport, we look for the highest number in the "Frequency" column of the table.
The highest frequency is 13.
This frequency corresponds to the Bike.
Therefore, the bike was the most used means of transport.
c. If you were there to collect this data, how could you do it? Write the steps or process.
If I had to collect this data myself, I would follow these steps to make sure my count is accurate:
Step 1: Preparation
I would get a notebook and pen and create a table with the names of different vehicles and a column for tally marks before starting.
Step 2: Observation Point
I would choose a safe spot by the road where I could clearly see all the passing vehicles.
Step 3: Recording Data
Starting at 9 am, I would watch the traffic. Every time a vehicle passed, I would make a tally mark ($|$) in the correct row of my table.
Step 4: Concluding Observation
I would continue recording until exactly 10 am and then stop.
Step 5: Final Count
After finishing the observation, I would count the tally marks for each vehicle to find the total frequency for each type.
a. The minimum number of times.
b. The maximum number of times.
c. Find numbers that appeared an equal number of times.
Answer:
This is an activity that you need to perform yourself. The answers will be different for everyone depending on the outcome of your die rolls.
Here is a sample answer based on an example set of 30 die rolls to show you how to do it.
Step 1: Record the Data
Let's pretend I rolled a die 30 times and got the following numbers:
3, 5, 1, 4, 6, 2, 5, 4, 1, 6, 3, 5, 2, 5, 4, 1, 6, 5, 2, 4, 5, 3, 1, 4, 6, 2, 5, 4, 3, 5
Step 2: Prepare the Frequency Distribution Table
Now, I will count how many times each number appeared and put the result in a table using tally marks.
| Number on Die | Tally Marks | Frequency (Number of Times) |
| 1 | $||||$ | 4 |
| 2 | $||||$ | 4 |
| 3 | $||||$ | 4 |
| 4 | $\bcancel{||||} |$ | 6 |
| 5 | $\bcancel{||||} |||$ | 8 |
| 6 | $||||$ | 4 |
a. The minimum number of times.
By looking at the table, the smallest frequency is 4. The numbers that appeared 4 times are 1, 2, 3, and 6.
b. The maximum number of times.
The largest frequency in the table is 8. The number that appeared 8 times is 5.
c. Find numbers that appeared an equal number of times.
From the table, we can see that the numbers 1, 2, 3, and 6 all appeared an equal number of times (4 times each).
Note: Remember to do this activity with your own die rolls and create your own table to find your own answers.
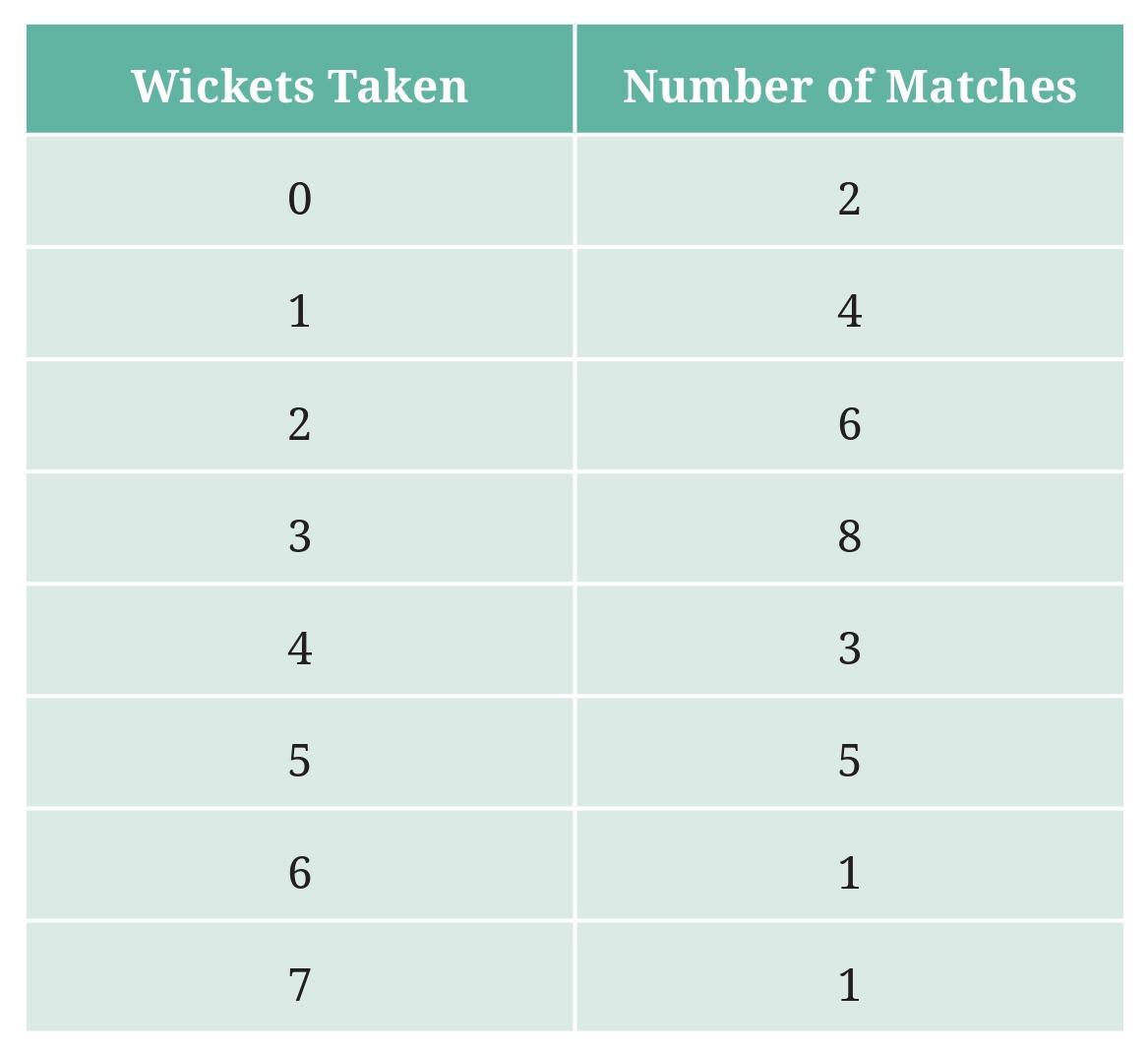
a. What information is this table giving?
b. What may be the title of this table?
c. What caught your attention in this table?
d. In how many matches has Bumrah taken 4 wickets?
e. Mayank says “If we want to know the total number of wickets he has taken in his last 30 matches, we have to add the numbers 0, 1, 2, 3 …, up to 7.” Can Mayank get the total number of wickets taken in this way? Why?
f. How would you correctly figure out the total number of wickets taken by Bumrah in his last 30 matches, using this table?
Answer:
Here is the data table for reference:
| Wickets Taken | Number of Matches |
| 0 | 2 |
| 1 | 4 |
| 2 | 6 |
| 3 | 8 |
| 4 | 3 |
| 5 | 5 |
| 6 | 1 |
| 7 | 1 |
a. What information is this table giving?
This table gives us information about Jaspreet Bumrah's bowling performance in his last 30 matches.
It tells us the frequency, which is the number of times he took a specific number of wickets (from 0 to 7) in a match.
b. What may be the title of this table?
A suitable title for this table would be: "Frequency of Wickets Taken by Jaspreet Bumrah in His Last 30 Matches".
c. What caught your attention in this table?
The most noticeable thing is that he took 3 wickets in 8 matches. This was his most common performance in the last 30 matches.
d. In how many matches has Bumrah taken 4 wickets?
We can find this information directly from the table. We look for the row where 'Wickets Taken' is 4.
The corresponding 'Number of Matches' is 3.
e. Mayank says “If we want to know the total number of wickets he has taken in his last 30 matches, we have to add the numbers 0, 1, 2, 3 …, up to 7.” Can Mayank get the total number of wickets taken in this way? Why?
No, Mayank's method is incorrect.
Reason: His method ignores how many times each event occurred. For example, Bumrah took 3 wickets in 8 different matches, not just one time. Simply adding the numbers from 0 to 7 doesn't use the frequency data and will give the wrong total.
f. How would you correctly figure out the total number of wickets taken by Bumrah in his last 30 matches, using this table?
To find the correct total number of wickets, we must multiply the wickets taken in each row by the number of matches for that row, and then add all these results together.
The calculation is as follows:
Total Wickets = $(0 \times 2) + (1 \times 4) + (2 \times 6) + (3 \times 8) + (4 \times 3) \ $$ + (5 \times 5) \ $$ + (6 \times 1) + (7 \times 1)$
$= 0 + 4 + 12 + 24 + 12 + 25 + 6 + 7$
$= 90$
The correct total number of wickets taken by Bumrah in his last 30 matches is 90.

Observe the pictograph and answer the following questions—
a. Which village has the smallest number of tractors?
b. Which village has the most tractors?
c. How many more tractors does Village C have than Village B?
d. Komal says, “Village D has half the number of tractors as Village E.” Is she right?
Answer:
Using the corrected data, let's list the number of tractors for each village:
- Village A: 6 tractors
- Village B: 5 tractors
- Village C: 8 tractors
- Village D: 3 tractors
- Village E: 6 tractors
a. Which village has the smallest number of tractors?
We compare the number of tractors in each village: 6, 5, 8, 3, 6.
The smallest number in this list is 3.
Therefore, Village D has the smallest number of tractors.
b. Which village has the most tractors?
Looking at the list of numbers again, the largest number is 8.
Therefore, Village C has the most tractors.
c. How many more tractors does Village C have than Village B?
To find out, we subtract the number of tractors in Village B from Village C.
Tractors in Village C = 8
Tractors in Village B = 5
Difference = $8 - 5 = 3$
Village C has 3 more tractors than Village B.
d. Komal says, “Village D has half the number of tractors as Village E.” Is she right?
Let's verify her statement with the data.
Number of tractors in Village D = 3
Number of tractors in Village E = 6
Now, we find what is half the number of tractors in Village E:
Half of 6 is $\frac{6}{2} = 3$.
Since Village D has 3 tractors, her statement is correct.
Yes, Komal is right.

Observe this pictograph and answer the following questions:
a. Which class has the least number of girl students?
b. What is the difference between the number of girls in Classs 5 and 6?
c. If 2 more girls were admitted in Class 2, how would the graph change?
d. How many girls are there in Class 7?
Answer:
First, let's understand the pictograph. The key says that one full symbol of a girl represents 4 girls. This means partial symbols represent fewer girls:
- A three-quarter symbol represents 3 girls.
- A half symbol represents 2 girls.
- A one-quarter symbol represents 1 girl.
Now, let's find the number of girls in each class:
| Class | Calculation | Number of Girls |
| 1 | 6 full symbols $\times$ 4 | 24 |
| 2 | 4 full symbols + 1 half symbol = (4 $\times$ 4) + 2 | 18 |
| 3 | 5 full symbols $\times$ 4 | 20 |
| 4 | 3 full symbols + 1 half symbol = (3 $\times$ 4) + 2 | 14 |
| 5 | 2 full symbols + 1 half symbol = (2 $\times$ 4) + 2 | 10 |
| 6 | 4 full symbols $\times$ 4 | 16 |
| 7 | 3 full symbols $\times$ 4 | 12 |
| 8 | 1 full symbol + 1 half symbol = (1 $\times$ 4) + 2 | 6 |
a. Which class has the least number of girl students?
By looking at our table, the smallest number of girls is 6. This corresponds to Class 8.
b. What is the difference between the number of girls in Class 5 and 6?
Number of girls in Class 6 = 16
Number of girls in Class 5 = 10
Difference = $16 - 10 = 6$
The difference is 6 girls.
c. If 2 more girls were admitted in Class 2, how would the graph change?
Currently, Class 2 has 18 girls (4 full symbols and 1 half symbol).
If 2 more girls are admitted, the total number of girls will be $18 + 2 = 20$.
To represent 20 girls, we need $20 \div 4 = 5$ full symbols.
So, the row for Class 2 would change from having 4 and a half symbols to having 5 full symbols.
d. How many girls are there in Class 7?
Looking at our table or the pictograph for Class 7, there are 3 full symbols.
Number of girls = $3 \times 4 = 12$.
There are 12 girls in Class 7.
Village A : 18, Village B : 36, Village C : 12, Village D : 48, Village E : 18, Village F : 24
Prepare a pictograph and answer the following questions:
a. What will be a useful scale or key to draw this pictograph?
b. How many symbols will you use to represent the dogs in Village B?
c. Kamini said that the number of dogs in Village B and Village D together will be more than the number of dogs in the other 4 villages. Is she right? Give reasons for your response.
Answer:
a. What will be a useful scale or key to draw this pictograph?
First, we look at the numbers of dogs in each village: 18, 36, 12, 48, 18, 24.
All of these numbers are multiples of 6. Therefore, a useful scale would be to have one symbol represent 6 dogs.
Scale: 🐶 = 6 Dogs
Pictograph of Mudhol Hounds in Six Villages
| Village | Number of Dogs (🐶 = 6 Dogs) |
| Village A (18) | 🐶🐶🐶 |
| Village B (36) | 🐶🐶🐶🐶🐶🐶 |
| Village C (12) | 🐶🐶 |
| Village D (48) | 🐶🐶🐶🐶🐶🐶🐶🐶 |
| Village E (18) | 🐶🐶🐶 |
| Village F (24) | 🐶🐶🐶🐶 |
b. How many symbols will you use to represent the dogs in Village B?
Village B has 36 dogs. According to our scale, one symbol represents 6 dogs.
Number of symbols = $36 \div 6 = 6$.
You will use 6 symbols to represent the dogs in Village B.
c. Kamini said that the number of dogs in Village B and Village D together will be more than the number of dogs in the other 4 villages. Is she right? Give reasons for your response.
Yes, Kamini is right.
Reason:
First, let's find the total number of dogs in Village B and Village D.
Total dogs in B and D = (Dogs in Village B) + (Dogs in Village D)
$= 36 + 48 = 84$ dogs.
Next, let's find the total number of dogs in the other four villages (A, C, E, and F).
Total dogs in other villages = (Dogs in A) + (Dogs in C) + (Dogs in E) + (Dogs in F)
$= 18 + 12 + 18 + 24$
$= 30 + 18 + 24$
$= 48 + 24 = 72$ dogs.
Now, we compare the two totals. Is 84 more than 72?
$84 > 72$.
Since the total number of dogs in Village B and D (84) is greater than the total in the other four villages (72), Kamini's statement is correct.

Draw a bar graph to illustrate the above data taking the scale of 1 unit length = 5 students. Which activity is preferred by most students other than playing?
Answer:
First, we will draw a bar graph for the given data using the specified scale.
Data:
- Playing: 45 students
- Reading story books: 30 students
- Watching TV: 20 students
- Listening to music: 10 students
- Painting: 15 students
Scale: 1 unit length = 5 students
Steps to Draw the Bar Graph:
1. Draw and Label Axes: Draw a horizontal X-axis for "Preferred Activity" and a vertical Y-axis for "Number of Students".
2. Mark the Scale: On the Y-axis, mark the numbers starting from 0 and going up in steps of 5 (e.g., 0, 5, 10, 15, ..., 45), because our scale is 1 unit = 5 students.
3. Calculate Bar Heights: Determine the height of each bar in units.
- Playing: $45 \div 5 = 9$ units
- Reading story books: $30 \div 5 = 6$ units
- Watching TV: $20 \div 5 = 4$ units
- Listening to music: $10 \div 5 = 2$ units
- Painting: $15 \div 5 = 3$ units
4. Draw the Bars: Draw the bars for each activity with the calculated height. Keep the width of the bars and the space between them equal.
5. Add a Title: Give the graph a title, such as "Preferred Free Time Activities of Students".
Completed Bar Graph:

Which activity is preferred by most students other than playing?
From the data table, we can see that "Playing" is the most preferred activity with 45 students.
To find the most preferred activity *other than playing*, we need to look at the remaining activities and find the one with the highest number of students.
The remaining activities and their student numbers are:
- Reading story books: 30
- Watching TV: 20
- Listening to music: 10
- Painting: 15
The highest number among these is 30, which corresponds to "Reading story books".
Therefore, the activity preferred by most students other than playing is Reading story books.
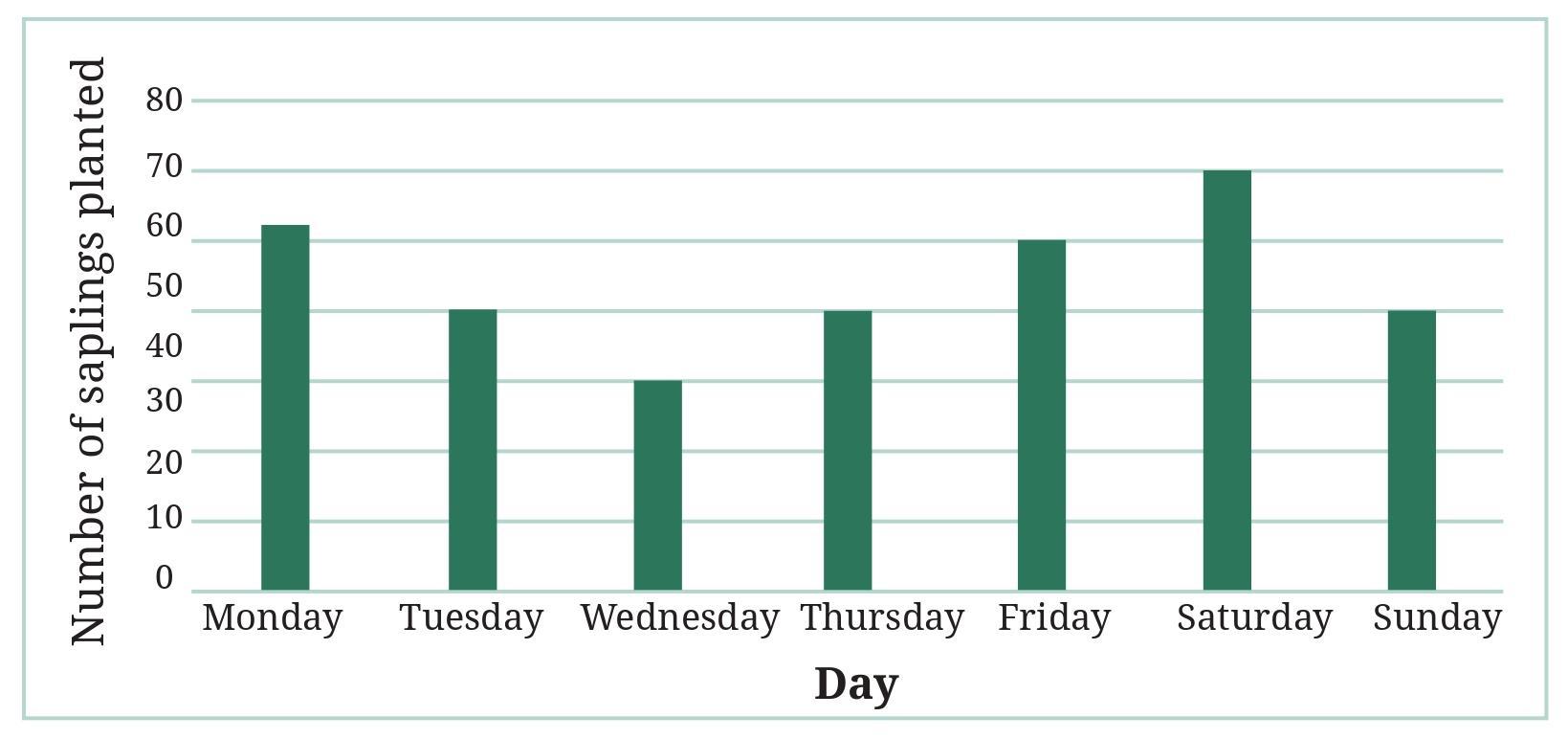
a. The total number of saplings planted on Wednesday and Thursday is ___________.
b. The total number of saplings planted during the whole week is ___________.
c. The greatest number of saplings were planted on ___________, and the least number of saplings were planted on ___________. Why do you think that is the case? Why were more saplings planted on certain days of the week and less on others? Can you think of possible explanations or reasons? How could you try and figure out whether your explanations are correct?
Answer:
First, let's read the number of saplings planted each day from the bar graph:
| Day | Number of Saplings Planted |
| Monday | 60 |
| Tuesday | 46 |
| Wednesday | 34 |
| Thursday | 46 |
| Friday | 58 |
| Saturday | 70 |
| Sunday | 46 |
a. The total number of saplings planted on Wednesday and Thursday is ___________ .
To find the total, we add the numbers for Wednesday and Thursday.
Saplings on Wednesday = 34
Saplings on Thursday = 46
Total = $34 + 46 = 80$
The total number of saplings planted on Wednesday and Thursday is 80.
b. The total number of saplings planted during the whole week is ___________ .
To find the total for the week, we add the numbers for all seven days.
Total = $60 + 46 + 34 + 46 + 58 + 70 + 46$
Total = $360$
The total number of saplings planted during the whole week is 360.
c. The greatest number of saplings were planted on ___________, and the least number of saplings were planted on ___________. Why do you think that is the case? Why were more saplings planted on certain days of the week and less on others? Can you think of possible explanations or reasons? How could you try and figure out whether your explanations are correct?
The greatest number of saplings (70) were planted on Saturday, and the least number of saplings (34) were planted on Wednesday.
Possible Explanations/Reasons:
- More saplings on Saturday: Saturday is a weekend day. More students and teachers, and possibly parents or people from the village, would be free to join the planting activity. More volunteers mean more saplings can be planted.
- Less saplings on Wednesday: Wednesday is a regular school day in the middle of the week. Students and teachers have classes and other schoolwork. There was probably less time available for planting, which is why fewer saplings were planted.
How to figure out if these explanations are correct?
- We could ask the teachers or the headmaster who organized the event. They would know the schedule and how many people participated each day.
- We could check the school's weekly timetable or a notice for the event. It might show that more time was set aside for planting on Saturday.
- We could survey the students who participated and ask them on which day they worked the longest or saw the most people helping.
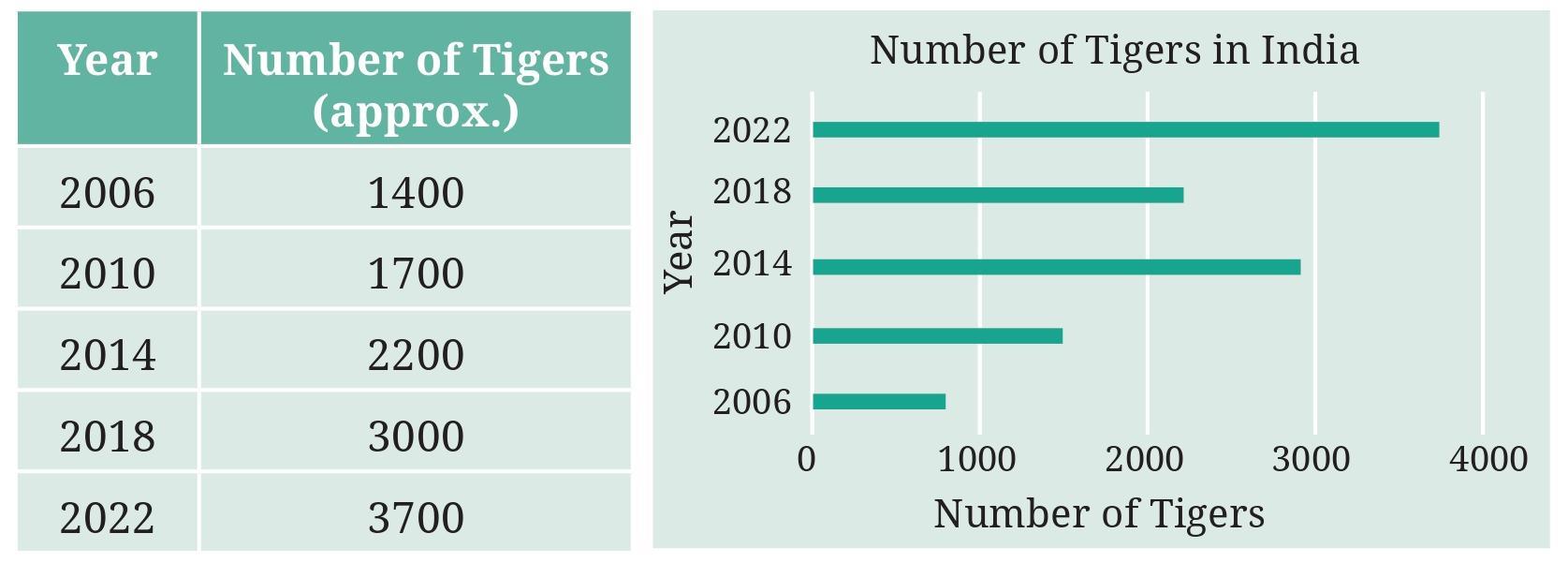
Answer:
To find and fix the mistakes, we need to carefully compare the data in the table with the bars shown in the graph.
Data from the table:
| Year | Number of Tigers (approx.) |
| 2006 | 1400 |
| 2010 | 1700 |
| 2014 | 2200 |
| 2018 | 3000 |
| 2022 | 3700 |
Identifying the Mistakes in the Bar Graph:
Let's check each bar one by one against the table data.
- Year 2006: The data is 1400 tigers. The bar in the graph ends near 1000, not 1400. This is a mistake.
- Year 2010: The data is 1700 tigers. The bar in the graph ends between 1000 and 2000, which looks correct for 1700. This bar seems correct.
- Year 2014: The data is 2200 tigers. The bar in the graph ends near 3000, not 2200. This is a mistake.
- Year 2018: The data is 3000 tigers. The bar in the graph ends near 2200, not 3000. This is a mistake.
- Year 2022: The data is 3700 tigers. The bar in the graph ends between 3000 and 4000, which looks correct for 3700. This bar seems correct.
Summary of Mistakes:
- The bar for the year 2006 is too short.
- The bar for the year 2014 is too long.
- The bar for the year 2018 is too short.
Corrected Bar Graph:
To fix the graph, we need to draw the bars with the correct lengths according to the data in the table.
- The bar for 2006 should end at 1400.
- The bar for 2010 should end at 1700 (this was correct).
- The bar for 2014 should end at 2200.
- The bar for 2018 should end at 3000.
- The bar for 2022 should end at 3700 (this was correct).
Here is what the corrected bar graph should look like:

Figure it Out (Page 103)
Question 1. If you wanted to visually represent the data of the heights of the tallest persons in each class in your school, would you use a graph with vertical bars or horizontal bars? Why?
Answer:
For representing the heights of the tallest persons in each class, it would be better to use a graph with vertical bars.
Reason:
Height is a measurement of how tall something is, which is a vertical direction (up and down).
Using vertical bars makes the graph easy and natural to understand. A taller bar directly looks like a taller person.
This makes it very easy to see at a glance which class has the tallest person, as our eyes naturally connect the height of the bar with the concept of height.
While a horizontal bar graph could show the same data, it would be less intuitive.
Question 2. If you were making a table of the longest rivers on each continent and their lengths, would you prefer to use a bar graph with vertical bars or with horizontal bars? Why? Try finding out this information, and then make the corresponding table and bar graph! Which continents have the longest rivers?
Answer:
For making a bar graph of the longest rivers on each continent, it is significantly better to use a graph with horizontal bars.
Reasons why a horizontal bar graph is better:
- Long Labels: River names (e.g., "Mississippi-Missouri-Jefferson") and continent names are long. On a horizontal graph, these names can be written horizontally next to the bars, making them easy to read. In a vertical graph, they would have to be rotated or tilted.
- Reading Direction: We read text from left to right. Placing the labels on the vertical axis allows the reader to scan the names naturally before looking at the length of the bar.
- Visual Analogy: Since rivers flow across the landscape, a horizontal bar more intuitively represents the concept of "length" compared to a vertical bar, which usually represents "height" or "quantity."
- Easy Ranking: It allows for a clean top-to-bottom ranking, placing the longest river at the top for immediate identification.
Table of Longest Rivers by Continent:
| Continent | Longest River System | Approximate Length (km) |
|---|---|---|
| Africa | Nile River | 6650 |
| South America | Amazon River | 6400 |
| Asia | Yangtze River | 6300 |
| North America | Mississippi-Missouri-Jefferson | 6275 |
| Australia | Murray-Darling | 3672 |
| Europe | Volga River | 3530 |
| Antarctica | Onyx River | 32 |
Bar Graph (Horizontal Bars):

Which continents have the longest rivers?
Based on the data and graph, Africa (Nile River) and South America (Amazon River) have the longest rivers in the world. Africa holds the record for the single longest river system at approximately 6,650 km.

