| Latest Maths NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
Chapter 10 The Other Side Of Zero
Welcome to the solutions guide for Chapter 10, "The Other Side of Zero," a pivotal chapter in the Class 6 Ganita Prakash textbook (NCERT, 2024-25 session) that significantly expands the students' numerical horizons. This chapter introduces the fundamental concept of Integers, moving beyond the familiar world of whole numbers to include negative values. These solutions are meticulously crafted to demystify negative numbers and provide clear, step-by-step guidance for understanding their properties and performing basic operations, which is crucial for future mathematical development.
The core idea presented in "The Other Side of Zero" is the set of Integers, often denoted by the symbol $\mathbb{Z}$. This set encompasses all the positive whole numbers ($1, 2, 3, \dots$), their negative counterparts ($-1, -2, -3, \dots$), and the crucial number zero ($0$). The solutions provide extensive clarity on this expanded number system. A key tool emphasized is the number line. Solutions illustrate how integers are arranged linearly, with zero at the center, positive integers extending infinitely to the right, and negative integers extending infinitely to the left. This visual representation is fundamental for understanding the order of integers: any number to the right is always greater than any number to its left (e.g., $-2 > -5$, and $1 > -3$). The solutions demonstrate how to accurately locate integers on the number line and use it effectively for comparing integers and arranging them in ascending or descending order.
A significant portion of this solutions guide is dedicated to mastering the arithmetic of integers, specifically addition and subtraction, which often presents initial challenges. The solutions systematically explain the rules governing these operations:
- Adding Integers:
- Same Signs: Add their absolute values (magnitudes) and retain the common sign. Example: $(+3) + (+4) = +7$; $(-5) + (-2) = -7$.
- Different Signs: Find the difference between their absolute values and assign the sign of the integer with the larger absolute value. Example: $(-8) + (+3) = -5$; $(+6) + (-4) = +2$.
- Subtracting Integers: The key principle explained is to convert subtraction into addition by adding the additive inverse (the opposite) of the integer being subtracted. Example: $(+7) - (+4) = (+7) + (-4) $$ = +3$; $(-5) - (-2) = (-5) + (+2) = -3$.
Furthermore, the concept of absolute value is often introduced, representing the non-negative distance of an integer from zero on the number line, denoted by vertical bars (e.g., $|-5| = 5$ and $|+5| = 5$). The solutions clarify this concept. They also tackle practical word problems where integers naturally arise. These problems often involve real-world contexts such as measuring temperature changes above and below $0^\circ C$, calculating depths below sea level and heights above it, or tracking financial transactions involving credits (positive) and debits (negative). By diligently working through these solutions for Chapter 10 of the Class 6 Ganita Prakash (NCERT 2024-25), students can effectively overcome common hurdles associated with negative numbers, build strong confidence in performing integer arithmetic, and appreciate the relevance of this expanded number system in describing real-world situations.
Intext Questions (Page 243)
Question: Can there be a number less than 0? Can you think of any ways to have less than 0 of something?
Answer:
Yes, there can be numbers less than 0. These numbers are called negative numbers.
We can definitely think of ways to have "less than 0" of something. While you cannot physically have a negative count of discrete objects (like -3 apples), negative numbers are used to represent quantities that can go below a reference point, which is often set as zero. Here are some examples:
- Temperature: Temperatures can go below $0^\circ$ Celsius (freezing point of water) or $0^\circ$ Fahrenheit. For example, $-5^\circ$C represents a temperature 5 degrees below freezing.
- Money: In a bank account, a negative balance (like -₹500) means you owe the bank money; you have less than zero rupees in your account. Similarly, incurring a debt represents a negative amount of money.
- Elevation/Altitude: Heights can be measured relative to sea level (defined as 0). Being below sea level is represented by a negative elevation, e.g., -10 meters means 10 meters below sea level.
- Depth: Similar to elevation, the depth of a mine or a submarine can be represented by a negative number relative to ground level or sea level.
- Golf Scores: In golf, a score below par (often considered the reference 0) is represented by a negative number (e.g., -2 means two strokes under par).
- Time: Time can be measured relative to an event. Time before the event can be represented by negative numbers (e.g., T-minus 10 seconds before launch is represented as -10 seconds).
- Change in a quantity: If a quantity decreases, the change can be negative. For example, a temperature drop of $5^\circ$C can be represented as a change of $-5^\circ$C.
In these contexts, "less than 0" represents a state below a chosen reference point, indicating deficit, debt, position below a standard level, etc.

Answer:
In an elevator, moving up is shown with a positive sign (+), and moving down is shown with a negative sign (-). The number tells us how many floors to move.
What do you press to go four floors up?
To go up, we use a positive sign (+).
To go up by four floors, we use the number 4.
Therefore, to go four floors up, you would press the button for +4.
What do you press to go three floors down?
To go down, we use a negative sign (-).
To go down by three floors, we use the number 3.
Therefore, to go three floors down, you would press the button for -3.
Intext Questions (Page 244)

Answer:
Solution
To number the floors of the "Building of Fun", we will use the concept of integers. The ground floor is considered the reference point and is numbered as 0. Floors above the ground level are represented by positive integers, and floors below the ground level (in the basement) are represented by negative integers.
In the given picture, the "Welcome hall" is the ground floor.
Based on this, we can number all the floors as follows:
| Floor Name | Floor Number |
| Space | +6 |
| Sports | +5 |
| Ice Cream | +4 |
| Books | +3 |
| Art Centre | +2 |
| Food Court | +1 |
| Welcome hall | 0 (Ground Floor) |
| Toys | -1 |
| Video Games | -2 |
| Cinema | -3 |
| Ghost House | -4 |
| Dinosaur | -5 |
So, the floors above ground are numbered from +1 to +6, and the basement floors are numbered from -1 to -5.
Intext Questions (Page 245)
Question: Start from the Food Court and press + 2 in the lift. Where will you reach? ____________
Answer:
Solution
We need to determine the destination floor after starting from the Food Court and moving up 2 floors.
Step 1: Find the starting floor number.
The "Welcome hall" is the ground floor (Level 0). The floors above are numbered with positive integers.
The Food Court is one floor above the Welcome hall. So, the starting floor is +1.
Step 2: Apply the movement.
Pressing "+2" in the lift means moving up by 2 floors from the current position.
Step 3: Calculate the destination floor.
We start at floor +1 and add 2 to find the new floor number.
$1 + 2 = 3$
So, the destination floor is +3.
Step 4: Identify the place at the destination floor.
Looking at the building directory, the floor at level +3 is the Books floor.
Answer: You will reach the Books floor.
Figure it Out (Page 245)
Question 1. You start from Floor + 2 and press – 3 in the lift. Where will you reach? Write an expression for this movement.
Answer:
We are asked to find the destination floor in "Bela's Building of Fun" after a specific lift movement.
Step 1: Identify the starting floor.
You start from Floor +2. Looking at the building directory, Floor +2 is the Art Centre.
Step 2: Understand the movement.
You press –3 in the lift. The negative sign means you are going down. The number 3 means you are moving 3 floors.
Step 3: Write the expression and calculate the destination.
The movement can be written as an addition of integers:
Starting Floor + Movement = Destination Floor
The expression for this movement is:
$(+2) + (–3)$
Calculating this, we get:
$2 - 3 = -1$
The destination floor is Floor -1.
Step 4: Identify the place at the destination floor.
Looking at the building directory, Floor -1 is the Toys floor.
Answer: You will reach the Toys floor.
Question 2. Evaluate these expressions (you may think of them as Starting Floor + Movement by referring to the Building of Fun).
a. (+ 1) + (+ 4) = _______
b. (+ 4) + (+ 1) = _______
c. (+ 4) + (– 3) = _______
d. (– 1) + (+ 2) = _______
e. (– 1) + (+ 1) = _______
f. 0 + (+ 2) = _________
g. 0 + (– 2) = _________
Answer:
We will evaluate each expression by performing integer addition.
a. (+ 1) + (+ 4)
Start at floor 1 and go up 4 floors. $1 + 4 = 5$.
(+ 1) + (+ 4) = +5
b. (+ 4) + (+ 1)
Start at floor 4 and go up 1 floor. $4 + 1 = 5$.
(+ 4) + (+ 1) = +5
c. (+ 4) + (– 3)
Start at floor 4 and go down 3 floors. $4 - 3 = 1$.
(+ 4) + (– 3) = +1
d. (– 1) + (+ 2)
Start at floor -1 and go up 2 floors. $-1 + 2 = 1$.
(– 1) + (+ 2) = +1
e. (– 1) + (+ 1)
Start at floor -1 and go up 1 floor. $-1 + 1 = 0$.
(– 1) + (+ 1) = 0
f. 0 + (+ 2)
Start at floor 0 and go up 2 floors. $0 + 2 = 2$.
0 + (+ 2) = +2
g. 0 + (– 2)
Start at floor 0 and go down 2 floors. $0 - 2 = -2$.
0 + (– 2) = -2
Question 3.
Starting from different floors, find the movements required to reach Floor – 5. For example, if I start at Floor + 2, I must press – 7 to reach Floor – 5. The expression is (+ 2) + (– 7) = – 5.
Find more such starting positions and the movements needed to reach Floor – 5 and write the expressions.
Answer:
We need to find different movements to reach the destination, which is Floor –5 (the Dinosaur floor). The general expression is:
Starting Floor + Movement = –5
Here are several examples using floors from the "Building of Fun":
| Starting Floor (Name) | Calculation for Movement | Movement Needed | Expression |
| +6 (Space) | $-5 - 6 = -11$ | -11 (Down 11 floors) | $(+6) + (-11) = -5$ |
| +1 (Food Court) | $-5 - 1 = -6$ | -6 (Down 6 floors) | $(+1) + (-6) = -5$ |
| 0 (Welcome Hall) | $-5 - 0 = -5$ | -5 (Down 5 floors) | $0 + (-5) = -5$ |
| -3 (Cinema) | $-5 - (-3) = -5 + 3 = -2$ | -2 (Down 2 floors) | $(-3) + (-2) = -5$ |
| -5 (Dinosaur) | $-5 - (-5) = -5 + 5 = 0$ | 0 (No movement) | $(-5) + 0 = -5$ |
Figure it out (Page 246)
Evaluate these expressions by thinking of them as the resulting movement of combining button presses:
a. (+ 1) + (+ 4) = _____________
b. (+ 4) + (+ 1) = _____________
c. (+ 4) + (– 3) + (– 2) = _______
d. (– 1) + (+ 2) + (– 3) = _______
Answer:
We can evaluate these expressions by thinking of each number as a button press in an elevator. A positive number (+) means moving up, and a negative number (–) means moving down. The final result is the total movement after all the button presses are combined.
a. (+ 1) + (+ 4)
This is like pressing "up 1 floor" and then "up 4 floors".
The total movement is 1 floor up + 4 floors up, which is a total movement of 5 floors up.
$(+1) + (+4) = +5$
b. (+ 4) + (+ 1)
This is like pressing "up 4 floors" and then "up 1 floor".
The total movement is 4 floors up + 1 floor up, which is a total movement of 5 floors up.
$(+4) + (+1) = +5$
c. (+ 4) + (– 3) + (– 2)
This is like pressing "up 4 floors", then "down 3 floors", and then "down 2 floors".
First, we can combine the "down" movements: (–3) + (–2) is a total of 5 floors down (–5).
So the expression becomes (+4) + (–5).
Going up 4 floors and then down 5 floors results in a total movement of 1 floor down.
$(+4) + (–3) + (–2) = -1$
d. (– 1) + (+ 2) + (– 3)
This is like pressing "down 1 floor", then "up 2 floors", and then "down 3 floors".
We can combine the "down" movements: (–1) + (–3) is a total of 4 floors down (–4).
So the expression becomes (+2) + (–4).
Going up 2 floors and then down 4 floors results in a total movement of 2 floors down.
$(–1) + (+2) + (–3) = -2$
Intext Questions (Page 246)
Question: Write the inverses of these numbers:
+4, –4, –3, 0, +2, –1.
Answer:
The additive inverse of a number is the number that, when added to the original number, results in a sum of zero. For any integer $a$, its additive inverse is $-a$, such that $a + (-a) = 0$ and $(-a) + a = 0$.
We need to find the additive inverse for each of the given numbers:
- The number is +4. The additive inverse of +4 is the number that sums with +4 to give 0. $(+4) + (-4) = 0$. The inverse of +4 is -4.
- The number is -4. The additive inverse of -4 is the number that sums with -4 to give 0. $(-4) + (+4) = 0$. The inverse of -4 is +4.
- The number is -3. The additive inverse of -3 is the number that sums with -3 to give 0. $(-3) + (+3) = 0$. The inverse of -3 is +3.
- The number is 0. The additive inverse of 0 is the number that sums with 0 to give 0. $0 + 0 = 0$. The inverse of 0 is 0.
- The number is +2. The additive inverse of +2 is the number that sums with +2 to give 0. $(+2) + (-2) = 0$. The inverse of +2 is -2.
- The number is -1. The additive inverse of -1 is the number that sums with -1 to give 0. $(-1) + (+1) = 0$. The inverse of -1 is +1.
The inverses of the given numbers are:
Inverse of +4 is -4.
Inverse of -4 is +4.
Inverse of -3 is +3.
Inverse of 0 is 0.
Inverse of +2 is -2.
Inverse of -1 is +1.
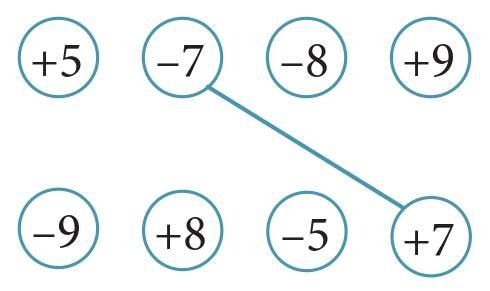
Answer:
Solution
The additive inverse of a number is the number that you add to it to get zero. For any number, its inverse has the opposite sign but the same numerical value. For example, the inverse of +10 is -10, and the inverse of -3 is +3.
We need to connect each number in the top row with its additive inverse in the bottom row.
Matching the Inverses:
- The inverse of +5 is -5.
- The inverse of -7 is +7. (This is already connected in the example).
- The inverse of -8 is +8.
- The inverse of +9 is -9.
The completed figure with all the inverses connected is shown below:
Question: Who is on the lowest floor?
1. Jay is in the Art Centre. So, he is on Floor +2.
2. Asin is in the Sports Centre. So, she is on Floor ___.
3. Binnu is in the Cinema Centre. So, she is on Floor ____.
4. Aman is in the Toys Shop. So, he is on Floor ____.
Answer:
To find out who is on the lowest floor, we first need to determine the floor number for each person based on the "Bela's Building of Fun" directory.
Floor Locations:
1. Jay is in the Art Centre. So, he is on Floor +2.
2. Asin is in the Sports Centre. So, she is on Floor +5.
3. Binnu is in the Cinema Centre. So, she is on Floor -3.
4. Aman is in the Toys Shop. So, he is on Floor -1.
Comparing the Floors:
Now, let's list the floor numbers for each person:
- Asin: +5 (highest floor)
- Jay: +2
- Aman: -1
- Binnu: -3 (lowest floor)
To find who is on the lowest floor, we need to find the smallest number among +5, +2, -1, and -3. On a number line, negative numbers are to the left of zero, and -3 is to the left of -1. Therefore, -3 is the smallest number.
Conclusion:
The person on the lowest floor is the one with the smallest floor number, which is -3.
Binnu is on the lowest floor.
Figure it Out (Page 247)
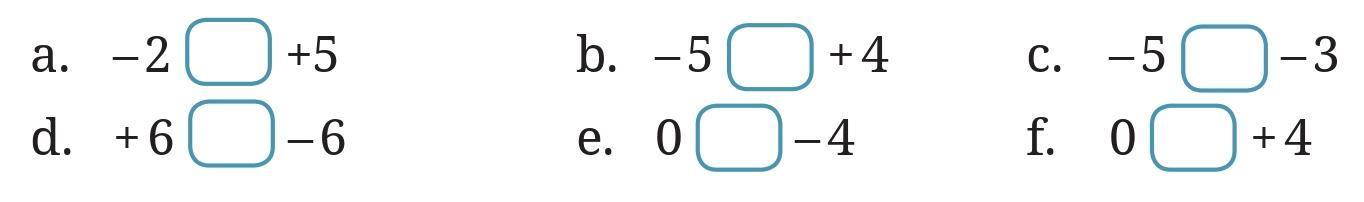
Notice that all negative number floors are below Floor 0. So, all negative numbers are less than 0. All the positive number floors are above Floor 0. So, all positive numbers are greater than 0.
Answer:
Solution
We need to compare the pairs of integers using the symbols for "less than" (<) or "greater than" (>). We can think of these numbers as floors in a building: a higher floor number is greater, and a lower floor number is smaller.
a. -2 ___ +5
Floor -2 is in the basement, while Floor +5 is above ground. Any negative number is less than any positive number.
So, -2 < +5.
b. -5 ___ +4
Floor -5 is in the basement, and Floor +4 is above ground. A negative number is always less than a positive number.
So, -5 < +4.
c. -5 ___ -3
Both floors are in the basement. Floor -5 is deeper (lower) than Floor -3. On a number line, -5 is to the left of -3.
So, -5 < -3.
d. +6 ___ -6
Floor +6 is high above ground, while Floor -6 is deep in the basement. A positive number is always greater than a negative number.
So, +6 > -6.
e. 0 ___ -4
Floor 0 is the ground floor, and Floor -4 is in the basement. The ground floor is higher than any basement floor. Zero is greater than any negative number.
So, 0 > -4.
f. 0 ___ +4
Floor 0 is the ground floor, and Floor +4 is above ground. Floor +4 is higher than the ground floor. Zero is less than any positive number.
So, 0 < +4.
Completed Expressions:
a. -2 < +5
b. -5 < +4
c. -5 < -3
d. +6 > -6
e. 0 > -4
f. 0 < +4

Answer:
Solution
We need to compare the pairs of integers using the symbols for "less than" (<) or "greater than" (>). A useful way to think about this is using a number line, where numbers on the left are smaller and numbers on the right are larger.
a. -10 ___ -12
On a number line, -10 is to the right of -12. Therefore, -10 is greater than -12.
So, -10 > -12.
b. +17 ___ -10
Any positive number is greater than any negative number.
So, +17 > -10.
c. 0 ___ -20
Zero is greater than any negative number.
So, 0 > -20.
d. +9 ___ -9
Any positive number is greater than any negative number.
So, +9 > -9.
e. -25 ___ -7
On a number line, -25 is to the left of -7. Therefore, -25 is less than -7.
So, -25 < -7.
f. +15 ___ -17
Any positive number is greater than any negative number.
So, +15 > -17.
Completed Expressions:
a. -10 > -12
b. +17 > -10
c. 0 > -20
d. +9 > -9
e. -25 < -7
f. +15 > -17
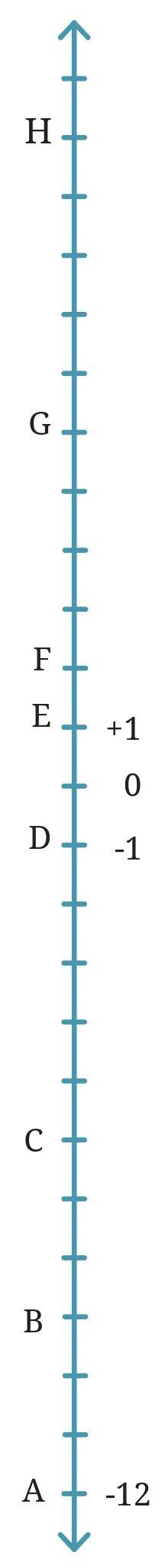
Question 3. If Floor A = – 12, Floor D = – 1 and Floor E = + 1 in the building shown on the right as a line, find the numbers of Floors B, C, F, G and H.
Answer:
To Find:
The integer values for the floors labeled B, C, F, G, and H.
Solution:
We are given the reference points D = -1, E = +1, and the location of 0 on the number line. By observing the marks between these points, we can see that each tick mark represents one floor.
We can find the number for each floor by counting the tick marks from the Ground Floor (0).
Floor B:
By counting, we find that Floor B is 9 tick marks below Floor 0. Therefore, the number for Floor B is -9.
Floor C:
Floor C is 6 tick marks below Floor 0. Therefore, the number for Floor C is -6.
Floor F:
Floor F is 2 tick marks above Floor 0. Therefore, the number for Floor F is +2.
Floor G:
Floor G is 6 tick marks above Floor 0. Therefore, the number for Floor G is +6.
Floor H:
Floor H is 11 tick marks above Floor 0. Therefore, the number for Floor H is +11.
Question 4. Mark the following floors of the building shown on the right.
a. – 7
b. – 4
c. + 3
d. – 10
Answer:
Using the floor numbers we determined (C=-6, B=-9, A=-12, F=+2, G=+6), we can locate and mark the required floors on the number line.
a. Mark – 7:
The floor –7 is one floor below C (–6) and two floors above B (–9). It is located on the tick mark that is 7 steps below 0.
b. Mark – 4:
The floor –4 is two floors above C (–6). It is located on the tick mark that is 4 steps below 0.
c. Mark + 3:
The floor +3 is one floor above F (+2). It is located on the tick mark that is 3 steps above 0.
d. Mark – 10:
The floor –10 is one floor below B (–9) and two floors above A (–12). It is located on the tick mark that is 10 steps below 0.
The locations are shown on the number line:
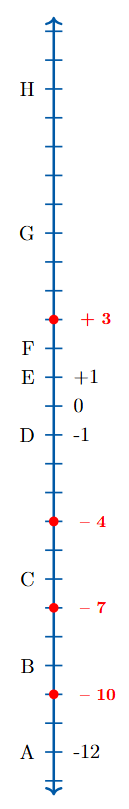
Intext Questions (Page 248)
Question: Evaluate 15 – 5, 100 – 10 and 74 – 34 from this perspective.
Answer:
The perspective referred to is likely standard subtraction within the set of integers, as discussed in the preceding context.
Evaluation of $15 - 5$:
$15 - 5 = 10$
Evaluation of $100 - 10$:
$100 - 10 = 90$
Evaluation of $74 - 34$:
$74 - 34 = 40$
Figure it Out (Page 249)
Complete these expressions. You may think of them as finding the movement needed to reach the Target Floor from the Starting Floor.
a. (+ 1) – (+ 4) = _______
b. (0) – (+ 2) = _________
c. (+ 4) – (+ 1) = _______
d. (0) – (– 2) = _________
e. (+ 4) – (– 3) = _______
f. (– 4) – (– 3) = ________
g. (– 1) – (+ 2) = _______
h. (– 2) – (– 2) = ________
i. (– 1) – (+1) = _______
j. (+ 3) – (– 3) = ________
Answer:
Here, we evaluate each expression by performing subtraction. Thinking in terms of floors, subtracting a number is equivalent to adding its opposite. The result represents the change in floor level (movement) from the starting floor to the target floor.
a. $(+1) - (+4)$
$+1 - 4 = -3$
Result: -3
b. $(0) - (+2)$
$0 - 2 = -2$
Result: -2
c. $(+4) - (+1)$
$+4 - 1 = 3$
Result: +3
d. $(0) - (-2)$
$0 - (-2) = 0 + 2 = 2$
Result: +2
e. $(+4) - (-3)$
$+4 - (-3) = 4 + 3 = 7$
Result: +7
f. $(-4) - (-3)$
$-4 - (-3) = -4 + 3 = -1$
Result: -1
g. $(-1) - (+2)$
$-1 - 2 = -3$
Result: -3
h. $(-2) - (-2)$
$-2 - (-2) = -2 + 2 = 0$
Result: 0
i. $(-1) - (+1)$
$-1 - 1 = -2$
Result: -2
j. $(+3) - (-3)$
$+3 - (-3) = 3 + 3 = 6$
Result: +6
Figure it Out (Page 251)
Complete these expressions.
a. (+ 40) + ______ = + 200
b. (+ 40) + _______ = – 200
c. (– 50) + ______ = + 200
d. (– 50) + _______ = – 200
e. (– 200) – (– 40) = _______
f. (+ 200) – (+ 40) = _______
g. (– 200) – (+ 40) = _______
Check your answers by thinking about the movement in the mineshaft.
Answer:
We complete the given expressions by performing the required addition or subtraction.
a. $(+40) + \underline{\hspace{1cm}} = +200$
Let the missing number be $x$.
$+40 + x = +200$
$x = +200 - (+40)$
$x = 200 - 40$
$x = 160$
So, $(+40) + \mathbf{+160} = +200$.
b. $(+40) + \underline{\hspace{1cm}} = –200$
Let the missing number be $x$.
$+40 + x = -200$
$x = -200 - (+40)$
$x = -200 - 40$
$x = -240$
So, $(+40) + \mathbf{-240} = –200$.
c. $(–50) + \underline{\hspace{1cm}} = +200$
Let the missing number be $x$.
$-50 + x = +200$
$x = +200 - (-50)$
$x = 200 + 50$
$x = 250$
So, $(–50) + \mathbf{+250} = +200$.
d. $(–50) + \underline{\hspace{1cm}} = –200$
Let the missing number be $x$.
$-50 + x = -200$
$x = -200 - (-50)$
$x = -200 + 50$
$x = -150$
So, $(–50) + \mathbf{-150} = –200$.
e. $(–200) – (–40) = \underline{\hspace{1cm}}$
$-200 - (-40) = -200 + 40 = -160$
So, $(–200) – (–40) = \mathbf{-160}$.
f. $(+200) – (+40) = \underline{\hspace{1cm}}$
$+200 - (+40) = 200 - 40 = 160$
So, $(+200) – (+40) = \mathbf{+160}$.
g. $(–200) – (+40) = \underline{\hspace{1cm}}$
$-200 - (+40) = -200 - 40 = -240$
So, $(–200) – (+40) = \mathbf{-240}$.
Intext Questions (Page 251)
Question: Try evaluating the following expressions by similarly drawing or imagining a suitable lift:
a. – 125 + (– 30)
b. + 105 – (– 55)
c. + 105 + (+ 55)
d. + 80 – (– 150)
e. + 80 + (+ 150)
f. – 99 – (– 200)
g. – 99 + (+ 200)
h. + 1500 – (– 1500)
Answer:
We can solve these problems by thinking about movements in a very tall lift. Adding a positive number means going up, adding a negative number means going down, and subtracting a negative number is the same as adding a positive number (it's like cancelling a "down" command, which makes you go up).
a. – 125 + (– 30)
Lift Analogy: Start at basement level 125 and then go down another 30 floors.
Calculation: You are going deeper into the basement.
$-125 - 30 = -155$
Result: -155
b. + 105 – (– 55)
Lift Analogy: Start at floor 105. Subtracting a "down 55" movement is the same as going up 55 floors.
Calculation: This is the same as $105 + 55$.
$+105 + 55 = 160$
Result: 160
c. + 105 + (+ 55)
Lift Analogy: Start at floor 105 and go up another 55 floors.
Calculation: This is a straightforward addition.
$105 + 55 = 160$
Result: 160
d. + 80 – (– 150)
Lift Analogy: Start at floor 80. Subtracting a "down 150" movement is the same as going up 150 floors.
Calculation: This is the same as $80 + 150$.
$80 + 150 = 230$
Result: 230
e. + 80 + (+ 150)
Lift Analogy: Start at floor 80 and go up another 150 floors.
Calculation: This is a straightforward addition.
$80 + 150 = 230$
Result: 230
f. – 99 – (– 200)
Lift Analogy: Start at basement level 99. Subtracting a "down 200" movement is the same as going up 200 floors.
Calculation: This is the same as $-99 + 200$. You will go past the ground floor and end up on a positive floor.
$200 - 99 = 101$
Result: 101
g. – 99 + (+ 200)
Lift Analogy: Start at basement level 99 and go up 200 floors.
Calculation: This is a straightforward addition.
$-99 + 200 = 101$
Result: 101
h. + 1500 – (– 1500)
Lift Analogy: Start at floor 1500. Subtracting a "down 1500" movement is the same as going up another 1500 floors.
Calculation: This is the same as $1500 + 1500$.
$1500 + 1500 = 3000$
Result: 3000
Intext Questions (Page 252)
Question:
In the other exercises that you did above, did you notice that subtracting a negative number was the same as adding the corresponding positive number?
Take a look at the ‘infinite lift’ above. Does it remind you of a number line? In what ways?
Answer:
Part 1: Subtracting a Negative Number
Yes, in the other exercises, subtracting a negative number was the same as adding the corresponding positive number.
This is a very important rule when working with integers. Let's look at the examples to see this pattern:
- We saw that + 105 – (– 55) gave the same result as + 105 + (+ 55). Both equaled 160.
- Similarly, – 99 – (– 200) was the same as – 99 + (+ 200). Both equaled 101.
Thinking about the lift helps to understand why. If you are on a floor and you "subtract" or "cancel" a movement to go down (a negative number), the overall effect is that you go up (adding a positive number).
The general rule is: Subtracting a negative is the same as adding a positive.
$a - (-b) = a + b$
Part 2: The Infinite Lift and the Number Line
Yes, the 'infinite lift' is very much like a number line. It's essentially a vertical number line.
Here are the ways they are similar:
- The Center Point (Origin): The Ground Floor in the lift is like the number 0 on the number line. It's the starting or reference point.
- Two Opposite Directions: The lift goes up and down from the Ground Floor. The number line goes right and left from 0.
- Positive and Negative Numbers: Floors above ground are represented by positive numbers (+1, +2, ...), just like numbers to the right of 0 are positive. Floors below ground (basement) are represented by negative numbers (–1, –2, ...), just like numbers to the left of 0 are negative.
- Ordering of Numbers: In the lift, a higher floor (+5) is always above a lower floor (+2 or -3). On a number line, a number to the right (+5) is always greater than a number to its left (+2 or -3).
- Infinite Extension: Both are imagined to go on forever in both directions.
Figure it Out (Page 253 - 254)

Question 1. Mark 3 positive numbers and 3 negative numbers on the number line above.
Answer:
Solution
To mark numbers on the number line, we need to remember a few simple rules:
- The number 0 is the center point.
- Positive numbers (+1, +2, +3, ...) are located to the right of 0.
- Negative numbers (-1, -2, -3, ...) are located to the left of 0.
We will choose three positive and three negative numbers to mark on the line. For example:
- Positive Numbers: +3, +7, +9
- Negative Numbers: -2, -5, -8
The number line with these numbers marked (for example, with a colored circle) is shown below:
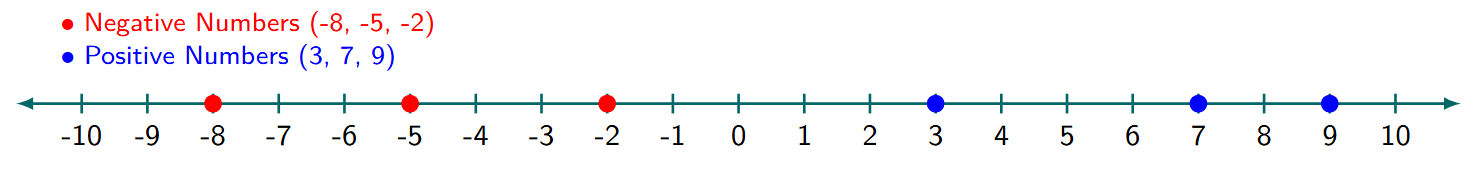

Answer:
Solution
In the previous exercise, the three negative numbers chosen and marked on the number line were -2, -5, and -8.
We will now write these three numbers into the boxes provided.
Question 3. Is 2 > – 3? Why? Is – 2 < 3? Why?
Answer:
First part: Is $2 > -3$?
Yes, $2 > -3$.
Reason: On a number line, numbers located further to the right are always greater than numbers located further to the left. The number $2$ is a positive integer, located $2$ units to the right of $0$. The number $-3$ is a negative integer, located $3$ units to the left of $0$. Since $2$ is located to the right of $-3$ on the number line, $2$ is greater than $-3$.
Second part: Is $-2 < 3$?
Yes, $-2 < 3$.
Reason: On a number line, numbers located further to the left are always less than numbers located further to the right. The number $-2$ is a negative integer, located $2$ units to the left of $0$. The number $3$ is a positive integer, located $3$ units to the right of $0$. Since $-2$ is located to the left of $3$ on the number line, $-2$ is less than $3$. Additionally, any negative number is always less than any positive number.
Question 4. What are
(i) – 5 + 0
(ii) 7 + (– 7)
(iii) – 10 + 20
(iv) 10 – 20
(v) 7 – (– 7)
(vi) – 8 – (– 10)
Answer:
We evaluate each of the given expressions:
(i) $-5 + 0$
Adding zero to any integer results in the same integer.
$-5 + 0 = -5$
(ii) $7 + (-7)$
Adding an integer to its additive inverse (opposite) results in zero.
$7 + (-7) = 7 - 7 = 0$
(iii) $-10 + 20$
To add integers with different signs, find the difference between their absolute values and take the sign of the integer with the larger absolute value.
$|-10| = 10$, $|20| = 20$. The difference is $20 - 10 = 10$. Since $|20| > |-10|$, the result is positive.
$-10 + 20 = +10$
(iv) $10 - 20$
Subtracting a larger number from a smaller number results in a negative number. Alternatively, $10 - 20$ can be written as $10 + (-20)$.
Adding integers with different signs: difference between absolute values is $20 - 10 = 10$. Since $|-20| > |10|$, the result is negative.
$10 - 20 = -10$
(v) $7 - (-7)$
Subtracting a negative integer is the same as adding its corresponding positive integer.
$7 - (-7) = 7 + 7 = 14$
(vi) $-8 - (-10)$
Subtracting a negative integer is the same as adding its corresponding positive integer.
$-8 - (-10) = -8 + 10$
Adding integers with different signs: difference between absolute values is $10 - 8 = 2$. Since $|10| > |-8|$, the result is positive.
$-8 + 10 = +2$
Intext Questions (Page 255)
Question: Use unmarked number lines to evaluate these expressions:
a. – 125 + (– 30) = _______
b. + 105 – (– 55) = _______
c. + 80 – (– 150) = _______
d. – 99 – (– 200) = _______
Answer:
We will evaluate each expression by visualizing movements on a number line. Adding a positive number means moving right, adding a negative number means moving left, and subtracting a negative number is the same as adding a positive number (moving right).
a. – 125 + (– 30)
Number Line Method:
1. Start at the position -125 on the number line.
2. The expression "+ (– 30)" means we need to add a negative number, which is a movement of 30 units to the left (in the negative direction).
3. Moving 30 units to the left from -125 brings us to -155.
$– 125 + (– 30) = -155$
b. + 105 – (– 55)
Number Line Method:
1. First, we simplify the expression. Subtracting a negative number is the same as adding its positive counterpart. So, $+ 105 – (– 55)$ becomes $+ 105 + (+ 55)$.
2. Start at the position +105 on the number line.
3. The expression "+ (+ 55)" means we move 55 units to the right (in the positive direction).
4. Moving 55 units to the right from +105 brings us to +160.
$+ 105 – (– 55) = 160$
c. + 80 – (– 150)
Number Line Method:
1. Simplify the expression: $+ 80 – (– 150)$ becomes $+ 80 + (+ 150)$.
2. Start at the position +80 on the number line.
3. The expression "+ (+ 150)" means we move 150 units to the right.
4. Moving 150 units to the right from +80 brings us to +230.
$+ 80 – (– 150) = 230$
d. – 99 – (– 200)
Number Line Method:
1. Simplify the expression: $– 99 – (– 200)$ becomes $– 99 + (+ 200)$.
2. Start at the position -99 on the number line.
3. The expression "+ (+ 200)" means we move 200 units to the right.
4. Moving 200 units to the right from -99 will cross 0 and go into the positive side. It takes 99 units to get to 0, and then we have $200 - 99 = 101$ more units to move to the right.
5. So, we land on +101.
$– 99 – (– 200) = 101$
Figure it Out (Page 257)
Question 1. Complete the additions using tokens.
a. (+ 6) + (+ 4)
b. (– 3) + (– 2)
c. (+ 5) + (– 7)
d. (– 2) + (+ 6)
Answer:
We use tokens to represent the integers. Let's use positive tokens for positive numbers and negative tokens for negative numbers. A positive token and a negative token cancel each other out, representing a sum of zero.
a. $(+6) + (+4)$
Represent +6 with 6 positive tokens.
Represent +4 with 4 positive tokens.
Combine the tokens: 6 positive tokens and 4 positive tokens.
Total number of positive tokens = $6 + 4 = 10$.
$(+6) + (+4) = \mathbf{+10}$.
b. $(–3) + (–2)$
Represent -3 with 3 negative tokens.
Represent -2 with 2 negative tokens.
Combine the tokens: 3 negative tokens and 2 negative tokens.
Total number of negative tokens = $3 + 2 = 5$.
$(–3) + (–2) = \mathbf{-5}$.
c. $(+5) + (–7)$
Represent +5 with 5 positive tokens.
Represent -7 with 7 negative tokens.
Combine the tokens: 5 positive tokens and 7 negative tokens.
Form pairs of one positive and one negative token. 5 positive tokens will cancel out 5 negative tokens.
Remaining tokens = $7 - 5 = 2$ negative tokens.
$(+5) + (–7) = \mathbf{-2}$.
d. $(–2) + (+6)$
Represent -2 with 2 negative tokens.
Represent +6 with 6 positive tokens.
Combine the tokens: 2 negative tokens and 6 positive tokens.
Form pairs of one positive and one negative token. 2 negative tokens will cancel out 2 positive tokens.
Remaining tokens = $6 - 2 = 4$ positive tokens.
$(–2) + (+6) = \mathbf{+4}$.
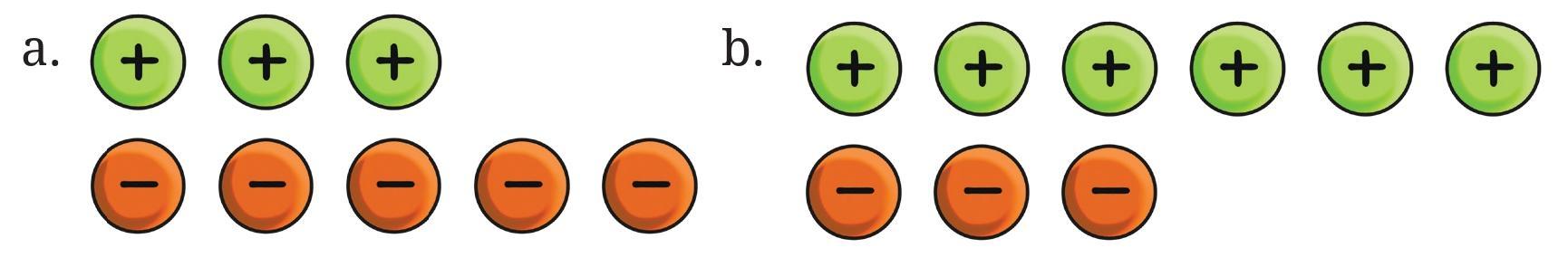
Answer:
Solution
This problem uses colored tokens to represent integer addition. Green tokens with a '+' sign represent positive numbers, and orange tokens with a '–' sign represent negative numbers. A "zero pair" consists of one positive token and one negative token, which cancel each other out because $(+1) + (-1) = 0$.
Case a.
1. Counting the Tokens:
- Number of positive tokens: 3 (representing +3)
- Number of negative tokens: 5 (representing -5)
2. Cancelling Zero Pairs:
We can form 3 zero pairs by matching each of the 3 positive tokens with 3 of the negative tokens. These 3 pairs cancel each other out and equal zero.
3. Remaining Tokens:
After cancelling the pairs, we are left with $5 - 3 = 2$ negative tokens.
4. Final Result:
The 2 remaining negative tokens represent the number -2. This means the lift attendant is on Floor -2.
5. Addition Statement:
The corresponding addition statement is:
$(+3) + (–5) = –2$
Case b.
1. Counting the Tokens:
- Number of positive tokens: 6 (representing +6)
- Number of negative tokens: 3 (representing -3)
2. Cancelling Zero Pairs:
We can form 3 zero pairs by matching each of the 3 negative tokens with 3 of the positive tokens.
3. Remaining Tokens:
After cancelling the pairs, we are left with $6 - 3 = 3$ positive tokens.
4. Final Result:
The 3 remaining positive tokens represent the number +3. This means the lift attendant is on Floor +3.
5. Addition Statement:
The corresponding addition statement is:
$(+6) + (–3) = +3$
Figure it Out (Page 258)
Question 1. Evaluate the following differences using tokens. Check that you get the same result as with other methods you now know:
a. (+ 10) – (+ 7)
b. (– 8) – (– 4)
c. (– 9) – (– 4)
d. (+ 9) – (+ 12)
e. (– 5) – (– 7)
f. (– 2) – (– 6)
Answer:
To evaluate the differences using tokens, we will represent positive integers with green '+' tokens and negative integers with orange '–' tokens. The operation "subtract" means "take away" the specified number of tokens.
a. (+ 10) – (+ 7)
Using Tokens:
- Start with 10 green '+' tokens to represent (+10).
- The problem asks to subtract (+7), which means we need to take away 7 green '+' tokens.
- We have enough green tokens, so we remove 7 of them.
- After removing them, we are left with $10 - 7 = 3$ green '+' tokens.
Result: The remaining 3 green '+' tokens represent the number +3.
Verification:
$(+10) – (+7) = 10 - 7 = 3$
b. (– 8) – (– 4)
Using Tokens:
- Start with 8 orange '–' tokens to represent (–8).
- The problem asks to subtract (–4), which means we need to take away 4 orange '–' tokens.
- We have enough orange tokens, so we remove 4 of them.
- After removing them, we are left with $8 - 4 = 4$ orange '–' tokens.
Result: The remaining 4 orange '–' tokens represent the number –4.
Verification:
$(–8) – (–4) = –8 + 4 = –4$
c. (– 9) – (– 4)
Using Tokens:
- Start with 9 orange '–' tokens to represent (–9).
- The problem asks to subtract (–4), which means we need to take away 4 orange '–' tokens.
- We have enough orange tokens, so we remove 4 of them.
- After removing them, we are left with $9 - 4 = 5$ orange '–' tokens.
Result: The remaining 5 orange '–' tokens represent the number –5.
Verification:
$(–9) – (–4) = –9 + 4 = –5$
d. (+ 9) – (+ 12)
Using Tokens:
- Start with 9 green '+' tokens to represent (+9).
- The problem asks to subtract (+12), which means we need to take away 12 green '+' tokens.
- We only have 9 green tokens, so we need 3 more. To get them, we add 3 zero pairs (3 green '+' tokens and 3 orange '–' tokens). Adding zero pairs does not change the total value.
- Now we have $9 + 3 = 12$ green '+' tokens and 3 orange '–' tokens.
- We can now take away 12 green '+' tokens.
- After removing them, we are left with 3 orange '–' tokens.
Result: The remaining 3 orange '–' tokens represent the number –3.
Verification:
$(+9) – (+12) = 9 - 12 = –3$
e. (– 5) – (– 7)
Using Tokens:
- Start with 5 orange '–' tokens to represent (–5).
- The problem asks to subtract (–7), which means we need to take away 7 orange '–' tokens.
- We only have 5 orange tokens, so we need 2 more. We add 2 zero pairs (2 orange '–' tokens and 2 green '+' tokens).
- Now we have $5 + 2 = 7$ orange '–' tokens and 2 green '+' tokens.
- We can now take away 7 orange '–' tokens.
- After removing them, we are left with 2 green '+' tokens.
Result: The remaining 2 green '+' tokens represent the number +2.
Verification:
$(–5) – (–7) = –5 + 7 = 2$
f. (– 2) – (– 6)
Using Tokens:
- Start with 2 orange '–' tokens to represent (–2).
- The problem asks to subtract (–6), which means we need to take away 6 orange '–' tokens.
- We only have 2 orange tokens, so we need 4 more. We add 4 zero pairs (4 orange '–' tokens and 4 green '+' tokens).
- Now we have $2 + 4 = 6$ orange '–' tokens and 4 green '+' tokens.
- We can now take away 6 orange '–' tokens.
- After removing them, we are left with 4 green '+' tokens.
Result: The remaining 4 green '+' tokens represent the number +4.
Verification:
$(–2) – (–6) = –2 + 6 = 4$
Question 2. Complete the subtractions:
a. (– 5) – (– 7)
b. (+ 10) – (+ 13)
c. (– 7) – (– 9)
d. (+ 3) – (+ 8)
e. (– 2) – (– 7)
f. (+ 3) – (+ 15)
Answer:
To complete these subtractions, we use the rule that subtracting an integer is the same as adding its opposite (additive inverse). The rule is: $a - b = a + (-b)$.
a. (– 5) – (– 7)
To subtract (–7), we add its opposite, which is (+7).
$(– 5) – (– 7) = (– 5) + (+ 7)$
$= – 5 + 7$
$= 2$
So, (– 5) – (– 7) = 2.
b. (+ 10) – (+ 13)
To subtract (+13), we add its opposite, which is (–13).
$(+ 10) – (+ 13) = (+ 10) + (– 13)$
$= 10 – 13$
$= –3$
So, (+ 10) – (+ 13) = –3.
c. (– 7) – (– 9)
To subtract (–9), we add its opposite, which is (+9).
$(– 7) – (– 9) = (– 7) + (+ 9)$
$= – 7 + 9$
$= 2$
So, (– 7) – (– 9) = 2.
d. (+ 3) – (+ 8)
To subtract (+8), we add its opposite, which is (–8).
$(+ 3) – (+ 8) = (+ 3) + (– 8)$
$= 3 – 8$
$= –5$
So, (+ 3) – (+ 8) = –5.
e. (– 2) – (– 7)
To subtract (–7), we add its opposite, which is (+7).
$(– 2) – (– 7) = (– 2) + (+ 7)$
$= – 2 + 7$
$= 5$
So, (– 2) – (– 7) = 5.
f. (+ 3) – (+ 15)
To subtract (+15), we add its opposite, which is (–15).
$(+ 3) – (+ 15) = (+ 3) + (– 15)$
$= 3 – 15$
$= –12$
So, (+ 3) – (+ 15) = –12.
Figure it Out (Page 259)
Question 1.
Try to subtract: – 3 – (+ 5).
How many zero pairs will you have to put in? What is the result?
Answer:
Given:
The subtraction problem is: $– 3 – (+ 5)$.
To Find:
- The number of zero pairs needed to perform the subtraction using tokens.
- The result of the subtraction.
Solution:
We will solve this using the token method. Let's assume orange '–' tokens represent negative integers and green '+' tokens represent positive integers.
Step 1: Represent the first number
The first number is –3. We represent this by placing 3 orange '–' tokens.
Step 2: Understand the subtraction
The problem asks us to subtract (+5), which means we need to "take away" 5 green '+' tokens from our collection.
Step 3: Check if we have enough tokens to take away
Currently, we only have 3 orange '–' tokens. We have no green '+' tokens to take away.
Step 4: Add zero pairs
To get the green '+' tokens we need, we must add "zero pairs". A zero pair consists of one green '+' token and one orange '–' token. Adding zero pairs does not change the total value of our collection because $(+1) + (–1) = 0$.
Since we need to take away 5 green '+' tokens, we need to add 5 zero pairs. This will give us 5 green '+' tokens and 5 orange '–' tokens.
Step 5: Perform the subtraction
Our collection of tokens now consists of:
- The original 3 orange '–' tokens.
- The 5 green '+' tokens from the zero pairs.
- The 5 orange '–' tokens from the zero pairs.
In total, we have 5 green '+' tokens and $3 + 5 = 8$ orange '–' tokens.
Now, we can perform the subtraction by taking away the 5 green '+' tokens.
Step 6: Determine the result
After removing the 5 green '+' tokens, we are left with 8 orange '–' tokens.
These 8 orange '–' tokens represent the integer –8.
Conclusion:
You will have to put in 5 zero pairs.
The result is –8.
Verification using standard method:
Subtracting a positive integer is the same as adding its negative counterpart.
– 3 – (+ 5) = – 3 + (– 5)
= – 8
The result matches the token method.
Question 2. Evaluate the following using tokens.
a. (– 3) – (+ 10)
b. (+ 8) – (– 7)
c. (– 5) – (+ 9)
d. (– 9) – (+ 10)
e. (+ 6) – (– 4)
f. (– 2) – (+ 7)
Answer:
To evaluate these expressions using tokens, we will follow these steps:
- Represent the first number with the corresponding tokens (green '+' for positive, orange '–' for negative).
- Determine the number and type of tokens that need to be "taken away" (subtracted).
- If we don't have enough tokens of the required type, we add "zero pairs" (one '+' token and one '–' token) until we do. Adding zero pairs does not change the total value.
- Take away the required tokens.
- The remaining tokens represent the final answer.
a. (– 3) – (+ 10)
- Start with 3 orange '–' tokens to represent (–3).
- We need to take away 10 green '+' tokens to subtract (+10).
- We have no green tokens, so we add 10 zero pairs. This gives us 10 green '+' tokens and 10 more orange '–' tokens.
- Our collection now consists of 10 green '+' tokens and a total of $3 + 10 = 13$ orange '–' tokens.
- We take away the 10 green '+' tokens.
- We are left with 13 orange '–' tokens.
Result: –13
b. (+ 8) – (– 7)
- Start with 8 green '+' tokens to represent (+8).
- We need to take away 7 orange '–' tokens to subtract (–7).
- We have no orange tokens, so we add 7 zero pairs. This gives us 7 orange '–' tokens and 7 more green '+' tokens.
- Our collection now consists of 7 orange '–' tokens and a total of $8 + 7 = 15$ green '+' tokens.
- We take away the 7 orange '–' tokens.
- We are left with 15 green '+' tokens.
Result: +15
c. (– 5) – (+ 9)
- Start with 5 orange '–' tokens to represent (–5).
- We need to take away 9 green '+' tokens to subtract (+9).
- We have no green tokens, so we add 9 zero pairs. This gives us 9 green '+' tokens and 9 more orange '–' tokens.
- Our collection now consists of 9 green '+' tokens and a total of $5 + 9 = 14$ orange '–' tokens.
- We take away the 9 green '+' tokens.
- We are left with 14 orange '–' tokens.
Result: –14
d. (– 9) – (+ 10)
- Start with 9 orange '–' tokens to represent (–9).
- We need to take away 10 green '+' tokens to subtract (+10).
- We have no green tokens, so we add 10 zero pairs. This gives us 10 green '+' tokens and 10 more orange '–' tokens.
- Our collection now consists of 10 green '+' tokens and a total of $9 + 10 = 19$ orange '–' tokens.
- We take away the 10 green '+' tokens.
- We are left with 19 orange '–' tokens.
Result: –19
e. (+ 6) – (– 4)
- Start with 6 green '+' tokens to represent (+6).
- We need to take away 4 orange '–' tokens to subtract (–4).
- We have no orange tokens, so we add 4 zero pairs. This gives us 4 orange '–' tokens and 4 more green '+' tokens.
- Our collection now consists of 4 orange '–' tokens and a total of $6 + 4 = 10$ green '+' tokens.
- We take away the 4 orange '–' tokens.
- We are left with 10 green '+' tokens.
Result: +10
f. (– 2) – (+ 7)
- Start with 2 orange '–' tokens to represent (–2).
- We need to take away 7 green '+' tokens to subtract (+7).
- We have no green tokens, so we add 7 zero pairs. This gives us 7 green '+' tokens and 7 more orange '–' tokens.
- Our collection now consists of 7 green '+' tokens and a total of $2 + 7 = 9$ orange '–' tokens.
- We take away the 7 green '+' tokens.
- We are left with 9 orange '–' tokens.
Result: –9
Figure it Out (Page 260)
Question 1. Suppose you start with 0 rupees in your bank account, and then you have credits of `30, `40, and `50, and debits of `40, `50, and `60. What is your bank account balance now?
Answer:
Given:
- Starting bank balance =
₹ 0 - Credits (deposits) =
₹ 30,₹ 40,₹ 50 - Debits (withdrawals) =
₹ 40,₹ 50,₹ 60
To Find:
The final bank account balance.
Solution:
We can represent credits as positive integers and debits as negative integers. The final balance is the sum of the starting balance and all transactions.
Final Balance = $0 + (+30) + (+40) + (+50) + (–40) + (–50) + (–60)$
We can rearrange the terms to group the credits and debits together.
Final Balance = $30 + 40 + 50 – 40 – 50 – 60$
We can notice that there is a credit of
Similarly, the credit of
The calculation simplifies to:
Final Balance = $30 + (40 – 40) + (50 – 50) – 60$
Final Balance = $30 + 0 + 0 – 60$
Final Balance = $30 – 60$
Final Balance = $–30$
Therefore, the bank account balance is
Question 2. Suppose you start with 0 rupees in your bank account, and then you have debits of `1, 2, 4, 8, 16, 32, 64, and 128, and then a single credit of `256. What is your bank account balance now?
Answer:
Given:
- Starting bank balance =
₹ 0 - Debits =
₹ 1,₹ 2,₹ 4,₹ 8,₹ 16,₹ 32,₹ 64,₹ 128 - Credit =
₹ 256
To Find:
The final bank account balance.
Solution:
First, we need to calculate the total amount of the debits.
Total Debits = $1 + 2 + 4 + 8 + 16 + 32 + 64 + 128$
These numbers form a geometric sequence where each number is double the previous one. There is a pattern in their sum:
$1 + 2 = 3$ (which is $4 - 1$)
$1 + 2 + 4 = 7$ (which is $8 - 1$)
$1 + 2 + 4 + 8 = 15$ (which is $16 - 1$)
Following this pattern, the sum of all the debits will be one less than the next number in the sequence (which would be 256).
Total Debits = $256 – 1 = 255$
So, the total amount withdrawn is
Now, we can find the final balance:
Final Balance = Starting Balance + Credit – Total Debits
Final Balance =
Final Balance =
Therefore, the bank account balance is
Question 3. Why is it generally better to try and maintain a positive balance in your bank account? What are circumstances under which it may be worthwhile to temporarily have a negative balance?
Answer:
Why it is generally better to maintain a positive balance:
- To Avoid Fees: Banks charge penalties, known as overdraft fees, when an account balance drops below zero without a prior arrangement. A positive balance ensures you avoid these extra costs.
- To Avoid Interest Charges: A negative balance is essentially a loan from the bank. The bank charges interest on this borrowed amount, making it more expensive than using your own funds.
- For Financial Security: A positive balance acts as a safety net for emergencies or unexpected expenses. It provides financial stability and peace of mind.
- To Maintain a Good Credit History: Consistently managing your account well and avoiding negative balances can contribute positively to your financial reputation and credit score, which is important for future loans.
Circumstances where a temporary negative balance might be worthwhile:
A temporary negative balance, usually through a planned overdraft facility, is a form of short-term borrowing. It can be useful in specific situations:
- Urgent Emergencies: To pay for an unexpected and critical expense, such as a medical emergency or urgent home repair, when no other funds are immediately available.
- Bridging a Short-Term Cash Flow Gap: When you need to make an essential payment (like rent or a bill) just before your salary is credited to your account. This can help avoid late fees or service disruptions.
- Seizing a Time-Sensitive Opportunity: In business or investment, a short-term loan (negative balance) might be used to take advantage of an opportunity that promises a return greater than the cost of the interest and fees.
In these cases, the negative balance is a calculated decision where the benefit of making the payment outweighs the cost of borrowing from the bank for a short period.
Figure it Out (Page 261)
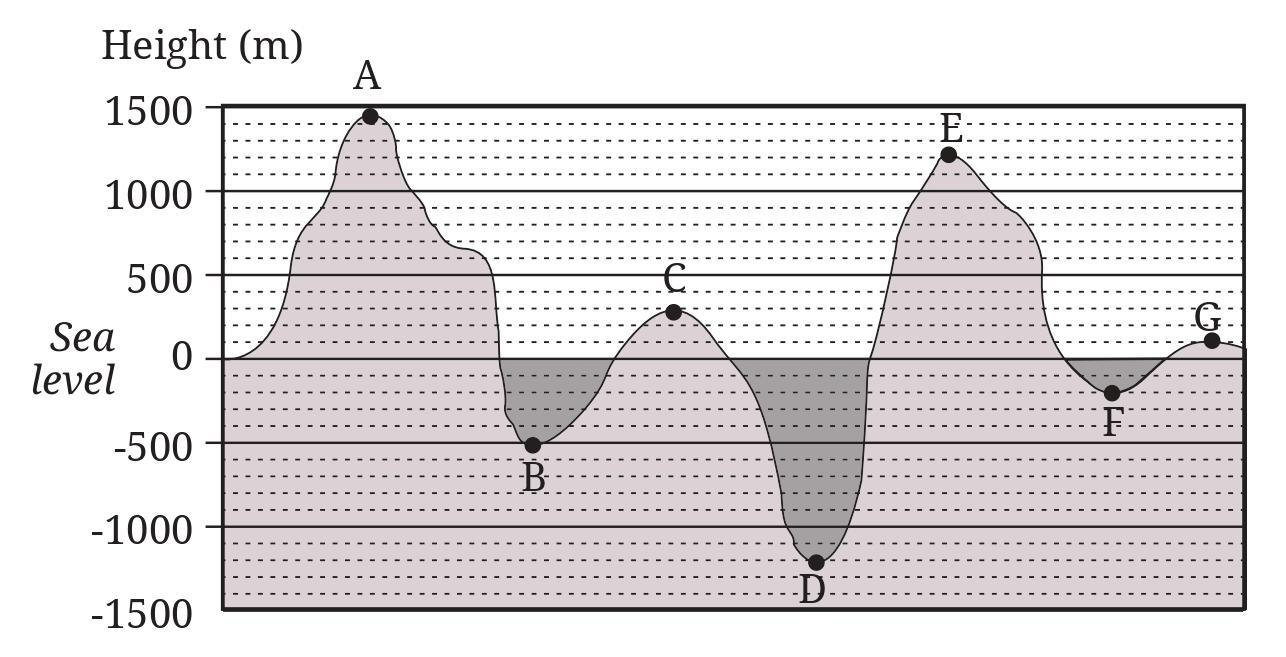
Answer:
By observing the geographical cross-section graph, we can determine the height of each marked point. The vertical axis represents the height in metres (m), with sea level at 0 m. Each major grid line represents an interval of 500 m, and each small dotted line between them represents an interval of 100 m.
The heights for the respective points are:
A: The point is located on the line marked 1500. Thus, its height is 1500 m.
B: The point is located on the line marked -500. Thus, its height is -500 m.
C: The point is located on the third dotted line above sea level (0 m). Thus, its height is 300 m.
D: The point is located on the second dotted line below the -1000 m line. Thus, its height is -1200 m.
E: The point is located on the second dotted line above the 1000 m line. Thus, its height is 1200 m.
F: The point is located on the third dotted line below sea level (0 m). Thus, its height is -300 m.
G: The point is located on the first dotted line above sea level (0 m). Thus, its height is 100 m.
Question 2. Which is the highest point in this geographical cross-section? Which is the lowest point?
Answer:
To find the highest and lowest points, we first list the heights of all the marked points from the graph:
- Point A: +1500 m
- Point B: -500 m
- Point C: +300 m
- Point D: -1200 m
- Point E: +1200 m
- Point F: -300 m
- Point G: +100 m
The highest point is the one with the greatest positive value. Comparing the positive heights (+1500, +1200, +300, +100), the largest value is +1500 m.
Therefore, the highest point is A.
The lowest point is the one with the smallest value (the most negative value). Comparing the negative heights (-500, -1200, -300), the smallest value is -1200 m.
Therefore, the lowest point is D.
Question 3. Can you write the points A, B, …, G in a sequence of decreasing order of heights? Can you write the points in a sequence of increasing order of heights?
Answer:
First, let's list the heights of each point:
- A: +1500 m
- B: -500 m
- C: +300 m
- D: -1200 m
- E: +1200 m
- F: -300 m
- G: +100 m
Sequence of decreasing order of heights (highest to lowest):
We arrange the heights from the largest value to the smallest value:
$+1500 > +1200 > +300 > +100 > -300 > -500 > -1200$
The corresponding sequence of points is:
A, E, C, G, F, B, D
Sequence of increasing order of heights (lowest to highest):
We arrange the heights from the smallest value to the largest value:
$-1200 < -500 < -300 < +100 < +300 < +1200 < +1500$
The corresponding sequence of points is:
D, B, F, G, C, E, A
Question 4. What is the highest point above sea level on Earth? What is its height?
Answer:
The highest point above sea level on Earth is the summit of Mount Everest, located in the Himalayas.
Its officially recognized height is 8,848.86 metres above sea level.
Question 5. What is the lowest point with respect to sea level on land or on the ocean floor? What is its height? (This height should be negative).
Answer:
The lowest point on the surface of the Earth is the Challenger Deep, which is located at the southern end of the Mariana Trench on the ocean floor in the western Pacific Ocean.
Its depth, expressed as a negative height with respect to sea level, is approximately -10,984 metres. (Note: Measurements vary slightly, but this is a commonly cited value).
Figure it Out (Page 262)
Question 1. Do you know that there are some places in India where temperatures can go below 0°C? Find out the places in India where temperatures sometimes go below 0°C. What is common among these places? Why does it become colder there and not in other places?
Answer:
Yes, there are many places in India where temperatures drop below 0°C, especially during the winter months. These places often experience snowfall and freezing conditions.
Some of these places include:
- Ladakh: Leh, Dras (often cited as one of the coldest inhabited places in India), and Kargil.
- Jammu and Kashmir: Srinagar, Gulmarg, and Pahalgam.
- Himachal Pradesh: Shimla, Manali, Kullu, Keylong, and Spiti Valley.
- Uttarakhand: Auli, Munsiyari, and Harsil.
- Sikkim: Lachen, Lachung, and Yumthang Valley.
- Arunachal Pradesh: Tawang and Bomdila.
What is common among these places?
The most significant common factor among all these places is their high altitude. They are all located in the Himalayan mountain ranges in the northern and northeastern parts of India.
Why does it become colder there and not in other places?
Several geographical factors contribute to the extremely low temperatures in these regions:
High Altitude: This is the primary reason. As you go higher up from sea level, the air becomes thinner (less dense). Thinner air is less effective at absorbing and retaining heat from the sun and the Earth's surface. As a general rule, the temperature decreases by about 6.5°C for every 1000 metres increase in altitude. This phenomenon is known as the normal lapse rate.
Distance from the Sea: These mountainous regions are far from the moderating influence of the sea. Coastal areas experience milder winters because the water cools down much more slowly than land, keeping the nearby air warmer. Inland areas do not have this benefit and thus experience more extreme temperatures.
Snowfall: These areas receive heavy snowfall in winter. Fresh snow is white and has a high albedo, which means it reflects most of the sunlight back into space instead of absorbing it. This prevents the ground and the air above it from warming up, keeping the temperatures very low.
Northern Latitude: Being located in the northern parts of India, these places receive slanting sun rays during the winter. Slanted rays spread the sun's energy over a larger area, making them less intense and providing less heat compared to the direct rays received in regions closer to the equator.
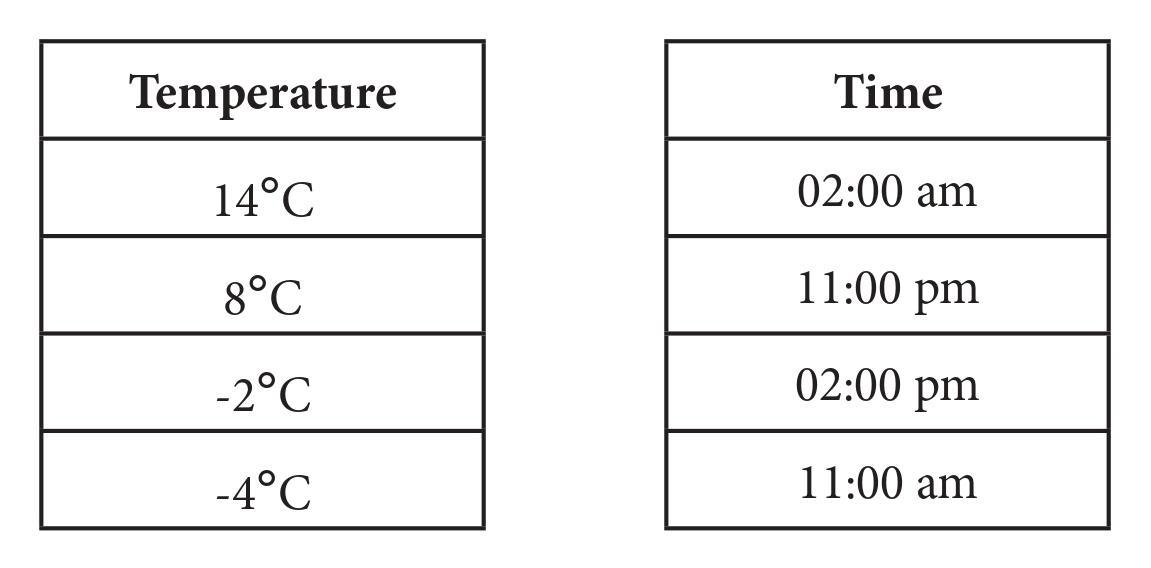
Answer:
To match the temperatures with the appropriate times, we need to consider the typical daily temperature cycle. Generally, the temperature is at its lowest in the early hours of the morning (before sunrise) and at its highest in the afternoon.
Let's apply this logic:
The highest temperature in the list is 14°C. This would most likely occur in the afternoon. The afternoon time given is 02:00 pm.
The lowest temperature in the list is -4°C. This would most likely occur in the coldest part of the night/early morning. The earliest morning time given is 02:00 am.
The remaining temperatures are 8°C and -2°C, and the remaining times are 11:00 am and 11:00 pm. At 11:00 am, the day is warming up, so the temperature would be moderately high. At 11:00 pm, the day has cooled down significantly, so the temperature would be low.
Therefore, 8°C corresponds to 11:00 am, and -2°C corresponds to 11:00 pm.
The correct matching is presented in the table below:
| Temperature | Time |
| 14°C | 02:00 pm |
| 8°C | 11:00 am |
| -2°C | 11:00 pm |
| -4°C | 02:00 am |
Figure it Out (Page 263 - 264)
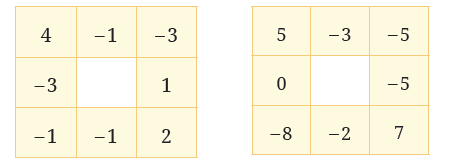
There is something special about the numbers in these two grids. Let us explore what that is.
| Top row: | $4 + (– 1) + (– 3) = 0$ | $5 + (– 3) + (– 5) =$ ____ |
| Bottom row: | $(– 1) + (– 1) + 2 = 0$ | $(– 8) + (– 2) + 7 =$ ____ |
| Left column: | $4 + (– 3) + (– 1) = 0$ | $5 + 0 + (– 8) =$ ____ |
| Right column: | $(– 3) + 1 + 2 = 0$ | $(– 5) + (– 5) + 7 =$ ____ |
In each grid, the numbers in each of the two rows (the top row and the bottom row) and the numbers in each of the two columns (the leftmost column and the rightmost column) add up to give the same number. We shall call this sum as the ‘border sum’. The border sum of the first grid is ‘0’.
Question 1. Do the calculations for the second grid above and find the border sum.
Answer:
To Find:
The border sum for the second grid.
Solution:
The "border sum" is the sum of the numbers in the top row, bottom row, left column, and right column. We need to calculate these sums for the second grid. The numbers in the second grid are:
| 5 | -3 | -5 |
| 0 | -5 | |
| -8 | -2 | 7 |
Let's perform the calculations for each border:
1. Top row:
$5 + (– 3) + (– 5) = 5 – 3 – 5 = 2 – 5 = -3$
2. Bottom row:
$(– 8) + (– 2) + 7 = –8 – 2 + 7 = –10 + 7 = -3$
3. Left column:
$5 + 0 + (– 8) = 5 – 8 = -3$
4. Right column:
$(– 5) + (– 5) + 7 = –5 – 5 + 7 = –10 + 7 = -3$
Since the sum of each border (top row, bottom row, left column, and right column) is the same, we can conclude that the border sum for the second grid is –3.
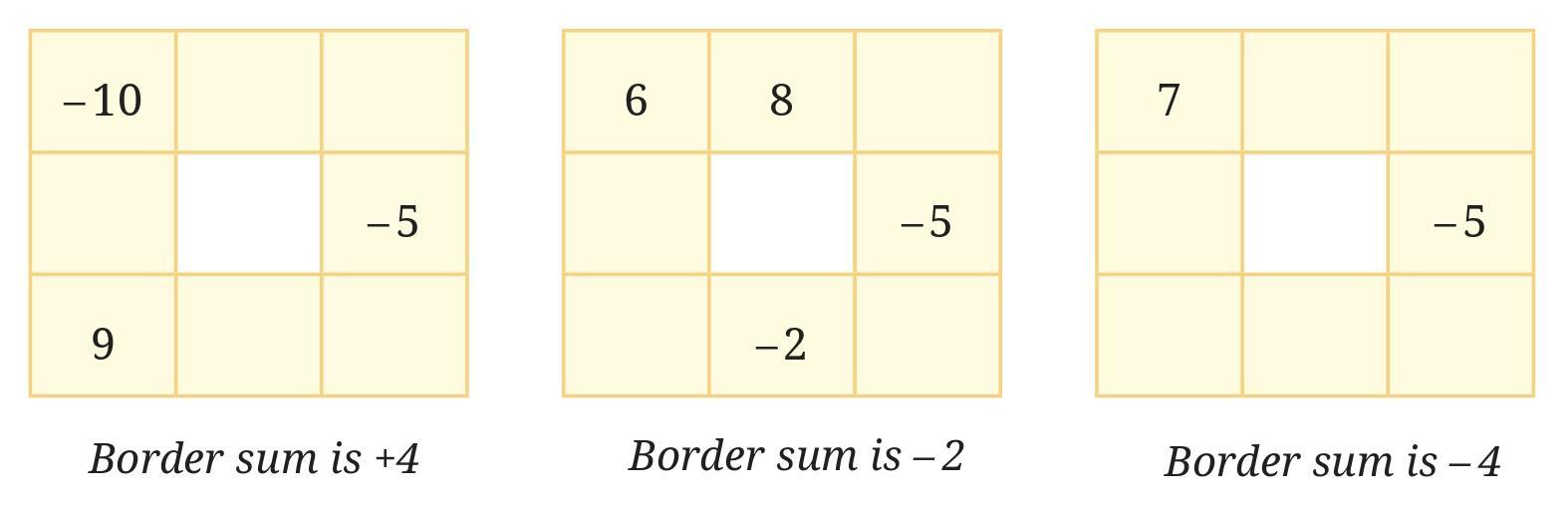
Answer:
To complete the grids, we need to fill in the blank cells on the border so that the sum of the numbers in the top row, bottom row, left column, and right column each equals the given 'border sum'.
Grid 1: Border sum is +4
First, we find any missing number that can be calculated directly. Let's look at the left column:
Left column: $(-10) + \text{Middle-left} + 9 = 4$
$(-1) + \text{Middle-left} = 4$
$\text{Middle-left} = 4 + 1 = 5$
Now we have to find the remaining four numbers. There are multiple possible solutions. We will find one valid solution. Let's assume the bottom-right number is 0.
Bottom-right = 0
Now we can solve for the other numbers:
Right column: $\text{Top-right} + (-5) + 0 = 4$
$\text{Top-right} = 4 + 5 = 9$
Bottom row: $9 + \text{Bottom-middle} + 0 = 4$
$\text{Bottom-middle} = 4 - 9 = -5$
Top row: $(-10) + \text{Top-middle} + 9 = 4$
$(-1) + \text{Top-middle} = 4$
$\text{Top-middle} = 4 + 1 = 5$
The completed grid is:
| -10 | 5 | 9 |
| 5 | -5 | |
| 9 | -5 | 0 |
Grid 2: Border sum is -2
We can find the missing numbers step-by-step:
1. Top row: We can find the top-right number.
$6 + 8 + \text{Top-right} = -2$
$14 + \text{Top-right} = -2$
$\text{Top-right} = -2 - 14 = -16$
2. Right column: Now we can find the bottom-right number.
$(-16) + (-5) + \text{Bottom-right} = -2$
$(-21) + \text{Bottom-right} = -2$
$\text{Bottom-right} = -2 + 21 = 19$
3. Bottom row: Now we can find the bottom-left number.
$\text{Bottom-left} + (-2) + 19 = -2$
$\text{Bottom-left} + 17 = -2$
$\text{Bottom-left} = -2 - 17 = -19$
4. Left column: Finally, we find the middle-left number.
$6 + \text{Middle-left} + (-19) = -2$
$\text{Middle-left} - 13 = -2$
$\text{Middle-left} = -2 + 13 = 11$
The completed grid is:
| 6 | 8 | -16 |
| 11 | -5 | |
| -19 | -2 | 19 |
Grid 3: Border sum is -4
For this grid, there are many possible solutions. We will find one by making some simple choices. Let's assume the top-right number is 0.
Top-right = 0
Now we can solve for the other numbers:
Top row: $7 + \text{Top-middle} + 0 = -4$
$\text{Top-middle} = -4 - 7 = -11$
Right column: $0 + (-5) + \text{Bottom-right} = -4$
$\text{Bottom-right} = -4 + 5 = 1$
Now let's assume the bottom-left number is 0.
Bottom-left = 0
Left column: $7 + \text{Middle-left} + 0 = -4$
$\text{Middle-left} = -4 - 7 = -11$
Bottom row: $0 + \text{Bottom-middle} + 1 = -4$
$\text{Bottom-middle} = -4 - 1 = -5$
The completed grid is:
| 7 | -11 | 0 |
| -11 | -5 | |
| 0 | -5 | 1 |
Question 3. For the last grid above, find more than one way of filling the numbers to get border sum – 4.
Answer:
The last grid is the third one, which has a required border sum of -4. The initial state of the grid is:
| 7 | ||
| -5 | ||
We need to find values for the blank border cells so that the top row, bottom row, left column, and right column each sum to -4. There are infinite solutions. Here are two possible ways.
Way 1:
Let's make some simple choices to start. Let the top-right corner be 1.
Top row: $7 + \text{Top-middle} + 1 = -4 $$ \implies 8 + \text{Top-middle} = -4 $$ \implies \text{Top-middle} = -12$
Right column: $1 + (-5) + \text{Bottom-right} = -4 $$ \implies -4 + \text{Bottom-right} = -4 $$ \implies \text{Bottom-right} = 0$
Now let's choose the bottom-left corner to be 0.
Left column: $7 + \text{Middle-left} + 0 = -4 \implies \text{Middle-left} = -11$
Bottom row: $0 + \text{Bottom-middle} + 0 = -4 $$ \implies \text{Bottom-middle} = -4$
The completed grid for Way 1 is:
| 7 | -12 | 1 |
| -11 | -5 | |
| 0 | -4 | 0 |
Way 2:
Let's make different initial choices. Let the top-right corner be -3.
Top row: $7 + \text{Top-middle} + (-3) = -4 $$ \implies 4 + \text{Top-middle} = -4 $$ \implies \text{Top-middle} = -8$
Right column: $(-3) + (-5) + \text{Bottom-right} = -4 $$ \implies -8 + \text{Bottom-right} = -4 $$ \implies \text{Bottom-right} = 4$
Now let's choose the bottom-left corner to be -1.
Left column: $7 + \text{Middle-left} + (-1) = -4 $$ \implies 6 + \text{Middle-left} = -4 $$ \implies \text{Middle-left} = -10$
Bottom row: $(-1) + \text{Bottom-middle} + 4 = -4 $$ \implies 3 + \text{Bottom-middle} = -4 $$ \implies \text{Bottom-middle} = -7$
The completed grid for Way 2 is:
| 7 | -8 | -3 |
| -10 | -5 | |
| -1 | -7 | 4 |
Question 4. Which other grids can be filled in multiple ways? What could be the reason?
Answer:
Actually, all of the grids in this puzzle can be filled in more than one correct way.
Reason:
The reason is that there are too many empty boxes and not enough starting numbers to force you into only one solution. This gives you the freedom to make a choice when you start filling in the numbers.
Let's look at the last grid where the border sum is – 4.
The top row has the number 7, followed by two empty boxes. The rule is that the sum of this row must be – 4.
$7 + \text{Box A} + \text{Box B} = -4$
Since there are two empty boxes, we have to choose a number for one of them to figure out the other. We can make different choices.
Example Choice 1:
Let's choose to put 0 in Box B. The equation becomes:
$7 + \text{Box A} + 0 = -4$
To make this true, Box A must be –11.
Example Choice 2:
Now, what if we choose to put 1 in Box B instead? The equation becomes:
$7 + \text{Box A} + 1 = -4$
$8 + \text{Box A} = -4$
To make this true, Box A must be –12.
Because you can make different starting choices that lead to different correct answers, there are multiple ways to fill the grid. This is true for any row or column in the puzzles that has more than one empty box.
Question 5. Make a border integer square puzzle and challenge your classmates.
Answer:
Here is a border integer square puzzle you can use.
Puzzle Challenge:
Complete the following grid by filling in the blank cells with integers. The 'border sum' for this grid must be +5. This means the sum of the numbers in the top row, bottom row, left column, and right column must each be equal to +5.
Grid to Solve:
| 8 | -2 | |
| -1 |
Solution (for you to check their answers):
There are multiple correct answers. Here is one possible solution:
Step 1: Top row. Let the top-middle cell be $x$.
$8 + x + (-2) = 5 \implies 6 + x = 5 \implies x = -1$.
Step 2: Left column. Let the bottom-left cell be $y$ and the middle-left be $z$.
$8 + z + y = 5$. We need to choose values. Let's pick $y = 0$.
$8 + z + 0 = 5 \implies z = -3$.
Step 3: Bottom row. Let the bottom-right cell be $w$.
$0 + (-1) + w = 5 \implies -1 + w = 5 \implies w = 6$.
Step 4: Right column. Let the middle-right cell be $v$. We can use this to check our work.
$(-2) + v + 6 = 5 \implies 4 + v = 5 \implies v = 1$.
One possible completed grid:
| 8 | -1 | -2 |
| -3 | 1 | |
| 0 | -1 | 6 |
Encourage your classmates to find different solutions!
Figure it Out (Page 265)
Below is a grid having some numbers. Follow the steps as shown until no number is left.
| 3 | 4 | 0 | 9 |
| -2 | -1 | -5 | 4 |
| 1 | 2 | -2 | 7 |
| -7 | -6 | -10 | -1 |
- Strike out the row and column of the chosen number
- Circle any number
- Circle any unstruck number
- When there are no more unstruck numbers, STOP. Add the circled numbers.
In the example below, the circled numbers are $-1$, $9$, $-7$, $-2$. If you add them, you get $-1$.
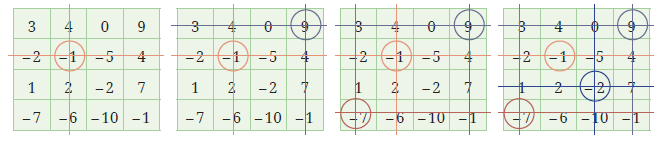
Question 1. Try afresh, choose different numbers this time. What sum did you get? Was it different from the first time? Try a few more times!
Answer:
Let's try the puzzle afresh with different choices and visualize the process. The grid of numbers is:
| 3 | 4 | 0 | 9 |
| -2 | -1 | -5 | 4 |
| 1 | 2 | -2 | 7 |
| -7 | -6 | -10 | -1 |
First New Attempt
- Let's start by circling the number 3 in the top-left corner. We strike out the first row and the first column.
- From the remaining unstruck numbers, let's circle 2 (in the third row, second column). We strike out the third row and second column.
- From the remaining unstruck numbers, let's circle -10 (in the fourth row, third column). We strike out the fourth row and third column.
- The only unstruck number left is 4 (in the second row, fourth column). We circle it.
The circled numbers in this attempt are: 3, 2, -10, 4.
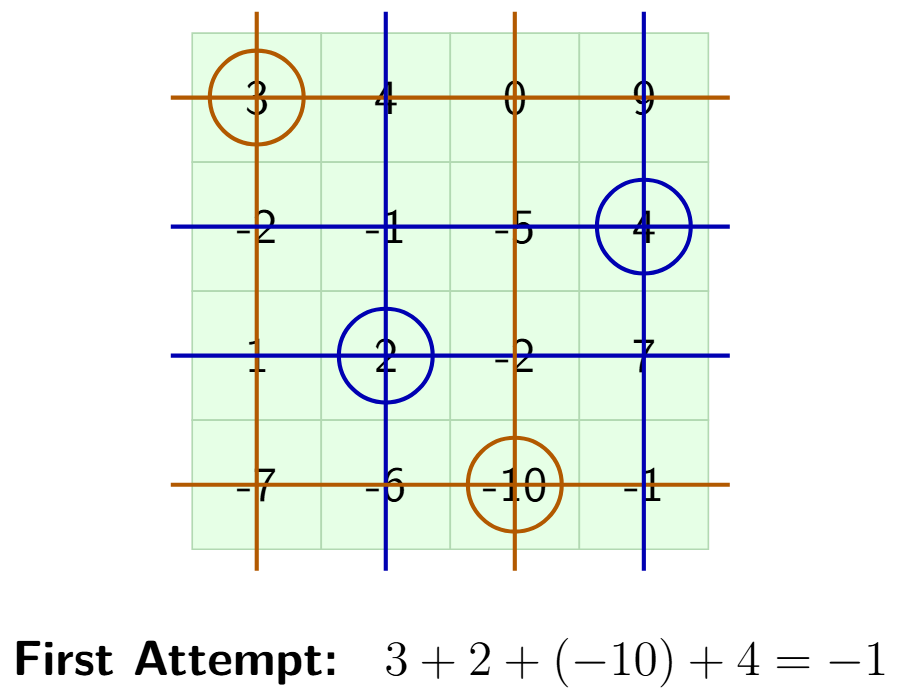
Now, let's calculate their sum:
$3 + 2 + (-10) + 4$
$ = 5 + (-10) + 4$
$ = -5 + 4$
$ = -1$
The sum is -1. This is the same sum as the one obtained in the example.
Second New Attempt
- Let's start by circling -1 in the bottom-right corner. We strike out the fourth row and fourth column.
- From the remaining unstruck numbers, let's circle 1 (in the third row, first column). We strike out the third row and first column.
- From the remaining unstruck numbers, let's circle 4 (in the first row, second column). We strike out the first row and second column.
- The only unstruck number left is -5 (in the second row, third column). We circle it.
The circled numbers in this attempt are: -1, 1, 4, -5.
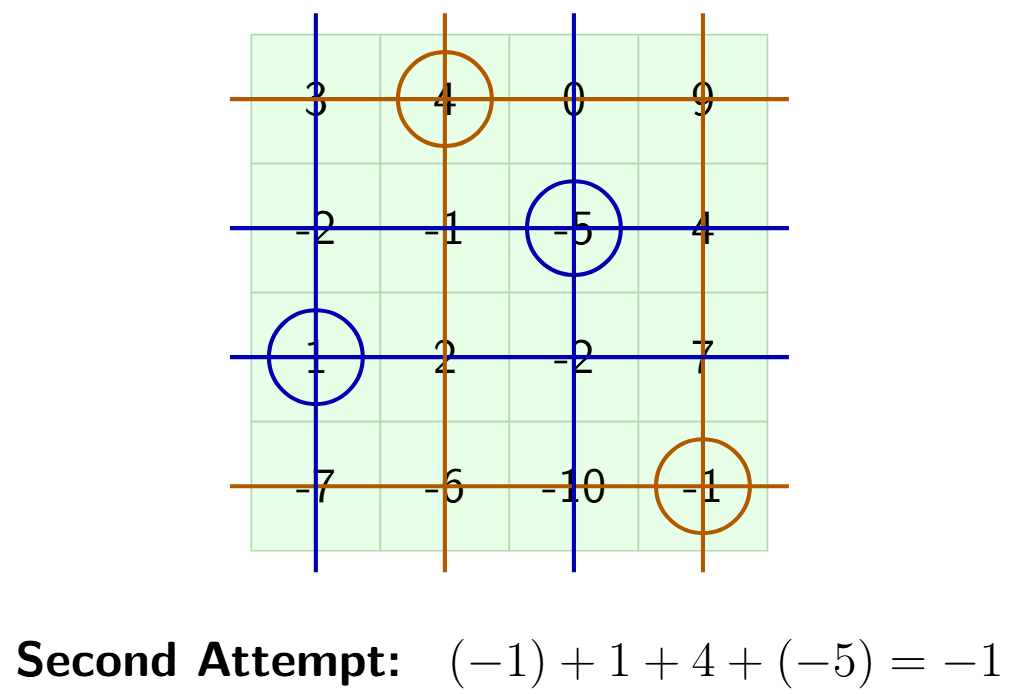
Now, let's calculate their sum:
$(-1) + 1 + 4 + (-5)$
$ = 0 + 4 + (-5)$
$ = 4 - 5$
$ = -1$
The sum is again -1.
Conclusion
The sum I got was -1. This was not different from the first time.
If you try a few more times with different starting numbers, you will discover that no matter which four numbers you circle according to the rules, their sum will always be -1. This is a special property of this particular grid of numbers.
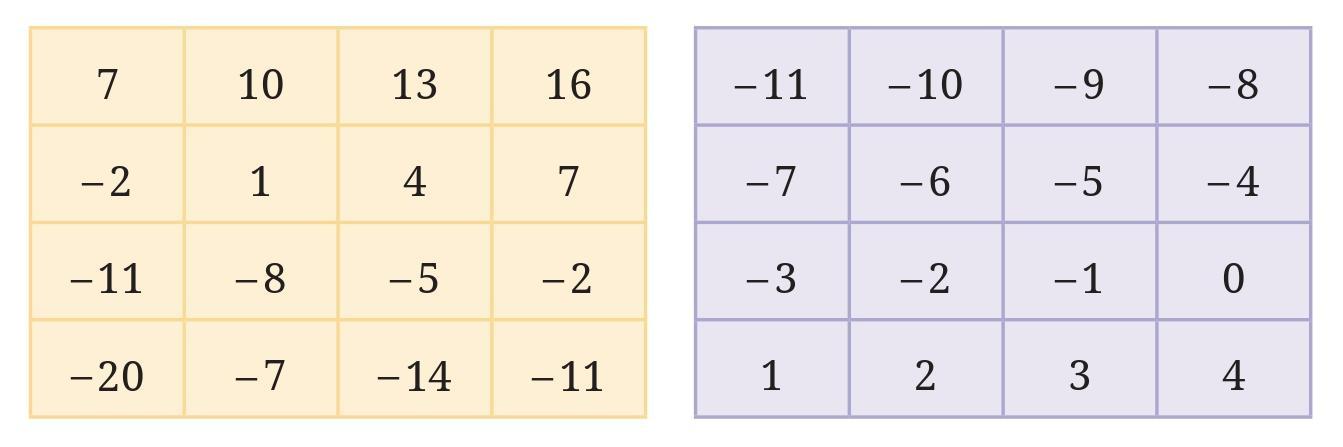
Answer:
We will play the game for each of the two grids provided by choosing a set of four numbers according to the rules, showing the process visually, and then finding their sum.
Grid 1 (Yellow Grid)
The first grid is:
| 7 | 10 | 13 | 16 |
| -2 | 1 | 4 | 7 |
| -11 | -8 | -5 | -2 |
| -20 | -7 | -14 | -11 |
Let's play the game with one possible set of choices:
- Circle the number 10 (in row 1, column 2). Strike out its row and column.
- From the remaining numbers, circle -2 (in row 2, column 1). Strike out its row and column.
- From the remaining numbers, circle -5 (in row 3, column 3). Strike out its row and column.
- The only number left is -11 (in row 4, column 4). Circle it.
The circled numbers are 10, -2, -5, and -11.
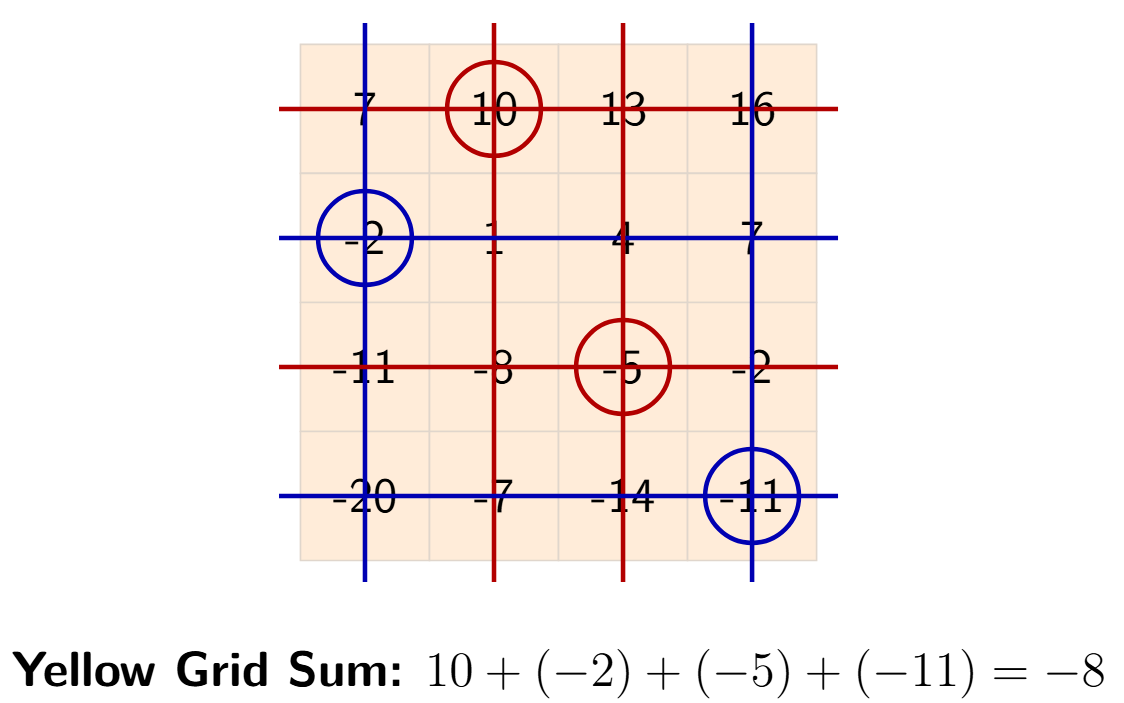
Let's find their sum:
$10 + (-2) + (-5) + (-11)$
$ = 8 + (-5) + (-11)$
$ = 3 + (-11)$
$ = -8$
The answer for the first grid is -8. (No matter which combination you choose, the sum will always be -8).
Grid 2 (Purple Grid)
The second grid is:
| -11 | -10 | -9 | -8 |
| -7 | -6 | -5 | -4 |
| -3 | -2 | -1 | 0 |
| 1 | 2 | 3 | 4 |
Let's play the game with one possible set of choices:
- Circle the number -11 (in row 1, column 1). Strike out its row and column.
- From the remaining numbers, circle -6 (in row 2, column 2). Strike out its row and column.
- From the remaining numbers, circle 0 (in row 3, column 4). Strike out its row and column.
- The only number left is 3 (in row 4, column 3). Circle it.
The circled numbers are -11, -6, 0, and 3.
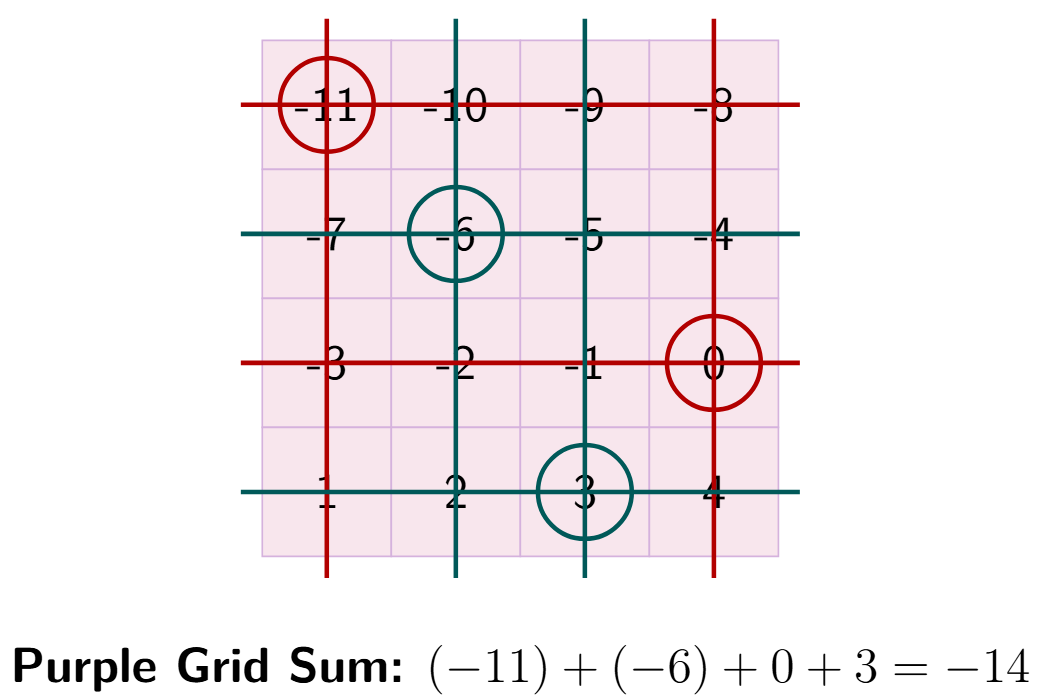
Let's find their sum:
$(-11) + (-6) + 0 + 3$
$ = -17 + 0 + 3$
$ = -17 + 3$
$ = -14$
The answer for the second grid is -14. (Again, any combination of choices will result in this same sum).
Question 3. What could be so special about these grids? Is the magic in the numbers or the way they are arranged or both? Can you make more such grids?
Answer:
What is so special about these grids?
The special property is that no matter which four numbers you circle following the "strike out the row and column" rule, their sum is always the same. For the first grid you played with, the sum is always -8. For the second grid, the sum is always -14. This constant sum is the "magic" of the grid.
Is the magic in the numbers or the way they are arranged or both?
The magic is in both the numbers and their arrangement. The numbers in the grid are not random; they are placed there according to a hidden pattern or rule.
Think of it like this: each grid is created from two secret lists of numbers. One list is for the rows, and one is for the columns.
- Let's say the secret list for the rows is [R1, R2, R3, R4].
- And the secret list for the columns is [C1, C2, C3, C4].
Every number in the grid is the sum of its secret row number and secret column number. For example, the number in the top-left corner is R1 + C1.
When you follow the rule of picking one number from each row and column, you are actually picking each secret number from the lists exactly once. So, your final sum is always:
$(R1 + R2 + R3 + R4) + (C1 + C2 + C3 + C4)$
Since the secret lists never change, this sum is always the same, no matter which cells you pick!
Can you make more such grids?
Yes, you can! Now that you know the secret, you can easily create your own magic grids. Here’s how to make a 3x3 grid:
Step 1: Choose 3 "secret row numbers".
Let's pick: 5, 10, -2
Step 2: Choose 3 "secret column numbers".
Let's pick: 4, -1, 0
Step 3: Create the grid by adding the numbers.
For each box in the grid, add the corresponding secret row number and secret column number.
- Top-left box = (Row 1 secret number) + (Column 1 secret number) = 5 + 4 = 9
- Top-middle box = 5 + (-1) = 4
- Middle-right box = 10 + 0 = 10
Here is the completed grid:
| $5 + 4 = \mathbf{9}$ | $5 + (-1) = \mathbf{4}$ | $5 + 0 = \mathbf{5}$ |
| $10 + 4 = \mathbf{14}$ | $10 + (-1) = \mathbf{9}$ | $10 + 0 = \mathbf{10}$ |
| $(-2) + 4 = \mathbf{2}$ | $(-2) + (-1) = \mathbf{-3}$ | $(-2) + 0 = \mathbf{-2}$ |
You can now challenge your friends with this grid! The magic sum will be the sum of all your secret numbers: $(5 + 10 - 2) + (4 - 1 + 0) = 13 + 3 = \mathbf{16}$.
Figure it Out (Page 265 - 266)
Question 1. Write all the integers between the given pairs, in increasing order.
a. 0 and – 7
b. – 4 and 4
c. – 8 and – 15
d. – 30 and – 23
Answer:
We list the integers between the given pairs in increasing order. "Between" means strictly greater than the smaller number and strictly less than the larger number.
a. Integers between 0 and –7 (i.e., between –7 and 0) in increasing order:
The integers greater than $-7$ and less than $0$ are $-6, -5, -4, -3, -2, -1$.
-6, -5, -4, -3, -2, -1
b. Integers between –4 and 4 in increasing order:
The integers greater than $-4$ and less than $4$ are $-3, -2, -1, 0, 1, 2, 3$.
-3, -2, -1, 0, 1, 2, 3
c. Integers between –8 and –15 (i.e., between –15 and –8) in increasing order:
The integers greater than $-15$ and less than $-8$ are $-14, -13, -12, -11, -10, -9$.
-14, -13, -12, -11, -10, -9
d. Integers between –30 and –23 in increasing order:
The integers greater than $-30$ and less than $-23$ are $-29, -28, -27, -26, -25, -24$.
-29, -28, -27, -26, -25, -24
Question 2. Give three numbers such that their sum is – 8.
Answer:
We need to find three integers that, when added together, result in a sum of -8.
There are many possible combinations. Here is one example:
Let the three numbers be -3, -2, and -3.
Let's find their sum:
$(-3) + (-2) + (-3) = -5 + (-3) = -5 - 3 = -8$
Another example:
Let the three numbers be 0, -5, and -3.
Let's find their sum:
$0 + (-5) + (-3) = -5 + (-3) = -5 - 3 = -8$
Another example:
Let the three numbers be +2, -10, and 0.
Let's find their sum:
$(+2) + (-10) + 0 = 2 - 10 + 0 = -8$
Three numbers such that their sum is -8 are, for example: -3, -2, and -3.
(Any set of three integers that add up to -8 is a valid answer.)
Question 3. There are two dice whose faces have these numbers: – 1, 2, – 3, 4, – 5, 6. The smallest possible sum upon rolling these dice is – 10 = (– 5) + (– 5) and the largest possible sum is 12 = (6) + (6). Some numbers between (– 10) and (+ 12) are not possible to get by adding numbers on these two dice. Find those numbers.
Answer:
Given:
We have two identical dice. The numbers on the faces of each die are {–1, 2, –3, 4, –5, 6}.
The smallest possible sum is $(–5) + (–5) = –10$.
The largest possible sum is $6 + 6 = 12$.
To Find:
The integer sums between –10 and 12 (inclusive) that are impossible to obtain by rolling these two dice.
Solution:
To find all possible sums, we can create a table that shows the result of adding the outcome of the first die to the outcome of the second die. Let's list the numbers on the faces in ascending order: {–5, –3, –1, 2, 4, 6}.
| + | –5 | –3 | –1 | 2 | 4 | 6 |
| –5 | –10 | –8 | –6 | –3 | –1 | 1 |
| –3 | –8 | –6 | –4 | –1 | 1 | 3 |
| –1 | –6 | –4 | –2 | 1 | 3 | 5 |
| 2 | –3 | –1 | 1 | 4 | 6 | 8 |
| 4 | –1 | 1 | 3 | 6 | 8 | 10 |
| 6 | 1 | 3 | 5 | 8 | 10 | 12 |
From the table, we can list all the unique possible sums in increasing order:
–10, –8, –6, –4, –3, –2, –1, 1, 3, 4, 5, 6, 8, 10, 12
Now, let's list all the integers from the smallest possible sum (–10) to the largest (12):
–10, –9, –8, –7, –6, –5, –4, –3, –2, –1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12
By comparing the two lists, we can find the numbers that are in the full range but are not possible to get as a sum. These numbers are:
–9, –7, –5, 0, 2, 7, 9, 11
These are the sums that cannot be obtained by rolling the two dice.

Answer:
Top Row Calculations
1. $8 - 13$
$8 - 13 = -5$
2. $(-8) - (13)$
$(-8) - (13) = -8 - 13 = -21$
3. $(-13) - (-8)$
Subtracting a negative number is the same as adding its positive counterpart.
$(-13) - (-8) = -13 + 8 = -5$
4. $(-13) + (-8)$
$(-13) + (-8) = -13 - 8 = -21$
Bottom Row Calculations
5. $8 + (-13)$
$8 + (-13) = 8 - 13 = -5$
6. $(-8) - (-13)$
Subtracting a negative number is the same as adding its positive counterpart.
$(-8) - (-13) = -8 + 13 = 5$
7. $(13) - 8$
$(13) - 8 = 13 - 8 = 5$
8. $13 - (-8)$
Subtracting a negative number is the same as adding its positive counterpart.
$13 - (-8) = 13 + 8 = 21$
Question 5. Find the years below.
a. From the present year, which year was it 150 years ago? ________
b. From the present year, which year was it 2200 years ago? _______
(Hint: Recall that there was no year 0.)
c. What will be the year 320 years after 680 BCE? ________
Answer:
To solve these, we can think of years on a number line. Let's represent CE (Common Era) years as positive integers and BCE (Before Common Era) years as negative integers. Let's assume the "present year" is 2024 CE.
a. From the present year, which year was it 150 years ago?
We subtract 150 from the present year.
$2024 - 150 = 1874$
The year was 1874 CE.
b. From the present year, which year was it 2200 years ago?
We subtract 2200 from the present year.
$2024 - 2200 = -176$
The timeline goes directly from 1 CE to 1 BCE, with no year 0. A result of 0 would mean 1 BCE, -1 would mean 2 BCE, and so on. So, a result of -176 means the year is 177 BCE.
c. What will be the year 320 years after 680 BCE?
We can represent 680 BCE as -680. "320 years after" means we add 320.
$-680 + 320 = -360$
A result of -360 corresponds to the year 360 BCE.
Question 6. Complete the following sequences:
a. (– 40), (– 34), (– 28), (– 22), _____, ______, ______
b. 3, 4, 2, 5, 1, 6, 0, 7, _____, _____, _____
c. _____, ______, 12, 6, 1, (– 3), (– 6), _____, ______, ______
Answer:
We need to find the pattern in each sequence to determine the missing terms.
a. (– 40), (– 34), (– 28), (– 22), _____, ______, ______
Let's find the difference between consecutive terms:
$(-34) - (-40) = 6$
$(-28) - (-34) = 6$
$(-22) - (-28) = 6$
The pattern is to add 6 to each term. The next terms are:
$-22 + 6 = -16$
$-16 + 6 = -10$
$-10 + 6 = -4$
The sequence is: (– 40), (– 34), (– 28), (– 22), –16, –10, –4.
b. 3, 4, 2, 5, 1, 6, 0, 7, _____, _____, _____
This sequence has two alternating patterns:
The numbers in the odd positions (1st, 3rd, 5th,...) form a sequence: 3, 2, 1, 0, ... The pattern is subtract 1.
The numbers in the even positions (2nd, 4th, 6th,...) form a sequence: 4, 5, 6, 7, ... The pattern is add 1.
Following these patterns:
The next term in the 'subtract 1' sequence is $0 - 1 = -1$.
The next term in the 'add 1' sequence is $7 + 1 = 8$.
The next term in the 'subtract 1' sequence is $-1 - 1 = -2$.
The sequence is: 3, 4, 2, 5, 1, 6, 0, 7, –1, 8, –2.
c. _____, ______, 12, 6, 1, (– 3), (– 6), _____, ______, ______
Let's look at the difference between the known terms:
$6 - 12 = -6$
$1 - 6 = -5$
$-3 - 1 = -4$
$-6 - (-3) = -3$
The amount being subtracted decreases by 1 each time. The pattern of differences is: ..., -7, -6, -5, -4, -3, -2, -1, 0, ...
To find the terms after –6:
$-6 - 2 = -8$
$-8 - 1 = -9$
$-9 - 0 = -9$
To find the terms before 12, we go backward. The difference before -6 was -7.
$12 - (-7) = 12 + 7 = 19$.
The difference before -7 was -8.
$19 - (-8) = 19 + 8 = 27$.
The sequence is: 27, 19, 12, 6, 1, (– 3), (– 6), –8, –9, –9.
Question 7. Here are six integer cards: (+ 1), (+ 7), (+ 18), (– 5), (– 2), (– 9).
You can pick any of these and make an expression using addition(s) and subtraction(s).
Here is an expression: (+ 18) + (+ 1) – (+ 7) – (– 2) which gives a value (+ 14). Now, pick cards and make an expression such that its value is closer to (– 30).
Answer:
Given Cards: (+1), (+7), (+18), (–5), (–2), (–9)
Target Value: Get a result as close as possible to –30.
Strategy:
To get a large negative number like –30, we should start with our negative cards and make them even more negative by subtracting the largest positive cards.
Let's try subtracting the two largest positive cards, (+18) and (+7), from one of our negative cards.
Attempt 1: Start with (–9).
$(–9) – (+18) – (+7) = -9 - 18 - 7 = -27 - 7 = -34$.
This is close to -30 (difference of 4).
Attempt 2: Start with (–5).
$(–5) – (+18) – (+7) = -5 - 18 - 7 = -23 - 7 = -30$.
This gives exactly –30, which is the closest possible value.
An expression whose value is closest to –30 is:
(–5) – (+18) – (+7)
The value of this expression is –30.
Question 8. The sum of two positive integers is always positive but a (positive integer) – (positive integer) can be positive or negative. What about
a. (positive) – (negative)
b. (positive) + (negative)
c. (negative) + (negative)
d. (negative) – (negative)
e. (negative) – (positive)
f. (negative) + (positive)
Answer:
Let's determine the outcome for each case.
a. (positive) – (negative)
Subtracting a negative is the same as adding a positive. Example: $5 - (-3) = 5 + 3 = 8$.
The result is always positive.
b. (positive) + (negative)
The result depends on which number has a larger absolute value.
- $10 + (-4) = 6$ (Positive)
- $10 + (-15) = -5$ (Negative)
- $10 + (-10) = 0$ (Zero)
The result can be positive, negative, or zero.
c. (negative) + (negative)
Adding two negative numbers results in a more negative number. Example: $(-5) + (-3) = -8$.
The result is always negative.
d. (negative) – (negative)
This is the same as (negative) + (positive). The result depends on which number has a larger absolute value.
- $(-4) - (-10) = -4 + 10 = 6$ (Positive)
- $(-10) - (-4) = -10 + 4 = -6$ (Negative)
- $(-10) - (-10) = -10 + 10 = 0$ (Zero)
The result can be positive, negative, or zero.
e. (negative) – (positive)
Subtracting a positive from a negative makes it more negative. Example: $(-5) - 3 = -8$.
The result is always negative.
f. (negative) + (positive)
This is the same operation as part (b). The result depends on the numbers' absolute values.
The result can be positive, negative, or zero.
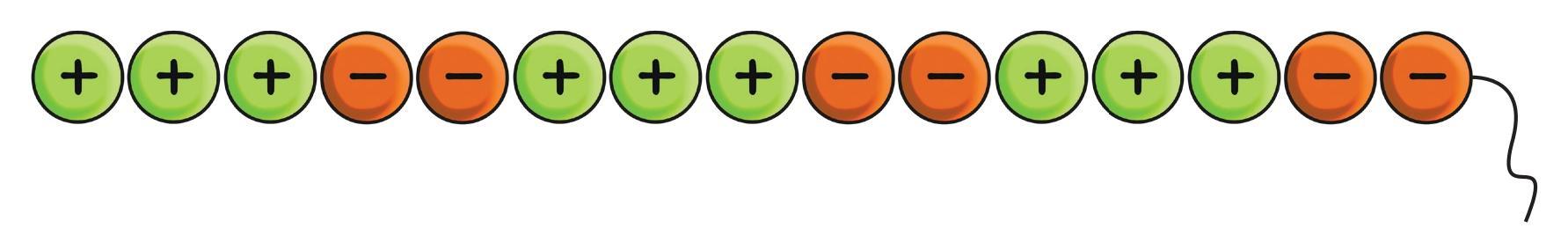
Answer:
Given:
A string contains a total of 100 tokens.
The tokens are arranged in a repeating pattern as shown in the image.
Green tokens represent positive integers (+1) and orange tokens represent negative integers (–1).
To Find:
The total value of the string of 100 tokens.
Solution:
First, we need to identify the repeating pattern in the string of tokens from the image.
By observing the image, we can see that the pattern is:
3 green (+) tokens followed by 2 orange (–) tokens.
This block of $(+++--)$ consists of $3+2=5$ tokens. This 5-token block is the basic repeating unit of the string.
Next, let's calculate the value of this single repeating block:
Value of one block = $(+1) + (+1) + (+1) + (–1) + (–1)$
= $3 - 2$
= $1$
So, each repeating block of 5 tokens has a total value of +1.
Now, we need to find out how many times this 5-token block repeats in a string of 100 tokens.
Number of blocks = $\frac{\text{Total number of tokens}}{\text{Number of tokens in one block}}$
Number of blocks = $\frac{100}{5} = 20$
The pattern repeats 20 times in the string.
Finally, to find the total value of the string, we multiply the number of blocks by the value of each block.
Total Value = (Number of blocks) $\times$ (Value of one block)
Total Value = $20 \times 1 = 20$
Therefore, the value of the string is +20.
Alternate Solution:
We know the string has 100 tokens and the pattern $(+++--)$ repeats. This means for every 5 tokens, 3 are positive and 2 are negative.
First, let's find the total number of positive and negative tokens in the entire string of 100 tokens.
The fraction of positive tokens is $\frac{3}{5}$.
Total positive tokens = $\frac{3}{5} \times 100 = 3 \times 20 = 60$.
The fraction of negative tokens is $\frac{2}{5}$.
Total negative tokens = $\frac{2}{5} \times 100 = 2 \times 20 = 40$.
Now, we can calculate the total value by summing the values of all positive and negative tokens.
Total Value = (Number of positive tokens $\times$ +1) + (Number of negative tokens $\times$ –1)
Total Value = $(60 \times 1) + (40 \times -1)$
= $60 - 40$
= $20$
Both methods confirm that the value of the string is +20.
Figure it Out (Page 268)
In 628 CE, the Indian mathematician Brahmagupta was the first to write down a complete set of rules for working with positive numbers, negative numbers, and zero. In his book, the Brāhma-sphuṭa-siddhānta, he explained how to perform operations like addition and subtraction in a way that is remarkably similar to the methods we use today.
Here is a summary of his key rules:
Brahmagupta's Rules for Addition
- Positive + Positive: The sum is always positive. (e.g., $2 + 3 = 5$)
- Negative + Negative: The sum is always negative. (e.g., $(-2) + (-3) = -5$)
- Positive + Negative: Find the difference between the numbers (ignoring their signs). The answer takes the sign of the larger original number. (e.g., $-5 + 3 = -2$)
- A Number + Its Opposite: The sum is always zero. (e.g., $2 + (-2) = 0$)
- A Number + Zero: The number remains unchanged. (e.g., $-2 + 0 = -2$)
Brahmagupta's Rules for Subtraction
- Subtracting a Negative: This is the most important rule. Subtracting a negative number is the same as adding its positive counterpart. (e.g., $2 - (-3)$ is the same as $2 + 3$)
- Positive – Positive: The result is positive if the first number is larger and negative if the second number is larger. (e.g., $3 - 2 = 1$ but $2 - 3 = -1$)
- A Number – Itself: The result is always zero. (e.g., $-2 - (-2) = 0$)
- Subtracting Zero: Subtracting zero from a number does not change it. However, subtracting a number from zero gives its opposite. (e.g., $0 - 5 = -5$)
Question 1. Can you explain each of Brahmagupta’s rules in terms of Bela’s Building of Fun, or in terms of a number line?
Answer:
Yes, we can explain Brahmagupta's ancient rules using the modern analogies of Bela's Building of Fun and a number line.
In Bela's Building of Fun, the ground floor ("Welcome Hall") is 0. Floors above are positive (+1, +2, ...), and basement floors are negative (–1, –2, ...). Addition means moving up or down, while subtraction means doing the opposite.
On a number line, 0 is the center. Positive numbers are to the right, and negative numbers are to the left. Addition means moving right (for positive) or left (for negative), while subtraction means moving in the opposite direction.
Brahmagupta’s Rules for Addition Explained
1. The sum of two positives is positive.
- Building of Fun: You start on a floor above ground (e.g., +2, Art Centre) and go up more floors (+3, to Ice Cream). You will end up on a higher floor (+5, Sports), which is still positive.
- Number Line: You start at a positive number on the right (e.g., +2) and move further to the right (+3). You will land on another positive number further to the right (+5).
2. The sum of two negatives is negative.
- Building of Fun: You start in the basement (e.g., –2, Video Games) and go down more floors (–3, to Dinosaur). You will end up on a lower floor (–5, Dinosaur), which is deeper in the basement (more negative).
- Number Line: You start at a negative number on the left (e.g., –2) and move further to the left (–3). You will land on another negative number further to the left (–5).
3. The sum of a positive and a negative.
- Building of Fun: You start on a floor, say +5 (Sports), and add a negative, which means you go down, say –8 floors. You will pass the ground floor and end up at –3 (Cinema). The result takes the sign of the direction you moved more.
- Number Line: You start at +5 and move 8 steps to the left. You will pass 0 and land at –3. The result depends on which number is further from 0.
4. The sum of a number and its inverse is zero.
- Building of Fun: You start on floor +3 (Books) and add –3 (go down 3 floors). You arrive at the Welcome Hall (Floor 0).
- Number Line: You start at +3 and move 3 steps to the left. You arrive at 0.
5. The sum of any number and zero is the same number.
- Building of Fun: You start on any floor (e.g., –4, Ghost House) and add 0 (don't move any floors). You stay on the same floor (–4).
- Number Line: You start at any point (e.g., –4) and move 0 steps. You stay at the same point (–4).
Brahmagupta’s Rules for Subtraction Explained
1 & 2. Subtracting a positive from a positive.
- Building of Fun: Subtraction means doing the opposite. Subtracting a positive (+3) means doing the opposite of going up 3 floors, which is going down 3 floors. If you start at +5 (Sports) and subtract +3, you go down 3 floors to +2 (Art Centre). If you start at +2 (Art Centre) and subtract +5, you go down 5 floors to –3 (Cinema).
- Number Line: Subtracting a positive (+3) means moving 3 steps to the left. If you start at +5 and move 3 left, you reach +2. If you start at +2 and move 5 left, you reach –3.
3. Subtracting a negative number is the same as adding the corresponding positive number.
- Building of Fun: Subtracting a negative (–3) means doing the opposite of going down 3 floors, which is going up 3 floors. So, starting at +2 (Art Centre) and subtracting –3 is the same as starting at +2 and going up 3 floors, landing at +5 (Sports).
- Number Line: Subtracting a negative (–3) means doing the opposite of moving 3 steps left, which is moving 3 steps right. So, $2 - (–3)$ is the same as $2 + 3$.
4. Subtracting a number from itself gives zero.
- Building of Fun: Start at floor –2 (Video Games). Subtracting –2 means doing the opposite of going down 2 floors, which is going up 2 floors. You arrive at the Welcome Hall (Floor 0).
- Number Line: Start at –2. Subtracting –2 means moving 2 steps to the right. You arrive at 0.
5. Subtracting zero from a number gives the same number. Subtracting a number from zero gives its inverse.
- Building of Fun: Starting at +3 (Books) and subtracting 0 means you don't move, so you stay at +3. Starting at 0 (Welcome Hall) and subtracting +3 means going down 3 floors to –3 (Cinema), which is the inverse of +3.
- Number Line: Starting at +3 and subtracting 0 means you don't move. Starting at 0 and subtracting +3 means moving 3 steps left to –3.
Question 2. Give your own examples of each rule.
Answer:
Here are my own examples for each of Brahmagupta's rules.
Brahmagupta’s Rules for Addition: Examples
1. The sum of two positives is positive.
$15 + 20 = 35$
2. The sum of two negatives is negative.
$(-10) + (-8) = -18$
3. The sum of a positive and a negative.
- When the negative number has a greater absolute value: $7 + (-12) = -5$
- When the positive number has a greater absolute value: $20 + (-5) = 15$
4. The sum of a number and its inverse is zero.
$(-33) + 33 = 0$
5. The sum of any number and zero is the same number.
- $42 + 0 = 42$
- $(-9) + 0 = -9$
Brahmagupta’s Rules for Subtraction: Examples
1. If a smaller positive is subtracted from a larger positive, the result is positive.
$50 - 10 = 40$
2. If a larger positive is subtracted from a smaller positive, the result is negative.
$10 - 50 = -40$
3. Subtracting a negative number is the same as adding the corresponding positive number.
- $12 - (-5) = 12 + 5 = 17$
- $(-10) - (-25) = -10 + 25 = 15$
4. Subtracting a number from itself gives zero.
$(-7) - (-7) = 0$
5. Subtracting zero from a number gives the same number. Subtracting a number from zero gives the number’s inverse.
- Subtracting zero from a number: $(-23) - 0 = -23$
- Subtracting a number from zero: $0 - 16 = -16$
- Subtracting a negative number from zero: $0 - (-9) = 9$

